1 Introduction

In recent years, power electronics-based multilevel voltage source inverters have become more popular in high-voltage and high-power applications. Diode-clamped, flying capacitor and cascaded H-bridge are the major types of inverter design [1]. Multilevel inverters provide a near sine wave output with low THD values, minimum voltage stress on the switches, reduced electromagnetic interference, and reduced common mode voltage and switching frequency [2]. Harmonic distortion in the output voltage can be minimized by progressive increment in the number of levels [3]. However, an increase in the number of levels results in the increased complexity of the control circuit and the number of isolated DC sources required. The SHE strategy helps to further reduce the harmonic in the output voltage. The switching instances of various unequal DC sources are obtained by solving transcendental equations for the SHE to eliminate chosen harmonics and to retain the fundamental content. The solution for the switching angles can be obtained using several iterative methods. In previous years, numerical techniques such as the Newton–Raphson [NR] technique [4] and Gauss Newton [5] have been utilized to solve non-linear transcendental equations. The switching angles obtained by these methods depend on various problems such as the initial value selection and require large computational times. Chiasson et al. [6] suggested the resultant theory to solve transcendental equations using an equivalent set of polynomials to reduce the harmonics in multilevel inverters. The switching angles for various modulation indices were estimated using an Artificial Neural Network (ANN) [7]. However, the training of the ANN for various switching angles increases its complexity. Currently, the Evolutionary Algorithm (EA) plays a key role in finding solutions to engineering problems. Several literatures are reported on the application of EAs for various complex problems. Non-linear equations of SHE were solved using genetic algorithm [8] and differential evolution algorithms [9]. It was found that these algorithms outperform classical algorithms for selective harmonic elimination. The optimal switching angle for SHE with non-equal DC sources was obtained using particle swarm optimization [10] and improved colonial competitive algorithm [11]. The gravitational search algorithm proposed by Rashedi et al [12] utilizes the Newtonian gravity and the laws of motion concepts, which yields better performance in finding solutions to various systems [13]. The HCLPSO algorithm was applied to standard benchmark problems and found its performing well when compared to other particle swarm algorithms [14]. The DSA [18], FireFly Algorithm (FFA) [19] and APSO algorithms [20] have been applied for selective harmonic elimination considering firing angle as a variable for optimization with fixed values for the modulation index and input voltage. The reported results obtained by the DSA and FFA provide minimum lower-order harmonics with large THD values. In the selective harmonic elimination of multilevel inverters reported in the literatures, using optimum switching angles to reduce lower-order harmonics was achieved using various conventional and algorithmic approaches. However, in all of the cases, the input voltage values and modulation indices are kept constant. In many power electronic applications, inverters need to be operated with minimum harmonics to achieve required quality.

  • In this paper, SHE is considered as optimization problem with modulation index and input voltage source values as variables along with switching angles to obtain minimum values of the lower-order harmonics and THD.

  • The performance of multilevel inverters for low modulation indices is also analyzed by considering the modulation index as one of the parameters in the optimization.

  • In this paper, GSA and HCLPSO algorithms are considered for optimizing variables. It is found that the HCLPSO provides a better solution with minimum lower-order harmonics when compared to PSO due to its exploration and exploitation capability, as well as its capacity to avoid getting stuck in local optimum due to its comprehensive learning process. Hence, it is proposed for SHE problem.

The paper is organized as follows. Section 2 describes a typical multilevel inverter topology. Mathematical implementation of the problem was elaborated in Sect. 3. Algorithms used for solving this problem were explained in Sect. 4. Section 5 discusses simulation results obtained and a comparison with existing literature. Section 6 presents experimental validation of these results. Section 7 gives the conclusion of the paper.

2 Multilevel inverter topology

2.1 Multilevel inverter

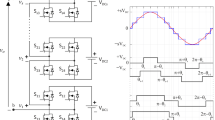
The cascaded H-bridge-type multilevel inverter (CHB MLI) is preferred over other MLIs due to its reduced numbers of components such as clamping diodes and voltage balancing capacitors, its ease in terms of fault detection due to its construction using simple H-bridge units, and the fact that modification can be easily made in the number of output voltage levels [15, 16]. In CHB-type multilevel inverters, ‘S’ numbers of H-bridge inverters are cascaded to synthesize ‘n’ levels in the output voltage, where n = 2S + 1 [17]. Hence, for generating 7 levels in the output voltage, 3 H-bridge units are needed, similarly for 11 levels, 5 units are needed as shown in Fig. 1.

Fig. 1
figure 1

Three-phase eleven-level cascaded H-bridge inverter

Full size image

2.2 Selective harmonic elimination PWM

Figure 1 shows a three-phase eleven-level CHB MLI with five H-Bridges connected in the cascade mode. The switching angles for various levels are α1, α2, α3, α4, and α5; while Vdc1, Vdc2, Vdc3, Vdc4, and Vdc5 are the unequal DC sources of each H-bridge unit. The Fourier series expansion of a staircase output voltage waveform for the unequal DC sources can be written as:

$$V\left( {\omega t} \right) = \mathop \sum \limits_{n = 1,3,5}^{\infty } \frac{{4V_{{{\text{dc}}}} }}{n\pi }\left( {\sum\nolimits_{i = 1}^{s} {k_{i} \times \cos n\alpha_{i} } } \right)\sin n\omega t.$$
(1)

The subsequent non-linear equations are used for calculating the switching angles with SHE for CHB MLI:

$$\begin{aligned} & H_{1} = \sum\nolimits_{i = 1 }^{5} {k_{i} } \times \cos \left( {\alpha_{i} } \right) = M \times S{,} \\ & H_{5} = \frac{{4V_{{{\text{dc}}}} }}{5\pi } \left[ {\sum\nolimits_{i = 1 }^{5} {k_{i} } \times \cos \left( {5\alpha_{i} } \right)} \right] = 0, \\ & H_{7} = \frac{{4V_{{{\text{dc}}}} }}{7\pi } \left[ {\sum\nolimits_{i = 1 }^{5} {k_{i} } \times \cos \left( {7\alpha_{i} } \right)} \right] = 0, \\ & H_{5} = \frac{{4V_{{{\text{dc}}}} }}{5\pi } \left[ {\sum\nolimits_{i = 1 }^{5} {k_{i} } \times \cos \left( {5\alpha_{i} } \right)} \right] = 0, \\ & H_{7} = \frac{{4V_{{{\text{dc}}}} }}{7\pi } \left[ {\sum\nolimits_{i = 1 }^{5} {k_{i} } \times \cos \left( {7\alpha_{i} } \right)} \right] = 0, \\ & H_{11} = \frac{{4V_{{{\text{dc}}}} }}{11\pi }\left[ {\sum\nolimits_{i = 1 }^{5} {k_{i} } \times \cos \left( {11\alpha_{i} } \right)} \right] = 0, \\ & H_{13} = \frac{{4V_{{{\text{dc}}}} }}{13\pi }\left[ {\sum\nolimits_{i = 1 }^{5} {k_{i} } \times \cos \left( {13\alpha_{i} } \right)} \right] = 0, \\ \end{aligned}$$
(2)

where \(k_{i} = \frac{{V_{{{\text{dc}}i}} }}{{V_{{{\text{dc}}}} }},S\) = number of DC sources, \(V_{{{\text{dc}}}}\) = nominal value of the DC voltage, Vdci = \(i\)th unequal DC voltage and \(i\) ranges from 1 to 5. The actual fundamental component of the output voltage is matched up with its desired value using the first equation from the above listed group. In addition, the remaining 5th-, 7th-, 11th-, and 13th-order harmonics are eliminated by solving the rest of the equations. The modulation index \(\left( M \right)\) is the ratio between the DC voltage and the fundamental component of the output voltage:

$${\text{Modulation}}\,{\text{index}},M = \frac{{H_{1} }}{{4 \times S \times V_{{{\raise0.7ex\hbox{${{\text{dc}}}$} \!\mathord{\left/ {\vphantom {{{\text{dc}}} \pi }}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$\pi $}}}} }}(0 \le M \le 1).$$
(3)

The required fundamental voltage can be acquired by changing the values of M from 0 to 1 to cover different values of H1. By solving ‘\(S\)’ no. of equations for and ‘\(i\)’ no. of switching angles, \(\left( {S - 1} \right)\) no. of harmonics can be eliminated from the output voltage. The value of \(S\) is equal to the number of DC sources of the CHBMLI.

3 Mathematical implementation

The selective harmonic elimination of multilevel inverter is formulated as an optimization problem to find the optimal switching angle, modulation index and input voltages by minimizing the considered objective function. The objective function considered for minimization is given in Eq. (4) and the variables considered are the switching angles, modulation index and input voltage source. The search space of the variables is given in Eq. (5):

$$\begin{aligned} & f = \mathop {\min }\limits_{{\alpha_{i} }} \left\{ {\left( {100\frac{{V_{1}^{*} - V_{1} }}{{V_{1} }}} \right)^{4} + \mathop \sum \limits_{s = 2}^{S} \frac{1}{{h_{s} }}\left( {50 \times \frac{{V_{{h_{s} }} }}{{V_{1} }}} \right)^{2} } \right\}, \\ & & i = 1,2, \ldots S, \\ \end{aligned}$$
(4)
$$\begin{aligned} & 0 \le \alpha_{1 } \le \alpha_{2 } \le \alpha_{3 } \le \alpha_{4 } \le \alpha_{5 } \le \frac{\pi }{2} \\ & 0 \le m \le 1 \\ & 0 \ge k_{1} \ge k_{2} \ge k_{3} \ge k_{4} \ge k_{5} \ge 1.1, \\ \end{aligned}$$
(5)

where \(V_{1}^{*}\) is the desired value of the fundamental component, \(S\) is the number of switching angles, and \(h_{s}\) is the number of the harmonic order to be eliminated (proposed 5th, 7th, 11th, and 13th harmonics). The ratio \(k_{i}\) varies from 0 to 110% of the nominal value of the DC voltage, \(V_{{{\text{dc}}}}\), i.e., 0–1.1. In the function, the first term is to regulate the fundamental component by minimizing the relative error to within 1%. The second term mitigates the amplitude of the proposed harmonic to under 2% of its fundamental component. The limit of harmonics below 2% is preferred as per IEEE-519 recommendations [21]. The standard limits harmonics by 3% of its fundamental component. In addition, in the function, the weighting method is adapted, i.e., each harmonic is weighted by its order to provide more importance to the elimination of lower-order harmonics than the higher-order harmonics.

4 Algorithm used for optimization

4.1 Gravitational search algorithm

The gravitational search algorithm (GSA) developed by Rashedi et al. [12] utilizes Newton’s laws of gravity and mass. As per this algorithm, the agents are assigned as objects and their masses give their performances. The global movement of all objects towards heavier mass objects is due to gravitational force. The objects with heavier and lighter masses give good optimal solutions and worst solutions, respectively. The four particulars of each mass are its position, inertial mass (Mi), active gravitational mass (Mga) and passive gravitational mass (Mgp). The solution is represented by the position of the masses, and the fitness function is calculated by the inertial mass and gravitational masses. The position of the \(i\)th agent in a N agent system is:

$$X_{i} = \left( {x_{i}^{1} , \ldots ,x_{i}^{d} , \ldots ,x_{i}^{n} } \right)\quad {\text{for}}\, i = 1,2, \ldots N,$$
(6)

\(x_{i}^{d}\) represents the dth dimensional position of the ith agent.

As per Newtonians law, the randomly assigned initial agents (masses) and the force exerted by the mass ‘j’ on mass ‘i’ at time ‘t’ is:

$$F_{ij}^{d} \left( t \right) = G\left( t \right)\frac{{M_{gpi} \left( t \right) \times M_{gaj} \left( t \right)}}{{R_{ij} \left( t \right) + \varepsilon }}\left( {x_{j}^{d} \left( t \right) - x_{i}^{d} \left( t \right)} \right),$$
(7)
$$R_{ij} \left( t \right) = \left\| {x_{i} \left( t \right),x_{j} \left( t \right)} \right\|_{2} ,$$
(8)

\(M_{gpi}\) is related to the mass of the ‘\(i\)’th agent, \(M_{gpj}\) is related to the mass of the ‘\(j\)’th agent, G(t) is the gravitational constant at time ‘\(t\)’, \(\varepsilon\) is a constant of small value, and the Euclidean distance of the two agents ‘\(i\)’ and ‘\(j\)’is \(R_{ij} \left( t \right)\).

The arbitrarily weighted sum of the \(d\)th component due to other agents is the net force on agent ‘\(i\)’ in the \(d\)th dimension:

$$F_{i}^{d} \left( t \right) = \sum\nolimits_{j = 1, j \ne i}^{N} {{\text{rand}}_{j} } F_{ij}^{d} \left( t \right).$$
(9)

At time ‘t’, the acceleration of the agent ‘i’ of the mass ‘Mii’ is given by the law of motion:

$$a_{i}^{d} \left( t \right) = \frac{{F_{i}^{d} \left( t \right)}}{{M_{ii} \left( t \right)}}.$$
(10)

The upcoming velocity of an agent is calculated by the sum of its acceleration and a fraction of its current velocity. The acceleration of an agent and a portion of its present velocity give its next velocity and the equation used to calculate the velocity and position are:

$$v_{i}^{d} \left( {t + 1} \right) = {\text{ rand}}_{i} \times v_{i}^{d} \left( t \right) + a_{i}^{d} \left( t \right),$$
(11)
$$x_{i}^{d} \left( {t + 1} \right) = x_{i}^{d} \left( t \right) + v_{i}^{d} \left( {t + 1} \right).$$
(12)

Search accuracy is controlled by the gravitational constant ‘G’ and it is a function of time ‘t’ and its initial value Go is:

$$G\left( t \right) = G\left( {G_{o} ,t} \right),$$
(13)
$$G\left( t \right) = G_{o} e^{{ - \alpha \frac{t}{T}}} .$$
(14)

The evaluation of fitness is found by inertial and gravitational masses. The agent that moves more slowly due to higher attraction, has a heavier mass and is considered a more efficient agent. The equations to update inertial and gravitational masses are:

$$M_{gai} = M_{gpi} = M_{ii} = M_{i} ,\quad i = 1,2, \ldots ,N$$
$$M_{i} \left( t \right) = \frac{{{\text{fit}}_{i} \left( t \right) - {\text{worst}}\left( t \right)}}{{{\text{best}}\left( t \right) - {\text{worst}}\left( t \right)}},$$
(15)
$$M_{i} \left( t \right) = \frac{{m_{i} \left( t \right)}}{{\mathop \sum \nolimits_{j = 1}^{N} m_{j} \left( t \right)}},$$
(16)

\({\text{fit}}_{i} \left( t \right)\) is the fitness value of the ith agent at time ‘t’. For the minimization problem, the worst and the best optimum values are:

$${\text{best}}\left( t \right) = \mathop {\min }\limits_{{j \in \left( {1, \ldots ,N} \right)}} {\text{fit}}_{j} \left( t \right),$$
(17)
$${\text{worst}}\left( t \right) = \mathop {\max }\limits_{{j \in \left( {1, \ldots ,N} \right)}} {\text{fit}}_{j} \left( t \right).$$
(18)

In GSA, every agent is located at some point in the search space, which gives problem solution at every instant. The new locations of the agents are determined as per the equation. Other algorithmic parameters are updated as per the equations mentioned in every cycle. The objective of the proposed work is to minimize selected lower-order harmonics. Hence, the harmonics are considered as masses and the velocities are considered as variables. The search algorithm helps in finding the minimum harmonics (maximization of the masses in the GSA) and the agents are the variables considered for finding best solution.

4.2 HCLPSO algorithm

Exploration means determining possible solution areas of the whole search space. In addition, exploitation helps to find optimal solutions from the available potential solution region. The particles move around the search space and determine the global optimum with the help of exploration and exploitation. The best position of each particle in the comprehensive learning particle swarm optimization (CLPSO) is updated from the best position of the same particles or other particles. The CLPSO is modified with an exploration sub population, and an exploitation sub population helps to overcome particles with a high exploration tendency that is influenced by high exploitation tendency particles. The HCLPSO algorithm, which has this improvement, was proposed in [14]. Two heterogeneous subpopulations are formed from the swarm. One of them is for improving exploration and the other is for improving exploitation. In addition, the exemplar for both subpopulations is generated by comprehensive learning along with a Pc curve. The velocity of the exploration-enhanced subpopulation is updated by:

$$V_{i}^{d} = wV_{i}^{d} + c \times {\text{rand}}_{i}^{d} \times \left( {p{\text{best}}V_{{f_{i} \left( d \right)}}^{d} - X_{i}^{d} } \right),$$
(19)

\(f_{i} \left( d \right) = \left[ {f_{i} \left( 1 \right),f_{i} \left( 2 \right), \ldots f_{i} \left( D \right)} \right]\) represents the ith particle following its own or other’s \(p{\text{best}}V_{i}^{d}\) for each dimension \(d\).

In addition, the velocity of the exploitation-enhanced subpopulation is updated by:

$$V_{i}^{d} = wV_{i}^{d} + c_{1} \times {\text{rand}}1_{i}^{d} \times \left( {p{\text{best}}V_{{f_{i} \left( d \right)}}^{d} - X_{i}^{d} } \right) + c_{2} \times {\text{rand}}2_{i}^{d} \times \left( {g{\text{best}}V_{{{\text{fit}}\left( d \right)}}^{d} - X_{i}^{d} } \right) .$$
(20)

The range of the inertia weight \(w\) (decreasing linearly with run time) is 0.99–0.2. In the exploration subpopulation group, the value of the time varying acceleration coefficient is \(c = 3\,{\text{to}}\,1.5\) in Eq. (21). Similarly, in the exploitation subpopulation group, the value of the time varying acceleration coefficients are \(c_{1}\) = 2.5 to 0.5 and \(c_{2} = 0.5\,{\text{to}}\,2.5\) in Eq. (22). The learning probability values \(P_{ci}\) of different particles ‘\(i\)’ is:

$$a + b \times \frac{{\left( {\exp \left( {\left( {10\left( {i - 1} \right)} \right)/\left( {{\text{ps}} - 1} \right)} \right) - 1} \right)}}{{\left( {\exp \left( {10} \right) - 1} \right)}},$$
(21)

where \(ps\) is the size of the population, \(a = 0, b = 0.25\). The exemplars direct both the exploration and the exploitation subpopulation particles. The random number is compared with the respective learning probability value. If it is smaller than the learning probability values, the particle learns from some other particles pbest. Otherwise, the particle will be trained on its own. A compromise between exploration and exploitation is obtained in the HCLPSO by avoiding the information flow between the exploration and exploitation sub particles. The exploration group has the ability to save. However, the exploitation group suffers from the local optima.

The diversity of the swarm is determined by:

$${\text{Diversity}}{\mkern 1mu} \left( {S\left( t \right)} \right) = \frac{1}{N}\sum\nolimits_{i = 1}^{N} {\sqrt {\sum\nolimits_{d = 1}^{D} ( x_{i}^{d} \left( t \right) - \overline{{X^{d} \left( t \right)^{2} }} } } ,$$
(22)
$$\overline{{X^{d} \left( t \right)}} = \frac{{\mathop \sum \nolimits_{i = 1}^{N} x_{i}^{d} \left( t \right)}}{N},$$
(23)

where \(S\) represents the swarm, \(N = \left| S \right|\) represents the swarm size, \(D\) is the problem dimensionality, \(x_{i}^{d}\) is the ‘\(i\)’th particle’s ‘\(d\)’th value in the population, and \(\overline{{X^{d} \left( t \right)}}\) is the mean of the ‘\(d\)’th dimension of all the particles in the swarm. The exploration subpopulation diversity is greater than the exploitation group. The diversity is maintained in the exploitation subpopulation group if the convergence of the group is within the acceptable region.

Equation (5) represents the search space of the particles for the proposed problem. The particles update to various positions using the velocity expression in Eqs. (19) and (20) to find the best position (minimization of harmonics shown in expression (4)) in the search space.

5 Simulation results and discussion

In this paper, the selective harmonic elimination for seven-level and eleven-level multilevel inverters are carried out to obtain an output voltage of inverter with minimum lower-order non-triplen harmonics and THD by tuning the control variables using evolutionary algorithms. The optimization algorithms, namely the HCLPSO, are used to determine the optimal values of the considered control parameters, such as the modulation index, switching angles and input voltages. Then these values are compared with the results obtained using GSA. Simulations are carried out using MATLAB 2014A. Simulations are performed by taking the population size as 100 with 2000 functional evaluations. The results obtained from both of the algorithms are compared with the previously reported results of the firefly algorithm for eleven-level MLI [19] and the DSA algorithm for seven-level MLI [18]. The DC input voltage source of the inverter is varied between 0.01 and 1.1% of 20 V and the load considered is R = 14.5 Ω and L = 12 mH for the seven-level and eleven-level inverters. The performance of the various algorithms is discussed in the following section:

5.1 Simulation results of GSA-based MLI

Optimal parameters such as the switching angles, modulation index, input voltage and fitness value obtained for seven-level and eleven-level MLI using GSA are given in the Tables 1, 2 and 3. From these tables, it is clear that GSA-based seven-level multilevel inverter gives an output voltage with reduced lower-order harmonics (5th and 7th order) and minimum THD when compared with DSA-based seven-level inverter [18]. Similarly, for an eleven-level MLI, the THD obtained is very low when compared with the firefly algorithm [19]-based eleven-level MLI. This clearly indicates that the GSA-based MLI outperforms the DSA and firefly algorithm-based multilevel inverters with acceptable lower-order harmonics and minimum THD. It is also clear that the variable voltage source and variable modulation index help to enhance the performance of the MLI with a minimum THD since they result in an appreciable reduction in the selected lower-order harmonics and a better fundamental component magnitude when compared with an equal voltage source and fixed modulation index-based MLI. Figures 2 and 3 show the output voltage waveforms and harmonic spectrum of seven-level and eleven-level GSA-tuned MLIs.

Table 1 Seven-level inverter input variables and output parameters
Full size table
Table 2 Eleven-level inverter input variables
Full size table
Table 3 Eleven-level inverter output parameters
Full size table
Fig. 2
figure 2

Simulation results of seven-level inverter using GSA with MI = 0.5289: a output phase voltage waveform; b harmonic spectrum of the phase voltage; c output line voltage waveform; d harmonic spectrum of the line voltage

Full size image
Fig. 3
figure 3

Simulation results of eleven-level inverter using GSA with MI = 0.5236: a output phase voltage waveform; b harmonic spectrum of the phase voltage; c output line voltage waveform; d harmonic spectrum of the line voltage

Full size image

Even though, the THD values of the voltage waveforms are high, due to the increased magnitude of the higher-order harmonics that can be easily filtered, the magnitude of the harmonics selected for elimination (5th and 7th orders for seven levels and 5th, 7th, 11th and 13th orders for eleven levels) have been significantly reduced.

5.2 Simulation results of HCLPSO-based MLI

The efficiency of the proposed HCLPSO algorithm is discussed below. The fitness function value of the HCLPSO is very low when compared with the GSA, which clearly shows that the HCLPSO provides commendable performance in all the considered aspects.

The optimal variables, lower-order harmonics value and fundamental component obtained from the HCLPSO are displayed in the Tables 1, 2 and 3. Figures 4 and 5 show the output voltage and harmonic spectrums of HCLPSO-based seven- and eleven-level multilevel inverter. It gives better results also for the lower modulation indices. The selected lower-order harmonics obtained from the HCLPSO for both of the considered levels is very low when compared with the GSA. Like the lower-order harmonics, the output voltage THD values of MLI tuned with HCLPSO are also minimum when compared with the GSA. From this, it is confirmed that the HCLPSO-based variable input voltage, variable modulation index- and variable switching angle-based MLI give better efficacy (this is also true for lower modulation indices) with minimum lower-order harmonics and THD when compared to a fixed voltage and fixed modulation index-based DSA, firefly MLI and GSA-tuned variable input voltage, variable modulation index and variable switching angle-based multilevel inverter. The input variables and output parameters for seven-level and eleven-level CHB MLIs are given in Tables 1, 2 and 3. Output voltage waveforms and harmonic spectrums for eleven-level MLI using HCLPSO are shown in Fig. 5.

Fig. 4
figure 4

Simulation results of seven-level inverter using HCLPSO with MI = 0.4412: a output phase voltage waveform; b harmonic spectrum of the phase voltage; c output line voltage waveform; d harmonic spectrum of the line voltage

Full size image
Fig. 5
figure 5

Simulation results of eleven-level inverter using HCLPSO with MI = 0.4776: a output phase voltage waveform; b harmonic spectrum of the phase voltage; c output line voltage waveform; d harmonic spectrum of the line voltage

Full size image

Figures 6 and 7 show a comparison of the total harmonic distortion values obtained for various algorithms. The comparison figure clearly indicates that the HCLPSO-based MLI gives lower THD value for both of the levels with minimum lower-order harmonics. The best fitness value, worst fitness value, as well as the mean and standard deviation of the fitness value obtained for 20 independent runs for the GSA and HCLPSO are reported in Tables 4 and 5.

Fig. 6
figure 6

Comparison of seven-level inverter THD values

Full size image
Fig. 7
figure 7

Comparison of eleven-level inverter THD values

Full size image
Table 4 Statistical performance values of seven-level inverter
Full size table
Table 5 Statistical performance values of eleven-level inverter
Full size table

In the FFT analysis, the THD values of the phase voltages are high when compared to the line voltage due to the triplen harmonics and the increase in the magnitude of the higher-order harmonics. The higher-order harmonics can be easily filtered using minimum filtering components. However, the selected harmonics for elimination have been reduced to below the IEEE-519 recommendation limit (below 2%).

From the table, it is clear that the HCLPSO provides better performance when compared with the GSA with minimum mean and standard deviation values. This proves the closeness of the results obtained in all twenty runs. The statistical performance values also show that the HCLPSO is superior to the GSA in finding optimal solutions to selective harmonic elimination problems.

6 Experimental results

The simulation results of the HCLPSO and GSA are validated experimentally. The experimental setup of cascaded H-bridge multilevel inverter (CHBMLI) is shown in Fig. 8. Each unit of the CHBMLI is built using metal oxide semiconductor field effect transistors (MOSFET) IRF840.

Fig. 8
figure 8

Experimental setup of three-phase eleven-level inverter

Full size image

The input DC source for each unit of the CHBMLI is 20 V. The gate signals for the MOSFET are generated using DSPIC30F2010 controller and applied to the gate through TLP250 MOSFET driver circuit. A Fluke 434 series II power quality analyzer is used to measure the voltage waveforms and frequency spectrum of MLIs. The output phase voltage waveforms and THD values corresponding to the simulation results reported for HCLPSO and GSA are shown and the obtained hardware results are nearer to the simulation results. The results have appreciable amount of reduction in the selected harmonics and THD. Phase voltage waveforms and harmonic spectrums of the experimental results are shown in Figs. 9 and 10. The %THD values obtained for the seven-level inverter are 12.1% for the HCLPSO and 13.1% for the GSA. Similarly, the phase voltage and harmonic spectrum of 3-phase eleven-level inverters for modulation indices of 0.4776 for the HCLPSO and 0.5236 for the GSA are shown in Figs. 11 and 12. The %THD values obtained for the HCLPSO and the GSA are 9.1% and 11.7%, respectively.

Fig. 9
figure 9

Experimental results of seven-level inverter using HCLPSO with MI = 0.4412: a output phase voltage waveform; b harmonic spectrum of the phase voltage

Full size image
Fig. 10
figure 10

Experimental results of seven-level inverter using GSA with MI = 0.5289: a output phase voltage waveform; b harmonic spectrum of the phase voltage

Full size image
Fig. 11
figure 11

HCLPSO Experimental results for eleven-level inverter with MI = 0.4776: a output phase voltage waveform; b harmonic spectrum of phase voltage

Full size image
Fig. 12
figure 12

Experimental results of eleven-level inverter using GSA with MI = 0.5236: a output phase voltage waveform; b harmonic spectrum of the phase voltage

Full size image

Even though, the THD values are slightly high, the magnitude of the harmonics selected for elimination is reduced to the minimum level, i.e., less than 3% as prescribed by IEEE.

The obtained experimental results are slightly differed from the simulation results since, in the simulations, the switches are considered as ideal with no resistance or losses. However, in the experimental verification, due to the losses in the switching devices, the voltage and THD values are slightly different.

7 Conclusion

In this paper, a recent optimization technique, Heterogeneous Comprehensive Learning Particle Swarm Optimization is applied for determining the optimum switching angles, modulation index and input voltage source values to reduce the 5th, 7th, 11th and 13th harmonics present in the output voltage of 3-phase H-bridge multilevel inverters, while simultaneously preserving the required fundamental component. The results are compared with the results obtained from the Gravitational Search Algorithm. The results of simulations and the experimental setup as well as the statistical performance for 7-level and 11-level inverters reveal that the HCLPSO-based multilevel inverter obtains precise values for the switching angles, modulation index and input voltage source values to reduce lower-order harmonics and total harmonic distortion when compared with the GSA and other fixed voltage and fixed modulation index cases even at the lower modulation indices. Since, the increased level of harmonics, especially at lower modulation indices, is a major issue in the operation of MLI. This variable voltage and variable modulation-based SHE can be used for applications where the inverter has to work with minimum lower-order harmonics, minimum total harmonic distortion, low switching frequency and lower modulation indices.