1 Introduction

In recent years, researchers are paying more attention in the areas of research related to bipedal robots due to its usability and adaptiveness in accomplishing various tasks. Controlling the locomotion of the biped robot is difficult to achieve in unknown terrains. Several studies [1,2,3,4,5,6] focused on the control of locomotion of the biped robot after utilizing the concept of zero moment point (ZMP). Most of the research work was focused on the analysis of walking stability of the biped robots on flat and uneven terrains. To maintain the stability, the trajectory-based methods are suitable, as the robots perform their walk based on predesigned trajectories. However, if the trajectories are fixed and the terrain conditions are varying, the robot may fail to move on those terrains. It is important to note that the polynomial interpolation methods may become incompetent, if the complexity of walking increases. Further, the increase in the order of the polynomial leads to enhanced computational time. To overcome this problem, Shih [1] developed a strategy that uses a cubic spline interpolation to estimate the foot trajectories. In [2], Huang et al. formulated the constraints for the foot trajectories to produce various types of trajectories on different terrain conditions. Further, Park et al. [5] proposed a trajectory generation method based on the combination of third-order polynomial and sinusoidal functions to realize the free gait for the biped walking. Human walking does not show the characteristics of precise trajectory tracking. But, the biological researches show that the human beings walk is a consequence and combination of inherent patterns and reflexes. Later on, researchers worked on the bio-inspired control methods based on the biomechanics of musculoskeletal system and the motors of neural networks [7, 8]. Inspired by the concept of ZMP, many researchers had developed stable walking for biped robots. Several studies were based on the equations of ZMP that express the relationship between the ZMP and centre of gravity (COG). In addition to the COG trajectory, the generation of ZMP equation is useful for the biped robot to walk on flat ground. The ZMP equation with constant COG height on flat ground was very simple. Vukobratovic and Stepanenko [9] proposed the concept of ZMP, which corresponds to the centre of pressure of floor reaction force on the sole of a biped robot. If the ZMP falls inside the foot support polygon, the sole of the foot does not leave the ground and the balanced walk is possible. The foot rotation indicator (FRI) is the extension of the ZMP, and was proposed by Goswami [10]. While the ZMP exists within the boundary of the foot support polygon, the FRI can be used as an indicator of the extent of balance of the robot. However, many researchers had proposed trajectory-planning methods for the balanced walking of biped robots. Kajita et al. [11] generated the walking pattern for the biped robot by the preview control of the ZMP. Here, the COG trajectory is generated by using the cart-table model. Further, Shibuya et al. [12] developed a linear pendulum model (LPM) and applied this to control the COG trajectory generation in the double-support phase. In addition to the above approaches, Erbatur and Kurt [13] proposed a reference generation algorithm based on the linear inverted pendulum model (LIPM) and moved the ZMP references.

Later on, some of the researchers had dealt with the walking of the biped mechanism on a slope surface to enhance the utility of the biped robot. Ching-Long and Chien-Jung [14] studied the motion control of statically stable biped robot with seven degrees of freedom (DOF) on an uneven floor. To maintain the statically stable walk, the COG of the biped had to fall inside the foot support polygon during the single- and double-support phases. Sung et al. [15] proposed a trajectory generation method for a biped robot to walk on an inclined surface. To generate the walking trajectory, three additional assumptions were used. First, the centre of mass was moved parallel to the slope surface. Second, the ZMP should be fixed with the supporting foot during the single-support phase. Third, when the slope of the surface is changed, the boundary conditions of the robot while walking are also changed. Cristiano et al. [16] proposed the concept of central pattern generator (CPG) for efficient locomotion control of the biped robots while ascending and descending the slope surface. The feedback signals were generated by the robot, i.e. the data from inertial and force sensors were directly fed to the CPG, and allowed the robot to automatically change the locomotion pattern over the flat and inclined terrains in real time. Further, the researchers not only worked on the generation of the dynamically balanced gaits of the biped robot using ZMP, COG, LPM and LIPM but also solved the problems related to the controlling of the generated gait of the biped robot using PID controllers. Tae et al. [17] discussed a hybrid self-organizing fuzzy (SOF) PID controller to tune the parameters of the multi-input multi-output nonlinear biped robot. They observed a better performance for hybrid SOF-PID controller when compared to SOF-PID controller. Safa et al. [18] developed a predictive PID controller for stable walking of the biped robot. The predictive PID controller was used to imitate the calculated time and reduce the complexity of the control. Moreover, Ho Pham et al. [19] proposed a novel adaptive neural PID (AN-PID) controller, which was suitable for the real-time control of the biped robot. The proposed AN-PID controller had a simpler and self-organising structure, fast online-tuning speed and flexibility in updating the online data. The above algorithm was capable of optimizing the gains and weights of MLPNN model integrated with AN-PID controller.

The PID controller is an electrical element, whose purpose is to reduce the error between a desired and actual process variable. In order to do so, it requires tuning of some of its essential parameters. But, tuning of the PID controller is a time-consuming process. Recently, some researchers are trying with different types of stochastic methods, population-based algorithms, nature-inspired and computational intelligence algorithms, such as artificial neural network, fuzzy systems and artificial immune systems [20], to tune the PID controller and train the biped robot [21]. In [22], the authors had constructed a modified triangular fuzzy PID controller and used a genetic algorithm (GA) to fine-tune the membership function parameters of fuzzy system, and to improve the quality of the system in terms of rise time, overshoot and steady-state error. Hang et al. [23] developed an intelligent tuning algorithm, i.e. bacterial forging optimization (BFO) technique, to tune the PID controller. The BFO algorithm uses natural selection to eliminate the entities with poor forging strategies for locating, capturing and ingesting the food. Further, Huseyin and Zafer [24] proposed a new nature-inspired optimization (i.e. ant algorithm) algorithm to tune the parameters of the PID controller. The results of the tuning process were compared with Ziegler–Nichols (ZN), iterative feedback tuning (IFT) and internal model control (IMC) methods. Dusan et al. [25] tuned the parameters of the PID controller using various optimization algorithms such as, differential evolution algorithm, genetic algorithm, bat algorithm, hybrid bat algorithm, particle swarm optimization algorithm and cuckoo search algorithm. The results were compared using statistical analysis and observed that PSO had exhibited better performance when compared with the other methods.

In the present research, the authors have implemented a torque-based PID controller to control the joint motors in a systematic manner. It is important to mention that ZMP-based PID controller, which was used by many of the researchers [26,27,28,29], is an indirect method of controlling the motor, as the error signal between the obtained and reference ZMP trajectory is used to design the gaits for various links of the biped robot. In this process, the controller may suggest some dynamically balanced postures which may not be kinematically feasible. Moreover, finding the most appropriate gait of the biped robot that fulfils the sequence-oriented criterion and repeatability conditions is difficult to achieve, whereas torque-based PID controller considers the error signal of each joint of the biped robot and tries to design the gains of the controller by minimizing the error between two consecutive gait angles of each joint of the biped robot. The gains of the PID controller are obtained by using the neural network (NN) (i.e. adaptive based). Further, the structure of NN is tuned with the help of a nature-inspired optimization algorithm, i.e. MCIWO (which is a variant of standard IWO algorithm). To improve the performance of the algorithm, in the present research the authors have added two new variables, namely cosine and chaotic variables. The cosine variable is used to increase the search space, and the chaotic variable is used to push the solution directly into global optimum position. Finally, the performance of the developed algorithm has been compared with another nature-inspired algorithm such as PSO. Further, the gait angels generated by the best algorithm are fed into the real robot for testing its performance.

The rest of the paper is organised as follows. Section 2 describes the kinematics, dynamics and design of PID controller of the biped robot. Section 3 discusses the structure of neural network. Section 4 explains the nature-inspired optimization algorithms which are used to tune the weights of the NN controller. Section 5 deals with the experiments and the results related to the MCIWO-NN- and PSO-NN-based PID controller algorithms. Further, the paper concludes with a summary of work and the suggestions for further improvement.

2 Modelling and design of controller of the biped robot

In this section, the model of the biped robot and the design of the corresponding PID controller are discussed.

2.1 Modelling

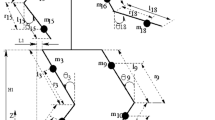
Day by day, the usage of biped robots in both the industrial and non-industrial applications is increasing enormously. An overview of the biped robot used in this research is shown in Fig. 1. All the joints of the robot are connected in a serial manner, and each joint has only one motor mounted on it. The robot is designed to have 6 DOF in each leg and 3 DOF in each hand.

Fig. 1
figure 1

Schematic diagram showing structure of the Robot

Full size image

To maintain the balanced walk, the foot of the biped robot is assumed to follow a particular polynomial trajectory. In this research, the authors had conducted a study on different polynomial trajectories, such as quadratic, cubic and fifth-order polynomials, and found that the cubic polynomial trajectory has produced dynamically more balanced gaits when compared with the other trajectories. The maximum angle of slope on which the robot can perform walk without slipping is decided by the value of coefficient friction (µ). To tackle the situation in an appropriate manner, all the joints are allowed to move in a coordinated manner. For moving the links in a systematic way without violating the kinematic constraints, the concept of inverse kinematics is applied. While walking, the foot of the robot is always kept parallel to the ground and the ZMP should fall within the foot support polygon. The equation for calculating the ZMP in X- and Y-directions is given by Eqs. (1) and (2), respectively.

$$x_{\text{ZMP}} = \frac{{\sum\nolimits_{i = 1}^{n} {\left( {I_{i} \dot{\omega }_{i} - m_{i} \ddot{x}_{i} z_{i} - m_{i} x_{i} (g + \ddot{z}_{i} )} \right)} }}{{\sum\nolimits_{i = 1}^{n} {\left( {m_{i} (\ddot{z}_{i} + g)} \right)} }}$$
(1)
$$y_{\text{ZMP}} = \frac{{\sum\nolimits_{i = 1}^{n} {\left( {I_{i} \dot{\omega }_{i} - m_{i} \ddot{y}_{i} z_{i} - m_{i} y_{i} (g + \ddot{z}_{i} )} \right)} }}{{\sum\nolimits_{i = 1}^{n} {\left( {m_{i} (\ddot{z}_{i} + g)} \right)} }}$$
(2)

where \(\dot{\omega }_{i}\), Ii, g and mi represent the angular acceleration (rad/s2), mass moment of inertia (kg m2) of the ith link, acceleration due to gravity (m/s2) and mass (kg) of the link i, respectively. Further, (xi, yi, zi) signify the coordinates of the ith lumped mass and \(\ddot{z}_{i}\) and \(\ddot{x}_{i}\) indicate the acceleration of the ith link moving in z- and x-directions (m/s2), respectively.

Once the ZMP is calculated, the dynamic balance margin of the biped robot in X- and Y-directions has been determined by using the mathematical Eqs. (3) and (4), respectively.

$$x_{\text{DBM}} = \left( {\frac{{f_{s} }}{2} \times \cos \alpha - \left| {x_{\text{ZMP}} } \right|} \right)$$
(3)
$$y_{\text{DBM}} = \left( {\frac{{f_{w} }}{2} \times \cos \alpha - \left| {y_{\text{ZMP}} } \right|} \right)$$
(4)

where fw and fs represent the width and length of the foot, respectively.

The gait generation methodology for the biped while descending the slope is very much similar to the ascending case with only one difference, that is, the acceleration due to gravity “g” is acting in the direction opposite to that of the movement of the root.

2.2 Controller

Once the model of the robot is generated after generating the balanced gaits on ascending and descending the sloping surfaces, the torque-based PID controllers are designed to control each joint of the biped robot in a coordinated manner. The torque required to move each joint of the biped robot is derived based on the Lagrange–Euler formulation (ref. Eq. 5).

$$\tau_{i,the} = \sum\limits_{j = 1}^{n} {M_{ij} } \left( q \right)\ddot{q}_{j} + \sum\limits_{j = 1}^{n} {\sum\limits_{k = 1}^{n} {C_{ijk} } } \dot{q}_{j} \dot{q}_{k} + G_{i} \quad i,j,k = 1,2 \ldots \ldots \ldots n$$
(5)

Further, the acceleration of the links plays an important role to control each joint of the biped robot. The expression that represents the acceleration of the link is obtained by rearranging the terms of the above equation and is given as follows.

$$\ddot{q}_{j} = \sum\limits_{j = 1}^{n} {M_{ij} } \left( q \right)^{ - 1} \left[ { - \sum\limits_{j = 1}^{n} {\sum\limits_{k = 1}^{n} {C_{ijk} } } \dot{q}_{j} \dot{q}_{k} - G_{i} } \right] + \left( {\sum\limits_{j = 1}^{n} {M_{ij} } \left( q \right)^{ - 1} *\tau_{i,the} } \right)\quad i,j,k = 1,2 \ldots \ldots \ldots n$$
(6)
$${\text{The}}\,{\text{ term}}\,\hat{\tau } = \sum\limits_{j = 1}^{n} {M_{ij} \left( q \right)^{ - 1} *\tau_{i,the} }$$
(7)

After substituting Eq. (7) in Eq. (6), it can be written as

$$\ddot{q}_{j} = \sum\limits_{j = 1}^{n} {M_{ij} } \left( q \right)^{ - 1} \left[ { - \sum\limits_{j = 1}^{n} {\sum\limits_{k = 1}^{n} {C_{ijk} } } \dot{q}_{j} \dot{q}_{k} - G_{i} } \right] + \hat{\tau }\quad i,j,k = 1,2 \ldots \ldots \ldots n$$
(8)

where the term \(\tau_{i, the}\) represents the theoretical torque required at each joint (N m) and \(q_{j}\), \(\dot{q}_{j}\) and \(\ddot{q}_{j}\) indicate the displacement in (rad), velocity in (rad/s) and acceleration in (rad/s2) of the joint, respectively. The actual torque required at various joints of the biped robot is calculated using the following expression.

$$\tau_{\text{act}} = K_{p} e(\theta_{i} ) + K_{d} e(\dot{\theta }_{i} ) + K_{i} \int {e(\theta_{i} ){\text{d}}t}$$
(9)
$$e\left( {\theta_{i} } \right) = \theta_{if} - \theta_{is}$$
(10)

where τact represents the actual torque required for each joint, Kp, Kd and Ki denote the proportional, derivative and integral gains of the controllers, respectively. Further, θis and θif are the initial and final angular positions. Further, the integral term in Eq. (9) needs to be substituted by its state variables, namely \(\dot{x}_{i}\) and its meaning is given as follows.

$$x_{i} = \int {e\left( {\theta_{is} } \right){\text{d}}t} \Rightarrow \dot{x}_{i} = \theta_{if} - \theta_{is} \quad i = 1,2, \ldots \ldots \ldots n$$
(11)

Now, substituting Eqs. (10 and 11) in Eq. (9), it can be written as

$$\tau_{{i,{\text{act}}}} = K_{pi} \left( {\theta_{if} - \theta_{is} } \right) - K_{di} \dot{\theta }_{is} + K_{ii} \dot{x}_{i} \quad i = 1,2, \ldots \ldots \ldots n$$
(12)

The above equation represents the torque-based PID controller equation used to reduce the error between the initial and final angular positions of each joint. The equation that represents the acceleration of the link, i.e. after substituting the actual torque expression, is given as follows.

$$\ddot{q}_{j} = \sum\limits_{j = 1}^{n} {M_{ij} } \left( q \right)^{ - 1} \left[ { - \sum\limits_{j = 1}^{n} {\sum\limits_{k = 1}^{n} {C_{ijk} } } \dot{q}_{j} \dot{q}_{k} - G_{i} } \right] + K_{pi} \left( {\theta_{if} - \theta_{is} } \right) - K_{di} \dot{\theta }_{is} + K_{ii} \dot{x}_{i}$$
(13)

3 Neural network-based PID controller

The working principle of neural network is similar to that of the human brain in the following two ways: firstly, the network attains the knowledge through learning, and secondly, the data are stored within the synaptic weights. The network consists of junctions which are connected with simple processing units to process the data. The structure of the network (that is, shown in Fig. 2) consists of three layers, that is, input, hidden and output layers, and each layer consists of number of neurons. The weighted sum of the inputs and the bias values are added to each neuron, and the values are passed through transfer functions [30]. The transfer functions, namely linear, log-sigmoid and tan-sigmoid functions, are assigned to the input, hidden and output layers, respectively.

Fig. 2
figure 2

Structure of the neural network

Full size image

In the present research work, the structure of the network consists of 12 neurons in the input layer that indicates the angular error at various joints of the biped robot at various instances of time. The output layer consists of 36 neurons that represent the proportional, integral and derivative gains of the PID controller for the 12 joints of the lower links of the biped robot. These gains are useful to control each joint of the biped robot. Further, the number of neurons in the hidden layer is decided with the help of a parametric study. It is important to note that the performance of neural network depends on the connecting weights between the input–hidden and hidden–output layers. During this study, the connecting weights, bias value of the network and the coefficients of transfer function values of individual layers are optimized with the help of the two nature-inspired metaheuristic algorithms MCIWO and PSO (that is, shown in Fig. 3). Moreover, the performance of the network highly depends on the number of neurons in its hidden layer. The NN-parameters, such as weights between input to hidden [v], hidden to output [w] and bias values [b], are generated as one string of the MCIWO and PSO algorithms. The length of the MCIWO/PSO string always depends on the topology of the NN. The MCIWO/PSO string can be represented as follows:

$$\underbrace {0 \ldots \ldots 1}_{{v_{11} }}\,\,\underbrace {1 \ldots \ldots 1}_{{v_{12} }}\underbrace {1 \ldots \ldots 0}_{{v_{13} }}\underbrace {0 \ldots \ldots 1}_{{v_{21} }}\underbrace {1 \ldots \ldots 0}_{{v_{22} }}\underbrace {0 \ldots \ldots 0}_{{v_{23} }} \ldots \ldots \ldots \ldots \underbrace {0 \ldots \ldots 1}_{{w_{11} }}\underbrace {1 \ldots \ldots 1}_{{w_{12} }}\underbrace {0 \ldots \ldots 1}_{{b_{1} }}\underbrace {0 \ldots \ldots 1}_{{b_{2} }}$$
Fig. 3
figure 3

Flow chart related to the MCIWO-NN and PSO-NN approaches

Full size image

The number of candidate NNs are considered as population of MCIWO/PSO strings, and the MCIWO/PSO will try to find the best one through search. To train the neural network, batch-mode training has been implemented. Initially, a set of data has been used for training the network with the help of evolutionary algorithms. The difference (∆θk = θj − θi) between the initial and final joint angles of all the 12 joints, ∆θ1, ∆θ2, ∆θ3, ∆θ4, ∆θ5, ∆θ6, ∆θ7, ∆θ8, ∆θ9, ∆θ10, ∆θ11, ∆θ12, is considered as inputs to the neural network. The adaptive gains of the PID controllers are predicted at the output of the network. It is called adaptive because the gains are varied for every instant of time based on the amount of error in angular displacement received at the input nodes.

Once the gains of the PID controllers are obtained, they are used to tune the PID controller. The variation in the RMS deviation of the angular displacement at the end of each interval (∝ijkf) and the beginning of the interval (∝ijki) is considered as the fitness (f) of each population and is given as follows.

$$f = \frac{1}{d}\sum\limits_{i = 1}^{d} {\left[ {\frac{1}{h}\sum\limits_{j = 1}^{b} {\sqrt {\frac{1}{2}\sum\limits_{k = 1}^{p} {\left( {\alpha_{ijkf} - \alpha_{ijks} } \right)^{2} } } } } \right]}$$

where d, h and p are the number of training scenarios, number of intervals considered in one step and number of joints, respectively, for which the controllers are designed.

4 Optimization algorithms used

In the present research work, the authors have used two nature-inspired optimization algorithms, namely a newly proposed MCIWO and a well-established PSO to train the structure of the neural network. The block diagram showing the proposed adaptive PID control algorithm is given in Fig. 4. The explanation related to the optimization algorithms is presented in the subsequent sub-sections.

Fig. 4
figure 4

Block diagram showing the proposed adaptive PID controller architecture

Full size image

4.1 MCIWO algorithm

The MCIWO algorithm is developed after making a modification to the standard invasive weed optimization (IWO) algorithm, which is a nature-inspired stochastic optimization algorithm proposed by Mehrabain and Lucas [31] in 2006.

The standard procedure used by the IWO algorithm is explained as follows:

  1. 1.

    Initially, a number of seeds are distributed randomly over the search space, Si = (x1,x2……….xn), where n is the number of selected variables, over the search space. Subsequently, each seed occupies random values for each variable in N-dimensional space.

  2. 2.

    The fitness of each individual seed is calculated after incorporating them into the optimization problem. The fittest seeds grow to flowering weeds and are able to produce new seeds.

  3. 3.

    Each individual weed is ranked based on its fitness value with respect to the subsequent weeds. Consequently, each weed produces new seeds based on its rank in the colony. The weeds which have attained more resources in the field have a better chance of producing more seeds. The number of seeds to be produced by each weed varies linearly from Nmin to Nmax which can be calculated using the following equation.

    $${\text{Number}}\, {\text{of}}\, {\text{seeds }} = \frac{{F_{i} - F_{\text{worst}} }}{{F_{\text{best}} - F_{\text{worst}} }}\left( {N_{ \hbox{max} } - N_{ \hbox{min} } } \right) + N_{ \hbox{min} }$$

    where Fi denotes the fitness of the ith weed. Fbest and Fworst represent the best and worst fitness in the weed colony. This mechanism ensures that every weed considered in the generation takes part in the reproduction process.

  4. 4.

    Once the seeds are generated, they are distributed normally over the search space with mean equal to zero and varying standard deviation σiter, which is described by

    $$\sigma_{\text{iter}} = \left( {\frac{{{\text{iter}}_{ \hbox{max} } - {\text{iter}}}}{{{\text{iter}}_{ \hbox{max} } - 1}}} \right)^{m} \left( {\sigma_{0} - \sigma_{f} } \right) + \sigma_{f}$$

    where iter and itermax represent the number of iterations and maximum number of iterations, respectively, σ0 and σf indicate the initial and final standard deviations, respectively, and m denotes the nonlinear modulation index. The modulation index is a critical parameter which can influence the convergence performance of the IWO algorithm.

  5. 5.

    Further, the fitness of each seed is calculated along with their parent weed and the whole population is ranked. Those weeds with less fitness are eliminated from the colony through competition to make the number of weeds equal to the maximum weeds allowed in the field.

  6. 6.

    The above process is repeated from step 2 until the maximum number of iterations allowed by the user is reached.

To enhance certain capabilities of IWO, such as improving the pre-mature convergence and exploring the better solution quickly by preventing the spread of the new solution in the search space, cosine and chaotic variables are introduced during the dispersal stage. In the present study, Chebyshev map is used to generate the random number used in the chaotic term and is given as follows.

$$X_{k + 1} = \cos \left( {k\cos^{ - 1} \left( {X_{k} } \right)} \right)$$

Further, the cosine term-added spatial dispersal scheme of the present study is given as follows.

$$\sigma_{\text{iter}} = \left( {\frac{{{\text{iter}}_{ \hbox{max} } - {\text{iter}}}}{{{\text{iter}}_{\hbox{max} } - 1}}} \right)^{m} *\left| {\cos \left( {\text{iter}} \right)} \right|*\left( {\sigma_{0} - \sigma_{f} } \right) + \sigma_{f}$$
figure a

4.2 PSO algorithm

PSO is a swarm-based optimization algorithm developed by Kennedy and Eberhart [32]. In PSO, each particle represents a candidate solution to the problem and the implementation of the algorithm is relatively easy. Initially, the position of the particle i is represented by Xi = (xi1, xi2, xi3………. xiD), which denotes a potential solution to the problem in D-dimensional space. Each particle is having a memory to store its previous best position Pbest, and it is calculated based on its velocity along each dimension, denoted as Vi = (vi1, vi2, vi3………. viD).

Once the initial swarm is generated, the fitness value of the problem is denoted in terms of the average error in angular position for all the joints of the biped robot, and will be calculated for all the swarms. The particle with best fitness is designated as Pbest. Further, the Gbest is calculated from the available local best swarm. After calculating the two best positions, the velocity and the new position of the particles in the swarm can be calculated by using the following two equations.

$$V_{i,D}^{t + 1} = W \times V_{i,D}^{t} + C_{1} \times {\text{rand}}_{1} \times \left( {P_{i,D}^{t} - X_{i,D}^{t} } \right) + C_{2} \times {\text{rand}}_{2} \times \left( {G_{i,D}^{t} - X_{i,D}^{t} } \right)$$
$$X_{i,D}^{t + 1} = X_{i,D}^{t} + V_{i,D}^{t + 1} \,\,\,\,i = 1,2, \ldots \ldots \ldots n$$

where W is the inertia weight, C1 and C2 determine the relative influence of the social and cognition components (learning factors), while rand1 and rand2 denote the two random numbers uniformly distributed in the interval [0, 1].

figure b

5 Results and discussion

The purpose of the research work is twofold: firstly to illustrate the good quality results attained by the adaptive PID controller tuned by the nature-inspired optimization algorithm to control the biped robot walking on a slope surface, and secondly, to carry out analysis on various performance measures of the controller and the behaviour of the biped robot, such as

  • An error study has been carried out for the selected nature-inspired algorithms on their capability to tune the gains of the PID controller.

  • Analysis is carried out in terms of the position of ZMP and torque required at various joints of the biped robot for both the optimization algorithms.

  • A comparative study has been carried out on the basis of the dynamic balance margin values obtained for ascending and descending the sloping surfaces using the said algorithms.

  • Finally, the gait angles obtained by the best nature-inspired optimization algorithm are fed to the real biped robot for testing.

The parameters related to the robot, that is, length, mass and inertia of the link, are given in Table 1. The results of convergence for the three approaches, namely MCIWO-NN, PSO-NN and BPNN, are given in Fig. 5. From this test, it can be observed that the MCIWO has shown better performance in terms of convergence of the solution when compared with the PSO and steepest descent method. However, both the MCIWO and PSO are seen to perform better than the steepest descent algorithm. It may be due to the fact that the solutions obtained from the back-propagation algorithm are prone to be stuck in the local minimum.

Table 1 Parameters related to the biped robot
Full size table
Fig. 5
figure 5

Graph showing the convergence of the fitness with different optimization algorithms

Full size image

In the present study, an attempt is made to tune the architecture of the NNs that provide the adaptive gains for the PID controller with the help of two nature-inspired algorithms MCIWO and PSO. The graph showing the effect of variation of neurons in the hidden layer on the performance of the controllers is shown in Fig. 6. The study is conducted by varying the number of hidden neurons between 14 and 22. From Fig. 6, it has been observed that the number of hidden neurons that are responsible for the better performance of MCIWO-NN and PSO-NN approach is seen to be equal to 18 and 16, respectively. The number of input and output neurons that correspond to the input and output layers is observed to be equal to 12 and 36, respectively. Therefore, the connecting weights for the MCIWO-NN and PSO-NN are found to be equal to 864 (12 × 18 + 18 × 36) and 768 (12 × 16 + 16 × 36). Alongside, two bias values are introduced at hidden and output layers of the network. Therefore, the total number of variables required to optimize the structure of NN with MCIWO and PSO is found to be equal to 866 and 770, respectively.

Fig. 6
figure 6

Graph showing the fitness value by varying the hidden neurons with different adaptive algorithms

Full size image

The parameter setting of these algorithms that are used to train the NN, which produce the gains of the controller for the robot while walking on ascending and descending the slope, is illustrated in Table 2. As nature-inspired algorithms are used in this study, the program is run for a minimum no. of generations (Gen) equal to 30, to set the other parameters of the algorithm. Further to obtain the final convergence, the two algorithms are terminated when the maximum number of fitness function evaluations is equal to 100. Further, each algorithm is run for ten times to determine its stochastic nature.

Table 2 Parametric settings of the ascending and descending the slope algorithm
Full size table

All the algorithms are implemented in the MATLAB 2013, and the simulations are carried out on a Dell Precision T1700 computer, having the following specifications:

  • Processor: Intel(R) Xeon(R) CPU E3-1226 v3 @ 3.30 GHz,

  • RAM: 8 GB,

  • Operating System: Windows 7 Professional, 64-bit.

The aim of the present study is to illustrate the behaviour of two nature-inspired metaheuristic-based optimization algorithms, i.e. MCIWO and PSO, on tuning the weights of the neural network. Further, the neural network controller is used to provide adaptive gains for the simple PID controller based on the error signal received at the input of NN. The performance of the MCIWO-NN- and PSO-NN-based controllers is compared in terms of error in angular position, torque required at each joint of the biped robot, variation of ZMP and DBM of the biped robot while ascending and descending the sloping surface.

5.1 Ascending the slope surface

Figure 7 shows the variation of angular error at various joints of the biped robot after using the MCIWO-NN and PSO-NN adaptive PID controllers. From the error plots, it can be observed that the error for all the joints of the biped robot has shown a certain amount of overshoot initially for both the said cases. Then the overshoot slowly decreases and coincides with zero. Further, it has also been observed that MCIWO-NN is seen to converge quickly when compared with the PSO-NN-based PID controller.

Fig. 7
figure 7

Error at various joints of the biped robot while ascending the slope surface. a Joint 2, b Joint 3, c Joint 4, d Joint 5, e Joint 8, f Joint 9, g Joint 10 and h Joint 11

Full size image

Later on, a comparative study has been made on the torque required by the two-legged robot to move each motor from one position to the next and is shown in Fig. 8. It can be observed that the motor mounted on joint 3 (that is, hip joint of the swing leg) has consumed more torque when compared with the other joint motors of the biped robot. It may be due to the fact that while shifting the leg, the hip joint carries other links and joint motors of the biped robot. Moreover, it has also been observed that PSO-NN-based PID controller is found to consume more torque when compared with the MCIWO-NN PID controller. It might have happened due to the large angular displacement obtained at that particular joint. This was also concluded from error plots in which the convergence took more time when compared with the MCIWO-NN approach (ref. Fig. 5(b)).

Fig. 8
figure 8

Torque required at various joints of the swing and stand leg while walking on ascending the sloping surface

Full size image

Further, a comparative study has also been carried out on the position of ZMP (that is, both in X- and Y-directions) obtained for the controlled gait determined by the MCIWO-NN- and PSO-NN-adaptive torque-based PID controllers (ref. Fig. 9). It can be observed that the ZMP is found to lie inside the foot support polygon for both the said controllers when the two-legged robot is ascending the slope surface. But, when compared to PSO-NN-based PID controller, the ZMP point of MCIWO-NN-based PID controller is seen to lie close to the centre of the foot. It is important to mention that when the ZMP is close to the centre of the foot, the robot is found to be more dynamically balanced. From this, it can be concluded that MCIWO-NN-based PID controller is found to derive more dynamically balanced gaits when compared with the PSO-NN-based PID controller.

Fig. 9
figure 9

Variation of zero moment point while ascending the slope surface

Full size image

5.2 Descending the slope surface

Like ascending the slope surface, analysis is also carried out on descending the slope surface. The variation of angular error at various joints of the biped robot is shown in Fig. 10. Similar to the ascending case, here also initially the error is seen to overshoot and then slowly settles down and coincides with zero. In descending case also the error is found to settle down and coincides quickly with zero in the MCIWO-NN-based PID controller when compared with PSO-NN-based PID controller.

Fig. 10
figure 10

Error at various joints of the biped robot while descending the slope surface a Joint 2, b Joint 3, c Joint 4, d Joint 5, e Joint 8, f Joint 9, g Joint 10 and h Joint 11

Full size image

Figure 11 shows the torque required to move the motors at various joints of the biped robot while descending the slope. Similar observation as that of ascending the slope, regarding the torque required hip joint, is conceived during descending the slope. It is also observed that the torque required for all the joints is less when the robot is descending the slope when compared with ascending the slope. This might have happened due to the smaller angular displacements of the links when compared with the ascending case.

Fig. 11
figure 11

Torque required at various joints of the swing and stand leg while descending the slope surface

Full size image

The variation of ZMP for the biped robot while descending the slope surface is given in Fig. 12. In this case also MCIWO-NN torque-based PID controller is observed to produce dynamically more balanced gaits when compared with the PSO-NN-based controller. The reason for this is also same as the one explained for the ascending case. Moreover, the DBM values obtained by the MCIWO-NN adaptive PID controller are seen to be high when compared with the PSO-NN adaptive PID controller in both X- and Y-directions. This may be due to the global optimal nature induced in the MCIWO by allowing all the weeds to participate in the reproduction process. Based on the above process, fitter plants will produce more seeds than less-fit plants, which is the reason to improve the convergence of the algorithm. Another important feature of MCIWO is that the weeds reproduce new seeds independently without mating and contribute towards the generation of fit plants. Further, additional experiments are conducted to study the advantage of MCIWO-NN over PSO-NN by varying the angle of slope from 0° to 5° (refer to Fig. 13). It can be observed that the MCIWO-NN-based PID controller has consistently outperformed PSO-NN-based PID controller in terms of dynamic balance margin of the biped robot while negotiating the slope surface.

Fig. 12
figure 12

Variation of zero moment point while moving on descending the sloping surface

Full size image
Fig. 13
figure 13

Graph showing the dynamic balance margin by varying the slope angle

Full size image

5.3 Comparative study

A comparative study has been conducted in terms of DBM in X- and Y-directions while ascending and descending the slope surfaces. From Fig. 14a, b, it can be observed that the DBM is high when the robot is ascending the slope surface when compared with descending the slope surface.

Fig. 14
figure 14

Dynamic balance margin in X- and Y-directions a X-DBM and b Y-DBM

Full size image

From the above analysis, it has been concluded that MCIWO-NN-based PID controller is found to perform better than the PSO-NN-based PID controller. The controlled gait obtained using the best controller (that is, MCIWO-NN-based PID controller) is fed to the real robot to test the performance of the controller. From Fig. 15a, b, it can be observed that the two-legged robot has successfully performed walk while ascending and descending the slope, respectively. Further, a qualitative comparison has been performed with other approaches provided in [1, 2, 7, 33,34,35,36]. They considered a 7-DOF biped robot and used analytical approach to generate the gaits of the robot. In the present approach, the authors have not only considered the gait generation issues of the biped robot, but also designed a PID controller to execute the generated gait in a smooth manner. Moreover, in [18, 26,27,28,29], some researchers had developed the ZMP-based PID controllers, which are an indirect way of controlling the motors mounted on the joints of the robot, whereas in the present study a torque-based PID controller directly deals with the error in angular displacements of the motors. Further, in [20,21,22,23,24,25], the researchers had used evolutionary algorithms that provide only one set of gain values for the PID controller to tune the gains of the same. However, in the present research, an evolutionary algorithm trained NN is used to predict the gains of the PID controller in an adaptive manner to suit the magnitude of error signals. The said algorithm is tested on a real biped robot.

Fig. 15
figure 15

Biped robot walking on different surfaces a ascending of the slope surface; and b descending of the slope surface

Full size image

6 Conclusion

In general, tuning of the PID controller is a process of determining the optimal values of its gains before the start of the run. Compared to other controllers, the simplified PID controllers are more popular and powerful control systems used in industrial and non-industrial applications. In the present research paper, an attempt is made to develop an adaptive torque-based PID controller with the help of MCIWO-NN and PSO-NN algorithms. The results of these adaptive algorithms are analysed in terms of error, torque required for each joint, variation of ZMP and DBM of the biped robot in order to obtain the best suitable algorithm for this purpose. In this analysis, the online response of the MCIWO-NN-based control algorithm is seen to be better when compared with the PSO-NN-based control algorithm. This might have happened due to the introduction of cosine and chaotic variables in the IWO algorithm. Further, the gait angles obtained by the best adaptive PID controller (i.e. MCIWO-NN) are fed to the real robot. It has been observed that the real biped robot has successfully performed walk on ascending and descending the slope surface.