A robust multi-objective humanitarian relief chain network design for earthquake response, with evacuation assumption under uncertainties

Abstract

In this paper, we have proposed a multi-objective mathematical model for the humanitarian supply chain design problem that minimizes: (1) total number of the injured not transferred to hospitals and total number of the homeless not evacuated from the affected area, and (2) total unmet relief commodity needs. In this model, such parameters as the demand and travel time have been considered as uncertain and two discrete robust counterpart models (with “ellipsoidal” and “box and polyhedral” uncertainty sets) have been developed to model uncertainties. Results found from Tehran Case Study have revealed that the one with the “box and polyhedral” uncertainty set performs better than the “ellipsoidal” set.

1 Introduction

Annually, people all over the world suffer from enormous life/financial losses due to such natural/unnatural (man-made) disasters as earthquakes, floods, tsunamis, terrorist attacks, and so on [1]. In recent years, much attention has been paid to disasters [2], but considering the progress in the science and technology, man has not yet been able to foresee and prevent them [3]. Materials commonly and mostly used in disasters include pharmaceuticals, canned food, water bottles, and tents [4]. In a disaster, rapid resource distribution is quite necessary for the minimization of the damage and fatalities. Since time and resources are limited, the relief logistics will decide on the allocation of time, budget, and other resources [5]. In a disaster, relief commodities are quite vital to reduce fatalities. Generally, very serious challenges of the crisis management include relief and logistic, reducing financial costs, and decreasing fatalities [6]. The main objective of the relief logistics is to set up shelters to help the victims and the disaster-affected people in the shortest possible time [7]. After a disaster, shelters and hospitals are appropriate places for taking care of the injured and the homeless to stay protected from different viruses, cold weather, and so on. The purposeful transferring of the affected people to these places can considerably reduce the fatalities. Since disasters are uncertain and unpredictable, flexibility in logistic activities is of the utmost importance. In a disaster, considering such issues as the uncertain demands, facilities capacities (to be used in the distribution process), transfer capacity, and the available resources is quite important for the decision makers [8]. The obvious problem in effective pre-disaster planning is the uncertainty about the disaster itself because the information about it is scarce [9]. It can be stated that before a disaster, there are no certainties about its occurrence, severity, and losses, and this is why the post-disaster relief logistics planning is usually associated with disorder and perturbation. Under such circumstances, the robust optimization (RO) has proven to be a very powerful tool to model uncertainties.

Although researches about the relief supply chain are not numerous, they can still be classified into two groups one of which has focused on evacuation planning and the other on the relief logistics; hence, their main differences lie in “man” and “commodity.” In one, the main goal is to evacuate people from the affected area, but in the other, it is logistic/commodity delivery.

1.1 Evacuation planning

In these problems, a large number of people reside in accident-prone areas and the aim is to evacuate and send them to safe places. For this purpose, people should usually cover a distance to reach the nearest evacuation station where vehicles are ready to move them. Some examples of such researches are as follows:

An et al. [10] have presented a model to locate evacuation transportation facilities under disruption conditions in order to plan the evacuation of a large number of people residing at accident-prone places. The objective of the research is to minimize the costs of the facility setup, transfer, and transportation through a preplanned evacuating facility disruption risk model. Guan [11] has proposed a model for locating emergency facilities to rescue people in accident-prone areas; the main objective is to minimize the average costs of facility setup and travel time. The travel time between distribution centers and demand points is uncertain, and the use of the stochastic programming approach has been made. Kulshrstha et al. [12] have presented a model for locating evacuation facilities and allocating buses under uncertain demand conditions. The objective of this paper is to minimize the total shipping time. Its demand is uncertain, and the uncertainty modeling has been done using the RO [13] approach. Gama et al. [14] have proposed a multi-period model of locating–allocating shelters for the evacuation of the people experiencing flood and storm. The primary concern of this research is to minimize the total transportation time, and it uses a heuristic approach to solve the proposed model.

1.2 Relief commodity delivery

The humanitarian supply chain consists of several main layers wherein the accident-prone areas that need emergency services are specified. The goals are to locate centers for the distribution of relief commodities, store pre-disaster supplies, and manage their distribution in post-disaster situations. Examples of such researches are as follows:

Using goal programming, Zhan and Liu [15] have developed a multi-objective model for relief logistics under uncertain conditions. The goal of the model is to minimize unmet demand with bi-objective programming: One objective function minimizes the expected service time, and the other minimizes the unmet demand. The demand and the maximum suppliers’ capacities are uncertain and are considered as discrete scenarios. Bozorgi-Amiri et al. [16] developed a modified particle swarm optimization model for relief logistics under uncertainty wherein the demand, suppliers’ capacities, and the costs of transportation and purchasing are assumed uncertain and the objective function is to minimize the total costs. In this problem, the objective is to locate the pre-disaster relief commodity distribution centers for the distribution of the commodities in the affected areas after the disaster. Murali et al. [17] have proposed a model for locating facilities to respond to natural disasters under uncertain demand conditions; the objective is to maximize the number of people who need service and to deal with uncertainties, the authors have used the chance constraint stochastic programming. Bozorgi-Amiri et al. [18] have presented a robust multi-objective model for the relief logistics planning under uncertainties; one objective function minimizes the total costs, and the other establishes justice in the distribution of relief goods. This paper uses the RO approach with such uncertain parameters as the demand, transfer costs, and supply preparation costs. Zhang and Jiang [19] have proposed a bi-objective robust optimization model for the planning of pharmaceutical services in emergency conditions. One objective function minimizes the total costs, and the other minimizes the response time. Here, the focus is mostly on locating the emergency facilities and regions are allocated to emergency centers. Deng and Yang [20] have developed a mathematical model for the transportation planning for the emergency operations management. The model objective is to minimize the transportation and inventory costs, and its total demand is uncertain. Rezaei Malek and Tavakoli-Moghadam [21] have developed a bi-objective RO [22] model for the logistic revival plan wherein one objective function minimizes the service time and the other minimizes the costs. The shipping time (from the warehouses to the demand points), demand, and the warehouses’ remaining capacities are considered uncertain. Bozorgi-Amiri and Khorsi [23] have presented a dynamic multi-objective model for the locating and routing of the logistic facilities under uncertain conditions. One objective function, in this 3-objective model, minimizes the maximum shortages, one minimizes the total travel time, and the third minimizes the total costs. Such parameters as the commodity purchase prices, shipping costs, demand for vital supplies, and the capacities of the suppliers and distribution centers are uncertain and are considered as discrete scenarios. Garrido et al. [24] have developed a model for the emergency planning of flood and storm with the stochastic programming approach. Its objective is to minimize transportation costs with uncertain demand. Zokaee et al. [25] have developed a RO [26] model for the design of the humanitarian supply chain consisting of three levels of suppliers, distribution centers, and affected areas; the objective of the model is to minimize total costs. Paul and Wang [27] have presented a robust location–allocation model for earthquake response under uncertain conditions. The objective function is to minimize total social costs. It has an uncertain casualty of severity level at demand node and transportation times which are considered as different scenarios. Jha et al. [28] have developed a multi-objective programming for humanitarian relief supply chain. This paper model is a humanitarian relief chain that includes a relief goods supply chain and an evacuation chain in case of a natural disaster. The objective functions are presented in the following: 1—demand satisfaction in relief chain, 2—demand satisfaction in evacuation chain, and 3—estimating/minimizing overall logistics cost. A multi-objective genetic algorithm, NSGA-II, is used to get dataset including Pareto solution. In Vahdani et al. [29], a multi-objective optimization model has been provided based on the travel time and total cost and reliability of the routes. In this model (during) the earthquake response activities, the damaged roads can be repaired. The relief supply chain comprises a set of distribution centers and affected areas.

1.3 The paper novelties

A literature review of the humanitarian supply chain in recent years reveals that the evacuation of the people (homeless and injured) from the affected area has not been dealt with properly; most papers have addressed only the delivery of the relief commodities in such areas and the number of papers dealing simultaneously with the distribution of the relief goods and evacuation of the people from these areas is not many. In an earthquake, some people need relief supplies, injuries of some are more severe and they should be immediately transferred to emergency centers, and those who are not injured should be sent to safe areas to be protected from the subsequent tremors, wildlife, and contagious diseases. Therefore, the need for a plan that can, at the same time, organize the distribution of the relief supplies, send the injured people to emergency centers, and evacuate homeless people to shelters is highly felt. In most studies regarding modeling, the use of the scenario-based programming has been made to deal with uncertainties in disasters and accidents, while in the real world, appropriate historical data are not available based on which scenarios can be defined; the distribution function of the random variable is also unknown [30]. Additionally, data uncertainty is assumed discrete in the scenario-based approach, while in reality it is continuous. Another weak point of the scenario-based approach is the challenge in defining and generating the scenarios [18]; the solution found under certain conditions may not be feasible for other observations and scenarios [30]. Assuming different scenarios are generated, the next problem will be solving them; when the number of scenarios is more and the problem size is large, the solution time will face a serious challenge [4]. Therefore, the reason for choosing a RO [26, 31, 32] to develop a novel mathematical model is based on the real-world assumptions and conditions. To model uncertainties, scenarios are modeled based on an observed example. What distinguishes this research from other similar ones is the simultaneous consideration of the distribution of relief goods, transferring injured people to hospitals, and evacuating the homeless people into shelters; the planning is multi-period and considers the means of transportation as well. To be as close to the real world as possible and face uncertainties, the use of two types of RO approaches has been made: box and polyhedral [26] and ellipsoidal [31] uncertainty sets. This programming is bi-objective: One minimizes the number of injured and homeless people of the affected area sent to the emergency centers and shelters, and the other minimizes the shortage of the relief supplies, emergency centers, and shelters. The main contributions of this paper can be given as follows:

• Developing a robust multi-objective model in the disaster relief supply chain;

• Developing and comparing two RO models in the relief supply chain;

• Comparing robust models with maximum constraint violation probability;

• Simultaneous addressing of evacuating, transferring the injured, and delivering commodities;

• The proposed model is applied on a real-world case study of disaster relief;

The rest of the paper is organized as follows. The concerned problem is defined in Sect. 2, and the proposed mathematical model for humanitarian relief chain network design is presented in Sect. 3. The robust counterpart models based on “box and polyhedral” and “ellipsoidal” uncertainty sets are elaborated in Sect. 4, and the employed solution method is presented in Sect. 5. Finally, an illustrative example and concluding remarks and some possible future works are presented in Sects. 6 and 7, respectively.

2 Problem description

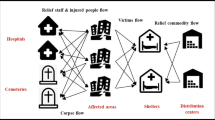
Suppose the relief supply chain (Fig. 1) consists of four levels including distribution centers, shelters, affected areas, and hospitals. In an earthquake, successive tremors are most likely; if some buildings remain partially undamaged in the first hit, they may get totally destroyed in the next tremors. Therefore, evacuation of the people from such places will become a very serious issue. Meanwhile, some people may be injured and need to be sent to emergency centers and hospitals for revival and more medication. In the proposed model, we have considered some relief–rescue revival centers and some evacuation shelters so that immediately after the disaster the injured may be sent to hospitals and the unhurt can be transferred to shelters. In a disaster, the unhurt are willing to help their relatives and other people and, for this purpose, they would require relief commodities (first aid supplies, water, food, etc.), and those who have been sent to hospitals and shelters would be in need of pharmaceuticals, drinks, and food stuff; hence, each level requires relief commodities. Here, there are some different capacity distribution centers that provide service to send relief commodities to each of these points [33].

Fig. 1

Network structure of the relief supply chain

In an earthquake, some of these service centers may be destroyed, and since no exact information is available about the earthquake intensity, we cannot specify the remaining capacities after it hits. To make sure not to miss some potential of the relief chain in a disaster, hospitals, shelters, and distribution centers are considered outside the disaster-prone areas. Under such circumstances, the service time (commodity distribution, people transportation, etc.) may be prolonged; if this service time exceeds a specified limit, the provided service may totally lose its desirability. This is why a maximum coverage time is considered for every service so that we may not face such adverse conditions.

The main assumptions of the relief supply chain design problem are as follows:

• 1. The planning horizon has three periods (3 × 24);

• 2. The number of candidate points for setting up distribution centers and shelters is known;

• 3. Capacities of the distribution centers, hospitals, and shelters are limited;

• 4. Three relief commodities (drinking water, food stuff, and pharmaceuticals) are distributed;

• 5. The number of the affected and homeless people, relief commodity demand, and the travel time between all nodes are considered uncertain;

• 6. The service time is not to exceed a specified amount;

• 7. The distribution centers can be established at only one level (large, medium, or small);

• 8. The number and capacities of the transportation vehicles are limited;

• 9. The planning budget is limited;

Considering the above assumptions, we have developed a bi-objective relief optimization model that minimizes, as its first objective, the number of people who have not been sent to the hospitals and shelters and, as its second objective, the total shortages of the relief commodities through making such decisions as locating shelters and distribution centers, determining the capacity level of the distribution centers, determining the number of people sent to hospitals and shelters, determining the flow of the relief commodities from distribution centers to the affected area, hospitals, and shelters, and dispatching transportation vehicles.

3 Model formulation

3.1 Indices and sets

t :

Planning horizon

i :

Set of the affected points

j :

Set of the candidate locations for setting up distribution centers

p :

Set of the shelters

k :

Set of the relief commodities

l :

Set of the distribution centers

v :

Set of the transportation vehicles

h :

Set of the losses and injuries

3.2 Parameters

$fp_{p}$ :

Fixed cost of setting up a shelter at location p

$fj_{jl}$ :

Fixed cost of setting up a distribution center with capacity l at location j

$di_{hi}$ :

Number of injured people type h available at affected area i

$dh_{i}$ :

Number of people at the affected area i that are to be evacuated

$dk_{kit}$ :

Demand for the relief commodity type k at the affected area i at time t

$ds_{kst}$ :

Demand for the relief commodity type k at the hospital s at time t

$Ci_{s}$ :

Capacity of the hospital s for the injured people

$Cw_{v}$ :

Weight capacity of the vehicle type v

$Cv_{v}$ :

Volume capacity of the vehicle type v

$Civ_{v}$ :

Capacity of the vehicle type v for shipping injured people

$Ch_{v}$ :

Capacity of the vehicle type v for evacuating the homeless people

${\text{Cap}}_{l}$ :

Capacity of distribution center level l

$Cps_{p}$ :

Capacity of shelter p

$dt_{vis}$ :

Travel time of vehicle v between the affected area i and the hospital s

$dt_{vip}$ :

Travel time of vehicle v between the affected area i and the shelter p

$dt_{vjs}$ :

Travel time of vehicle v between the distribution center j and the hospital s

$dt_{vjp}$ :

Travel time of vehicle v between the distribution center j and the shelter p

$dt_{vji}$ :

Travel time of vehicle v between the distribution center j and the affected area i

$Wt_{k}$ :

Weight of one unit relief commodity type k

$Vl_{k}$ :

Volume of one unit relief commodity type k

$nk_{k}$ :

Number of the relief commodity type k required per person in a shelter

$A_{jv}$ :

Number of the vehicle type v available at the distribution center j when the planning horizon begins

$B_{iv}$ :

Number of the vehicle type v available at the affected area i at the beginning of the planning horizon

$B_{o}$ :

Maximum accessible budget

Tc :

Coverage time

$M_{big}$ :

A very big positive number

3.3 Variables

$y_{p}$ :

A binary variable to set up a shelter at location p

$y_{li}$ :

A binary variable to set up a distribution center with capacity l at the location j

$x_{kjst}$ :

No. of the relief commodity type k sent from the distribution center j to the hospital s at time t

$x_{kjpt}$ :

No. of the relief commodity type k sent from the distribution center j to the shelter p at time t

$x_{kjit}$ :

No. of the commodity type k sent from the distribution center j to the affected area i at time t

$Ni_{hist}$ :

No. of injured people type h sent from the affected area i to the hospital s at time t

$Nh_{ipt}$ :

No. of people sent from the affected area i to the shelter p at time t

$Nvh_{ipvt}$ :

No. of the vehicle type v sent from the affected area i to the shelter p at time t

$Nvi_{isvt}$ :

No. of the vehicle type v sent from the affected area i to the hospital s at time t

$Nvk_{jpvt}$ :

No. of the vehicle type v sent from the distribution center j to the shelter p at time t

$Nvji_{jivt}$ :

No. of the vehicle type v sent from the distribution center j to the affected area i at time t

$Nvjs_{jsvt}$ :

No. of the vehicle type v sent from the distribution center j to the hospital s at time t

$dv_{kpt}$ :

Demand for the relief commodity type k in the shelter p at time t

$av_{ivt}$ :

No. of the vehicle type v available at the affected area i at time t

3.4 Objective functions and constraints

The proposed mathematical model for humanitarian relief chain network design (HRCND) is as follows:

HRCND:

$${\text{Min}}\;{\text{z}}_{ 1} = \mathop \sum \limits_{h} \mathop \sum \limits_{i} \left( {di_{hi} - \mathop \sum \limits_{s} \mathop \sum \limits_{t} Ni_{hist} } \right) + \mathop \sum \limits_{s} \left( {dh_{i} - \mathop \sum \limits_{p} \mathop \sum \limits_{t} Nh_{ipt} } \right)$$

(1)

$${\text{Min}}\;{\text{z}}_{ 2} = \mathop \sum \limits_{k} \mathop \sum \limits_{i} \mathop \sum \limits_{t} \left( {dk_{kit} - \mathop \sum \limits_{j} x_{kjit} } \right) + \mathop \sum \limits_{k} \mathop \sum \limits_{s} \mathop \sum \limits_{t} \left( {ds_{kst} - \mathop \sum \limits_{j} x_{kjst} } \right) + \mathop \sum \limits_{k} \mathop \sum \limits_{p} \mathop \sum \limits_{t} \left( {dv_{kpt} - \mathop \sum \limits_{j} x_{kjpt} } \right)$$

(2)

subject to

$$\mathop \sum \limits_{p} f_{p} y_{p} + \mathop \sum \limits_{j} \mathop \sum \limits_{l} f_{jl} y_{jl} \le B_{o}$$

(3)

$$\mathop \sum \limits_{l} y_{lj} \le 1\quad \forall j \in J$$

(4)

$$\mathop \sum \limits_{i} \mathop \sum \limits_{t} Nh_{ipt} \le Cps_{p} \cdot y_{p} \quad \forall p \in P$$

(5)

$$\mathop \sum \limits_{i} \mathop \sum \limits_{t} \mathop \sum \limits_{h} Ni_{hist} \le Ci_{s} \quad \forall s \in S$$

(6)

$$\mathop \sum \limits_{i} Nh_{ipt} nk_{k} = dv_{kpt} \quad \forall k \in K,p \in P,t \in K$$

(7)

$$\mathop \sum \limits_{k} \mathop \sum \limits_{p} \mathop \sum \limits_{t} x_{kjpt} + \mathop \sum \limits_{k} \mathop \sum \limits_{s} \mathop \sum \limits_{t} x_{kjst} + \mathop \sum \limits_{k} \mathop \sum \limits_{i} \mathop \sum \limits_{t} x_{kjit} \le \mathop \sum \limits_{l} Cap_{l} .y_{jl} \quad \forall j \in J$$

(8)

$$\mathop \sum \limits_{P} \mathop \sum \limits_{t} Nh_{ipt} \le dh_{i} \quad \forall i \in I$$

(9)

$$\mathop \sum \limits_{s} \mathop \sum \limits_{t} Ni_{hist} \le di_{hi} \quad \forall h \in H, i \in I$$

(10)

$$\mathop \sum \limits_{j} x_{kjit} \le dk_{kit} \quad \forall k \in K, i \in I,t \in T$$

(11)

$$\mathop \sum \limits_{j} x_{kjst} \le ds_{kst} \quad \forall k \in K,\;s \in S,\;t \in T$$

(12)

$$\mathop \sum \limits_{j} x_{kjpt} \le dv_{kpt} \quad \forall k \in K,p \in P,t \in T$$

(13)

$$\mathop \sum \limits_{k} wt_{k} x_{kjpt} \le \mathop \sum \limits_{v} Cw_{v} .Nvk_{jpvt} \quad \forall j \in J, p \in P ,t \in T$$

(14)

$$\mathop \sum \limits_{k} Vl_{k} x_{kjpt} \le \mathop \sum \limits_{v} Cv_{v} .Nvk_{jpvt} \quad \forall j \in J,p \in P,t \in T$$

(15)

$$\mathop \sum \limits_{k} wt_{k} x_{kjst} \le \mathop \sum \limits_{v} Cw_{v} Nvjs_{jsvt} \quad \forall j \in J,s \in S,t \in T$$

(16)

$$\mathop \sum \limits_{k} Vl_{k} .x_{kjst} \le \mathop \sum \limits_{v} Cv_{v} Nvjs_{jsvt} \quad \forall j \in J,s \in S,t \in T$$

(17)

$$\mathop \sum \limits_{k} wt_{k} x_{kjit} \le \mathop \sum \limits_{v} Cw_{v} Nvji_{jivt} \quad \forall j \in J, i \in I ,t \in T$$

(18)

$$\mathop \sum \limits_{k} Vl_{k} x_{kjit} \le \mathop \sum \limits_{v} Cv_{v} Nvji_{jivt} \quad \forall j \in J,i \in I,t \in T$$

(19)

$$\mathop \sum \limits_{h} Ni_{hist} \le \mathop \sum \limits_{v} Civ_{v} Nvi_{isvt} \quad \forall i \in I,s \in S,t \in T$$

(20)

$$Nh_{ipt} \le \mathop \sum \limits_{v} Chv_{v} Nvh_{ipvt} \quad \forall i \in I,p \in P,t \in T$$

(21)

$$Nvk_{jpvt} \le M_{big} y_{p} \quad \forall j \in J,p \in P,v \in V,t \in T$$

(22)

$$Nvk_{jpvt} \le \mathop \sum \limits_{l} M_{big} y_{jl} \quad \forall j \in J,p \in P,v \in V,t \in T$$

(23)

$$Nvji_{jivt} \le \mathop \sum \limits_{l} M_{big} y_{jl} \quad \forall j \in J,i \in I,v \in V,t \in T$$

(24)

$$Nvjs_{jsvt} \le \mathop \sum \limits_{l} M_{big} y_{jl} \quad \forall j \in J,p \in P,v \in V,t \in T$$

(25)

$$dt_{vis} Nvi_{isvt} \le tc\quad \forall i \in I,s \in S,v \in V,t \in T$$

(26)

$$dt_{vip} Nvh_{ipvt} \le tc\quad \forall i \in I,s \in S,v \in V,t \in T$$

(27)

$$dt_{vjs} Nvjs_{jsvt} \le tc\quad \forall j \in J,s \in S,v \in V,t \in T$$

(28)

$$dt_{vjp} Nvk_{jpvt} \le tc\quad \forall j \in J,p \in P,v \in V,t \in T$$

(29)

$$dt_{vji} Nvji_{jivt} \le tc\quad \forall j \in J,i \in I,v \in V,t \in T$$

(30)

$$\mathop \sum \limits_{p} \mathop \sum \limits_{t} Nvk_{jpvt} + \mathop \sum \limits_{i} \mathop \sum \limits_{t} Nvji_{jivt} + \mathop \sum \limits_{s} \mathop \sum \limits_{t} Nvjs_{jsvt} \le A_{jv} \quad \forall j \in J,v \in V$$

(31)

$$av_{ivt} = av_{ivt - 1} + \mathop \sum \limits_{j} Nvji_{jivt} - \mathop \sum \limits_{p} Nvh_{ipvt} - \mathop \sum \limits_{s} Nvi_{isvt} \forall i \in I,v \in V,t \in T$$

(32)

$$av_{iv0} = B_{iv} \quad \forall i \in I,v \in V$$

(33)

$$y_{p} , y_{lj} \in \left\{ {0,1} \right\}x_{kjpt } ,x_{kjst} ,x_{kjit} ,dv_{kpt} ,Ni_{hist} Nh_{ipt} ,Nvh_{ipvt} Nvi_{isvt} ,Nvk_{jpvt} ,Nvji_{jivt} ,Nvjs_{jsvt} ,av_{ivt} \ge 0,\;{\text{and}}\;\text{int}$$

(34)

In the above model, the first objective function (1) minimizes the total number of people who have not been sent to hospitals and shelters, while the second objective function (2) minimizes the total shortages of the relief commodities in the affected area, hospitals, and shelters. Constraint (3) ensures that the setup fixed costs may not exceed the available budget. Constraint (4) specifies the setup capacity of each distribution center. Constraint (5) keeps the number of the people sent to a shelter below its capacity. Constraint (6) limits a hospital capacity for the injured people. Constraint (7) limits the shelter demand for relief commodities. Constraint (8) ensures that the total relief commodities sent from a distribution center to other nodes should be less than their capacities. Constraints (9 and 10) ensure that the total number of people sent to hospitals and shelters should not exceed the population of the affected area. Constraints (11–13) ensure that the total number of relief commodities sent from a distribution center to other nodes should not exceed their demands. Constraints (14–19) deal with the vehicles’ weights and volumes limitations. Constraints (20 and 21) show a vehicle’s human capacity. Constraint (22) ensures that sending people to a shelter is possible only if it already exists. Constraints (23–25) ensure that the relief commodity flow from a distribution center to other nodes is possible only if they already exist. Constraints (26–30) ensure that the time of each service should not exceed the maximum coverage time Constraint (31) ensures that the number of vehicles dispatched from distribution centers to affected areas, hospitals, and shelters cannot be more than the total number of the available vehicles. Constraints (32 and 33) balance the vehicles in the affected area. And, finally, constraint (34) specifies the sign of each variable.

4 The proposed robust model

The concept of the RO was first introduced by Soyster [32], who assumed that all uncertainty data assume values in a closed interval and, with this assumption, he determined these values so that the worst possible state may be imposed on the model; if the model is feasible with this logic, then it is so in realization. Although Soyster’s logic solved the problem of the parameters’ stochasticity to some extent, it was far from reality because the probability that all the parameters may be in their worst possible state simultaneously is almost nil. To control the conservatism degree appropriately and create more conformity between the RO and reality, many researchers developed their models on this basis. To start their works, Ben-Tal and Nemirovski [31] assumed an ellipsoidal set formation for the uncertainty data, but Bertsimas and Sim’s [26] assumption was a counterpart “box and polyhedral” set. These sets show that all the parameters cannot be in their worst possible states simultaneously.

These two approaches have been proposed against Soyster’s traditional model and may yield different results. The goal is to compare them in disaster conditions and see which one, under similar situations, yields better results so that the decision maker can perform better under such circumstances.

4.1 Robust optimization with ellipsoidal uncertainty set

This modeling was first introduced by Ben-Tal and Nemirovski [31]. Consider the following mathematical model:

$$\begin{array}{*{20}l} {{\text{RO}}:\;\hbox{min}\, z = \mathop \sum \limits_{j} c_{j} x_{j} } \hfill \\ {{\text{Subject}}\;{\text{to}}} \hfill \\ {\mathop \sum \limits_{j} \tilde{a}_{ij} x_{j} \le b_{i} } \hfill \\ \end{array}$$

(35)

where the uncertain vector ($\tilde{a}_{ij}$) assumes value in the interval [$\varvec{ }\bar{a}_{ij} + \hat{a}_{ij}$ and $\varvec{ }\bar{a}_{ij} - \hat{a}_{ij}$] ($\bar{a}_{ij}$) is the nominal value of the uncertain parameter, and ($\hat{a}_{ij}$) is the perturbation vector. Considering the ellipsoidal uncertainty set, the robust counterpart of Ben-Tal and Nemirovski’s model is shown as follows:

$$\begin{array}{*{20}l} {\hbox{min}\, z = \mathop \sum \limits_{j} c_{j} x_{j} } \hfill \\ {{\text{Subject}}\;{\text{to}}} \hfill \\ {\mathop \sum \limits_{j} a_{ij} x_{j} + \varOmega \sqrt {\mathop \sum \limits_{{j \in J_{i} }} \hat{a}_{ij}^{2} x_{i}^{2} } \le b_{i} } \hfill \\ \end{array}$$

(36)

where ($\varOmega$) corresponds to the conservatism degree of the ellipsoidal uncertainty set. For instance, consider the first part of the objective function (1), constraints (9 and 26), in problem (HRCND):

$${\text{Min}}\;z$$

(37)

Subject to

$$\mathop \sum \limits_{h} \mathop \sum \limits_{i} \left( {di_{hi} - \mathop \sum \limits_{s} \mathop \sum \limits_{t} Ni_{hist} } \right) \le z$$

(38)

$$\mathop \sum \limits_{P} \mathop \sum \limits_{t} Nh_{ipt} \le {\text{d}}h_{i} \quad \forall i \in I$$

(39)

$${\text{d}}t_{\text{vis}} Nvi_{isvt} \le tc\quad \forall i \in I,s \in S,v \in V,t \in T$$

(40)

Making use of the auxiliary variables k_hi and k_i, the above model can be rewritten as follows:

$${\text{Min}}\;z$$

(41)

Subject to

$$\mathop \sum \limits_{h} \mathop \sum \limits_{i} di_{hi} k_{hi} \le \mathop \sum \limits_{h} \mathop \sum \limits_{i} \mathop \sum \limits_{s} \mathop \sum \limits_{t} Ni_{hist} + z$$

(42)

$$k_{i} dh_{i} \le - \mathop \sum \limits_{p} \mathop \sum \limits_{t} Nh_{ipt} \quad \forall i \in I$$

(43)

$$dt_{vis} Nvi_{isvt} \le tc\quad \forall i \in I,s \in S,v \in V,t \in T$$

(44)

The robust counterpart of the above model is as follows:

$${\text{Min}}\;z$$

(45)

Subject to

$$\mathop \sum \limits_{h} \mathop \sum \limits_{i} \overline{d} i_{hi} k_{hi} + \varOmega \sqrt {\mathop \sum \limits_{{h \in H_{O} }} \mathop \sum \limits_{{i \in I_{O} }} \widehat{di}_{hi}^{2} k_{hi}^{2} } \le \mathop \sum \limits_{h} \mathop \sum \limits_{i} \mathop \sum \limits_{s} \mathop \sum \limits_{t} Ni_{hist} + z$$

(46)

$$\overline{dh}_{i} k_{i} + \varOmega \sqrt {\widehat{dh}_{i}^{2} k_{i}^{2} } \le - \mathop \sum \limits_{p} \mathop \sum \limits_{t} Nh_{ipt} \quad \forall i \in I$$

(47)

$$\overline{{{\text{d}}t}}_{vis} Nvi_{isvt} + \varOmega \sqrt {\widehat{dt}_{vip}^{2} Nvi_{isvt}^{2} } \le tc\quad \forall i \in I,s \in S,v \in V,t \in T$$

(48)

Now, substituting the values of the auxiliary variables ($k_{hi} = 1$ and $k_{i} = - 1$), we will get:

$${\text{Min}}\;z$$

(49)

Subject to

$$\mathop \sum \limits_{h} \mathop \sum \limits_{i} \overline{di}_{hi} + \varOmega \sqrt {\mathop \sum \limits_{{h \in H_{O} }} \mathop \sum \limits_{{i \in I_{O} }} \widehat{di}_{hi}^{2} } \le \mathop \sum \limits_{h} \mathop \sum \limits_{i} \mathop \sum \limits_{s} \mathop \sum \limits_{t} Ni_{hist} + z$$

(50)

$$\mathop \sum \limits_{p} \mathop \sum \limits_{t} Nh_{ipt} \le \overline{dh}_{i} - \varOmega \widehat{dh}_{i} \quad \forall i \in I$$

(51)

$$\overline{dt}_{vis} Nvi_{isvt} + \varOmega \widehat{dt}_{vis} Nvi_{isvt} \le tc\quad \forall i \in I,s \in S,v \in V,t \in T$$

(52)

We can see that the nonlinear model with the ellipsoidal uncertainty set has turned into a linear programming. Finally, the robust counterpart of the multi-objective relief problem with ellipsoidal uncertainty set (RCRES) is shown as follows:

RCRES:

$${\text{Min}}\;z1$$

(53)

$${\text{Min}}\;z2$$

(54)

Subject toConstrains (3–8) (13–25) and (31–34)

$$\mathop \sum \limits_{h} \mathop \sum \limits_{i} \overline{di}_{hi} + \varOmega \sqrt {\mathop \sum \limits_{{h \in H_{O} }} \mathop \sum \limits_{{i \in I_{O} }} \widehat{dh}_{hi}^{2} } - \mathop \sum \limits_{h} \mathop \sum \limits_{i} \mathop \sum \limits_{s} \mathop \sum \limits_{t} Ni_{hist} + \mathop \sum \limits_{i} \overline{di}_{i} + \varOmega \sqrt {\mathop \sum \limits_{{i \in I_{O} }} \widehat{dh}_{i}^{2} } - \mathop \sum \limits_{i} \mathop \sum \limits_{p} \mathop \sum \limits_{t} Nh_{ipt} \le z 1$$

(55)

$$\mathop \sum \limits_{k} \mathop \sum \limits_{i} \mathop \sum \limits_{t} \overline{dk}_{kit} + \varOmega \sqrt {\mathop \sum \limits_{{k \in K_{o} }} \mathop \sum \limits_{{i \in I_{o} }} \mathop \sum \limits_{{t \in T_{o} }} \widehat{dk}_{kit}^{2} } - \mathop \sum \limits_{k} \mathop \sum \limits_{j} \mathop \sum \limits_{i} \mathop \sum \limits_{t} x_{kjit} + \mathop \sum \limits_{k} \mathop \sum \limits_{s} \mathop \sum \limits_{t} \overline{ds}_{kst} + \varOmega \sqrt {\mathop \sum \limits_{{k \in K_{o} }} \mathop \sum \limits_{{s \in S_{o} }} \mathop \sum \limits_{{t \in T_{o} }} \widehat{ds}_{kst}^{2} } - \mathop \sum \limits_{k} \mathop \sum \limits_{j} \mathop \sum \limits_{s} \mathop \sum \limits_{t} x_{kjst} + \mathop \sum \limits_{k} \mathop \sum \limits_{p} \mathop \sum \limits_{t} \left( {dv_{kpt} - \mathop \sum \limits_{j} x_{kjpt} } \right) \le z2$$

(56)

$$\mathop \sum \limits_{p} \mathop \sum \limits_{t} Nh_{ipt} \le \overline{dh}_{i} - \varOmega \widehat{dh}_{i} \quad \forall i \in I$$

(57)

$$\mathop \sum \limits_{s} \mathop \sum \limits_{t} Ni_{hist} \le \overline{di}_{hi} - \varOmega \widehat{di}_{hi} \quad \forall h \in H,\;i \in I$$

(58)

$$\mathop \sum \limits_{j} x_{kjit} \le \overline{dk}_{kit} - \varOmega \widehat{dk}_{kit} \quad \forall k \in K,\;i \in I,\;t \in T$$

(59)

$$\mathop \sum \limits_{j} x_{kjst} \le \overline{ds}_{kst} + \varOmega \widehat{ds}_{kst} \quad \forall k \in K,\;s \in S,\;t \in T$$

(60)

$$\overline{dt}_{vis} Nvi_{isvt} + \varOmega \widehat{dt}_{vis} Nvi_{isvt} \le tc\quad \forall i \in I,\;s \in S,\;v \in V,\;t \in T$$

(61)

$$\overline{dt}_{vjs} Nvjs_{jsvt} + \varOmega \widehat{dt}_{vjs} Nvjs_{jsvt} \le tc\quad \forall j \in J,\;s \in S,\;v \in V,\;t \in T$$

(62)

$$\overline{dt}_{vjp} Nvk_{jpvt} + \varOmega \widehat{dt}_{vjp} Nvk_{jpvt} \le tc\quad \forall j \in J,\;p \in P,\;v \in V,\;t \in T$$

(63)

$$\overline{dt}_{vip} Nvh_{ipvt} + \varOmega \widehat{dt}_{vip} Nvh_{ipvt} \le tc\quad \forall p \in P,\;i \in I,\;v \in V,\;t \in T$$

(64)

$$\overline{dt}_{vis} Nvji_{vt} + \varOmega \widehat{dt}_{vij} Nvji_{jivt} \le tc\quad \forall j \in J,\;i \in I,\;v \in V,\;t \in T$$

(65)

4.2 Robust optimization with box and polyhedral uncertainty sets

This modeling was first introduced by Bertsimas and Sim [26]. In this modeling, it is assumed that some stochastic data are influenced by uncertainty and they assume value in their worst possible state.

Considering linear programming (RO), the robust counterpart of this model with box and polyhedral uncertainty sets is as follows:

$$\begin{array}{*{20}l} {\hbox{min}\, z = \mathop \sum \limits_{j} c_{j} x_{j} } \hfill \\ {{\text{Subject}}\;{\text{to}}} \hfill \\ {\mathop \sum \limits_{j} \bar{a}_{ij} x_{j} + { \hbox{max} }_{{\{ s_{i} \cup \left\{ {t_{i} } \right\}|s_{i} \subseteq J_{i} ,\left| {s_{i} } \right| = \left[ {\varGamma_{i} } \right],t_{i} \in J_{i} \backslash s_{i} \} }} \{ \mathop \sum \limits_{{j \in s_{i} }} \hat{a}_{ij} |x_{j} | + \left( {\varGamma_{i} - { \lfloor }\varGamma_{i} { \rfloor }} \right)\hat{a}_{{it_{i} }} \left| {x_{{it_{i} }} } \right|\} \le b_{i} } \hfill \\ \end{array}$$

(66)

where ($J_{i}$) is an integer, is the total number of uncertain parameters available in constraint i, and ($\varGamma_{i}$) is the uncertainty robustness budget ($\varGamma_{i} = \left[ {0,\left| {J_{i} } \right|} \right]$). To turn the above problem into a single optimization problem, the protection function against uncertainty β (x, $\varGamma_{i}$) is introduced as follows:

$$\beta \left( {x,\varGamma_{i} } \right) = \max_{{\{ s_{i} \cup \left\{ {t_{i} } \right\}|s_{i} \subseteq J_{i} ,\left| {s_{i} } \right| = d\varGamma_{i} t,t_{i} \in J_{i} \backslash s_{i} \} }} \left\{ {\mathop \sum \limits_{{j \in s_{i} }} \hat{a}_{ij} |x_{j} | + \left( {\varGamma_{i} - d\varGamma_{i} t} \right)\hat{a}_{{it_{i} }} \left| {x_{{it_{i} }} } \right|} \right\}$$

(67)

The protection function optimization problem is equivalent to the following problem:

$$\begin{array}{*{20}l} {{\text{Max}}\mathop \sum \limits_{{j \in J_{i} }} \hat{a}_{ij} z_{ij} |x_{j} |} \hfill \\ {{\text{Subject}}\;{\text{to}}} \hfill \\ {\mathop \sum \limits_{j} z_{ij} \le \varGamma_{i} } \hfill \\ {0 \le z_{ij} \le } \hfill \\ \end{array}$$

(68)

The dual of the above problem is written as follows:

$$\begin{array}{*{20}l} {{\text{Min}}\;\varGamma_{i} p_{i} + \mathop \sum \limits_{{j \in J_{i} }} q_{ij} } \hfill \\ {{\text{Subject}}\;{\text{to}}} \hfill \\ {p_{i} + q_{ij} \ge \hat{a}_{ij} |x_{j} |\quad \forall i \in I,\;j \in J_{i} } \hfill \\ {p_{i} ,q_{ij} \ge 0} \hfill \\ \end{array}$$

(69)

$q_{ij}$ and $p_{i}$ are the dual variables. Consequently, the robust counterpart of problem (RO) is written as follows:

$$\begin{array}{*{20}l} {\hbox{min}\,z = \mathop \sum \limits_{j} c_{j} x_{j} } \hfill \\ {\mathop \sum \limits_{j} a_{ij} x_{j} + \varGamma_{i} p_{i} + \mathop \sum \limits_{{j \in J_{i} }} q_{ij} \le b_{i} } \hfill \\ \begin{aligned} p_{i} + q_{ij} \ge \hat{a}_{ij} u_{j} \hfill \\ - u_{j} \le x_{j} \le u_{j} \hfill \\ p_{i} ,q_{ij} ,u_{j} \ge 0 \hfill \\ \end{aligned} \hfill \\ \end{array}$$

(70)

Finally, the robust counterpart of the multi-objective relief problem with box and polyhedral uncertainty sets (RCRBPS) is shown as follows:

RCRBPS:

$${\text{Min}}\;z1$$

(71)

$${\text{Min}}\;z2$$

(72)

Subject to

Constrains (3–5) (8–13) and (31–34)

$$\mathop \sum \limits_{h} \mathop \sum \limits_{i} \left( {\overline{di}_{hi} - \mathop \sum \limits_{s} \mathop \sum \limits_{t} Ni_{hist} } \right) + \mathop \sum \limits_{{h \in H_{o} }} \mathop \sum \limits_{{i \in I_{o} }} q_{hi}^{di} + P_{o}^{di} \varGamma_{o}^{di} + \mathop \sum \limits_{s} \left( {\overline{dh}_{i} - \mathop \sum \limits_{p} \mathop \sum \limits_{t} Nh_{ipt} } \right) + \mathop \sum \limits_{{i \in I_{o} }} q_{i}^{dh} + P_{o}^{dh} \varGamma_{o}^{dh} \le z1$$

(73)

$$\mathop \sum \limits_{k} \mathop \sum \limits_{i} \mathop \sum \limits_{t} \left( {\overline{dk}_{kit} - \mathop \sum \limits_{j} x_{kjit} } \right) + \mathop \sum \limits_{{k \in K_{o} }} \mathop \sum \limits_{{i \in I_{o} }} \mathop \sum \limits_{{t \in T_{O} }} q_{kit}^{dk} + P_{o}^{dk} \varGamma_{o}^{dk} + \mathop \sum \limits_{k} \mathop \sum \limits_{s} \mathop \sum \limits_{t} \left( {\overline{ds}_{kst} - \mathop \sum \limits_{j} x_{kjst} } \right) + \mathop \sum \limits_{{k \in K_{o} }} \mathop \sum \limits_{{s \in S_{o} }} \mathop \sum \limits_{{t \in T_{o} }} q_{kst}^{ds} + P_{o}^{ds} \varGamma_{o}^{ds} + \mathop \sum \limits_{k} \mathop \sum \limits_{p} \mathop \sum \limits_{t} \left( {dv_{kpt} - \mathop \sum \limits_{j} x_{kjpt} } \right) \le z$$

(74)

$$\mathop \sum \limits_{P} \mathop \sum \limits_{t} Nh_{ipt} \le \overline{dh}_{i} - \varGamma_{i}^{dh} \widehat{dh}_{i} \quad \forall i \in I$$

(75)

$$\mathop \sum \limits_{s} \mathop \sum \limits_{t} Ni_{hist} \le \overline{di}_{hi} - \varGamma_{hi}^{dh} \widehat{di}_{hi} \quad \forall h \in H,\;i \in I$$

(76)

$$\mathop \sum \limits_{j} x_{kjit} \le \overline{dk}_{kit} - \varGamma_{kit}^{dk} \widehat{dk}_{kit} \quad \forall k \in K,\;i \in I,\;t \in T$$

(77)

$$\mathop \sum \limits_{j} x_{kjst} \le \overline{ds}_{kst} + \varGamma_{kst}^{ds} \widehat{ds}_{kst} \quad \forall k \in K,\;s \in S,\;t \in T$$

(78)

$$\overline{dt}_{vis} Nvi_{isvt} + q_{vis}^{tvis} + P_{vis}^{tvis} \varGamma_{vis}^{tvis} \le tc\quad \forall i \in I,\;s \in S,\;v \in V,\;t \in T$$

(79)

$$\overline{dt}_{vip} Nvh_{ipvt} + q_{vip}^{tvip} + P_{vip}^{tvip} \varGamma_{vip}^{tvip} \le tc \quad \forall i \in I,\;p \in P,\;v \in V,\;t \in T$$

(80)

$$\overline{dt}_{vjs} Nvjs_{jsvt} + q_{vjs}^{tvjs} + P_{vjs}^{tvjs} \varGamma_{vjs}^{tvjs} \le tc\quad \forall j \in J,\;s \in S,\;v \in V,\;t \in T$$

(81)

$$\overline{dt}_{vji} Nvji_{jivt} + q_{vji}^{tvji} + P_{vji}^{tvji} \varGamma_{vji}^{tvji} \le tc\quad \forall j \in J,\;i \in I,\;v \in V,\;t \in T$$

(82)

$$q_{hi}^{di} + P_{o}^{di} \ge \widehat{di}_{hi} \quad \forall h \in H,\;i \in I$$

(83)

$$q_{i}^{dh} + P_{o}^{dh} \ge \widehat{dh}_{i} \quad \forall i \in I$$

(84)

$$q_{kit}^{dk} + P_{o}^{dk} \ge \widehat{dk}_{kit} \quad \forall k \in K,\;i \in I,\;t \in T$$

(85)

$$q_{kst}^{ds} + P_{o}^{ds} \ge \widehat{dk}_{kst} \quad \forall k \in K,\;s \in S,\;t \in T$$

(86)

$$q_{vis}^{tvis} + P_{vis}^{tvis} \ge \widehat{dt}_{vis} Nvi_{isvt} \quad \forall v \in v,\;i \in I,\;s \in S,\;t \in T$$

(87)

$$q_{vip}^{tvip} + P_{vip}^{tvip} \ge \widehat{dt}_{vip} Nvh_{ipvt} \quad \forall i \in I,\;p \in P,\;v \in V,\;t \in T$$

(88)

$$q_{vjs}^{tvjs} + P_{vjs}^{tvjs} \ge \widehat{dt}_{vjs} Nvjs_{jsvt} \quad \forall j \in J,\;s \in S,\;v \in V,\;t \in T$$

(89)

$$q_{vjp}^{tvjp} + P_{vjp}^{tvjp} \ge \widehat{dt}_{vjp} Nvk_{jpvt} \quad \forall j \in J,\;p \in P,\;v \in V,\;t \in T$$

(90)

$$q_{vji}^{tvji} + P_{vji}^{tvji} \ge \widehat{dt}_{vji} Nvji_{jivt} \quad \forall j \in J,\;i \in I,\;v \in V,\;t \in T$$

(91)

$$q_{hi}^{di} , \;P_{o}^{di} ,\;q_{i}^{dh} ,\;P_{o}^{dh} ,\;q_{kit}^{dk} ,\;P_{o}^{dk} ,\;q_{kst}^{ds} ,\;P_{o}^{ds} ,\;q_{kst}^{ds} ,\;P_{o}^{ds} ,\;q_{vis}^{tvis} ,\;P_{vis}^{tvis} ,\;q_{vip}^{tvip} ,\;P_{vip}^{tvip} ,\;q_{vjs}^{tvjs} ,\;P_{vjs}^{tvjs} ,\;q_{vjp}^{tvjp} ,\;P_{vjp}^{tvjp} ,\;q_{vji}^{tvji} ,\;P_{vji}^{tvji} \ge 0$$

(92)

In mathematical model (RCRBPS), there is only one uncertain parameter in the set of constraints (75–82). The maximum value of the robustness budget of these constraints is 1 and its minimum is 0. We determine a total robustness budget for a specified datum (e.g., $dk_{kit}$) and consider the share of each constraint in the total budget equal. In other words, we consider the parameter uncertainty of these constraints column-wise instead of row-wise [25]; this will facilitate the work and simplify the computations. Therefore, constraints (75–82) of model (RCRBPS) are extended as follows:

$$\mathop \sum \limits_{P} \mathop \sum \limits_{t} Nh_{ipt} \le dh_{i} - \frac{{\varGamma_{O}^{dh} }}{I}\widehat{dh}_{i} \quad \forall i \in I$$

(93)

$$\mathop \sum \limits_{s} \mathop \sum \limits_{t} Ni_{hist} \le di_{hi} - \frac{{\varGamma_{O}^{dh} }}{H.I}\widehat{di}_{hi} \quad \forall h \in H,\;i \in I$$

(94)

$$\mathop \sum \limits_{j} x_{kjit} \le dk_{kit} - \frac{{\varGamma_{O}^{dk} }}{K.I.T}\widehat{dk}_{kit} \quad \forall k \in K,\;i \in I,\;t \in T$$

(95)

$$dt_{vis} Nvi_{isvt} + q_{vis}^{tvis} + P_{vis}^{tvis} \frac{{\varGamma^{tvis} }}{V.I.S} \le tc\quad \forall i \in I,\;s \in S,\;v \in V,\;t \in T$$

(96)

$$dt_{vip} Nvh_{ipvt} + q_{vip}^{tvip} + P_{vip}^{tvip} \frac{{\varGamma^{tvip} }}{V.I.P} \le tc\quad \forall i \in I,p \in P,v \in V,t \in T$$

(97)

$$dt_{vjs} Nvjs_{jsvt} + q_{vjs}^{tvjs} + P_{vjs}^{tvjs} \frac{{\varGamma^{tvjs} }}{V.J.S} \le tc\quad \forall j \in J,\;s \in S,\;v \in V,\;t \in T$$

(98)

$$dt_{vjp} Nvk_{jpvt} + q_{vjp}^{tvjp} + P_{vjp}^{tvjp} \frac{{\varGamma^{tvjp} }}{V.J.P} \le tc\quad \forall j \in J,\;p \in P,\;v \in V,\;t \in T$$

(99)

4.3 Maximum probability of constraint violation in the robust optimization

Consider the following uncertain constraint:

$$\mathop \sum \limits_{j} \tilde{a}_{ij} x_{j}^{*} \le b_{i} \quad \forall i \in I$$

(100)

As we know, the left-side coefficients ($\tilde{a}_{ij}$) are uncertain. RO is more after the solution robustness of constraint (100) under realization; therefore, it is possible to establish a relationship between the degree of conservatism and the probability of constraint violation. Ben-Tal and Nemirovski [34] have shown the maximum probability of constraint (100) violation as follows:

$$\Pr \left( {\mathop \sum \limits_{j} \tilde{a}_{ij} x_{j}^{*} \ge b_{i} } \right) \le e^{{\left( { - \varOmega_{i}^{2} } \right)}} \quad \forall i \in I$$

(101)

Although the above relation is to find the maximum probability of the constraint violation of the RO with box and polyhedral uncertainty sets, it is true for the RO with ellipsoidal uncertainty set as well [35].

Bertsimas and Sim [26], have introduced the maximum probability of constraint (100) violation with box and polyhedral uncertainty sets as follows:

$$\Pr \left( {\mathop \sum \limits_{j} \tilde{a}_{ij} x_{j}^{*} \ge b_{i} } \right) \le 1 - \varPhi \left( {\frac{{\varGamma_{i} - 1}}{{\sqrt {|J_{i|} } }}} \right)$$

(102)

In constraint (102), $\varPhi \left( {\frac{{\varGamma_{i} - 1}}{{\sqrt {|J_{i|} } }}} \right)$ is the cumulative probability of the normal distribution function.

To compare the performances of models (RCRES) and (RCRBPS) against uncertainty, the probabilities of the constraint violation are assumed equal and the conservatism degree is calculated for each model and compared under similar conditions.

5 Solution procedure

In the related literature, the extensive use of the multi-objective optimization problems has been made [36,37,38]. In this paper, we have used the Lexicographic Weighted Tchebycheff (LWT) method where every objective is first optimized individually and then a new objective is defined which is after minimizing the maximum weight deviation of each objective function from its optimum value [39]. Consider a multi-objective model with n variables and m objective functions as follows:

$$\begin{array}{*{20}l} {{\mathbf{LWT}}:{\text{Min }}H(x) = \{ h_{1} (x), \, h_{2} (x), \, h_{3} (x), \, \ldots , \, h_{m} (x)\} } \hfill \\ {{\text{Subject}}\;{\text{to}}} \hfill \\ {x \in X_{h} } \hfill \\ \end{array}$$

(103)

where $(x_{f} \subseteq x) x$ is the set of the feasible solutions, H(x) is the set of the decision variables in the decision space $x:\left[ {x = x_{1} ,x_{2} ,x_{3} , \ldots , \, x_{n} } \right]$ and the solution space $z:\left[ {z = z_{1} ,z_{2} ,z_{3} , \ldots , \, z_{m} } \right]$.

First, the optimum value of each objective function is found as follows:

$$z_{i}^{*} = {\text{Min}}\{ h_{i} (x|x \in x_{h} )\} - \varepsilon_{i}$$

(104)

where ε_i is a very small positive value. The multi-objective model LWT is turned into a single objective model (namely LWTS) as follows:

$$\begin{array}{*{20}l} {{\mathbf{LWTS}}:{\text{Min}}\;\alpha } \hfill \\ {S.t} \hfill \\ \begin{aligned} \alpha \ge \lambda_{i} \left( {h_{i} \left( x \right) - \, z_{i}^{*} } \right) \hfill \\ \mathop \sum \limits_{i = 1}^{m} \lambda_{i} \, = 1\quad 0 \le \lambda_{i} \le 1,\;x \in x_{h } \hfill \\ \end{aligned} \hfill \\ \end{array}$$

(105)

where (λ_i) is the importance of each objective function.

Problem LWTS minimizes the maximum weight deviation of each objective function from its optimum value and may produce weak Pareto optimum solutions. Therefore, some of the solutions may dominate the weak Pareto solutions for the elimination of which we can use the model as follows if we define x_w as the Pareto optimum solution of model LWTS:

$$\begin{array}{*{20}l} {{\text{Min}}\mathop \sum \limits_{i = 1}^{m} \left( {h_{i} \left( x \right) - z_{i}^{*} } \right)} \hfill \\ {{\text{Subject}}\;{\text{to}}} \hfill \\ {x \in x_{w} } \hfill \\ \end{array}$$

(106)

6 Case study

Tehran, with a population of more than 8 million, is the largest metropolitan city in Iran. With this population, many people may face irrecoverable difficulties in case of an earthquake. Tehran is an earthquake-prone city because of its famous faults (Rey, Mosha, North Tehran, etc.).

6.1 Case description

Figure 2 shows that there are relatively many faults in the northern part of Tehran meaning that the first five districts (out of 22) are among the high-risk places. Therefore, the centers of these five districts have been considered as the affected areas. As shown in Fig. 3, the hospitals and the candidate locations to set up shelters and distribution centers are outside the affected areas.

Fig. 2

Map of Tehran faults

Fig. 3

Affected areas, hospitals, candidate locations to set up shelters and distribution centers

The main sources of data for this case study are the reports provided by this region’s disaster management experts, the Red Crescent Society, Japan International Cooperation Agency, and online available data on population and available resources. The data helped us calculate the location of the affected area, the number of injured people, the number of relief commodities, transportation times between all nodes of the network and the costs parameters, and the number and capacities of distribution centers, shelters, hospitals, and vehicles.

Each distribution center can be large, medium, or small, and the relief commodities stored in them include water, food, and pharmaceuticals. Capacities and setup costs of each type are shown in Table 1.

Table 1 The capacity level of distribution centers and their setup costs

In this issue, there are five candidate locations to set up the distribution centers; the districts addresses and the candidate locations are shown in Table 2.

Table 2 Candidate locations for distribution centers

There are six different capacity hospitals at different locations, the names and capacities of which are shown in Table 3.

Table 3 Locations and capacities of hospitals

There are five candidate locations to set up shelters with different capacities; their brief information is provided in Table 4.

Table 4 Candidate locations for shelters

Tables 5 and 6 show the transportation vehicles’ features and the weight/volume of every 1000 units of the relief commodities, respectively.

Table 5 Capacities of vehicles

Table 6 Weight and volume of the relief commodities

And, finally, Table 7 shows the uncertainty interval for every stochastic parameter.

Table 7 The sources of random generation of the nominal data

As mentioned before, hospitals, shelters, and distribution centers are located outside the affected areas to make most of their capacities and capabilities because if they are inside, some of them may get totally destroyed and some may lose their efficiencies in case an earthquake or other disasters occur.

7 Results

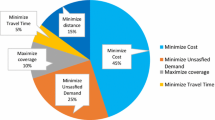
As discussed in the earlier sections, the goal is a comparison between the optimization models (RCRES) and (RCRBPS) to see which one performs better in facing uncertainties. But, establishing a direct relationship between these models’ conservatism degree is not an easy task, and for us in order to do it, we use another trick. If we take the probabilities of all the constraints violations of both models equal, we will be able to calculate their robustness budgets. For this purpose and to do the sensitivity analyses and models tests, we have considered five levels (0.1, 0.15, 0.2, 0.25, and 0.3) for the maximum probabilities of constraints violations and three levels (5, 10, and 15%) for the deviation of the uncertainty data from the nominal data. We have already pointed out that there are five affected areas, six hospitals, five candidate locations (to set up shelters), and five candidate locations (to set up distribution centers). Also, there are three types of transportation vehicles, two types of injured people, and three periods in the planning horizon. Problems (RCRES) and (RCRBPS) and also the deterministic problem (HRCND) have been solved using nominal data, DELL Laptop (core i5 and RAM4), GAMS Optimization Software (Ver. 24.0.1), and CPLEX Powerful Solver. Five different weight sets (λ₁ and λ₂) have been considered for the objective functions.

By reducing the maximum probabilities of the constraints violations, we make the conditions more severe for the mathematical model; it means that if this maximum is reduced in each step, the conservatism budgets ($\Omega$ and $\varGamma$) will increase and, as we know, the optimum solution can suffer with this increase. Again, if the maximum deviation from the nominal data is increased, the conditions will get more difficult for modeling and, under such circumstances, the optimum solution may get worse. The summary of the results found from the solution of models (HRCND), (RCRES), and (RCRBPS) is provided in Tables 8, 9, 10, 11, 12, 13. As shown, the objective function has improved in each step by increasing the maximum probabilities of the constraints violations (which reduces the conservatism degree) and keeping the deviations from the nominal data constant.

Table 8 Results from the deterministic model tests with the nominal data

Table 9 Results from two uncertainty sets tests with a maximum constraint violation probability of (0.1)

Table 10 Results from two uncertainty sets tests with a maximum constraint violation probability of (0.15)

Table 11 Results from two uncertainty sets tests with a maximum constraint violation probability of (0.2)

Table 12 Results from two uncertainty sets tests with a maximum constraint violation probability of (0.25)

Table 13 Results from two uncertainty sets tests with a maximum constraint violation probability of (0.3)

In Tables 8, 9, 10, 11, 12, 13, z_i* is the optimum value of the ith objective function when the problem is single objective and (z⁻_i) is the worst value of the ith objective function when the problem is single objective (with another objective function). By “weight,” we mean the importance given to the first and second objective functions [(λ₁) and (λ₂), respectively] in multi-objective cases (λ₁, λ₂ ≤ 1, and λ₁+ λ₂ = 1). Also, (α) is the value of the objective function of the multi-objective programming when importance λ₁ is given to the first objective function (z₁) and λ₂ is given to the second objective function (z₂). MPCV and DFNV stand, respectively, for “Maximum Probability of Constraint Violation” and “Deviation from Nominal Value.”

For instance, Fig. 4 is drawn for the first objective function (z₁) of the deterministic model, robust ellipsoidal model, and robust box and polyhedral models and Fig. 5 is prepared for the second objective function (z₂) for 5% deviation from the nominal data for all levels of the maximum probabilities of constraints violations. We can see that an increase in the maximum probability has improved the first and second objective functions in each step. It is worth mentioning that the worst case for robust models has occurred at 0.1 and 15%, respectively, for maximum probability of constraint violation and deviation of the stochastic data from the nominal data; this is the highest conservatism degree among all degrees introduced. Both robust models have been worse, in all cases, than the deterministic model. To achieve solution robustness, the robust modeling is after optimization under bad conditions (considering a specified conservatism degree) in such a way that the mathematical model will stay feasible under realization.

Fig. 4

First objective function with respect to the maximum constraint violation probability with 5% deviation from the nominal data

Fig. 5

Second objective function with respect to the maximum constraint violation probability with 5% deviation from the nominal data

Objective functions values have been worse compared with those of the deterministic model.

Moreover, with an increase in the deviation from the nominal data, the optimum values of the objective functions of the robust models have become worse in each step. For example, the values of the first and the second objective functions (z₁ and z₂, respectively) are drawn in Figs. 6 and 7, respectively, considering 0.1 for the maximum probability of constraint violation with deviations of 5, 10, and 15% from the nominal data.

Fig. 6

First objective function with respect to the uncertainty data deviation from the nominal data and the maximum constraint violation probability of 0.1

Fig. 7

Second objective function with respect to the stochastic data deviation from the nominal data and the maximum constraint violation probability of 0.1

We can see that with an increase in the deviation from the nominal data, the optimum values of the objective functions have obtained worse in each step. If the uncertainty interval is increased, we expect that the optimum value of the objective function has obtained worse in each step. In other levels of the maximum probability of constraint violation and deviation of the uncertainty data from the nominal data, the trend has been the same and the results have conformed to our expectations.

In optimization, if the first objective function (z₁) gets a 100% importance (λ₁ = 1), the optimum value of the objective function of the robust model will perform better with ellipsoidal set than box and polyhedral model, but if λ₁ < 1, sometimes the solution optimality is displaced among the ellipsoidal, box, and polyhedral models. If the 100% importance (λ₂ = 1) is given to the second objective function (z₂), the robust model with the ellipsoidal set will perform worse than the box and polyhedral models. Solutions of the robust models have been calculated in (75) cases (5 levels of maximum probability of constraint violation, 3 levels of deviation from nominal data, and 5 weight sets) without giving the 100% importance to one objective function (λ₁ < 1, λ₂ < 1, and λ₁ + λ₂ = 1). If we count the number of the cases where the value of (z₁) in the robust model with box and polyhedral uncertainty sets has become better than that with the ellipsoidal set, in (56) cases the robust model with box and polyhedral uncertainty sets has performed better. If the same comparison is made for (z₂), again the robust model with box and polyhedral uncertainty sets has outperformed in (74) cases. Therefore, the point average of the robust model with box and polyhedral uncertainty sets has been better compared to that with the ellipsoidal set.

Since RO approaches based on the box and polyhedral and ellipsoidal uncertainty sets are quite different, their direct comparison is very difficult. If the MPCV is considered equal in both methods and appropriate robustness budgets are calculated from relations (101) and (102), their comparison will be possible under such similar conditions; this comparison method has been used in the proposed model. As explained in the paper (page 25 Paragraph 1), if robust models are solved with a single objective, the ellipsoidal uncertainty set will perform better than the box and polyhedral uncertainty set (as regards the first objective function), but as regards the second objective function, it is vice versa. If robust models are solved with multi-objective approaches considering weight (importance) for the objective functions, the box and polyhedral uncertainty set will perform better than the ellipsoidal uncertainty set. Therefore, on average, the robust method based on the box uncertainty set performs better than the ellipsoidal uncertainty set.

Strong Pareto solutions have been produced at all levels of the maximum probability of constraint violation and different percentages of deviation from the nominal data. For instance, Pareto (Fig. 8) has been drawn for models (RCRES), (RCRBPS), and (HRCND) at the maximum probability of constraint violation of 0.2 and 10% deviation from the nominal data. The vertical axis of the Pareto figure shows the value of (z₁), and the horizontal axis shows that of (z₂). When Pareto solutions are reported, one solution set should not dominate another one at the same level considering a known conservatism degree. Decision makers decide based on the importance they attach to each objective function. With a decrease in (z₁), (z₂) increases in each step; the same is true for (z₂) as well. When the Pareto figure gets closer to the horizontal axis, it means that (z₁) has been more important than (z₂). Similarly, when it gets nearer to the vertical axis, (z₂) has been more important. Uniform slope of Fig. 8 is an indication that strong Pareto solutions have been produced.

Fig. 8

Pareto diagrams of deterministic and robust models at a maximum constraint violation probability of 0.2 and a 10% deviation from the nominal data

Figure 8 shows Pareto diagrams of deterministic and robust models at a maximum constraint violation probability of 0.2 and a 10% deviation from the nominal data.

8 Conclusions

Considering the importance of transferring the injured/homeless people and distributing relief commodities in earthquakes, a bi-objective rescue–relief model under uncertainty has been developed. The first objective minimizes the total number of the injured/homeless people who have not been transferred from the affected area, and the second objective is after minimizing the total shortages of the relief commodities. To model uncertainty, two approaches have been developed: (1) RO with ellipsoidal uncertainty set and (2) RO with box and polyhedral uncertainty sets. To do sensitivity analyses and compare deterministic and robust models, the use of Tehran Case Study has been made. The results obtained from solving the deterministic and robust models show that the robust models resulted in more conservative solutions in all cases. Also, by comparing the two proposed robust models, it can be concluded that using the box and polyhedral uncertainty sets results in a better performance than the ellipsoidal uncertainty set.

Finally, suggestions for future studies are: (1) Routing can be added to commodity distribution and injured/homeless transfer, (2) using exact and meta-heuristic algorithms for large-scale problems, and (3) using other uncertainty sets such as box–ellipsoidal and ellipsoidal–polyhedral to see which RO model with uncertainty sets outperforms the other alternatives.