Bipolar $\delta$-equal complex fuzzy concept lattice with its application

Abstract

Recently, bipolar as well as vague concept lattice visualization is introduced for precise representation of inconsistency and incompleteness in data sets based on its acceptation and rejection part simultaneously. In this process, a problem is addressed while measuring the periodic fluctuation in bipolar information at the given phase of time. This changes in human cognition used coexist often in our daily life where the sentiments (i.e., love or hatred) for anyone may change several times from morning to evening office time. In this case precise representation of this type of bipolar information and measuring its pattern is a major issue for the researchers. To deal with this problem, the current paper proposes three methods for adequate representation of bipolar complex data set using the calculus of complex fuzzy matrix, $\delta$-equality and the calculus of granular computing, respectively. Hence, the proposed method provides an umbrella way to navigate or decompose the bipolar complex data sets and their semantics using an illustrative example. The results obtained from the proposed methods are also compared to validate the results.

1 Introduction

Extracting some of the meaningful information from a given data set is a major concern for the research community [18]. Solving the particular problem of a given research field is based on user requirements. To deal with this problem, one of the mathematical model is introduced by Wille [56] based on applied abstract algebra. The algebra of this tool is recently enhanced via mathematics of fuzzy set [16] and its extensive properties [17]. It given a way to deal with uncertainty and vagueness in fuzzy attributes precisely when compared to binary setting [48]. This new tool generally takes the input in form of a fuzzy context ${\mathbf{K}} = \left( {X,Y,\tilde{R}} \right)$ having some set of objects set (X), some set of fuzzy attributes (Y), and an L-relation among X and Y such that, $\tilde{R}$: $\textit{X}\times \textit{Y} \rightarrow \textit{L}$. It means the relation $\tilde{R}(\textit{x},\textit{y})\in L$ represents the membership value at which the object $x\in \textit{X}$ has the attribute $y\in \textit{Y}$ in L-set [26]. L is a support set of some complete residuated lattice ${\mathbf{L}} )=(L,\wedge ,\vee ,\otimes ,\rightarrow ,0,1)$ where, 0 and 1 represent the least and greatest elements, respectively [37]. This becomes complete residuated lattice having following properties: (i) $(L,\wedge ,\vee ,0,1)$ is a bounded complete lattice with bound 0 and 1, (ii) $(L,\otimes ,1)$ is commutative monoid, (iii) $\otimes$ and $\rightarrow$ are adjoint operators (called multiplication and residuum, respectively), that is $a \otimes b \le c$ iff $a\le b\rightarrow c, \forall a,b,c\in \textit{L}$ [55]. The operators $\otimes$ and $\rightarrow$ are defined distinctly by Lukasiewicz: $a \otimes b = \hbox {max} (\textit{a}+\textit{b}-1, 0)$, $a \rightarrow b=\hbox {min} (1-\textit{a}+\textit{b}, 1)$; G$\ddot{o}$del: $a \otimes b = \hbox {min} (\textit{a}, \textit{b})$, $a \rightarrow b = 1$ if $a \le b$, otherwise b; Goguen: $a \otimes b = a \cdot b$, $a \rightarrow b = 1$ if $a \le b$, otherwise b/a. For any L-set A$\in L^{\tiny {\textit{X}}}$ of objects, an L-set A$^{\uparrow }\in L^{\tiny {\textit{Y}}}$ of attributes can be obtained using $\uparrow$ operator A$^{\uparrow } (y)=\wedge _{x\in {\textit{X}}}( \textit{A}(x) \rightarrow \tilde{R}(\textit{x},\textit{y}))$. Similarly, for any L-set $\textit{B} \in L^{\tiny {\textit{Y}}}$ of attributes, an L-set $\textit{B}^{\downarrow }\in L^{\tiny {\textit{X}}}$ of objects can be discovered using $\downarrow$ operator, i.e., $\textit{B}^{\downarrow } (x)=\wedge _{y\in {\textit{Y}}}( \textit{B}(y) \rightarrow \tilde{R}(\textit{x},\textit{y}))$. Here, $\textit{A}^{\uparrow } (y)$ is interpreted as the L-set of attribute y$\in \textit{Y}$ shared by all objects from A. Similarly, $\textit{B}^{\downarrow } (x)$ is interpreted as the L-set of all objects $\textit{x}\in \textit{X}$ having the same attributes from B in common. The formal fuzzy concept is a pair of $(\textit{A}, \textit{B})\in L^{\tiny {\textit{X}}}\times L^{\tiny {\textit{Y}}}$ satisfying $\textit{A}^{\uparrow }=\textit{B}$ and $\textit{B}^{\downarrow }=\textit{A}$, where fuzzy set of objects A is called an extent and fuzzy set of attributes B is called an intent [24]. The set of obtained formal fuzzy concepts from a given fuzzy context K defines the partial ordering principle, i.e., $(\textit{A}_{1},\textit{B}_{1})\le (\textit{A}_{2},\textit{B}_{2})\Longleftrightarrow \textit{A}_{1}\subseteq \textit{A}_{2}(\Longleftrightarrow \textit{B}_{2}\subseteq \textit{B}_{1})$. Together with this ordering, there exists an infimum and a supremum for the generated formal fuzzy concepts in the complete lattice, i.e., (i) $\wedge _{j\in J}(A_{j}, B_{j})=(\bigcap _{j\in J} A_{j}, (\bigcup _{j\in J}B_{j})^{\downarrow \uparrow })$, (ii) $\vee _{j\in J} (A_{j}, B_{j})=((\bigcup _{j \in J} A_{j})^{\uparrow \downarrow },\bigcap _{j\in J} B_{j})$ [22]. The operators ($\uparrow , \downarrow$) are known as Galois connection [28]. In this way, the calculus of fuzzy concept lattice provides some of the interesting patterns hidden in the data with fuzzy attributes. In this process, a problem arises when the attributes contain bipolar information and its uncertainty changes at each given phase of time. To conquer this problem, current paper focuses on the depth analysis of complex or dynamic data set having bipolar fuzzy attributes using the calculus of bipolar complex fuzzy set and its graphical properties.

Table 1 A comparative study on complex fuzzy, interval, vague and bipolar set

Fig. 1

Graphical understanding of bipolar complex fuzzy concept learning

The bipolarity is nothing but a generalized mathematical representation of Yin Yang logic [69, 71]. Generally, it exists in two forms: (1) linear bipolarity, i.e., pass and fail or, (2) interactive bipolarity among the attributes, i.e., conflict or common interest side [23, 68]. It means a bipolar information can be represented through combination of a positive and negative membership of a defined bipolar fuzzy space $[-1, 0) \times (0, 1]$ where 1 represents positive pole true, − 1 represents negative pole true and 0 as false [2]. In this case, a bipolar fuzzy set J in Z can be represented as $\textit{J}=\left\{ (z, \mu ^{\mathrm{P}}(z),\mu ^{\mathrm{N}}(z))|z\in Z \right\}$ where $\mu ^{\mathrm{P}}:\textit{Z}\rightarrow [0, 1]$ and $\mu ^{\mathrm{N}}:\textit{Z}\rightarrow [-1, 0]$ are mappings [10]. This mathematical model provides a precise representation of bipolar information given by any user for further analysis. However, the preference and opinion of any user change at each interval of time [45]. The bipolar cognitions as well as bipolarity in sentiments used to find in each of the human couple. In which, they love each other maximally at the beginning and hate minimally to each other, whereas it changes after some time and vice versa. This type of fluctuation is used to find in each daily life where a user prefers specific product to purchase at morning official time and some thing different at evening returning time. This can be measured in day, month and yearly basis also [4]. Analyzing this type of periodic or non-periodic bipolar or multi-polar information using the properties of mathematics [14] or graphs [13] is a major issue for the researchers of current time [45]. The problem computing with these types of multi-valued [64] complex linguistics words is an intensive issue due to lack of incomplete data [33, 63]. To deal with these types of multi-valued linguistic words properties of complex fuzzy set [59] and its calculus is extensively studied [60]. Among them the calculus of bipolar complex fuzzy set and its application is at infancy stage. However, its properties provide a precise representation of chages in bipolar information when compared to other available approaches as shown in Table 1. Due to this reason, current paper focuses on analysis of bipolar complex fuzzy context and its compact visualization in the concept lattice for knowledge processing tasks. The motivation is to extract some meaningful information from the given bipolar complex fuzzy context based on their objects and attributes set. To achieve this goal, recently Prem Kumar Singh [45] tried to analyze the given bipolar context [39] and its concept lattice visualization [40] using the amplitude and phase term of a complex fuzzy set. The current paper is distinct from any of the available approaches in following ways:

• (i) The current paper focuses on empirical analysis of bipolar complex fuzzy context for multi-decision process,

• (ii) The current paper aimed at providing a graphical analytics of periodic bipolar data sets and their pattern,

• (iii) The current provides $\delta$-equal decomposition or navigation of bipolar complex fuzzy concept lattice at user required complex granules for refining the knowledge. It can be considered as one of the novel and significant output of the proposed method in field of knowledge discovery and representation tasks.

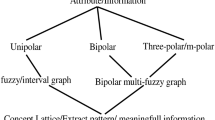
To understand the necessity of the proposed method, a graphical structure classification of available data process is shown in Fig. 1. It shows that the bipolar complex fuzzy concept lattice and its calculus are vital requirements to handle the data with bipolar complex fuzzy attributes. To achieve this goal, three subsequent methods are proposed in this paper: (i) the first method aims at investigating all the bipolar complex fuzzy concepts based on user required subset of attributes, (ii) the second method aims at selecting $\delta$-equal bipolar complex fuzzy concepts based on their computed distance, and (iii) the third method focuses on decomposition of given bipolar complex fuzzy context at user-defined complex granules with an illustrative example. All of these methods and their obtained results are compared with each other to validate the results and their uses for the appropriate contexts.

Remaining parts of this paper is constituted as follows: Sect. 2 contains some of the required mathematical notations about bipolar complex fuzzy set and its graphical representation. Section 3 includes the proposed methods for handling the bipolar complex fuzzy data sets. The step-by-step demonstration of the proposed methods is shown in Sect. 4 using an illustrative example. Section 5 provides discussions followed by conclusions and references.

2 Preliminaries

In the last decade, bipolar fuzzy concept lattice [39] and its properties in complex vague plane [45] are considered as one of the most potential tool. The reason is it given a mathematical way to represent the positive and negative side of bipolar information, independently when compared to vague set [40]. Recently, Prem Kumar Singh [45] addressed a issue in this regard that precise representation of bipolar information in the dynamic or complex data sets is computationally expensive task. It becomes more difficult when the user or expert wants to analyze and visualize them in using applied abstract algebra or graphical format. The reason is uncertainty and its existence in the bipolar attributes changes at each given phase of time [51, 52]. To resolve this issue, the current paper focuses on utilizing the properties of bipolar complex fuzzy graph, $\delta$-equality and complex granules as given below:

Definition 1

(Complex fuzzy set) [49, 50]: A complex fuzzy set Z can be defined over a universe of discourse U having a single fuzzy membership value at given phase of time. The complex-valued grade of membership of an element $z \in U$ can be characterized by $\mu _{Z}(z)$. The membership values that $\mu _{Z}(z)$ may receive all lie within the unit circle in the complex plane in the form $\mu _{Z} (z) =r_{z}(x) e^{iw_z(x)}$, where $i=\sqrt{-1}$, both $r_{Z}(z)$ and $w_Z(z)$ are real-valued and $r_{Z}(z)$$\in$ [0, 1]. The complex fuzzy set Z may be represented as the set of ordered pairs:

$$\begin{aligned} Z=\left\{ (z,\mu _{Z}(z)):z \in U \right\} = \left\{ (z, r_{Z}(z) e^{iw_{Z}(z)}): z \in U \right\} \end{aligned}$$

Example 1

Let us suppose, a company wants to manufacture a car ($x_1$) using the opinion of an expert ($y_1$). The expert gives 60% opinion that the production of car can be done in the third or fourth month of the given year. This complex linguistics words can be represented via properties of complex fuzzy set as follows: $x_1= 0.6e^{i0.7 \pi }/y_1$. Similarly, the opinion of more than two experts can be analyzed using the union and intersection of complex fuzzy sets $\mu _{z_1}(z)=r_{z_1}(z).e^{i arg_{z_1}(z)}$ and $\mu _{z_2}(z)=r_{z_2}(z).e^{i arg_{z_2}(z)}$ as given below [4]:

• $\mu _{z_{1} \cup z_{2}}= r_{z_{1} \cup z_{2}}(z).e^{i arg_{z_{1} \cup z_{2}}(z)} = max(r_{z_1}(z), r_{z_2}(z))$. $e^{i max(arg_{z_1}(z), arg_{z_2}(z))}$.

• $\mu _{z_{1} \cap z_{2}}= r_{z_{1} \cap z_{2}}(z).e^{i arg_{z_{1} \cap z_{2}}(z)} = min(r_{z_1}(z), r_{z_2}(z))$. $e^{i min(arg_{z_1}(z), arg_{z_2}(z))}$.

Example 2

Let us suppose, two experts provide their opinion for the production of car in the third or fourth months. One of the expert agreed 60 percent for the production, whereas the second expert agreed 40 percent in the given phase of time. In this case, the opinion of two experts can be analyzed using the intersection and union operator among the complex number: $z_1 (z)= 0.6e^{i0.7 \pi }/y_1$ and $z_2= 0.4e^{i0.7 \pi }/y_1$ as follows [21]:

• $\mu _{z_{1} \cup z_{2}}= 0.6e^{i0.7 \pi }/y_1$.

• $\mu _{z_{1} \cap z_{2}}= 0.4e^{i0.7 \pi }/y_1$.

It can be observed that the expert gives 60% opinion for the production of car in the third or fourth month which includes his/her 40% disagreement also. To represent this type of bipolar attributes, the calculus of bipolar fuzzy set and bipolar fuzzy graph can be utilized in the complex fuzzy set.

Definition 2

(Bipolar fuzzy set) [30]: A bipolar fuzzy set J in Z represents the positive and negative side of a given attributes, consequently. It is represented in the form $\textit{J}=\left\{ (z, \mu ^{\mathrm{P}}(z),\mu ^{\mathrm{N}}(z))|z\in Z \right\}$ where $\mu ^{\mathrm{P}}(z):\textit{Z}\rightarrow [0, 1]$ and $\mu ^{\mathrm{N}}(z):\textit{Z}\rightarrow [-1, 0]$ are mappings. The positive membership degree $\mu ^{\mathrm{P}}(z)$ is to denote the satisfaction degree of an element z to the property corresponding to a bipolar fuzzy set J, and the negative membership degree $\mu ^{\mathrm{N}}(z)$ is to denote the satisfaction degree of an element z to some implicit counter-property corresponding to a bipolar fuzzy set J. The following can be defined for any given two bipolar fuzzy sets $\textit{I}=(\mu ^{\mathrm{P}}_{I}, \mu ^{\mathrm{N}}_{I})$ and $\textit{J}=(\mu ^{\mathrm{P}}_{J}, \mu ^{\mathrm{N}}_{J})$:

• (1) $(\textit{I} \bigcap \textit{J})(\textit{z})= \hbox {min}(\mu ^{\mathrm{P}}_{I}(z),\mu ^{\mathrm{P}}_{J}(z))$, max$(\mu ^{\mathrm{N}}_{I}(z),\mu ^{\mathrm{N}}_{J}(z))$,

• (2) $(\textit{I} \bigcup \textit{J})(\textit{z})=\hbox {max}(\mu ^{\mathrm{P}}_{I}(z),\mu ^{\mathrm{P}}_{J}(z))$, min$(\mu ^{\mathrm{N}}_{I}(z),\mu ^{\mathrm{N}}_{J}(z))$.

Definition 3

(Bipolar complex fuzzy set) [5]: A bipolar complex fuzzy set Z can be defined over a universe of discourse U. The bipolar complex fuzzy membership of an element $z \in U$ can be characterized by positive $0 < r_{P_z} \le 1$, negative membership value $-1 \le r_{N_z} <0$, whereas the membership value 0 means the element is somehow irrelevant to the given context. It can be observed that the “amplitude” term in bipolar complex fuzzy set satisfies the property $0 \le r_{P_{z}}+r_{N_{z}} \le 2$, whereas the “phase” term can be characterized by $w^{r}_{P_z}$ and $2\pi -w^{r}_{N_z}$ in real-valued interval $(0, 2\pi ]$ and $i=\sqrt{-1}$. It can be represented as $Z=\left\{ (z, [r_{P_z}, r_{N_z} ] \times e^{w^{r}_{P_{z}}, 2\pi -w^{r}_{N_{z}}}:z \in U \right\}$. Similarly, the bipolar complex fuzzy relations and their partial ordering can be defined based on their positive and negative membership for their amplitude and phase terms, independently.

Example 3

Let us suppose, a company wants to manufacture a car ($x_1$) based on the expert opinion ($y_1$). The expert agreed 60% for the production of car in third or fourth month, whereas 30% disagreed in production of car in eight month. To represent, this type of complex fuzzy word this paper introduces the properties of bipolar complex fuzzy set as follows $x_1= (0.5e^{i0.7 \pi }, -0.4e^{i1.2 \pi })/y_1$. Now for the visualization the properties of bipolar complex fuzzy graph and its calculus are given below with a suitable example.

Definition 4

(Bipolar fuzzy graph) [3, 58]: A bipolar fuzzy graph $\textit{G}=(\textit{I}, \textit{J})$ is complete iff:

• $\mu ^{\mathrm{P}}_{J}(\left\{ v_{1}, v_{2}\right\} )= min(\mu ^{\mathrm{P}}_{I}(v_{1}), \mu ^{\mathrm{P}}_{I}(v_{2}))$ and,

• $\mu ^{\mathrm{N}}_{J}(\left\{ v_{1}, v_{2}\right\} ) =max(\mu ^{\mathrm{N}}_{I}(v_{1}), \mu ^{\mathrm{N}}_{I}(v_{2}))$

for all $v_{1}, v_{2} \in \textit{V}$ and $(v_{1}, v_{2}) \in V \times V$.

Example 4

Let us suppose, the expert $\textit{V}=(v_{1}, v_{2}, v_{3})$ provides a bipolar information and its fluctuation in context of production of cars. It can be shown mathematically using the calculus of bipolar fuzzy sets as shown in Table 2. Subsequently, their corresponding relationship can be shown through fuzzy set of edges $\textit{E}=(v_{1}v_{2}, v_{2}v_{3}, v_{3}v_{1})$ given in Table 3. This can be visualized using vertices and edges of a bipolar fuzzy complete graph as shown in Fig. 2.

Table 2 A bipolar fuzzy subset of V for Example 1

Table 3 A bipolar fuzzy subset of E for Example 1

Fig. 2

A bipolar fuzzy complete graph visualization for the fuzzy set shown in Tables 2 and 3

Definition 5

(Bipolar complex fuzzy graph) [54]: A bipolar complex fuzzy graph $G=(V, \mu _c, \rho _c)$ is a non-empty set in which the value of vertices $\mu _c: \textit{V} \rightarrow r_{c}(v).e^{i arg_{c}(v)}$ and edges $\rho _c: V \times V\rightarrow r_{c}(v\times v).e^{i arg_{c}(v\times v)}$ may receive the membership values within the unit circle of a complex argand plane. In this case, $r_{c}(v)$, $r_{c}(v \times v) \in [-1, 1]$ and $e^{i arg_{c}(v)}$, $e^{i arg_{c}(v\times v)}$ is periodic function. It means the vertices (V) and Edges (E) of a complex fuzzy graph can be characterized by an amplitude and phase term of defined complex fuzzy set such that:

$$\begin{aligned} r^{\mathrm{P}}_{c}(v_{i}\times v_{j}).e^{i arg^{\mathrm{P}}_{c}(v_{i} \times v_{j})} &\le min\left( r^{\mathrm{P}}_{c}(v_{i}), r_{c}(v_{i})\right) . e^{i min \left( arg^{\mathrm{P}}_{c}(v_{i}), arg_{c} (v_{j})\right) }.\\ r^{\mathrm{N}}_{c}(v_{i}\times v_{j}).e^{i arg^{\mathrm{N}}_{c}(v_{i} \times v_{j})} &\le min\left( r^{\mathrm{N}}_{c}(v_{i}), r_{c}(v_{i})\right) . e^{i min \left( arg^{\mathrm{N}}_{c}(v_{i}), arg_{c} (v_{j})\right) }. \end{aligned}$$

The given complex fuzzy graph is complete iff:

$$\begin{aligned} r_{c}(v_{i}\times v_{j}).e^{i arg_{c}(v_{i} \times v_{j})} = min\left( r_{c}(v_{i}), r_{c}(v_{i})\right) . e^{i min \left( arg_{c}(v_{i}), arg_{c} (v_{j})\right) }. \end{aligned}$$

Example 5

Let us combine Examples 3 and 4. This provides a complex bipolar information about the production of car as shown in Table 4. Similarly, the corresponding complex bipolar relationship among each of the car can be represented through a bipolar complex fuzzy set as shown in Table 5. These two contexts can be visualized in a compact format using the vertices V and edges E of a bipolar complex fuzzy graph as shown in Fig. 3. This representation is still unable to solve the problem of a company to analyze the preference of user for purchasing the car. To encounter this problem, a method is proposed in the next section using the properties of bipolar complex fuzzy graph and its $\delta$-granulation.

Table 4 A bipolar complex fuzzy context for the opinion of expert toward production of car

Table 5 A bipolar complex fuzzy edges exists among the car

Fig. 3

A bipolar complex fuzzy graph visualization of context shown in Tables 4 and 5

3 Proposed method

Knowledge discovery from a given complex data set having bipolar fuzzy attributes is a computationally expensive task [40, 45]. In this process, two technical issues arises one with their mathematical representation whereas the second one with their graphical visualization. To resolve this issue current paper proposes three methods to process the bipolar complex fuzzy context using the calculus of applied abstract algebra, bipolar complex fuzzy graphs and properties of $\delta$-granulation.

3.1 A proposed method for bipolar complex fuzzy concepts generation

This section introduces a method for extracting the interesting patterns in the given bipolar complex fuzzy context based on their objects and common attribute set using the amplitude and phase term of a defined complex fuzzy connected with Galois closure operator. The discovered bipolar complex fuzzy concepts and their hierarchical ordering are shown using the mathematical properties of bipolar complex fuzzy graph and its ordering. To achieve this goal, the expert or user can decide the acceptance of bipolar complex attributes based on his/her desired requirements to solve the particular problem. In this paper, the author has considered maximal acceptance of bipolar complex fuzzy attribute, i.e., 1.0 membership value for the positive amplitude and 0.0 for negative amplitude at given phase of time, i.e. ($2 \pi$, 0) where $2 \pi$ represents a periodic year. In general, the amplitude represents uncertainty hidden in the bipolar information, whereas the phase term represents fluctuations in the uncertainty at given phase of time. The amplitude and phase term can be decided by user or expert to measure the uncertainty in the bipolar complex data set as shown in Table 6. The proposed method in this paper aims at partially complete information about amplitude and phase term to generate the complex pattern as given below:

Table 6 Some potential classification of bipolar complex fuzzy data set based on amplitude and phase term

Let us suppose, a bipolar complex fuzzy context is defined on the universe of discourse U. The bipolar complex-valued grade of membership of an element $z \in U$ includes the positive $r_{P_z}$ and negative membership value $r_{N_z}$ for the amplitude term where $0 < r_{P_{z}}\le 1$$-1 \le r_{P_{z}} <0$. The amplitude with 0 membership values means it is not relevant to the corresponding property. The phase term is represented by $w^{r}_{P_z}$ and $w^{r}_{N_z}$ in real-valued interval $(0, 2\pi ]$ and $i=\sqrt{-1}$ which can be represented in composed form as given below: $Z=\left\{ (z, (r_{P_z}e^{w^{r}_{P_{z}}}, r_{N_z}) e^{w^{r}_{N_{z}}}):z \in U \right\}$. Similarly, the bipolar complex fuzzy relationship among objects and attributes of a given bipolar complex fuzzy context ${\mathbf {F}} = ({X}, {Y}, \tilde{R})$$\mu _{Z}(z)$ can be represented through positive and negative membership using the amplitude and phase terms. The membership values that $\mu _{Z}(z)$ may receive all lie within the unit circle in the complex plane in the form $\mu _{Z} (z) =r_{z}(x) e^{iw_z(x)}$, where $\hbox {i}=\sqrt{-1}$, both $r_{Z}(z)$ and $w_Z(z)$ are real-valued and $r_{Z}(z) \in [0,1]$.

Step 1.:

Let us choose any bipolar complex fuzzy set of attribute as given below:

$$\begin{aligned} (y_{j},(r_{P_{y_{j}}}e^{w^{r}_{P_{y_j}}}, r_{N_{y_{j}}}e^{w^{r}_{N_{y_j}}})). \end{aligned}$$

Now, a pattern can be investigated based on their amplitude and phase term of objects–attributes set.

Step 2.:

Decide the partial acceptance of chosen attributes based on its amplitude and phase term to investigate the user interest patterns from the given bipolar complex data set. In this case, generally a user tries to choose the maximal acceptance of attributes. It means the maximal positive membership value, i.e., 1.0 and minimal, i.e., 0.0 membership value for the amplitude term in the given phase of time. This provides positive regions (0.0, 1.0) for the amplitude and phase term to choose subset of attributes $(y_{j},(r_{P_{y_{j}}}e^{w^{r}_{P_{y_j}}}, r_{N_{y_{j}}}e^{w^{r}_{N_{y_j}}}))$. Similarly, ($0, 2 \pi$) can be considered as phase term for measuring minimal fluctuation $(e^{w^{r}_{P_{y_j}}}, e^{w^{r}_{N_{y_j}}})$.

Step 3.:

Now, the pattern can be discovered from the given bipolar complex fuzzy context using $\downarrow$ of Galois connection to find their maximal covering objects set based on their amplitude and phase term as given below:

$$\begin{aligned} (y_{j},(r_{P_{y_{j}}}e^{w^{r}_{P_{y_j}}}, r_{N_{y_{j}}}e^{w^{r}_{N_{y_j}}}))^{\downarrow }= (x_{i}, (r_{P_{x_{i}}}e^{w^{r}_{P_{x_i}}}, r_{N_{x_{i}}} e^{w^{r}_{N_{x_i}}})), \end{aligned}$$

for all $y_{j} \in$Y where $j=1,2,{\ldots}, m$ and $i=1,2,3,{\ldots},n$.

Step 4.:

The membership value of the obtained bipolar complex fuzzy set of objects can be computed for the amplitude and phase term as follows:

Amplitude:

min ($x_{i}, r_{P_{x_i}})$ for the positive membership value, and

max ($x_{i}, r_{N_{x_i}})$ for negative membership value.

Phase term:

min $(e^{w^{r}_{P_{x_i}}})$ for positive phase, and

max $(e^{w^{r}_{N_{x_i}}})$ for negative phase term.

Step 5.:

Now, apply the operator $\uparrow$ on these constituted objects set to find their maximal covering attributes based on amplitude and phase term as follows:

$$\begin{aligned} (x_{i},(r_{P_{x_{i}}}e^{w^{r}_{P_{x_i}}}, r_{N_{x_{i}}}e^{w^{r}_{N_{x_i}}}))^{\uparrow } = (y_{j},(r_{P_{y_{j}}}e^{w^{r}_{P_{y_j}}}, r_{N_{y_{j}}}e^{w^{r}_{N_{y_j}}})), \end{aligned}$$

for all $x_{i} \in$X where $i=1,2,{\ldots}, n$ and $j=1,2,3,{\ldots},m$.

Step 6.:

The membership value of the obtained attributes (new attributes) using $\uparrow$ on the constituted objects set can be computed as follows:

Amplitude:

min ($y_{j}, r_{P_{y_j}})$ for positive membership value and,

max ($y_{j}, r_{N_{y_j}})$ for negative membership value.

Phase term:

min $(e^{w^{r}_{P_{y_j}}})$ for positive phase term and,

max ($e^{w^{r}_{N_{y_j}}})$ for negative phase term.

Step 7.:

The investigated pair of bipolar complex fuzzy objects and their common attributes (A, B) using the Galois connection forms a pattern (i.e., concept) for knowledge processing tasks.

Step 8.:

In this way, all the bipolar complex fuzzy concepts can be generated.

Step 9.:

Draw the bipolar complex fuzzy concept lattice using the super and sub-concept ordering of distinct complex concepts.

Step 10.:

Discover the knowledge for empirical analysis. The above given steps are shown in a form of an algorithm as shown in Table 7.

Table 7 A proposed algorithm for generating the bipolar complex fuzzy concepts

Complexity: The proposed algorithm shown in Table 7 starts the analysis from the given subset of bipolar complex fuzzy set of attributes. In this case, the proposed method takes O($2^{m}$) computational time to find the subset and O(n) time to connect with its covering objects set based on amplitude and phase term. This takes overall O($n^{2}.2^{m}$) computational time to investigate the bipolar complex fuzzy concepts. One of the major advantages of the proposed method is that it provides complete information about positive and negative membership of the given bipolar information in $[-1, 1]$ at a given phase term [0, 2$\pi$]. This unique representation of the proposed method helps precisely in knowledge processing tasks when compared to other approaches.

3.2 A method for extracting bipolar $\delta$-equal complex fuzzy concepts

It can be observed that the method shown in Table 7 provides several bipolar complex fuzzy concepts for knowledge processing tasks in exponential computational time. In this case, extracting some of the interesting patterns based on chosen information granules is very rigorous. To shoot this problem, a method is proposed in this section using the calculus of complex granulation [66]. The granulation [36] is an umbrella term which includes many different mathematical ways to process the large and complex data via a small chunk of information [53]. This small chunk of information provides a simpler solution for the given problem with an improved descriptions [36]. Due to that, its calculus is applied in formal fuzzy context [29, 38], interval-valued context [46] and bipolar fuzzy context [40] for concept lattice reduction [41]. To decompose or navigate the concept lattice at user required information granulation [7, 42]. In this way, the properties of granulation help more approximately for precise analysis of knowledge processing tasks [57] using different multi-granulation [32]. These advantages of granular computing methods motivated to navigate the bipolar complex fuzzy concept lattice using the user required $\delta$-granulation. To achieve this goal, the current paper focuses on utilizing the different distance metric of complex fuzzy set [66] and its other available measurements [5, 20, 60]. The steps of the proposed method are given as follows:

Step 1.:

Let us suppose, a user or experts want a bipolar complex fuzzy concept $C_{1}=(A_{1}, B_{1})$ having similar amplitude and phase term for the knowledge processing tasks.

Step 2.:

To discover the similar information in the given complex data set, choose any bipolar complex fuzzy concepts investigated from the given context, i.e., $C_{2}=(A_{2}, B_{2})$.

Step 3.:

Now find their distance based on intent (or extent), i.e., bipolar complex fuzzy set of attributes, i.e., $(r_{P_{B_{1}}}e^{iarg {P_{B_1}}}, r_{N_{B_{1}}}e^{iarg_{N_{B_1}}})$$r_{B_{1}}(y).e^{i arg_{B_{1}}(y)}$ and $(r_{P_{B_{2}}}e^{iarg {P_{B_2}}}, r_{N_{B_{2}}}e^{iarg_{N_{B_2}}})$$r_{B_{2}}(y).e^{i arg_{B_{2}}(y)}$ as given below:

$$\begin{aligned} d(B_{1}, B_{2})= \hbox {max}(\hbox {sup}(|r_{P_{B_1}}- r_{P_{B_{2}}}|, |r_{N_{B_1}}- r_{N_{B_{2}}}|), \frac{1}{2\pi }\hbox { sup } (|arg_{P_{B_1}} -arg_{P_{B_{2}}}|, |arg_{N_{B_1}} -arg_{N_{B_{2}}}|)). \end{aligned}$$

Step 4.:

The total distance among two concepts is the sum of all the distances among each of the attributes in their intents, i.e., $\sum d(B_{1}, B_{2})$.

Step 5.:

Now, the average distance can be computed among the given concepts as follows:

$AV(d)= \frac{\sum d(B_{1}, B_{2})}{m}$ where m is total number of attributes in the given bipolar complex fuzzy concepts.

Step 6.:

Define a $\delta$-granulation for deciding the similarity level to refine the knowledge.

Step 7.:

The chosen bipolar complex fuzzy concept $C_2$ can be considered as $\delta$-granules to user required concept $C_1$ iff: $d(C_{1}, C_{2}) \le 1 -\delta$.

Step 8.:

In this way a user required $\delta$-granules bipolar complex fuzzy concepts can be selected from the investigates concepts.

Step 9.:

Write all the $\delta$-similar concepts based on their distance.

Step 10.:

Interpret the obtained concepts for the knowledge processing tasks.

Table 8 A proposed algorithm for extracting $\delta$-equal bipolar complex fuzzy concepts

Complexity: The proposed algorithm shown in Table 8 finds the $\delta$-equal bipolar complex fuzzy concepts based on user required information granules. To achieve this goal, the proposed method compares the amplitude and phase term for each of the given attributes (or objects) set which may take $m^2$ computational time for the amplitude and phase term, respectively. In this way, the overall time complexity of the proposed method can be O($m^{4}$). This reduced complexity is helpful for the experts in quick analysis of concept learning when compared to any other approaches.

3.3 A method for decomposition of bipolar complex fuzzy context

Analyzing dynamic or complex data set based on small chunk of variables is a major concern for data analysis and processing tasks [61, 71]. Recently, some of the researchers have paid attention toward processing the given fuzzy context based on user-defined granules [38]. The advantage of using the properties of granular computing is that it provides many ways to process the given context based on small chunk of information [32, 36]. Due to which, its calculus is utilized on processing the fuzzy context [29], interval-valued fuzzy context [22, 46], bipolar fuzzy context [40] for concept lattice reduction [9, 41, 70]. This paper focuses on decomposition of complex fuzzy matrix [67] for knowledge processing [31]. The motivation is to apply the properties of granular computing for navigating the bipolar complex fuzzy context to measure the changes in bipolar queries [65]. For this purpose, a method is proposed in Table 8 based on amplitude and phase term of given complex fuzzy relations. It can be observed that the proposed method provides many ways to a user or expert for processing the given complex fuzzy context based on obtained binary context.

Table 9 A proposed algorithm for decomposition of the bipolar complex fuzzy context

Complexity: The proposed algorithm shown in Table 9 provides a way to find many binary context based on user-defined complex fuzzy granules. To achieve this goal, the proposed method finds the entries in complex fuzzy matrix which have maximal amplitude and phase term from the chosen complex granules. In this case, the proposed method takes total $m \times n$ searches to find the chosen complex information granules. Hence, the total complexity taken by the proposed method cannot exceed the O($n.m^{2}$) or O($m.n^{2}$) computational time in case of n-number of objects and m-number of complex fuzzy attributes. In this way, the proposed method reduces the time complexity to process the complex fuzzy context when compared to the proposed method shown in Tables 7 and 8. To validate the extracted information, the knowledge discovered from the proposed method is compared with other two proposals in this paper.

4 Illustration

In this section, each of the proposed methods shown in Table 7, 8 and 9 is demonstrated one by one with an illustrative example.

4.1 Bipolar complex fuzzy concept lattice

Concept learning from data with bipolar information is a major issue for the researchers of current time [40, 71]. The reason is it exists at many time of our daily life from morning to evening [45]. Some of notable bipolarity and its existing conditions are as follows: (1) Coexistence, (2) Equilibrium, (3) Negation, (4) Linear and (5) Integrity [6, 68]. This paper focuses on negation condition to explore the bipolar complex fuzzy context and its fluctuation using the properties of bipolar complex fuzzy set. In the last decade some of the researchers tried to analyze the bipolar information through visualization in the graph [3, 11] and concept lattice [12, 39]. The problem arises when the uncertainty in bipolar information fluctuates at a given phase of time in the complex data sets [26, 27]. Modeling this type of bipolar information [25] and its compact visualization in the graph [34, 45] is computationally expensive tasks. To deal with this issues, current paper tries to model the bipolar information in complex data sets using the extensive properties of complex fuzzy set [45] and its different metric [60] to discover all the bipolar complex fuzzy pattern hidden in a given bipolar complex data set. To achieve this goal, Example 5 is extended as given below:

Example 6

To illustrate the proposed method Example 5 is extended in this section. Let us suppose the car company wants to analyze the production based on Cost ($y_1$), Fuel efficient ($y_2$), Speed ($y_3$), Beautiful ($y_4$), Luxurious $(y_5)$, Durability ($y_6$), Modern technology ($y_7$), maximum payload $(y_8)$, reliability ($y_{9}$) and maintenance charges ($y_{10}$) based on the user or experts feedback $\left\{ x_1, x_2, x_3, x_4\right\}$. It is observed that most of the users focused on four parameters cost ($y_1$), fuel efficient ($y_2$), speed ($y_3$), beautiful ($y_4$). Suppose an expert says that the car $x_1$ cost $y_1$ may fluctuate to 60 percent within three to four months, the fuel efficiency $y_2$ may fluctuate to 40% at each two to three month, Speed $y_3$ of car may fluctuate to 70% at each two to three month, whereas Beauty ($y_4$) of car may fluctuate to 60% within one month of its production. This complex expression given by expert can be written using the amplitude and phase term of a defined complex fuzzy set as follows:

• (i) $x_1 = 0.6e^{i 0.7\pi }/y_1 + 0.4e^{i 0.5\pi } / y_2 + 0.7e^{i 0.5\pi }/ y_3 + 0.6e^{i 0.2\pi }$$y_4$.

This paper considers a production year as 2$\pi$ for the phase term and its analysis. Similarly, the opinion of expert can be written for the remaining cars to analyze its production:

• (ii) $x_2 = 0.5e^{i 1.6\pi } /y_1 + 0.7e^{i 0.4\pi } /y_2 + 0.6e^{i 1.9\pi } /y_3 + 0.7e^{i 0.4\pi } /y_4$.

• (iii) $x_3 = 0.3e^{i 1.4 \pi } /y_1 + 0.4e^{i 1.3 \pi } /y_2 + 0.5e^{i 0.2\pi } /y_3 + 0.2e^{i 0.5 \pi }/y_4$.

• (iv) $x_4 = 0.4e^{i 0.7\pi }/y_1 + 0.6e^{i 0.5\pi }/y_2 + 0.5e^{i 1.2\pi }/y_3 + 0.4e^{i 0.2\pi } /y_4$.

This positive opinion of experts can be written in the form of a complex fuzzy matrix as shown in Table 10. The negative opinion of experts can be derived from this context through complement as shown in Table 11. Now, the problem arises with company in analysis of this positive and negative opinion of the expert for the production of suitable car. To encounter this problem, a method is proposed in Table 7 of this paper for finding all the complex fuzzy pattern hidden in the given context. To achieve this goal, the constituted bipolar fuzzy context for Tables 10 and 11 is shown in Table 12 where x represents the car, i.e., objects set, and y represents the attributes of the car, and entries represent bipolar complex fuzzy relationship among them. The complex fuzzy concepts from this context can be generated as given below:

Table 10 A positive opinion of experts about the given cars in form of complex fuzzy set

Table 11 A negative opinion of experts about the given cars in form of complex fuzzy set

Table 12 A bipolar complex fuzzy set representation of experts opinion about the given set of cars

Step (1) There are four attributes $\left\{ y_1, y_2, y_3, y_4\right\}$ in the given bipolar complex fuzzy context shown in Table 12 which provides following subsets to find the pattern in the data:

• 1. $\left\{ \oslash \right\}$,

• 2. $\left\{ (0.0, 1.0)e^{i (0, 2\pi )})/y_{1}\right\}$,

• 3. $\left\{ (0.0, 1.0)e^{i (0, 2\pi )})/y_{2}\right\}$,

• 4. $\left\{ (0.0, 1.0)e^{i (0, 2\pi )})/y_{3}\right\}$,

• 5. $\left\{ (0.0, 1.0)e^{i (0, 2\pi )})/y_{4}\right\}$,

• 6. $\left\{ (0.0, 1.0)e^{i (0, 2\pi )})/y_{1}+ 1.0e^{i2\pi }/y_{2}\right\}$,

• 7. $\left\{ (0.0, 1.0)e^{i (0, 2\pi )})/y_{1}+ (0.0, 1.0)e^{i (0, 2\pi )})/y_{3}\right\}$,

• 8. $\left\{ (0.0, 1.0)e^{i (0, 2\pi )})/y_{1}+ (0.0, 1.0)e^{i (0, 2\pi )})/y_{4}\right\}$,

• 9. $\left\{ (0.0, 1.0)e^{i (0, 2\pi )})/y_{2}+ (0.0, 1.0)e^{i (0, 2\pi )})/y_{3}\right\}$,

• 10. $\left\{ (0.0, 1.0)e^{i (0, 2\pi )})/y_{2}+ (0.0, 1.0)e^{i (0, 2\pi )})/y_{4}\right\}$,

• 11. $\left\{ (0.0, 1.0)e^{i (0, 2\pi )})/y_{3}+ (0.0, 1.0)e^{i (0, 2\pi )})/y_{4}\right\}$,

• 12. $\left\{ (0.0, 1.0)e^{i (0, 2\pi )})/y_{1}+ (0.0, 1.0)e^{i (0, 2\pi )})/y_{2}+ (0.0, 1.0)e^{i (0, 2\pi )})/y_{3}\right\}$,

• 13. $\left\{ (0.0, 1.0)e^{i (0, 2\pi )})/y_{1}+ (0.0, 1.0)e^{i (0, 2\pi )})/y_{2}+ (0.0, 1.0)e^{i (0, 2\pi )})/y_{4}\right\}$,

• 14. $\left\{ (0.0, 1.0)e^{i (0, 2\pi )})/y_{1}+ (0.0, 1.0)e^{i (0, 2\pi )})/y_{3}+ (0.0, 1.0)e^{i (0, 2\pi )})/y_{4}\right\}$,

• 15. $\left\{ (0.0, 1.0)e^{i (0, 2\pi )})/y_{2}+ (0.0, 1.0)e^{i (0, 2\pi )})/y_{3}+ (0.0, 1.0)e^{i (0, 2\pi )})/y_{4}\right\}$,

• 16. $\{(0.0, 1.0)e^{i (0, 2\pi )})/y_{1}+ (0.0, 1.0)e^{i (0, 2\pi )})/y_{2}+ (0.0, 1.0)e^{i (0, 2\pi )})/y_{3}+ (0.0, 1.0)e^{i (0, 2\pi )})/y_{4}\}$.

Now the complex fuzzy concepts can be generated using the above subsets from the context shown in Table 12. In this process, the proposed method considers maximal acceptance of complex fuzzy subsets of attributes in the given year, i.e. (0, 1)-amplitude and (0, 2$\pi$)-phase term.

Step (2) Apply the $\downarrow$ on the first subset $\left\{ \oslash \right\} ^\downarrow$ which provide following covering objects:

$$\begin{aligned} \{(0.7e^{i 0.5\pi }, -0.3e^{i 1.5\pi })/x_1+ (0.7e^{i 0.4\pi }, -0.3e^{i 1.6\pi })/x_2+ (0.5e^{i 0.2\pi }, -0.5e^{i 1.8\pi })/x_3+ (0.6e^{i 0.5\pi }, -0.4e^{i 1.5\pi }) /x_4 \}. \end{aligned}$$

Similarly, apply the $\uparrow$ on these constituted objects which provide following bipolar complex fuzzy set of attributes:

$$\begin{aligned} \{(0.3e^{i 1.4 \pi }, -0.7e^{i 0.6 \pi })/y_1+ (0.4e^{i 0.5\pi }, -0.6e^{i 1.5\pi })/y_2+ (0.5e^{i 0.2\pi }, -0.5e^{i 1.8\pi })/y_3+ (0.2e^{i 0.5 \pi }, -0.8e^{i 1.5 \pi })/y_4\}. \end{aligned}$$

In this way the first subset provides following bipolar complex fuzzy concepts from Table 12:

1.:

Extent: $\{(0.7e^{i 0.5\pi }, -0.3e^{i 1.5\pi })/x_1+ (0.7e^{i 0.4\pi }, -0.3e^{i 1.6\pi })/x_2+ (0.5e^{i 0.2\pi }, -0.5e^{i 1.8\pi })/x_3+ (0.6e^{i 0.5\pi }, -0.4e^{i 1.5\pi }) /x_4 \}$.

Intent: $\{(0.3e^{i 1.4 \pi }, -0.7e^{i 0.6 \pi })/y_1+ (0.4e^{i 0.5\pi }, -0.6e^{i 1.5\pi })/y_2+ (0.5e^{i 0.2\pi }, -0.5e^{i 1.8\pi })/y_3+ (0.2e^{i 0.5 \pi }, -0.8e^{i 1.5 \pi })/y_4\}$.

Step (3) Similarly, following concepts can be generated using other subsets of complex fuzzy attributes shown in step 1:

2.:

Extent: $\{(0.6e^{i 0.7\pi }, -0.4e^{i 1.3\pi })/x_1+ (0.5e^{i 1.6\pi }, -0.5e^{i 0.4\pi })/x_2+ (0.3e^{i 1.4\pi }, -0.7e^{i 0.6\pi })/x_3+ (0.4e^{i 0.7\pi }, -0.6e^{i 1.3\pi }) /x_4 \}$.

Intent: $\{(0.0, 1.0)e^{i (0, 2\pi )})/y_{1}+ (0.4e^{i 0.4\pi }, -0.3e^{i 0.7\pi })/y_2+ (1.0e^{i 0.2\pi }, -0.3e^{i 0.1\pi }/y_3+ (0.2e^{i 0.2 \pi }, -0.3e^{i 1.5 \pi })/y_4\}$.

3.:

Extent: $\{(0.4e^{i 0.5\pi }, -0.6e^{i 1.5\pi })/x_1+ (0.7e^{i 0.4\pi }, -0.3e^{i 1.6\pi })/x_2+ (0.4e^{i 1.3\pi }, -0.7e^{i 0.7\pi })/x_3+ (0.6e^{i 0.5\pi }, -0.4e^{i 1.5\pi }) /x_4 \}$.

Intent: $\{(0.3e^{i 0.7\pi }, -0.4e^{i 0.4\pi })/y_{1} +(0.0, 1.0)e^{i (0, 2\pi )})/y_{2}+ (0.5e^{i 0.2\pi }, -0.3e^{i 0.1\pi })/y_3+ (0.2e^{i 0.5 \pi }, -0.3e^{i 1.5 \pi })/y_4\}$.

4.:

Extent: $\{(0.7e^{i 0.5\pi }, -0.3e^{i 1.5\pi })/x_1+ (0.6e^{i 1.9\pi }, -0.4e^{i 0.1\pi })/x_2+ (0.5e^{i 0.2\pi }, -0.5e^{i 1.8\pi })/x_3+ (0.5e^{i 1.2\pi }, -0.5e^{i 0.8\pi }) /x_4 \}$.

Intent: $\{(0.3e^{i 0.7\pi }, -1.0e^{i 0.4\pi })/y_{1} +(0.4e^{i 0.4\pi }, -0.3e^{i 0.7\pi })/y_2 + (0.0, 1.0)e^{i (0, 2\pi )})/y_{3}+ (0.2e^{i 0.5 \pi }, -0.3e^{i 1.5 \pi })/y_4\}$.

5.:

Extent: $\{(0.6e^{i 0.2\pi }, -0.4e^{i 1.8\pi })/x_1+ (0.7e^{i 0.4\pi }, -0.3e^{i 1.6\pi })/x_2+ (0.2e^{i 0.5\pi }, -0.8e^{i 1.5\pi })/x_3+ (0.4e^{i 0.2\pi }, -0.6e^{i 1.8\pi }) /x_4 \}$.

Intent: $\{(0.3e^{i 0.7\pi }, -0.4e^{i 0.4\pi })/y_{1} +(0.4e^{i 0.4\pi }, -0.3e^{i 0.7\pi })/y_2 + (0.5e^{i 0.2\pi }, -0.3e^{i 0.1\pi })/y_3+ (0.0, 1.0)e^{i (0, 2\pi )})/y_{4}\}$.

6.:

Extent: $\{(0.4e^{i 0.5\pi }, -0.4e^{i 1.3\pi })/x_1+ (0.5e^{i 0.4\pi }, -0.3e^{i 0.4\pi })/x_2+ (0.3e^{i 1.3\pi }, -0.6e^{i 0.6\pi })/x_3+ (0.4e^{i 0.5\pi }, -0.4e^{i 1.3\pi }) /x_4 \}$.

Intent: $\{(0.0, 1.0)e^{i (0, 2\pi )})/y_{1}+(0.0, 1.0)e^{i (0, 2\pi )})/y_{2} + (1.0e^{i 0.2\pi }, -0.3e^{i 0.1\pi })/y_3+ (0.2e^{i 0.2 \pi }, -0.3e^{i 1.5 \pi })/y_4\}$.

7.:

Extent: $\{(0.6e^{i 0.5\pi }, -0.3e^{i 1.3\pi })/x_1+ (0.5e^{i 1.6\pi }, -0.4e^{i 0.1\pi })/x_2+ (0.3e^{i 0.2\pi }, -0.5e^{i 0.6\pi })/x_3+ (0.4e^{i 0.7\pi }, -0.5e^{i 0.8\pi }) /x_4 \}$.

Intent: $\{(0.0, 1.0)e^{i (0, 2\pi )})/y_{1}+ (0.4e^{i 0.4\pi }, -0.3e^{i 0.7\pi })/y_{2}+(0.0, 1.0)e^{i (0, 2\pi )})/y_{3}+ (0.2e^{i 0.2 \pi }, -0.3e^{i 1.5 \pi })/y_4\}$.

8.:

Extent: $\{(0.6e^{i 0.2\pi }, -0.4e^{i 1.3\pi })/x_1+ (0.5e^{i 0.4\pi }, -0.3e^{i 0.4\pi })/x_2+ (0.2e^{i 0.5\pi }, -0.7e^{i 0.6\pi })/x_3+ (0.4e^{i 0.2\pi }, -0.6e^{i 1.3\pi }) /x_4 \}$.

Intent: $\{(0.0, 1.0)e^{i (0, 2\pi )})/y_{1}+ (0.4e^{i 0.4\pi }, -0.3e^{i 0.7\pi })/y_{2}+ (0.5e^{i 0.2\pi }, -0.3e^{i 0.1\pi })/y_{3} + (0.0, 1.0)e^{i (0, 2\pi )})/y_{4}\}$.

9.:

Extent: $\{(0.4e^{i 0.5\pi }, -0.3e^{i 1.5\pi })/x_1+ (0.6e^{i 0.4\pi }, -0.3e^{i 0.1\pi })/x_2+ (0.4e^{i 0.2\pi }, -0.5e^{i 0.7\pi })/x_3+ (0.5e^{i 0.5\pi }, -0.4e^{i 0.8\pi }) /x_4 \}$.

Intent: $\{(0.3e^{i 0.7\pi }, -1.0e^{i 0.4\pi })/y_{1}+ (0.0, 1.0)e^{i (0, 2\pi )})/y_{2}+ (0.0, 1.0)e^{i (0, 2\pi )})/y_{3} + (0.2e^{i 0.2 \pi }, -1.0e^{i 1.5 \pi })/y_4\}$.

10.:

Extent: $\{(0.4e^{i 0.2\pi }, -0.4e^{i 1.5\pi })/x_1+ (0.7e^{i 0.4\pi }, -0.3e^{i 1.6\pi })/x_2+ (0.2e^{i 0.5\pi }, -0.8e^{i 0.7\pi })/x_3+ (0.4e^{i 0.2\pi }, -0.4e^{i 1.5\pi }) /x_4 \}$.

Intent: $\{(0.3e^{i 0.7\pi }, -0.4e^{i 0.4\pi })/y_{1}+ (0.0, 1.0)e^{i (0, 2\pi )})/y_{2}+ (0.5e^{i 0.2\pi }, -0.3e^{i 0.1\pi })/y_{3} + (0.0, 1.0)e^{i (0, 2\pi )})/y_{4}\}$.

11.:

Extent: $\{(0.6e^{i 0.2\pi }, -0.3e^{i 1.5\pi })/x_1+ (0.6e^{i 0.4\pi }, -0.3e^{i 0.1\pi })/x_2+ (0.2e^{i 0.2\pi }, -0.5e^{i 1.5\pi })/x_3+ (0.4e^{i 0.2\pi }, -0.5e^{i 0.8\pi }) /x_4 \}$.

Intent: $\{(0.3e^{i 0.7\pi }, -0.4e^{i 0.4\pi })/y_{1}+ (0.4e^{i 0.4\pi }, -0.3e^{i 0.7\pi })/y_{2}+ (0.0, 1.0)e^{i (0, 2\pi )})/y_{3}+ (0.0, 1.0)e^{i (0, 2\pi )})/y_{4}\}$.

12.:

Extent: $\{(0.4e^{i 0.5\pi }, -0.3e^{i 1.3\pi })/x_1+ (0.5e^{i 0.4\pi }, -0.3e^{i 0.1\pi })/x_2+ (0.3e^{i 0.2\pi }, -0.5e^{i 0.6\pi })/x_3+ (0.4e^{i 0.5\pi }, -1.0e^{i 0.2\pi }) /x_4 \}$.

Intent: $\{(0.0, 1.0)e^{i (0, 2\pi )})/y_{1}+ (0.0, 1.0)e^{i (0, 2\pi )})/y_{2}+ (0.0, 1.0)e^{i (0, 2\pi )})/y_{3}+ (0.2e^{i 0.5 \pi }, -0.3e^{i 1.5 \pi })/y_4\}$.

13.:

Extent: $\{(0.4e^{i 0.2\pi }, -0.4e^{i 1.3\pi })/x_1+ (0.5e^{i 0.4\pi }, -0.3e^{i 0.4\pi })/x_2+ (0.2e^{i 0.5\pi }, -0.6e^{i 0.6\pi })/x_3+ (0.4e^{i 0.2\pi }, -0.4e^{i 1.3\pi }) /x_4 \}$.

Intent: $\{(0.0, 1.0)e^{i (0, 2\pi )})/y_{1}+ (0.0, 1.0)e^{i (0, 2\pi )})/y_{2}+(1.0e^{i 0.2\pi }, -0.3e^{i 0.1\pi })/y_{3} +(0.0, 1.0)e^{i (0, 2\pi )})/y_{4}\}$.

14.:

Extent: $\{(0.6e^{i 0.2\pi }, -0.3e^{i 1.3\pi })/x_1+ (0.5e^{i 0.4\pi }, -0.3e^{i 0.1\pi })/x_2+ (0.2e^{i 0.2\pi }, -0.5e^{i 0.6\pi })/x_3+ (0.4e^{i 0.2\pi }, -0.5e^{i 0.8\pi }) /x_4 \}$.

Intent: $\{(0.0, 1.0)e^{i (0, 2\pi )})/y_{1}+(0.4e^{i 0.4\pi }, -1.0e^{i 0.7\pi })/y_{2}+(0.0, 1.0)e^{i (0, 2\pi )})/y_{3}+ (0.0, 1.0)e^{i (0, 2\pi )})/y_{4}\}$.

15.:

Extent: $\{(0.4e^{i 0.2\pi }, -0.3e^{i 1.5\pi })/x_1+ (0.6e^{i 0.4\pi }, -0.3e^{i 0.1\pi })/x_2+ (0.2e^{i 0.2\pi }, -0.5e^{i 0.7\pi })/x_3+ (0.4e^{i 0.2\pi }, -0.4e^{i 0.8\pi }) /x_4 \}$.

Intent: $\{ (0.3e^{i 0.7\pi }, -1.0e^{i 0.4\pi })/y_{1}+(0.0, 1.0)e^{i (0, 2\pi )})/y_{2}+ (0.0, 1.0)e^{i (0, 2\pi )})/y_{3}+ (0.0, 1.0)e^{i (0, 2\pi )})/y_{4}\}$.

16.:

Extent: $\{(0.4e^{i 0.2\pi }, -0.3e^{i 1.3\pi })/x_1+ (0.5e^{i 0.4\pi }, -0.3e^{i 0.1\pi })/x_2+ (0.2e^{i 0.2\pi }, -0.5e^{i 0.6\pi })/x_3+ (0.4e^{i 0.2\pi }, -0.4e^{i 0.8\pi }) /x_4 \}$.

Intent: $\{ (0.0, 1.0)e^{i (0, 2\pi )})/y_{1}+(0.0, 1.0)e^{i (0, 2\pi )})/y_{2}+ (0.0, 1.0)e^{i (0, 2\pi )})/y_{3}+ (0.0, 1.0)e^{i (0, 2\pi )})/y_{4}\}$.

Fig. 4

A bipolar complex fuzzy concept lattice for the context shown in Table 12

The bipolar complex fuzzy concept lattice for the above generated concepts is shown in Fig. 4 reflecting 16 as the most specialized and 1 as the more generalized concepts. The specialized concept 16 shows that the car $(0.5e^{i 0.4\pi }, -0.3e^{i 0.1\pi })/x_2$ will be considered as first preference due to its maximal acceptance whereas car $(0.4e^{i 0.2\pi }, -0.3e^{i 1.3\pi })/x_1$ as second preference. The generalized concept 1 shows that user preference of car is based on attribute $(0.5e^{i 0.2\pi }, -0.5e^{i 1.8\pi })/y_3$ and $(0.4e^{i 0.5\pi }, -0.6e^{i 1.5\pi })/y_2$ maximally. It means that the preference analysis of user is based on the concepts having maximal acceptance of these attributes, i.e., concepts number 4, 3, 9 will be useful due to their maximal acceptance of attributes $y_1$ and $y_2$. The concept number 4 represents that the car $(0.7e^{i 0.5\pi }, -0.3e^{i 1.5\pi })/x_1$ will be considered as the first preference whereas the car $(0.6e^{i 1.9\pi }, -0.4e^{i 0.1\pi })/x_2$ as the second preference due to their maximal acceptance of attribute $y_3$. Similarly, the concept number 3 represents that the car $(0.7e^{i 0.4\pi }, -0.3e^{i 1.6\pi })/x_2$ will be considered as the first preference whereas car $(0.6e^{i 0.5\pi }, -0.4e^{i 1.5\pi }) /x_4$ as the second preference due to their maximal acceptance of attribute $y_2$. The concept number 9 represents that the car $(0.6e^{i 0.4\pi }, -0.3e^{i 0.1\pi })/x_2$ will be considered as the first preference due to its maximal acceptance of attributes $y_{2}, y_{3}$. These extracted information together approves that the car $x_2$ will considered as the first preference of user while purchasing the car in the given year. This conclusion helps to the company and its production department to increase its profit in the given financial year. Similarly, other meaningful information can be extracted. To provide this extraction, the current paper takes exponential time. This becomes computationally expensive in case the user wants to analyze the concepts based on his/her requirements. To deal with this problem, another method is proposed in Table 8 of Sect. 3.2. This method provides a way to find all $\delta$-equal complex fuzzy concepts based on user required complex granules. In the next section illustration of this method is given for the given context. In addition, the analysis derived from both of the method is compared to validate the results.

4.2 $\delta$-equal bipolar complex fuzzy concepts

The previous section shows that the number of bipolar complex fuzzy concepts may be exponential based on small changes in amplitude and phase terms. In this case, finding some of the important or similar bipolar fuzzy concepts at user-defined granulation is an expensive task. To solve this problem, a method is proposed in Sect. 3.2. In this section, the proposed method is illustrated using the same context shown in Table 12. The problem is that the company wants to analyze the preferences of user to purchase the car using this bipolar complex fuzzy context. To solve this problem, current paper considers maximal acceptance of each attributes as given below:

$$\begin{aligned} C_1= \{ (0.0, 1.0)e^{i (0, 2\pi )})/y_{1}+(0.0, 1.0)e^{i (0, 2\pi )})/y_{2}+ (0.0, 1.0)e^{i (0, 2\pi )})/y_{3}+ (0.0, 1.0)e^{i (0, 2\pi )})/y_{4}\}. \end{aligned}$$

The distance of each car $x_1, x_2, x_3, x_4$ from the user preference is given in Tables 13, 14, 15, and 16, respectively.

Table 13 $\delta$-equal computation of car $x_1$ using proposed method shown in Table 8

Table 14 $\delta$-equal computation of car $x_2$ using proposed method shown in Table 8

Table 15 $\delta$-equal computation of car $x_3$ using proposed method shown in Table 8

Table 16 $\delta$-equal computation of car $x_4$ using proposed method shown in Table 8

Table 17 Selection of $\delta$-equal complex fuzzy concepts at user requirements

Table 17 represents the $\delta$-granulation of a given bipolar complex fuzzy concepts and shows that the car $x_2$ will be considered as first preference. This extracted information corresponds to its bipolar complex fuzzy concepts (shown in Fig. 3) with less computational time, i.e., O($m^{4}$) or O($n^{4}$). It should be noted that both of proposed methods have different advantages to solve the particular problem of a given bipolar complex fuzzy context. In the next section, another method is proposed to navigate the bipolar complex fuzzy concept lattice based on user-defined complex granules.

4.3 Decomposition of bipolar complex fuzzy concepts

In the last decade, many researchers tried to read the large or complex data set using the properties of granular computing. This provides a simpler way to solve the particular problem with an improved descriptions [36]. Due to which, recently some of the researchers tried to navigate the formal fuzzy context [29], interval-valued context [46] and bipolar fuzzy context [40] at different granulation [38, 53]. This paper focuses on decomposition of bipolar complex fuzzy context at user required $\delta$-granulation using the proposed method shown in Sect. 3.3. For this purpose, a context shown in Table 12 is considered. Now the problem is to decide a level of granulation to analyze this context. To achieve this goal, some of the potential levels are shown in Table 18. Table 19 shows the decomposition of context shown in Table 12 using the granulation level-4 i.$e. (0.5, -0.5)e^{ (0,2\pi )}$ for finding the interesting concepts.

Table 18 Some of the complex granules to analyze the preference in a given phase of time

Table 19 A $(0.5, -\,0.5)e^{ (0,2\pi )}$ decomposition of bipolar complex fuzzy context shown in Table 12

Fig. 5

A concept lattice generated from the context shown in Table 19

The concept lattice generated from Table 19 is shown in Fig. 5 which shows that $x_2$ is specialized concept and $x_3$ as generalized concepts. In this case the company can conclude that the user will prefer the $x_3$ as first preference. This analysis corresponds to its bipolar complex fuzzy concept lattice shown in Fig. 4 as well as its $\delta$-distance shown in Sect. 4.2. However, to achieve this goal the proposed method takes O($n.m^{2}$) or O($m.n^{2}$) time complexity. This is one of the major advantages of the proposed method toward reduction of time complexity.

5 Results and discussion

Recently, bipolar fuzzy graph representation of concept lattice [40] is studied for graphical analytics of data with bipolar fuzzy attributes. In this process, a major issue was addressed by Prem Kumar Singh [45] that the bipolar cognition of human changes at given phase of time. In this case, precise measurement of bipolarity exists in given data sets which is a major problem for multi-decision making process [47]. To deal with this problem, the current paper focused on measuring the changes in bipolar fuzzy attributes and its pattern at given phase of time. This research field has just got significant attention of the various researchers in the world [45, 60]. The bipolar complex fuzzy context and its navigation in the graph are still at infancy stage. To achieve this goal, a subset based method is proposed to discover all the bipolar complex fuzzy concepts and its graphical visualization as basis of further research. It is well known that this method takes exponential time to build the concept lattice [8]. To resolve this issue, two other methods are proposed for navigating the bipolar complex data set using the distance [5] and granular computing [66] metric. The motivation is to mathematically represent the bipolar complex data set [60] for its various applications [51] in knowledge processing task [52]. The objective is to extract some of the meaningful information from the given bipolar complex fuzzy context using its compact display in the concept lattice. To fulfill this need, following methods are proposed: (1) the first one focused on investigating all the bipolar complex fuzzy concepts and its graphical structure visualization in the complex fuzzy graph, (2) the second one focused on selecting some of the similar complex fuzzy concepts, whereas (3) the third one focused on decomposition or navigation of bipolar complex fuzzy concept lattice based on user required granulation. It can be observed that each of the proposed methods has some advantages and disadvantages which can be decided by experts to solve the complexity of the particular problem (as demonstrated in Sect. 4). For better understanding, a comparative analysis on them is shown in Table 20 based on several parameters. It can be observed that second and third methods are useful for analyzing the bipolar fuzzy context at user-defined granulation in less computational time. However, the first method provides more rigorous analysis and pattern in the given bipolar complex data set, whereas it takes exponential time.

Table 20 Comparison of proposed methods in this paper

Table 21 shows the comparison of some available approaches based on their novel ideas to understand the necessity of the proposed method. It can be observed that each of the method has its own mathematics and graphical analytics to deal with semantics of bipolar information. However, the proposed methods in this paper are distinct from any of the available approaches in complex fuzzy set as shown in Table 22. It represents some of the significance difference of the proposed methods when compared to any of the approaches in bipolar space. Some of the most interesting and noted differences are as follows:

• (1) The first proposed method provides a methods to visualize the bipolar complex fuzzy matrix in the concept lattice using their subset of attributes, i.e., O($n^{2}.2^{m}$) time complexity which can work as a basis for further research,

• (2) The second proposed method gives a way to choose some of the closest bipolar complex fuzzy pattern based on user required distance within O($m^{4}$) or O($n^{4}$) time complexity,

• (3) The third proposed method provides many ways to decompose or navigate the bipolar complex fuzzy concept lattice at user-defined granulation within O($n.m^{2}$) or O($m.n^{2}$) time complexity to solve the particular problem.

• (4) It can be observed that the proposed methods in this paper gives a compact display of bipolar complex fuzzy matrix in the graph which is more helpful in knowledge processing tasks when compared to any other approaches.

Table 21 Some benchmark work on data with bipolar and complex fuzzy attributes

Table 22 Comparison of the proposed methods by available approaches in bipolar space

Table 22 provides a comparative analysis between the proposed methods and other available approaches on various parameters. Among them the complex vague concept lattice introduced in [45] is considered as one of the most relevant. In this case, to validate the obtained results this method is considered in this paper. It can be observed that the obtained results from Example 6 by each of the proposed methods in this paper is concordant with the subset based method shown in [45]. However, the proposed method in this paper provides multiple ways to zoom in and zoom out the bipolar complex fuzzy contexts in less computational time when compared to subset based method [45] as illustrated in Sects. 4.2 and 4.3, respectively. It is one of the major advantages of the proposed method while handing the bipolar complex fuzzy contexts. However, to accomplish this tasks proposed method takes exponential time in its graphical structure visualization. Same time the proposed method is unable to measure the uncertainty in periodic data beyond the three-polar [46] or multi-polar space [1, 47]. To resolve these issues the author will focus on introducing other metrics of complex fuzzy sets [5, 60] or its composition [43] in near future using different metric like entropy [41].

6 Conclusions

This paper establishes that bipolar complex fuzzy matrix data set can be visualized in the compact format of concept lattice for knowledge processing tasks. In this process a major problem is addressed dealing with exponential size of bipolar complex fuzzy concept lattice. To resolve this issue two methods are used to navigate or decompose the bipolar complex fuzzy concept lattice within O($m.n^{2}$) and O($m.n^{2}$) time complexity, respectively. It is one of the significant output of the proposed method toward reducing the time complexity while dealing with bipolar periodic data set. However the proposed method is unable to measure the fluctuation in uncertainty beyond the three-polar or multi-polar space. To deal with this problem, the author will focus on introducing other metrics of bipolar complex fuzzy sets in the concept lattice theory.