1 Introduction

Due to the constant growing of electrical loads, the existed VAR sources became insufficient which resulted in gradual drop of the system nodes voltage. Thus, VAR resources shall be planned and disseminated throughout the power systems to meet the future demands and ensure system performance which is indicated as RPP.

The control variables of RPP problem are the generator bus voltages, the injected reactive power from existing, additional reactive power sources and tap ratio of transformers. It has been exceedingly solved by various classical optimization methods (COMs) such as linear, quadratic, mixed integer, nonlinear programming techniques and interior point algorithm. COMs have still been implemented and developed for solving the RPP. A NLP solver has been applied in [1], while LP-based IP method has been used in the second stage to minimize both the power losses and the generator’s reactive cost function for each zone by approximating it to a piecewise-linear function [2]. Both NLP and MINLP solver using GAMS software have also been implemented in [3]. Also, multiple stages of a stochastic nonlinear RPP model have been handled using MINLP [4]. A dual projected pseudoquasi-newton method has been utilized as a solution procedure in [5] for the capacitor placement patterns to reduce the transmission losses, while the investment cost for VAR sources has been handled as budget constraint. For the same purpose, IP method has been employed where the weak buses have been selected as candidates to install VAR sources based on L-index as a voltage stability index [6].

In the last two decades, the RPP has been widely solved using various meta-heuristic optimizers (MOs) such as GA [7, 8], real-coding GA (RGA) [9], modified nondominated sorted GA-II (MNSGA-II) [10], multi-objective fuzzy LP (MFLP) [11,12,13], covariance matrix adaptation evolution strategy (CMAES) [14], PSO [15,16,17], evolutionary programming [18, 19], seeker optimizer (SO) [20], differential search algorithm [21] and DE [22,23,24,25,26,27,28,29]. In [26], an improved model of it has been presented where the mutation factor changed dynamically instead of being constant. In [27, 28], the original DE strategy has been modified using a self-tuned mutation parameter. In [29], two DE versions have been applied to the RPP for minimizing the costs of operation and VAR investment. In spite of these multi-executed references of the DE algorithm to the RPP problem, the only applied DE strategy uses a randomly chosen base vector mutated by appending a scaled random difference vector [30]. In [31], a hybrid between DE algorithm and the ant system has been proposed to minimize the power losses, voltage deviation and operating costs. In [32], gravitational search algorithm has been utilized to enhance the voltage profile, the voltage stability or minimize the power losses. Furthermore, optimal planning of reactive power sources is proposed for enhancing the power systems under contingencies [33].

The RPP problem could be formulated with single or multiple objectives. However, modeling of each objective function has different formulations [34]. The searching for optimal solution is enhanced with unexpected locations for new VAR sources when all load buses are considered as candidate buses. However, the searching space, time-consuming, complexity and computational burden will be high, especially in large power systems [35]. Thus, the optimal placement of new reactive power sources may be considered a first step in RPP which have maximum effect on the technical and economical objects in power systems where different methods have been implemented to choose the candidate locations [36]. The reactive power dispatch problem is solved by several integrated strategies of backtracking search and ant colony algorithms in [37, 38], respectively.

In the optimization field, several novel optimizers of bioinspired meta-heuristic algorithms have been still proposed for solving global numerical optimization problems such as earthworm optimization algorithm [39], monarch butterfly optimization [40] and krill herd algorithm incorporated a mutation scheme [41]. In [42], a novel chaotic cuckoo search optimizer has been presented by emerging chaotic effect into cuckoo search technique. Another novel improved version of firefly algorithm has been applied for global numerical optimization [43]. In [44], a hybridized technique between krill herd and quantum PSO is presented for handling engineering optimization problems. In [45], the fruit fly optimization algorithm was developed for solving global optimization problem and applied for the optimal design of shape design of tubular linear synchronous motor.

COMs have been widely applied to solve the RPP for years [1,2,3,4,5,6] because they are fast and so they provide the capability to solve a high number of single optimizations in case of different loading conditions and contingencies. However, their main drawbacks are that they are usually based on some simplifications such as linear approximations of nonlinear functions and constraints or using their first and second differentiations. Another shortage of COMs is the weakness treatment of multi-objective nonlinear optimization problems [35]. They may trap in a local optimum result in divergences in solving RPP problems [19, 35]. Furthermore, they cannot handle the nondifferentiable factor in VAR sources installation function [8, 14].

This paper proposes two-step procedure on account of solving the reactive power planning (RPP). In the first step, the candidate VAR locations are selected based on the weakness voltage levels of the load buses with iterative VAR injection. In the second step, various DE strategies are proposed for handling the RPP. The proposed strategies are distinguished with diverse exploration and exploitation search capability which give diversified solutions. They are analyzed in a comparison with the computation intelligence techniques which have often been used to solve this problem. Else, the optimal tuning of the mutation and crossover parameters of the proposed algorithm is discussed. Its robustness indices are checked in comparison with the other optimization algorithms. Added to that, the proposed two-step procedure was assessed compared to single-step RPP procedure.

In [46], a two-step approach has been implemented analytically for voltage support by use of the design of experiment (DOE) method where the optimal locations of the VAR devices have been firstly identified and then a sizing process of those devices has been carried out. Compared to the proposed procedure, the DOE approach [44] has been tested on a small distribution networks (28-bus radial medium voltage network) based on some simplifications by reducing the number of control variables (only 2) in the second stage which may not be suitable for medium- and large-scale power systems. The DOE approach employed the screening approach over a small set of buses to identify the optimal VAR locations, and it did not discuss the effects of the others. However, the reduction of the losses and including the voltage profile has been utilized as objectives in the DOE approach, minimizing the costs of operation, and VAR investment is a considerable objective function in the planning problem [35] since it has great effects on the optimal decision.

However, the presented paper deals with one of the important optimization problems in power systems which has been taken into consideration in many previous published articles; it provides various contributions as follows:

  • Three types of objective function are investigated: (1) minimizing system power losses, (2) minimizing the costs of operation and VAR investment and (3) improving the voltage profile distribution.

  • Several strategies of differential algorithm are proposed, compared and examined on IEEE 30 bus and West Delta network (WDN) as a section in the Egyptian power system. The strategies robustness and consistency are compared to genetic algorithm (GA), particle swarm optimizer (PSO) and DE.

  • Also, application of the proposed method is carried out on large-scale power system of 354-bus test system.

  • The proposed two-step procedure using the proposed DE strategy is assessed compared to single-step RPP procedure.

  • Furthermore, its mutation and crossover scales are optimally specified. Simulation outcomes denote that the proposed DE strategy is excessively superior, more powerful and consistent than the other compared optimizers which indicate that the proposed strategy of DE algorithm can be very efficient to solve the RPP. The proposed strategies are proven as alternative solution strategies, especially for large-scale power systems.

  • Nevertheless, the evolution of the system considering the annual growth rate of peak load in the Egyptian system has been taken into consideration with different loading levels.

The rest sections of this paper are ordered as follows: Sect. 2 presents the RPP formulation. Section 3 introduces the suggested procedure for solving the RPP. The simulation results of the case studies are presented in Sect. 4, while the last section represents the conclusion of the work.

2 Formulation of the reactive power planning

Conventionally, the RPP objective is to minimize the investment cost of new VAR sources and the system operational cost [27,28,29].

2.1 Objectives

2.1.1 Minimizing the costs of energy loss and investment

The operational cost (OC) is related to the annual cost of energy losses, while the investment cost (IC) has two components, fixed installation part and variable purchase cost as follows:

$$\begin{aligned} {\text{Min}}\,F & = {\text{Min }}(O_{\text{C}} + I_{\text{C}} ) \\ {\text{where}},O_{\text{C}} & = H\sum\limits_{L = 1}^{{N_{\text{Load}} }} {d_{L} P_{\text{loss}}^{L} } {\text{and}}\,I_{\text{C}} = \sum\limits_{i = 1}^{{N_{c} }} {e_{i} + C_{{c_{i} }} |Q_{{c_{i} }}^{n} |} \\ \end{aligned}$$
(1)
$$P_{\text{loss}} = \sum\limits_{{i,j \in N_{b} }} {g_{ij} \left( {V_{i}^{2} + V_{j}^{2} - 2V_{i} V_{j} \cos \theta_{ij} } \right)}$$
(2)

where NLoad indicates the number of load levels; H indicates the energy cost in per unit; dL refers to each load duration (hours); \(P_{\text{Loss}}^{L}\) is the losses during each load period L; Nc is the reactive compensator buses; e refers to fixed installation cost of VAR sources; \(C_{{c_{i} }}\) is its corresponding purchase cost; \(Q_{\text{C}}^{n}\) refers to the reactive power output of the additional VAR source; Nb indicates the buses number; gij and θij indicate the branch conductance and voltage angle difference between buses i and j, respectively; V refers to the voltage magnitude.

2.1.2 Improvement in voltage profile

The enchantment of voltage profile can be formulated by minimizing the deviation of the load voltages (VD) at NPQ load buses as:

$${\text{Min}}\;{\text{VD}} = \left( {\sum\limits_{i = 1}^{{N_{PQ} }} {\left| {V_{i} - V_{i}^{\text{ref}} } \right|} } \right)$$
(3)

This objective could be simply included to the classical objective of the RPP using the weighted sum approach [35]:

$${\text{Min}}\;F = {\text{Min}}\,(O_{C} + I_{C} ) + \omega *VD$$
(4)

where ω is a suitable weight factor selected by the planner to give an importance to each one of the objective functions.

2.2 Equality and inequality constraints

The electric power networks have to maintain the equality constraints, which are denoted by the load flow balance equations and the inequality operational constraints of the operational variables. These constraints could be formulated as:

$$Q_{gi} - Q_{Li} + Q_{{_{Ci } }}^{n} + Q_{Ci} - V_{i} \sum\limits_{j = 1}^{{N_{b} }} {V_{j} (G_{ij} \sin \theta_{ij} - B_{ij} \cos \theta_{ij} )} = 0, \quad i = 1,2, \ldots N_{PQ}$$
(5)
$$P_{gi} - P_{Li} - V_{i} \sum\limits_{j = 1}^{{N_{b} }} {V_{j} (G_{ij} \cos \theta_{ij} + B_{ij} \sin \theta_{ij} )} = 0,\quad i = 1,2, \ldots N_{b} - {\text{slack}}$$
(6)
$$Q_{gi}^{\hbox{min} } \le Q_{gi} \le Q_{gi}^{\hbox{max} } ,\quad i = 1,2, \ldots N_{pv}$$
(7)
$$V_{i}^{\hbox{min} } \le V_{i} \le V_{i}^{\hbox{max} } ,\quad i = 1,2, \ldots N_{b}$$
(8)
$$T_{q}^{\hbox{min} } \le T_{q} \le T_{q}^{\hbox{max} } ,\quad q = 1,2, \ldots N_{t}$$
(9)
$$\left| {S_{L}^{\text{flow}} } \right| \le S_{L}^{\hbox{max} } ,\quad L = 1,2, \ldots N_{L}$$
(10)
$$0 \le Q_{Cx} \le Q_{Cx}^{\hbox{max} } , \ldots x = 1,2, \ldots N_{C}$$
(11)
$$0 \le Q_{Cj}^{n} \le Q_{Cj}^{\hbox{max} (n)} ,\quad j \in {\text{candidate}}\,{\text{buses}}$$
(12)
$$P_{s}^{\hbox{min} } \le P_{s} \le P_{s}^{\hbox{max} }$$
(13)

where Qg, QL and QC are the reactive power of generator, power demand and for the existing VAR injections, respectively; Gij and Bij are mutual conductance and susceptance between bus i and j, respectively; Pg and PL are the active power output of generator and the active demand, respectively; Npv is the voltage-controlled buses number; Tq and Nt are the tapping change of a transformer q and their total number, respectively; Sflow, Smax and NL refer to the MVA flow through the transmission lines, their maximum MVA rating and their total number, respectively. \(Q_{{c_{x} }}\) and \(Q_{c}^{\hbox{max} }\) are the existing VAR injection at bus x and its capacity; Ps, \(P_{s}^{\hbox{min} }\) and \(P_{s}^{\hbox{max} }\) are the slack active power, its minimum and maximum limits.

In the equality constraints, the tapping change of a transformer (Tk) is modeled inside the bus admittance matrix where the branches, phase shifters and transformers are formulated with the standard π model [47]. Each transmission line is modeled with branch admittance matrix (Ybr) as follows:

$$Y_{\text{br}} = \left[ {\begin{array}{*{20}l} {\left( {y_{k} + j\frac{{b_{k} }}{2}} \right)\frac{1}{{T_{k}^{2} }}} \hfill & { - y_{k} \frac{1}{{T_{k} e^{{ - j\theta_{\text{shift}} }} }}} \hfill \\ { - y_{k} \frac{1}{{T_{k} e^{{j\theta_{{{\text{shif}}t}} }} }}} \hfill & {y_{k} + j\frac{{b_{k} }}{2}} \hfill \\ \end{array} } \right]$$
(14)

where yk and bc are the series admittance and the total charging capacitance of the line; θshift is the phase shift angle of the transformer.

3 Proposed procedure for reactive power planning

3.1 Salient stages of DE algorithm

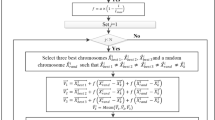
The major stages of DE algorithm are shown in Fig. 1. As shown, it begins with initialization step after identifying its parameters, the population size (NP) of the individuals (X) with D-dimensional variables and the maximum iterations number (Imax). The individuals in this initial population are randomly distributed over the D-dimensional search space. Then, the objective value of each individual is evaluated. After that, each individual is updated according to the mutation and crossover operations as follows:

$$X_{i,j} (I + 1) = \left\{ {\begin{array}{*{20}l} {V_{i,j} (I + 1) = X_{r1,j} (I) + F*(X_{r2,j} (I) - X_{r3,j} (I))} \hfill & {{\text{if}}\quad rand(0,1) < Cr} \hfill \\ {X_{i,j} (I)} \hfill & {\text{else}} \hfill \\ \end{array} } \right.$$
(15)

where Xr1, Xr2 and Xr3 are three randomly chosen and similar vectors, V is the mutant vector, F is the mutation constant in the range of [0.4–1], and Cr is the crossover probability within the range [0, 1]. Then, the corresponding objectives of the individuals are evaluated. Afterward, each new individual is compared with the previous one on the basis of the objective value and new population is selected in the next iteration which provides better solutions. These steps are reiterated until the maximum number of iterations is achieved or other stopping method is applied.

Fig. 1
figure 1

Flowchart of the proposed two-step procedure

Full size image

3.2 DE strategies

In Table 1, a summary is presented to define the basic difference of different DE strategies from the DE algorithm stated above. These strategies differ from each other based on mutation operator. Each one is addressed as DE/a/b/c. a indicates the kind of perturbation, b indicates the number of difference individuals, and c indicates the kind of crossover.

Table 1 Table summary of the different DE strategies [30]
Full size table

In Table 1, r1–r5 are random integers within the range [1, NP], and they are unlike the vector i. Xbest refers to the vector with best objective value. These DE strategies are worked with the binomial crossover operator as Eq. 15. Added to that, the individual is reinitialized randomly if any dimensional variable is exceeded its limits, while the dependent variables augmented as penalty terms inside the objective function as follows:

$$f = F + {\rm K}_{v} \sum\limits_{{Nv_{V} }} {\Delta V_{\text{Load}}^{2} } + {\rm K}_{q} \sum\limits_{{Nv_{Q} }} {\Delta Q_{g}^{2} } + {\rm K}_{Ps} \Delta P_{s}^{2} + {\rm K}_{Sf} \sum\limits_{{Nv_{Sf} }} {\Delta S_{f}^{2} }$$
(16)

where Kv, Kq, KPs, KSf are the penalty factors, NvV refers to the set of violated load voltages, NvQ refers to the set of violated reactive outputs of generators, NvSf refers to the overflow set of branches, ΔVLoad, ΔQg, ΔPs and ΔSf are defined as follows:

$$\Delta V_{\text{Load}} = \left\{ {\begin{array}{*{20}l} {V_{\text{Load}}^{\hbox{min} } - V_{\text{Load}} } \hfill & {\text{if}} \hfill & {V_{\text{Load}} < V_{\text{Load}}^{\hbox{min} } } \hfill \\ {V_{\text{Load}}^{\hbox{max} } - V_{\text{Load}} } \hfill & {\text{if}} \hfill & {V_{\text{Load}} > V_{\text{Load}}^{\hbox{max} } } \hfill \\ \end{array} } \right.$$
(17)
$$\Delta Q_{g} = \left\{ {\begin{array}{*{20}l} {Q_{g}^{\hbox{min} } - Q_{g} } \hfill & {\text{if}} \hfill & {Q_{g} < Q_{g}^{\hbox{min} } } \hfill \\ {Q_{g}^{\hbox{max} } - Q_{g} } \hfill & {\text{if}} \hfill & {Q_{g} > Q_{g}^{\hbox{max} } } \hfill \\ \end{array} } \right.$$
(18)
$$\Delta P_{s} = \left\{ {\begin{array}{*{20}l} {P_{s}^{\hbox{min} } - P_{s} } \hfill & {\text{if}} \hfill & {P_{s} < P_{s}^{\hbox{min} } } \hfill \\ {P_{s}^{\hbox{max} } - P_{s} } \hfill & {\text{if}} \hfill & {P_{s} > P_{s}^{\hbox{max} } } \hfill \\ \end{array} } \right.$$
(19)
$$\Delta S_{f} = S_{f}^{\hbox{max} } - S_{f} \quad {\text{if}}\quad S_{f} > S_{f}^{\hbox{max} }$$
(20)

where superscripts “min” and “max” indicate the minimum and maximum of a variable.

3.3 Proposed procedure

A two-step procedure is proposed to handle the RPP. An IM is introduced to place the additional sources of reactive power and their associated maximum sizes in the first step as depicted in Fig. 1. As shown, an AC load flow is performed and if there are any violations of load buses voltage out of the desired specified limits, the bus with the exceeded/lowest voltage is determined. Subsequently, an identified step size of a reactor/capacitor is added to that violated, respectively. An AC load flow is performed again and so until the voltage of the load buses is to be inside the desired identified limits. This IM is flexible that it can find different strategies for the RPP which is helpful for various trends to operate the power system. This can be achieved based on identifying the step size and the desired voltage limits. The output of this IM is the candidate VAR buses and their associated maximum sizes to be utilized in the second step. For this purpose, the compensation step and the minimum desired voltage are specified at 0.1 MVAR and 1 p.u., respectively, while Imax is 1000.

In the second step, various DE strategies are suggested for handling the RPP. To assess the single-step optimization procedure, only the second step of the two-step optimization procedure is employed to obtain the RPP solution considering all buses as candidate buses.

4 Applications

To estimate the performance and efficiency of the suggested strategies to handle the RPP, IEEE 30 bus and the WDN are used. These power systems are considered at their peak loads, while the active power outputs are predefined. Additional case study is applied for IEEE 354-bus test network [49, 50] as a large-scale power system.

For simulation studies, GA with crossover factor = 0.80 and mutation factor = 0.20 [7], DE/rand/1, and PSO with learning factors = 2, and inertia factors (ωmax = 0.90 and ωmin = 0.40) are utilized. The velocities related to PSO are reinitialized if they are violated 80% of their concerned particles. The DE’s crossover and mutation factors are 0.90 and 0.60, respectively. h, ei and Cci (Eq. 1) have been considered equal to 60 $/MWh, 1000 $ and 30,000 $/MVAR, respectively, as taken in most articles [8,9,10, 13, 15, 17, 18, 22, 26,27,28]. NP = 50 and Imax = 300. To show the capability of the proposed strategies, three cases have been studied as follows:

  • Case 1: Minimization of system power losses.

  • Case 2: Minimization of total costs of operation and VAR investment.

  • Case 3: Voltage profile improvement.

Added to that, a comparative to the single-step optimization procedure is presented. The effects of discrete model are discussed compared to the continuous model of decision variables.

4.1 Simulation results for IEEE 30-bus system

It comprises of 30 buses, 6 generators, 41 lines, 4 on-load tap change transformers and 2 existed VAR sources at buses 10 and 24. The generator, load voltages and tap changing of transformer are bounded between 0.90 and 1.10. The data of IEEE 30-bus system are taken from MATPOWER 5.0b1 [50].

In the first step, the proposed IM is carried out. Initially, the weakest location is node 30 with lower voltage of 0.901 p.u. Thus, node 30 is firstly chosen and injected by a VAR step (Qstep) equals 0.1 MVAR step (0.1 MVAR). Then, power flow program is run again and so until the voltage of the load buses is inside the desired identified limits. Finally, the VAR candidate buses are identified at 18, 19, 21, 23, 24, 26, 27, 29 and 30 and their associated maximum sizes are 0.70, 7.10, 7.70, 1.30, 11.40, 4.70, 2.10, 2.40 and 8.10 MVAR, respectively.

In the second step, GA, PSO and the proposed DE strategies are employed. Tables 2 and 3 show the corresponding results for Cases 1 and 2, respectively. In these tables, Psave and Csave denote the percentage saving of the power losses and the costs of energy loss and investment, respectively, with respect to the initial condition. For minimizing the power losses, DE 2 and DE 3 achieved the highest reduction of losses with 18.98 and 18.99%, respectively, where DE 1 and DE 4 attained reductions of 18.92 and 18.93%, respectively. DE 5, GA and PSO accomplished lower costs reduction of 18.28, 17.11 and 16.63, respectively.

Table 2 Simulation results of the compared approaches to minimize the losses for IEEE 30-bus test system (Case 1)
Full size table
Table 3 Simulation results of the compared approaches to minimize the costs of energy loss and investment for IEEE 30-bus test system (Case 2)
Full size table

For minimizing the costs of energy loss and investment (Case 2), the obtained results by the proposed strategies of DE algorithm are compared with other MOs such as evolutionary programming (EP) [18, 19], DE [22, 29], improved GA [8], RGA [22], improved GA [8] and CMAES [14] and COMs such as Broyden–Fletcher–Goldfarb–Shanno method [19], sequential QP (SQP) [14] and LP [8] in Table 3. From this comparison, the greatest costs reduction is acquired using DE 2 and DE 3 except the best solution that got hold of DE [29], but it is an infeasible solution that the reactive outputs at generator buses 2 and 4 were −25.25 and 85.6914 MVAR, respectively, which exceeded their corresponding limits [49]. Thus, the proposed algorithm outperforms these MOs and COMs which establish the efficacy of the proposed RPP methodology.

Figure 2 shows the convergence features of the GA, PSO and the proposed DE strategies for both studied cases. It was explicated that DE 2 and DE 3 converged to the minimum objective at the 80th and 70th iteration for both Cases 1 and 2, respectively. DE 1 and DE 4 continued through the 300 iterations and remained minimizing the objective, while PSO got stuck in a local minimum at the 100th and 80th iteration for both Cases 1 and 2, respectively.

Fig. 2
figure 2

Convergence characteristics of the compared approaches for solving the RPP (IEEE 30-bus test system). a Case 1, b Case 2

Full size image

4.2 Results for West Delta network

This second network comprises of 52 bus, 8 generator buses and 108 lines [12] as illustrated in Fig. 3. The generator and load voltages are bounded between 0.94 and 1.06, while tap changing of transformer is between 0.9 and 1.1 p.u. Its nominal power demand equals (889.75 + j539.98) MVA. The voltages at load buses 18 and 20–22 exceeded their minimum value.

Fig. 3
figure 3

Single-line diagram of West Delta network [12]

Full size image

Similarly, the VAR candidate buses are identified at 18, 19, 20, 21, 24, 32, 33, 35, 49 and 50 and their associated maximum sizes are 13.70, 0.80, 24.20, 12.70, 0.10, 10, 26.50, 3, 4.20 and 4.70 MVAR, respectively. Tables 4 and 5 represent the simulation results of GA, PSO and DE strategies for Cases 1 and 2, respectively.

Table 4 Simulation results of the compared approaches to minimize the losses for WDN (Case 1)
Full size table
Table 5 Simulation results of the compared approaches to minimize the costs of energy loss and investment for WDN (Case 2)
Full size table

For Case 1, the minimal power losses are obtained by the proposed strategies DE 2 and DE 3 with 23.29% (from 19.015 to 14.586 MW) and 23.25% (from 19.015 to 14.5936 MW), respectively. Very close results are accomplished by DE 1 and DE 4 which attained real losses reduction of 23.13 and 23.09%, respectively. DE 5, PSO and GA achieved less reduction of 21.93, 20.93 and 20.63%, respectively.

For Case 2, the greatest costs reduction is attained by DE 3 and DE 2 that procured reduction of 15.41 and 15.408%, respectively. On the other hand, DE 1 and DE 4 acquired a relative reduction of 15.406 and 15.403%, respectively, while DE 5 and PSO achieved a significant reduction of 15.09 and 14.491%, respectively.

In this case, although the IM is developed to identify the candidate buses, DE 2 and DE 3 acquired the minimal losses without installing additional VAR sources compared to other algorithms for IEEE 30 bus and WDN. This illustrates that the optimal solutions found by proposed DE 2 and DE 3 strategies are achieved via controlling the generator voltages and tap settings of transformers which are sufficient for Case 2.

Figure 4 displays the convergence features of GA, PSO and DE strategies which illustrates that DE 2 and DE 3 converge to the minimum objective at the 70th and 50th iteration for Cases 1 and 2, respectively. DE 1, DE 4 and DE 5 take the 300 iterations still reducing the objective. PSO achieves similar costs reduction; nevertheless, it remains stuck within a local minimum, while GA’s solution remains unchanged for a large number of iterations and obtained higher objective value compared to other approaches.

Fig. 4
figure 4

Convergence characteristics of the compared approaches for solving the RPP (WDN). a Case 1, b Case 2

Full size image

Taking into consideration the evolution of the system, the annual growth rate of peak load in the Egyptian system is approximately 6–8% in the previous year’s [51]. For this purpose, the proposed algorithm (DE 3) is performed for three-year plan with 8% annual growth rate of peak load. Therefore, the active and reactive power loads are increased with 8% and consequently the active power generations are increased with the same percentage. As planning for installing fixed capacitors, their values are considered optimally fixed for the three-year plan, while the generator bus voltages and tap ratio of transformers are optimally varied with increasing loading level. Table 6 shows the corresponding results for handling Case 1 which demonstrates the capability of the proposed algorithm to obtain savings of 22.93, 22.87 and 24.06% for the consecutive three years, respectively. Besides that, the initial voltages are improved and become within the acceptable range since the minimum voltages after installing the new VAR sources are recorded at bus 44 with values of 1.001, 0.996 and 1.000 p.u. for the consecutive 3 years, respectively.

Table 6 Simulation results for WDN considering its evolution by 8% annual growth rate (Case 1)
Full size table

To discuss the sensitivity of the optimal sizing and positioning of the VAR sources for the system state changes due to different loading situations and considering the annual growth rate of these loading, three loading conditions are taken into account as shown in Table 7.

Table 7 RPP for different loading conditions and their duration for WDN
Full size table

Table 8 shows the related simulation results for WDN for handling Case 1. Great savings are obtained using the proposed algorithm at each loading situation through the consecutive three years, respectively. This proves the ability of the proposed procedure to deal with different loading situations and considering the annual growth rate which provide some kind of dynamic optimization on a larger set of system states instead of implementing on a static state of the power system.

Table 8 Simulation results considering different loading conditions and their growth rate for WDN (Case 1)
Full size table

4.3 Statistical analysis

In evolutionary optimization, the definition of robustness is not uniform, but a solution is commonly defined as a robust solution if it behaves well with slightly diverse situations [52]. Therefore, the algorithm that provided a robust solution against diverse initial populations due to the randomization existed in evolutionary optimization is considered a robust one.

For this purpose, the compared approaches have been applied for 30 runs in each case study and the statistics of best, worst, mean, standard deviation (Std) and standard error (Ste) are listed in Table 9 to solve the RPP for IEEE 30-bus test system and WDN. Added to that, the convergence frequency in obtaining the minimal losses or total costs is recorded in Tables 10 and 11 for IEEE 30 bus and WDN, respectively. Moreover, statistical tests to judge the significance of the obtained results by the proposed method are carried out in Table 12 using a parametric test of paired t test and a nonparametric test of Wilcoxon’s rank-sum test [53].

Table 9 Comparison between the compared approaches to solve the RPP
Full size table
Table 10 Convergence frequency of IEEE 30-bus test system
Full size table
Table 11 Convergence frequency of WDN
Full size table
Table 12 t test and Wilcoxon’s rank-sum test between DE 3 and the compared approaches to solve the RPP (Case 2) for IEEE 30-bus test system
Full size table

From Tables 9, 10, 11 and 12, it can be concluded as follows:

  • The proposed DE 3 strategy is the most robust algorithm to handle the RPP compared to the other approaches.

  • DE 3 achieved trivial Std and Ste in Case 1 with 1.12E−04 and 2.05E−05 for IEEE 30-bus system and 3.23E−04 and 5.89E−05 for the WDN system, respectively. This states the high potency of the proposed DE 3 strategy to find the global minimal regardless of the initial guesses.

  • Moreover, its superiority over the compared approaches is proven as the DE 3 strategy always obtains mean objective very near to its obtained best and lower than the achieved best of the other compared approaches except DE 2 best of WDN for Case 2.

  • The proposed DE 3 strategy is the most consistent algorithm to solve the RPP problem as its success rates compassed always perfect (100%) in the first range for both systems and higher than other methods. The nearest results are obtained by DE 2 strategy with perfect success rates (100%) in the first range for both systems in Case 2.

  • In Table 12, z values are evaluated based on Wilcoxon’s rank-sum test so it does not be varied except for DE 2–DE 3. This is due to that the obtained worst objective value using the proposed DE 3 is better than the best values of GA, PSO, DE 1, DE 4 and DE 5.

  • Table 12 indicates that the p values of the statistical t test and Wilcoxon’s rank-sum test prove that the obtained results of the proposed method do not happen by chance in spite of the stochastic nature of the meta-heuristic algorithms. Thus, the significance of the obtained results is verified.

4.4 Parametric analysis of the suggested DE 3 strategy for solving the RPP

In DE algorithm, two parameters have to be adjusted which are Cr and F. The parameter Cr controls the number of individuals to be varied in each iteration, while F guides the directions and the appended values through the search space. In this section, a parametric analysis of the suggested DE 3 strategy by varying Cr and F on the costs of energy loss and investment is studied. Figures 5 and 6 show the effects of simultaneous varying Cr and F of the proposed DE 3 strategy for Cases 1 and 2 for IEEE 30 and WDN, respectively. For minimizing the power losses, the optimal ranges of F and Cr, as illustrated in Fig. 5, are inside [0.50, 0.90] and [0.10, 0.90] for IEEE 30-bus system and WDN. For Case 2, the optimal ranges of F and Cr, as illustrated in Fig. 6, are inside [0.50, 0.80] and [0.30, 0.90] for IEEE 30-bus system, respectively. Similarly for the WDN, the optimal ranges of F and Cr are inside [0.50, 0.80] and [0.10, 0.90], respectively. By crossing these ranges, F and Cr of the proposed DE 3 strategy are recommended to be within [0.50, 0.80] and [0.30, 0.90], respectively, to handle the RPP for any electrical network.

Fig. 5
figure 5

Effects of varying Cr and F of DE 3 strategy on the power losses (Case 1). a IEEE 30-bus test system. b WDN

Full size image
Fig. 6
figure 6

Effects of varying Cr and F of DE 3 strategy on the total costs (Case 2). a IEEE 30-bus test system. b WDN

Full size image

4.5 Solving the RPP problem including the voltage profile improvement for IEEE 30-bus system

For solving the RPP problem including the voltage profile improvement (Case 3), a robust DE variant (DE/best/1) is employed with high ability of global exploitation and fast convergence as proven previously. Table 13 tabulates the related results for IEEE 30-bus system where the system voltage profile obtained by the proposed DE variant in all studied cases compared to the initial case is shown in Fig. 7. It is evident that the voltage profile distribution is quite improved compared to the initial case and Cases 1–2.

Table 13 Application of the proposed DE 3 strategy for voltage profile improvement for IEEE 30-bus test system
Full size table
Fig. 7
figure 7

Voltage profile using the DE strategy for all studied cases with IEEE 30-bus test system

Full size image

4.6 Application of the proposed DE 3 strategy for the RPP on large-scale power system

In order to show the efficiency of the proposed approach in solving the RPP for large-scale systems, a 354-bus system [49, 50] is used. The concerned results using the proposed DE 3 strategy to minimize the total costs of both of system operational losses and VAR investment are illustrated in Table 14. As shown, 57 new VAR sources are installed where the power losses are 390.82 MW. All the bus voltages are within its bounds where the minimum voltage is 0.95597 p.u. at bus 1091 and the maximum one is 1.04359 p.u. at bus 2041.

Table 14 Application of the proposed DE 3 strategy to solve the RPP for 354-bus test system (Case 2)
Full size table

4.7 Application of single-step optimization procedure

The RPP problem could be solved using single- step optimization procedure for searching for the optimal solution considering all load buses as candidate VAR locations. Table 15 shows a comparison between single-step and two-step procedures using DE 3 to minimize the total costs for IEEE 30-bus system. As shown the two-step procedure achieved more reduction of the total costs (16.57%) where the single-step method recorded 12.93%. Thus, it is evident that reducing the search space with the effective VAR buses enables the optimization algorithm to find the optimal results.

Table 15 Comparison between single-step optimization and proposed two-step procedure using DE 3 to minimize the total costs for IEEE 30-bus system
Full size table

4.8 Effect of discretizing the noncontinuous variables

DE algorithm can be adjusted to handle the discrete variables using a rounding operator which is involved after the initialization and mutation process [51]. Thus, the capacitor banks step is chosen of 0.1 MVAR, while 32 steps of on-load tap changers are considered as it generally provides ±10% automatic adjustment regulation [54]. Table 16 shows the discretization effect compared to its continuous considerations for Cases 1 and 2. As shown, the optimal settings and results are slightly changed and so the optimization process is influenced to a small degree.

Table 16 Optimal RPP solution considering discrete and continuous variables for Cases 1 and 2
Full size table

5 Conclusions

This paper proposes a two-step procedure for handling the reactive power planning problem. The candidate locations for installing new VAR sources and their concerned maximum sizes are identified by employing a proposed iterative method. In addition, various strategies of DE algorithm are suggested as solution tools in order to solve the RPP optimization problem. A performance comparison with GA, PSO and the original DE variant DE/rand/1 is discussed and examined on the IEEE 30 bus and the WDN. An additional application to large-scale power system is implemented on IEEE 354-bus system.

The minimization of the power losses is considered as single objective function, while the minimization of both the VAR investment and costs of energy loss is handled using the mathematical sum approach. Additional technical objective is considered to enhance the voltage profile. Although DE/rand/1 strategy is exceedingly utilized for solving the RPP optimization that accomplished greater reduction in energy losses and costs, DE/rand to best/1 and DE/best/1 are able to obtain lesser values, but also they demonstrate more speedy convergence and the load voltages are ameliorated. While DE/rand/1 and DE/best/2 achieved a comparable reduction percentage of the power losses or the total costs, they recorded further reduction with more generations. DE and its strategies have better performance over PSO and GA. Also, robustness statistics are evaluated of the optimizing algorithms in solving the RPP problem which indicates that the suggested DE/best/1 strategy is frequently superior and highly robust than the other compared approaches for minimizing the real power losses or the total costs and its ability to converge near optimally values distinguishes DE/best/1 strategy over others. Though the DE/rand/2 performance shows worse than the other DE strategies, it is generally more robust and consistent than PSO and GA, especially for minimizing the total costs of VAR investment and operational power losses. Furthermore, a parametric analysis of the crossover and mutation factors related to the suggested DE/best/1 algorithm is studied and their optimal tuning is declared.

The proposed optimization procedure was checked for discrete and continuous models of decision variables. A comparative study between the single-step optimization procedure and the proposed two-step procedure was studied.