A simple yet effective grouping evolutionary strategy (GES) algorithm for scheduling parallel machines

Abstract

As a novel evolutionary technique, grouping evolutionary strategy (GES) has proved efficient and effective on grouping problems in which the task is to partition a set of items into disjoint groups. This paper investigates the first application of GES to tackle the parallel-machines scheduling problem as a well-known grouping problem in which machines can be treated as groups and jobs can be regarded as the items and the task is to partition a set of jobs into disjoint groups (and process all jobs in a same group by the same machines) to minimize makespan (C _max) criterion. The main features of GES algorithm that make it different from the typical evolutionary approaches proposed for the parallel-machines scheduling problem, lie in exploiting a suitable chromosomal representation and a well-designed mutation operator that works with the set of jobs assigned to each machine instead of jobs isolatedly, and uses a two-phase procedure to generate the new schedules more effectively. In addition, we hybridized GES with an efficient local search heuristic and proved that it has an important descent property. To verify the performance of our proposed algorithm, comparisons are made using available methodologies in the literature. Computational results signify that the proposed approach is fast and competitive in providing high quality results.

1 Introduction

Identical parallel-machines scheduling problem is formally described as follows: a set of n independent jobs, $J = \{ J_{1} ,J_{2} , \ldots ,J_{n} \}$, each having an associated processing time p _i , i = 1,…,n, are to be processed on a set $M = \{ M_{1} ,M_{2} , \ldots ,M_{m} \}$ of $m$ machines. Each job should be processed on one of the machines, and preemption is not allowed during processing. The subset of jobs assigned to machine M _j in a schedule is denoted by $S_{{M_{j} }}$. Furthermore, each machine can only process one job at a time, and there is no precedence relation between jobs. The paper investigates the problem of optimal assignment of jobs to machines in order to minimize the completion time of the last job, i.e., the makespan criterion (C _max). Due to the fact that this problem is NP-hard [13], it is unlikely to obtain the optimal schedule through polynomial time-bounded algorithms. Over the years extensive research has been carried out to develop efficient approaches for the problem. As a member of a family of algorithms known as list-scheduling algorithms, the well-known longest processing time (LPT) rule of Graham [15] has received considerable attention because it tends to perform better in terms of performance guarantee. According to LPT rule, we start with an empty schedule and iteratively assign a nonscheduled job with the longest processing time of all remaining jobs to the machine with currently minimal workload. This method generates a schedule that is no worse than $\frac{{C_{\hbox{max} } (LPT)}}{{C_{\hbox{max} }^{*} }} \le \frac{4}{3} - \frac{1}{3m}$, where C _max(LPT) denotes the makespan obtained based on the LPT rule. Coffman et al. [7] developed an algorithm entitled MULTIFIT that establishes the relation between bin-packing and makespan problems. Although the performance guarantee for MULTIFIT algorithm is tighter than that of LPT algorithm, it does not imply that MULTIFIT algorithm will yield better makespan than LPT algorithm for any given problem.

Min and Cheng [37] proposed a modified version of genetic algorithm based on machine code for minimizing the makespan on identical machines scheduling problem. Fatemi Ghomi and Jolai Ghazvini [12] developed an algorithm for the problem that is also applicable to schedule nonidentical parallel-machines and also the case of non-simultaneous job arrivals. With the idea that the variance of the last job’s completion times on each machine in the presence of job preemption is zero, they tried to minimize sum of ranges of machine finish times instead of the makespan. Gupta and Ruiz-Torres [16] proposed a heuristic named LISTFIT based on bin-packing problem and list scheduling that its worst-case performance bound is no worse than that of MULTIFIT algorithm. Their computational results demonstrated that the heuristic outperforms the LPT algorithm, the MULTIFIT algorithm and the COMBINE methods of Lee and Massey [33] that utilizes the output of LPT algorithm as an initial solution for the MULTIFIT algorithm. Mokotoff [38] proposed an exact cutting plane algorithm for minimizing the makespan in parallel-machines scheduling problem. Dell’Amico and Martello [8] provided a note, demonstrating that their proposed exact algorithm in Dell’Amico and Martello [9] outperforms the exact algorithm proposed by Mokotoff [38] in terms of time and quality of solutions for minimizing makespan. Gharbi and Haouari [14] proposed an approximate decomposition algorithm that calls for iteratively solving a sequence of two-machine problems. Iori and Martello [28] reviewed, evaluated and compared scatter search algorithms for two generalizations of identical parallel machine scheduling problem. Mellouli et al. [36] studied the identical parallel-machines scheduling problem with a planned maintenance period on each machine with the objective of minimizing the sum of completion times. They proposed three exact methods to solve the problem at hand: mixed integer–linear programming method, a dynamic programming-based method and a branch-and-bound method. Lee et al. [34] presented a simulated annealing (SA) algorithm for the problem and evaluated its performance in comparison to LISTFIT and PI algorithms. They asserted that their approach outperforms comparator algorithms for all experimental frameworks. Husseinzadeh Kashan et al. [23] introduced a local search heuristic for enhancing the performance of the genetic algorithm for scheduling parallel batch-processing machines. Husseinzadeh Kashan and Karimi [20] proposed a discrete particle swarm optimization algorithm and its hybridized version for the problem of scheduling identical parallel machines and evaluated their performance in comparison to the SA algorithm. Jing et al. [29] proposed a discrete harmony search (HS) algorithm to solve identical parallel-machines scheduling problem. They embedded a local search in the HS algorithm to enhance its performance. Balin [3] proposed a new crossover operator and a new optimality criterion to adapt genetic algorithm to nonidentical machines scheduling problem. A dynamic harmony search (DHS) was presented by Chen et al. [6] to minimize makespan in a parallel-machines system. The proposed algorithm was also incorporated with a VNS-based local search to improve its effectiveness. Bathrinath et al. [4] proposed a genetic algorithm and a simulated annealing algorithm to solve parallel-machines scheduling problem with the objectives of simultaneous minimization of makespan and number of tardy jobs. The effectiveness of the proposed algorithms was compared by solving benchmark problems. Zarandi and Kayvanfar [42] compared NSGAII and NRGA in scheduling identical parallel-machines considering controllability of processing times and just-in-time (JIT) philosophy, when minimizing total cost and makespan. Hashemian et al. [17] considered the existence of non-availability periods of machines in their proposed model and utilized constructive and backtracking heuristics to solve the model. Bathrinath et al. [5] compared a VNS-based heuristic with an SA-based heuristic in parallel-machines scheduling problem with weighted objective function of makespan and number of tardy jobs. Kuruvilla and Paletta [32] proposed and evaluated a heuristic algorithm combining LPT and MULTIFIT heuristics to solve the parallel-machines scheduling problem with the objective of minimizing the makespan. Diana et al. [10] proposed an immune-inspired algorithm incorporating greedy randomized adaptive search (GRASP) and variable neighborhood descent (VND) algorithms for minimizing the makespan and compared it to three recently proposed genetic algorithm (GA), ant colony optimization (ACO) algorithm and simulated annealing (SA) algorithm for the parallel-machines scheduling problem. Pakzad-Moghaddam [39] presented a mixed integer programming formulation with the objectives of makespan and total hiring cost for the problem and proposed a particle swarm optimization (PSO) algorithm, embedded with Lévy flights in replacement for random walks, to solve large-sized problems. Kowalczyk and Leus [31] proposed a branch-and-price algorithm for the problem of parallel-machines scheduling with conflicts by combining bin-packing, scheduling and graph coloring methods. They demonstrated the algorithm’s efficiency for problems with and without conflicting jobs. Low and Wu [35] proposed two ACO algorithms for the problem where parallel machines are unrelated and each job can be processed on a subset of machines and compared the algorithms on different sizes of the problem.

2 Motivation

Since its introduction in 1994, grouping genetic algorithm (GGA) is the most predominant algorithm for grouping problems in which the aim is to group a set of items in disjoint groups [11]. Many NP-hard combinatorial optimization problems such as graph coloring problem, bin-packing problem, batch-processing machine scheduling problem, line-balancing problem, timetabling problem, parallel-machines scheduling problem, cell formation problem and pickup and delivery problem are well-used examples of grouping problems.

Grouping evolution strategies (GES) which has been introduced in 2009 [24] is one of the latest evolutionary algorithms introduced just for grouping problems. GES is the grouping version of the well-known evolution strategies which have been heavily modified to suit the structure of grouping problems. GES has been successfully applied to bin-packing problem [24, 26], batch-processing machine scheduling problem [26] and fuzzy data clustering [25]. Results showed that on bin-packing problem and batch-processing machine scheduling problem, GGA is inferior to GES. Moreover, the design of GES gives it some advantages over GGA.

Given the fact that parallel-machines scheduling problem is a grouping problem, the aim of this paper is to propose an algorithm which takes into account the structural knowledge along with the grouping nature of this problem. The aim of the paper is to propose a GES-based algorithm for the parallel-machines scheduling problem. We believe that it is not straightforward to propose a GGA with its classic operators for this problem, because:

• When the structure of the grouping problem is in such a way that the number of groups is very small, the use of GGA to form the groups may be irrelevant. Short chromosome lengths imposed by the very small number of groups make the GGA operators less applicable. For example, in the parallel-machines scheduling problem with two machines, every solution (i.e., grouping of jobs) has inevitably two groups. Here, the GGA crossover and mutation operators as those described in [11] are completely inapplicable because there are only three positions for crossing sections (given that the operators work with groups). The performance of GGA is worsened due to the fact that the chromosomes become proportionally shorter in length, thus placing possible limitations on the search capabilities of the GGA operators. Hopefully, GES does not suffer from this deficiency.

• While we can simply apply GES on grouping problems with nonidentical groups, this is not true for GGA. Let us consider the parallel-machines scheduling problem with nonidentical machines and the objective of minimizing makespan. Since the classic GGA performs under whole-group sharing rationale, it cannot be applied to this scheduling problem. However, under subgroup sharing rationale which is followed by GES, there is no matter whether groups are identical or nonidentical [26] .

The remainder of the paper is organized as follows. In the following section, we give a brief introduction to evolution strategies (ES) and its source of inspiration. The grouping version of evolution strategies (GES) for parallel-machines scheduling problems is presented in Sect. 4. Section 5 generalizes the proposed methodology for job scheduling on nonidentical machines. Section 6 investigates the effectiveness of GES through computational experiments. The paper will be concluded in Sect. 7.

3 An introduction to evolution strategies (ES)

According to Darwin’s theory about the development of species, the most important characteristics of the evolution process are inheritance, mutation and selection. Only these properties of the biological evolution had to be translated into mathematical terms to develop a most general and effective optimization technique. Evolution strategies (ES) of Rechenberg [40] are methods which translate the properties of the Darwinian biological evolution into mathematical terms to formulate a general optimization method.

The family of evolution strategies is introduced by $(\mu /\rho ^{ + } ,\lambda ) - ES$ notation. All members operate with a population $\varPi^{t}$ of μ candidate solutions. In every time step t, a set $Q^{t}$ of µ candidate solutions is generated from $\varPi^{t}$ by employing the recombination and mutation operators. The symbol ρ indicates the number of parental solutions involved in the generation of every single offspring solution. When $\rho = 1$, it will be omitted. To form $\varPi^{t + 1}$, the candidate solutions are selected on the basis of their fitness. Selection which is the goal-directed element of the evolutionary search is represented by “$\begin{array}{*{20}c} \begin{subarray}{l} + \\ \, , \end{subarray} \\ \end{array}$”, denoting the two mutually exclusive selection types. Employing “+” selection, the $\mu$ best of $\mu + \lambda$ candidates in $\varPi^{t} \cup Q^{t}$ are selected to form $\varPi^{t + 1}$. Using “,” selection, it is the $\mu$ best of $\lambda$ candidate solutions in $Q^{t}$ that form $\varPi^{t + 1}$.

Generation of an offspring candidate solution is supported via mutation. Mutation consists of adding to centroid, a random noise drawn from an isotropic normal distribution. For a population $\varPi^{t} = \left\{ {X_{1}^{t} ,X_{2}^{t} , \ldots ,X_{\mu }^{t} } \right\}$ in which $X_{k}^{t} = \left( {x_{k1}^{t} ,x_{k2}^{t} , \ldots ,x_{\text{km}}^{t} } \right)$ $\forall k = 1, \ldots ,\mu$, is a m-dimensional solution vector in a continuous search space, the set $Q^{t}$ will be composed of offspring candidate solutions $Y_{i}^{t} = \left( {y_{i1}^{t} ,y_{i2}^{t} , \ldots ,y_{im}^{t} } \right)$ $\forall i = 1, \ldots ,\lambda$, where:

$$y_{ij}^{t} = x_{{i_{k} j}}^{t} + z_{j}^{t} , \, \forall j = 1, \ldots ,m, \, \forall i = 1, \ldots ,\lambda$$

(1)

with $z_{j}^{t} = \sigma^{t} N_{j} (0,1)$, where $N_{j} (0,1)$ is a random number associated to dimension j generated from a standardized normal distribution (i.e., the variation source). The positive scalar variable $\sigma^{t} ,$ which is learnt during the evolution process is referred to as the strategy parameter or mutation strength and determines the expected distance (variation) of an offspring candidate solution from the centroid of its parents. Index i _k is drawn with replacement from the set $\{ 1, \ldots ,\mu \}$.

Too low values for mutation strength can slow down the progress while too high values may lead to divergence. Therefore, the mutation strength $\sigma^{t}$ should be adapted in course of search. The first mutation strength adaptation strategy was proposed for $(1 + 1) - ES$ by Rechenberg [41]. Rechenberg’s recommendation was to monitor success probabilities (i.e., the probability that an offspring candidate solution is superior to its parent) by averaging over the number of time steps. The mutation strength is increased if the observed estimate of the success probability is >0.2 and it is decreased if the success probability is <0.2. This mutation strength adaptation scheme is known as 1/5-success rule.

4 Grouping evolution strategies (GES) for parallel-machines scheduling problems

In this section our aim is to propose an efficient and effective algorithm for parallel-machines scheduling problem based on GES. The algorithm employs an encoding scheme which is called assignments encoding. A particular mutation operator is used which works based on the composition of job assignments to machines and not the jobs isolatedly. The mutation strategy is implemented via a two-phase heuristic.

4.1 The structure of assignments encoding

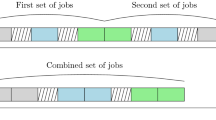
When optimizing a continuous function by ES, each solution is represented by a chromosome of length m of real numbers (m is the problem dimension, i.e., the number of variables). Similarly, for parallel-machines scheduling problem, one can represent a solution as a structure whose length is equal to the number of machines. The content of each element in the structure demonstrate all jobs assigned to the relevant machine (see the left part in Fig. 1). Figure 1 demonstrates a schedule for a five jobs and two machines problem. Any feasible schedule must inevitably partition the set of jobs into two groups. In the exampled schedule, jobs J ₁, J ₂ and J ₅ are assigned to machine M ₁ and form the first group. Jobs J ₃, J ₄ are assigned to machine M ₂ which forms the second group. Thus, machines play the role of groups. Adopting the structure of assignments encoding, GES works with the sets {J ₁, J ₂, J ₅}, {J ₃, J ₄} as a chromosomal structure with only two genes (one gene for each group). Hence, the GES operations are designed based on the set/groups of jobs rather than jobs isolatedly. The rationale is that in a grouping problem like parallel-machines scheduling problem, these are the job groups that are the innate building blocks of the problem, which can convey information on the expected quality of the schedule they are part of, and not the particular positions of any one job on its own.

Fig. 1

Structure of assignments encoding

4.2 The GES mutation operator

Given the structure of assignments encoding, the aim of this section is to adapt mutation (1) to obtain the one which works with the whole jobs assigned to a machine instead of scalars. Reconstructing (1) to work with whole jobs assigned to a machine, the major idea would be to use suitable operators as a substitute for arithmetic operators. In particular, we substitute “–” operator with a dissimilarity measure. Similar to “–” operator that measures the magnitude of difference between two scalars, a dissimilarity measure quantifies the distance/dissimilarity between two pattern of job assignments. We use “Distance” to address such a measure.

Let A and $A^{\prime}$ be two different subset of jobs assigned to a given machine (say M ₁) in two different solutions of the problem, respectively. Let $|A|$ denotes the cardinality of A. Measuring the degree of similarity between A and $A^{\prime}$ helps us to determine how similar the assignments are to each other or how far apart they are from each other. One of the most commonly used measures to determine the degree of dissimilarity between A and $A^{\prime}$ is the Jaccard’s coefficient of dissimilarity defined as follows:

$$Dis \text{(}A,A^{\prime}\text{)} = 1 - \frac{{|A \cap A^{\prime}|}}{{|A \cup A^{\prime}|}} \,$$

(2)

It is obvious that $0 \le Dis \, \text{(}A,A^{\prime}\text{)} \le \text{1}$. To develop an analogous Gaussian mutation let us reshape (1) in form of $y_{ij}^{t} - x_{{i_{k} j}}^{t} = z_{j}^{t}$ and substitute “–” by “Dis.” The Gaussian mutation can be introduced as follows:

$$Dis\text{(}y_{ij}^{t} ,x_{{i_{k} j}}^{t} ) \approx z_{j}^{t}$$

(3)

where $j = 1, \ldots ,m, \, i = 1, \ldots ,\lambda$ and $z_{j}^{t} = \sigma^{t} N_{j} (0,1)$. While in (1), $x_{{i_{k} j}}^{t}$ and $y_{ij}^{t}$ are scalars, in (3) $x_{{i_{k} j}}^{t}$ and $y_{ij}^{t}$ denote the subset of jobs assigned to a machine M _j in schedules $X_{{i_{k} }}^{t}$ and $Y_{i}^{t}$, respectively.

In (4), “≈” implies “approximately equal to.” We use this symbol instead of “=” because it may not be possible to form the new group of jobs $(y_{ij}^{t} )$ assigned to machine M _j in the offspring schedule $Y_{i}^{t}$ in such a way that the value of $Dis\text{(}y_{ij}^{t} ,x_{{i_{k} j}}^{t} )$ becomes exactly equal to $z_{j}^{t}$.

In place of Jaccard coefficient of dissimilarity, it may be used the Kulczynski’s coefficient or Sørensen–Dices’ coefficient. However, presumably the most widely used dissimilarity measure is the Jaccard’s coefficient of dissimilarity. Moreover, both of these measures can perform equivalent to the Jaccard’s coefficient of dissimilarity in our case.

The component $z_{j}^{t}$ makes use of variations depending on the selected mutation strength $\sigma^{t}$. If $\sigma^{t}$ increases, there is more likelihood for $z_{j}^{t}$ to go far away beyond the origin, and if $\sigma^{t}$ decreases, there is more likelihood for $z_{j}^{t}$ to fall around the origin. While $z_{j}^{t}$ can get any arbitrary real value unrestricted in sign (i.e., $z_{j}^{t} \in \left( { - \infty ,\infty } \right)$), the range of $Dis\text{(}.,.)$ is only real values in [0,1]. This is evidence that $z_{j}^{t}$ may not be an appropriate source of variation in GES.

Hence, we should devise a different type of random variable as an alternative source of variations. It is highly desirable that the candidate random variable take values just in [0,1]. Moreover, similar to the normal PDF in which changing the value of scale parameter $\sigma^{t}$ changes the chance of getting a random normal value in a specific range, it is of interest to devise a flexible PDF that provides different chances for getting a value in a specific sub-range in [0,1] by means of the PDF input parameter(s). The Beta distribution which is denoted by $B(\alpha ,\beta )$ is an intended PDF which is defined in [0,1] and models skew quite well. We are therefore at the point to use Beta distribution in place of isotropic normal distribution typically used in ES, as the source of variation in GES. Beta distribution is flexible in shape and takes all forms of J shape, humped shape and U shape. But we need only J-shaped and humped-shaped Beta distributions. We can achieve these shapes via considering the value of one of the shape parameters, say β, greater than one. From (3), we finally obtain the mutation relation in GES as follows:

$$Dis \, \text{(}y_{ij}^{t} ,x_{{i_{k} j}}^{t} \text{)} \approx Beta{}_{j}(\alpha^{t} ,\beta )\text{, }\forall j = 1, \ldots ,m , { }\forall i = 1, \ldots ,\lambda , \, i_{k} \in \{ 1, \ldots ,\mu \}$$

(4)

where $Beta{}_{j}(\alpha^{t} ,\beta )$ is a Beta random number associated to machine M _j with shape parameters $\alpha^{t}$ and $\beta$. Keeping the value of $\beta$ constant, we can only consider $\alpha^{t}$ as the endogenous strategy parameter just similar to the classic ES.

4.3 Generating a new schedule

Generation of the new schedule in GES requires two phases. The first phase, the inheritance phase, includes deciding about those parts of the parent that the offspring inherits. During this phase a number of jobs may remain unassigned. Therefore, the second phase is the post-assignment or reinsertion phase in which the unassigned jobs are reassigned to machines.

The inheritance phase is handled through (4). By (4) it is implied that the construction of the new assignment of jobs to machine M _j (i.e., $y_{ij}^{t}$) in the offspring schedule during the inheritance phase should be in such a way that its degree of dissimilarity with its counterpart in the parent schedule (i.e., $x_{{i_{k} j}}^{t}$) be around the value $Beta{}_{j}(\alpha^{t} ,\beta )$. This means that the degree of similarity between two assignments should be approximately equal to $1 - Beta_{j} (\alpha^{t} ,\beta ).$. In other words, we seek the number of jobs shared between $x_{{i_{k} j}}^{t}$ and $y_{ij}^{t}$ (i.e.,$n_{id}^{t} = |y_{ij}^{t} \cap x_{{i_{k} j}}^{t} |$) in such a way that the value of $Dis \, \text{(}y_{ij}^{t} ,x_{{i_{k} j}}^{t} \text{)}$ gets close to the value of $Beta{}_{j}(\alpha^{t} ,\beta )$. Indeed, the shared jobs between $x_{{i_{k} j}}^{t}$ and $y_{ij}^{t}$ are one of the parts that offspring schedule $Y_{i}^{t}$ inherits from parent schedule $X_{{i_{k} }}^{t}$. During the inheritance phase, it is reasonable to assume that $y_{ij}^{t} \subseteq x_{{i_{k} j}}^{t}$ (because, $y_{ij}^{t}$ can inherit up to all jobs of $x_{{i_{k} j}}^{t}$). Starting from (4) we have:

$$Dis \, (y_{ij}^{t} ,x_{{i_{k} j}}^{t} ) = 1 - \frac{{n_{ij}^{t} }}{{|x_{{i_{k} j}}^{t} |}} \approx Beta{}_{j}(\alpha^{t} ,\beta ) \Rightarrow n_{ij}^{t} = \left\lfloor {(1 - Beta{}_{j}(\alpha^{t} ,\beta ))|x_{{i_{k} j}}^{t} |} \right\rfloor$$

(5)

The following algorithm describes the steps of generating the offspring schedule $Y_{i}^{t}$ based on the parent schedule $X_{{i_{k} }}^{t}$.

Problem-dependent heuristics can be employed at both steps of NSG algorithm. We select jobs in Step 1 of NSG algorithm in a greedy fashion based on their attribute values (e.g., processing times). Selecting $n_{ij}^{t}$ number of jobs with the longest processing times helps us to use the structural knowledge of the problem to generate possibly better schedules. Such a selection strategy is inspired from LPT rule. However, we apply such a selection strategy in a probabilistic manner. That is, everytime for each machine M _j a random number is drawn from [0, 1]. If it becomes less than 0.1, selection is done based on job processing times. Otherwise, job selection is done randomly.

At step 2 of NSG algorithm any constructive heuristic can be employed. Again we use LPT rule to iteratively assign a remaining job with the longest processing time of all remaining jobs, which has not been selected during Step 1, to the machine with currently minimal workload.

The selection process in GES is deterministic and similar to what was explained in Sect. 3. Similar to the notation employed to introduce the multi-member ES, we can use $(\mu \begin{array}{*{20}c} \begin{subarray}{l} + \\ \, , \end{subarray} \\ \end{array} \lambda ) - GES$ notation to introduce the family of GES algorithms. In a manner similar to “1/5-success rule,” starting from $\alpha^{0}$, we increase $\alpha^{t}$ if the observed estimate of the success probability exceeds a given threshold ($P_{s}$) during G successive iterations and decrease it if the success probability gets below the threshold.

To improve the performance of GES, we hybridize it with a pairwise interchange algorithm (PIA). For a given schedule, PIA tries to reduce the makespan through suitable pairwise interchange of jobs between machines. The structure of PIA is in such a way that it either terminates without any improvement gained over the input schedule or it will decrease the makespan value of the input schedule via job interchanges. In this way it performs as a descent algorithm.

In our implementation, we use $(1 + 1) - GES$ family which is elaborated as follows. Since $\mu = 1$, we omit index i _k .

5 Generalization to the case of nonidentical machines

In the nonidentical parallel-machines scheduling problem there are a set of n independent jobs $J = \{ J_{1} ,J_{2} , \ldots ,J_{n} \}$, each of which has to be scheduled on one of m machines $M_{1} ,M_{2} , \ldots ,M_{m}$. A job can run on only one machine at a time, and a machine can process at most one job at a time. If a job J _i is processed on a machine M _j , it will take a positive processing time p _ij . When $p_{ij} = p_{i}$ for all i and j, the machines have the same speed and the machines are called identical. When $p_{ij} = {{p_{i} } \mathord{\left/ {\vphantom {{p_{i} } {s_{j} }}} \right. \kern-0pt} {s_{j} }}$ where p _i is the processing time of job J _i and s _j is the speed of machine M _j , then the machines are called uniform. If the p _ij ’s are arbitrary then the machines are called unrelated. Both of the uniform and unrelated cases belong to nonidentical parallel-machines scheduling problem.

The structure of GES allows it to simply work for scheduling jobs on nonidentical parallel-machines. We need only

• adapt the LPT rule properly for the case of nonidentical machines, just to use it in the body of NSG algorithm. For example, for the case of uniform machines the following two rules can be referred to as the LPT rule. In the case of identical processors these methods give the same schedule.

  • 1. As a machine finishes a job it chooses from the queue of waiting jobs the one with the longest processing time.

  • 2. Assign jobs, in the order of non-increasing processing times, to the machine on which they will have the earliest finishing time.

• adapt the pairwise interchange algorithm to work for the case of scheduling jobs on nonidentical machines. For this purpose we should only modify the job selection step of PIA which says “Find a job $J_{a} \in S_{{M_{i} }}$ and a job (or dummy job) $J_{b} \in S_{{M_{j} }}$ such that $0 \,< \,p_{b} - p_{b} \,<\, C_{{\max_{i} }} - C_{{\max_{j} }}$.” The following lemmas help us to determine suitable conditions for job selection.

Lemma 1

Suppose $p_{aj}$ and $p_{bj}$ be the processing time of job J _a and J _b on machine M _j , respectively; let also $C_{{{ \hbox{max} }_{j} }} = \sum\nolimits_{{J_{r} \in S_{{M_{j} }} }} {p_{{_{r} }} } ,$ be the load time of machine M _j . If the conditions $0 < p_{ai} - p_{bi} < C_{{\max_{i} }} - C_{{\max_{j} }}$ and $0 < p_{aj} - p_{bj} < C_{{\max_{i} }} - C_{{\max_{j} }}$ are held for any jobs $J_{a} \in S_{{M_{i} }}$ and $J_{b} \in S_{{M_{j} }} ,$ the following inequalities hold after interchanging job J _a and J _b between M _i and M _j ($C^{\prime}_{{{ \hbox{max} }_{j} }}$ is the load time of machine M _j after interchange.

• 1.
  $$\left| {C^{\prime}_{{\max_{i} }} - C^{\prime}_{{\max_{j} }} } \right| \le C_{{\max_{i} }} - C_{{\max_{j} }}$$
• 2.
  $$\hbox{max} (C^{\prime}_{{\max_{i} }} ,C^{\prime}_{{\max_{j} }} ) < C_{{\max_{i} }}$$

Proof

By interchanging job J _a and J _b between M _i and M _j we will have $C^{\prime}_{{\max_{i} }} = C_{{\max_{i} }} - p_{ai} + p_{bi}$ and $C^{\prime}_{{\max_{j} }} = C_{{\max_{j} }} + p_{aj} - p_{bj}$. As a result we have $C^{\prime}_{{\max_{i} }} - C^{\prime}_{{\max_{j} }} = C_{{\max_{i} }} - C_{{\max_{j} }} - (p_{ai} - p_{bi} ) - (p_{aj} - p_{bj} ).$ Following the assumptions we have $- (p_{ai} - p_{bi} ) - (p_{aj} - p_{bj} ) > - 2(C_{{\max_{i} }} - C_{{\max_{j} }} )$. We therefore arrive at $C^{\prime}_{{\max_{i} }} - C^{\prime}_{{\max_{j} }} > - (C_{{\max_{i} }} - C_{{\max_{j} }} )$. On the other hand, from our assumptions we have $- \left( {p_{ai} - p_{bi} } \right){-}\left( {p_{aj} - p_{bj} } \right) < 0$ which forces that $C^{\prime}_{{\max_{i} }} - C^{\prime}_{{\max_{j} }} < (C_{{\max_{i} }} - C_{{\max_{j} }} )$. We conclude that $\left| {C^{\prime}_{{\max_{i} }} - C^{\prime}_{{\max_{j} }} } \right| \le C_{{\max_{i} }} - C_{{\max_{j} }}$. To prove the second inequality, we have $C^{\prime}_{{\max_{i} }} = C_{{\max_{i} }} - (p_{ai} - p_{bi} ) < C_{{\max_{i} }}$ and $C^{\prime}_{{\max_{j} }} = C_{{\max_{j} }} + (p_{aj} - p_{bj} ) < C_{{\max_{j} }} + C_{{\max_{i} }} - C_{{\max_{j} }} = C_{{\max_{i} }}$. We finally get $\hbox{max} (C^{\prime}_{{\max_{i} }} ,C^{\prime}_{{\max_{j} }} ) < C_{{\max_{i} }} .$

Remark 1

When doing a job interchange during execution of PIA, if we have $J_{a} \in S_{{M_{i} }}$, then the value of makespan will be decreased.

Remark 2

When the scheduling criterion is the minimization of total flow time, any job interchange during execution of PIA will decrease the value of total flow time.

To adapt the pairwise interchange algorithm to work for the problem of scheduling jobs on nonidentical machines, we only modify the job selection step of PIA as follows: “Find a job $J_{a} \in S_{{M_{i} }}$ and a job (or dummy job) $J_{b} \in S_{{M_{j} }}$ such that: $0 \,<\, p_{ai} - p_{bi} \,<\, C_{{\max_{i} }} - C_{{\max_{j} }}$ and $0 \,<\, p_{aj} - p_{bj} \,<\, C_{{\max_{i} }} - C_{{\max_{j} }}$.”

6 Computational experiments

In this section, we investigate a comparison study on the effectiveness of the proposed GES algorithm on a large number of test problem instances. We benchmark the experimental frameworks used in Lee et al. [34] that have originally been designed by Gupta and Ruiz-Torres [16], Lee and Massey [33] and Kedia [30]. Four experimental frameworks, namely E ₁, E ₂, E ₃ and E ₄ are considered each of them having three influencing variables: the number of machines (m); the number of jobs (n); and the type of discrete uniform distribution used to generate job processing times (p).

Table 1 presents a summary of the experimental framework which is composed of 120 problems. Given the problem parameters of Table 1, 50 test instances are generated for each problem. This yields 6000 test problem instances in total.

Table 1 Summary of the computational experiments

To implement our GES and its hybridized version, GES + PIA, the following set of parameters are used. The maximum number of iterations is 1000. Only 1000 schedules are generated and evaluated. G is 6, P _s is 6⁻¹, a is 0.98, β is 5 and α ⁰ is 10. Every generated offspring in GES + PIA is selected to be improved by PIA with probability of 0.1. We found these values suitable through preliminary experiments. We have done the value selection process in a greedy fashion, though GES is relaxed to the exact tuning of parameters.

Tables 2, 3, 4, 5, 6 and 7 report the results acquired from the computations. The column with the title “Mean” reports the mean performance obtained by the corresponding algorithm. The ratio of the makespan over the lower bound is averaged for 50 replications to obtain the mean performance of an algorithm for an experiment. It should be mentioned that the mean performance values are given by four digits precision without rounding. The column with the title “Time (s)” reports the average running time (in seconds) to solve each of 50 test instances of a problem. The last three columns demonstrate the relative performance of the algorithms. Each cell in these three columns indicate the number of times, out of 50, a given algorithm reports a better makespan compared to the other algorithm. For instance, a value of c versus d in GES versus SA column means that, out of 50 replications, there are c test instances for which GES performs better than SA, d problems for which SA finds a better schedule, and 50-c-d test instances for which GES and SA yield the same makespan.

Table 2 Results for experiment E ₁

Table 3 Results for experiment E ₂

Table 4 Results for experiment E ₃: p ~ U(1,100)

Table 5 Results for experiment E ₃: p ~ U(100,200)

Table 6 Results for experiment E ₃: p ~ U(100,800)

Table 7 Results for experiment E ₄

We have implemented both of GES and GES + PIA algorithms in MATLAB and run them on a laptop computer with 2.67 GHz of CPU speed and 4 GB of RAM. The results of GES and GES + PIA are compared with the SA algorithm of Lee et al. [34].

The results for the experiment E ₁ are summarized in Table 2. In terms of the mean performance there is a negligible difference between GES and GES + PIA algorithms. Only on two problems (e.g., m = 4, n = 8, p ~ U(20,50) and m = 5, n = 15, p ~ U(20,50)) GES + PIA performs slightly better than GES. SA’s mean performance is inferior to GES and GES + PIA algorithms on seven problems, but superior on three problems. As the number of jobs increases, at a fixed level of m, the mean performance of all algorithms improves. Here, SA performs faster than others on average.

Table 3 reports the results on experimental framework E ₂. Here the superiority of GES + PIA over SA and GES algorithms is more pronounced in terms of the mean performance. Comparing SA with GES algorithm, there are many problems on which GES performs better than SA. In terms of the mean performance, there is no problem in which SA could dominate either GES or GES + PIA. However, there are some problems for which all algorithms perform the same. Among 20 problems in this experiment, SA finds the optimal makespan of all 50 test instances of five problems. While GES performs optimal on six problems, GES + PIA performs optimal on 13 problems. However, on the optimality of performance on the rest of problems we cannot make any judgment since the lower bound values may not be optimal and the optimal solutions are also unknown. One can find that as the number of jobs and the number of machines increase, GES + PIA can report the optimal makespan for all of test problems. Results indicate that GES + PIA performs better than SA on average on 32.20 out of 50 test instances of each of 20 problems. While this record is only 0.1 out of 50 for SA over GES + PIA. Such a trend is also visible for GES + PIA versus GES. GES + PIA performs better than GES on average on 30.40 out of 50 test instances of each problem. This record is only 0.15 out of 50 for GES over GES + PIA. Finally GES performs better than SA on average in 19.50 out of 50 test instances of each problem. The reverse scenario occurs only on average on nine test instances of each problem. Tracking the trends in the mean performance of the algorithms reveals that for a given number of jobs, as the number of machines increases, the mean performance decreases. Comparing the execution times, as the number of jobs increases, the time taken by the algorithms becomes longer. Also, increasing the number of machines adds to the running times.

The point is that the rate of increment is very smooth and much less than that of SA. SA times may even exceed from 40 s but for GES and GES + PIA all times are <2 s. This is because that GES and GES + PIA are able to find the optimum schedules faster and get stop sooner before reaching the maximum allowed number of schedule evaluations. But, SA fails to get the optimal schedules more frequently and has to do its search until getting the maximum allowed number of schedule evaluation.

Tables 4, 5 and 6 present the results for experimental framework E ₃ when the processing times are generated within U(1,100), U(100,200) and U(100,800), respectively. As can be found, both GES and GES + PIA algorithms reveal better performance than SA on all problems in each table. There is no problem for which the mean performance of SA becomes less than that of GES or GES + PIA. There is also no instance (among $3 \times 24 \times 50$ test instances) for which GES could report a better performance in comparison with GES + PIA. This indicates that the mean performance of SA is not optimal since all of its ratios in Tables 4, 5 and 6 are greater than one. This means that for each problem, there are some test instances for which SA is not able to find the optimal makespan. Such an observation is almost true but less highlighted for GES. In Table 4, there are at least 13 problems out of 24 problems that GES + PIA is able to find the optimal makespan in all of 50 trials. This record is 11 out of 24 for GES + PIA in Table 5. As the range of processing times becomes wider, the gap between GES + PIA and SA in terms of the success rate becomes more sensible. In Table 4, on average on 25.16 test instances out of 50, GES + PIA performs better than SA. This record is 40.83 and 44.20 out of 50 in Tables 5 and 6, respectively. The sensible gap between the success rate of GES + PIA and GES, and between the success rate of GES and SA is also observable. Therefore, when the range gets broader, GES + PIA is expected to strictly outperform other algorithms.

Table 7 presents the results for experiment E ₄. For the experiments in E ₄ since the problem sizes are small, all of the algorithms perform almost similar. However, again GES + PIA algorithm performs slightly better. From the above discussions and from the results on the mean performance and success rate of algorithms we can conclude that the relation GES + PIA > GES > SA is held where “>” indicates better performance.

In Tables 3, 4 and 5, from the row with the caption “Average,” it can be inferred that the average time taken by GES + PIA algorithm is shorter than GES. This is due to the fact that hybridizing with PIA algorithm speeds up converging toward the global optimum. Hence, our second stopping condition, which is getting the lower bound value, is fired soon and GES + PIA algorithm stops. Paradoxically in Table 6, the time needed for GES is less than GES + PIA. Here the reason for the increment in the required running time of GES + PIA is most probably related to the performance of the lower bound. Inevitably, GES + PIA should generate the maximum allowable number of schedules before being stopped. We do not conduct the execution time comparison between SA and GES or GES + PIA since these algorithms have been run on different machines (the results of SA have been adopted from Husseinzadeh Kashan and Karimi [20]). All we say is that both of GES and GES + PIA are computationally efficient and can produce very good results for problems with 100 jobs and 10 machines in less than a second.

7 Conclusions and future research

The paper proposed a new solution methodology based on grouping evolution strategies (GES) for parallel-machines scheduling problem to minimize makespan. The proposed GES algorithm owns a mutation operator which is founded based on dissimilarity measure between the set of jobs assigned to a machine to work with job groups rather than jobs isolatedly. Therefore, these are the job groups that constitute the underlying building blocks of the solution in the parallel-machines scheduling problem. The rationale of the new mutation operator is analogous to the original mutation of ES. It works in the real-valued space while the consequences are used in the body of a two-phase algorithm to generate an offspring schedule in the discrete space with the aid of LPT rule. A pairwise interchange algorithm (PIA) was hybridized with GES to improve its local performance. Additionally, we generalized the design of PIA to work also for the problem of scheduling with nonidentical parallel-machines and proved that under suitable conditions it has descent property. Results acquired from extended computational experiments justify the competitive performance of the proposed algorithms compared to an already existing simulated annealing algorithm.

GES is very easy for implementation and can be regarded as a promising solver of the wide class of scheduling problems. For future research, the effectiveness of GES is worth examining on parallel-machines scheduling problem while taking account of machines’ failure rates and the case of machines’ unavailability. Considering criteria other than makespan and even multiple objectives would be worthwhile. Additionally, developing the grouping version of the recently introduced real-valued algorithms such as, league championship algorithm [18, 22], Optics Inspired Optimization [19] and Find-Fix-Finish-Exploit-Analyze (F3EA) metaheuristic algorithm [27] and evaluating their effectiveness on parallel-machines scheduling problem is particularly encouraged. Finally, applications of GES on other types of scheduling problems, e.g., task scheduling in cloud computing environment [1, 2] or scheduling batch processing machines [21], is of great interest.