1 Introduction

The steering system plays the substantial role in the dynamics, handling and specially the yaw stability control of all road vehicles. Due to possible sudden unpredictable and unexpected driving condition changing, having a sense of efficient steering control is unavoidable. As an applicable index, any change in the road coefficient of friction and its effect on the yaw stability control has been considered in some articles [1, 2]. Fast and accurate response to changes in road conditions enforces engineers to design and introduce efficient controls so that the answer is minimized for the probably late drivers. In the literature, several approaches such as direct yaw moment control, four-wheel steering system, active differential braking and active front steering control have been proposed to control the yaw rate of vehicles.

The active front steering (AFS) [2] arrangement is one of the efficient ones that works by adding an additional angle to that previously made by conventional steering system [3]. In the literature, several studies have been done using simple arrangement controllers to reach economical applicable solutions. For example, in [4], a fractional-order PID controller was designed as the AFS to control the yaw stability of a vehicle. Boada et al. [5] designed a fuzzy logic controller to control both the yaw rate and sideslip angle of a vehicle. Hajjaji and Bentalba [6] designed a Sugeno-type fuzzy logic controller for their control scheme. Masao et al. [7] designed a steering controller using the state feedback of both yaw rate and sideslip angle and utilizing active rear wheel steering and direct yaw moment control systems jointly. Zeyada et al. [8] developed a fuzzy logic controller to improve the handling of a vehicle by using both differential braking and active front steering control systems.

Others used almost simplified models for vehicle dynamics. Rezai and Heidari Shirazi [9] designed a QFT (quantitative feedback theory) robust controller to control the yaw rate of a 7-degree-of-freedom vehicle by means of active front steering system. Their controller was adjusted for a range of offline road coefficients of friction; thus, it failed to modify the vehicle behavior completely and properly. Ma et al. [10] designed a fuzzy logic AFS controller for an eight-degree-of-freedom car. Although the degrees of freedom grew up, it did not lead to a precise behavior. Wu et al. in [11], used the back propagation of error as a learning method for a neural networks AFS controller. Then, an optimization was done using genetics algorithm, but the road condition was assumed unchanged during the maneuvers.

It can be found that some studies employed combined algorithms and methods to overcome the resultant errors. Masao et al. [12] designed an optimal control for a vehicle to enhance the handling quality of the front steering angle by controlled distribution of moment on all four wheels. Elbeheiry et al. [13] developed a sliding mode control that combines both active front steering and active roll moment control (ARMC) system in order to enhance vehicle stability and handling of vehicle in emergency maneuvers. Yihu et al. [14] designed a fuzzy logic controller to improve yaw stability of a vehicle by integrated yaw moment control and active front steering. Their study did not consider unpredictable situation, for example, changes in road friction.

Although these combination methods can improve the vehicle handling, they are not economical controllers and usually increase the overall cost of manufacturing and production.

Some works have been focused on improving the controller performances using superimposed methods. Zhanga et al. [15] optimized a fuzzy logic controller for a four-wheel steering vehicle by a combination of genetic algorithm, nonlinear programming quadratic line search (NPQL) and response surface model (RSM) in a fixed road condition.

Motoki and Masao designed a controller by using direct yaw moment control to manipulate the yaw rate of a vehicle in different road surface conditions. They used sideslip angle regulating as the feed forward and both the sideslip angle and yaw rate as the feedback signal [16]. Halvai et al. developed an adaptive neuro-fuzzy controller and studied the effect of sudden changes of road friction coefficient for right side wheels of the vehicle [17]. It is noted that the proposed controller can steer to desired conditions for almost limited variation.

Most of the controllers, which have been recommended in the literature, were based on the simplified vehicle dynamic models or assumed constant road and parameter conditions. Due to unpredictable and unexpected parameter changes, an applicable and efficient controller must be developed in order to adjust itself with these various conditions. It is necessary to design a controller that adapts its parameters during maneuvers to improve the handling of vehicle.

In this study, an applicable and economic but simultaneously efficient and adaptive neural network controller was proposed. In order to design an efficient neural network controller, some problems must first be noticed and solved. First, it is noted that an efficient network has many neuron interconnections and unknown parameters that must be optimized. Second, the ranges of neural network’s parameters are not initially specified. Third, during the training of the network, the parameters (layer weights) may be trapped in local optimums.

For not dealing with these problems, first a general PID controller with only three unknown parameters but almost specified ranges of variation is picked up. Then, utilizing the PSO (particle swarm optimization) algorithm, the PID controller parameters are optimized. PSO algorithm works with both the local and global solutions; therefore, the final global optimal solution can be reached. By means of the neural network toolbox in MATLAB software and data obtained from optimized PID controller, the neural network is trained. This integrated controller is applied to the vehicle, and again by using back propagation of error as a learning algorithm, the controller can modify its weights to improve the handling for different road conditions. The proposed controller satisfies both the applicability and effectiveness due to joint use of PID and adaptive neural network controllers.

2 Vehicle model description

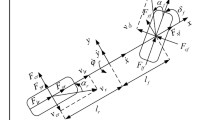
In this section, both the reference and actual models for our system will be introduced. With respect to Fig. 1, the reference model is a 2D reduction of a real 3D vehicle whose two rear and front wheels were replaced by a set of wheels. In a real vehicle, the best condition for minimized slipping and optimal handling occurs when the wheels rotate about a point. This introduced model can satisfy these optimal conditions for desired handling simply. One advantage of this simple model is that the trajectory response of vehicle under step input of steering is a circle or the yaw rate is a constant value [18, 19].

Fig. 1
figure 1

The schematic diagram of the reference model

Full size image

With reference to Fig. 1, the 2D governing equations of motion become:

$$m(\dot{v}_{y} + \dot{\psi }v_{x} ) = F_{\text{cr}} + F_{\text{cf}} \cos \delta_{\text{f}}$$
(1)
$$m( - \dot{\psi }v_{y} ) = - F_{\text{cf}} \sin \delta_{\text{f}}$$
(2)
$$I_{z} \ddot{\psi } = l_{\text{f}} F_{\text{cf}} - l_{\text{r}} F_{\text{cr}}$$
(3)

where m is the total mass of car, v y and v x are the velocities along y-direction and x-direction, respectively, F cr and F cf are the lateral forces exerted to the rear and front wheels, \(\delta_{\text{f}}\) is the steering angle of front wheel, \(I_{z}\) is the mass moment of inertia, and ψ is yaw angle.

l f and l r are the interspaces between front/rear wheels and the center of mass, l is the distance between rear and front axles, and \(\alpha_{\text{f}}\) and \(\alpha_{\text{r}}\) are the lateral slip angle of front rear wheels, respectively.

Assuming the constant cornering stiffness for rear and front tire leads someone to rewrite the lateral forces as:

$$F_{\text{cf}} = C_{\text{f}} \alpha_{\text{f}} \Rightarrow F_{\text{cf}} = C_{\text{f}} \left( {\beta + \frac{{\dot{\psi }l_{\text{f}} }}{{v_{x} }} - \delta_{\text{f}} } \right)$$
(4)
$$F_{\text{cr}} = C_{\text{r}} \alpha_{\text{r}} \Rightarrow F_{\text{cr}} = - C_{\text{r}} \left( {\beta - \frac{{\dot{\psi }l_{\text{r}} }}{{v_{x} }}} \right)$$
(5)

where C f, C r and β are the cornering stiffness of front and rear wheels and sideslip angle of the car, respectively. By introducing β and dψ/dt as the state variables, one can simply reach to such following state space equation between δ f and defined state variables:

$$\left[ {\begin{array}{*{20}c} {\dot{\beta }} \\ {\ddot{\psi }} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - \frac{{(C_{\text{f}} + C_{\text{r}} )}}{{mv_{x} }}} & { - 1 - \frac{{(l_{\text{f}} C_{\text{f}} - l_{\text{r}} C_{\text{r}} )}}{{mv_{x}^{2} }}} \\ { - \frac{{(l_{\text{f}} C_{\text{f}} - l_{\text{r}} C_{\text{r}} )}}{{I_{z} }}} & { - \frac{{(l_{\text{f}}^{2} C_{\text{f}} + l_{\text{r}}^{2} C_{\text{r}} )}}{{mv_{x}^{2} }}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} \beta \\ {\dot{\psi }} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\frac{{C_{\text{f}} }}{{mv_{x} }}} \\ {\frac{{l_{\text{f}} C_{\text{f}} }}{{I_{z} }}} \\ \end{array} } \right]\delta_{f}$$
(6)

A simple calculation results in the transfer function between the yaw rate and the steer angle of the front wheel as:

$$\frac{{\dot{\psi }}}{{\delta_{\text{f}} }} = \frac{{A_{1} s + A_{2} }}{{B_{1} s^{2} + B_{2} s + B_{3} }}$$
(7)

where s is the Laplace operator and the coefficients A 1 , A 2 , B 1 , B 2 and B 3 are:

$$\begin{aligned} A_{1} & = mv_{x} l_{\text{f}} C_{\text{f}} \\ A_{2} & = LC_{\text{f}} C_{\text{r}} \\ B_{1} & = mv_{x} I_{z} \\ B_{2} & = I_{z} (C_{\text{f}} + C_{\text{r}} ) + m(l_{\text{f}}^{2} C_{\text{f}} + l_{\text{r}}^{2} C_{\text{r}} ) \\ B_{3} & = \frac{{C_{\text{f}} C_{\text{r}} }}{{v_{x} }}(l_{\text{f}} + l_{\text{r}} )^{2} \left[ {1 + \frac{{mv_{x}^{2} (l_{\text{r}} C_{\text{r}} - l_{\text{f}} C_{\text{f}} )}}{{C_{\text{f}} C_{\text{r}} (l_{\text{f}} + l_{\text{r}} )^{2} }}} \right] \\ \end{aligned}$$
(8)

With respect to Fig. 1, it can be shown that:

$$\delta_{\text{f}} - \alpha_{\text{f}} + \alpha_{\text{r}} = \frac{l}{R} \to \delta_{\text{f}} = \alpha_{\text{f}} - \alpha_{\text{r}} + \frac{l}{R}$$
(9)

Also, by rewriting Eqs. (4) and (5), we have:

$$\alpha_{\text{f}} = \frac{{F_{\text{cf}} }}{{C_{\text{f}} }} = \frac{{m_{\text{f}} }}{{C_{\text{f}} }}\frac{{v^{2} }}{R}$$
(10)
$$\alpha_{\text{r}} = \frac{{F_{\text{cr}} }}{{C_{\text{r}} }} = \frac{{m_{\text{r}} }}{{C_{\text{r}} }}\frac{{v^{2} }}{R}$$
(11)

where m f and m r show the distributed masses on the rear and front axles in nonoperating situation. Substituting Eqs. (10) and (11) to (9), one can reach to:

$$\begin{aligned} \delta_{\text{f}} & = \frac{l}{R} + \left( {\frac{{m_{\text{f}} }}{{C_{\text{f}} }} - \frac{{m_{\text{r}} }}{{C_{\text{r}} }}} \right)\frac{{v^{2} }}{R} \\ & = \frac{l}{R} + \left( {\frac{{m_{\text{f}} }}{{C_{\text{f}} }} - \frac{{m_{\text{r}} }}{{C_{\text{r}} }}} \right)a_{y} \\ & = \frac{l}{R} + K_{u} a_{y} \\ \end{aligned}$$
(12)

where \(a_{y}\) is the lateral acceleration and K u is known as the understeering coefficient, with such following relation:

$$K_{u} = \frac{{m_{\text{f}} }}{{C_{\text{f}} }} - \frac{{m_{\text{r}} }}{{C_{\text{r}} }} = \left( {\alpha_{\text{f}} - \alpha_{\text{r}} } \right)\frac{R}{{v^{2} }}$$
(13)

Finally, using Eqs. (10)–(13), one can rearrange the transfer function between the yaw rate of vehicle and steering angle (Eq. (7)) as:

$$\dot{\psi } = \frac{{v\delta_{\text{f}} }}{{l + k_{u} v^{2} }}$$
(14)

Equation (14) prepares the reference signal for our control simulation arrangement, while, in this paper, a virtual but completely efficient software is used to model the actual plant. CarSim software as one of the MATLAB Simulink toolbox is used to model an actual vehicle with real and different road conditions and other true situations. Many studies have used this software package to simulate the vehicle responses in their control schemes (see for example [12, 13, 20, 21]).

The parameters of the vehicle, we used in this study, are shown in Table 1. In this table, \(R_{\text{w}}\) is the nominal radius of the wheel, \(I_{\text{w}}\) is the mass moment of inertia of the wheel, h is the height of the center of gravity of the sprung mass, and \(l_{\text{w}}\) is the width between right and left wheels.

Table 1 The parameters of the vehicle used in our simulations
Full size table

3 Controller design pattern

In this section, the logic and procedure of selecting and designing the proposed controller will be described. Since the whole controlling process happens in a very short time interval, it should be able to demonstrate more efficient and precise behaviors rather than simple conventional controllers.

Here, and due to simplicity, generality and widespread use of PID controllers, a general PID controller is picked up for a determined and fixed road condition. After using the particle swarm optimization method and an artificial neural network, the PID coefficients have been optimized and updated throughout such a smart planned process in real time. This advanced and smart combination can improve the handling of the vehicle in different road coefficients of friction in short intervals of time.

3.1 Particle swarm optimization algorithm

The particle swarm optimization (PSO) is a random search algorithm, which was imitated from the social behavior of the bird flocks or fish schools, to find the best value of a cost function. This algorithm was first introduced by Kennedy and Eberhart [22] and can be used to optimize binary discrete optimization problems as well as the continuous ones [23]. The ability of algorithm in finding optimized candidate has been studied in some works (see for example [24–26]). In this optimization algorithm, first a set of population (swarm) of n particles was created (initialization step). Then, the fitness function for these particles was evaluated. The best position for each particle (personal best) and the best position among all particles (global best) were selected and be named as “Pbest” and “Gbest,” respectively [27, 28]. If the stopping criterion was satisfied, the process stopped and the final Gbest was reported as the optimal population.

In our simulation, each particle includes three parameters, i.e., the coefficient of a general PID controller. They are named as x i1  = k p , x i2  = k int and x i3  = k d where i is the ith particle. First a set of 3D particles is created. Then, the fitness function (the integral of squared error) for these particles is evaluated and the “Pbest” and “Gbest” are computed. Each particle can be defined by its current velocity and position. The position of each particle changes according to the following update formula [28]:

$$x_{ij} \left( {n + 1} \right) = x_{ij} \left( n \right) + v_{ij} (n + 1)$$
(15)

where \(x_{ij}\) and \(v_{ij}\) are the position and the velocity of the parameter j of ith particle of the whole population. Also, the update rule for the velocity is [28]:

$$v_{ij} \left( {n + 1} \right) = wv_{ij} \left( n \right) + c_{1} r_{1j} (n)[Pbest_{ij} - x_{ij} ] + c_{2} r_{2j} (n)[Gbest_{j} - x_{ij} ]$$
(16)

The first term at the right side of Eq. 16 is known as the inertia term and makes the particle moves in the same direction and with the same velocity. The second term which is known as “the personal influence” makes the particle come back to a possibly better previous position, while the third term which is known as “the social influence” makes the particle monitor the best neighbor direction. In these terms, \(r_{1j}\) and \(r_{2j}\) are some random values in the range of [0, 1], while w, c 1 and c 2 are the weighting factors. These weighting factors enable one to manipulate the rate of convergence and also the magnitude of each effect in the searching process. See for example [29, 30] that presented some methods to select optimal values of above weighting factors. The flowchart of the PSO algorithm is schematically drawn in Fig. 2.

Fig. 2
figure 2

The schematic flowchart of the PSO algorithm

Full size image

The constant values that are used in our PSO algorithm are also tabulated in Table 2.

Table 2 The values of parameters that are used in our PSO algorithm
Full size table

3.2 Proposed neural network controller

As it can be seen in many works, an artificial neural network is an imitation of making a decision with respect to previous trained behaviors and data in the biological human brain [31–33]. After an ANN has been trained by some defined and determined input/output signals, it may decide about a suitable response due to an unknown input [33]. The efficiency and correctness of this method has been discussed in many applications including control systems. See for example [34–36].

Figure 3 shows the architecture of a two-layer feed-forward neural network controller that is used in this study. In this model, all the activation functions (f) of first layer are hyperbolic tangent sigmoid functions, while that of second layer are all linear. With reference to this architecture, the outlets of first layer are:

$$z_{i} = f\left( {\mathop \sum \limits_{{\varvec{j} = 1}}^{2} \varvec{w}_{{\varvec{ij}}} \varvec{x}_{\varvec{j}} } \right)\quad (i = 1,2, \ldots 30)$$
(17)
Fig. 3
figure 3

The architecture of the network used in our simulation

Full size image

While the output signals of the second layer become:

$$u = f\left( {\mathop \sum \limits_{{\varvec{l} = 1}}^{30} \varvec{v}_{\varvec{l}} \varvec{z}_{\varvec{l}} } \right)$$
(18)

Here w ij ’s and v l ’s are the layer weights between the input, intermediate and output neurons.

During the simulation/training and in each iteration, the error signal is computed via the following relation:

$$e\left( n \right) = Y_{\text{ref}} - y(n)$$
(19)

and the cost function is defined as:

$$E = \frac{1}{2}{\text{e}}^{2} \left( n \right)$$
(20)

To minimize the cost function (Eq. 20), the back-propagation method is used. The method was first introduced by Werbos [37] and then used in neural networks as a learning algorithm in [38]. Here, this method is used to update the weights iteratively to reach an optimal value for the desired cost function. In fact, the back-propagation algorithm together with the delta learning rule [39, 40] is used to compute layer weights for minimizing the cost function E (Eq. 20) in this study. Based on above methods, the weight variation in each iteration must be proportional to the minus gradient of the cost function with respect to that layer weight, i.e.,

$$\begin{aligned} \Delta w_{ij} & \propto - \frac{\partial E}{{\partial w_{ij} }}\mathop = \limits^{{{\text{Chain}}\,{\text{rule}}}} - \frac{\partial E}{\partial e(n)} \frac{\partial e(n)}{\partial y(n)}\frac{\partial y}{\partial u}\frac{\partial u}{{\partial w_{ij} }} \\ \Delta v_{i} & \propto - \frac{\partial E}{{\partial v_{i} }}\mathop = \limits^{{{\text{Chain}}\,{\text{rule}}}} - \frac{\partial E}{\partial e(n)} \frac{\partial e(n)}{\partial y(n)}\frac{\partial y}{\partial u}\frac{\partial u}{{\partial v_{i} }} \\ \end{aligned}$$
(21)

A simple calculation leads someone to reach such following relation for layer weight changing rule:

$$\begin{aligned} \Delta w_{ij} & = \eta e\left( n \right)\frac{\partial u}{{\partial w_{ij} }} \\ \Delta v_{i} & = \eta e\left( n \right)\frac{\partial u}{{\partial v_{i} }} \\ \end{aligned}$$
(22)

where η is the coefficient of training. This coefficient must be selected such that both the stability of iterations and the speed of training will be satisfied. In this study, η = 0.0002 satisfies both conditions; therefore, the updating law of layer weights becomes:

$$\begin{aligned} w_{ij} \left( {n + 1} \right) & = w_{ij} \left( n \right) + \eta e(n) \frac{\partial u}{{\partial w_{ij} }} \\ v_{i} \left( {n + 1} \right) & = v_{i} \left( n \right) + \eta e(n) \frac{\partial u}{{\partial v_{i} }} \\ \end{aligned}$$
(23)

More specifically, first the parameters of a conventional PID controller, i.e., K p , K d and K i , are optimized for a specified road condition using particle swarm optimization algorithm. After that, train the NN controller to set the weights of NN controller, and then, the weights of NN are adjusted during the control process. Here the PSO (particle swarm optimization) algorithm has utilized to optimize the PID controller that must train the NN controller, and ANN (artificial neural network) has used to control the yaw rate of vehicle.

Briefly, the parameters of a conventional PID controller, i.e., K p , K d and K i , are optimized when the road coefficient of friction is equal to one by using particle swarm optimization algorithm. After that, a two-layer neural network is designed and trained. The trained layer weights of the network can tune the controller signal for other road conditions. In the next section, the efficiency and effectiveness of the controller for three types of road conditions will be justified in real time for some famous vehicle maneuvers.

4 Simulation results

In what follows, the adeptness and the ability of the designed controller for three famous maneuvers, i.e., J-turn, fishhook and change lane in three different road friction conditions, are investigated. Figure 4 shows these three famous maneuvers.

Fig. 4
figure 4

Three famous maneuvers that must be tracked in our simulations

Full size image

In this study, the coefficient of friction as an unpredictable condition was selected and varied from a road with coefficient of friction equal to one to a road with coefficient of friction equal to 0.2. As an analogical study, the behaviors of the system under the PID that was optimized by PSO and when it was integrated to ANN are compared. In the following figure legends, “PID” is the abbreviation of PID controller optimized by SFO, while “neural network” is the abbreviation of PID controller optimized by SFO and integrated by the ANN.

Figure 5 shows the desired, uncontrolled and controlled yaw rate of the vehicle for the change lane maneuver at different road conditions under mentioned controllers.

Fig. 5
figure 5

The desired, uncontrolled and controlled yaw rate of the vehicle for the change lane maneuver when the road coefficient of friction is a 1, b 0.6 and c 0.2

Full size image

According to this figure, in first road coefficient of friction, i.e., the case (a) of Fig. 5, both the controllers can track the desired path, properly. It is completely expectable since the PSO algorithm is used to find optimized controller for this road condition only and the neural network has been trained at this road condition. Of course, when road coefficient of friction decreases, the optimized PID controller cannot control the vehicle alone and employing an auxiliary adaptive ANN is unavoidable as Fig. 5b, c indicates this matter.

The simulation is repeated for other two maneuvers, i.e., the J-turn and fishhook. Figures 6 and 7 show the superiority of the integrated optimized PID plus ANN controller with respect to optimized PID controller alone in tracking the desired trajectories.

Fig. 6
figure 6

The desired, uncontrolled and controlled yaw rate of the vehicle for the J-turn maneuver when the road coefficient of friction is a 1, b 0.6 and c 0.2

Full size image
Fig. 7
figure 7

The desired, uncontrolled and controlled yaw rate of the vehicle for the fishhook maneuver when the road coefficient of friction is a 1, b 0.6 and c 0.2

Full size image

In Table 3, one can compare the performance of the mentioned controllers of previous cases quantitatively and entirely.

Table 3 The integral of squared error between the desired and actual trajectories for our case studies
Full size table

5 Conclusion

It was tried to introduce an active steering control scheme for vehicle handling that satisfies both the applicability and effectiveness criteria. An integrated optimized PID and artificial neural network controller was designed, and its performance was investigated for three famous yaw rate maneuvers in different road frictions. An analogical study was also done between the PID that was optimized by particle swarm algorithm and the entire represented controller. It was shown that in regular road friction, both the controllers can steer the vehicle well, but for rainy and icy roads, only the integrated PID plus adaptive ANN can follow the desired trajectory precisely.