1 Headings

Traditionally, the trajectory tracking problem either in a kinematic or in a dynamic control level is well known that under the assumption of the model is appropriate simplification. However, for complex robots such as wheeled mobile manipulators (WMMs), it is more realistic to consider the tracking problem with system uncertainties, nonlinearity, and coupling to realize high-performance control. In kinematic control level, authors have studied the tracking problem using adaptive controls and robust controls considering system uncertainties and nonlinearity as disturbances [1–5]. However, the dynamics usually cannot be neglected if accurate motion is required. Some adaptive controls and robust controls have been developed to confront the uncertainties and nonlinearity in the dynamics of the systems. In [6, 7], adaptive control techniques were employed to solve the tracking problem of WMM with unknown inertia parameters. In [8, 9], a robust adaptive controller was designed for robot systems with model uncertainties. Dong et al. [10] have studied the motion/force control for a mobile manipulator. In addition, they have proposed some adaptive robust control strategies. In [11], robust adaptive controllers were proposed for dynamic systems with parametric and nonparametric uncertainties, in which adaptive control techniques were used to compensate for the parametric uncertainties and sliding mode control was used to suppress the bounded disturbances. In [12–16], robust control strategies were presented systematically in the presence of uncertainties and disturbances. However, the major problem of the adaptive robust control approach is that certain functions must satisfy the assumption of “linearity in the parameters,” and tedious preliminary computation is required to determine “regression matrices.”

In the past decade, great progress has been achieved in the study of using neural networks to control nonlinear systems with uncertain. Extensive works demonstrate that adaptive neural control is particularly suitable for controlling highly uncertain, nonlinear, and complex systems [17–20]. In these neuro-adaptive control schemes, the neural network is used to study dynamic system or compensate the effects of system nonlinearity and uncertainties. Therefore, the stability, convergence, and robustness of the control system can be improved. A multilayer perception network-based controller was suggested by Fierro and Lewis [21] to deal with parametric or nonparametric uncertainties for a mobile robot without any prior knowledge of the uncertainties. Other neural networks, such as radial basis function (RBF) neural network [22], wavelet network [23, 24], and fuzzy neural network (FNN), were also adopted for the robust control of mobile manipulators.

The FNN has been widely used for trajectory tracking control of WMMs owing to the advantages in stability, convergence, and robustness. The FNN is essentially a neural network. In this network, the structure is determined using a number of fuzzy rules. The key to evaluate a FNN is to see its generalization ability. The most important effect of the generalization ability is the network structure of the selection. If the number of nodes is not appropriate, it can easily lead to the problem, of over-fitting or training phenomenon, and reduce the generalization ability of the neural network. The traditional learning method mostly uses the back-propagation algorithm, which has low speed, easy to fall into local minimum [25]. Others have used unsupervised procedures (e.g., k-means clustering or Kohonen’s self-organizing maps [26]) for selecting the centers [27]. Theoretical justification of the suitability of such a strategy is presented in [28]. Nevertheless, in order to acquire optimal performance, the centers training procedure should also include the target data [29], leading to a form of supervised learning that proved to be superior in several applications [30]. Owning to the advantage of quick converge and converge to global minima, extended Kalman filters (EKFs) have been used extensively with neural networks. They have been used to train multilayer perceptron [31–33] and recurrent networks [34, 35]. They have also been used to train RBF networks [36, 37].

In this study, we propose an effective tracking control method based on FNN and EKF to track a reference trajectory (e.g., trajectory for opening a door or grasping an object) in the proposed WMM system. Firstly, we identify the WMM system, FNN, and EKF using a simple description. Secondly, to deal with complex dynamics system, we developed a FNN to approximate the dynamics model. In order to decrease the computational effort of the training algorithm, a pair of parallel EKF is used to sequentially update both the weights and centers, following the line of previous work related to considering the training procedure of a neural network as an estimation problem [38–40]. Thirdly, an effective tracking control law for the WMM system is proposed with system stability analysis. Finally, the proposed tracking control method facilitates precise tracking performance, which was demonstrated using some simulations and experiments.

This paper is organized as follows. The background of the WMM system, FNN, and EKF are introduced in Sect. 2. Section 3 discusses the FNN learning scheme, and a pair of parallel EKF is used to sequentially update both the weights and centers of the network. The effective tracking control strategy for the WMM system is proposed based on the stability analysis in Sect. 4. Some simulations and experiments are presented in Sect. 5. Finally, some conclusions are presented in Sect. 6.

2 Background

2.1 WMM model

In this study, consider the WMM consisting of the wheeled mobile vehicle and 6-link manipulator, as shown in Fig. 1. The dynamics of WMM can be given by the dynamics of wheeled mobile vehicle and 6-link manipulator [41].

Fig. 1
figure 1

Coordinate of wheeled mobile manipulator

Full size image
$${\varvec{M}}(\varvec{q}) \ddot{\varvec{{q}}} + {\varvec{C}}({\varvec{q}},{\dot{\varvec{q}}}){\dot{\varvec{q}}} + {\varvec{G}}({\varvec{q}}) + {\varvec{F}}({\varvec{q}},{\dot{\varvec{q}}}) + {\varvec{\Gamma}}^{ - 1} {\varvec{\uptau}}_{s} = {\varvec{B}}({\varvec{q}}){\varvec{\uptau}} - {\varvec{J}}^{\text{T}} ({\varvec{q}}){\varvec{\uplambda}}$$
(1)

where \({\varvec{q}},\,{\dot{\varvec{q}}},\,\ddot{\varvec{{q}}}\) are the joint angles, velocities, and accelerations of the mobile manipulator, respectively. \({\varvec{M}}({\varvec{q}}) \in \Re^{8 \times 8}\) is the symmetric bounded positive definite inertia matrix, \({\varvec{C}}({\varvec{q}},{\dot{\varvec{q}}}) \in \Re^{8 \times 8}\) denotes the centripetal and Coriolis torques, \(\varvec{G}({\varvec{q}}) \in \Re^{8 \times 1}\) is gravity matrix, \(\varvec{F}({\varvec{q}},{\dot{\varvec{q}}}) \in \Re^{8 \times 1}\) is a vector representing frictional force, \({\varvec{\uptau}}_{s} \in \Re^{8 \times 1}\) denotes the coupling torque, \({\varvec{\Gamma}} \in \Re^{8 \times 8}\) denotes the reduction radio of the speed reducer, \(\tau \in \Re^{8 \times 1}\) is the actuation input, \(\varvec{B}(\varvec{q}) \in \Re^{8 \times 8}\) is a full-rank input transformation matrix, which is assumed to be known because it is a function of the fixed geometry of the system, \({\varvec{J}}^{{\varvec{T}}} ({\varvec{q}}) \in \Re^{8 \times 8}\) is the Jacobian matrix, and \({\varvec{\uplambda}} \in \Re^{8 \times 1}\) denotes the constraining force. From Fig. 1, we can define \({\varvec{q}} = \left[ {\begin{array}{*{20}c} {\vartheta_{\text{Bl}} } & {\vartheta_{\text{Br}} } & {q_{M1} } & {q_{M2} } & {q_{M3} } & {q_{M4} } & {q_{M5} } & {q_{M6} } \\ \end{array} } \right]^{\text{T}}\).

By analogy with a similar concept introduced in [41], the dynamics model of WMM considering kinematics can be derived as follows.

$$\tilde{\varvec{M}}(\varvec{q})\dot{\varvec{v}} + \tilde{\varvec{C}}(\varvec{q},\dot{\varvec{q}})\varvec{v} + \tilde{\varvec{G}}(\varvec{q}) + \tilde{F}(\varvec{q},\dot{\varvec{q}}) + \tilde{\varvec{\tau }}_{s} = \tilde{\varvec{\tau }}$$
(2)
$$\tilde{\varvec{M}}(\varvec{q})\,\triangleq\,\varvec{S}^{\text{T}} (\varvec{q}_{\text{B}} )\varvec{M}(\varvec{q})\varvec{S}(\varvec{q}_{\text{B}} )$$
$$\tilde{\varvec{C}}(\varvec{q},\dot{\varvec{q}})\,\triangleq\,\varvec{S}^{\text{T}} (\varvec{q}_{\text{B}} )\{ \varvec{M}(\varvec{q})\dot{\varvec{S}}(\varvec{q}_{\text{B}} ) + \varvec{C}(\varvec{q},\dot{\varvec{q}})\varvec{S}(\varvec{q}_{\text{B}} )\}$$
$$\tilde{\varvec{G}}(\varvec{q})\,\triangleq\,\varvec{S}^{\text{T}} (\varvec{q}_{\text{B}} )\varvec{G}(\varvec{q})$$
$$\tilde{\varvec{F}}(\varvec{q},\dot{\varvec{q}})\,\triangleq\,\varvec{S}^{\text{T}} (\varvec{q}_{\text{B}} )\varvec{F}(\varvec{q},\dot{\varvec{q}})$$
$$\tilde{\varvec{\tau }}_{s}\,\triangleq\,\varvec{S}^{\text{T}} (\varvec{q}_{\text{B}} )\varGamma^{ - 1}\varvec{\tau}_{s}$$
$$\tilde{\varvec{\tau }}_{s}\,\triangleq\,\varvec{S}^{\text{T}} (\varvec{q}_{\text{B}} )\varvec{B}(\varvec{q})\varvec{\tau}$$

2.2 Fuzzy neural network

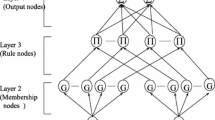
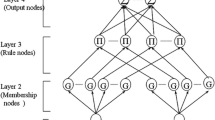
In this paper, a FNN is used, as shown in Fig. 2. Here, r is the number of input variables; x i (i = 1, 2,…, r) is the input linguistic variables; y i (i = 1, 2,…, m) is the output of the system; MF ij is the i-th input variables of the j-th membership function; R j is the j-th fuzzy rule; w mj is a result parameter of the j-th rule; and u is the rule number of the system.

Fig. 2
figure 2

Structure of a two-layer FNN

Full size image

The following is a detailed description for all the sub-layers of the network.

The first layer is the input layer. Each node represents a variable input language.

The second layer is the membership function layer. Each node represents a membership function. The membership function is the Gauss function

$$\mu_{ij} (x_{i} ) = \exp \left[ { - \frac{1}{{\sigma_{ij}^{2} }}||x_{i} - c_{ij} ||^{2} } \right];i = 1,2, \ldots ,r,\;j = 1,2, \ldots ,u$$
(3)

where r is the number of input variables, u is numbers of membership functions, also represents the total number of rules; \(\mu_{ij}\) is the j-th Gaussian membership function of \(x_{i}\); \(c_{ij}\) is the j-th Gaussian membership function center of \(x_{i}\); and \(\sigma_{ij}\) is the j-th Gaussian membership function width of \(x_{i}\).

The third layer is a T-norm layer. Each node represents the IF part of the possible fuzzy rules, also on behalf of the NN units, and the layer node number reflects the number of fuzzy rules. If the T-norm operator used to compute each rule’s firing strength is multiplication, the output of the j-th rule \(R_{j} (j = 1,2, \ldots ,u)\) in the third layer is

$$\varphi_{\text{j}} = \exp \left[ { - \sum\limits_{i = 1}^{r} {\frac{1}{{\sigma_{ij}^{2} }}\left\| {x_{i} - c_{ij} } \right\|^{2} } } \right]\quad j = 1,2,\; \ldots ,\;u$$
(4)

The fourth layer is the output layer. Each node in this layer represents an output variable as the weighted summation of incoming signals. In this study, we consider multi-input and multi-output systems in the following analysis.

$$\text{y}_{j} = \sum\limits_{i = 1, j = 1}^{i = p, j = u} {w_{ij} \varphi_{j} }$$
(5)

where \(\text{y}_{j}\) is the value of j-th output variable and w ij is the THEN-part (consequent parameters) or connection weight of the i-th rule.

From the above, the fuzzy rule numbers and the third-layer numbers of the FNN units are same. The first layer is used to realize input variables language; the second layer is equivalent to the fuzzy generator, which is used to calculate the membership functions; the third layer is equivalent to the fuzzy rule base, using the T-norm operator multiplication on the degree of membership of the second layer; and the fourth layer is used to obtain the output. The rule from the input to output is defined as

$$R^{j} :{\text{IF}}\,x_{1} \,{\text{is}}\,{\text{MF}}_{1j} \,{\text{and}} \ldots {\text{and}}\,x_{r} \,is\,{\text{MF}}_{rj} ,\,{\text{THEN}}\,{\text{y}}_{j} \,{\text{is}}\,w_{j}$$

where \(w_{j}\) is a real number, a system based on fuzzy S model is used to realize the network, and the output of the S model is

$${\varvec{y}}({\varvec{x}}) = \sum\limits_{j = 1}^{u} {a_{j0} } \exp \left[ { - \frac{1}{{\sigma_{j}^{2} }}\left\| {{\varvec{x}} - {\varvec{C}}_{j} } \right\|^{2} } \right]$$
(6)

Assume n observation data has produced a u fuzzy rule, the third layer of the FNN units output can be written in matrix form as follows

$$\phi = \left[ {\begin{array}{*{20}c} {\varphi_{11} } & \cdots & {\varphi_{1n} } \\ \vdots & \vdots & \vdots \\ {\varphi_{u1} } & \cdots & {\varphi_{un} } \\ \end{array} } \right]$$

where \(\varphi_{ij}\) is the output of the third layer of the i-th neurons when the j-th training data reaches the network.

The output of the system can be obtained using Eq. (5), and hence, Eq. (5) can be rewritten as follows

$${\varvec{W}}\phi = {\varvec{Y}}$$
(7)

where \({\varvec{W}} = \left[ {\begin{array}{*{20}c} {w_{11} } & {w_{12} } & \cdots & {w_{1u} } \\ {w_{21} } & {w_{22} } & \cdots & {w_{2u} } \\ \vdots & \vdots & \vdots & \vdots \\ {w_{n1} } & {w_{n2} } & \cdots & {w_{nu} } \\ \end{array} } \right],\,\,\,{\varvec{Y}} = \left[ {\begin{array}{*{20}c} {{\text{y}}_{1} } & {y_{2} } & \cdots & {y_{n} } \\ \end{array} } \right] .\)

2.3 Extended Kalman filter

The Kalman filter is usually used to estimate the state variables of a discrete process using a linear stochastic differential equation as \({\varvec{x}} \in \Re^{n}\) [42]. However, if the relationship between the process and (or) the observed variables and the observed variables are nonlinear, the direct use of the Kalman filter is not the case. The Kalman filter, which is expected to be linear with the covariance, is known as the EKF, which is used to solve the problem of nonlinear filtering.

In the nonlinear case, the partial derivative of the process and observation equation can be used to estimate the state of the process by using the partial derivative and observation equation. The state vector is assumed as \({\varvec{x}} \in \Re^{n}\), the state equation is a nonlinear stochastic differential equation given as:

$${\varvec{x}}_{k} = {\varvec{f}}({\varvec{x}}_{k - 1} ,{\varvec{u}}_{k - 1} ,{\varvec{w}}_{{k{ - 1}}} )$$
(8)

The observation variable is given as \({\varvec{z}} \in \Re^{m}\) and can be defined as

$${\varvec{z}}_{k} \in {\varvec{h}}({\varvec{x}}_{k} ,{\varvec{v}}_{k} )$$
(9)

where the random variables \({\varvec{w}}_{k}\) and \({\varvec{v}}_{k}\) are the process noise and observation noise, respectively. These variables, which are Gauss white noise, are independent of each other. In differential Eq. (8), the nonlinear function \({\varvec{f}}\) maps the state to the present moment k, and its parameters include driving function \({\varvec{u}}_{k - 1}\) and zero mean noise \({\varvec{w}}_{k}\). The nonlinear function h in Eq. (9) is connected with the state variable \({\varvec{x}}_{k}\) and the observed variable \({\varvec{v}}_{k}\).

Equation (10) is the estimation function of the state vector and Eq. (11) is the estimation function of the observation vector. \({\varvec{w}}_{k}\) and \({\varvec{v}}_{k}\) are the process noise and observation noise, respectively, which are not easy to be estimated by mathematical formula, in practical applications. So, we did not consider them in this step. That is to say, they are regarded as zero.

$${\tilde{\varvec{x}}}_{k} = {\varvec{f}}({\tilde{\varvec{x}}}_{k - 1} ,{\varvec{u}}_{k - 1} ,0)$$
(10)
$${\tilde{\varvec{z}}}_{k} = {\varvec{h}}({\tilde{\varvec{x}}}_{k} ,0)$$
(11)

where the \({\tilde{\varvec{x}}}_{k}\) is a posteriori estimation of the state relative to the first time k.

In order to include the process of a nonlinear difference and observation error in practical applications, we can use the new control equation by Eqs. (12) and (13)

$${\varvec{x}}_{k} \approx {\tilde{\varvec{x}}}_{k} { + }{\varvec{A}}({\varvec{x}}_{k - 1} { - }{\hat{\varvec{x}}}_{k - 1} ){ + }{\varvec{Ww}}_{k - 1}$$
(12)
$${\varvec{z}}_{k} \approx {\tilde{\varvec{z}}}_{k} { + }{\varvec{H}}({\varvec{x}}_{k} { - }{\tilde{\varvec{x}}}_{k} ){ + }{\varvec{Vv}}_{\text{k}}$$
(13)

where \({\varvec{x}}_{k}\) is the actual value of the state vector. \({\varvec{z}}_{k}\) is the actual value of the observation vector. \({\tilde{\varvec{x}}}_{k}\) is obtained using Eq. (10) and is the observation value of the state vector. \({\tilde{\varvec{z}}}_{k}\) is calculated using Eq. (11), which is the observation value of the observation vector. \({\hat{\varvec{x}}}_{k}\) is a posteriori estimation of the state vector of the k moment. The random variables \({\varvec{w}}_{k}\) and \({\varvec{v}}_{k}\) are the process noise and observation noise, in practical applications, which are feedback from sensors. A is the Jacoby matrix of the partial derivative of f to x, which can be rewritten as

$${\varvec{A}}_{[i,j]} = \frac{{\partial {\varvec{f}}_{[i]} }}{{\partial {\varvec{x}}_{[j]} }}({\hat{\varvec{x}}}_{k - 1} ,{\varvec{u}}_{k - 1} , 0)$$
(14)

W is the Jacoby matrix of the partial derivative of f to w.

$${\varvec{W}}_{[i,j]} = \frac{{\partial {\varvec{f}}_{[i]} }}{{\partial {\varvec{w}}_{[j]} }}({\hat{\varvec{x}}}_{k - 1} ,{\varvec{u}}_{k - 1} , 0)$$
(15)

H is the Jacoby matrix of the partial derivative of h to x.

$${\varvec{H}}_{[i,j]} = \frac{{\partial {\varvec{h}}_{[i]} }}{{\partial {\varvec{x}}_{[j]} }}({\tilde{\varvec{x}}}_{k} , 0)$$
(16)

V is the Jacoby matrix of the partial derivative of h to v.

$${\varvec{V}}_{[i,j]} = \frac{{\partial {\varvec{h}}_{[i]} }}{{\partial {\varvec{v}}_{[j]} }}({\tilde{\varvec{x}}}_{k} , 0)$$
(17)

Prediction error is

$${\tilde{\varvec{e}}}_{{{\varvec{X}}_{{\varvec{k}}} }} \equiv {\varvec{x}}_{{\varvec{k}}} - {\tilde{\varvec{x}}}_{{\varvec{k}}}$$
(18)

The residuals of the observed variables are

$${\tilde{\varvec{e}}}_{{{\varvec{z}}_{{\varvec{k}}} }} \equiv {\varvec{z}}_{{\varvec{k}}} - {\tilde{\varvec{z}}}_{{\varvec{k}}}$$
(19)

Furthermore, the expression of the error can be recorded as Eqs. (20) and (21).The covariance matrix is

$${\tilde{\varvec{e}}}_{{\varvec{x}}_{\varvec{k}}} \approx {\varvec{A}}({\varvec{x}}_{k - 1} - {\tilde{\varvec{x}}}_{k - 1} ) + {\varvec{\upvarepsilon}}_{k}$$
(20)
$${\tilde{\varvec{e}}}_{{\varvec{z}}_{\varvec{k}}} \approx {\varvec{H}}\,{\tilde{\varvec e}}_{{\varvec{x}}_{\varvec{k}}} + {\varvec{\upeta}}_{k}$$
(21)

where \({\varvec{\upvarepsilon}}_{k}\) and \({\varvec{\upeta}}_{k}\) are zero mean. The covariance matrix is the independent random variables of \({\varvec{WQW}}^{\text{T}}\) and \({\varvec{VRV}}^{\text{T}}\). Q is obtained from \({\varvec{p}}({\varvec{w}}) \sim {\varvec{N}}(0,{\varvec{Q}})\), R is obtained from \({\varvec{p}}({\varvec{v}}) \sim {\varvec{N}}(0,{\varvec{R}})\). Q and R are Gauss white noise series which are independent of each other and have normal distribution.

By using the observation residuals \({\tilde{\varvec{e}}}_{{{\varvec{z}}_{{\varvec{k}}} }}\) in Eq. (19) and the second Kalman filter (hypothesis) estimates \({\tilde{\varvec{e}}}_{{{\varvec{x}}_{{\varvec{k}}} }}\) in Eq. (20), the estimation results denoted as \({\hat{\varvec{e}}}_{{\varvec{k}}}\), combining Eq. (18) together to obtain the initial nonlinear process a posteriori state estimation, i.e.,

$${\hat{\varvec{x}}}_{k} = {\tilde{\varvec{x}}}_{k} + {\hat{\varvec{e}}}_{k}$$
(22)

The random variables in Eqs. (20) and (21) are approximate to the probability distribution.

$${\varvec{p}}({\tilde{\varvec{e}}}_{{{\varvec{x}}_{{\varvec{k}}} }} ) \sim {\varvec{N}}(0,{\varvec{E}}[{\tilde{\varvec{e}}}_{{{\varvec{x}}_{{\varvec{k}}} }} {\tilde{\varvec{e}}}_{{{\varvec{x}}_{{\varvec{k}}} }}^{\text{T}} ])$$
(23)
$${\varvec{p}}({\varvec{\upvarepsilon}}_{k} ) \sim {\varvec{N}}(0,{\varvec{WQW}}^{\text{T}} )$$
(24)
$${\varvec{p}}({\varvec{\upeta}}_{k} ) \sim {\varvec{N}}(0,{\varvec{VR}}_{{\varvec{k}}} {\varvec{V}}^{\text{T}} )$$
(25)

According to the above approximation, the Kalman filter is used to estimate the equation. \({\hat{\varvec{e}}}_{k}\) can be written as

$${\hat{\varvec{e}}}_{k} = {\varvec{K}}_{k} {\tilde{\varvec{e}}}_{{z_{k} }}$$
(26)

Substituting Eqs. (26) and (19) into Eq. (22), we can observe that the second Kalman filter is not actually required

$${\hat{\varvec{x}}}_{k} = {\tilde{\varvec{x}}}_{k} { + }{\varvec{K}}_{k} {\tilde{\varvec{e}}}_{{z_{k} }} = {\tilde{\varvec{x}}}_{k} { + }{\varvec{K}}_{k} ({\varvec{z}}_{k} - {\tilde{\varvec{z}}}_{k} )$$
(27)

Equation (27) can be used to extend the observation variables of Kalman filtering, where \({\hat{\varvec{x}}}_{k}\) and \({\tilde{\varvec{z}}}_{k}\) are derived from Eqs. (10) and (11), respectively.

3 A self-organizing learning algorithm

In general, training a neural network is a challenging nonlinear optimization problem. Various derivative-based methods have been used to train neural networks. However, they typically tend to converge more slowly or tend to converge to local minima. The Kalman filter is a well-known estimation procedure of a vector of parameters from the available measured data. They have been used to train multilayer perceptions and recurrent networks. The need essential of recursive Kalman filtering algorithm for neural network training, except an orderly way to update the weights and centers of the network, is a two-order differential information approximation error variance matrix that also needs to be maintained and updated, which has the advantage of converging quickly and converge to global minima in the training process. In this study, we extend the use of the Kalman filters to train general multi-input multi-output FNN based on using a pair of parallel EKF to sequentially update both the weights and centers of the network known as the self-organizing learning algorithm.

As mentioned in Sect. 2, the third layer of each node represents the IF part of the possible fuzzy rules or the FNN units. If the number of fuzzy rules requires an identification system, we cannot select the pre-structure of the fuzzy neural networks. Therefore, this study presents a new learning algorithm, which can automatically determine the fuzzy rules of the system, to achieve the system of specific performance.

3.1 Production standards of fuzzy rules

In the fuzzy neural network, if the fuzzy rule number is too high, it will not only increase the system complexity and computational burden, but also reduce the generalization ability of the network. If it is too low, the system will not be able to contain input and output state space completely, and will degrade the network performance. Joining the new fuzzy rules or not depends on three important factors: the system error, accommodate boundary, and the error reduction rate.

3.1.1 The system error

The error criterion can be described as follows: for the i-th observation data \(({\varvec{x}}_{{{\text{o}}i}} ,\;{\varvec{y}}_{{{\text{o}}i}} )\), where \({\varvec{x}}_{{{\text{o}}i}}\) is the input vector; \({\varvec{y}}_{{{\text{o}}i}}\) is the desired output. The current structure of the network of all outputs \({\varvec{y}}_{i}\) is calculated by using Eq. (3). System error is defined as:

$$\left\| {{\varvec{e}}_{i} } \right\| = \left\| {{\varvec{y}}_{{{\text{o}}i}} - {\varvec{x}}_{{{\text{o}}i}} } \right\|;\;i = 1,2, \ldots ,n$$
(28)

If

$$\left\| {{\varvec{e}}_{i} } \right\| > k_{e} ;\;k_{e} = \hbox{max} \left[ {{\varvec{e}}_{\hbox{max} } \times \beta^{i} ,\;{\varvec{e}}_{\hbox{min} } } \right]$$
(29)

then a new rule should be considered; otherwise, new rules should not be produced. The term \(k_{e}\) consists of preselected values according to the expected network precision. \({\varvec{e}}_{\hbox{max} }\) is a pre-defined maximum error, \({\varvec{e}}_{\hbox{min} }\) is the desired output accuracy, and \(\beta (0 < \beta < 1)\) is the convergence factor.

3.1.2 Accommodate boundary

In a way, the efficient performance of FNN learning is the partition of the input space. The FNN structure and performance and the input membership functions are closely related. In this study, we use the Gauss membership function, and output decreases with increase in the center distance. If a new sample is located in a preexisting Gaussian membership function within the scope of coverage, the new samples can use the existing Gaussian membership function, and they do not need the network to generate new Gaussian units.

Accommodate boundary: For the i-th observation data \(({\varvec{x}}_{i} ,\;{\varvec{y}}_{i} )\), we calculated the i-th input values \({\varvec{x}}_{i}\) with the existing FNN units in the center of the \({\varvec{c}}_{i}\) between distance \(d_{i} (j)\)

$$d_{i} (j) = \left\| {{\varvec{x}}_{i} - {\varvec{c}}_{j} } \right\|;\;i = 1,2, \ldots ,n;\;j = 1,2, \ldots ,u$$
(30)

where u is the number of existing fuzzy rules or NN unit.

Define

$$d_{i,\hbox{min} } = \arg \,\hbox{min} \,(d_{i} (j))$$
(31)

If

$$d_{i,\hbox{min} } > k_{d} ,k_{d} = \hbox{max} [d_{\hbox{max} } \times \gamma^{i} ,d_{\hbox{min} } ]$$
(32)

then the existing input membership functions cannot effectively partition the input space. It is necessary to add a new fuzzy rule. If not, the observation data will be represented by using the existing nearest FNN units. The term \(k_{d}\) is the effective radius of the accommodate boundary, \(d_{\hbox{max} }\) is the maximum length of the input space, \(d_{\hbox{min} }\) is the minimum length, and \(\gamma (0 < \gamma < 1)\) is the attenuation factor.

3.1.3 The error reduction rate

In traditional learning algorithms, the learning speed will be reduced because of the pruning process, and increase the computational burden [45, 46]. In this study, a new growth criterion is proposed. The algorithm does not need the pruning process; thus, the learning process will speed up.

Given n input/output data \(({\varvec{x}}_{i} ,\;{\varvec{y}}_{i} ),\;i = 1,2, \ldots ,n\), consider Eq. (3) as a special case of a linear regression model; the linear regression model can be rewritten as

$${\varvec{y}}(i) = \sum\limits_{j = 1}^{u} {{\varvec{h}}_{j} (i){\varvec{\uptheta}}_{j} } + {\varvec{\upvarepsilon}}(i)$$
(33)

Equation (9) can be abbreviated as

$${\varvec{D}} = {\varvec{H}}\varTheta + {\varvec{E}}$$
(34)

where \({\varvec{D}} = {\varvec{T}}^{\text{T}} \in \Re^{n}\) is the expected output, \({\varvec{H}} = {\varvec{\Psi}}^{\text{T}} \in \Re^{n \times u}\) is a regressor, and \(\varTheta = {\varvec{W}}^{\text{T}} \in \Re^{u}\) is a weighting vector; suppose that \({\varvec{E}} \in \Re^{n}\) is not correlated with the regression error vector quantity.

For matrix \({\varvec{\Psi}}\), if its line number is greater than the number of columns, by the decomposition of QR:

$${\varvec{H}} = {\varvec{PQ}}$$
(35)

H transforms into a set of orthogonal basis vectors set \({\varvec{P}} = \left[ {\begin{array}{*{20}c} {{\text{p}}_{1} ,} & {{\text{p}}_{2} ,} & { \ldots ,} & {{\text{p}}_{u} } \\ \end{array} } \right] \in \Re^{n \times u}.\) The dimension is same as that of H, the column vector consists of an orthogonal basis, and \({\varvec{Q}} \in \Re^{{{\text{u}} \times u}}\) is an upper triangular matrix. Through this transformation, it is possible to calculate the contribution of each component to the expected energy output from each base vector. Substituting Eq. (11) into Eq. (10), one can obtain

$${\varvec{D}} = {\varvec{PQ\varTheta }}\,+\,{\varvec{E}} = {\varvec{PG}}\,+\,{\varvec{E}}$$
(36)

Linear least-squares solution of G is \({\varvec{G}}{ = (}{\varvec{P}}^{\text{T}} {\varvec{P}})^{ - 1} {\varvec{P}}^{\text{T}} {\varvec{D}}\), or

$${\text{g}}_{k} = \frac{{p_{k}^{\text{T}} {\varvec{D}}}}{{p_{k}^{\text{T}} p_{k} }};\;k = 1,\;2,\; \ldots ,\;u$$
(37)

\({\varvec{Q}}\) and \({\varvec{\Theta}}\) satisfy the following equation

$${\varvec{Q\varTheta }} = {\varvec{G}}$$
(38)

When \(k \ne l\), \(p_{k}\) and \(p_{l}\) is orthogonal; the quadratic sum of D is given by Eq. (15)

$${\varvec{D}}^{{\varvec{T}}} {\varvec{D}} = \sum\limits_{k = 1}^{u} {g_{k}^{2} p_{k}^{\text{T}} p_{k} + {\varvec{E}}^{{\varvec{T}}} {\varvec{E}}}$$
(39)

On eliminating the mean, the variance of D is given by Eq. (16)

$$n^{ - 1} {\varvec{D}}^{{\varvec{T}}} {\varvec{D}} = n^{ - 1} \sum\limits_{{{\text{k}} = 1}}^{u} {g_{k}^{2} p_{k}^{\text{T}} p_{k} + n^{ - 1} {\varvec{E}}^{{\varvec{T}}} {\varvec{E}}}$$
(40)

From Eq. (16), we can see that \({{n}}^{ - 1} \sum\nolimits_{{{\text{k}} = 1}}^{u} {g_{k}^{2} p_{k}^{\text{T}} p_{k} }\) is a part of expected output variance brought about by regressor \(p_{k}\). Thus, the error rate of decline of \(p_{k}\) can be defined as

$${\text{err}}_{k} = \frac{{g_{k}^{2} p_{k}^{\text{T}} p_{k} }}{{{\varvec{D}}^{{\varvec{T}}} {\varvec{D}}}},\;1 \le k \le u$$
(41)

Substituting Eq. (13) into Eq. (17), one can obtain

$${\text{err}}_{k} = \frac{{(p_{k}^{\text{T}} {\varvec{D}})^{2} }}{{p_{k}^{\text{T}} p_{k} {\varvec{D}}^{{\varvec{T}}} {\varvec{D}}}},\;1 \le k \le u$$
(42)

Equation (18) provides a simple and effective method to return the vales of the quantum set, its significance lies in \({\text{err}}_{k}\) revealed the similarity of \(p_{k}\) and \({\varvec{D}}\). The larger the value of \({\text{err}}_{k}\) and \({\varvec{D}}\), said \(p_{k}\) similarity is greater, and it has a greater effect on output \(p_{k}\). Using \({\text{err}}_{k}\) defining generalized factor (GF), GF can test the generalized ability of the algorithm, and this further simplifies and speeds up the learning process. Definition:

$${\text{GF}} = \sum\limits_{k = 1}^{u} {{\text{err}}_{k} }$$
(43)

Equation (43) can be used to calculate the fuzzy rule numbers. If \({\text{GF}} < k_{\text{GF}}\), then it is necessary to increase additional new fuzzy rules; otherwise, the additional new rules is not necessary where the value of \(k_{\text{GF}}\) is a preselected thresholds value.

3.2 Parameter training by extended Kalman filter

Please note that irrespective of newly generated hidden nodes or those that are already present, the network parameters need to be adjusted. In this study, we have used the EKF method to adjust the parameters of the network. A neural network of nonlinear system equations can be written as

$${\varvec{\uptheta}}_{{k{ + 1}}} = {\varvec{\uptheta}}_{k}$$
(44)
$${\varvec{y}}_{k} = {\varvec{h}} ({\varvec{\uptheta}}_{k} )$$
(45)

where \({\varvec{h}} ({\varvec{\uptheta}}_{k} )\) is a nonlinear mapping between the input and the output of the network. To achieve a stable EKF algorithm, process noise and observation noise are added to the system Eqs. (44) and (45), which can be rewritten as

$${\varvec{\uptheta}}_{{k{ + 1}}} = {\varvec{\uptheta}}_{k} { + }{\varvec{\upomega}}_{\text{k}}$$
(46)
$${\varvec{y}}_{k} = {\varvec{h}} ({\varvec{\uptheta}}_{k} ){ + }{\varvec{v}}_{k}$$
(47)

where \({\varvec{\upomega}}_{\text{k}}\) and \({\varvec{v}}_{k}\) denote the added noise.

In fact, by using the EFK, one can adjust all the parameters of the network. However, the global method will involve large matrix operations and increase the computational burden. Therefore, we can divide the global problem into a series of sub-problems. Because the center and width of the network are nonlinear, it can be adjusted using the EKF algorithm.

The adjustment of the parameters of the former parts: Because of the nonlinear characteristics of the front end of the network, it can be used as follows: The EKF algorithm is used to update the center and width parameters of the membership function of Gauss.

$${\varvec{K}}_{i}^{\delta } = {\varvec{P}}_{i - 1}^{\delta } {\varvec{G}}_{i}^{\text{T}} [{\varvec{R}}_{i} + {\varvec{G}}_{i} {\varvec{P}}_{i - 1}^{\delta } {\varvec{G}}_{i}^{\text{T}} ]^{ - 1}$$
(48)
$${\varvec{\updelta}}_{\text{i}} = {\varvec{\updelta}}_{i - 1} + {\varvec{K}}_{i}^{\delta } ({\varvec{T}}_{i} - {\varvec{W}}_{i - 1} \phi_{i} )$$
(49)
$${\varvec{P}}_{\text{i}}^{\delta } = {\varvec{P}}_{i - 1}^{\delta } - {\varvec{K}}_{i}^{\delta } {\varvec{G}}_{i} {\varvec{P}}_{i - 1}^{\delta } + {\varvec{Q}}_{i}$$
(50)

where \({\varvec{\updelta}}_{\text{i}}\) is the center or width of the membership function of Gauss, \({\varvec{K}}_{i}^{\delta }\) is Kalman gain matrix, and \({\varvec{G}}_{i}\) is the partial derivative of the center or width parameter of the network output for the membership function of Gauss \({\varvec{\updelta}}\). \({\varvec{P}}_{{i}}^{\delta }\) is the forecast error variance matrix, \({\varvec{Q}}_{i}\) is a process noise covariance matrix, and \({\varvec{R}}_{i}\) is the measurement noise covariance matrix.

$${\varvec{G}}_{i} = \left. {\frac{{\partial {\varvec{Y}}_{\text{i}} }}{{\partial {\varvec{\updelta}}_{i - 1} }}} \right|_{{\delta = \hat{\delta }_{i - 1} }} = - 2{\varvec{\updelta}}_{i - 1} \left\| {{\varvec{X}}_{i} - {\varvec{C}}_{j} } \right\|^{2} \sum\limits_{j = 1}^{u} {{\varvec{w}}_{j} \varphi_{j} }$$
(51)

After adjustment of the parameters: Because the back end of the network has a linear feature, the following Kalman filtering algorithm can be used to update the parameters.

$${\varvec{K}}_{i}^{\text{w}} = {\varvec{P}}_{i - 1}^{w} \phi_{i}^{\text{T}} [{\varvec{R}}_{i} + \phi_{i} {\varvec{P}}_{i - 1}^{w} \phi_{i}^{\text{T}} ]^{ - 1}$$
(52)
$${\varvec{W}}_{\text{i}} = {\varvec{W}}_{i - 1} + {\varvec{\rm K}}_{i}^{\text{w}} ({\varvec{T}}_{i} - {\varvec{W}}_{i - 1} \phi_{i} )$$
(53)
$${\varvec{P}}_{\text{i}}^{\text{w}} = {\varvec{P}}_{i - 1}^{w} - {\varvec{K}}_{i}^{w} \phi_{i} {\varvec{P}}_{i - 1}^{w} + {\varvec{Q}}_{i}$$
(54)

where \({\varvec{W}}_{\text{i}}\) is a post-parameter matrix, \({\varvec{K}}_{i}^{\text{w}}\) is Kalman gain matrix, \({\varvec{P}}_{\text{i}}^{\text{w}}\) is the forecast error variance matrix, \({\varvec{Q}}_{i}\) is a process noise covariance matrix, and \({\varvec{R}}_{i}\) is the measurement noise covariance matrix.

3.3 The process of adding fuzzy rules

In the algorithm, the process of adding fuzzy rules is as follows.

Initial parameter allocation: When the first observation data \(({\varvec{x}}_{1} ,{\varvec{y}}_{1} )\) is obtained, the network is not yet established, so the data will be selected as the first fuzzy rule: \({\varvec{C}}_{1} = {\varvec{x}}_{1} = \left[ {\begin{array}{*{20}c} {{{x}}_{11} } & {x_{21} } & \ldots & {x_{r1} } \\ \end{array} } \right]^{\text{T}}\), \({\varvec{\upsigma}}_{1} = {\varvec{\upsigma}}_{0}\), \({\varvec{w}}_{1} = {\varvec{y}}_{1}\), where \({\varvec{\upsigma}}_{0}\) is a pre-defined constant.

Growth process: When the i-th observation data \(({\varvec{x}}_{\text{i}} ,{\varvec{y}}_{i} )\) is obtained, in the third layer, there is a u-th hidden neuron. According to Eqs. (28), (31), and (43), respectively, we can calculate \({\varvec{e}}_{i} ,d_{i,\hbox{min} } ,{\text{GF}}.\)

If

$$\left\| {{\varvec{e}}_{i} } \right\| \ge k_{e} ,d_{i,\hbox{min} } > k_{d} ,{\text{and}}\;{\text{GF}} < k_{\text{GF}}$$
(55)

then add a new hidden neuron, where \(k_{e} ,k_{d}\) are given in Eqs. (29) and (32), respectively. The new increase in the center of the hidden neurons and weights assigned to the center as \({\varvec{C}}_{\text{u + 1}} = {\varvec{x}}_{i} = \left[ {\begin{array}{*{20}c} {x_{1i} } & {x_{2i} } & \ldots & {x_{ri} } \\ \end{array} } \right]^{\text{T}}\), \({\varvec{\updelta}}_{{u{ + 1}}} = {\varvec{k}}_{0} d_{i,\hbox{min} }\), \({\varvec{w}}_{{u{ + 1}}} = {\varvec{e}}_{i}\), where \({\varvec{k}}_{0} (\left\| {{\varvec{k}}_{0} } \right\| > 1)\) is the overlap factor.

Parameter adjustment: When the new neurons are added, the parameters of all the existing neurons are adjusted by using Eqs. (48–54).

Figure 3 illustrates the application of EKF to the training of general multi-input, multi-output FNN for both weights and centers.

Fig. 3
figure 3

Signal flow graph of FNN training based on using a pair of parallel EKF

Full size image

4 Tracking controller design

Define \({\varvec{v}}_{\text{d}}\) as reference velocity. Take \({\varvec{v}}_{\text{d}}\) into the dynamics model of WMM (2), which can be rewritten as

$${\tilde{\varvec{M}}}({\varvec{q}}){\dot{\varvec{v}}}_{\text{d}} + {\tilde{\varvec{C}}}({\varvec{q}},{\dot{\varvec{q}}}){\varvec{v}}_{d} + {\tilde{\varvec{G}}}({\varvec{q}}) + {\tilde{\varvec{F}}}({\varvec{q}},{\dot{\varvec{q}}}) + {\tilde{\varvec{\tau }}}_{s} = {\tilde{\varvec{\tau }}}$$
(56)

The velocity error vector is defined as

$$\varvec{E = }\left[ {\begin{array}{*{20}c} {\varvec{v}_{d} } & { - \varvec{v}} \\ {\dot{\varvec{v}}_{d} } & { - \dot{\varvec{v}}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} \xi \\ {\dot{\xi }} \\ \end{array} } \right].$$
(57)

Differentiating Eq. (57), using Eq. (2), and the mobile robot dynamics can be rewritten in terms of the velocity tracking error as

$${\tilde{\varvec{M}}}({\varvec{q}}){\dot{\varvec{\xi }}}{ = - }{\tilde{\varvec{C}}}({\varvec{q}},{\dot{\varvec{q}}}){\varvec{\upxi}} + {\varvec{g}}({\varvec{\uptheta}}) + {\tilde{\varvec{\tau }}}_{s} { - }{\tilde{\varvec{\tau }}}$$
(58)

where the important nonlinear mobile robot function is defined as

$${\varvec{g}}({\varvec{\uptheta}}) = {\tilde{\varvec{M}}}({\varvec{q}}){\dot{\varvec{v}}}_{\text{d}} { + }{\tilde{\varvec{C}}}({\varvec{q}},{\varvec{v}}){\varvec{v}}_{\text{d}} + {\tilde{\varvec{G}}}({\varvec{q}}) + {\tilde{\varvec{F}}}({\varvec{q}},{\varvec{v}}) + {\tilde{\varvec{\tau }}}_{s} { - }{\tilde{\varvec{\tau }}}$$
(59)

Here, the vector \({\varvec{\uptheta}}\) can be measured by \({\varvec{\uptheta}} \equiv \left[ {\begin{array}{*{20}c} {{\varvec{v}}_{d}^{\text{T}} } & {{\dot{\varvec{v}}}_{d}^{\text{T}} } & {{\varvec{v}}^{\text{T}} } \\ \end{array} } \right]^{\text{T}}\).

Function \({\varvec{g}}({\varvec{\uptheta}})\) contains all the mobile manipulator parameters, such as mass, moments of inertia, and friction coefficients. The system function \({\varvec{g}}({\varvec{\uptheta}})\) is approximated using the FNN described by Eq. (7). The function \({\varvec{g}}({\varvec{\uptheta}})\) can be rewritten as

$${\varvec{g}}({\varvec{\uptheta}}) = {\varvec{w}}^{\text{T}} \phi ({\varvec{\uptheta}}) + {\varvec{\upvarepsilon}}({\varvec{\uptheta}})$$
(60)

where \({\varvec{w}} \in \Re^{(L + 1)}\) is the vector of the ideal threshold and their weights. The bounds described by Eq. (60) are modified for w and \({\varvec{\upvarepsilon}}({\varvec{\uptheta}})\) and expressed as

$$||{\varvec{w}}|| \le b_{w}\,{\text{and}}\,|\varepsilon (\varvec{\theta})| \le b_{\varepsilon } \forall \varvec{\theta}.$$
(61)

The FNN controller is connected in parallel with the PD controller and robust term to generate a compensated control signal. Theoretically, one can directly control the motor movement by the FNN controller. But in our real test process, we found it easy to diverge in joint tracking control process, since the errors in sensors signal acquisition and data fusion process exist. So we use a PD controller to prevent the divergence which caused by signal errors in the system and a robust term to ensure the robustness. They form the inner closed-loop system that controls the velocity error. The control law is given by:

$${\tilde{\varvec{\tau }}} = {\tilde{\varvec{g}}} + {\varvec{KE}} + d\text{sgn} ({\varvec{\upxi}})$$
(62)

where \({\tilde{\varvec{g}}}\) is an estimate of g. KE is the torque produced by the PD controller, and \(d\text{sgn} ({\varvec{\upxi}})\) is the robust term. An estimate of \({\varvec{g}}({\varvec{\uptheta}})\) can be given by:

$${\tilde{\varvec{g}}}({\varvec{\uptheta}}) = {\tilde{\varvec{w}}}^{\text{T}} \tilde{\phi }({\varvec{\uptheta}})$$
(63)

where \({\tilde{\varvec{w}}} \in \Re\) is the vector of the estimated threshold and weights. There is no simple or standard method of judging which choice is the best; hence, our assumption about \(\tilde{\phi } = \phi\) is always feasible. A pair of parallel running extended Kalman filters then can be used to sequentially update both the weights and the centers of the network \({\tilde{\varvec{g}}}\) as description in Sect. 3.

KE is given by

$${\varvec{KE}} = {\varvec{K}}_{\text{P}} {\varvec{\upxi}}{ + }{\varvec{K}}_{\text{D}} {\dot{\varvec{\xi }}}$$
(64)

where \({\varvec{K}}{ = [}{\varvec{K}}_{\text{P}} \quad {\varvec{K}}_{\text{D}} ]\), \({\varvec{K}}_{P} = {\text{diag}}(k_{4} ,k_{5} )]\), and \({\varvec{K}}_{\text{D}} {\text{ = diag}}(k_{6} ,k_{7} )\) are positive matrix with real numbers.

Using the estimated function \({\tilde{\varvec{g}}}({\varvec{\uptheta}})\) given by Eq. (63), the system control law (62) becomes:

$${\tilde{\varvec{\tau }}} = {\tilde{\varvec{w}}}^{\text{T}} \phi ({\varvec{\uptheta}}) + {\varvec{K}}_{P} {\varvec{\upxi}} + {\varvec{K}}_{D} {\dot{\varvec{\xi }}} + d\text{sgn} ({{\varvec{\upxi}} \mathord{\left/ {\vphantom {{\varvec{\upxi}} {\varvec{\updelta}}}} \right. \kern-0pt} {\varvec{\updelta}}})$$
(65)

and the parameter d is defined as:

$$d \ge b_{\varepsilon } + b_{d} + \frac{1}{4}\kappa b_{w}^{2} + \in$$
(66)

which is related to the bounds described by Eq. (59), the parameter \(\kappa\) in Eq. (65), and a strictly positive constant \(\in\).

The structure of the proposed tracking controller scheme is as shown in Fig. 4. The control system is shown in terms of the composition of a compensated controller and a Fuzzy neural network controller.

Fig. 4
figure 4

Structure of the proposed fuzzy neural network-based motion control methodology

Full size image

Next, we perform the system stability analysis of the closed-loop behavior of the proposed control methodology. Substituting the control input (65) into the mobile manipulator dynamics system described by Eq. (56) yields

$$({\tilde{\varvec{M}}} + {\varvec{K}}_{D} ){\dot{\varvec{\xi }}}{ = - (}{\varvec{K}}_{{\varvec{P}}} + {\tilde{\varvec{C}}}){\varvec{\upxi}} + {\hat{\varvec{g}}} - d\text{sgn} ({\varvec{\upxi}})$$
(67)

where \({\hat{\varvec{g}}} = {\varvec{g}}{ - }{\tilde{\varvec{g}}}\) is the function estimation error.

This estimation error is expressed in terms of Eq. (57) as

$${\hat{\varvec{g}}}({\varvec{\uptheta}}) = {\hat{\varvec{w}}}^{\text{T}} \phi ({\varvec{\uptheta}}) + {\varvec{\upvarepsilon}}({\varvec{\uptheta}})$$
(68)

where \({\hat{\varvec{w}}}\) is the vector of the threshold and weight estimation errors, defined as

$${\hat{\varvec{w}}} = {\varvec{w}} - {\tilde{\varvec{w}}}$$
(69)

Therefore, Eq. (62) can be written as

$$({\tilde{\varvec{M}}} + {\varvec{K}}_{D} ){\dot{\varvec{\xi }}}{ = - (}{\varvec{K}}_{{\varvec{P}}} + {\tilde{\varvec{C}}}){\varvec{\upxi}} + {\hat{\varvec{w}}}^{\text{T}} \phi ({\varvec{\uptheta}}) + {\varvec{\upvarepsilon}}({\varvec{\uptheta}}){ - }d\text{sgn} ({\varvec{\upxi}})$$
(70)

Consider the following Lyapunov function candidate

$$\begin{aligned} {\text{V(}}{\varvec{\upxi}},t ) = \frac{1}{2}{\varvec{\upxi}}^{\text{T}} {{\tilde{\varvec M}\xi }} + \frac{1}{2}{\varvec{\upxi}}^{\text{T}} {\varvec{K}}_{D} {\varvec{\upxi}} + \frac{1}{2}\left[ {({\varvec{w}} - {\tilde{\varvec{w}}})^{\text{T}} ({\varvec{\dot{\tilde{w}}}})} \right] \end{aligned}$$
(71)

Differentiation yields

$$\begin{aligned} {\text{{V}(}}{\varvec{\upxi}},t )& = {\varvec{\upxi}}^{\text{T}} {\varvec{\tilde{M}\dot{\xi }}} + \frac{1}{2}{\varvec{\upxi}}^{\text{T}} {\varvec{\dot{\tilde{M}}\dot{\xi }}}{ + }{\varvec{\upxi}}^{\text{T}} {\varvec{K}}_{D} {\dot{\varvec{\xi }}} + {\text{tr}}\left[ {({\varvec{w}} - {\tilde{\varvec{w}}})^{\text{T}} ({\varvec{\dot{\tilde{w}}}})} \right] \\ & = {\varvec{\upxi}}^{\text{T}} ( - \tilde{C}{\varvec{\upxi}} + {\tilde{\varvec{w}}}^{\text{T}} \phi - {\varvec{K}}_{D} {\dot{\varvec{\xi }}} - {\varvec{K}}_{P} {\varvec{\upxi}} + {\varvec{\upvarepsilon}} + {\tilde{\varvec{\tau }}}_{s} { - }d\text{sgn} ({\varvec{\upxi}})) \\ & \quad + \frac{1}{2}{\varvec{\upxi}}^{\text{T}} {\varvec{\tilde{M}\dot{\xi }}} + {\varvec{\upxi}}^{\text{T}} {\varvec{K}}_{D} {\dot{\varvec{\xi }}} - {\text{tr}}\left[ {{\tilde{\varvec{w}}}^{\text{T}} (\phi {\varvec{\upxi}}^{\text{T}} - \kappa \left\| {\varvec{\upxi}} \right\|{\tilde{\varvec{w}}})} \right] \\ & = \frac{1}{2}{\varvec{\upxi}}^{\text{T}} ({\varvec{\dot{\tilde{M}}}} - 2\dot{\tilde{C}}){\varvec{\upxi}} + {\varvec{\upxi}}^{\text{T}} {\tilde{\varvec{w}}}^{\text{T}} \phi - {\varvec{\upxi}}^{\text{T}} {\varvec{K}}_{P} {\varvec{\upxi}}{ - }d\left\| {\varvec{\upxi}} \right\| \\ & \quad + {\varvec{\upxi}}^{\text{T}} ({\varvec{\upvarepsilon}} + {\tilde{\varvec{\tau }}}_{s} ) - {\text{tr}}\left[ {{\tilde{\varvec{w}}}^{\text{T}} \phi {\varvec{\upxi}}^{\text{T}} - \kappa {\tilde{\varvec{w}}}^{\text{T}} \left\| {\varvec{\upxi}} \right\|{\tilde{\varvec{w}}})} \right] \\ & = {\varvec{\upxi}}^{\text{T}} {\tilde{\varvec{w}}}^{\text{T}} \phi - {\varvec{K}}_{P} \left\| {\varvec{\upxi}} \right\|^{2} - d\left\| {\varvec{\upxi}} \right\| + {\varvec{\upxi}}^{\text{T}} ({\varvec{\upvarepsilon}} + {\tilde{\varvec{\tau }}}_{s} ) \\ & \quad - {\text{tr}}\left[ {{\varvec{\upxi}}^{\text{T}} {\tilde{\varvec{w}}}^{\text{T}} \phi } \right]{\text{ + tr}}\left[ {\kappa {\tilde{\varvec{w}}}\left\| {\varvec{\upxi}} \right\|({\varvec{w}} - {\tilde{\varvec{w}}})} \right] \\ & \le - {\varvec{K}}_{P} \left\| {\varvec{\upxi}} \right\|^{2} { - }d\left\| {\varvec{\upxi}} \right\| + \left\| {\varvec{\upxi}} \right\|(\varepsilon + {\tilde{\varvec{\tau }}}_{s} ){ - }\kappa \left\| {\varvec{\upxi}} \right\|\left\| {{\tilde{\varvec{w}}}} \right\|^{2} + \kappa \left\| {\varvec{\upxi}} \right\|\left\| {{\tilde{\varvec{w}}}} \right\|b_{w} \\ & = - {\varvec{K}}_{P} \left\| {\varvec{\upxi}} \right\|^{2} { - }d\left\| {\varvec{\upxi}} \right\| + \left\| {\varvec{\upxi}} \right\|(b_{e} + b_{d} ){ - }\kappa \left\| {\varvec{\upxi}} \right\|(\left\| {{\tilde{\varvec{w}}}} \right\|^{2} - \left\| {{\tilde{\varvec{w}}}} \right\|b_{w} ) \\ & \quad - \frac{1}{4}\kappa b_{w}^{2} \left\| {\varvec{\upxi}} \right\| + \frac{1}{4}\kappa b_{w}^{2} \left\| {\varvec{\upxi}} \right\| \\ & = - {\varvec{K}}_{P} \left\| {\varvec{\upxi}} \right\|^{2} { - }d\left\| {\varvec{\upxi}} \right\| + \left\| {\varvec{\upxi}} \right\|(b_{e} + b_{d} ){ - }\kappa \left\| {\varvec{\upxi}} \right\| \\ & \quad \left( {\left\| {{\tilde{\varvec{w}}}} \right\|^{2} - \left\| {{\tilde{\varvec{w}}}} \right\|b_{w} { + }\frac{1}{4}b_{w}^{2} } \right) + \frac{1}{4}\kappa b_{w}^{2} \left\| {\varvec{\upxi}} \right\| \\ & = - {\varvec{K}}_{P} \left\| {\varvec{\upxi}} \right\|^{2} { - }\left\| {\varvec{\upxi}} \right\|\left\{ {d - b_{e} - b_{d} { + }\kappa \left[ {\left( {\left\| {{\tilde{\varvec{w}}}} \right\| - \frac{1}{2}b_{w} } \right)^{2} - \frac{1}{4}b_{w}^{2} } \right]} \right\} \\ & \le - {\varvec{K}}_{P} \left\| {\varvec{\upxi}} \right\|^{2} { - }\left\| {\varvec{\upxi}} \right\|{ + }\kappa \left[ {\varepsilon { + }\left( {\left\| {{\tilde{\varvec{w}}}} \right\| - \frac{1}{2}b_{w} } \right)^{2} } \right] \\ \end{aligned}$$
(72)

Thus, \(\text{V} \ge 0\) and \(\dot{V} \le 0\) are guaranteed to be negative, and this shows that \(\text{V} \to 0\) and implies \(\xi \to 0\), while \(\dot{\xi } \to 0\) as \(t \to \infty\). Furthermore, Eq. (72) shows \(\text{V} = 0\) if and only if \(\xi \to 0\). Therefore, \({\varvec{v}} \to {\varvec{v}}_{d}\), as \(t \to \infty\).

Remark

In practice, the velocity and tracking errors are not exactly equal to zero when using control law (66). The best we can guarantee is that the error converges in the neighborhood of the origin. The discontinuous function “sign” will give rise to control chattering because of imperfect switching in the computer control. This is undesirable because the unmodeled high-frequency dynamics might become excited. To avoid this, we use the boundary layer technique [43] to smooth the control signal. In a small neighborhood of the velocity error (\({\varvec{\upxi}} = 0\)), the discontinuous function “sign” is replaced by a boundary saturation function \({\text{sat}}({{\varvec{\upxi}} \mathord{\left/ {\vphantom {{\varvec{\upxi}} {\varvec{\updelta}}}} \right. \kern-0pt} {\varvec{\updelta}}})\). Thus, based on dynamics control, the robust neural network motion tracking control law (66) becomes

$${\tilde{\varvec{\tau }}} = {\tilde{\varvec{w}}}^{\text{T}} \phi ({\varvec{\uptheta}}) + {\varvec{K}}_{P} {\varvec{\upxi}} + {\varvec{K}}_{D} {\dot{\varvec{\xi }}} + {\text{dsat}}({{\varvec{\upxi}} \mathord{\left/ {\vphantom {{\varvec{\upxi}} {\varvec{\updelta}}}} \right. \kern-0pt} {\varvec{\updelta}}})$$
(73)

5 Simulation and experimental results

5.1 Trajectory tracking for simulation

In this simulation, we show the process of identification of the dynamic system of a manipulator and predict the future value using proposed control methodology. The dynamic system of the manipulator with two joints is described using Eq. (74), which is defined as:

$${\varvec{M}} (\varvec{q} ){\ddot{\textit{{\varvec q}}}}{ + }{\varvec{V}} ({\varvec{q}} ,{\dot{\varvec{q}}} ){\dot{\varvec{q}}} + {\varvec{G}}({\varvec{q}}) + {\varvec{F}}({\dot{\varvec{q}}}) + {\varvec{\uptau}}_{d} = {\varvec{\uptau}}$$
(74)

where \({\varvec{M}} ({\varvec{q}} ) = \left[ {\begin{array}{*{20}c} {{\text{p}}_{1} + {\text{p}}_{2} + 2p_{3} \cos q_{2} } & {{\text{p}}_{2} + p_{3} \cos q_{2} } \\ {{\text{p}}_{2} + p_{3} \cos q_{2} } & {{\text{p}}_{2} } \\ \end{array} } \right]\), \({\varvec{V}} ({\varvec{q}},{\dot{\varvec{q}}} ) = \left[ {\begin{array}{ll}- {{\text{ p}}_{3} \dot{q}_{2} \sin q_{2} } &\quad- {{\text{ p}}_{3} ( {\dot{\text{q}}}_{1} + \dot{q}_{2} )\sin q_{2} } \\ {{\text{p}}_{3} \dot{q}_{1} \sin q_{2} } & \quad0 \\ \end{array} } \right]\), \({\varvec{G}}({\varvec{q}}) = \left[ {\begin{array}{*{20}c} {{\text{p}}_{4} g\cos q_{1} + {\text{p}}_{5} g\cos (q_{1} + q_{2} )} \\ {{\text{p}}_{5} g\cos (q_{1} + q_{2} )} \\ \end{array} } \right]\), \({\varvec{F}}({\dot{\varvec{q}}}) = 0.02\text{sgn} ({\dot{\varvec{q}}})\), \({\varvec{\uptau}}_{\text{d}} = \left[ {\begin{array}{*{20}c} {20\sin (t)} & {20\sin (t)} \\ \end{array} } \right]^{\text{T}}\).

The reference positions for training of the two joints can be given as \({\text{q}}_{1d} = 0.1\sin (t)\), \({\text{q}}_{2d} = 0.1\sin (t)\). The reference positions for prediction of the two joints can be given as \({\text{q}}_{1d} = 0.5\sin (t)\), \({\text{q}}_{2d} = 0.5\cos (t)\). \({\varvec{p}} = \left[ {\begin{array}{*{20}c} {p_{1} ,} & {p_{2} ,} & {p_{3} ,} & {p_{4} ,} & {p_{5} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {2.9,} & {0.76,} & {0.87,} & {3.04,} & {0.87} \\ \end{array} } \right].\) The parameters of controller (73) are selected as: \({\varvec{K}}_{\text{P}} = {\text{diag}}\{ 35.26,38.45\}\), \({\varvec{K}}_{\text{D}} = {\text{diag}}\{ 25.45,\,20.15\}\), \({\text{b}}_{\varepsilon } = 0.20\), \({\text{b}}_{\text{d}} = 0.10\), \(\kappa {\text{ = b}}_{w} = \iota = 0.01\). In order to obtain the time series, using Eq. (74) to generate 7200 data as the input. We use the first 6000 data pairs as training data sets and the last 1200 data pairs to validate the model’s predictive performance.

Figure 5 shows that the number of fuzzy rules of the algorithm is 12. The algorithm has good generalization ability at the same time. Figures 6, 7, 8 and 9 show the good performance of the algorithm.

Fig. 5
figure 5

Fuzzy rule generation

Full size image
Fig. 6
figure 6

Desired output and training output

Full size image
Fig. 7
figure 7

Desired output and predicted output

Full size image
Fig. 8
figure 8

Predicted error

Full size image
Fig. 9
figure 9

Model uncertainty and estimate

Full size image

5.2 Trajectory tracking for real MRR

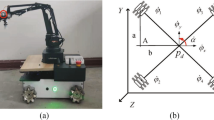
At this stage, a real-life wheeled mobile manipulator is used for the tracking experiment. The robot is named RCAMC-1 (see Fig. 10) [43]. It consists of arm from SCHUNK LWA4/SDH, providing 6 DOF, a four-wheel mobile base with two active wheels (front), and two passive wheels (back). We have written all our software based on VC++ and made use of a variety of open-source packages including KDL (knowledge description language), ROBOOP (an object-oriented toolbox in C++ for robotics simulation), and MATLAB. The API (Automated Precision Inc.) T3 laser tracker system is used for the aided experiment (Fig. 11).

Fig. 10
figure 10

Mobile manipulator used in this study

Full size image
Fig. 11
figure 11

Reference trajectory of the platform

Full size image

In this study, using the main control points as shown in Table 1, a smooth trajectory for mobile manipulator is proposed to be used with the open-door task. The smooth orientation trajectory is generated by interpolating key orientations with the spherical spline quaternion interpolation method, as shown in Fig. 12, and a Hermite cubic polynomial is used to connect these position points to create a rudimentary position trajectory, as shown in Fig. 13. The key joint positions are solved with the inverse kinematics algorithm according to discrete pose sampled with specific accuracy of the task need, and then smooth joint trajectories with stable start–stop motion and continuous jerk are obtained through interpolating key joint positions with B-spline, as shown in Figs. 11 and 14. Next, Eq. (73) is used as the trajectory tracking control law, to realize the planned trajectory tracking. This controller is realized using C++ programming with a cycle of 20 ms (Table 2).

Table 1 Trajectory control points of mobile manipulator
Full size table
Fig. 12
figure 12

Reference pose trajectory of the manipulator

Full size image
Fig. 13
figure 13

Reference orientation trajectory of the manipulator

Full size image
Fig. 14
figure 14

Reference joints trajectory of the manipulator

Full size image
Table 2 Control parameters
Full size table

The response of FNN–EKF-based controller is described under conditions that the dynamic model of the system is not exactly known. The input and output sample data generated from [44]. Figure 15 shows the comparison and errors of reference trajectory and real trajectory for wheeled platform in task space. Figure 16 shows the comparison and errors of reference trajectory and real trajectory for the manipulator in joint space.

Fig. 15
figure 15

Reference and real trajectory of the platform

Full size image
Fig. 16
figure 16

Reference and real trajectory of the manipulator

Full size image

6 Conclusion

The new method for mobile manipulator tracking the desired motion trajectory was developed using fuzzy neural network (FNN) and extended Kalman filter (EKF) approach and the robust control algorithm. The FNN is trained to generate a feedforward torque. For parameter tuning of the FNN, an online EKF methodology is derived to sequentially update both the output weights and centers, so that the tracking velocity and converge property can be guaranteed. When external disturbances and unknown system parameters changed, not only the connecting weights but also the centers are adjusted online. This training scheme will increase the learning capability of the FNN. By several simulations and experiments, it is obvious that the tracking performance was advantageous. The method can be extended to more complex robot configurations, such as tracks or legs, although a method is never the perfect solution. Even so, this paper contribution focuses on the development of a new method for mobile manipulator tracking the desired motion trajectory that provides a better solution of the high-performance control. Experiments were conducted to contrasting the utility and validity of the proposed method. The method proposed in this study supplies another option for similar robots’ process.