1 Introduction

Numerous power conditioning systems are widely seen in industry, such as photovoltaic energy systems, wind energy systems, and hydrogen fuel cell systems. The PCS performance depends on the inverter-LC filter unit, whose task is to transform the DC to AC voltages. Thus, the capability of promising low distorted PCS inverter output voltage under nonlinear loading and fast transient response under phase-controlled loading must be attained; this can be fulfilled by utilizing feedback control strategies. The PI control is frequently applied; but while the loading is highly nonlinear and uncertain, the low distorted output voltage and fast transient response cannot be obtained [1, 2]. Many advanced control technologies derived for power conditioning systems are also cited, such as deadbeat control, repetitive control, and mu-synthesis. As reported in [3], deadbeat control has been successfully applied to control PCS, but this method depends on parameters exactness and PCS output waveform has a noticeable distortion. A multilevel PCS with the use of deadbeat control is presented in [4]; although the proposed system has good steady-state performance, this technique is complex and the transient response is unsatisfactory. A modified deadbeat control methodology is suggested for PCS. The system exhibits very fast dynamic response, but this methodology is sensitive to variations of plant parameter, leading to nonzero steady-state errors [5]. The deadbeat control with robust predictors is applied to the dual-loop regulation of the PCS. Although the scheme presents excellent dynamic response in transient phase of the PCS, the steady-state performance of this scheme with a nonlinear loading is somewhat mediocre [6]. The repetitive control associated with the concept of an adaption-type is proposed for PCS to perform zero steady-state errors and to lessen output voltage distortion in face of nonlinear loading. Nevertheless, such an algorithm suffers from complicated control algorithms [7]. The PCS output is developed by a simpler repetitive scheme, and it attenuates the harmonic components. This scheme has simple control structure and shows low output voltage distortion, but obtains poor transient response in the presence of nonlinear loading [8]. The mu-synthesis is proposed as a choice to PCS control since it resolves the problem of system uncertainties, but its complex algorithm makes digital realization difficult and the steady-state error occurs when the load is highly nonlinear [9, 10]. Sliding mode control (SMC) is inherently robust against internal parameter variations and external interferences [11, 12]. The SMC has displayed that it is a good choice of techniques in PCS design [13–18]. In [13], a reduced state feedback method for PCS is proposed. But, a conventional SMC is employed and such a method results in output voltage distortion in steady-state execution with a nonlinear loading. The tracking control scheme based on input–output feedback linearization SMC technique has also been adopted for PCS design. The high-quality output voltage cannot be seen between steady-state and transient state [14]. Reference [15] utilizes an integral sliding control law to achieve PCS tracking control. This method has poor dynamic response and an undesirable chattering phenomenon. The digital SMC with dual-loop in PCS design is presented [16]; the tracking trajectory runs away target sliding surface and therefore output voltage distortion exists in nonlinear loading. In the works of [17, 18], they adopt continuous-time SMC scheme suitable for power conditioning systems, showing fast dynamic and satisfactory steady state. Nevertheless, owing to nominal loading deviation, the reliability of the SMC deteriorates. As above-mentioned [13–18], the lessened output voltage distortion and fast transient response in SMC design have been reported. But, these use fixed sliding surfaces. For classic SMC design with the fixed sliding surface, the sliding mode exists while the tracking trajectory hits and keeps in the sliding surface. Therefore, a reaching phase indicates the trajectory from an arbitrary primary circumstance tending towards sliding surface; the trajectory is not robust to system interferences before the sliding mode happens [19, 20]. To solve such a problem, the TVSMC with the use of rotating and shifting from arbitrary primary circumstances tending towards the target sliding surface can be utilized. By applying the concept of TVSMC, the insensitivity to system uncertainties can be decreased through speeding up the reaching phase [21, 22]. But, if a highly nonlinear loading is applied, the chattering and steady-state errors will occur in TVSMC system, thus yielding severe output voltage distortion and even degrading PCS performance. The grey prediction (GP) has been successfully applied in a wide variety of fields. The GP without difficult computation and complex mathematical structure is capable of building a grey model by a few data sampling only that can precisely forecast serial system state [23–26]. This paper uses the GP with mathematically simple and arithmetically efficient GP for attenuating the chattering or steady-state errors if the overestimate or underestimate of system uncertainties bounds occurs. Additionally, an adaptive neuro-fuzzy inference system (ANFIS) associating the training ability of neural network with approximate human reasoning of fuzzy logic is popular artificial intelligence technique in many engineering areas [27–30]. The ANFIS assists in generating and optimizing the fuzzy membership functions as well as the fuzzy rules [31–35]. By such a hybrid learning technique, the error between desired and actual output can be minimized [36–39]. Thus, the ANFIS is employed to tune GP-compensated TVSMC control gains optimally so that more precise tracking control can be obtained. By combining TVSMC, GP, and ANFIS, the proposed methodology produces a closed-loop power conditioning system with low total harmonic distortion, fast transient response, chattering alleviation, and steady-state errors attenuation under various loadings. Simulations and experiments are finally shown to validate the performance of the proposed methodology. Section II presents the dynamic modelling of the power conditioning system. The proposed methodology is represented in section III. Sections IV and V represent the simulation and experimental results and conclusions, respectively.

2 System modelling

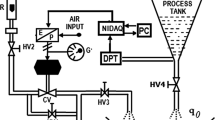
Figure 1 represents the structure of a static power supply, which can be used in power conditioning system. The LC filter and R can be regarded as a plant. The output voltage v c of the plant has to be requested to follow an AC reference v r , by the proposed methodology.

Fig. 1
figure 1

Structure of power conditioning system

Full size image

The plant can be written as

$$\dot{x}_{\text{p}} = A_{\text{p}} x_{\text{p}} + B_{\text{p}} u_{\text{p}} + d$$
(1)

where \(x_{\text{p}} = \left[ {\begin{array}{*{20}c} {x_{{{\text{p}}1}} } & {x_{{{\text{p}}2}} } \\ \end{array} } \right]^{T} = \left[ {\begin{array}{*{20}c} {v_{\text{c}} } & {\dot{v}_{\text{c}} } \\ \end{array} } \right]^{T}\), \(A_{\text{p}} = \left[ {\begin{array}{*{20}c} 0 & 1 \\ { - \frac{1}{\text{LC}}} & { - \frac{1}{\text{RC}}} \\ \end{array} } \right]\), \(B_{\text{p}} = \left[ {\begin{array}{*{20}c} 0 \\ {\frac{1}{\text{LC}}} \\ \end{array} } \right]\), u p is the plant control input, and d is the interference.

The reference model with a sinusoidal reference frequency ω 0 can be represented as

$$\dot{x}_{\text{m}} = A_{\text{m}} x_{\text{m}} + B_{\text{m}} u_{\text{m}}$$
(2)

where \(x_{\text{m}} = \left[ {\begin{array}{*{20}c} {x_{{{\text{m}}1}} } & {x_{{{\text{m}}2}} } \\ \end{array} } \right]^{T} = \left[ {\begin{array}{*{20}c} {v_{\text{r}} } & {\dot{v}_{\text{r}} } \\ \end{array} } \right]^{T}\), \(A_{\text{m}} = \left[ {\begin{array}{*{20}c} 0 & 1 \\ {\omega_{0}^{2} } & 0 \\ \end{array} } \right]\), \(B_{\text{m}} = \left[ {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \right]\), and u m is the model control input.

Thus, the error differential equation yields

$$\left\{ {\begin{array}{*{20}l} {e = x_{\text{m}} - x_{\text{p}} \, } \hfill \\ {\dot{e} = A_{\text{m}} e + (A_{\text{m}} - A_{\text{p}} )x_{\text{p}} + B_{\text{m}} u_{\text{m}} - B_{\text{p}} u_{\text{p}} - d} \hfill \\ \end{array} } \right.$$
(3)

The control goal is to design a control law u p, and then the plant state x p can follow the demanded control x m specified by a reference model. The tracking error e = x m − x p is therefore formulated to carry out the control aim. A control methodology has to be designed for driving the tracking error to zero between the model and the plant states. The control design is developed in the following.

3 Control design

3.1 Time-varying sliding mode control (TVSMC)

The time-varying sliding surface is designed as

$$s = \rho (t)e - \gamma (t)$$
(4)

where ρ(t) = Et + F, γ(t) = Gt + H, and E, F, G, H are constants. The constitution of the proposed methodology by time-varying sliding surface is represented in Fig. 2.

Fig. 2
figure 2

Constitution of the proposed methodology using time-varying sliding surface

Full size image

Figures 3 and 4 indicate that the time-varying sliding surface is composed of rotating sliding surface (RSS) and shifting sliding surface (SSS). The rotating and shifting can be operated by several ways. In the beginning the rotating or shifting relies on the primary state position. When the rotating is applied, the rotating will keep till the trajectory is convergent. When the shifting is applied, the surface is moved as this algorithm demands. Simultaneously, the feasibility of the rotating is checked. If it is feasible, the rotating will continue until the trajectory convergence. Even though the rotating is infeasible, the shifting can guarantee the state converged to the target surface and then move forward to the origin. The algorithms of the RSS and the SSS are outlined below.

Fig. 3
figure 3

RSS structure

Full size image
Fig. 4
figure 4

SSS structure

Full size image

Assume a system with primary circumstance (\(e(t_{0} ), \, \dot{e}(t_{0} )\)) and let the target sliding surface be

$$s = \dot{e} + k_{t} e.$$
(5)

Rotating sliding surface: The primary sliding surface can be selected as

$$s = \dot{e}_{0} + \rho_{0} e_{0}$$
(6)

where \(\rho_{0} {{ = - \dot{e}(t_{0} )} \mathord{\left/ {\vphantom {{ = - \dot{e}(t_{0} )} {e(t_{0} )}}} \right. \kern-0pt} {e(t_{0} )}}\). The sliding surface can be decided as the following.

The new value ρ new can be obtained by the sliding surface moving every Δ τ second.

$$\left| s \right| = \left| {\dot{e} + \rho_{\text{new}} e} \right| = \Delta_{r}$$
(7)

where Δ r must be small so that the system behaviour can maintain on the sliding surface, and a Δ τ needs to be determined, thus moving the system from s(t) = Δ r to s(t + Δ τ ) = 0. In (7), two solutions satisfy the ρ new. When ρ 0 > k t or ρ 0 < k t , the smaller or larger value of the ρ new is applied, and the ρ is decreased or increased. When ρ 0 < k t or ρ 0 > k t , the rotating stops under the circumstance of ρ new ≥ k t or ρ new ≤ k t , and then ρ new = k t is allowed.

Shifting sliding surface: When \(e(t_{0} ), \, \dot{e}(t_{0} ) > 0\), the rotating is infeasible, incurring a non-Hurwitz sliding surface. The shifting with a sliding surface will pass through \(e(t_{0} ), \, \dot{e}(t_{0} )\), and then γ 0 = γ(t 0). The γ = 0 must be obtained and the trajectory is converged to (7).

The new value γ new can be chosen as

$$\left| s \right| = \left| {\dot{e} + \rho e + \gamma_{\text{new}} } \right| = \varDelta_{s}$$
(8)

When γ 0 < 0 or γ 0 > 0, the larger or smaller value of the γ new is applied, and the γ is increased or decreased. When γ 0 > 0 or γ 0 < 0, the shifting stops under the circumstance of γ new ≤ 0 or γ new ≥ 0, and then let γ new = 0.

Differential sliding surface can be expressed as

$$\dot{s} = Ee_{1} + \rho (t)\dot{e} + G$$
(9)

Substituting (3) into (9) gives

$$\begin{aligned} \dot{s} & = Ee_{1} + \rho (t) \times [A_{\text{m}} e + (A_{\text{m}} - A_{p} )x_{\text{p}} \\ \quad + B_{\text{m}} u_{\text{m}} - B_{\text{p}} u_{\text{p}} - d] + G \\ \end{aligned}$$
(10)

The control input is set as

$$u_{\text{p}} = u_{\text{e}} + u_{\text{s}}$$
(11)

where u e indicates the equivalent control that allows the execution of requested sliding mode while system uncertainties are zero. The u s represents the sliding control component that guarantees sliding mode existence and can remove system uncertainties.

The sliding control u s is defined as

$$u_{\text{s}} = Ke + K_{n}$$
(12)

Then, the Lyapunov function can be expressed as

$$V = \frac{1}{2}ss^{2}$$
(13)

By Lyapunov criterion, the control law u p guarantees \(\dot{V} = s\dot{s} < 0\) for satisfying sliding mode existence; thus, the system is asymptotically stable.

3.2 Grey prediction (GP)

The GM(2,1) is adopted to create a grey prediction model, and the grey modelling process is stated in the following.

  • Step 1: Collecting the original sample data sequence

$$x^{(0)} = \left\{ {x^{(0)} (n),\quad n = 1,2, \ldots ,k} \right\}$$
(14)

  • Step 2: Mapping generating operation (MGO)

The system data sequence may be positive or negative, and then the MGO is used to map the negative data to the related positive data.

$$x_{\text{gy}}^{(0)} = \left\{ {x^{(0)} (n) + {\text{BIAS}},\quad k = 1,2, \ldots ,n} \right\}$$
(15)

where BIAS is a constant.

  • Step 3: Taking accumulated generating operation (AGO) for x (0)gy

$$x_{\text{gy}}^{(1)} (n) = \sum\limits_{j = 1}^{n} {x_{\text{gy}}^{(0)} (j),} \quad n = 1,2, \ldots ,k$$
(16)

  • Step 4: Constructing GM(2,1) model

The difference GP model can be written as

$$x_{\text{gy}}^{(1)} (n + 2) + Px_{\text{gy}}^{(1)} (n + 1) + Qx_{\text{gy}}^{(1)} (n) = 0$$
(17)

where P and Q are the coefficients of the GM(2,1) that requires estimating their values.

Equation (17) can be rewritten as

$$\left[ {\begin{array}{*{20}c} { - x_{\text{gy}}^{(1)} (n + 1)} & { - x_{\text{gy}}^{(1)} (n)} \\ \end{array} } \right] \, \left[ {\begin{array}{*{20}c} P \\ Q \\ \end{array} } \right] = \left[ {x_{\text{gy}}^{(1)} (n + 2)} \right]$$
(18)

Letting \(n = 1,2, \ldots ,k - 2\) and (18) becomes

$$\left[ {\begin{array}{*{20}c} { - x_{\text{gy}}^{(1)} (2)} & { - x_{\text{gy}}^{(1)} (1)} \\ { - x_{\text{gy}}^{(1)} (3)} & { - x_{\text{gy}}^{(1)} (2)} \\ \vdots & \vdots \\ { - x_{\text{gy}}^{(1)} (k - 1)} & { - x_{\text{gy}}^{(1)} (k - 2)} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} P \\ Q \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {x_{\text{gy}}^{(1)} (3)} \\ {x_{\text{gy}}^{(1)} (4)} \\ \vdots \\ {x_{\text{gy}}^{(1)} (k)} \\ \end{array} } \right]$$
(19)

Assume \(Y = \left[ {\begin{array}{*{20}c} {x_{\text{gy}}^{(1)} (3)} \\ {x_{\text{gy}}^{(1)} (4)} \\ \vdots \\ {x_{\text{gy}}^{(1)} (k)} \\ \end{array} } \right]\), \(B = \left[ {\begin{array}{*{20}c} { - x_{\text{gy}}^{(1)} (2)} & { - x_{\text{gy}}^{(1)} (1)} \\ { - x_{\text{gy}}^{(1)} (3)} & { - x_{\text{gy}}^{(1)} (2)} \\ \vdots & \vdots \\ { - x_{\text{gy}}^{(1)} (n - 1)} & { - x_{\text{gy}}^{(1)} (n - 2)} \\ \end{array} } \right]\), and \(J = \left[ {\begin{array}{*{20}c} P \\ Q \\ \end{array} } \right]\), then the estimated parameters P and Q can be solved by the least square estimation method as follows:

$$J = \left[ {P, \, Q} \right]^{T} = (B^{T} B)^{ - 1} B^{T} Y$$
(20)

The solution of (20) can be found by defining x (1)gy (n) = β n, x (1)gy (n + 1) = β n+1, and x (1)gy (n + 2) = β n+2, and thus the following equation is obtained as

$$\beta^{n + 2} + P\xi^{n + 1} + Q\xi^{n} = \beta^{n} (\beta^{2} + P\xi + Q) = 0$$
(21)

The roots for satisfying (21) are given as

$$\left\{ {\begin{array}{*{20}c} {\beta_{1} = \frac{{ - P + \sqrt {P^{2} - 4Q} }}{2}} \\ {\beta_{2} = \frac{{ - P - \sqrt {P^{2} - 4Q} }}{2}} \\ \end{array} } \right.$$
(22)

  • Step 5: Taking IAGO

$$\hat{x}_{\text{gy}}^{(0)} (n) = \hat{x}_{\text{gy}}^{(1)} (n) - \hat{x}_{\text{gy}}^{(1)} (n - 1)$$
(23)

  • Step 6: Inversing IMGO

Using IMGO for \(\hat{x}_{\text{gy}}^{(0)}\), the forecasted value of the original data sequence \(\hat{x}^{(0)}\) yields

$$\hat{x}^{(0)} (n + 1) = \hat{x}_{\text{gy}}^{(1)} (n + 1) - \hat{x}_{\text{gy}}^{(1)} (n) - {\text{BIAS}}$$
(24)

The control law of (11) can be restated as

$$u_{\text{p}} (n) = u_{\text{e}} (n) + u_{\text{s}} (n) + u_{\text{gy}} (n)$$
(25)

where the difference GP control, u gy can remove the chattering or attenuate steady-state errors.

$$u_{\text{gy}} (n) = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {\left| {\hat{s}(n)} \right| \le \varepsilon } \hfill \\ {K_{\text{gy}} \hat{s}(n)\text{sgn} (s(n)\hat{s}(n)),} \hfill & {\left| {\hat{s}(n)} \right| \ge \varepsilon } \hfill \\ \end{array} } \right.$$
(26)

where \(\hat{s}(n)\) denotes the predicted value of s(n) and ɛ represents the system boundary.

3.3 Adaptive neuro-fuzzy inference system (ANFIS)

Firstly, a Takagi–Sugeno (T–S) fuzzy structure is created by the ANFIS and then the given training data are modelled.

Then, the ANFIS is written as

$$\begin{aligned} {\text{Rule }}n:{\text{ If }}e_{1} {\text{ is }}A_{n1} {\text{ and }}e_{k} {\text{ is }}A_{nk} \, \hfill \\ {\text{Then }}u_{n} = p_{n1} e_{1} + \cdots + p_{nk} e_{k} + r_{n} \hfill \\ \end{aligned}$$
(27)

where \({\text{Rule }}n\) represents the \(n{\text{th}}\) fuzzy rules, \(n = 1,2, \ldots q\), A ni denotes the fuzzy set in the antecedent associated with the \(i{\text{th}}\) input variable at the \(n{\text{th}}\) fuzzy rule, and p n1, … p nk and r n are the fuzzy resulting parameters.

By the use of the ANFIS, the u p can be obtained as

$$\begin{aligned} u_{\text{p}} & = \frac{{w_{1} }}{{w_{1} + \cdots + w_{\text{q}} }}u_{1} + \cdots + \frac{{w_{\text{q}} }}{{w_{1} + \cdots + w_{\text{q}} }}u_{\text{q}} \\ = \bar{w}_{1} u_{1} + \cdots + \bar{w}_{\text{q}} u_{\text{q}} \\ \end{aligned}$$
(28)

where \(\bar{w}_{1} = \frac{{w_{1} }}{{w_{1} + \cdots + w_{q} }}\) and \(\bar{w}_{q} = \frac{{w_{q} }}{{w_{1} + \cdots + w_{q} }}\).

Owing to \(u_{n} = p_{n1} e_{1} + \cdots + p_{nk} e_{k} + r_{n}\), (28) can be restated as

$$\begin{aligned} u_{\text{p}} & = \bar{w}_{1} u_{1} + \cdots + \bar{w}_{\text{q}} u_{\text{q}} \\ = (\bar{w}_{1} e_{1} )p_{11} + \cdots + (\bar{w}_{1} e_{k} )p_{{1{\text{k}}}} + \bar{w}_{1} r_{1} \\ \quad + \\ \quad \vdots \\ \quad + \, (\bar{w}_{q} e_{1} )p_{{{\text{q}}1}} + \cdots + (\bar{w}_{\text{q}} e_{\text{k}} )p_{qk} + \bar{w}_{\text{q}} r_{\text{q}} \\ \end{aligned}$$
(29)

Equation (29) implies the proposed ANFIS with five-layer structure. More precisely, the concept of the neural network learning algorithm developed in [34] can directly be applied to (29). From the architecture of (29), it can be explored that when the values of premise parameters are given, the overall output can be written as a linear combination of the consequent parameters. More specifically speaking, in the forward pass of the ANFIS, functional signals move ahead till layer 4 and the consequent parameters are recognized by the least squares estimation; in the backward pass, the error rates propagate backward and the premise parameters are updated by the gradient descent method. Figure 5 displays the structure of the ANFIS and concisely summarizes the activities in each pass. The layer 1 represents for inputs, and every node is an adaptive node with a node function. The membership function for A can be any proper parameterized membership function. The layer 2 is for fuzzification, and every node is a fixed node labelled whose output is the product of all the incoming signals. Each node output denotes the firing strength of a rule. The layers 3 and 4 indicate for fuzzy rule evaluation. Every node of the layer 3 is a fixed node labelled N. The outputs of this layer are normalized firing strengths given, and in layer 4, every node is an adaptive node with a node function. Parameters in this layer are referred to as consequent parameters. The layer 5 denotes for defuzzification, and this layer with a fixed node labelled computes the overall output as the summation of all incoming signals.

Fig. 5
figure 5

Structure of the ANFIS

Full size image

4 Simulation and experimental results

To verify the effective operation of the proposed methodology, simulations and experiments are performed. The parameters of the PCS are given as follows: DC-bus voltage V D = 210 V; output voltage v c = 110 V; output frequency f = 60 Hz; filter inductor L = 1.2 mH; filter capacitor C = 10 μF; switching frequency f s = 12 kHz; rated loading R = 12Ω. Figures 6 and 7 show the simulated output voltage and the output current obtained using the proposed methodology and the classic SMC under phase-controlled loading from no load to R = 12Ω at a 90° firing angle every half cycle, respectively. As shown in Fig. 6, a close examination of the waveforms shows that there are a slight voltage droop and a rapid steady-state recovery. But, the voltage waveform shown in Fig. 7 achieves poor dynamic response and very visible period distortion. Evidently, as an abrupt loading disturbance is applied to the AC power conditioner, the proposed controller not only maintains the inherent robustness but has fast dynamic response. To test the performance of the AC power conditioner with the proposed methodology under nonlinear loading consisted of a full-wave diode bridge rectifier with an electrolytic capacitor of 200 μF and load resistance of 55Ω, the simulated output voltage and the output current waveforms are displayed in Fig. 8. The output voltage is very close to sinusoidal waveform with low THD (%THD equals 1.53 %), and high steady-state accuracy is obtained. Compared with the proposed methodology, the simulated waveforms obtained using the classic SMC under nonlinear loading are reported in Fig. 9. The high harmonic distortion exists in output voltage (%THD equals 9.04 %), thus yielding inaccurate steady-state response. Figure 10 displays the experimental output voltage and the output current with the proposed methodology under phase-controlled loading from no load to R = 12Ω. As can be seen, a fast steady-state recovery is achieved. Nevertheless, the experimental waveform with the classic SMC shown in Fig. 11 has unsatisfactory voltage sag compensation. In addition, Figs. 12 and 13 compare the experimental output voltage waveforms of the power conditioning system controlled by the proposed methodology and the classic SMC under LC filter parameter values undergoing 50–250 % variations of 12Ω nominal resistive values. The proposed PCS is more insensitive to the parameter variations than the classic sliding mode controlled PCS. Table 1 displays the simulated and experimental output voltage THD values of the proposed controlled PCS and the classic SMC-controlled PCS under different loads. In final summation, it is well confirmed that the proposed methodology always gives better steady-state accuracy, lower waveform distortion, and quicker convergence rate under various loading conditions, as compared to the classic SMC. The proposed methodology is thus more suitable for use in PCS design.

Fig. 6
figure 6

Simulated waveforms under phase-controlled loading with the proposed methodology (100 V/div; 30A/div; 5 ms/div)

Full size image
Fig. 7
figure 7

Simulated waveforms under phase-controlled with the classic SMC (100 V/div; 30A/div; 5 ms/div)

Full size image
Fig. 8
figure 8

Simulated waveforms under nonlinear loading with the proposed methodology (100 V/div; 30A/div; 5 ms/div)

Full size image
Fig. 9
figure 9

Simulated waveforms under nonlinear loading with the classic SMC (100 V/div; 30A/div; 5 ms/div)

Full size image
Fig. 10
figure 10

Experimental waveforms under phase-controlled loading with the proposed methodology (100 V/div; 20A/div; 5 ms/div)

Full size image
Fig. 11
figure 11

Experimental waveforms under phase-controlled loading with the classic SMC (100 V/div; 20A/div; 5 ms/div)

Full size image
Fig. 12
figure 12

Experimental waveforms under LC parameter variations with the proposed methodology (100 V/div; 5 ms/div)

Full size image
Fig. 13
figure 13

Experimental waveforms under LC parameter variations with the classic SMC (100 V/div; 5 ms/div)

Full size image
Table 1 Simulated and experimental output voltage %THD
Full size table

5 Conclusions

An ANFIS-based grey compensated TVSMC is presented to increase the tracking behaviour of the PCS, even a severe interference is applied. The TVSMC can reduce the reaching phase and is robust to parameter variations and interferences, thus enhancing the robustness of the system. But, while the loading is highly nonlinear, the chattering and steady-state errors yield. For achieving high tracking accuracy, the GP is used to remove the chattering and attenuate steady-state errors, which exists in TVSMC. Moreover, using the ANFIS with reduced rule numbers, faster operation speed and without modifying membership function by conventional trial and error, the control gains of the TVSMC with GP can be optimally tuned. Simulations and DSP-based experiments show that low output voltage distortion, fast dynamic response, chattering reduction, and steady-state errors attenuation are achieved in the presented PCS under both linear loading and nonlinear loading.