Time series forecasting by recurrent product unit neural networks

Abstract

Time series forecasting (TSF) consists on estimating models to predict future values based on previously observed values of time series, and it can be applied to solve many real-world problems. TSF has been traditionally tackled by considering autoregressive neural networks (ARNNs) or recurrent neural networks (RNNs), where hidden nodes are usually configured using additive activation functions, such as sigmoidal functions. ARNNs are based on a short-term memory of the time series in the form of lagged time series values used as inputs, while RNNs include a long-term memory structure. The objective of this paper is twofold. First, it explores the potential of multiplicative nodes for ARNNs, by considering product unit (PU) activation functions, motivated by the fact that PUs are specially useful for modelling highly correlated features, such as the lagged time series values used as inputs for ARNNs. Second, it proposes a new hybrid RNN model based on PUs, by estimating the PU outputs from the combination of a long-term reservoir and the short-term lagged time series values. A complete set of experiments with 29 data sets shows competitive performance for both model proposals, and a set of statistical tests confirms that they achieve the state of the art in TSF, with specially promising results for the proposed hybrid RNN. The experiments in this paper show that the recurrent model is very competitive for relatively large time series, where longer forecast horizons are required, while the autoregressive model is a good selection if the data set is small or if a low computational cost is needed.

1 Introduction

Times series (TS) consist on a succession of data values chronologically sorted that belongs to a magnitude or phenomenon that has been sampled at a certain rate. An example of TS could be the evolution of the maximum daily temperature, the unemployment rate of a country or the amplitude of the seismic waves of an earthquake. Time series is present in most of the science fields like flood forecasting [1], weather forecasting [2] or energy consumption [3].

Nowadays, TS research is focused on TS analysis (TSA) and TS forecasting (TSF). The goal of TSA is to extract the main features and characteristics that describe the underlying phenomena, while the objective of TSF is to find a function to predict the next value of the time series using its p lagged values. It is worth mentioning that the TSA is primordial to reach a good accuracy for TSF, so TSA is usually applied as a preprocessing step in TSF. Finally, TSF can be tackled by univariate or multivariate models. This paper focuses on the former type of models.

Artificial neural networks (ANNs) are a very popular machine learning (ML) tool used for TSF [4]. Feedforward neural networks (FFNNs) are the most common and simplest type of ANNs, where the information moves in a forward direction. For example, the time delay neural network (TDNN) consists on a FFNN whose inputs are the delayed values of the TS [5]. Instead, recurrent neural networks (RNNs) are based on a different architecture where the information through the system moves constituting a direct cycle [6]. This cycle can storage information from previous data in the internal memory of the network, which can be useful for certain kind of applications. RNNs have shown competitive performance in several real-world problems. For example, RNNs based on the method of penalty functions were proposed to solve the bilevel linear programming problem [7]. Furthermore, a RNN approach was also recently proposed to robustly model predictive control for constrained discrete-time nonlinear systems with unmodeled dynamics affected by bounded uncertainties [8]. One example of RNN is the long short-term memory neural network (LSTMNN) [9], whose main characteristic is the capability of its nodes to remember a time series value for an arbitrary length of time. Echo state networks (ESNs) are RNNs whose architecture includes a random number of neurons whose interconnections are also randomly decided. This provides the network with a long-term memory and a competitive generalisation performance [10–12]. In this direction, the minimal complexity which is required for the construction of a competitive RNN is investigated in [12], concluding that a simple deterministically constructed cycle reservoir is comparable to the standard ESN methodology. From the analysis of ANNs in the context of TSF, it can be derived that one of the main differences between FFNNs and RNNs lies on their storage capacity. RNNs have a long-term memory because of the architecture of the model, whereas the memory of FFNNs is provided by the lagged terms at the input of the network.

On the other hand, the parameter estimation algorithm is also very important when analysing the different proposals. The more complex the structure of a neural network is, the more challenging its weight matrix estimation turns. Traditional backpropagation (BP) algorithms can result in a very high computational cost, specially when dealing with complex nonlinear error surfaces [13]. The extreme learning machine (ELM) is an example of an algorithm that can estimate the parameters of a FFNN model efficiently [14]. It is a popular algorithm that determines the hidden layer parameters randomly and the output layer ones by using the Moore–Penrose (MP) generalised inverse [15], providing a better generalisation performance than traditional gradient-based learning algorithms for some problems.

This paper is focused on product unit neural networks (PUNNs) and its application on TSF. The basis function of the hidden neurons of PUNNs is the product unit (PU) function, where the output of the neuron is the product of their inputs raised to real-valued weights. PUNNs are an alternative to sigmoidal neural networks and are based on multiplicative nodes instead of additive ones [16]. Durbin and Rumelhart [16] empirically determined that the information capacity of a single product unit (as measured by its capacity for learning random boolean patterns) is approximately 3N, compared to 2N for a single summation unit, where N is the number of inputs to the units. This model has the ability to express strong interactions between input variables, providing large variations at the output from small variations at the inputs. Consequently, it has increased storage information capability and promising potential for TSF. However, they result in a highly convoluted error function, plenty of local minima. This handicap makes convenient the use of global search algorithms, such as genetic algorithms [17, 18], evolutionary algorithms [19] or swarm optimisation algorithms [20], in order to find the parameters minimising the error function. PUNNs have been widely used in classification [21] and regression problems [22], but scarcely applied to TSF, with the exception of some attempts on hydrological TSA [23, 24]. It is important to point out that, in TSF, there is an autocorrelation between the lagged values of the series. In this way, theoretically, PUNNs should constitute an appropriate model for TSF because they can easily model the interactions (correlations) between the lagged values of the time series.

The first goal of this paper is to evaluate the performance of autoregressive product unit neural networks (ARPUNNs) on TSF. The ARPUNN model should yield high performance for TSF, as it fulfils the requirements that allow the modelling of TS: ability to express the interactions between inputs and increased storage capability. However, as mentioned above, long-term memory ANNs usually obtain better results than FFNNs [25]. For this reason, a second goal of this work is to propose a hybrid ANN combining an ARPUNN with a reservoir network [26] with the objective of increasing the final storage capability. The short-term memory is provided by the different lags of the TS included in the input layer, and the long-term memory is supplied by a reservoir network included as one of the inputs of the system. The final model is called recurrent product unit neural network (RPUNN).

From the point of view of the learning algorithm, the complex error surface associated with PUs implies serious difficulties for searching the best parameters minimising the error function. A hybrid algorithm is proposed in this work to alleviate these difficulties. It combines the exploration abilities of global search algorithms with the exploitation ones of local search methods. The covariance matrix adaptation evolution strategy (CMA-ES) algorithm [27, 28] is used to calculate the parameter values of the hidden layer, whereas the weights of the output layer are determined by means of the MP generalised inverse. CMA-ES has been successfully applied to estimate the weights of neural networks with fixed topologies [29]. Recently, the CMA-ES was also modified to allow the simultaneous determination of topology and weights in neural networks [30]. This combination of an EA and a local search method provides us with a hybrid training of a hybrid model, able to afford the difficulties of TSF and obtain a competitive performance. Although some of the previous works also consider the combination of evolutionary algorithms and PUNNs [21, 22], both the model structure and the training algorithm considered in this paper are different and specifically adapted to TSF.

The model proposed can be seen as a generalisation of the multiplicative neuron model ANN (MNN-ANN) [31]. MNM has only one neuron in the hidden layer. Therefore, the problem of determining the number of neurons in hidden layer is automatically solved when MNM is employed [32]. Previous works have tackled the estimation of MNN-ANN parameters by cooperative random learning particle swarm optimisation (CRPSO), PSO, backpropagation algorithm and genetic algorithms [33]. The model was extended and generalised based on the concept of generalised mean of all multiplicative inputs [34]. Furthermore, the recurrent multiplicative neuron artificial neural network model (RMNM-ANN) was also proposed recently. The RMN-ANN incorporates not just AR terms but moving average terms in the model [35]. The model proposed in this paper provides a greater flexibility for modelling the complex interactions of real-world time series but also have a higher computational complexity if it is compared to the standard MNN-ANN model.

Summarising, the main contributions of this paper are the following:

• The use of PU basis functions in the field of TSF. PU basis functions were already investigated in the field of regression and classification [16, 21, 22]. However, their mathematical expression makes them specially interesting for addressing TSF problems (due to their increased storage capability and their ability to model correlations in the input space).

• A new hybrid RNN combining reservoir computing (RC) models (specifically, ESNs) and FFNs with PU basis functions, with the goal of providing to the model with a long-term memory.

• The use of the CMA-ES algorithm for the parameter estimation of the proposed models. Neural networks based on PU basis functions tend to generate complex error functions with multiple local minima. The use of this standard genetic algorithm allows the proposed models to converge to global minima.

This paper is organised as follows: Sect. 2 describes the ANN hybrid model proposed in this paper to be applied in TSF. Section 3 explains the hybrid search algorithm designed to get the parameters which optimise the error function. Sections 4 and 5 explain the experiments that were carried out and the results obtained. Finally, Sect. 6 summarises the conclusions of this work.

2 Models

In this section, we first introduce an ARPUNN model, which is then extended by considering a reservoir to result in the RPUNN model. The models proposed addressed the TSF problem. This problem is mathematically formulated as follows. Let $\{y_{n}\}_{n = 1}^{N+p}$ be a TS to be predicted, where $N+p$ values are given for training. In this way, the function $f{:}\,{\mathbb {R}}^p \rightarrow {\mathbb {R}}$ is estimated from a training set of N patterns, ${\mathbf {D}} = ({\mathbf {X}},{\mathbf {Y}}) = \{ ({\mathbf {x}}_{n}, y_{n+p})\}_{n=1}^{N}$ where ${\mathbf {x}}_{n}=\{y_{n},\ldots ,y_{n+p-2},y_{n+p-1}\}$ is the vector of input characteristics (p past values of the TS) taking values in the space $\Omega \subset {\mathbb {R}}^p$, and the label, $y_{n+p}$, is the value of the TS for the $n+p$ instant. Both models are explained in the following subsections.

2.1 Short memory model: autoregressive product unit neural network (ARPUNN)

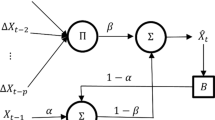
This section presents the first model proposed to address the TSF problem, the so-called ARPUNN. The suggested architecture is based on considering PUs as the basis functions for the hidden layer of the network. PUNN models have the ability to express strong interactions between the input variables. The model is composed by an input, hidden and output layers. The input layer has p input units that correspond to the lagged values of the TS providing the network with a short memory. The hidden layer of the network is composed by S PUs, and the output layer contains only one neuron. A representation of model proposed is shown in Fig. 1.

Fig. 1

Architecture of the autoregressive product unit neural network (ARPUNN)

The final model is linear in the basis function space together with the initial variables. A similar architecture (which is usually referred to as skip-layer connections) was also considered for classification in previous works for PUs [36]. The TS value is estimated by ${\widehat{y}}_{n+p}=f({\mathbf {x}}_{n},{\varvec{\uptheta }}): {\mathbb {R}}^{p} \rightarrow {\mathbb {R}}$, where the final output of the model is defined as:

$$\begin{aligned} f\left( {\mathbf {x}}_{n},{\varvec{\uptheta }}\right) = \beta _0+\mathop {\sum }_{s=1}^{S}\beta _s B_s\left( {\mathbf {x}}_{n},{\mathbf {w}}_s\right) +\mathop {\sum }_{k=1}^{p}\alpha _k y_{n+p-k}, \end{aligned}$$

(1)

where $\beta _s \in {\mathbb {R}}$ denotes the weight of the connection between the hidden neuron s and the output neuron ($s= 1,2,\ldots ,S$), leading the structure that provides the nonlinear contribution of the inputs. The ${\varvec{\upbeta }}$ vector includes all the parameters connecting the hidden with the output layer and the bias ${\varvec{\upbeta }} = (\beta _{0},\beta _1,\beta _2,\ldots ,\beta _{S}) \in {\mathbb {R}}^{S+1}$. The linear contribution of the inputs is controlled by $\alpha _{k}$ which is the weight of the connection between the input k and the output layer ($k=1,2,\ldots ,p$). The vector ${\varvec{\upalpha }}$ contains all the parameters connecting the input and the output layer, ${\varvec{\upalpha }} = (\alpha _{1},\alpha _{2},\ldots ,\alpha _{p}) \in {\mathbb {R}}^{p}$. Another kind of weights, ${\mathbf {w}}_s \in {\mathbb {R}}^{p}$, represents the connections of the hidden neuron s and the input layer. The ${\varvec{\uptheta }}$ vector contains the full parameter vector (${\varvec{\uptheta }}= \{{\mathbf {w}}_1,{\mathbf {w}}_2,\ldots ,{\mathbf {w}}_S,{\varvec{\upbeta }}, {\varvec{\upalpha }}\}$). Finally, $B_s({\mathbf {x}}_{n},{\mathbf {w}}_s): {\mathbb {R}}^{p} \rightarrow {\mathbb {R}}$ represents the output of the sth PU basis function, and it is defined as:

$$\begin{aligned} B_s\left( {\mathbf {x}}_{n},{\mathbf {w}}_s\right) = \prod _{i=1}^{p}\left( y_{n+p-i}\right) ^{w_{is}},\quad s =\left\{ 1 ,\ldots ,S\right\} , \end{aligned}$$

(2)

where $w_{is}\in {\mathbb {R}}$ is the weight of the connection between the ith input node and the sth basis function and $y_{n+p-i}$ denotes the ith lagged past value of the TS.

2.2 Long memory model: recurrent product unit neural network (RPUNN)

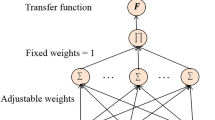
In this section, the long memory model is presented (called recurrent product unit neural network, RPUNN). The RPUNN model reuses the network architecture of the ARPUNN model. One aspect that should be considered on TSF is the memory or the amount of information that can be stored in the network. Traditionally, ANNs with longer memory have an enhanced performance for TSF [25]. The main difference between ARPUNN and RPUNN lies in the inclusion on a new structure as an input, a reservoir network. The reservoir network provides the whole model with long-term and dynamic memory. The structure of the RPUNN is depicted in Fig. 2.¹

Fig. 2

Architecture of the recurrent product unit neural network (RPUNN)

As can be seen, the network inherits the architecture of ARPUNN with the linear and nonlinear combination of the inputs described in the previous section. The output layer contains only one neuron, while the hidden layer of the network is composed by S neurons with the PU basis function. The input layer considered has $p+m$ neurons that correspond to the p lagged values of the TS plus the m outputs of the reservoir network. The p lagged values provide the network with the short memory. The reservoir part is formed by a set of m nodes, and the output of each of these nodes is considered as an input to the PUs, providing the whole structure with a dynamic memory. The only input considered for the reservoir is the first lagged value of the TS. The estimated TS value is defined by the final output of the model, ${\widehat{y}}_{n+p}=f({\mathbf {x}}_{n},{\varvec{\uptheta }}): {\mathbb {R}}^{m+p} \rightarrow {\mathbb {R}}$, as follows:

$$\begin{aligned} f\left( {\mathbf {x}}_{n},{\varvec{\uptheta }}\right) = \beta _0+\mathop {\sum }_{s=1}^{S}\beta _s B_s\left( {\mathbf {x}}_{n},{\varvec{\uppsi }}^{(n)},{\mathbf {w}}_s\right) + \mathop {\sum }_{k=1}^{p}\alpha _k y_{n+p-k} \end{aligned}$$

(3)

where ${\varvec{\uppsi }}^{(n)}\in {\mathbb {R}}^{m}$ is the reservoir state vector for time n, and ${\varvec{\uptheta }}=\{{\mathbf {w}}_1,{\mathbf {w}}_2,\ldots , {\mathbf {w}}_S,{\varvec{\upbeta }}, {\varvec{\upalpha }},{\varvec{\kappa }}\}$ represents the set of the network weights, composed by the vectors ${\varvec{\upbeta }}\in {\mathbb {R}}^{S}$ and ${\varvec{\upalpha }}\in {\mathbb {R}}^{p}$ (previously defined), ${\mathbf {w}}_s \in {\mathbb {R}}^{m+p}$, which represents the connections of the hidden neurons and the input layer, $s=1,\ldots ,S$, and, finally, the matrix of the connections for the reservoir network, ${\varvec{\kappa }}\in {\mathbb {R}}^{m\times (m+2)}$. At last, $B_s({\mathbf {x}}_{n},{\varvec{\uppsi }}^{(n)},{\mathbf {w}}_s): {\mathbb {R}}^{m+p}\rightarrow {\mathbb {R}}$ represents the basis function considered in the hidden layer yielding the following nonlinear output for the model:

$$\begin{aligned} B_s\left( {\mathbf {x}}_{n},{\varvec{\uppsi }}^{(n)},{\mathbf {w}}_s\right) =\mathop {\prod }_{i=1}^{p}\left( y_{n+p-i}\right) ^{w_{is}} \mathop {\prod }_{j=p+1}^{p+m}\left( \psi _j^{(n)}\right) ^{w_{js}} \end{aligned}$$

(4)

where $s = 1, \ldots , S$, ${\mathbf {w}}_s=(w_{1s}, \ldots ,w_{ps}, w_{(p+1)s},\ldots$, $w_{(p+m)s}) \in {\mathbb {R}}^{m+p}$ is the hidden layer weight vector, $w_{is}\in {\mathbb {R}}$ is the weight of the connection between the input neuron i and the hidden neuron s, $i = 1,\ldots ,p$, and $w_{(p+j)s}$ is the weight of the connection between the jth reservoir node and the hidden neuron s, $j = 1,\ldots ,m$. Finally, $\psi _j^{(n)}$ represents the output of the jth reservoir node at time n, $j= 1,\ldots ,m$ and the corresponding vector is ${\varvec{\uppsi }}^{(n)} =\left\{ \psi _1^{(n)}, \ldots ,\psi _m^{(n)}\right\}$.

The reservoir consists of a sparsely connected group of nodes, where each neuron output is randomly assigned to the input of another neuron. This allows the reservoir reproducing specific temporal patterns. All the reservoir nodes are sigmoidal nodes, as this model is more adequate in order to keep the long-term memory:

$$\begin{aligned} \psi _j^{(n)}& = R_j\left( {\varvec{\uppsi }}^{(n-1)},{\varvec{\kappa }}_j\right) \nonumber \\& = \sigma \left( \kappa _{0j}+\mathop {\sum }_{i=1}^{m} \kappa _{ij}\psi _i^{(n-1)} +\kappa _{(m+1)j}y_{n-1}\right) , \end{aligned}$$

(5)

where $\sigma (x)=1/(1+\exp (-x))$ is the sigmoidal activation function and ${\varvec{\kappa }}_j$ is the vector of parameters corresponding to the jth reservoir neuron

$$\begin{aligned} {\varvec{\kappa }}_j=\left\{ \kappa _{0j},\kappa _{1j},\ldots ,\kappa _{mj}, \kappa _{(m+1)j}\right\} , \end{aligned}$$

with $m+2$ elements. As can be observed, self-connections are allowed. The internal structure of the reservoir is randomly fixed and kept constant during the learning process, in the same vein than it is done with ESNs [11].

3 Parameter estimation

This section discusses the training algorithm proposed to fit ARPUNN and RPUNN parameters. As stated above, PUNNs exhibit a highly convoluted error surface, which can easily make the training algorithm get stuck in local minima and, in consequence, avoid that the optimum parameters are obtained. In general, this can be overcome by using global search algorithms, but instead they can be slow to reach the global optimum. The method considered in this work focuses in obtaining a trade-off between both extremes, which is achieved by a hybrid algorithm. The parameter set to be optimised in the ARPUNN model is

$$\begin{aligned} {\varvec{\uptheta }}=\left\{ {\varvec{\upbeta }},{\varvec{\upalpha }}, {\mathbf {w}}_1,{\mathbf {w}}_2,\ldots ,{\mathbf {w}}_S\right\} , \end{aligned}$$

which is composed by the set of weights of the hidden layer nodes (${\mathbf {w}}_1,{\mathbf {w}}_2, \ldots ,{\mathbf {w}}_S$) and the set of weights of the output layer, ${\varvec{\upbeta }}$ and ${\varvec{\upalpha }}$. In the case of the RPUNN, it is also required to estimate the values of the parameters included in the vector ${\varvec{\kappa }}$, i.e. the weights of the reservoir interconnections.

The beginning of the algorithm involves the CMA-ES method as a global optimisation procedure [27]. CMA-ES is an evolutionary algorithm for difficult nonlinear non-convex optimisation problems in continuous domain. The evolution strategy defined in this algorithm is based on the use of a covariance matrix that represents the pairwise dependencies between the candidate values of the variables to be optimised. The distribution of the covariance matrix is updated by means of the covariance matrix adaptation method that attempts to learn a second-order model of the cost function similar to the optimisation made in the quasi-Newton methods [37]. The CMA-ES has several invariance properties and does not require a complex parameter tuning. In this paper, the uncertainty is undertaken as proposed in [38] and a subtractive update of the covariance matrix is done as in [28]. Another consideration is to adapt only the diagonal of the covariance matrix for a number of initial iterations, as stated in [39], leading to a faster learning. The upper and lower bounds of the parameters are handled as proposed in [38]. The standard deviation considered in the initialisation stage is set to 0.3. For both ARPUNN and RPUNN models, the target parameters under optimisation by the CMA-ES algorithm are the weights from the input layer to the hidden layer $\{{\mathbf {w}}_1,{\mathbf {w}}_2,\ldots ,{\mathbf {w}}_S\}$. The hybrid algorithm starts by randomly generating the values for these weights. Although the rest of the weights are needed to obtain the cost function, they can be analytically calculated by using the MP generalised inverse, as done in the ELM [15]. This process has to be performed on each iteration of the CMA-ES algorithm and for each individual of the population. Let ${\varvec{\upphi }}=(\beta _1,\ldots , \beta _S,\alpha _1,\ldots ,\alpha _p)^{{\mathrm{T}}}$ denote the weights of the links connecting hidden and output layers. The calculation of ${\varvec{\upphi }}$ can be done by taking into account that the system is linear if the basis function space is considered. In this way, the nonlinear system can be converted into a linear system:

$$\begin{aligned} {\mathbf {Y}} = {\mathbf {H}}{\varvec{\upphi }}, \end{aligned}$$

(6)

where ${\mathbf {H}}=\{h_{ij}\}$ ($i=1,\ldots ,N$ and $j=1,\ldots ,S+p$) represents the hidden and input layers output matrix: if $j = 1,\ldots ,S$, $h_{ij}=B_{j}({\mathbf {x}}_{i},{\mathbf {w}}_{j})$ (for the ARPUNN model) or $h_{ij} = B_j({\mathbf {x}}_{i},{\varvec{\uppsi }}^{(i)},{\mathbf {w}}_j)$ (for the RPUNN model); if $j = S+1, \ldots , S+p$, $h_{ij}= y_{i+p-j}$. Finally, the determination of ${\varvec{\upphi }}$ can be obtained by finding the least-square solution of the equation:

$$\begin{aligned} {\hat{{\varvec{\upphi }}}} = {\mathbf {H}}^\dagger {\varvec{Y}} \end{aligned}$$

(7)

where ${\mathbf {H}}^{\dagger }$ is the MP generalised inverse of the matrix ${\mathbf {H}}$. The solution provided by this method is unique, and it has the smallest norm within all least-square solutions. In addition, it obtains a high generalisation performance that decreases the time required to learn the sequence as states [40].

The parameters of the reservoir for the RPUNN model are randomly fixed before starting the CMA-ES optimisation and then kept constant for the whole evolution, given that, otherwise, the computational cost and the complexity of the final model would increase significantly. Sparsity is achieved by randomly setting to 0 a percentage (in our case, $\sim 90\,\%$) of the weights for the connections between reservoir nodes (i.e. $\kappa _{ij}=0$, for some randomly selected i and j values, $i = 1,\ldots ,m$, $j = 1,\ldots ,m$). The reservoir is composed of 30 sigmoidal nodes that are not considered in the value computed as number of hidden neurons (NHNs) of the experimental part. The spectral radius $\alpha$ is set to 0.5. The weights of the reservoir are randomly initialised from a uniform distribution over $[-1, 1]$. After this initialisation, the weights of the reservoir are normalised to a spectral radius $\alpha < 1$, by scaling them using the factor $\alpha /|\lambda _{{\mathrm {max}}}|$, where $\lambda _{{\mathrm {max}}}$ is the largest eigenvalue of the vector of weights (as suggested in [41]). Finally, isolated reservoir neurons are not allowed in the model to guarantee the consistency of the network.

4 Experiments

In order to analyse the performance of the proposed methods, an experimental study was carried out. The TS data selected, the metrics considered to evaluate the performance of the models and the algorithms used for comparison purposes are described in the following subsections.

4.1 Data sets selected

The time series used for the experimental set-up belongs to the NNGC1, Acont, B1dat, D1dat and Edat forecasting competitions.² These data sets were selected based on the TSF task proposed in [42]. A total of 29 time series available in the KEEL-data set repository³ [43] have been considered.

The NNGC1 data sets contain transportation data, including highway traffic, traffic data of cars in tunnels, traffic at automatic payment systems on highways, traffic of individuals on subway systems, domestic aircraft flights, shipping imports, border crossings, pipeline flows and rail transportation that are sampled with a weekly, daily or hourly frequency. Specifically, 24 time series belonging to this set have been used. In the case of the Acont data set, only one time series has been used that contains a laser univariate time record of a single observed quantity, measured in a physics laboratory experiment. On the other hand, B1dat is a multivariate data set recorded from a patient in the sleep laboratory of the Beth Israel Hospital, in Boston, Massachusetts. The lines in the original data set file are spaced by 0.5 s. The data set contains three physiological measurements: the first is the heart rate, the second is the chest volume (respiration force), and the third is the blood oxygen concentration (measured by ear oximetry). The Edat is a set of measurements of the light curve (time variation of the intensity) of the variable white dwarf star PG1159-035 during March 1989, and it was recorded by the Whole Earth Telescope (a coordinated group of telescopes distributed around the Earth that permits the continuous observation of an astronomical object). Finally, the Ddat is a time series data set generated synthetically by a computer. Table 1 describes the main features of the time series used in the experiments.

Table 1 Characteristics of the benchmark data sets, alphabetically ordered

Following the procedures used in [42], the augmented Dickey–Fuller [44] test has been applied to the series in order to consider only stationary series. In addition, linearity test has been performed during the building procedure in order to exclude data sets that exhibit linear properties. The lag set was adjusted using an uniform embedding with a constant time lag through adjacent input channels. Specifically, four lagged values were considered. Although other alternative embeddings could be considered [45], this decision was taken to simplify the experimentation.

Finally, the data sets have been preprocessed to adapt the inputs to the mathematical characteristics of the PU-based models: input variables have been scaled in the rank [0.1, 0.9].⁴ The experimental design was conducted using a fivefold cross-validation, with 10 repetitions per each fold.

4.2 Metrics considered for evaluation

The metrics considered in this paper are the mean absolute percentage error (MAPE) (in the generalisation set, ${{\mathrm {MAPE}}}_{{\mathrm {G}}}$) and the number of hidden nodes (NHN). Given that all the models consider fully connected neurons, NHN is a measure of the size of the neural network. Neural networks are very sensitive to this value (generally, large networks require a longer processing time [46]).

4.3 Algorithms selected for comparison purposes

In order to evaluate the performance of the RPUNN and ARPUNN models, they have been compared to some of the most promising neural networks models for TSF. Aiming to outline different characteristics of the methods, the compared methods have been grouped in two sets. The main objective behind the first set of models is comparing ARPUNN and RPUNN methods to baseline algorithms. This set is composed by the following methods:

• The minimum complexity echo state network (MCESN) [12]. This model is constructed deterministically unlike the standard ESNs. The architecture used is the simple cycle reservoir (SCR) one due to its competitive accuracy as reported in [12].

• The nonlinear autoregressive neural network (NARNN) proposed in [47].

• The standard echo state network (ESN) [26].

• The extreme learning machine method (ELM) [15].

The second set of models is selected with the purpose of analysing the performance of PU basis functions for TSF. Due to this, the two models proposed are compared to ANN models trained with the same algorithm, but considering other basis functions. The models employed in this set are:

• The nonlinear autoregressive radial basis function neural network (NARRBFNN).

• The nonlinear autoregressive sigmoidal neural network (NARSIGNN).

All the hyperparameters considered in this paper were estimated by a nested fivefold cross-validation procedure. The most important hyperparameter was the NHN, and the corresponding range of possible values considered for model selection depends on the model in the following manner:

• In the case of the NARNN, NARRBFNN, NARSIGNN, ARPUNN and RPUNN algorithms, the experiment was carried out using neural networks with 5, 10, 15 and 20 hidden nodes.

• The MCESN, ESN and ELM algorithms require a higher number of hidden neurons that can supply the network with sufficiently informative random projections [12, 15]. In this case, neural networks with 10, 20, 50, 100, 150, 200 and 300 hidden nodes were considered.

In order to control the overfitting of the models developed in this paper, three approaches have been implemented:

• The output weights of the models were determined through the MP pseudoinverse, ensuring that these parameters have the smallest norm within all least-square solutions.

• As previously discussed, the NHN was determined through a fivefold cross-validation procedure over the training set.

• Different boundaries for the weights connecting the input and the hidden layer were considered:

  • The hidden layer weights of the ARPUNN and RPUNN algorithms are initialised randomly within the interval $[-5,5]$, which is also the boundary considered for their input weights.

  • In the case of the NARRFBNN algorithm, the boundary established for the centroids of the RBFs, as well as the limits for input variable normalisation, were [0.1, 0.9].

  • The weights of NARSIGNN and ELM algorithms were randomly initialised in the interval [0, 1].

The range considered was determined after preliminary experiments and an analysis of the characteristic of the basis functions of each model. Furthermore, these bounds were already tested in the literature for PUNN models in function approximation and classification problems [36, 48].

Once the test prediction with a given model has been done, some considerations have been considered in order to provide a fair comparison between the different tested algorithms. The architecture of the ESN and MCESN methods requires several cycles until a proper predicted value can be obtained. The first cycles of the model are used to accommodate for a washout of the arbitrary (random or zero) initial reservoir state needed at time 1. For this reason, part of the first samples of the data set need to be discarded. In the experiments undertaken, a discard rate of the 25 % of the first samples of each data set has been considered. This constraint has been applied to every data set independently of the method used for TSF, in order to assure equitable MAPE values.

5 Results

For all of the 29 data series, models were trained, predictions were made on the test set, and the MAPE and NHN were computed. A ranking has been established (${\overline{R}}_{{\mathrm{MAPE}}}$ and ${\overline{R}}_{{\mathrm{NHN}}}$) for each method in each data set depending on the value obtained for MAPE and NHN ($R=1$ stands for the best performing method and $R=8$ for the worst one). The complete table of results has been included in a separated document.⁵ Analysing the results obtained for the MAPE from a descriptive point of view, it can be seen that the proposed models in this study achieved a considerable competitive performance. The ARPUNN method obtains the best results in 2 out of the 29 data sets considered, while the improved version of the ARPUNN, the RPUNN, achieves the best results in 14 out of the 29 data sets tested. With regard to the NHN metric, it is worth mentioning the competitive results achieved by the ARPUNN model. This model yielded the second best ranking for the NHN metric, being outperformed only by MCESN.

Additionally, Table 2 also reports the averaged results over all the series for the methods compared (including the averaged value for the metric and the averaged ranking). As shown in Table 2, the RPUNN model yielded the best mean in MAPE (${\overline{{\mathrm{MAPE}}}}=0.1345$ and ${\overline{R}}_{{\mathrm{MAPE}}_{{\mathrm {G}}}}=2.2758$) followed by the ARPUNN model (${\overline{{\mathrm{MAPE}}}}=0.1400$ and ${\overline{R}}_{{\mathrm{MAPE}}_{{\mathrm {G}}}}=3.4827$). The minimum ${\overline{{\mathrm{NHN}}}}$ is obtained by the MCESN model with a mean of 11.17 followed by the ESN model with a mean of 12.06. In terms of NHN ranking, the best results are obtained by the MCESN model with a 2.86 mean position, followed by the ARPUNN model with a 3.17 mean position. The RPUNN model leads to a ${\overline{{\mathrm{NHN}}}}$ of 15.10 and a ${\overline{R}}_{{\mathrm{NHN}}}$ of 4.79. After the examination of the experimental results,⁶ we can conclude that the RPUNN model seems to obtain lower error if the data set to be forecasted is relatively large, because longer forecast horizons are required (note that the best results for RPUNN are obtained when large data sets are evaluated). However, its computational cost is higher than that of ARPUNN (see the end of this section). On the contrary, the ARPUNN model is more precise if the data set is relatively small (shorter memory is required), and it should be selected when the competitive computational cost is a must. A boxplot of the results obtained for the ranking of the ${\mathrm{MAPE}}_{{\mathrm {G}}}$ and NHN is shown in Fig. 3 where it can be appreciated the performance above mentioned.

Table 2 Summary of results for MAPE and NHN as the test variables

Fig. 3

Boxplot for the average ranking of ${{\mathrm {MAPE}}}_{{\mathrm {G}}}$ (MAPE over the generalisation set) and NHN over the 29 data sets. a Test variable: R${{\mathrm {MAPE}}}_{{\mathrm {G}}}$, b Test Variable: R_NHN

The significance of the experimental results was assessed by using nonparametric statistical tests. Following the methodology recommended by Demsar [49] for this type of multiple comparisons, we have used Friedman, Nemenyi and Holm statistical tests. Friedman test checks whether there are significant differences in the results, while Nemenyi is used to detect which of all the comparable pairs are significantly different. Holm test can be applied when a control method is considered and corrects the statistics for multiple comparisons. A detailed description of these tests can be found in Zar’s book [50] and in [51–53]. This kind of statistical validation has been extensively applied in time series forecasting [42, 54–56]. The pre-hoc Friedman test has been performed with the ranking obtained in the MAPE and NHN of the best models as test variables. The test shows that the effect of the method used for forecasting is statistically significant at a significance level of 10 %, as the confidence interval is $C_0=(0,F_{0.10}=1.809)$ and the F-distribution statistical values are $F^*=19.47 \not \in C_0$ for NHN and $F^*=17.40 \not \in C_0$ for MAPE. Therefore, null hypothesis is rejected stating that all algorithms perform equally in mean ranking.

According to the previous rejection results, the Nemenyi post hoc test has been used in order to compare all the models to each other. The Nemenyi test analyses the performance of different models considering that a model is significantly different if its mean rank differs by at least the critical difference (CD) defined by:

$$\begin{aligned} {\mathrm{CD}} = q \sqrt{\frac{K(K+1)}{6D}} \end{aligned}$$

(8)

where K and D are the number of models and data sets used and q is derived from the studentised range statistic divided by $\sqrt{2}$. The results of the Nemenyi test for $\alpha = 0.10$ are shown in Fig. 4, where the CD is shown for MAPE and NHN, and the mean ranking of each algorithm is represented in the scale. When the mean rankings of two algorithms differ more than the CD, then significant differences can be assessed.

Fig. 4

Ranking test diagrams for the mean generalisation MAPE and NHN $(\alpha = 0.10)$. a Nemenyi CD diagram comparing the generalization MAPE mean rankings of the different methods, b Nemenyi CD diagram comparing NHN mean rankings of the different methods

The results of the Nemenyi test for $\alpha = 0.10$ in the case of the MAPE metric show that the RPUNN model is significantly better than the state-of-the-art models considered in our experiments except ARPUNN and NARNN. Regarding the NHN parameter, there are no significant differences between the models that present the best results: MCESN, ARPUNN, ESN, NARNN and NARBFNN. The rest of the models present a lower performance due to their complex architecture that requires a higher NHN.

Table 3 Results of the Holm test considering the ${\mathrm{MAPE}}_{{\mathrm {G}}}$ and NHN as the test variables

Generally, the results of the Nemenyi test comparing all models to each other in a post hoc are not as sensitive as the approach of comparing all the models to a given one, that is used as a control method. This is the philosophy followed by the Holm test presented now. The results of the Holm test are available in Table 3. The control methods used for the ${{\mathrm {MAPE}}}_{{\mathrm {G}}}$ and NHN measures are RPUNN and MCESN, as they have the best ranking performances, respectively.

The results given by the Holm test show slightly different results than those obtained with the Nemenyi test. In the case of the Holm test, it can be appreciated that the RPUNN model performs significantly better (in MAPE) than the rest of the models. Regarding the NHN metric, the MCESN method shows a significant lower complexity than the RPUNN, NARSIGNN and ELM methods.

Finally, the computational time of the proposed methods is analysed and compared to that of the algorithms already presented in the experimental section. The computational time recorded included the whole training process: cross-validation, training and test. This time is shown in Table 4. The number of hyperparameters of each method is decisive for the final time spent in running the algorithms, given that they have to be adjusted using a time-consuming cross-validation process. It is clear that the methods proposed in this paper (NARRBFNN, NARSIGNN, ARPUNN and RPUNN) have a higher computational cost, which is mainly due to the application of the CMA-ES evolutionary algorithm. From the three autoregressive models (NARRBFNN, NARSIGNN and ARPUNN), the lowest time is obtained with sigmoidal nodes, followed by PUs. The exponentiation of PUs implies a higher computational time than sigmoidal basis functions, while lower than that of RBFs. On the other hand, the use of the reservoir (RPUNN) increases the computational time with respect to RPUNN.

Table 4 Average of computational time results in seconds (cross-validation, training and test) for the 29 data sets considered and all the methods

The application of EAs is a controversial topic in ANN literature. evolutionary algorithms (EAs) and, in general, global search algorithms are computationally expensive especially when compared to local search algorithms, but the evolution of weights enables ANNs to avoid local minima in different data sets without human intervention or multiple repetitions [57], usually leading to better accuracy. In any case, ARPUNN and RPUNN are intended for environments where the training time is not a critical feature. Searching in a space with very few restrictions allows more solutions to be explored, but it is also more time-consuming. The improvement of accuracy obtained for the different data sets justifies the computational time.

6 Conclusions

This paper proposes two new models of ANNs based on the use of PUs as a basis function for time series forecasting (TSF). The interest on the use of PUs arises from its ability to express strong interactions between input variables, a feature truly important in TSF where there is autocorrelation between the lagged values of the time series (TS). Two models of PUNNs have been implemented, the ARPUNN and the RPUNN, which consists on an enhanced version of the ARPUNN. The architecture of ARPUNN considers a short-term memory provided by the lagged values of the TS, whereas the RPUNN model includes an additional set of inputs supplied by a reservoir network which provides a long-term memory to the model. The parameters of the models were determined by a hybrid learning algorithm that combines a global and a local search methods (the CMA-ES algorithm and the use of the MP generalised inverse, respectively).

TS data sets available in the community have been used as benchmark test sets. Five baseline algorithms from the state-of-the-art TSF literature (NARNN, NARRBFNN, ESN, ELM and NARSIGNN) and one advanced recurrent neural network model have been used for comparison and the model performance has been evaluated using the mean absolute percentage error (MAPE) and the number of hidden nodes (NHN) measures. Finally, nonparametric statistical tests have been performed to validate the results and the models have been compared also in terms of computational efficiency. The results show that the introduced models present a very good performance in terms of MAPE and NHN, at the cost of a higher computational cost.

Some suggestions for future research are the following: to use the proposed algorithms on other real-world applications, such as detection of tipping points [58] or stock market forecasting,⁷ to investigate the use of other advanced basis functions such as the generalised radial basis function [59] in the place of the product unit basis functions, and to analyse the impact of regularisation procedures in the models proposed.