RETRACTED ARTICLE: Solutions of Bagley–Torvik and Painlevé equations of fractional order using iterative reproducing kernel algorithm with error estimates

Abstract

This paper presents iterative reproducing kernel algorithm for obtaining the numerical solutions of Bagley–Torvik and Painlevé equations of fractional order. The representation of the exact and the numerical solutions is given in the $\hat{W}_{2}^{3} \left[ {0,1} \right]$, $W_{2}^{3} \left[ {0,1} \right]$, and $W_{2}^{1} \left[ {0,1} \right]$ inner product spaces. The computation of the required grid points is relying on the $\hat{R}_{t}^{{\left\{ 3 \right\}}} \left( s \right)$, $R_{t}^{{\left\{ 3 \right\}}} \left( s \right)$, and $R_{t}^{{\left\{ 1 \right\}}} \left( s \right)$ reproducing kernel functions. An efficient construction is given to obtain the numerical solutions for the equations together with an existence proof of the exact solutions based upon the reproducing kernel theory. Numerical solutions of such fractional equations are acquired by interrupting the $n$-term of the exact solutions. In this approach, numerical examples were analyzed to illustrate the design procedure and confirm the performance of the proposed algorithm in the form of tabulate data, numerical comparisons, and graphical results. Finally, the utilized results show the significant improvement in the algorithm while saving the convergence accuracy and time.

1 Introduction

Fractional calculus theory is a branch of the mathematical analysis that studies the possibility of taking real number powers of the differentiation and the integration operators. This generalized calculus is one of the most valuable and suitable tools to refine the description of numerous physical phenomena in science and engineering, which are indeed nonlinear. In mechanics, for example, fractional-order derivatives have been successfully used to model damping forces with memory effect or to describe state feedback controllers [1–5]. In particular, the $1/2$-order derivative or $3/2$-order derivative describe the frequency-dependent damping materials quite satisfactorily, and the Bagley–Torvik equation with $1/2$-order derivative or $3/2$-order derivative describes motion of real physical systems, an immersed plate in a Newtonian fluid and a gas in a fluid, respectively [6, 7]. In fact, many physical phenomena can be modeled by fractional differentia equations (FDEs), which have different applications in various areas of science and engineering such as thermal systems, turbulence, image processing, fluid flow, mechanics, and viscoelastic [1–5].

In this paper, iterative form of the reproducing kernel algorithm (RKA) has been investigated systematically for the development, analysis, and implementation of an accurate algorithm for the use of some form of concurrent processing technique for solving Bagley–Torvik and Painlevé equations of fractional order. More precisely, we consider the following set of FDEs:

• The fractional Bagley–Torvik equation:

  $$ \left\{ {\begin{array}{l} {a_{1} \left( t \right)y^{\prime \prime } \left( t \right) + a_{2} \left( t \right)D^{1.5} y\left( t \right) + a_{3} \left( t \right)y^{\prime } \left( t \right) + a_{4} \left( t \right)D^{0.5} y\left( t \right) + a_{5} \left( t \right)y\left( t \right) = f\left( t \right),} \hfill \\ {y\left( 0 \right) = \gamma_{0} , y^{\prime } \left( 0 \right) = \gamma_{1} ,} \hfill \\ {y\left( 0 \right) = \gamma_{0} , y\left( 1 \right) = \gamma_{1} .} \hfill \\ \end{array} } \right. $$

  (1)

• The first fractional Painlevé equation:

  $$ \left\{ {\begin{array}{l} {D^{\alpha } y\left( t \right) = 6y^{2} \left( t \right) + t,} \hfill \\ {y\left( 0 \right) = \gamma_{0} , y^{{\prime }} \left( 0 \right) = \gamma_{1} .} \hfill \\ \end{array} } \right. $$

  (2)

• The second fractional Painlevé equation:

  $$ \left\{ {\begin{array}{l} {D^{\alpha } y\left( t \right) = 2y^{3} \left( t \right) + ty\left( t \right) + \lambda , } \hfill \\ {y\left( 0 \right) = \gamma_{0} , y^{\prime } \left( 0 \right) = \gamma_{1} .} \hfill \\ \end{array} } \right. $$

  (3)

Here, $0 \le t \le 1$, $1 < \alpha \le 2$, $a_{i} \left( t \right),\;f\left( t \right) \in C\left[ {0,1} \right]$, $\gamma_{0} ,\gamma_{1} ,\lambda \in {\mathbb{R}}$, and $y \in \left\{ {W_{2}^{3} \left[ {0,1} \right],\hat{W}_{2}^{3} \left[ {0,1} \right]} \right\}$ are unknown functions to be determined while $D^{\alpha }$ denotes the Caputo fractional derivative operator of order $m - 1 < \alpha < m$ of a function $y\left( t \right)$ and defined as

$$ D^{\alpha } y(t) = \frac{1}{\Gamma (m - \alpha)}\int_{0}^{t} {(t - \tau )^{m - 1 - \alpha } y^{(m)} (\tau ){\text{d}}}t.$$

(4)

In general, fractional form of Bagley–Torvik and Painlevé equations do not always have solutions which we can obtain using analytical methods. In fact, many of real physical phenomena encountered are almost impossible to solve by this technique. Due to this, some authors have proposed numerical methods to approximate the solutions of such FDEs. The reader is request to go through [8–25] in order to know more details and descriptions about these methods and analyze.

The reproducing kernel theory has developed into an important tool in many areas, especially statistics and machine learning, and they play a valuable role in complex analysis, probability, group representation theory, finance, and the theory of differential and integral operators [26–29]. The RKA is a useful framework for constructing numerical solutions of great interest to applied sciences. In the recent years, based on this theory, extensive work has been proposed and discussed for the numerical solutions of several integral and differential operators side by side with their theories. The reader is kindly requested to go through [30–44] in order to know more details about the RKA, including its modification and scientific applications, its characteristics and key features, and others.

The structure of the present paper is as follows. In the next section, three inner product spaces and three reproducing kernel functions are constructed. In Sect. 3, some essential theoretical results are presented based upon the reproducing kernel theory. In Sect. 4, an efficient iterative technique for the solutions is described, while convergent theorem of the solutions is also presented. In order to capture the behavior of the numerical solutions, error estimations and error bounds are derived in Sect. 5. Numerical algorithm and numerical outcomes are discussed as utilized in Sect. 6. Finally, in Sect. 7, some concluding remarks and brief conclusions are provided.

2 Constructing of reproducing kernel spaces

In linear algebra, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors. Inner products allow the rigorous introduction of intuitive geometrical notions such as the length of a vector or the means of defining orthogonality between vectors. In this section, several inner product spaces and several reproducing kernel functions are constructed on the finite domain [0, 1].

Let $H$ be a Hilbert space of function $\theta :\Omega \to H$ on a set $\Omega$. A function $R:\Omega \times\Omega \to {\mathbb{C}}$ is a reproducing kernel of $H$ if the following conditions are met. Firstly, $R\left( { \cdot ,t} \right) \in H$ for each $t \in \varOmega$. Secondly, $\langle \theta \left( \cdot \right),R\left( { \cdot ,t} \right)\rangle = \theta \left( t \right)$ for each $\theta \in H$ and each $t \in \varOmega$. The condition $\langle \theta \left( \cdot \right),R\left( { \cdot ,t} \right)\rangle = \theta \left( t \right)$ is called the reproducing property, which means that the value of $\theta$ at the point $t$ is reproducing by the inner product of $\theta$ with $R\left( { \cdot ,t} \right)$. Indeed, a Hilbert space which possesses a reproducing kernel is called a reproducing kernel Hilbert space (RKHS).

Definition 1

([30]) The space $W_{2}^{1} \left[ {0,1} \right]$ is defined as $W_{2}^{1} \left[ {0,1} \right] = \{ z:z$ is absolutely continuous function on $\left[ {0,1} \right]$ and $z^{{\prime }} \in L^{2} [0,1]\}$ while the inner product and the norm of $W_{2}^{1} \left[ {0,1} \right]$ are given as

$$ \left\{ {\begin{array}{l} {\langle z_{1} \left( t \right),z_{2} \left( t \right)\rangle_{{W_{2}^{1} }} = z_{1} \left( 0 \right)z_{2} \left( 0 \right) + \int_{0}^{1} {z_{1}^{{\prime }} \left( t \right)z_{2}^{{\prime }} \left( t \right){\text{d}}t,} } \hfill \\ {\left\| {z_{1} } \right\|_{{W_{2}^{1} }}^{2} = \langle z_{1} \left( t \right),z_{1} \left( t \right)\rangle_{{W_{2}^{1} }} .} \hfill \\ \end{array} } \right. $$

(5)

Definition 2

([31]) The space $W_{2}^{3} \left[ {0,1} \right]$ is defined as $W_{2}^{3} \left[ {0,1} \right] = \{ z:z,z^{{\prime }} ,z^{{\prime \prime }}$ are absolutely continuous functions on $\left[ {0,1} \right]$, $z^{{{\prime \prime \prime }}} \in L^{2} \left[ {0,1} \right]$, and $z\left( 0 \right) = 0,z^{\prime}\left( 0 \right) = 0\}$ while the inner product and the norm of $W_{2}^{3} \left[ {0,1} \right]$ are given as

$$ \left\{ {\begin{array}{l} {\langle z_{1} \left( t \right),z_{2} \left( t \right)\rangle_{{W_{2}^{3} }} = \mathop \sum \limits_{i = 0}^{2} z_{1}^{\left( i \right)} \left( 0 \right)z_{2}^{\left( i \right)} \left( 0 \right) + \int_{0}^{1} {z_{1}^{\prime\prime\prime} \left( t \right)z_{2}^{\prime\prime\prime} \left( t \right){\text{d}}t,} } \hfill \\ {\left\| {z_{1} } \right\|_{{W_{2}^{3} }}^{2} = z_{1} \left( t \right),z_{1} \left( t \right)_{{W_{2}^{3} }} .} \hfill \\ \end{array} } \right. $$

(6)

Definition 3

([31]) The space $\hat{W}_{2}^{3} \left[ {0,1} \right]$ is defined as $\hat{W}_{2}^{3} \left[ {0,1} \right] = \{ z:z,z^{{\prime }} ,z^{{\prime \prime }}$ are absolutely continuous functions on $\left[ {0,1} \right]$, $z^{{{\prime \prime \prime }}} \in L^{2} \left[ {0,1} \right]$, and $z\left( 0 \right) = 0,z\left( 1 \right) = 0\}$ while the inner product and the norm of $\hat{W}_{2}^{3} \left[ {0,1} \right]$ are given as

$$ \left\{ {\begin{array}{l} {\langle z_{1} \left( t \right),z_{2} \left( t \right)\rangle_{{\hat{W}_{2}^{3} }} = \mathop \sum \limits_{i = 0}^{1} z_{1}^{\left( i \right)} \left( 0 \right)z_{2}^{\left( i \right)} \left( 0 \right) + z_{1} \left( 1 \right)z_{2} \left( 1 \right) + \int_{0}^{1} {z_{1}^{{{\prime \prime \prime }}} \left( t \right)z_{2}^{{{\prime \prime \prime }}} \left( t \right){\text{d}}t,} } \hfill \\ {\left\| {z_{1} } \right\|_{{\hat{W}_{2}^{3} }}^{2} = \langle z_{1} \left( t \right),z_{1} \left( t \right)\rangle_{{\hat{W}_{2}^{3} }} .} \hfill \\ \end{array} } \right. $$

(7)

Next, before any further discussion, we need to obtain the reproducing kernels functions of the spaces $W_{2}^{1} \left[ {0,1} \right]$, $W_{2}^{2} \left[ {0,1} \right]$, and $\hat{W}_{2}^{3} \left[ {0,1} \right]$. Those functions are symmetric, positive definite and have unique representations in the mentioned spaces [26–29].

Theorem 1

([30]) The Hilbert space$W_{2}^{1} \left[ {0,1} \right]$is a complete reproducing kernel with the reproducing kernel function

$$ R_{t}^{{\left\{ 1 \right\}}} \left( s \right) = \left\{ {\begin{array}{*{20}l} {1 + s,} \hfill & {s \le t,} \hfill \\ {1 + t,} \hfill & {s > t.} \hfill \\ \end{array} } \right. $$

(8)

Theorem 2

([31]) The Hilbert space$W_{2}^{3} \left[ {0,1} \right]$is a complete reproducing kernel with the reproducing kernel function

$$ R_{t}^{{\left\{ 3 \right\}}} \left( s \right) = \left\{ {\begin{array}{*{20}l} {\frac{1}{120}s^{2} \left( {s^{3} - 5s^{2} t + 10t^{2} \left( {s + 3} \right)} \right),} \hfill & {s \le t,} \hfill \\ {\frac{1}{120}t^{2} \left( {t^{3} - 5t^{2} s + 10s^{2} \left( {t + 3} \right)} \right),} \hfill & {s > t.} \hfill \\ \end{array} } \right. $$

(9)

Theorem 3

([31]) The Hilbert space$\hat{W}_{2}^{3} \left[ {0,1} \right]$is a complete reproducing kernel with the reproducing kernel function

$$ \hat{R}_{t}^{{\left\{ 3 \right\}}} \left( s \right) = \left\{ {\begin{array}{*{20}l} {\frac{1}{120}\left( {1 - t} \right)s\left[ {st^{4} - 4st^{3} + 6st^{2} + \left( {s^{4} - 5s^{3} - 120s + 120} \right)t + s^{4} } \right],} \hfill & {s \le t,} \hfill \\ {\frac{1}{120}\left( {1 - s} \right)t\left[ {ts^{4} - 4ts^{3} + 6ts^{2} + \left( {t^{4} - 5t^{3} - 120t + 120} \right)s + t^{4} } \right],} \hfill & {s > t.} \hfill \\ \end{array} } \right. $$

(10)

Throughout this paper and without the loss of generality, we are focusing on the construction proof by using $W_{2}^{3} \left[ {0,1} \right]$ as the domain space. Actually, in the same manner, we can employ our construction if $\hat{W}_{2}^{3} \left[ {0,1} \right]$ is the domain space.

3 Representation of the numerical solutions

In this section, we will show how to solve the fractional form of Bagley–Torvik and Painlevé equations subject to the given constraint conditions by using the RKA in detail and we will see what the influence choice of the continuous linear operator. Anyhow, the formulation and the implementation algorithm of the solutions are given in $W_{2}^{1} \left[ {0,1} \right]$, $W_{2}^{3} \left[ {0,1} \right]$, and $\hat{W}_{2}^{3} \left[ {0,1} \right]$.

Let us consider the following general form of the FDE that described completely Eqs. (1)–(3):

$$ \left\{ {\begin{array}{*{20}l} {a_{1} \left( t \right)D^{\alpha } y\left( t \right) + a_{2} \left( t \right)D^{1.5} y\left( t \right) + a_{3} \left( t \right)y^{{\prime }} \left( t \right) + a_{4} D^{0.5} y\left( t \right) + a_{5} \left( t \right)y\left( t \right) = f\left( {t,y\left( t \right)} \right),} \hfill \\ {y\left( 0 \right) = y_{0} , y^{{\prime }} \left( 0 \right) = y_{1} ,} \hfill \\ {y\left( 0 \right) = \gamma_{0} , y\left( 1 \right) = \gamma_{1} ,} \hfill \\ \end{array} } \right. $$

(11)

where $1 < \alpha \le 2$, $0 \le t \le 1$, and $y_{0} ,y_{1} \in {\mathbb{R}}$. Note that, for example, when $a_{1} \left( t \right) = 1$, $a_{2} \left( t \right) = a_{3} \left( t \right) = a_{4} \left( t \right) = 0$, $a_{5} \left( t \right) = - t$, and $f\left( {t,y\left( t \right)} \right) = 2y^{3} \left( t \right) + \lambda$, then the second fractional Painlevé equation well be obtained.

In order to put the constraint conditions in Eq. (11) into the space $W_{2}^{3} \left[ {0,1} \right]$ or $\hat{W}_{2}^{3} \left[ {0,1} \right]$, we must homogenize the mentioned initial or boundary conditions, for the convenience, we still denote the solution of the new equation by $y\left( t \right)$. So, let

$$ y\left( t \right): \to \left\{ {\begin{array}{*{20}l} {y\left( t \right) - \left( {\gamma_{1} t + \gamma_{0} } \right),} \hfill & {y\left( 0 \right) = \gamma_{0} , y^{\prime}\left( 0 \right) = \gamma_{1} ,} \hfill \\ {y\left( t \right) - \left( {\left( {\gamma_{1} - \gamma_{0} } \right)t + \gamma_{0} } \right),} \hfill & {y\left( 0 \right) = \gamma_{0} , y\left( 1 \right) = \gamma_{1} .} \hfill \\ \end{array} } \right. $$

(12)

Throughout remainder sections, we will focusing our constructions and results on the initial conditions type only in order not to increase the length of the paper without the loss of generality for the remaining boundary conditions type and its results. Actually, in the same manner, we can employ the RKA to construct the exact and the numerical solutions.

Now, to apply the RKA, we will define the following fractional differential linear operator:

$$ \left\{ {\begin{array}{*{20}l} {L:W_{2}^{3} \left[ {0,1} \right] \to W_{2}^{1} \left[ {0,1} \right],} \hfill \\ {Ly\left( t \right) = a_{1} \left( t \right)D^{\alpha } y\left( t \right) + a_{2} \left( t \right)D^{1.5} y\left( t \right) + a_{3} \left( t \right)y^{{\prime }} \left( t \right) + a_{4} \left( t \right)D^{0.5} y\left( t \right) + a_{5} \left( t \right)y\left( t \right).} \hfill \\ \end{array} } \right. $$

(13)

Thus, based on this, the fractional form of Bagley–Torvik and Painlevé equations can be converted into the following equivalent form:

$$ \left\{ {\begin{array}{*{20}l} {Ly\left( t \right) = f\left( {t,y\left( t \right)} \right),} \hfill \\ {y\left( 0 \right) = 0, y^{{\prime }} \left( 0 \right) = 0,} \hfill \\ \end{array} } \right. $$

(14)

in which $y \in W_{2}^{3} \left[ {0,1} \right]$ and $f \in W_{2}^{1} \left[ {0,1} \right]$. Here, $f\left( {t,y\left( t \right)} \right): \to f\left( {t,y\left( t \right) - \left( {\gamma_{1} t + \gamma_{0} } \right)} \right) + g\left( t \right)$, where $g\left( t \right) = \gamma_{1} \left( {a_{1} \left( t \right)D^{\alpha } t + a_{2} \left( t \right)D^{1.5} t + a_{3} \left( t \right) + a_{4} \left( t \right)D^{0.5} t + ta_{5} \left( t \right)} \right) + \gamma_{0} a_{5} \left( t \right)$.

Lemma 1

The operator$L:W_{2}^{3} \left[ {0,1} \right] \to W_{2}^{1} \left[ {0,1} \right]$is bounded and linear.

Proof

It is enough to show that $\left\| {Lu} \right\|_{{W_{2}^{1} }}^{2} \le M\left\| u \right\|_{{W_{2}^{3} }}^{2}$. From the definition of the inner product and the norm of $W_{2}^{1} \left[ {0,1} \right]$, we have $\left\| {Ly} \right\|_{{W_{2}^{1} }}^{2} = \langle Ly\left( t \right),Ly\left( t \right)\rangle_{{W_{2}^{1} }} = \left[ {Ly\left( 0 \right)} \right]^{2} + \int_{0}^{1} {[(Ly)^{{\prime }} (t)]^{2} {\text{d}}t}$. By the reproducing property of $R_{t}^{{\left\{ 3 \right\}}} \left( s \right)$, we have $y\left( t \right) = \langle y\left( s \right),R_{t}^{{\left\{ 3 \right\}}} \left( s \right)\rangle_{{W_{2}^{3} }}$ and $\left( {Ly} \right)^{\left( i \right)} \left( t \right) = \langle y\left( s \right),(LR_{t}^{{\left\{ 3 \right\}}} )^{\left( i \right)} \left( s \right)\rangle_{{W_{2}^{3} }}$, $i = 0,1$. Again, by the Schwarz inequality, one can write

$$ \begin{aligned} \left| {\left( {Ly} \right)^{\left( i \right)} \left( t \right)} \right| & = \left| {\left\langle {y\left( t \right),\left( {LR_{t}^{{\left\{ 2 \right\}}} } \right)^{\left( i \right)} \left( t \right)} \right\rangle_{{W_{2}^{3} }} } \right| \\ & \le \left\| {\left( {LR_{t}^{{\left\{ 2 \right\}}} } \right)^{\left( i \right)} \left( t \right)} \right\|_{{W_{2}^{1} }} \left\| y \right\|_{{W_{2}^{3} }} \\ & \le M^{{\left\{ i \right\}}} \left\| y \right\|_{{W_{2}^{3} }} , \quad i = 0,1. \\ \end{aligned} $$

(15)

Thus, $\left\| {Ly} \right\|_{{W_{2}^{1} }}^{2} \le \left( {\left( {M^{{\{ 0\} }} } \right)^{2} + \int\limits_{0}^{1} {\left( {M^{{\{ 1\} }} } \right)^{2} {\text{d}}t} } \right)\left\| y \right\|_{{W_{2}^{3} }}^{2}$ or $\left\| {Ly} \right\|_{{W_{2}^{1} }} \le M\left\| y \right\|_{{W_{2}^{3} }}$, where $M^{2} = \left( {M^{{\left\{ 0 \right\}}} } \right)^{2} + \left( {M^{{\left\{ 1 \right\}}} } \right)^{2}$.

Next, we construct an orthogonal function systems of $W_{2}^{3} \left[ {0,1} \right]$ as follows: put $\varphi_{i} \left( t \right) = r_{{t_{i} }} \left( t \right)$ and $\psi_{i} \left( t \right) = L^{ *} \varphi_{i} \left( t \right)$, where $L^{ *}$ is the adjoint operator of $L$, $R_{t}^{{\left\{ 1 \right\}}} \left( s \right)$ is the reproducing kernel function of $W_{2}^{1} \left[ {0,1} \right]$, and $\left\{ {t_{i} } \right\}_{i = 1}^{\infty }$ is dense on $\left[ {0,1} \right]$.

Algorithm 1

The orthonormal function systems $\left\{ {\bar{\psi }_{i} \left( t \right)} \right\}_{i = 1}^{\infty }$ of $W_{2}^{3} \left[ {0,1} \right]$ can be derived from the Gram-Schmidt orthogonalization process of $\left\{ {\psi_{i} \left( t \right)} \right\}_{i = 1}^{\infty }$ as follows.

• Step 1 For $i = 1,2, \ldots$ and $k = 1,2, \ldots ,i$ set

  $$ \mu_{ik} = \left\{ {\begin{array}{*{20}l} {\left\| {\psi_{1} } \right\|_{{W_{2}^{3} }}^{ - 1} ,} \hfill & {i = k = 1,} \hfill \\ {\left( {\left\| {\psi_{i} } \right\|_{{W_{2}^{3} }}^{2} - \mathop \sum \limits_{p = 1}^{i - 1} \left\langle {\psi_{i} \left( t \right),\bar{\psi }_{p} \left( t \right)} \right\rangle_{{W_{2}^{3} }}^{2} } \right)^{ - 0.5} ,} \hfill & {i = k \ne 1,} \hfill \\ {\left( {\left\| {\psi_{i} } \right\|_{{W_{2}^{3} }}^{2} - \mathop \sum \limits_{p = 1}^{i - 1} \left\langle {\psi_{i} \left( t \right),\bar{\psi }_{p} \left( t \right)} \right\rangle_{{W_{2}^{3} }}^{2} } \right)^{ - 0.5} \mathop \sum \limits_{p = k}^{i - 1} - \left\langle {\psi_{i} \left( t \right),\bar{\psi }_{p} \left( t \right)} \right\rangle_{{W_{2}^{3} }} \mu_{pk} ,} \hfill & {i > k;} \hfill \\ \end{array} } \right. $$

  (16)

• Step 2 For $i = 1,2, \ldots$ set

  $$ \bar{\psi }_{i} \left( t \right) = \mathop \sum \limits_{k = 1}^{i} \mu_{ik} \psi_{k} \left( t \right). $$

  (17)

The subscript $s$ by the operator $L$, denoted by $L_{s}$, indicates that the operator $L$ applies to the function of $s$. Indeed, it is easy to see that, $\psi_{i} \left( t \right) = L^{*} \varphi_{i} \left( t \right) = \langle L^{*} \varphi_{i} \left( s \right),R_{t}^{{\left\{ 3 \right\}}} \left( s \right)\rangle_{{W_{2}^{3} }} = \langle \varphi_{i} \left( s \right),L_{s} R_{t}^{{\left\{ 3 \right\}}} \left( s \right)\rangle_{{W_{2}^{1} }} = \left. {L_{s} R_{t}^{{\left\{ 3 \right\}}} \left( s \right)} \right|_{{s = t_{i} }} \in W_{2}^{3} \left[ {0,1} \right]$. Thus, $\psi_{i} \left( t \right)$ can be expressed in the form of $\psi_{i} \left( t \right) = \left. {L_{s} R_{t}^{{\left\{ 3 \right\}}} \left( s \right)} \right|_{{s = t_{i} }}$.

Theorem 4

For Eq. (14), if$\left\{ {t_{i} } \right\}_{i = 1}^{\infty }$is dense on$\left[ {0,1} \right]$, then$\left\{ {\psi_{i} \left( t \right)} \right\}_{i = 1}^{\infty }$is the complete function systems of$W_{2}^{3} \left[ {0,1} \right]$.

Proof

Similar to the proof of Theorem 2 in [32].

Theorem 5

If$\left\{ {t_{i} } \right\}_{i = 1}^{\infty }$is dense on$\left[ {0,1} \right]$and the solution of Eq. (14) is unique, then its exact solution satisfies

$$ \left\{ {\begin{array}{*{20}l} {y\left( t \right) = \mathop \sum \limits_{i = 1}^{\infty } A_{i} \bar{\psi }_{i} \left( t \right),} \hfill \\ {A_{i} = \mathop \sum \limits_{k = 1}^{i} \mu_{ik} f\left( {t_{k} ,y\left( {t_{k} } \right)} \right).} \hfill \\ \end{array} } \right. $$

(18)

Proof

Applying Theorem 4, it is easy to see that $\left\{ {\bar{\psi }_{i} \left( t \right)} \right\}_{i = 1}^{\infty }$ is the complete orthonormal basis of $W_{2}^{3} \left[ {0,1} \right]$. Since, $\langle y\left( t \right),\varphi_{i} \left( t \right)\rangle_{{W_{2}^{3} }} = y\left( {t_{i} } \right)$ for each $y \in W_{2}^{3} \left[ {0,1} \right]$, while $\sum\nolimits_{i = 1}^{\infty } {\langle y\left( t \right),\bar{\psi }_{i} \left( t \right)\rangle_{{W_{2}^{3} }} \bar{\psi }_{i} \left( t \right)}$ is the Fourier series expansion about $\left\{ {\bar{\psi }_{i} \left( t \right)} \right\}_{i = 1}^{\infty }$. Then $\sum\nolimits_{i = 1}^{\infty } {\langle y\left( t \right),\bar{\psi }_{i} \left( t \right)\rangle_{{W_{2}^{3} }} \bar{\psi }_{i} \left( t \right)}$ is convergent in the sense of $\left\| \cdot \right\|_{{W_{2}^{3} }}$. Thus, using Eq. (17), we have

$$ \begin{aligned} y\left( t \right) & = \mathop \sum \limits_{i = 1}^{\infty } \langle y\left( t \right),\bar{\psi }_{i} (t)\rangle_{{W_{2}^{3} }} \bar{\psi }_{i} (t) \\ & = \mathop \sum \limits_{i = 1}^{\infty } \langle y(t),\sum\limits_{k = 1}^{i} {\mu_{ik} \psi_{k} (t)\rangle_{{W_{2}^{3} }} \bar{\psi }_{i} (t)} \\ & = \mathop \sum \limits_{i = 1}^{\infty } \mathop \sum \limits_{k = 1}^{i} \mu_{ik} \langle y(t),L^{*} \varphi_{k} (t)\rangle_{{W_{2}^{3} }} \bar{\psi }_{i} (t) \\ & = \mathop \sum \limits_{i = 1}^{\infty } \mathop \sum \limits_{k = 1}^{i} \mu_{ik} \langle Ly(t),\varphi_{k} (t)\rangle_{{W_{2}^{1} }} \bar{\psi }_{i} (t) \\ & = \mathop \sum \limits_{i = 1}^{\infty } \mathop \sum \limits_{k = 1}^{i} \mu_{ik} \langle f\left( {t,y(t)} \right),\varphi_{k} (t)\rangle_{{W_{2}^{1} }} \bar{\psi }_{i} (t) \\ & = \mathop \sum \limits_{i = 1}^{\infty } \mathop \sum \limits_{k = 1}^{i} \mu_{ik} f\left( {t_{k} ,y(t)} \right)_{i} (t). \\ \end{aligned} $$

(19)

Therefore, the form of Eq. (18) is the exact solution of Eq. (14). So, the proof of the theorem is complete.

Anyhow, since $W_{2}^{3} \left[ {0,1} \right]$ is a Hilbert space, it is clear that $\sum\nolimits_{i = 1}^{\infty } {A_{i} \bar{\psi }_{i} \left( t \right) < \infty }$. Therefore,

$$ y_{n} \left( t \right) = \mathop \sum \limits_{i = 1}^{n} A_{i} \bar{\psi }_{i} \left( t \right), $$

(20)

is convergent in the sense of the norm of $W_{2}^{3} \left[ {0,1} \right]$, and the numerical solution $y_{n} \left( t \right)$ can be calculated by Eq. (20).

4 Convergence analysis of the algorithm

In this section, we consider Eq. (14) and construct an iterative technique to find its solution for linear and nonlinear case simultaneously. Further, the numerical solutions of the same equation, obtained using proposed algorithm with existing initial conditions are proved to converge to the exact solution.

The basis of our RKA for solving Eq. (14) is summarized below. Firstly, we shall make use of the following facts about the linear and the nonlinear case depending on the internal structure of the function $f$.

Case 1

If $f$ is linear, then the exact and the numerical solutions can be obtained directly from Eqs. (18) and (20), respectively.

Case 2

If $f$ is nonlinear, then the exact and the numerical solutions can be obtained by using the following iterative process.

According to Eq. (18), the representation form of the exact solution of Eq. (14) can be written as

$$ y\left( t \right) = \mathop \sum \limits_{i = 1}^{\infty } A_{i} \bar{\psi }_{i} \left( t \right). $$

(21)

For numerical computations, we define the $n$-term numerical solution of $y\left( t \right)$ and its coefficients $B_{i}$ as:

$$ \left\{ {\begin{array}{*{20}l} {y_{n} \left( t \right) = \mathop \sum \limits_{i = 1}^{n} B_{i} \bar{\psi }_{i} \left( t \right),} \hfill \\ {B_{i} = \mathop \sum \limits_{k = 1}^{i} \mu_{ik} f\left( {t_{k} ,y_{k - 1} \left( {t_{k} } \right)} \right).} \hfill \\ \end{array} } \right. $$

(22)

In the iterative process of Eq. (22), we can guarantee that the numerical solution $y_{n} \left( t \right)$ satisfies the initial conditions of Eq. (14). Now, we will proof that the numerical solution $y_{n} \left( t \right)$ is converge to the exact solution $y\left( t \right)$.

Theorem 6

If$y \in W_{2}^{3} \left[ {0,1} \right]$, then$\left| {y\left( t \right)} \right| \le \frac{7}{2}\left\| y \right\|_{{W_{2}^{3} }}$, $\left| {y^{{\prime }} \left( t \right)} \right| \le 3\left\| y \right\|_{{W_{2}^{3} }}$, and$\left| {y^{{\prime \prime }} \left( t \right)} \right| \le 2\left\| y \right\|_{{W_{2}^{3} }}$.

Proof

Noting that $y^{{\prime \prime }} (t) - y^{{\prime \prime }} (0) = \int_{0}^{t} {y^{{{\prime \prime \prime }}} (p){\text{d}}p}$, where $y^{{\prime \prime }} \left( t \right)$ is absolute continuous on $\left[ {0,1} \right]$. If this is integrated again from $0$ to $t$, the result is $y^{{\prime }} \left( t \right)$ itself as; $y^{\prime } (t) - y^{\prime } (0) - y^{\prime \prime } (0)t = \int_{0}^{t} {\left( {\int_{0}^{z} {y^{{{\prime \prime \prime }}} (p){\text{d}}p} } \right){\text{d}}z}$. Again, integrated from $0$ to $t$, yield that $y\left( t \right) - y\left( 0 \right) - y^{\prime } \left( 0 \right)t - \frac{1}{2}y^{\prime \prime } \left( 0 \right)t^{2} = \int_{0}^{t} {\left( {\int_{0}^{w} {\left( {\int_{0}^{z} {y^{{{\prime \prime \prime }}} (p){\text{d}}p} } \right){\text{d}}z} } \right)} {\text{d}}w$. So, $\left| {y\left( t \right)} \right| \le \left| {y\left( 0 \right)} \right| + \left| {y^{{\prime }} \left( 0 \right)} \right|\left| t \right| + \frac{1}{2}\left| {y^{{\prime \prime }} \left( 0 \right)} \right|\left| t \right|^{2} + \int_{0}^{1} {\left| {y^{{{\prime \prime \prime }}} (p)} \right|{\text{d}}p}$ or $\left| {y\left( t \right)} \right| \le \left| {y\left( 0 \right)} \right| + \left| {y^{\prime } \left( 0 \right)} \right| + \frac{1}{2}\left| {y^{\prime \prime } \left( 0 \right)} \right| + \int_{0}^{1} {\left| {y^{{{\prime \prime \prime }}} (p)} \right|{\text{d}}p}$. By using the Holder’s inequality and Eq. (6), we can note the following relation inequalities:

$$ \left\{ {\begin{array}{ll} {\left| {y\left( 0 \right)} \right| = \sqrt {y^{2} \left( 0 \right)} \le \left\| y \right\|_{{W_{2}^{3} }} ,} \hfill \\ {\left| {y^{\prime } \left( 0 \right)} \right| = \sqrt {\left( {y^{\prime } \left( 0 \right)} \right)^{2} } \le \left\| y \right\|_{{W_{2}^{3} }} ,} \hfill \\ {\left| {y^{\prime \prime } \left( 0 \right)} \right| = \sqrt {\left( {y^{\prime \prime } \left( 0 \right)} \right)^{2} } \le \left\| y \right\|_{{W_{2}^{3} }} ,} \hfill \\ {\int_{0}^{1} {\left| {y^{{{\prime \prime \prime }}} (p)} \right|{\text{d}}p \le \sqrt {\int_{0}^{1} {\left( {y^{{{\prime \prime \prime }}} (p)} \right)^{2} {\text{d}}p} } } \le \left\| y \right\|_{{W_{2}^{3} }} .} \hfill \\ \end{array} } \right. $$

(23)

Thus, $\left| {y\left( t \right)} \right| \le \frac{7}{2}\left\| y \right\|_{{W_{2}^{3} }}$, $\left| {y^{\prime}\left( t \right)} \right| \le 3\left\| y \right\|_{{W_{2}^{3} }}$, and $\left| {y^{\prime\prime}\left( t \right)} \right| \le 2\left\| y \right\|_{{W_{2}^{3} }}$. This completes the proof.

Corollary 1

If$\left\| {y_{n} - y} \right\|_{{W_{2}^{3} }} \to 0$as$n \to \infty$, then the numerical solution$y_{n} \left( t \right)$and its derivatives$y_{n}^{\left( i \right)} \left( t \right)$, $i = 1,2$are converging uniformly to the exact solution$y\left( t \right)$and all their derivatives up to order two as$n \to \infty$.

Theorem 7

If$\left\| {y_{n - 1} - y} \right\|_{{W_{2}^{3} }} \to 0$, $t_{n} \to s$as$n \to \infty$, $\left\| {y_{n - 1} } \right\|_{{W_{2}^{3} }}$is bounded, and$f\left( {t,y\left( t \right)} \right)$is continuous, then$f\left( {t_{n} ,y_{n - 1} \left( {t_{n} } \right)} \right) \to f\left( {s,y\left( s \right)} \right)$as$n \to \infty$.

Proof

Firstly, we will prove that $y_{n - 1} \left( {t_{n} } \right) \to y\left( s \right)$. Clearly,

$$ \begin{aligned} \left| {y_{n - 1} \left( {t_{n} } \right) - y\left( s \right)} \right| & = \left| {y_{n - 1} \left( {t_{n} } \right) - y_{\eta - 1} \left( s \right) + y_{n - 1} \left( s \right) - y\left( s \right)} \right| \\ & \le \left| {y_{n - 1} \left( {t_{n} } \right) - y_{n - 1} \left( s \right)} \right| + \left| {y_{n - 1} \left( s \right) - y\left( s \right)} \right| \\ & \le \left| {\left( {y_{n - 1} } \right)^{'} \left( \xi \right)} \right|\left| {t_{n} - s} \right| + \left| {y_{n - 1} \left( s \right) - y\left( s \right)} \right|, \\ \end{aligned} $$

(24)

where $\xi$ lies between $t_{n}$ and $s$. From Theorem 6, it follows that $\left| {y_{n - 1} \left( s \right) - y\left( s \right)} \right| \le \frac{7}{2}\left\| {y_{n - 1} - y} \right\|_{{W_{2}^{3} }}$ which gives $\left| {y_{n - 1} \left( s \right) - y\left( s \right)} \right| \to 0$ as $n \to \infty$, while $\left| {\left( {y_{n - 1} } \right)^{{\prime }} \left( \xi \right)} \right| \le 3\left\| {y_{n - 1} } \right\|_{{W_{2}^{3} }}$. In terms of the boundedness of $\left\| {y_{n - 1} } \right\|_{{W_{2}^{3} }}$ and the fact that $t_{n} \to s$, one can obtains that $\left| {y_{n - 1} \left( {t_{n} } \right) - y_{n - 1} \left( s \right)} \right| \to 0$ as $n \to \infty$. As a result, by the means of the continuation of $f$, it is implies that $f\left( {t_{n} ,u_{n - 1} \left( {t_{n} } \right)} \right) \to f\left( {s,u\left( s \right)} \right)$ as $\eta \to \infty$. So, the proof of the theorem is complete.

Theorem 8

Suppose that$\left\| {y_{n} } \right\|_{{W_{2}^{3} }}$is bounded in Eq. (22), $\left\{ {t_{i} } \right\}_{i = 1}^{\infty }$is dense on$\left[ {0,1} \right]$, and Eq. (14) has a unique solution. Then the$n$-term numerical solution$y_{n} \left( t \right)$converges to the exact solution$y\left( t \right)$with$y\left( t \right) = \sum\nolimits_{i = 1}^{n} {A_{i} \bar{\psi }_{i} \left( t \right)}$.

Proof

Similar to the proof of Theorem 5 in [32].

5 Error estimations and error bounds

Considerable errors of measurement become inadmissible in solving complicated mathematical, physical, and engineering problems. The reliability of the numerical result will depend on an error estimate or bound; therefore, the analysis of error and the sources of error in numerical methods are also a critically important part of the study of numerical technique. In this section, we derive an error bounds for the present algorithm and problems.

In the next results, we suppose that $T = \left\{ {t_{1} ,t_{2} , \ldots ,t_{n} } \right\} \subset \left( {0,1} \right)$ such that $0 < t_{1} \le t_{2} \le \cdots \le t_{n} < 1$ be the selected points for generating the basis functions $\left\{ {\bar{\psi }_{i} \left( t \right)} \right\}_{i = 1}^{\infty }$, $h = { \hbox{max} }_{0 \le i \le n} \left| {t_{i + 1} - t_{i} } \right|$ is the fill distance for the uniform partition of $\left[ {0,1} \right]$ such that $t_{0} = 0$ and $t_{n + 1} = 1$, $\left\| g \right\|_{\infty } = { \hbox{max} }_{{t_{i} \le t \le t_{i + 1} }} \left| {g\left( t \right)} \right|$, and $\left\| {L^{ - 1} } \right\| = \sup_{{0 \ne y \in W_{2}^{3} \left[ {0,1} \right]}} \frac{{\left\| {L^{ - 1} } \right\|_{{W_{2}^{3} }} }}{{\left\| y \right\|_{{W_{2}^{1} }} }}$.

Lemma 2

Let$y\left( t \right)$and$y_{n} \left( t \right)$are given by Eqs. (18) and (20), respectively. Then,$Ly_{n} \left( {t_{j} } \right) = Ly\left( {t_{j} } \right)$, $t_{j} \in T$.

Proof

Define the projective operator $P_{n} :W_{2}^{3} \left[ {0,1} \right] \to \left\{ {\sum\nolimits_{j = 1}^{n} {c_{j} \psi_{j} \left( t \right),c_{j} \in {\mathbb{R}}} } \right\}$. Then, we have

$$ \begin{aligned} Ly_{n} \left( {t_{j} } \right) & = \left\langle {y_{n} \left( t \right),L_{{t_{k} }} R_{{t_{k} }}^{{\left\{ 3 \right\}}} \left( t \right)} \right\rangle_{{W_{2}^{3} }} = \langle y_{n} \left( t \right),\psi_{k} \left( t \right)\rangle_{{W_{2}^{3} }} \\ & = \langle P_{n} y\left( t \right),\psi_{j} \left( t \right)\rangle_{{W_{2}^{3} }} = \langle y\left( t \right),P_{n} \psi_{j} \left( t \right)\rangle_{{W_{2}^{3} }} \\ & = \langle y\left( t \right),\psi_{j} \left( t \right)\rangle_{{W_{2}^{3} }} = \left\langle {y\left( t \right),L_{{t_{j} }} R_{{t_{j} }}^{{\left\{ 3 \right\}}} \left( t \right)} \right\rangle_{{W_{2}^{3} }} \\ & = L_{{t_{j} }} \left\langle {y\left( t \right),R_{{t_{j} }}^{{\left\{ 3 \right\}}} \left( t \right)} \right\rangle_{{W_{2}^{3} }} = L_{{t_{j} }} y\left( {t_{j} } \right) = Ly\left( {t_{j} } \right). \\ \end{aligned} $$

(25)

Lemma 3

Suppose that$g \in C^{m} \left[ {0,1} \right]$and$g^{{\left( {m + 1} \right)}} \in L^{2} \left[ {0,1} \right]$for some$m \ge 1$. If$g$vanishes at$T$with$n \ge m + 1$, then$g \in W_{2}^{1} \left[ {0,1} \right]$and there is a constant$A$such that

$$ \left\| g \right\|_{{W_{2}^{1} }} \le Ah^{m} \mathop { \hbox{max} }\limits_{0 \le t \le 1} \left| {g^{{\left( {m + 1} \right)}} \left( t \right)} \right|. $$

(26)

Proof

Since $g \in C^{m} \left[ {0,1} \right]$ and $g^{{\left( {m + 1} \right)}} \in L^{2} \left[ {0,1} \right]$ for some $m \ge 1$, it is easy to see that $g \in W_{2}^{1} \left[ {0,1} \right]$. Now, for each fixed $t \in \left[ {t_{i} ,t_{i + 1} } \right]$, $i = 1,2, \ldots n$, one can write

$$ \begin{aligned} \left| {g\left( t \right)} \right| & = \left| {g\left( t \right) - g\left( {t_{i} } \right)} \right| = \left| {\int_{{\tau_{i} }}^{t} {g^{{\prime }} (\tau ){\text{d}}\tau } } \right| \\ & \le \left| {t - t_{i} } \right|\mathop { \hbox{max} }\limits_{{t_{i} \le t \le t_{i + 1} }} \left| {g^{{\prime }} \left( t \right)} \right| \le h\left\| {g^{{\prime }} } \right\|_{\infty } . \\ \end{aligned} $$

(27)

Again, on $\left[ {t_{i} ,t_{i + 1} } \right]$, the application of the Roll’s theorem to $g$ yields that $g^{\prime}\left( {\tau_{i} } \right) = 0$, where $\tau_{i} \in \left( {t_{i} ,t_{i + 1} } \right)$, $i = 1,2, \cdots n - 1$. Thus, for fixed $t$ there exist $\tau_{i}$ such that $\left| {t - \tau_{i} } \right| < 2h$. Similarly, one can write

$$ \begin{aligned} \left| {g^{{\prime }} \left( t \right)} \right| & = \left| {g^{{\prime }} \left( t \right) - g^{{\prime }} \left( {\tau_{i} } \right)} \right| = \left| {\int_{{\tau_{i} }}^{t} {g^{{\prime \prime }} (\tau ){\text{d}}\tau } } \right| \\ & \le \left| {t - \tau_{i} } \right|\mathop { \hbox{max} }\limits_{{t_{i} \le t \le t_{i + 1} }} \left| {g^{{\prime \prime }} \left( t \right)} \right| \le 2h\left\| {g^{{\prime \prime }} } \right\|_{\infty } . \\ \end{aligned} $$

(28)

Thus, we get $\left| {g\left( t \right)} \right| \le 2h^{2} \left\| {g^{{\prime \prime }} } \right\|_{\infty }$. In a similar manner, there exists a constant $C_{1}$ such that $\left| {g\left( t \right)} \right| \le C_{1} h^{m + 1} \left\| {g^{{\left( {m + 1} \right)}} } \right\|_{\infty }$ and $\left| {g^{{\prime }} \left( t \right)} \right| \le C_{1} h^{m} \left\| {g^{{\left( {m + 1} \right)}} } \right\|_{\infty }$. Using these results, clearly

$$ \begin{aligned} \left\| g \right\|_{{W_{2}^{1} }} & = \left( {\left( {g(0)} \right)^{2} + \int_{0}^{1} {\left( {g^{{\prime }} (\tau )} \right)^{2} {\text{d}}\tau } } \right)^{{\frac{1}{2}}} \\ & \le Ah^{m} \mathop { \hbox{max} }\limits_{0 \le t \le 1} \left| {g^{{\left( {m + 1} \right)}} \left( t \right)} \right|, \\ \end{aligned} $$

(29)

where $A = C_{1} \sqrt {h + 1}$ on $\left[ {0,1} \right]$.

Theorem 9

Let$y\left( t \right)$and$y_{n} \left( t \right)$are given by Eqs. (18) and (20), respectively. If$R_{n} \left( t \right) = Ly_{n} \left( t \right) - f\left( {t,y\left( t \right)} \right)$is the residual error at$t \in \left[ {0,1} \right]$, then there is a constant$E$such that

$$ \left\| {y^{\left( i \right)} - y_{n}^{\left( i \right)} } \right\|_{\infty } \le Eh^{m} \mathop { \hbox{max} }\limits_{0 \le t \le 1} \left| {R_{n}^{{\left( {m + 1} \right)}} \left( t \right)} \right|,\quad i = 0,1,2. $$

(30)

Proof

The proof will be obtained by mathematical induction as follows: from Eq. (20) for $j \le n$, we see that

$$ \begin{aligned} Lu_{n} \left( {t_{j} } \right) & = \mathop \sum \limits_{i = 1}^{n} A_{i} L\bar{\psi }_{i} \left( {t_{j} } \right) \\ & = \mathop \sum \limits_{i = 1}^{n} A_{i} \langle L\bar{\psi }_{i} \left( t \right),\varphi_{j} \left( t \right)\rangle_{{W_{2}^{1} }} \\ & = \mathop \sum \limits_{i = 1}^{n} A_{i} \langle \bar{\psi }_{i} \left( t \right),L_{j}^{*} \varphi \left( t \right)\rangle_{{W_{2}^{3} }} \\ & = \mathop \sum \limits_{i = 1}^{n} A_{i} \langle \bar{\psi }_{i} \left( t \right),\psi_{j} \left( t \right)\rangle_{{W_{2}^{3} }} . \\ \end{aligned} $$

(31)

Using the orthogonality of $\left\{ {\bar{\psi }_{i} \left( t \right)} \right\}_{i = 1}^{\infty }$, yields that

$$ \begin{aligned} \mathop \sum \limits_{l = 1}^{j} \mu_{jl} Lu_{n} \left( {t_{l} } \right) & = \mathop \sum \limits_{i = 1}^{n} A_{i} \left\langle {\bar{\psi }_{i} \left( t \right),\mathop \sum \limits_{l = 1}^{j} \mu_{jl} \psi_{l} \left( t \right)} \right\rangle_{{W_{2}^{3} }} \\ & = \mathop \sum \limits_{i = 1}^{n} A_{i} \langle \bar{\psi }_{i} \left( t \right),\bar{\psi }_{j} \left( t \right)\rangle _{{W_{2}^{3} }} = A_{j} . \\ \end{aligned} $$

(32)

Now, if $j = 1$, then $Ly_{n} \left( {t_{1} } \right) = f\left( {t_{1} ,y_{0} \left( {t_{1} } \right)} \right)$. Again, if $j = 2$, then $\beta_{21} Ly_{n} \left( {t_{1} } \right) + \beta_{22} Ly_{n} \left( {t_{2} } \right) = \beta_{21} f\left( {t_{1} ,y_{0} \left( {t_{1} } \right)} \right) + \beta_{22} f\left( {t_{2} ,y_{1} \left( {t_{2} } \right)} \right)$. Thus, $Ly_{n} \left( {t_{2} } \right) = f\left( {t_{2} ,y_{1} \left( {t_{2} } \right)} \right)$, while on the other hand, it is easy to obtain the general pattern form $Ly_{n} \left( {t_{j} } \right) = f\left( {t_{j} ,y_{j - 1} \left( {t_{j} } \right)} \right)$, $j = 1,2, \ldots ,n$. For the conduct of proceedings in the proof, clearly $R_{n} \in C^{m} \left[ {0,1} \right]$ and $R_{n}^{{\left( {m + 1} \right)}} \in L^{2} \left[ {0,1} \right]$. Thus, from Lemma 3, it is follows that:

$$ \left\| {R_{n} } \right\|_{{W_{2}^{1} }} \le Ah^{m} \mathop { \hbox{max} }\limits_{0 \le t \le 1} \left| {R_{n}^{{\left( {m + 1} \right)}} \left( t \right)} \right|. $$

(33)

Remember that $R_{n} \left( t \right) = Ly_{n} \left( t \right) - f\left( {t,y\left( t \right)} \right) = Ly_{n} \left( t \right) - Ly\left( t \right) = L\left( {y_{n} \left( t \right) - y\left( t \right)} \right)$. Hence, $y - y_{n} = L^{ - 1} R_{n}$, then there exists a constant $C$ such that

$$ \begin{aligned} \left\| {y - y_{n} } \right\|_{{W_{2}^{3} }} & = \left\| {L^{ - 1} R_{n} } \right\|_{{W_{2}^{3} }} \le \left\| {L^{ - 1} } \right\|\left\| {R_{n} } \right\|_{{W_{2}^{1} }} \\ & \le ACh^{m} \mathop { \hbox{max} }\limits_{0 \le t \le 1} \left| {R_{n}^{{\left( {m + 1} \right)}} \left( t \right)} \right|. \\ \end{aligned} $$

(34)

Finally, from Theorem 6, one can find that

$$ \begin{aligned} \left| {y^{\left( i \right)} - y_{n}^{\left( i \right)} } \right| & \le D\left\| {y - y_{n} } \right\|_{{W_{2}^{3} }} \\ & \le ACDh^{m} \mathop { \hbox{max} }\limits_{0 \le t \le 1} \left| {R_{n}^{{\left( {m + 1} \right)}} \left( t \right)} \right|,\quad i = 0,1,2, \\ \end{aligned} $$

(35)

or in terms of the $\infty$ th norm, $\left\| {y^{\left( i \right)} - y_{n}^{\left( i \right)} } \right\|_{\infty } \le Eh^{m} { \hbox{max} }_{0 \le t \le 1} \left| {R_{n}^{{\left( {m + 1} \right)}} \left( t \right)} \right|$, $i = 0,1,2$, where $E = ACD$. This completes the proof.

Corollary 2

Let$y\left( t \right)$and$y_{n} \left( t \right)$are given by Eqs. (18) and (20), respectively. If$e_{n} \left( t \right) = y_{n} \left( t \right) - y\left( t \right)$is the nature error at$t \in \left[ {0,1} \right]$, then there is a constant$F$such that

$$ \left\| {y^{\left( i \right)} - y_{n}^{\left( i \right)} } \right\|_{\infty } \le Fh,\quad i = 0,1,2. $$

(36)

Proof

From Lemma 2 and Theorem 9, we obtain that $Ly_{n} \left( {t_{j} } \right) = Ly\left( {t_{j} } \right)$, $j = 1,2, \cdots ,n$. Therefore, $Ly_{n} \left( {t_{j} } \right)$ is the interpolating function of $Ly\left( {t_{j} } \right)$, where $t_{j}$ are the interpolation nodes in $\left[ {0,1} \right]$. By means of the value theorem for differentials, we have

$$ \begin{aligned} Ly\left( t \right) - Ly_{n} \left( t \right) & = Ly\left( t \right) - Ly\left( {t_{j} } \right) + Ly_{n} \left( {t_{j} } \right) - Ly_{n} \left( t \right) \\ & = \left( {Ly\left( {\xi_{1} } \right)} \right)^{{\prime }} \left( {t - t_{j} } \right) + \left( {Ly_{n} \left( {\xi_{2} } \right)} \right)^{{\prime }} \left( {t_{j} - t} \right) \\ & = \left( {t_{j + 1} - t_{j} } \right)\left( {\left( {Ly\left( {\xi_{1} } \right)} \right)^{{\prime }} \frac{{t - t_{j} }}{{t_{j + 1} - t_{j} }} + \left( {Ly_{n} \left( {\xi_{2} } \right)} \right)^{{\prime }} \frac{{t_{j} - t}}{{t_{j + 1} - t_{j} }}} \right) \\ & = h\delta \left( t \right), \\ \end{aligned} $$

(37)

where $\xi_{1}$ lies between $t,t_{j}$ with respect to $y$ and $\xi_{2}$ lies between $t_{j} ,t$ with respect to $y_{n}$. Here, $\delta \left( t \right) = \left( {Ly\left( {\xi_{1} } \right)} \right)^{{\prime }} \frac{{t - t_{j} }}{{t_{j + 1} - t_{j} }} + \left( {Ly_{n} \left( {\xi_{2} } \right)} \right)^{{\prime }} \frac{{t_{j} - t}}{{t_{j + 1} - t_{j} }}$. Clearly, $\delta \left( t \right),L^{ - 1} \delta \left( t \right) \in L^{2} \left[ {0,1} \right]$ and $\left\| {L^{ - 1} \left( \delta \right)} \right\|$ is bounded. So, it follows that:

$$ \begin{aligned} \left| {y^{\left( i \right)} - y_{n}^{\left( i \right)} } \right| & \le D\left\| {y - y_{n} } \right\|_{{W_{2}^{3} }} \\ & = D\left\| {L^{ - 1} \left( {h\delta } \right)} \right\| = Dh\left\| {L^{ - 1} \left( \delta \right)} \right\|,\quad i = 0,1,2, \\ \end{aligned} $$

(38)

or in terms of the $\infty$ th norm, $\left\| {y^{\left( i \right)} - y_{n}^{\left( i \right)} } \right\|_{\infty } \le Fh$, where $F = Dh\left\| {L^{ - 1} \left( \delta \right)} \right\|$, $i = 0,1,2$.

Here, the error estimate of the preceding results shows that the accuracy of the numerical solution is closely related to the fill distance $h$. So, more accurate solutions can be obtained using more mesh points.

6 Numerical algorithm and numerical outcomes

The key features of the RKA are as follows; firstly, it can produce good globally smooth numerical solutions, and with ability to solve many FDEs with complex constraint conditions, which are difficult to solve; secondly, the numerical solutions and their derivatives are converge uniformly to the exact solutions and their derivatives, respectively; thirdly, the algorithm is mesh-free, easily implemented and capable in treating various FDEs and various constraint conditions; fourthly, since the algorithm needs no time discretization, there is no matter, in which time the numerical solutions is computed, from the both elapsed time and stability problem, point of views.

Anyhow, to demonstrate the simplicity and effectiveness of the RKA, numerical solutions for some fractional form of Bagley–Torvik and Painlevé equations are constructed in this section. The results reveal that the algorithm is highly accurate, rapidly converge, and convenient to handle a various physical problems in fractional calculus.

Algorithm 2

To approximate the solution $y_{n} \left( t \right)$ of $y\left( t \right)$ for Eq. (14), we do the following steps.

• Step 1 Choose $n$ collocation points in the independent domain $\left[ {0,1} \right]$;

• Step 2 Set $\psi_{i} \left( {t_{i} } \right) = L_{s} \left[ {R_{{t_{i} }}^{{\left\{ 3 \right\}}} \left( s \right)} \right]_{{s = t_{i} }}$;

• Step 3 Obtain the orthogonalization coefficients $\mu_{ik}$ using Algorithm 1;

• Step 4 Set $\bar{\psi }_{i} \left( t \right) = \mathop \sum \nolimits_{k = 1}^{i} \mu_{ik} \psi_{k} \left( t \right)$ for $i = 1,2, \ldots ,n$;

• Step 5 Choose an initial approximation $u_{0} \left( {t_{i} } \right)$;

• Step 6 Set $i = 1$;

• Step 7 Set $B_{i} = \sum\nolimits_{k = 1}^{i} {\mu_{ik} f\left( {t_{k} ,y_{k - 1} \left( {t_{k} } \right)} \right)}$;

• Step 8 Set $y_{i}(t) = \sum\nolimits_{k = 1}^{i} B_{k} \bar{\psi}_{k}(t)$;

• Step 9 If $i < n$, then set $i = i + 1$ and go to step 7, else stop.

Using RKA, taking $t_{i} = \frac{i - 1}{n - 1}$, $i = 1,2, \ldots ,n = 21$ in $y_{n} \left( {t_{i} } \right)$ of Eq. (20), generating the reproducing kernel functions $R_{t}^{{\left\{ 1 \right\}}} \left( s \right),R_{t}^{{\left\{ 3 \right\}}} \left( s \right),\hat{R}_{t}^{{\left\{ 3 \right\}}} \left( s \right)$, and applying Algorithm 2 throughout the numerical computations; some results are presented and discussed quantitatively at some selected grid points on $\left[ {0,1} \right]$ to illustrate the numerical solutions for the following fractional form of Bagley–Torvik and Painlevé equations. In the process of computation, all the symbolic and the numerical computations are performed by using Mathematica $9$ software package.

Example 1

Consider the following fractional initial Bagley–Torvik equation:

$$ \left\{ {\begin{array}{*{20}l} {y^{{\prime \prime }} \left( t \right) + D^{1.5} y\left( t \right) + y\left( t \right) = 2 + 4\sqrt {\frac{t}{\pi }} + t^{2} ,} \hfill \\ {y\left( 0 \right) = 0, y^{{\prime }} \left( 0 \right) = 0.} \hfill \\ \end{array} } \right. $$

(39)

Here, the exact solutions is $y\left( t \right) = t^{2}$.

Example 2

Consider the following fractional initial Bagley–Torvik equation:

$$ \left\{ {\begin{array}{*{20}l} {y^{{\prime \prime }} \left( t \right) + D^{1.5} y\left( t \right) + y\left( t \right) = t + 1,} \hfill \\ {y\left( 0 \right) = 1, y^{{\prime }} \left( 0 \right) = 1.} \hfill \\ \end{array} } \right. $$

(40)

Here, the exact solutions is $y\left( t \right) = t + 1$.

Example 3

Consider the following fractional boundary Bagley–Torvik equation:

$$ \left\{ {\begin{array}{*{20}l} {y^{{\prime \prime }} \left( t \right) + 0.5D^{0.5} y\left( t \right) + y\left( t \right) = 3 + t^{2} \left( {\frac{1}{{\Gamma \left( {2.5} \right)}}t^{ - 0.5} + 1} \right),} \hfill \\ {y\left( 0 \right) = 1, y\left( 1 \right) = 2.} \hfill \\ \end{array} } \right. $$

(41)

Here, the exact solutions is $y\left( t \right) = t^{2} + 1$.

Example 4

Consider the following fractional boundary Bagley–Torvik equation:

$$ \left\{ {\begin{array}{*{20}l} {y^{\prime \prime } \left( t \right) + D^{0.5} y\left( t \right) + y\left( t \right) = 2 + t^{2} \left( {\frac{2}{{\Gamma \left( {2.5} \right)}}t^{ - 0.5} + 1} \right) - t\left( {\frac{1}{{\Gamma \left( {1.5} \right)}}t^{ - 0.5} + 1} \right),} \hfill \\ {y\left( 0 \right) = 0, y\left( 1 \right) = 0.} \hfill \\ \end{array} } \right. $$

(42)

Here, the exact solutions is $y\left( t \right) = t^{2} - t$.

Example 5

Consider the following first fractional Painlevé equation:

$$ \left\{ {\begin{array}{*{20}l} {D^{\alpha } y\left( t \right) = 6y^{2} \left( t \right) + t, } \hfill \\ {y\left( 0 \right) = 0, y^{{\prime }} \left( 0 \right) = 1.} \hfill \\ \end{array} } \right. $$

(43)

Here, the exact solution is not available in term of closed form expression.

Example 6

Consider the following second fractional Painlevé equation:

$$ \left\{ {\begin{array}{*{20}l} {D^{\alpha } y\left( t \right) = 2y^{3} \left( t \right) + ty\left( t \right) + 2, } \hfill \\ {y\left( 0 \right) = 1, y^{{\prime }} \left( 0 \right) = 0.} \hfill \\ \end{array} } \right. $$

(44)

Here, the exact solution is not available in term of closed form expression.

Our next goal is to illustrate some numerical results of the RKA approximate solutions of the aforementioned FDEs in numeric values. In fact, results from numerical analysis are an approximation, in general, which can be made as accurate as desired. Because a computer has a finite word length, only a fixed number of digits are stored and used during computations. Next, the agreement between the exact and the numerical solutions is investigated for Examples 1, 2, 3, and 4 at various $t$ in $\left[ {0,1} \right]$ by computing the numerical approximating of their exact solutions for the corresponding equivalent fractional equations as shown in Tables 1, 2, 3, and 4, respectively, while Tables 5 and 6 show the numerical results for Examples 5 and 6 when $\alpha = 2$ and $\alpha \in \left\{ {1.7,1.8,1.9} \right\}$.

Table 1 Numerical values of the dependent variables $y_{n} \left( t \right)$ in Example 1

Table 2 Numerical values of the dependent variables y_n(t) in Example 2

Table 3 Numerical values of the dependent variables y_n(t) in Example 3

Table 4 Numerical values of the dependent variables y_n(t) in Example 4

Table 5 Numerical values of the dependent variables y_n(t) when α ϵ {1.7, 1.8, 1.9, 2} in Example 5

Table 6 Numerical values of the dependent variables y_n(t) when α ϵ {1.7, 1.8, 1.9, 2} in Example 6

To further show the advantage of the RKA proposed in this paper, we now present comparison experiments for Examples 1, 2, 5, and 6 at various $t$ in $\left[ {0,1} \right]$. The numerical methods that are used for comparison include the following:

• For Example 1: variational iteration method (VIM) [8], Podlubny matrix method (PMM) [9], hybrid genetic algorithm with pattern search technique (HGA-PST) [10], and homotopy analysis method (HAM) [11].

• For Example 2: pattern search technique (PST) [10], hybrid genetic algorithm (HGA) [10], HGA-PST [10], and HAM [11].

• For Example 5: VIM [17], homotopy perturbation method (HPM) [17], HAM [17], particle swarm optimization algorithm (PSOA) [18], and neural networks algorithm (NNA) [19].

• For Example 6: Adomian decomposition method (ADM) [20], HPM [20], Legendre Tau method (LTM) [20], sinc collocation method (SCM) [21], and VIM [21].

Anyhow, Tables 7 and 8 show comparisons between the absolute errors of our RKA together with the other aforementioned methods for Examples 1 and 2, while Tables 9 and 10 show comparisons for Examples 5 and 6 when $\alpha = 2$ which is the most important case, because the others fractional solutions are take the same behaviors in general.

Table 7 Numerical comparison of absolute errors for y_n(t) in Example 1

Table 8 Numerical comparison of absolute errors for y_n(t) in Example 2

Table 9 Numerical comparison of absolute errors for y_n(t) when α = 2 in Example 5

Table 10 Numerical comparison of approximate solutions for y_n(t) when α = 2 in Example 6

It is clear from the tables that, for Examples 1 and 5, the VIM is suited for the starting few nodes and failed at the ending nodes, the HGA-PST is suited with great difficulty for Examples 1 and 2, while when solving Example 2, the HGA is suited with great difficulty too. As a result, it was found that the RKA in comparison is much better with a view to accuracy and applicability. Anyhow, to analyze the most comprehensive and accurate, the following comments and results are clearly observed:

• The best method for the solutions is the RKA.

• The average absolute errors for the RKA are the lowest one among all other aforementioned numerical ones.

• For Examples 1 and 2, the average absolute errors using the RKA are relatively of the same order which is of the order between $0$ and $10^{ - 16}$.

• For Example 5, the average absolute errors using the RKA are of the order between $10^{ - 7}$ and $10^{ - 10}$.

• The results obtained in these tables make it very clear that the RKA out stands the performance of all other existing methods in terms of accuracy and applicability.

As we mentioned earlier, it is possible to pick any point in $\left[ {0,1} \right]$ and as well the numerical solutions and all their derivatives up to order two will be applicable. Next, numerical results of approximating the first derivatives of the numerical solutions for Examples 1 and 2 at various $t$ in $\left[ {0,1} \right]$ are given in Tables 11 and 12, respectively. Again, to further show the advantage of the RKA, comparison experiments for the first derivative of the numerical solutions of Examples 1, 2, and 6 at various $t$ in $\left[ {0,1} \right]$ are tabulated as given in Tables 13, 14, and 15, respectively.

Table 11 Numerical values for the first derivative of the dependent variables $y_{n}^{{\prime }} \left( t \right)$ in Example 1

Table 12 Numerical values for the first derivative of the dependent variables $y_{n}^{{\prime }} \left( t \right)$ in Example 2

Table 13 Numerical comparison of absolute errors for the first derivative $y_{n}^{{\prime }} \left( t \right)$ in Example 1

Table 14 Numerical comparison of absolute errors for the first derivative $y_{n}^{{\prime }} \left( t \right)$ in Example 2

Table 15 Numerical comparison of approximate values for the first derivative $y_{n}^{{\prime }} \left( t \right)$ when α = 2 in Example 6

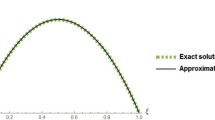
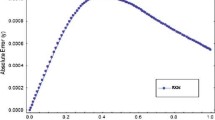
Next, the geometric behaviors of the absolute value of the nature error function $\left| {e_{n} \left( t \right)} \right| = \left| {y_{n} \left( t \right) - y\left( t \right)} \right|$ are discussed. Anyhow, Fig. 1 (left and right) gives the relevant data of the RKA results at various $t$ in $\left[ {0,1} \right]$ for Examples 1 and 2, respectively. It is observed that the increase in the number of node results in a reduction in the absolute error and correspondingly an improvement in the accuracy of the obtained solutions. This goes in agreement with the known fact, the error is monotone decreasing in the sense of the used norm, where more accurate solutions are achieved using an increase in the number of nodes. On the other hand, the cost to be paid while going in this direction is the rapid increase in the number of iterations required for convergence.

Fig. 1

Absolute value of the nature errors function $\left| {e_{n} \left( t \right)} \right|$ of the RKA approximate solutions of: Example 1 (left graph) and Example 2 (right graph)

The geometric behaviors of the memory and hereditary properties of the RKA approximate solutions and their level characteristics are studied next. Anyhow, the comparisons between the computational values of the RKA approximate solutions when $\alpha = 2$ and $\alpha \in \left\{ {1.7,1.8,1.9} \right\}$ for Examples 5 and 6 have been depicted on the domain $\left[ {0,1} \right]$ as shown in Fig. 2 (left and right), respectively. It is clear from the Fig. 2 that each of the graphs is nearly coinciding and similar in their behaviors with good agreement with RKA approximate solutions when $\alpha = 2$, while each of the subfigures is nearly identical and in excellent agreement to each other in terms of the accuracy. As a result, one can note that the RKA approximate solutions continuously depend on the fractional derivative.

Fig. 2

Comparisons between the computational values of the RKA approximate solutions when $\alpha = 2$ and $\alpha \in \left\{ {1.7,1.8,1.9} \right\}$: black$\alpha = 2$; purple$\alpha = 1.9$; brown$\alpha = 1.8$; green$\alpha = 1.7$ for: Example 5 (left graph) and Example 6 (right graph)

While one cannot know the absolute errors without knowing the exact solutions, in most cases, the residual errors can be used as a reliable indicators in the iteration progresses. Next, we present this type of errors which is mentioned in Theorem 9 in order to measure the extent of agreement with unknowns closed form solutions and to measure the accuracy of the RKA in finding and predicting the solutions. Anyhow, in Fig. 3 (left and right) the absolute value of the residual error functions

$$ \begin{array}{*{20}c} {\left| {R_{n} \left( t \right)} \right| = \left| {Ly_{n} \left( t \right) - f\left( {t,y_{n} \left( t \right)} \right)} \right|,} \\ \end{array} $$

(45)

where $1 < \alpha \le 2$ and $L:W_{2}^{3} \left[ {0,1} \right] \to W_{2}^{1} \left[ {0,1} \right]$ have been plotted when $\alpha = 2$ for Examples 5 and 6, respectively.

Fig. 3

Absolute value of the residual errors function $\left| {R_{n} \left( t \right)} \right|$ when $\alpha = 2$ of the RKA approximate solutions of: Example 5 (left graph) and Example 6 (right graph)

As the plots show, while the value of $t$ moving a way from the boundary of $\left[ {0,1} \right]$, the values of $\left| {R_{n} \left( t \right)} \right|$ various along the horizontal axis by satisfying the initial conditions for the dependent variables of the corresponding FDEs. We recall that the accuracy and duration of a simulation depend directly on the size of the steps taken by the solver. Generally, decreasing the step size increases the accuracy of the results, while increasing the time required to simulate the problem.

7 Concluding remarks

Numerical methods for the solutions of FDEs are essential for the analysis of physical and engineering phenomena. Strong solvers are necessary when exploring characteristics of equations that depend on description of memory and hereditary level properties. In this paper, we introduced the RKA as strong novel solver for some certain types of FDEs which are Bagley–Torvik and Painlevé equations to enlarge its applications range. The algorithm is applied in a direct way without using linearization, transformation, or restrictive assumptions. It is analyzed that the proposed algorithm is well suited for use in FDEs of volatile orders and resides in its simplicity in dealing with initial or boundary conditions. Results obtained by the proposed algorithm are compared systematically with some other well-known methods and are found outperforms in terms of accuracy and generality. It is worth to be pointed out that the RKA is still suitable and can be employed for solving other strongly linear and nonlinear FDEs.