Synthesis of linear antenna array using flower pollination algorithm

Abstract

Linear antenna array (LAA) design is a classical electromagnetic problem. It has been extensively dealt by number of researchers in the past, and different optimization algorithms have been applied for the synthesis of LAA. This paper presents a relatively new optimization technique, namely flower pollination algorithm (FPA) for the design of LAA for reducing the maximum side lobe level (SLL) and null control. The desired antenna is achieved by controlling only amplitudes or positions of the array elements. FPA is a novel meta-heuristic optimization method based on the process of pollination of flowers. The effectiveness and capability of FPA have been proved by taking difficult instances of antenna array design with single and multiple objectives. It is found that FPA is able to provide SLL reduction and steering the nulls in the undesired interference directions. Numerical results of FPA are also compared with the available results in the literature of state-of-the-art algorithms like genetic algorithm, particle swarm optimization, cuckoo search, tabu search, biogeography based optimization (BBO) and others which also proves the better performance of the proposed method. Moreover, FPA is more consistent in giving optimum results as compared to BBO method reported recently in the literature.

1 Introduction

Antennas are part and parcel of wireless communication. Without antennas, it is difficult to imagine wireless communication. For long distance communication, a single antenna is not capable as it does not have sufficient gain. Hence, antenna arrays are used to overcome this problem. In antenna arrays, number of same type of element antennas are arranged suitably to have required antenna characteristics. Antenna arrays are of different types depending upon the geometry, namely, linear antenna array (LAA), circular antenna array, hexagonal antenna array and so on. Antenna arrays find their application in number of fields like radar, satellite, radio and many more [1]. The synthesis of antenna array is a nonlinear and complex problem. Gradient methods require initial guess for obtaining good solution and may stuck in local minima. Hence, these are not good choice for optimization of antenna arrays. So, different global optimization techniques have emerged as good alternative for antenna array optimization.

LAA synthesis using global optimization methods too has received wide interest in researchers due to its geometrical simplicity and large applications. Tabu search (TS) has been applied for the designing of LAA by Merad et al. [2]. Particle swarm optimization (PSO) has been used for optimizing element positions of linear array to reduce side lobe level (SLL) and null placement [3–5]. Rattan et al. [6] have designed aperiodic LAA using genetic algorithm (GA) and compared the results with PSO [3]. Cengiz and Tokat [7] have evaluated the performance of GA, TS and memetic algorithm (MA) for the design of three different linear arrays. Lin et al. [8] have investigated the performance of differential evolution (DE) for symmetric aperiodic LAA. They have also shown the effect of angle resolution. The performance of self-adaptive differential evolution (SADE) and Taguchi’s method (TM) for design LAA has been compared in [9]. Biogeography based optimization (BBO) has been applied for obtaining linear antennas with low SLL and null placement in desired directions [10–12]. Ant colony optimization (ACO) has been applied for the synthesis of nonuniform LAA [13]. Multi-objective variant of DE called MOEA/D-DE has been employed to synthesize LAA. In their work, the authors have shown that MOEA/D-DE provides better trade-off curves between null placement and SLL as compared to single-objective optimization methods [14]. Goudos et al. [15] have applied an advance version of PSO, namely comprehensive learning particle swarm optimization (CLPSO) to three unequally spaced LAA for SLL reduction, null placement and beamwidth control. LAA has been also designed using a variant of DE called fitness adaptive differential evolution (FiADE) by Chowdhury et al. [16]. Harmony search algorithm (HSA) has been employed for SLL reduction and null placement [17]. Singh and Rattan [18] have used cuckoo optimization algorithm (COA) for synthesis of LAA and have obtained lower SLL and better null values as compared to other popular methods. Moreover, they have shown that the convergence of COA is faster than other algorithms used for the design of LAA. Khodier [19] has used cuckoo search (CS) for the design of LAA and Yagi-Uda array. Guney and Durmus [20] have used backtracking search algorithm (BSA) for pattern nulling of LAA. Babayigit et al. [21] have used clonal selection algorithm for null synthesis of LAA by controlling element amplitudes. An immune algorithm has been used for the null steering of LAA by optimizing element amplitude excitations [22]. Position only pattern nulling of LAA using clonal selection algorithm has been done by Guney et al. [23]. LAA design problem has been investigated extensively in the past using different well-known algorithms. So, it makes sense to apply a new algorithm to the same problem and evaluate its results with those available in the literature. In this paper, flower pollination algorithm (FPA) is used for optimization of LAA for reduction of maximum SLL and null control. FPA given by Yang [24] is a new algorithm inspired from the nature. It has been shown to be better than PSO and GA for ten benchmark problems. Moreover, it has been successfully used as an optimizer to solve problems in different engineering fields [25–29]. To show the strength and capability of FPA as an optimizer, different LAA design problems have been taken up for optimization that have been studied in the past using various optimization methods. A comprehensive comparisons of results have been made with the results of TS [2], GA [6, 7], MA [7], PSO [3, 4], SADE [9], TM [9], MOEA/D-DE [14], FiADE [16], BBO [10–12], ACO [13], BSA [20], HSA [17], CLPSO [15], COA [18] and CS [19] techniques.

The rest of the paper is organized as follows: Sect. 2 presents basic FPA algorithm, while in Sect. 3, results and discussion related to LAA are presented. Finally, in Sect. 4, the paper is concluded.

2 Flower pollination algorithm

The Darwinian theory of natural selection accounting for survival of the fittest is well known and is also applicable to flowers where different species of flowers pollinate. The pollination process in flowers paves way for optimal production of best fit flowers. Almost 250,000 (80 %) of all plants species are flowering, hence, dominating landscape aging from Cretaceous period (more than 125 million years) [30, 31]. From biological and evolutionary point of view, the main function of flowers is to reproduce and the process is pollination. In pollination, the transfer of pollen takes place which is further associated with pollinators such as insects, birds and others. Some flowers attract only specific species of insects or birds for pollination resulting into specialized flower-pollinator partnership [32].

The major forms of pollination are biotic and abiotic. Biotic pollination in flowers is associated with pollinators such as insects, birds, bats, honey bees and other animals. It constitutes about 90 % of flowering plants. In contrary to biotic, abiotic pollination does not require any pollinators. As in case of grass where wind or diffusion in water help in pollination [32]. Pollinators also called pollen vectors are very diverse (at least 200,000 varieties) and can also develop flower constancy. Constancy means pollinators tend to visit certain species and bypass other species. This maximizes the transfer of pollens to the same species of flower or conspecific plants and also increases reproduction rate of the same flower species. The pollinators in turn also get benefited as in case of honey bee, they visit only certain species to collect nectar maintaining minimum cost and more intake of nectar [33].

Pollination can also be achieved by self-pollination or cross-pollination. Self-pollination is the one in which fertilization takes among different flowers of same species or same flower, while in case of cross-pollination or allogamy, pollination occurs between pollens of flowers of different plants. Cross-pollination can be biotic and occurs over long distances, thus also considered as global pollination. Pollinators such as bees, bats and flies are examples of biotic cross-pollinators. These pollinators follow a Lévy flight behavior with steps obeying Lévy distribution [34].

FPA was proposed by Yang [24] and was inspired from the pollination process and constancy of flowering plants. The algorithm is idealized into four general rules:

• Rule 1 Movement of pollen carrying pollinators obeys Lévy flights, and biotic and cross-pollination are considered as global pollination.

• Rule 2 Abiotic and self-pollination are used for local pollination.

• Rule 3 Flower constancy which is proportional to the similarity of two flowers can be considered as the reproduction probability.

• Rule 4 Switch probability $p\,\epsilon$ [0, 1] controls the local and global pollination. Physical proximity and factors such as wind, bias the pollination activities towards local pollination.

As each plant has multiple flowers, and each flower patch release millions of pollen gametes. For present case, we assume only a single flower producing only a single pollen gamete. Thus, a single pollen gamete, flower or plant acts as potential solution of the problem under consideration.

The above-mentioned four rules are converted into proper equations. Global and local pollination are the main steps of FPA. In global pollination, pollinators carry pollen gametes even over long distances. Here Rule 1 and Rule 3 are used to formulate new equation as

$$x_{i}^{t + 1} = x_{i}^{t} + \alpha L\left( \mu \right)\left( {R_{*} - x_{i}^{t} } \right)$$

(1)

where x ^t _i is the potential solution at t iteration, R _* is the current best solution, α is the scaling factor to control step size of L(μ), the Lévy flight-based step size corresponding to strength of pollination. As pollinators travel variable distance steps, so Lévy flight is used and is given by

$$L\sim\left\{ {\frac{{\mu \left( \lambda \right)\sin \left( {\pi \mu /2} \right)}}{\pi }\frac{1}{{s^{1 + \mu } }},} \right. \quad (s \gg s_{0} > 0)$$

(2)

where Γ(μ) is the standard gamma function with step size s > 0 and theoretically s ₀ ≫ 0, but practically it can be as small as 0.1. The pseudorandom step size obeying Lévy distribution is obtained from Mantegna algorithm by using two Gaussian distributions. In local pollination, Rule 2 and Rule 3 can be represented mathematically as

$$x_{i}^{t + 1} = x_{i}^{t} + \epsilon \left( {x_{j}^{t} - x_{k}^{t} } \right)$$

(3)

where x ^t _j and x ^t _k are pollens from different flowers of same plants. Hence, flower constancy occurs in limited space corresponding to a local random walk drawn from a uniform distribution $\epsilon$ in [0, 1]. The flowchart of FPA is given Fig. 1.

Fig. 1

Flowchart of FPA

3 Design examples

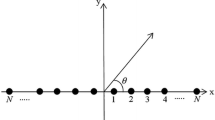
A LAA consists of N antenna elements arranged in a straight line. A symmetric LAA along the x-axis with 2 N elements is shown in Fig. 2. The elements are divided into two groups of N elements on each side of the origin. This symmetric arrangement helps in providing symmetric radiation pattern which is desirable for many applications. The symmetry also reduces computational complexity as only N elements have to be optimized instead on 2 N. The array factor (AF) in x–y plane (azimuth plane) is given by [1]:

$$AF\left( \emptyset \right) = 2\mathop \sum \limits_{n = 1}^{N} I_{n} \cos \left[ {kx_{n} \cos \left( \emptyset \right) + \varphi_{n} } \right]$$

(4)

where I _n , φ _n and x _n are amplitude excitation, phase and position of nth element, respectively, and $k = 2\pi /\lambda$ is the wave number. Hence, AF is a function of I _n , φ _n , and x _n . In equally spaced or uniform antennas, the element positions are kept fixed to λ/2 but the element excitations are varied to get the required radiation pattern. On the other hand, unequally spaced antennas have uniform element excitation but element positions are maneuvered to get the desired antenna. In this work, FPA is used to find the optimum design of both equally and unequally spaced LAA.

Fig. 2

A 2 N element linear antenna array

In this section, FPA is implemented for synthesis of uniform and nonuniform LAA. The performance of FPA has been evaluated by taking several different examples which have been studied in the literature. The aim is to obtain an antenna having radiation pattern with minimum possible SLL and nulls in the desired directions. The fitness or objective function to achieve the desired goal is given by:

$${\text{Fitness}} = k_{1} f_{\text{SL}} \left( \emptyset \right) + k_{2} f_{\text{NS}} \left( \emptyset \right)$$

(5)

where k ₁ and k ₂ are the weights of the two goals. $f_{\text{SL}} (\theta )$ and $f_{\text{NS}} (\theta )$ are given by:

$$f_{\text{SL}} \left( \emptyset \right) = \hbox{max} \left[ {AF\left( \emptyset \right)} \right]$$

(6)

$$f_{\text{NS}} \left( \emptyset \right) = \left[ {\max_{k = 1 \ldots \ldots \ldots K} \left( {AF\left( {\emptyset_{k}^{\text{null}} } \right)} \right)} \right]$$

(7)

and SL is the feasible region of sidelobes and $\emptyset_{k}^{\text{null}}$ is the k-th null direction. In the above equations, the value of AF is in decibels.

3.1 Equally spaced linear arrays

The performance of FPA is evaluated by applying it to the established LAA antenna design problem. Firstly, three equally spaced antennas of different sizes are considered for the optimization. The goal of optimization is to reduce maximum SLL by perturbing the element amplitude excitations. In this work, the element phase excitations are assumed to be uniform and equal to zero, i.e., φ _n  = 0°. To maintain a distance of λ/2 between two elements on either side of origin, the position of first element is taken as x ₁ = λ/4. The AF given in (4) for equally spaced array now becomes:

$$AF\left( \emptyset \right) = 2\mathop \sum \limits_{n = 1}^{N} I_{n} \cos \left[ {\left( {n - 0.5} \right)\pi \cos \left( \emptyset \right)} \right]$$

(8)

In the first example, a 10-element antenna array is taken for having minimum SLL only. To achieve the desired design, the value of k ₁ = 1 and k ₂ = 0 is taken in the fitness function. The aim is to suppress the maximum SLL in the region $\emptyset \in$ [104°, 180°]. As this is a symmetric array, there are only five element amplitudes that are to be optimized. Hence, the number of parameters to be optimized is five. The amplitudes of the elements allowed to vary between [0, 1]. For the FPA algorithm, the population size is taken as 20 and maximum number of iterations are fixed to 500. The value of probability switch p = 0.8 is taken, and for Levy flight, μ is fixed to 1.5. The results obtained by FPA are listed in Table 1. The convergence characteristics of FPA are shown in Fig. 3. The results are compared with the antenna array obtained by PSO [4], TM [9] and BBO [11] for the same objective in Table 2. The FPA has obtained SLL of −25.32 dB as compared to PSO [4], TM [9] and BBO [11] antenna which have SLL of −24.62, −24.88 and −25.21 dB, respectively. The radiation pattern of FPA optimized array is shown in Fig. 4 along with the radiation pattern of PSO [4], BBO [11] and TM [9] arrays. The performance of BBO [11] and FPA is compared in Table 3 in terms of standard deviation (SD). The SD of FPA is quite less and is 0.0063 which indicates that FPA is consistent in giving better solutions. Moreover, when compared to BBO [11], it turns out to be more robust as it has lower SD. Figure 5 shows the distribution of SLL for 20 runs of FPA.

Table 1 Optimum amplitude excitations obtained using FPA for 10-element LAA

Fig. 3

Convergence characteristics of FPA for 10-element LAA

Table 2 Comparison of results of different algorithms for 10-element LAA

Fig. 4

Radiation pattern of FPA optimized 10-element LAA compared to other optimization methods

Table 3 Comparison of performance of FPA with BBO [11] for 10-element LAA in 20 runs

Fig. 5

Distribution of maximum SLL for 20 runs of FPA for 10-element LAA

In the second example, FPA is used for maximum SLL reduction and null placement of a 20-element LAA. The single null is to be placed in the direction of 104°. In this case, the value of k ₁ = 20 and k ₂ = 1 is taken. The others parameters for optimization are same as in the previous example with the exception that the algorithm is run for 1000 iterations. The optimum excitation amplitudes obtained after optimization are given in Table 4. The results of FPA and other popular algorithms are compared in Table 5 with respect to SLL and null value obtained. Clearly it can be seen that FPA has provided the better results in terms of reduced SLL as compared to BSA [20] and HSA [17] arrays. The null in the direction of 104° has a value of −120.9 dB. It is pertinent to mention that any value of AF lesser than −60 dB is considered as a null. The array patterns of FPA, BSA [20] and HSA [17] optimized arrays with null at 104° direction are shown in Fig. 6.

Table 4 Optimum amplitude excitations obtained using FPA for 20-element LAA with null at 104°

Table 5 Comparison of results of different algorithms for 20-element LAA with null at 104°

Fig. 6

Radiation pattern of FPA optimized 20-element LAA with null at 104° compared to other optimization methods

To test the proficiency of FPA for synthesis of LAA with multiple nulls in any direction, in the next example, it is used to optimize again a 20-element LAA for maximum SLL reduction and null placement in two directions, i.e., at 104° and 116°. The normalized excitation amplitudes obtained after FPA optimization are given in Table 6. As can been observed from Table 7, the SLL obtained by FPA is least as compared to BSA [20], HSA [17] and BBO [12] algorithms. Moreover, FPA successfully imposed nulls of −98.45 and −102.6 dB in 104° and 116° directions, respectively. The radiation pattern of FPA optimized LAA along with that of BSA [20], HSA [17] and BBO [12] optimized arrays is shown in Fig. 7.

Table 6 Optimum amplitude excitations obtained using FPA for 20-element LAA with null at 104° and 116°

Table 7 Comparison of results of different algorithms for 20-element LAA with null at 104° and 116°

Fig. 7

Radiation pattern of FPA optimized 20-element LAA with null at 104° and 116° compared to other optimization methods

3.2 Unequally spaced linear arrays

The synthesis of unequally spaced linear array has been very popular antenna array problem in the recent past. The nonuniform spacing between the elements results in an aperiodic array factor. This aperiodic attribute of the array factor aids in attaining lower SLL with lesser number of antenna elements for a given aperture size. Moreover, due to uniform excitation of elements, the cost and complexity of the feed network is reduced. But since the relationship between array factor and positions of elements is nonlinear and non-convex, the design of unequally spaced arrays is intricate. The AF of a nonuniform array with uniform amplitude excitations, i.e., I _n  = 1 and φ _n  = 0° is given by:

$$AF\left( \phi \right) = 2\mathop \sum \limits_{n = 1}^{N} \cos \left[ {kx_{n} \cos \left( \phi \right)} \right]$$

(9)

In order to rank FPA as one of the good optimizers, it is imperative that a comparison of its performance is made with other well-known methods. Again in this case, five different problems of different array size are taken from the literature which have been designed using state-of-the-art algorithms.

In the first example for nonuniform linear arrays, a 12-element LAA is taken for FPA optimization. The aim is to reduce SLL in the region $\emptyset \in$ [98°, 180°] by optimizing the element positions. To achieve the required antenna, the value of k ₁ = 1 and k ₂ = 0 is chosen in the fitness function given in (5). Again for this optimization, number of iterations are 1000 with other parameters remaining the same. The FPA optimized positions for 12-element LAA are given in Table 8. The convergence graph for FPA optimization is shown in Fig. 8. The performance of FPA in terms of SLL attained is compared with that of FiADE [16], TS [7], MA [7], GA [7] and PSO [16]. The maximum SLL achieved by FPA is −20.764 dB which is least in Table 9. For the same problem, the SLL obtained by FiADE [16], TS [7], MA [7], GA [6] and PSO [16] is 18.96, −18.40, −19.10, −18.79 and −17.90 dB. The optimized radiation pattern for FPA LAA is given in Fig. 9. Also in the same figure for the purpose of comparison, radiation patterns of GA [7], PSO [16], FiADE [16] are also plotted. Table 10 shows the performance of FPA for 20 runs for this example. Clearly, it can be observed that FPA is very consistent in obtaining optimum solutions as the SD value is quite low. The maximum SLLs obtained for the 20 runs are shown in Fig. 10.

Table 8 Optimum element positions obtained using FPA for 12-element unequally spaced LAA

Fig. 8

Convergence characteristics of FPA for 12-element unequally spaced LAA

Table 9 Comparison of results of different algorithms for 12-element unequally spaced LAA

Fig. 9

Radiation pattern of FPA optimized 12-element unequally spaced LAA

Table 10 Performance of FPA algorithm for 12-element unequally spaced LAA in 20 runs

Fig. 10

Distribution of maximum SLL for 20 runs of FPA for 12-element unequally spaced LAA

In the next example, a 22-element is considered for FPA optimization. The aim is to suppress the SLL in the region $\emptyset \in$ [98°, 180°] and also to impose a null in the direction of 99°. For this optimization, the weighting factors k ₁ = 25 and k ₂ = 1 in the fitness function have been taken. The optimum element positions obtained using FPA are given in Table 11. In Table 12, the results of FPA are compared with BSA [20], TS [7], GA [7], MA [7], HSA [17], PSO [16] and MOEA/D-DE [14] methods in terms of peak SLL obtained and value of null in the desired direction. The SLL obtained by FPA for LAA is −23.81 dB which is better than other techniques listed in Table 12. The null value is also −101.71 dB which is deeper than GA [7], TS [7] MS [7], PSO [16] and MOEA/D-DE [14] optimized antennas. Figure 11 shows the plot of radiation patterns of BSA [20], HSA [19], MOEA/D-DE [14] and FPA optimized LAA which also indicates that the suppression of SLL is maximum for FPA optimized LAA and also null placement in the 99° direction.

Table 11 Optimum element positions obtained using FPA for 22-element unequally spaced LAA with null at 99°

Table 12 Comparison of results of different algorithms for 22-element unequally spaced LAA with null at 99°

Fig. 11

Radiation pattern of FPA optimized 22-element unequally spaced LAA with null at 99°

In the third example for nonuniform LAA, a 26-element array is designed for having minimum SLL in band $\emptyset \in$ [100°, 180°] and nulls in the directions of 120° and 168°. The value of k ₁ = 15 and k ₂ = 1 in the fitness function yielded optimum results for this design problem. The optimum geometry obtained after FPA optimization is shown in Table 13. In Table 14, the SLL and null values are compared with the results of MOEA/D-DE [14], TS [7], GA [7], MA [7] and PSO [16]. As it is obvious from the table, the SLL reduction is maximum in case of FPA optimized LAA. The SLL of FPA synthesized LAA is −21.65 dB. The null values at 120° and 168° are −126.9 and −116.2 dB, respectively. The radiation patterns of GA [7], MA [7], PSO [16] and FPA arrays are shown in Fig. 12.

Table 13 Optimum element positions obtained using FPA for 26-element unequally spaced LAA with nulls at 120° and 168°

Table 14 Comparison of results of different algorithms for 26-element unequally spaced LAA with null at 120° and 168°

Fig. 12

Radiation pattern of FPA optimized 26-element unequally spaced LAA with null at 120° and 168°

To test the proficiency of FPA in steering multiple nulls in the desired directions, a 28-element LAA is designed in this example. The aim is to impose the nulls in 120°, 122.5° and 125°. The SLL is reduced in the region $\emptyset \in$ [100°, 180°]. The optimized array geometry is given in Table 15. The optimized radiation pattern is shown in Fig. 13. For the sake of comparison, radiation plots of quadratic programming method (QPM) [3], HSA [17] and BSA [20] are also shown in the same figure. The comparison of performance of different algorithms is made in Table 16. Clearly, it is evident from the comparison that the SLL attained by FPA is least and is equal to −22.60 dB. The SLL is better than the closest competitor algorithm BSA [20] by −0.7 and −9.36 dB than QPM [3]. Moreover, the null values at directions 120°, 122.5° and 125° are −78.45, −96.51 and −82.58 dB, respectively, which are also quite less than the desired value of −60 dB.

Table 15 Optimum element positons obtained using FPA for 28-element unequally spaced LAA with nulls at 120°, 122.5°, and 125°

Fig. 13

Radiation pattern of FPA optimized 28-element unequally spaced LAA. LAA with nulls at 120°, 122.5° and 125°

Table 16 Comparison of results of different algorithms for 28-element unequally spaced LAA with nulls at 120°, 122.5°, and 125°

In the last example, to compare the performance of FPA with the other popular optimization methods, a well-known problem of optimizing 32-element LAA for SLL reduction and null placement is taken up. This problem has been optimized by popular optimization methods like PSO [3], CLPSO [15], GA [6], HSA [17], BSA [20], CS [19] and QPM [3]. The aim is to synthesize 32-element LAA for SLL reduction in the region $\emptyset \in$ [93°,180°] and null placement in the direction of 99°. The optimum array geometry achieved after FPA optimization is given in Table 17. Table 18 presents the comparison of results of different algorithms that have been used to optimize the same antenna. Clearly, FPA has achieved better results in terms of SLL reduction and null placement. The maximum SLL of FPA antenna is −23.10 dB, and null value is −130.60 dB which are least when compared with BSA [20], PSO [3], HSA [17], QPM [3], CS [19], GA [6], CLPSO [15] optimized antennas. The array pattern of FPA, HSA [17], PSO [3] and CS [19] optimized antenna are shown in Fig. 14.

Table 17 Optimum element positions obtained using FPA for 32-element unequally spaced LAA with null at 99°

Table 18 Comparison of results of different algorithms for 32-element unequally spaced LAA with null at 99°

Fig. 14

Radiation pattern of FPA optimized 32-element unequally spaced LAA with null at 99°

4 Conclusions

In this paper, FPA is presented for synthesis of LAA for suppressing the sidelobes and placing nulls in certain directions. The desired antenna arrays have been achieved by controlling either amplitude excitations or element positions. Results show that FPA is able to synthesize array pattern with minimum SLL and nulls in the directions of interferences. A comprehensive comparison of results of FPA optimization has been made with PSO, TS, TM, BBO, GA, PSO, HSA, BSA, TA, CS, ACO, COA and CLSPO. The results of FPA are found to be superior in terms of better SLL reduction and null placement than other algorithms. The results also show the robustness of the proposed technique as it consistently obtained the optimum antenna arrays. FPA is simple and easy to implement. In comparison with other methods, FPA requires few parameters to be tuned for optimization. The results of LAA obtained using FPA prove the strength and competence of the method and hence, can be used for solving other electromagnetic and real-world problems.