1 Introduction

The research of neural networks has received intensive attention due to their wide applications in classification of pattern recognition, static image processing, signal processing, optimization problems, mechanics of structures and materials, smart antenna arrays and other scientific areas during the past few decades [1–13]. In the hardware implementation of neural networks, time delays in particular time-varying delays are unavoidably encountered in the signal transmission among the neurons due to the finite speed of switching and transmitting signals, which may cause undesirable dynamical behaviors such as instability and oscillation [14–20]. However, there exists another type of time delays, namely, distributed time-varying delays, which have begun to receive much attention [21–23]. The main reason is that neural networks (NNs) usually have the spatial nature due to the presence of an amount of parallel pathways of a variety of axon sizes and lengths. Therefore, continuously distributed delays should be introduced in modeling of the NNs over a certain duration of time. Taking account of this, the authors in [21–23] investigated the stability of equilibrium points and (almost) periodic solutions of neural networks with both discrete time delays and distributed delays. Meanwhile, when we are modeling real nervous systems, parameter uncertainties are probably the main source of performance degradation of neural networks that in turn affect dynamical behaviors of the systems. Moreover, in practical applications, it is hard to well describe the accurate form by using purely neural networks, and neural networks with parameter uncertainties become more practice. Therefore, the stability analysis for uncertain neural networks (UNNs) with distributed time-varying delays becomes increasingly significant.

However, in some practical situations, we always hope to obtain faster or even finite-time convergent speed. So, it is necessary to make a study for finite-time stabilization. The concept of finite-time stability (FTS) has been first introduced in the control literature [24]. A system is said to be finite-time stable if its state does not exceed a certain threshold during a specified time interval. Compared with the Lyapunov stability, finite-time stability concerns the boundedness of system during a fixed finite-time interval. Up to date, many researchers have devoted much effort to finite-time stability and synchronization [25–29]. For example, finite-time stability was considered in [30–33] for some continuous nonlinear systems without delay. In [35], authors researched the delay-dependent stability of uncertain neural networks with time-varying delays. In [36], the authors studied the robust finite-time stabilization with guaranteed cost control for a class of delayed neural networks. Furthermore, in [25, 28, 32, 34, 38], authors investigated the finite-time stabilization and synchronization of delays neural networks in different kinds of methods. It should be noted that seldom authors have been reported concerning the finite-time stability and stabilization of UNNs with distributed time-varying delays. This is because UNNs with distributed time-varying delays bring difficulties in studying the finite-time stability and stabilization of the system. Moreover, it is difficult to find a Lyapunov function satisfying the derivative condition of the finite-time stability of system with distributed time-varying delays, because the systems with distributed time-varying delays generally have more complex dynamic behaviors than the systems without distributed time-varying delays.

Motivated by the above discussions, we study the finite-time stability of UNNs with the general activation functions through a designed feedback controller. Based on the Lyapunov stability theory and integral inequality technique, a proper feedback controller is designed to achieve the finite-time stability of UNNs with distributed time varying, and the upper bound of the settling time for stabilization is estimated. In addition, by choosing different parameters and different control strengths for the system, we consider two-dimensional distributed time-varying delay UNNs with different activation functions to verify the effectiveness of the obtained results. Our results are applicable to model and stabilize the high-dimensional nonlinear systems, specially high-order neural networks due to their excellent approximation capabilities. To our best knowledge, few works have been reported to control the UNNs with distributed time-varying delays arriving at its equilibrium point within a finite-time period in the existing literature, so our results compliment the previous results [25–33, 36, 38].

This paper is organized as follows: In the following section, the theoretical model for uncertain neural networks with distributed time-varying delays, some definitions and lemmas are presented. In Sect. 3, the finite-time stabilization of uncertain neural network is analyzed. Three examples are provided to demonstrate the effectiveness of the obtained results in Sect. 4. Finally, the conclusion is drawn in Sect. 5.

2 Problem statement and preliminaries

Notations The notations used in this paper are quite and fairly standard. Throughout this paper, \(\mathbb {R}^n\) and \(\mathbb {R}^{n\times n}\) denote, respectively, the n-dimensional Euclidean space and the set of all \(n\times n\) real matrices. \(\Vert x\Vert =\sqrt{x^\mathrm {T}x}\) refers to the Euclidean vector norm. \(A^\mathrm {T}\) represents the transpose of matrix A. I is the identity matrix with compatible dimension. \(diag\{\cdots \}\) represents a block-diagonal matrix. Matrices, if not explicitly specified, are assumed to have compatible dimensions.

In this paper, we consider a class of neural networks with distributed time-varying delays as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x}(t)=-Ex(t)+Af(x(t))+Bf(x(t-(\tau (t)))+C\int ^t_{t-\tau (t)}f(x(s))\hbox {d}s+u(t),\,t>0,\\ x(t)=\phi (t),\quad \forall \,t\in [-\tau _2,0], \end{array}\right. } \end{aligned}$$
(1)

where \(x(t)=[x_1(t),x_2(t),\ldots ,x_n(t)]^T\) is the state vector of the network at time t, n corresponds to the number of neurons; \(f(x(t))=[f_1(x_1(t)),f_2(x_2(t)),\ldots ,f_n(x_n(t))]^T\in \mathbb {R}^n\) is the neuron activation function; \(u(t)=(u_1(t),u_2(t),\ldots ,u_n(t))^T\) is the control input. \(E=diag(e_1,e_2,\ldots ,e_n)\) is the diagonal matrix with \(e_i>0\), \(i=1,2,\ldots ,n\); \(A\in \mathbb {R}^{n\times n}\) is the connection weight matrix; \(B\in \mathbb {R}^{n\times n}\) is the delayed connection weight matrix; and \(C\in \mathbb {R}^{n\times n}\) is the distributed delayed connection weight matrix; \(\phi (t)\) is a vector-valued initial function; \(\tau (t)\) denotes the time-varying delay and is assumed to satisfy the following condition:

$$\begin{aligned} 0<\tau _1\le \tau (t)\le \tau _2,\quad \mu _1\le \dot{\tau }(t)\le \mu _2,\quad \mu _2\ge 0 \end{aligned}$$

where \(\tau _1,\tau _2,\mu _1,\mu _2\) are known real constants.

The initial condition of system (1) is in the form of \(x(t)=\phi (t)\in \mathcal {C}([-\tau _2,0],\mathbb {R}^n),\) \(f:\mathbb {R}^n\rightarrow \mathbb {R}^n\) is continuous function satisfying \(f(0)=0\), and we also assume that the activation function \(f_i(\cdot )\) satisfies the Lipschitz condition with the Lipschitz constant \(l_i>0 \,(i=1,2,\ldots ,n)\) for all \(x_i, y_i\in \mathbb {R}\), i.e.,

$$\begin{aligned} |f_i(x_i)-f_i(y_i)|\le l_i|x_i-y_i|. \end{aligned}$$

Before studying the finite-time stabilization of system (1), we need the following useful definition and lemmas which play an important role in the derivation of the main results.

Definition 2.1

[37] The system (1) is finite-time stabilizable if there exists a constant \(T>0\) such that

$$\begin{aligned} \lim \limits _{t\rightarrow T}\Vert x(t)\Vert =0\hbox { and }\Vert x(t)\Vert =0\hbox { if }t>T. \end{aligned}$$

Lemma 2.2

[38] Assume that a continuous, positive definite function V(t) satisfies the following differential inequality:

$$\begin{aligned} \dot{V}(t)\le -\lambda V^\eta (t),\quad \forall t\ge t_0,\quad V(t_0)\ge 0, \end{aligned}$$
(2)

where \(\lambda >0,0<\eta <1\) are all constants. Then, for any given \(t_0\), V(t) satisfies the following inequality:

$$\begin{aligned} V^{1-\eta }(t)\le V^{1-\eta }(t_0)-\lambda (1-\eta )(t-t_0),\quad t_0\le t\le T , \end{aligned}$$
(3)

and \(V(t)=0,\,\forall t\ge T,\) with T given by

$$\begin{aligned} T=t_0+\frac{V^{1-\eta }(t_0)}{\lambda (1-\eta )}. \end{aligned}$$
(4)

Lemma 2.3

[39] Given any real matrices \(\Sigma _1,\Sigma _2,\Sigma _3\) of appropriate dimensions and a scalar \(s>0\), such that \(0<\Sigma _3=\Sigma _3^T\). Then the following inequality holds:

$$\begin{aligned} \Sigma _1^T\Sigma _2+\Sigma _2^T\Sigma _1\le s\Sigma _1^T\Sigma _3\Sigma _1+s^{-1}\Sigma _2^T\Sigma _3^{-1}\Sigma _2. \end{aligned}$$

Lemma 2.4

[40] For any positive definite matrix \(M\in \mathbb {R}^{n\times n}\), scalars \(h_2>h_1>0,\) vector function \(w:[h_1,h_2]\rightarrow \mathbb {R}^n\) such that the integrations concerned are well defined, the following inequality holds:

$$\begin{aligned} & -(h_2-h_1)\int _{t-h_2}^{t-h_1}w^T(s)Mw(s)\hbox {d}s\\ & \quad \le -\left( \int _{t-h_2}^{t-h_1}w(s)\hbox {d}s\right) ^TM\left( \int _{t-h_2}^{t-h_1}w(s)\hbox {d}s\right) \end{aligned}$$

3 Main results

In this section, we will address the finite-time stabilization of system (1) by means of the aforementioned lemmas. The feedback control law \(u(t)=(u_1(t),u_2(t),\ldots ,u_n(t))^T\) is given as follows:

$$\begin{aligned} u(t)&=-k_1x(t)-(k_2x^T(t-\tau (t))x(t-\tau (t))+k_3\int _{t-\tau (t)}^tf^T(x(s))f(x(s))\hbox {d}s)\frac{x(t)}{\Vert x(t)\Vert ^2}\nonumber \\&-\lambda (x^T(t)x(t)+\int _{t-\tau (t)}^tf^T(x(s))f(x(s))\hbox {d}s)^{\gamma }\frac{x(t)}{\Vert x(t)\Vert ^2} \end{aligned}$$
(5)

where \(x(t)=(x_1(t),x_2(t),\ldots , x_n(t))^T\), \(\lambda >0,\,0<\gamma <1\) are all constants, and \(k_1,k_2,\,k_3\) denote control strength.

In order to ensure the finite-time stability of system (1), we will establish some sufficient LMI conditions.

Theorem 3.1

Suppose that there exist positive constants \(s_1,s_2,s_3,\lambda , 0<\gamma <1\), and the feedback control strength \(k_1,k_2,k_3\) satisfying the following conditions:

  1. 1.

    \(-E-E^T+s_1AA^T+s_2BB^T+s_3CC^T+s_1^{-1}L_f^2+L_f^2-2k_1I\le 0\);

  2. 2.

    \(s_2^{-1}L_f^2-(1-\mu _2)L_f^2-2k_2I\le 0\);

  3. 3.

    \(s_3^{-1}\tau _2-2k_3\le 0\).

where \(L_f=diag(l_1,l_2,\ldots ,l_n)\), \(0\le \tau _1\le \tau (t)\le \tau _2\), \(\mu _1\le \dot{\tau }(t)\le \mu _2,\,\mu _2>1\). Then the system (1) is finite-time stability via the controller (5), and the settling time is estimated by \(T=t_0+\frac{V^{1-\gamma }(t_0)}{2\lambda (1-\gamma )}\)

Proof

Consider the following Lyapunov functional:

$$\begin{aligned} V(t)=x^T(t)x(t)+\int _{t-\tau (t)}^tf^T(x(s))f(x(s))\hbox {d}s \end{aligned}$$
(6)

According to Lemma 2.3, we have the following results:

$$\begin{aligned}&x^T(t)Af(x(t))+f^T(x(t))A^Tx(t)\le s_1x^T(t)AA^Tx(t)+s_1^{-1}f^T(x(t))f(x(t)) \end{aligned}$$
(7)
$$\begin{aligned}&x^T(t)Bf(x(t-\tau (t)))+f^T(x(t-\tau (t)))B^Tx(t)\le s_2x^T(t)BB^Tx(t)\nonumber \\&\quad +\,s_2^{-1}f^T(x(t-\tau (t)))f(x(t-\tau (t))) \end{aligned}$$
(8)
$$\begin{aligned}& x^T(t)C\int _{t-\tau (t)}^tf(x(s))\hbox {d}s+\left[ \int _{t-\tau (t)}^tf(x(s))\hbox {d}s\right] ^TC^Tx(t) \\ \quad & \le s_3x^T(t)CC^Tx(t)\nonumber \\ \quad & +\,s_3^{-1}\left[ \int _{t-\tau (t)}^tf(x(s))\hbox {d}s\right] ^T\int _{t-\tau (t)}^tf(x(s))\hbox {d}s \end{aligned}$$
(9)

According to Eqs. (7–9) and Lemma 2.4, the derivative of Eq. (6) with respect to time t along the trajectories of the system (1) is calculated and estimated as follows.

$$\begin{aligned} \dot{V}(t)& =2x^T(t)\dot{x}(t)+f^T(x(t))f(x(t))-f^T(x(t-\tau (t)))f(x(t-\tau (t)))(1-\dot{\tau }(t))\nonumber \\&\le \, 2x^T(t)\left[ -Ex(t)+Af(x(t))+Bf(x(t-\tau (t)))+C\int _{t-\tau (t)}^tf(x(s))\hbox {d}s+u(t)\right] \nonumber \\&\quad +\, f^T(x(t))f(x(t))-(1-\mu _2)f^T(x(t-\tau (t)))f(x(t-\tau (t)))\nonumber \\&=\, 2x^T(t)(-E)x(t)+2x^T(t)Af(x(t))+2x^T(t)Bf(x(t-\tau (t))) +2x^T(t)C\int _{t-\tau (t)}^tf(x(s))\hbox {d}s\nonumber \\&\quad +\, 2x^T(t)u(t)+f^T(x(t))f(x(t))-(1-\mu _2)f^T(x(t-\tau (t)))f(x(t-\tau (t)))\nonumber \\&\le\, x^T(t)\left[ -E-E^T+s_1AA^T+s_2BB^T+s_3CC^T+s_1^{-1}L_f^2+L_f^2\right] x(t)\nonumber \\&\quad +\, x^T(t-\tau (t))\left[ s_2^{-1}L_f^2-(1-\mu _2)L_f^2\right] x(t-\tau (t))\nonumber \\&\quad +s_3^{-1}\left[ \int _{t-\tau (t)}^tf(x(s))\hbox {d}s\right] ^T\left[ \int _{t-\tau (t)}^tf(x(s))\hbox {d}s\right] +2x^T(t)u(t)\nonumber \\&\le\, x^T(t)\left[ -E-E^T+s_1AA^T+s_2BB^T+s_3CC^T+s_1^{-1}L_f^2+L_f^2\right] x(t)\nonumber \\&\quad +\, x^T(t-\tau (t))\left[ s_2^{-1}L_f^2-(1-\mu _2)L_f^2\right] x(t-\tau (t))\nonumber \\&\quad +\, s_3^{-1}\tau _2\int _{t-\tau (t)}^tf^T(x(s))f(x(s))\hbox {d}s+2x^T(t)u(t)\nonumber \\ \end{aligned}$$
(10)

Note also that

$$\begin{aligned} 2x^T(t)u(t)&=-2k_1x^T(t)x(t)-2k_2x^T(t-\tau (t))x(t-\tau (t))-2k_3\int _{t-\tau (t)}^tf^T(x(s))f(x(s))\hbox {d}s \\ &\quad -2\lambda (x^T(t)x(t)+\int _{t-\tau (t)}^tf^T(x(s))f(x(s))\hbox {d}s)^{\gamma } \end{aligned}$$
(11)

Substituting Eq. 11 into Eq. 10, we have the following inequality:

$$\begin{aligned} \dot{V}(t)& \le\,x^T(t)\left[ -E-E^T+s_1AA^T+s_2BB^T+s_3CC^T+s_1^{-1}L_f^2+L_f^2-2k_1\right] x(t)\nonumber \\&+\quad x^T(t-\tau (t))\left[ s_2^{-1}L_f^2-(1-\mu _2)L_f^2-2k_2I\right] x(t-\tau (t))\nonumber \\&\quad +(s_3^{-1}\tau _2-2k_3)\int _{t-\tau (t)}^tf^T(x(s))f(x(s))\hbox {d}s\nonumber \\& \quad -2\lambda (x^T(t)x(t)+\int _{t-\tau (t)}^tf^T(x(s))f(x(s))\hbox {d}s)^{\gamma }\nonumber \\ \le&-2\lambda V^\gamma (t) \end{aligned}$$
(12)

Therefore, we have

$$\begin{aligned} T=t_0+\frac{V^{1-\gamma }(t_0)}{2\lambda (1-\gamma )}\quad t_0\le t\le T, \end{aligned}$$
(13)

and, we can also get \(V(t)=0, \quad \forall t\ge T\).

Therefore, the UNNs system x(t) is globally finite-time stability, and the settling time is estimated by \(T=t_0+\frac{V^{1-\gamma }(t_0)}{2\lambda (1-\gamma )}\).

The proof is completed. \(\square\)

Based on Theorem 3.1, it is easy to obtain the following corollary:

Corollary 3.2

If there exist positive constants \(s_1,s_2,s_3,\lambda ,\gamma\), and control strength \(k_1,k_2,k_3\) such that

  1. 1.

    \(k_1\ge \lambda _{\max }(-E-E^T+s_1AA^T+s_2BB^T+s_3CC^T+s_1^{-1}L_f^2+L_f^2)/2\)

  2. 2.

    \(k_2\ge (s_2^{-1}+\mu _2-1)/2\)

  3. 3.

    \(k_3\ge \tau _2/2s_3\)

where \(L_f=diag(l_1,l_2,\ldots ,l_n)\), \(0\le \tau _1\le \tau (t)\le \tau _2\), \(\mu _1\le \dot{\tau }(t)\le \mu _2,\,\mu _2>1\). Then the system (1) is finite-time stability via the controller (5), and the finite-time is estimated by \(T=t_0+\frac{V^{1-\gamma }(t_0)}{2\lambda (1-\gamma )}\)

Remark 3.3

From Corollary 3.2, it is easy to see that the control strength \(k_1\) just depends on the maximum eigenvalue of \(AA^T,\,BB^T, \,CC^T,\,L_f,\,-E-E^T\) and all the constants \(s_1,\,s_2,\,s_3\) and the control strength \(k_2\) relies on \(s_2\) and \(\mu _2\), and \(k_3\) relies on \(s_3\) and the maximum value of \(\tau (t)\), that is \(\tau _2\). Thus, compared with Theorem 3.1, Corollary 3.2 is an inequality, which is the simplified form of Theorem 3.1. And we can see that Theorem 3.1 is a LMI, which can be solved by using the LMI Control Toolbox in MATLAB. Then we can note that Corollary 3.2 is more specific than Theorem 3.1.

In the following, we will discuss the application of Theorem 3.1 in some special cases.

When there is no distributed time-varying delays, system (1) reduces to

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x}(t)=-Ex(t)+Af(x(t))+Bf(x(t-(\tau (t)))+u(t),\quad t>0,\\ x(t)=\phi (t), \quad \forall \,\,t\in [-\tau _2,0], \end{array}\right. } \end{aligned}$$
(14)

The feedback control law \(u(t)=(u_1(t),u_2(t),\ldots ,u_n(t))^T\) is given

$$\begin{aligned} u(t)&=-\tilde{k}_1x(t)-\tilde{k}_2x^T(t-\tau (t))x(t-\tau (t))\frac{x(t)}{\Vert x(t)\Vert ^2}\nonumber \\&-\tilde{\lambda }(x^T(t)x(t)+\int _{t-\tau (t)}^tf^T(x(s))f(x(s))\hbox {d}s)^{\tilde{\gamma }}\frac{x(t)}{\Vert x(t)\Vert ^2} \end{aligned}$$
(15)

Applying Theorem 3.1 to system (14), we obtain the following result.

Corollary 3.4

If there exist positive constants \(\tilde{s}_1,\tilde{s}_2,\tilde{\lambda },\tilde{\gamma }\), and control strength \(\tilde{k}_1,\tilde{k}_2\) such that

  1. 1.

    \(-E-E^T+\tilde{s}_1AA^T+\tilde{s}_2BB^T+\tilde{s}_1^{-1}L_f^2+L_f^2-2\tilde{k}_1I\le 0\)

  2. 2.

    \(\tilde{s}_2^{-1}L_f^2-(1-\mu _2)L_f^2-2\tilde{k}_2I\le 0,\)

where \(L_f=diag(l_1,l_2,\ldots ,l_n)\), \(0\le \tau _1\le \tau (t)\le \tau _2\), \(\mu _1\le \dot{\tau }(t)\le \mu _2,\,\mu _2>1\). Then the system (14) is finite-time stability via the controller (15), and the finite-time is estimated by \(T=t_0+\frac{V^{1-\tilde{\gamma }}(t_0)}{2\tilde{\lambda }(1-\tilde{\gamma })}\)

Proof

Considering the same Lyapunov functional as Eq. (6), the proof of this corollary is similar to Theorem 3.1; thus, we omit it.

Then, we have

$$\begin{aligned} T=t_0+\frac{V^{1-\tilde{\gamma }}(t_0)}{2\tilde{\lambda }(1-\tilde{\gamma })},\quad t_0\le t\le T, \end{aligned}$$
(16)

and, we can also get \(V(t)=0, \quad \forall t\ge T\).

Therefore, the system (14) is globally finite-time stability, and the settling time is estimated by \(T=t_0+\frac{V^{1-\tilde{\gamma }}(t_0)}{2\tilde{\lambda }(1-\tilde{\gamma })}\).

Remark 3.5

Although the stabilization of delays neural networks has been investigated in the past few years [7, 9, 10, 21], and finite-time stability of delays neural networks also has been investigated in [22, 25, 27, 29, 34]. Compared with the traditional method, it is noted that Corollary 3.4 studies the finite-time stabilization of UNNs without distributed time-varying delays, which is similar to the general neural networks. In this corollary, only two feedback control strengths \(\tilde{k}_1, \tilde{k}_2\) are designed to ensure the finite-time stabilization of system (14). Our results complement and extend the previous results of UNNs.

When there is no discrete delays and distributed time-varying delays, system (1) reduces to

$$\begin{aligned} \dot{x}(t)=-Ex(t)+Af(x(t))+u(t) \end{aligned}$$
(17)

The feedback control law \(u(t)=(u_1(t),u_2(t),\ldots ,u_n(t))^T\) is given

$$\begin{aligned} u(t)&=-\hat{k}_1x(t)-\hat{\lambda }(x^T(t)x(t))^{\hat{\gamma }}\frac{x(t)}{\Vert x(t)\Vert ^2} \end{aligned}$$
(18)

The following corollary can be easily obtained from Theorem 3.1 and Corollary 3.4.

Corollary 3.6

If there exist positive constants \(\hat{s}_1,\hat{\lambda },\hat{\gamma }\), and control strength \(\hat{k}_1\) such that

$$\begin{aligned} -E-E^T+\hat{s}_1AA^T+\hat{s}_1^{-1}L_f^2-2\hat{k}_1I\le 0 \end{aligned}$$

Then the system (17) is finite-time stability via the controller (18), and the finite-time is estimated by \(T=t_0+\frac{V^{1-\hat{\gamma }}(t_0)}{2\hat{\lambda }(1-\hat{\gamma })}.\)

Proof

Construct the following Lyapunov function:

$$\begin{aligned} V(t)= \,x^T(t)x(t) \end{aligned}$$
(19)

Then the derivative of Eq. (19) with respect to time t along the trajectories of the system (17) is calculated and estimated as follows.

$$\begin{aligned} \dot{V}(t)& =2x^T(t)\dot{x}(t)\nonumber \\ \le&2x^T(t)\left[ -Ex(t)+Af(x(t))+u(t)\right] \nonumber \\ \le&x^T(t)\left[ -E-E^T+\hat{s}_1AA^T+\hat{s}_1^{-1}L_f^2\right] x(t)+2x^T(t)u(t)\nonumber \\ \le&x^T(t)\left[ -E-E^T+\hat{s}_1AA^T+\hat{s}_1^{-1}L_f^2-2\hat{k}_1I\right] (t)-2\hat{\lambda }(x^T(t)x(t))^{\hat{\gamma }}\nonumber \\ \le&-2\hat{\lambda } V^{\hat{\gamma }}(t)\nonumber \\ \end{aligned}$$
(20)

where

$$\begin{aligned} 2x^T(t)u(t)&=-2\hat{k}_1x^T(t)x(t)-2\hat{\lambda }(x^T(t)x(t))^{\hat{\gamma }} \end{aligned}$$
(21)

Then, we have

$$\begin{aligned} T=t_0+\frac{V^{1-\hat{\gamma }}(t_0)}{2\hat{\lambda }(1-\hat{\gamma })},\quad t_0\le t\le T, \end{aligned}$$
(22)

and, we can also get \(V(t)=0, \quad \forall t\ge T\).

Therefore, the system (17) is globally finite-time stability, and the settling time is estimated by \(T=t_0+\frac{V^{1-\hat{\gamma }}(t_0)}{2\hat{\lambda }(1-\hat{\gamma })}\).

Remark 3.7

System (17) is the specific form of system (1), which is without time delays. And only a feedback control strength \(\hat{k}_1\) is needed to ensure the finite-time stabilization of system (17). However, time-delay systems have more complicated dynamic behaviors and are more difficult to deal with than system without delays. In [30], finite-time stability of neural networks was studied, but the systems in these papers are without delays, similar to system (17) in this paper. Since delays are unavoidable in the hardware implementation of neural networks, it is necessary to take the delays into consideration in the finite-time stability problem. In this paper, the neural networks with time-varying delays and distributed time-varying delays are considered, which make our results general compared with the existing results [9, 10, 21, 22, 25, 27, 29, 30, 32, 34].

4 Numerical example

In this section, three examples are provided to verify the effectiveness of the obtained results in the previous section. Program Euler algorithm in MATLAB can be used to solve distributed time-varying delay UNNs, and the LMI Control Toolbox in MATLAB can be used to solve the LMIs.

Example 1

Consider the two-dimensional distributed time-varying delay UNNs

$$\begin{aligned} \dot{x}(t)=-Ex(t)+Af(x(t))+Bf(x(t-(\tau (t)))+C\int ^t_{t-\tau (t)}f(x(s))\hbox {d}s, \end{aligned}$$
(23)

where \(x(t)=(x_1(t),x_2(t))^T, \,\)

$$\begin{aligned} E & = \left[ {{\begin{array}{ll} {1} &{} \quad 0 \\ 0 &{} \quad {1} \\ \end{array} }} \right] ,\quad A=\left[ {{\begin{array}{ll} {2} &{} \quad -0.1 \\ -5 &{} \quad {4.5} \\ \end{array} }} \right] ,\\ B & = \left[ {{\begin{array}{ll} {-1.5} &{}\quad -0.1 \\ -0.2 &{} \quad {-4} \\ \end{array} }} \right] ,\quad C=\left[ {{\begin{array}{ll} {-0.05} &{} \quad 0.07 \\ 0.37 &{} \quad {-0.18} \\ \end{array} }} \right] , \end{aligned}$$

The activation functions are assumed to be

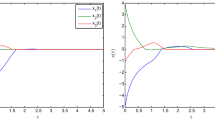
$$\begin{aligned} f_i(x_i)=\tanh (x_i),\quad i=1,2. \end{aligned}$$

In this example, we choose the time-varying delay \(\tau (t)=1+2.75sin(t)\), which implies \(0<\tau _1\le \tau (t)\le \tau _2=3.75\). Then we can get \(\dot{\tau }(t)=2.75cos(t)\), which implies \(\mu _1=-2.75\le \dot{\tau }(t)\le \mu _2=2.75\). Figure 1 depicts without the feedback control u(t) by setting \(x(0)=[-1.6, 1.2]^T\).

Fig. 1
figure 1

Phase plot of UNNs system without controller

Full size image

The controller is designed as

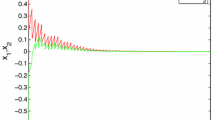
$$\begin{aligned} u(t)& =-k_1x(t)-(k_2x^T(t-\tau (t))x(t-\tau (t))+k_3\int _{t-\tau (t)}^tf^T(x(s))f(x(s))\hbox {d}s)\frac{x(t)}{\Vert x(t)\Vert ^2}\nonumber \\&-\lambda (x^T(t)x(t)+\int _{t-\tau (t)}^tf^T(x(s))f(x(s))\hbox {d}s)^{\gamma }\frac{x(t)}{\Vert x(t)\Vert ^2} \end{aligned}$$
(24)

Noting that \(\lambda _{\max }(AA^T)=47.7468,\lambda _{\max }(BB^T)=16.0755,\lambda _{\max }(CC^T)=0.1751,L_f=[1\,\,0;0\,\,1]\). For numerical simulation, we select \(\lambda =6,\gamma =0.9,s_1=0.1,s_2=5,s_3=1\), and system (23) can be finite-time stabilized via the controller (24) according to Corollary 3.2. Setting \(k_1=50,k_2=1,k_3=2\), the settling time for stabilization satisfies \(T=1.4657\). Under the controller (24), we get the state trajectories of variables \(x_1(t)\) and \(x_2(t)\) which are shown in Fig. 2.

Fig. 2
figure 2

State transient behaviors of variables \(x_1(t)\) and \(x_2(t)\) of system (23) under the controller (24)

Full size image

Remark 4.1

In the simulations, the Euler algorithm with step size 0.01 in MATLAB is used to solve distributed time-varying delay differential equations. When we select the appropriate initial values for system (23), it is noted that the system is chaotic as shown in Fig. 1. Meanwhile, our objective is to seek the appropriate \(k_1, k_2,k_3\) which guarantee the system (23) to be stabilized. Notice that the conditions of Theorem 3.1 are a linear matrix inequality, then the feedback control gains \(k_1,k_2,k_3\) can be solved by using MATLAB. Figure 2 shows the time–response curve of the UNNs with the feedback controller, which implies the parameters we chose are correct. From the numerical example, we found that the value of \(s_1,s_2,s_3\) satisfies Theorem 3.1 and all the conditions of Corollary 3.2 are also satisfied, while \(\gamma =0.9\). Therefore, the simulation results have a good agreement with the theoretical analysis obtained in the paper.

Example 2

Similar to Example 1, we adopt the Euler algorithm in MATLAB to calculate numerically the UNNs with step size 0.005. We will consider a different activation function of two-dimensional distributed time-varying delay UNNs with Example 1:

$$\begin{aligned} \dot{x}(t)=-Ex(t)+Af(x(t))+Bf(x(t-(\tau (t)))+C\int ^t_{t-\tau (t)}f(x(s))\hbox {d}s, \end{aligned}$$
(25)

where \(x(t)=(x_1(t),x_2(t))^T, \,\)

$$\begin{aligned} E & = \left[ {{\begin{array}{ll} {1} &{} \quad 0 \\ 0 &{} \quad {1} \\ \end{array} }} \right] ,\quad A=\left[ {{\begin{array}{ll} {1.8} &{} \quad -1.5 \\ 0.1 &{} \quad {1.8} \\ \end{array} }} \right] ,\\ B & = \left[ {{\begin{array}{ll} {-1.4} &{} \quad 0.1 \\ 0.1 &{}\quad {-1.4} \\ \end{array} }} \right] ,\quad C=\left[ {{\begin{array}{ll} {-0.03} &{} \quad 0.09 \\ 0.29 &{} \quad {-0.25} \\ \end{array} }} \right] , \end{aligned}$$

The activation functions are assumed to be

$$\begin{aligned} f_i(x_i)=0.5(|x_i+1|-|x_i-1|),\quad i=1,2. \end{aligned}$$

In this example, we choose the time-varying delay \(\tau (t)=5+1.05sin(t)\), which implies \(0<\tau _1\le \tau (t)\le \tau _2=6.05\). Then we can get \(\dot{\tau }(t)=1.05cos(t)\), which implies \(\mu _1=-1.05\le \dot{\tau }(t)\le \mu _2=1.05\). Figure 3 depicts without the feedback control u(t) by setting \(x(0)=[-3, 4]^T\).

Fig. 3
figure 3

Phase plot of UNNs system without controller

Full size image

The controller is designed as

$$\begin{aligned} u(t)&=-k_1x(t)-(k_2x^T(t-\tau (t))x(t-\tau (t))+k_3\int _{t-\tau (t)}^tf^T(x(s))f(x(s))\hbox {d}s)\frac{x(t)}{\Vert x(t)\Vert ^2}\nonumber \\&-\lambda (x^T(t)x(t)+\int _{t-\tau (t)}^tf^T(x(s))f(x(s))\hbox {d}s)^{\gamma }\frac{x(t)}{\Vert x(t)\Vert ^2} \end{aligned}$$
(26)

Noting that \(\lambda _{\max }(AA^T)=7.4610,\lambda _{\max }(BB^T)=2.25,\lambda _{\max }(CC^T)=0.1533,L_f=[1\,\,0;0\,\,1]\). For numerical simulation, we select \(\lambda =2,\gamma =0.8,s_1=1,s_2=10,s_3=4\), and system (25) can be finite-time stabilized via the controller (26) according to Corollary 3.2. Setting \(k_1=18,k_2=0.1,k_3=2\), the settling time for stabilization satisfies \(T=0.2862\). Under the controller (26), we get the state trajectories of variables \(x_1(t)\) and \(x_2(t)\) which are shown in Fig. 4.

Fig. 4
figure 4

State transient behaviors of variables \(x_1(t)\) and \(x_2(t)\) of system (25) under the controller (26)

Full size image

Remark 4.2

It should be highly pointed out that, in the previous literature, authors in [9, 10, 21, 22, 25, 27, 29] investigated the problems with time-varying delays with different approaches. However, when they are simulated, the delays they selected are always constant. So far, it is noted that in this paper, the time-varying delays and distributed time-varying delays \(\tau (t)\) are assumed to be differentiable. Therefore, as a result, some less conservative stability criteria are derived by considering the relationship between time-varying delay and its intervals, which have wider applications than [9, 10, 21, 22, 25, 27, 29, 32, 34], the existing ones because independent upper bounds of the delay derivative in the various delay intervals are taken into account.

Remark 4.3

Recently, the stabilization and synchronization of neural networks have been intensively investigated [9, 10, 21, 22, 25, 27, 29, 30, 32] and many interesting and useful results have been obtained. However, to the best of our knowledge, there are few results concerning the stabilization and synchronization schemes for uncertain neural networks with distributed time-varying delays via periodically intermittent control or impulsive control. This is an interesting problem and will become the subject of our future investigation.

Example 3

Similarly, the Euler algorithm with step size 0.02 in MATLAB is used to solve distributed time-varying delay differential equations in this example. To further show the validity of our results, we consider the three-dimensional distributed time-varying delay UNNs

$$\begin{aligned} \dot{x}(t)=-Ex(t)+Af(x(t))+Bf(x(t-(\tau (t)))+C\int ^t_{t-\tau (t)}f(x(s))\hbox {d}s, \end{aligned}$$
(27)

where \(x(t)=(x_1(t),x_2(t),x_3(t))^T, \,\)

$$\begin{aligned} E & = \left[ {{\begin{array}{lll} {0.9} &{}\quad 0 &{} \quad 0 \\ 0 &{}\quad {1.1} &{}\quad 0 \\ 0&{} \quad 0 &{}\quad 1\\ \end{array} }} \right] ,\quad A=\left[ {{\begin{array}{lll} {2} &{}\quad -0.1 &{}\quad -6 \\ -1.5 &{}\quad {-0.1} &{}\quad -0.8 \\ 4 &{} \quad 0.4 &{}\quad -0.2\\ \end{array} }} \right] ,\\ B & = \left[ {{\begin{array}{lll} {-5} &{} \quad 4.5 &{} \quad 7 \\ -0.2 &{}\quad {-4} &{} \quad 0.4 \\ -4 &{} \quad 3 &{}\quad 0.2\\ \end{array} }} \right] ,\quad C=\left[ {{\begin{array}{lll} {-0.5} &{}\quad 0.7 &{}\quad -0.4 \\ 0.3 &{} \quad {-0.18} &{} \quad 1 \\ -0.2 &{}\quad 0.5 &{}\quad -0.1 \end{array} }} \right] , \end{aligned}$$

The activation functions are assumed to be

$$\begin{aligned} f_i(x_i)=0.5(|x_i+1|-|x_i-1|),\quad i=1,2,3. \end{aligned}$$
Fig. 5
figure 5

Phase plot of UNNs system without controller

Full size image

In this example, we choose the time-varying delay \(\tau (t)=1+5sin(t)\), which implies \(0\le \tau _1\le \tau (t)\le \tau _2=6\). Then we can get \(\dot{\tau }(t)=5cos(t)\), which implies \(\mu _1=-5\le \dot{\tau }(t)\le \mu _2=5\). Figure 5 depicts without the feedback control u(t) by setting \(x(0)=[4, 0.6, 0.2]^T\).

The controller is designed as

$$\begin{aligned} u(t)&=-k_1x(t)-(k_2x^T(t-\tau (t))x(t-\tau (t))+k_3\int _{t-\tau (t)}^tf^T(x(s))f(x(s))\hbox {d}s)\frac{x(t)}{\Vert x(t)\Vert ^2}\nonumber \\&-\lambda (x^T(t)x(t)+\int _{t-\tau (t)}^tf^T(x(s))f(x(s))\hbox {d}s)^{\gamma }\frac{x(t)}{\Vert x(t)\Vert ^2} \end{aligned}$$
(28)

Noting that \(\lambda _{\max }(AA^T)=43.127,\lambda _{\max }(BB^T)=111.9566,\lambda _{\max }(CC^T)=1.8642,L_f=[1\,\,0\,\,0;0\,\,1\,\,0;0\,\,0\,\,1]\). For numerical simulation, we select \(\lambda =0.3,\gamma =0.8,s_1=0.2,s_2=0.1,s_3=5\), and system (27) can be finite-time stabilized via the controller (28) according to Corollary 3.2. Setting \(k_1=17,k_2=9,k_3=0.7\), the settling time for stabilization satisfies \(T=6.5571\). Under the controller (28), we get the state trajectories of variables \(x_1(t)\), \(x_2(t)\) and \(x_3(t)\) which are shown in Fig. 6.

Fig. 6
figure 6

State transient behaviors of variables \(x_1(t), x_2(t)\) and \(x_3(t)\) of system (27) under the controller (28)

Full size image

Remark 4.4

It is worthy to note that Example 1 and Example 2 depict the two-dimensional UNNs with different activation function, and to further show the validity of our results, we consider the three-dimensional distributed time-varying delay UNNs in this example. Compared with the precious works [9, 10, 21, 22, 25, 27, 29, 32], most authors discussed the two-dimensional NNs with or without delays. Our results are applicable to stabilize the high-dimensional nonlinear systems, specially high-order neural networks due to their excellent approximation capabilities.

5 Conclusions

This paper focuses on finite-time stability analysis of uncertain neural networks (UNNs) with distributed time-varying delays by using analysis technique. The proposed methods have been applied to two-dimensional and three-dimensional distributed time-varying delays to demonstrate the effectiveness of the results. By adding feedback controllers, the general finite-time stability criterion conditions, together with its simplified versions, have been obtained. Evidently, our results are novel and easily verified. In this paper, the distributed time-varying delays are taken into consideration in studying finite-time stability problem, which achieve a valuable improvement compared with corresponding previous works [25–36, 38]. Therefore, our results are less conservative and more general. Moreover, the finite-time stabilization of delayed neural networks without distributed time-varying delays has been intensively investigated in [27, 32, 34–36, 38], and the finite-time stabilization of uncertain neural networks with distributed time-varying delays also has been obtained in this paper. However, to the best of our knowledge, there are few results concerning the finite-time stabilization problem of uncertain neural networks (UNNs) with distributed time-varying delays under impulsive perturbations. Hence, one of the future tasks will be to improve the stability criteria for uncertain neural networks (UNNs) with distributed time-varying delays under impulsive effects.