Abstract
QUALIFLEX is a very efficient outranking method to handle multi-criteria decision-making (MCDM) involving cardinal and ordinal preference information. Based on a likelihood-based comparison approach, this paper develops two interval-valued hesitant fuzzy QUALIFLEX outranking methods to handle MCDM problems within the interval-valued hesitant fuzzy context. First, we define the likelihoods of interval-valued hesitant fuzzy preference relations that compare two interval-valued hesitant fuzzy elements (IVHFEs). Then, we propose the concepts of the concordance/discordance index, the weighted concordance/discordance index and the comprehensive concordance/discordance index. Moreover, an interval-valued hesitant fuzzy QUALIFLEX model is developed to solve MCDM problems where the evaluative ratings of the alternatives and the weights of the criteria take the form of IVHFEs. Additionally, this paper propounds another likelihood-based interval-valued hesitant fuzzy QUALIFLEX method to accommodate the IVHFEs’ evaluative ratings of alternatives and non-fuzzy criterion weights with incomplete information. Finally, a numerical example concerning the selection of green suppliers is provided to demonstrate the practicability of the proposed methods, and a comparison analysis is given to illustrate the advantages of the proposed methods.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
In multi-criteria decision-making (MCDM) [13, 38, 56], the evaluative ratings of the alternatives with respect to the criteria are often expressed by fuzzy sets [51], interval-valued fuzzy sets [52], intuitionistic fuzzy sets [1, 2], interval-valued intuitionistic fuzzy sets [3] and type-2 fuzzy sets [14]. In real applications, however, the decision-makers may hesitate among several possible precise values when expressing their assessments of the alternatives based on the criteria. To address such cases, Torra [39] and Torra and Narukawa [40] introduced the concept of hesitant fuzzy sets (HFSs), which permits the degree of membership to have different possible precise values between 0 and 1. Recently, Chen et al. [11, 12] used interval numbers within [0, 1] instead of crisp numbers to express the membership degrees in hesitant fuzzy sets and then introduced the concept of interval-valued hesitant fuzzy sets (IVHFSs), which permit the membership degrees of an element to have several different interval values within [0, 1]. Since their introduction, IVHFSs have been successfully used in many practical problems, especially in MCDM fields. MCDM within the interval-valued hesitant fuzzy environment is called interval-valued hesitant fuzzy MCDM. The existing interval-valued hesitant fuzzy MCDM methods can be generally divided into two classes. The first class is comprised of methods that use interval-value hesitant fuzzy aggregation operators [11, 24, 31, 45, 46, 53, 54]. For example, Chen et al. [11] proposed a series of operators to aggregate interval-valued hesitant fuzzy information, such as the interval-valued hesitant fuzzy weighted averaging (IVHFWA) operator, the interval-valued hesitant fuzzy weighted geometric (IVHFWG) operator, the generalized interval-valued hesitant fuzzy weighted averaging (GIVHFWA) operator, the generalized interval-valued hesitant fuzzy weighted geometric (GIVHFWG) operator, the interval-valued hesitant fuzzy ordered weighted averaging (IVHFOWA) operator, the interval-valued hesitant fuzzy ordered weighted geometric (IVHFOWG) operator, the generalized interval-valued hesitant fuzzy ordered weighted averaging (GIVHFOWA) operator, the generalized interval-valued hesitant fuzzy ordered weighted geometric (GIVHFOWG) operator, the interval-valued hesitant fuzzy hybrid averaging (IVHFHA) operator, the interval-valued hesitant fuzzy hybrid geometric (IVHFHG) operator, the generalized interval-valued hesitant fuzzy hybrid averaging (GIVHFHA) operator and the generalized interval-valued hesitant fuzzy hybrid geometric (GIVHFHG) operator. Zhang et al. [53] developed several induced generalized aggregation operators for interval-valued hesitant fuzzy information, including the induced generalized interval-valued hesitant fuzzy ordered weighted averaging (IGIVHFOWA) operator and the induced generalized interval-valued hesitant fuzzy ordered weighted geometric (IGIVHFOWG) operator. The second class is comprised of methods based on distance measures [12, 16, 17, 26, 32, 43, 50]. For example, Farhadinia [16] investigated the entropy, the similarity measure and the distance measure for IVHFSs. Chen et al. [12] proposed some correlation coefficient formulas for IVHFSs and applied them to clustering analysis in interval-valued hesitant fuzzy environments. Wei et al. [43] put forward a family of distance and similarity measures for interval-valued hesitant fuzzy sets. Xu and Zhang [50] used TOPSIS and the maximizing deviation method to develop an approach for handling MCDM problems in which the evaluative ratings of the alternatives are expressed by interval-valued hesitant fuzzy elements (IVHFEs) and the information regarding the criterion weights is incomplete.
However, two main disadvantages of the existing interval-valued hesitant fuzzy MCDM methodologies have emerged. (1) Different interval-valued hesitant fuzzy aggregation operators are involved in different operations, and this can lead to different results. Moreover, if interval-valued hesitant fuzzy aggregation operators include a large number of IVHFEs, the number of operations and the magnitudes of the results will be very large. The deterioration caused by these complexities may limit the application of interval-valued hesitant fuzzy aggregation operators. (2) In any associated distance measure, two IVHFEs must be of equal length and must be arranged in ascending order. Otherwise, it is necessary to add a specific interval value to the shorter of the two until they are both of equivalent length. It should be noted that filling some artificial interval values into an IVHFE would change the information in the original IVHFE. Moreover, different methods of extension can produce different results. Thus, such an approach is less well justified theoretically and less reliable practically. Outranking methods can overcome these drawbacks [4, 25, 34–36] and should be used to manage MCDM problems with IVHFSs. The QUALIFLEX (i.e., QUALItative FLEXible) multiple criteria method is a very popular outranking method. However, most of the existing interval-valued hesitant fuzzy decision-making methods only focus on scoring or compromise models, and until now no investigations on interval-valued hesitant fuzzy outranking models, particularly interval-valued hesitant fuzzy QUALIFLEX methods, have been found. Therefore, it is very natural for us to present some interval-valued hesitant fuzzy QUALIFLEX methods that circumvent the aforementioned drawbacks in the existing interval-valued hesitant fuzzy decision-making methods.
By generalizing Jacquet-Lagreze’s permutation method [21], Paelinck [27–29] developed the QUALIFLEX method, which approaches MCDM problems by testing how each possible ranking order of alternatives is supported by different criteria [6, 19, 20, 22, 33, 50]. Recently, some meaningful extensions of the classical QUALIFLEX method have been proposed, such as the intuitionistic fuzzy permutation method [10], the interval-valued fuzzy permutation method [9], the QUALIREG (qualitative regression) method [18], the intuitionistic fuzzy QUALIFLEX method with optimism and pessimism [8], the QUALIFLEX-based method with incomplete information [5], the interval-valued intuitionistic fuzzy QUALIFLEX method [6], the QUALIFLEX method based on interval type-2 trapezoidal fuzzy (IT2TrF) numbers [7, 41] and the hesitant fuzzy QUALIFLEX method [55]. However, all of these QUALIFLEX methods fail to address the IVHFEs’ decision data. To overcome this drawback, this paper extends the QUALIFLEX method to accommodate interval-valued hesitant fuzzy decision environments, which we call interval-valued hesitant fuzzy QUALIFLEX methods and then develops two interval-valued hesitant fuzzy QUALIFLEX methods to address MCDM problems with the interval-valued hesitant fuzzy information. First, we define the likelihoods of interval-valued hesitant fuzzy preference relations, based on which we present the concepts of the concordance/discordance index (CDI), the weighted concordance/discordance index (WCDI) and the comprehensive concordance/discordance index (CCDI). Second, we plug the likelihoods of interval-valued hesitant fuzzy preference relations into the classical QUALIFLEX method and then propose the interval-valued hesitant fuzzy QUALIFLEX (IVHF-QUALIFLEX) method to address the MCDM problems in which IVHFEs are used to represent the evaluative ratings of the alternatives and the weights of the criteria. Third, similar to the interval-valued intuitionistic fuzzy QUALIFLEX method proposed in [6], we develop another likelihood-based IVHF-QUALIFLEX method to address the IVHFEs’ evaluative ratings of alternatives and non-fuzzy criterion weights with incomplete information.
The structure of this paper is as follows: Sect. 2 reviews the concepts of IVHFSs. Section 3 formulates an MCDM problem within the interval-valued hesitant fuzzy context and then introduces the likelihoods of interval-valued hesitant fuzzy preference relations. In Sect. 4, a likelihood-based interval-valued hesitant fuzzy QUALIFLEX method is first developed to solve a MCDM problem involving interval-valued hesitant fuzzy criterion weights. Furthermore, this section also proposes a likelihood-based interval-valued hesitant fuzzy QUALIFLEX method for addressing incomplete certain information of criterion weights. Section 5 employs a practical example to justify the proposed methods. This section also carries out a comparative analysis with other interval-valued hesitant fuzzy MCDM methods. Section 6 ends this paper with some concluding remarks.
2 Preliminaries
Definition 2.1
[39, 40]. Let \(X\) be a reference set. A hesitant fuzzy set (HFS) \(A\) on \(X\) is defined in terms of a function \(h_{A} (x)\) that, when applied to \(X\), returns a subset of \(\left[ {0,1} \right]\).
An HFS \(A\) can be expressed by the following mathematical symbol [47]:
where \(h_{A} (x)\) is a set of values in \(\left[ {0,1} \right]\) and denotes all of the possible membership degrees of the element \(x \in X\) to the set \(A\). For convenience, Xia and Xu [47] called \(h = h_{A} \left( x \right)\) a hesitant fuzzy element (HFE).
Throughout this paper, let \(D([0,1])\) denote the set of all closed subintervals of \(\left[ {0,1} \right]\), i.e., \(D\left( {\left[ {0,1} \right]} \right) = \left\{ {\left. {\tilde{a} = \left[ {a^{L} ,a^{U} } \right]} \right|a^{L} \le a^{U} ,a^{L} ,a^{U} \in \left[ {0,1} \right]} \right\}\).
To compare two intervals \(\tilde{a} = \left[ {a^{L} ,a^{U} } \right]\) and \(\tilde{b} = \left[ {b^{L} ,b^{U} } \right]\), three possibility degree formulae have been developed by Facchinetti et al. [15], Wang et al. [42], and Xu and Da [49] and have been further proved to be equivalent by Xu and Chen [48]. In the following, we review Xu and Da’s possibility degree formula that is used throughout the paper.
Definition 2.2
[49]. Let \(\tilde{a} = \left[ {a^{L} ,a^{U} } \right],\tilde{b} = \left[ {b^{L} ,b^{U} } \right] \in D\left( {\left[ {0,1} \right]} \right)\), and let \(l_{{\tilde{a}}} = a^{U} - a^{L}\) and \(l_{{\tilde{b}}} = b^{U} - b^{L}\). Then, the degree of possibility of \(\tilde{a} \ge \tilde{b}\) is defined as:
The degree of possibility \(p\left( {\tilde{a} \ge \tilde{b}} \right)\) has the following properties [49]:
-
1.
\(0 \le p\left( {\tilde{a} \ge \tilde{b}} \right) \le 1\);
-
2.
\(p\left( {\tilde{a} \ge \tilde{b}} \right) + p\left( {\tilde{b} \ge \tilde{a}} \right) = 1\). In particular, \(p\left( {\tilde{a} \ge \tilde{a}} \right) = 0.5\);
-
3.
\(p\left( {\tilde{a} \ge \tilde{b}} \right) = 1\) if and only if \(b^{U} \le a^{L}\);
-
4.
\(p\left( {\tilde{a} \ge \tilde{b}} \right) = 0\) if and only if \(a^{U} \le b^{L}\);
-
5.
\(p\left( {\tilde{a} \ge \tilde{b}} \right) \ge 0.5\) if and only if \(a^{L} + a^{U} \ge b^{L} + b^{U}\). In particular, \(p\left( {\tilde{a} \ge \tilde{b}} \right) = 0.5\) if and only if \(a^{L} + a^{U} = b^{L} + b^{U}\);
-
6.
Let \(\tilde{a},\tilde{b},\tilde{c} \in D\left( {\left[ {0,1} \right]} \right)\), if \(p\left( {\tilde{a} \ge \tilde{b}} \right) \ge 0.5\) and \(p\left( {\tilde{b} \ge \tilde{c}} \right) \ge 0.5\), then \(p\left( {\tilde{a} \ge \tilde{c}} \right) \ge 0.5\).
Definition 2.3
[11, 12]. An interval-valued hesitant fuzzy set (IVHFS) \(\tilde{A}\) on the set \(X\) is defined in terms of a function that, when applied to \(X\), returns a subset of \(D\left( {\left[ {0,1} \right]} \right)\).
An IVHFS \(\tilde{A}\) can be expressed as the following mathematical symbol [11]:
where \(\tilde{h}_{{\tilde{A}}} \left( x \right)\) denotes all of the possible interval degrees of \(x \in X\) to \(\tilde{A}\). For simplicity, \(\widetilde{h} = \tilde{h}_{{\tilde{A}}} \left( x \right)\) is said to be an interval-valued hesitant fuzzy element (IVHFE) [11]. If \(\tilde{\gamma } \in \widetilde{h}\), then \(\tilde{\gamma }\) is an interval number and can be denoted by \(\tilde{\gamma } = \left[ {\gamma^{L} ,\gamma^{U} } \right]\), where \(\gamma^{L} = \inf \tilde{\gamma }\) and \(\gamma^{U} = \sup \tilde{\gamma }\) are the lower and upper limits of \(\tilde{\gamma }\), respectively. Obviously, if \(\gamma^{L} = \gamma^{U}\) for any \(\tilde{\gamma } \in \widetilde{h}\), then the IVHFE reduces to the HFE.
For convenience, we denote an IVHFE as \(\tilde{h} = \left\{ {\left. {\tilde{\gamma }} \right|\tilde{\gamma } \in \widetilde{h}} \right\} = \left\{ {\left[ {\left( {\gamma^{1} } \right)^{L} ,\left( {\gamma^{1} } \right)^{U} } \right],\left[ {\left( {\gamma^{2} } \right)^{L} ,\left( {\gamma^{2} } \right)^{U} } \right], \ldots ,\left[ {\left( {\gamma^{{l_{{\tilde{h}}} }} } \right)^{L} ,\left( {\gamma^{{l_{{\tilde{h}}} }} } \right)^{U} } \right]} \right\}\), where \(l_{{\tilde{h}}}\) is the number of interval values in \(\tilde{h}\). The lower bound of \(\tilde{h}\) is \(h^{ - } = \hbox{min} \left\{ {\left( {\gamma^{1} } \right)^{L} ,\left( {\gamma^{2} } \right)^{L} , \ldots ,\left( {\gamma^{{l_{{\tilde{h}}} }} } \right)^{L} } \right\}\), and the upper bound of \(\tilde{h}\) is \(h^{ + } = \hbox{max} \left\{ {\left( {\gamma^{1} } \right)^{U} ,\left( {\gamma^{2} } \right)^{U} , \ldots ,\left( {\gamma^{{l_{{\tilde{h}}} }} } \right)^{U} } \right\}\).
Example 2.1
Let \(X = \left\{ {x_{1} ,x_{2} ,x_{3} } \right\}\), \(\tilde{A} = \left\{ {\left\langle {x_{1} ,\left\{ {\left[ {0.7,0.8} \right],\left[ {0.5,0.6} \right]} \right\}} \right\rangle ,\left\langle {x_{2} ,\left\{ {\left[ {0.3,0.5} \right],\left[ {0.3,0.4} \right],\left[ {0.2,0.3} \right]} \right\}} \right\rangle ,\left\langle {x_{3} ,\left\{ {\left[ {0.6,0.8} \right],\left[ {0.6,0.7} \right]} \right\}} \right\rangle } \right\}\), and \(\tilde{h} = \left\{ {\left[ {0.3,0.5} \right],\left[ {0.3,0.4} \right],\left[ {0.2,0.3} \right]} \right\}\). Then \(\tilde{A}\) is an IVHFS on \(X\), \(\tilde{h}\) is an IVHFE, and \(l_{{\tilde{h}}} = 3\).
3 Likelihood defined on the interval-valued hesitant fuzzy environment
In this section, we first construct an MCDM problem within the interval-valued hesitant fuzzy decision environment. We then define the likelihood of the interval-valued hesitant fuzzy preference relations.
3.1 Interval-valued hesitant fuzzy decision context
Consider an MCDM problem within the interval-valued hesitant fuzzy context in which both the evaluative ratings of alternatives and the weights of criteria are given in the form of IVHFEs. Denote a set of alternatives by \(Z = \left\{ {z_{1} ,z_{2} , \ldots ,z_{m} } \right\}\). Denote a set of criteria by \(C = \left\{ {c_{1} ,c_{2} , \ldots ,c_{n} } \right\}\). We use an IVHFE \(\tilde{h}_{ij} = \left\{ {\tilde{\gamma }_{ij}^{1} ,\tilde{\gamma }_{ij}^{2} , \ldots ,\tilde{\gamma }_{ij}^{{l_{ij} }} } \right\}\) to express the evaluative rating of the alternative \(z_{i} \in Z\) with respect to the criterion \(c_{j} \in C\). Therefore, an interval-valued hesitant fuzzy decision matrix is established as below.

This paper explores MCDM problems involving two different preference information structures of criterion importance: interval-valued hesitant fuzzy importance weights and non-fuzzy importance weights with incomplete certain information.
3.2 Likelihood of interval-valued hesitant fuzzy preference relations
Within the decision context of IVHFSs, let two IVHFEs \(\tilde{h}_{\alpha j} = \left\{ {\tilde{\gamma }_{\alpha j}^{1} ,\tilde{\gamma }_{\alpha j}^{2} , \ldots ,\tilde{\gamma }_{\alpha j}^{{l_{\alpha j} }} } \right\}\) and \(\tilde{h}_{\beta j} = \left\{ {\tilde{\gamma }_{\beta j}^{1} ,\tilde{\gamma }_{\beta j}^{2} , \ldots ,\tilde{\gamma }_{\beta j}^{{l_{\beta j} }} } \right\}\) be the evaluative ratings of the alternatives \(z_{\alpha }\) and \(z_{\beta }\), respectively, with respect to the criterion \(c_{j} \in C\). Let \(\tilde{h}_{\alpha j} \ge \tilde{h}_{\beta j}\) be an interval-valued hesitant fuzzy preference relation that denotes the alternative \(z_{\alpha }\) not being inferior to the alternative \(z_{\beta }\) with respect to the criterion \(c_{j} \in C\). Let \(L\left( {\tilde{h}_{\alpha j} \ge \tilde{h}_{\beta j} } \right)\) denote the likelihood of the interval-valued hesitant fuzzy preference relation \(\tilde{h}_{\alpha j} \ge \tilde{h}_{\beta j}\) for each pair of alternatives \(\left( {z_{\alpha } ,z_{\beta } } \right)\). Using Eq. (2), we determine \(L\left( {\tilde{h}_{\alpha j} \ge \tilde{h}_{\beta j} } \right)\) using the following method.
Definition 3.1
Let \(\tilde{h}_{\alpha j} = \left\{ {\tilde{\gamma }_{\alpha j}^{1} ,\tilde{\gamma }_{\alpha j}^{2} , \ldots ,\tilde{\gamma }_{\alpha j}^{{l_{\alpha j} }} } \right\}\) (where \(l_{\alpha j}\) is the number of intervals in \(\tilde{h}_{\alpha j}\)) and \(\tilde{h}_{\beta j} = \left\{ {\tilde{\gamma }_{\beta j}^{1} ,\tilde{\gamma }_{\beta j}^{2} , \ldots ,\tilde{\gamma }_{\beta j}^{{l_{\beta j} }} } \right\}\) (where \(l_{\beta j}\) is the number of intervals in \(\tilde{h}_{\beta j}\)) be two IVHFEs. The likelihood \(L\left( {\tilde{h}_{\alpha j} \ge \tilde{h}_{\beta j} } \right)\) of an interval-valued hesitant fuzzy preference relation \(\tilde{h}_{\alpha j} \ge \tilde{h}_{\beta j}\) is defined as:
Example 3.1
Let \(\tilde{h}_{\alpha j} = \left\{ {\left[ {0.3,0.5} \right],\left[ {0.3,0.4} \right],\left[ {0.2,0.3} \right]} \right\}\) and \(\tilde{h}_{\beta j} = \left\{ {\left[ {0.1,0.2} \right],\left[ {0.3,0.4} \right]} \right\}\) be two IVHFEs. Then, the likelihood \(L\left( {\tilde{h}_{\alpha j} \ge \tilde{h}_{\beta j} } \right)\) of \(\tilde{h}_{\alpha j} \ge \tilde{h}_{\beta j}\) is calculated as:
Theorem 3.1
Let \(\tilde{h}_{\alpha j} = \left\{ {\tilde{\gamma }_{\alpha j}^{1} ,\tilde{\gamma }_{\alpha j}^{2} , \ldots ,\tilde{\gamma }_{\alpha j}^{{l_{\alpha j} }} } \right\}\) and \(\tilde{h}_{\beta j} = \left\{ {\tilde{\gamma }_{\beta j}^{1} ,\tilde{\gamma }_{\beta j}^{2} , \ldots ,\tilde{\gamma }_{\beta j}^{{l_{\beta j} }} } \right\}\) be two IVHFEs, where \(l_{\alpha j}\) and \(l_{\beta j}\) are the number of interval values in \(\tilde{h}_{\alpha j}\) and \(\tilde{h}_{\beta j}\) , respectively. Let the lower bounds of \(\tilde{h}_{\alpha j}\) and \(\tilde{h}_{\beta j}\) be \(h_{\alpha j}^{ - }\) and \(h_{\beta j}^{ - }\) , and the upper bounds of \(\tilde{h}_{\alpha j}\) and \(\tilde{h}_{\beta j}\) be \(h_{\alpha j}^{ + }\) and \(h_{\beta j}^{ + }\) , respectively. The likelihood \(L\left( {\tilde{h}_{\alpha j} \ge \tilde{h}_{\beta j} } \right)\) of \(\tilde{h}_{\alpha j} \ge \tilde{h}_{\beta j}\) satisfies the following relationships:
-
1.
\(0 \le L\left( {\tilde{h}_{\alpha j} \ge \tilde{h}_{\beta j} } \right) \le 1\);
-
2.
\(L\left( {\tilde{h}_{\alpha j} \ge \tilde{h}_{\beta j} } \right) = 0\) if and only if \(h_{\alpha j}^{ + } \le h_{\beta j}^{ - }\);
-
3.
\(L\left( {\tilde{h}_{\alpha j} \ge \tilde{h}_{\beta j} } \right) = 1\) if and only if \(h_{\beta j}^{ + } \le h_{\alpha j}^{ - }\);
-
4.
\(L\left( {\tilde{h}_{\alpha j} \ge \tilde{h}_{\beta j} } \right) + L\left( {\tilde{h}_{\beta j} \ge \tilde{h}_{\alpha j} } \right) = 1\);
-
5.
\(L\left( {\tilde{h}_{\alpha j} \ge \tilde{h}_{\beta j} } \right) = L\left( {\tilde{h}_{\beta j} \ge \tilde{h}_{\alpha j} } \right) = 0.5\) if \(L\left( {\tilde{h}_{\alpha j} \ge \tilde{h}_{\beta j} } \right) = L\left( {\tilde{h}_{\beta j} \ge \tilde{h}_{\alpha j} } \right)\);
-
6.
\(L\left( {\tilde{h}_{\alpha j} \ge \tilde{h}_{\alpha j} } \right) = 0.5\).
Proof
The lower bound of \(\tilde{h}_{\alpha j}\) is \(h_{\alpha j}^{ - } = \hbox{min} \left\{ {\left( {\gamma_{\alpha j}^{1} } \right)^{L} ,\left( {\gamma_{\alpha j}^{2} } \right)^{L} , \ldots ,\left( {\gamma_{\alpha j}^{{l_{\alpha j} }} } \right)^{L} } \right\}\), and the upper bound of \(\tilde{h}_{\alpha j}\) is \(h_{\alpha j}^{ + } = \hbox{max} \left\{ {\left( {\gamma_{\alpha j}^{1} } \right)^{U} ,\left( {\gamma_{\alpha j}^{2} } \right)^{U} , \ldots ,\left( {\gamma_{\alpha j}^{{l_{\alpha j} }} } \right)^{U} } \right\}\). The lower bound of \(\tilde{h}_{\beta j}\) is \(h_{\beta j}^{ - } = \hbox{min} \left\{ {\left( {\gamma_{\beta j}^{1} } \right)^{L} ,\left( {\gamma_{\beta j}^{2} } \right)^{L} , \ldots ,\left( {\gamma_{\beta j}^{{l_{\beta j} }} } \right)^{L} } \right\}\), and the upper bound of \(\tilde{h}_{\beta j}\) is \(h_{\beta j}^{ + } = \hbox{max} \left\{ {\left( {\gamma_{\beta j}^{1} } \right)^{U} ,\left( {\gamma_{\beta j}^{2} } \right)^{U} , \ldots ,\left( {\gamma_{\beta j}^{{l_{\beta j} }} } \right)^{U} } \right\}\).
-
1.
Because \(0 \le p\left( {\tilde{\gamma }_{\alpha j}^{k} \ge \tilde{\gamma }_{\beta j}^{s} } \right) \le 1\), for any \(k = 1,2, \ldots ,l_{\alpha j}\) and \(s = 1,2, \ldots ,l_{\beta j}\), we have \(0 \le \sum\limits_{k = 1}^{{l_{\alpha j} }} {\sum\limits_{s = 1}^{{l_{\beta j} }} {p\left( {\tilde{\gamma }_{\alpha j}^{k} \ge \tilde{\gamma }_{\beta j}^{s} } \right)} } \le l_{\alpha j} \cdot l_{\beta j}\); thus, \(0 \le L\left( {\tilde{h}_{\alpha j} \ge \tilde{h}_{\beta j} } \right) \le 1\).
-
2.
If \(L\left( {\tilde{h}_{\alpha j} \ge \tilde{h}_{\beta j} } \right) = 0\), then \(p\left( {\tilde{\gamma }_{\alpha j}^{k} \ge \tilde{\gamma }_{\beta j}^{s} } \right) = 0\) for any \(k = 1,2, \ldots ,l_{\alpha j}\) and \(s = 1,2, \ldots ,l_{\beta j}\), thus \(\left( {\gamma_{\alpha j}^{k} } \right)^{U} \le \left( {\gamma_{\beta j}^{s} } \right)^{L}\) for any \(k = 1,2, \ldots ,l_{\alpha j}\) and \(s = 1,2, \ldots ,l_{\beta j}\). We then have \(h_{\alpha j}^{ + } \le h_{\beta j}^{ - }\). Conversely, if \(h_{\alpha j}^{ + } \le h_{\beta j}^{ - }\), then \(\left( {\gamma_{\alpha j}^{k} } \right)^{U} \le \left( {\gamma_{\beta j}^{s} } \right)^{L}\) for any \(k = 1,2, \ldots ,l_{\alpha j}\) and \(s = 1,2, \ldots ,l_{\beta j}\); thus, \(p\left( {\tilde{\gamma }_{\alpha j}^{k} \ge \tilde{\gamma }_{\beta j}^{s} } \right) = 0\) for any \(k = 1,2, \ldots ,l_{\alpha j}\) and \(s = 1,2, \ldots ,l_{\beta j}\), and we then have \(L\left( {\tilde{h}_{\alpha j} \ge \tilde{h}_{\beta j} } \right) = 0\).
-
3.
If \(L\left( {\tilde{h}_{\alpha j} \ge \tilde{h}_{\beta j} } \right) = 1\), then \(p\left( {\tilde{\gamma }_{\alpha j}^{k} \ge \tilde{\gamma }_{\beta j}^{s} } \right) = 1\) for any \(k = 1,2, \ldots ,l_{\alpha j}\) and \(s = 1,2, \ldots ,l_{\beta j}\), thus \(\left( {\gamma_{\beta j}^{s} } \right)^{U} \le \left( {\gamma_{\alpha j}^{k} } \right)^{L}\) for any \(k = 1,2, \ldots ,l_{\alpha j}\) and \(s = 1,2, \ldots ,l_{\beta j}\); we then have \(h_{\beta j}^{ + } \le h_{\alpha j}^{ - }\). Conversely, if \(h_{\beta j}^{ + } \le h_{\alpha j}^{ - }\), then \(\left( {\gamma_{\beta j}^{s} } \right)^{U} \le \left( {\gamma_{\alpha j}^{k} } \right)^{L}\) for any \(k = 1,2, \ldots ,l_{\alpha j}\) and \(s = 1,2, \ldots ,l_{\beta j}\); thus, \(p\left( {\tilde{\gamma }_{\alpha j}^{k} \ge \tilde{\gamma }_{\beta j}^{s} } \right) = 1\) for any \(k = 1,2, \ldots ,l_{\alpha j}\) and \(s = 1,2, \ldots ,l_{\beta j}\); we then have \(L\left( {\tilde{h}_{\alpha j} \ge \tilde{h}_{\beta j} } \right) = 1\).
-
4.
Using Eq. (2), \(p\left( {\tilde{\gamma }_{\alpha j}^{k} \ge \tilde{\gamma }_{\beta j}^{s} } \right) + p\left( {\tilde{\gamma }_{\beta j}^{s} \ge \tilde{\gamma }_{\alpha j}^{k} } \right) = 1\), for any \(k = 1,2, \ldots ,l_{\alpha j}\) and \(s = 1,2, \ldots ,l_{\beta j}\); therefore
$$\begin{aligned} L\left( {\tilde{h}_{\alpha j} \ge \tilde{h}_{\beta j} } \right) + L\left( {\tilde{h}_{\beta j} \ge \tilde{h}_{\alpha j} } \right) & = \frac{1}{{l_{\alpha j} \cdot l_{\beta j} }}\sum\limits_{k = 1}^{{l_{\alpha j} }} {\sum\limits_{s = 1}^{{l_{\beta j} }} {p\left( {\tilde{\gamma }_{\alpha j}^{k} \ge \tilde{\gamma }_{\beta j}^{s} } \right)} } + \frac{1}{{l_{\beta j} \cdot l_{\alpha j} }}\sum\limits_{s = 1}^{{l_{\beta j} }} {\sum\limits_{k = 1}^{{l_{\alpha j} }} {p\left( {\tilde{\gamma }_{\beta j}^{s} \ge \tilde{\gamma }_{\alpha j}^{k} } \right)} } \\ & = \frac{1}{{l_{\alpha j} \cdot l_{\beta j} }}\sum\limits_{k = 1}^{{l_{\alpha j} }} {\sum\limits_{s = 1}^{{l_{\beta j} }} {\left( {p\left( {\tilde{\gamma }_{\alpha j}^{k} \ge \tilde{\gamma }_{\beta j}^{s} } \right) + p\left( {\tilde{\gamma }_{\beta j}^{s} \ge \tilde{\gamma }_{\alpha j}^{k} } \right)} \right) = 1} } \\ \end{aligned}$$(5) and (6) can be easily derived from (4).
4 Likelihood-based interval-valued hesitant fuzzy QUALIFLEX methods
In this section, we first present a comparison approach to identifying the CDI for all permutation of the rankings of the alternatives. We then develop a likelihood-based interval-valued hesitant fuzzy QUALIFLEX (IVHF-QUALIFLEX) method for addressing MCDM problems involving interval-valued hesitant fuzzy importance weights and a likelihood-based QUALIFLEX method to handle MCDM problems involving non-fuzzy importance weights with incomplete information.
4.1 Proposed method involving interval-valued hesitant fuzzy importance weights
Consider an MCDM problem in which both the evaluative ratings of the alternatives and the importance weights of the criteria take the form of IVHFEs. Let \(Z\) be an alternative set with \(m\) alternatives; then, we have \(m!\) permutations of the ranking of the alternatives. Let \(P_{l}\) denote the \(l\)th permutation as:
where \(z_{\alpha } ,z_{\beta } \in Z\) and the alternative \(z_{\alpha }\) is ranked greater than or equal to \(z_{\beta }\).
Let \(\tilde{h}_{\alpha j} = \left\{ {\tilde{\gamma }_{\alpha j}^{1} ,\tilde{\gamma }_{\alpha j}^{2} , \ldots ,\tilde{\gamma }_{\alpha j}^{{l_{\alpha j} }} } \right\}\) (where \(l_{\alpha j}\) is the number of interval values in \(\tilde{h}_{\alpha j}\)) and \(\tilde{h}_{\beta j} = \left\{ {\tilde{\gamma }_{\beta j}^{1} ,\tilde{\gamma }_{\beta j}^{2} , \ldots ,\tilde{\gamma }_{\beta j}^{{l_{\beta j} }} } \right\}\) (where \(l_{\beta j}\) is the number of interval values in \(\tilde{h}_{\beta j}\)) be the evaluative ratings of the alternatives \(z_{\alpha }\) and \(z_{\beta }\), respectively, with respect to the criterion \(c_{j} \in C\). Comparisons between two interval-valued hesitant fuzzy evaluative ratings \(\tilde{h}_{\alpha j}\) and \(\tilde{h}_{\beta j}\) can be obtained by using the likelihood \(L\left( {\tilde{h}_{\alpha j} \ge \tilde{h}_{\beta j} } \right)\) of the interval-valued hesitant fuzzy preference relations \(\tilde{h}_{\alpha j} \ge \tilde{h}_{\beta j}\). According to (5) in Definition 3.1, if \(L\left( {\tilde{h}_{\alpha j} \ge \tilde{h}_{\beta j} } \right) = L\left( {\tilde{h}_{\beta j} \ge \tilde{h}_{\alpha j} } \right)\), it follows that \(L\left( {\tilde{h}_{\alpha j} \ge \tilde{h}_{\beta j} } \right) = L\left( {\tilde{h}_{\beta j} \ge \tilde{h}_{\alpha j} } \right) = 0.5\). Therefore, the concordance/discordance index (CDI) \(\varphi_{j}^{l} \left( {z_{\alpha } ,z_{\beta } } \right)\) for each pair of alternatives \(\left( {z_{\alpha } ,z_{\beta } } \right)\) with respect to the criterion \(c_{j} \in C\) and the permutation \(P_{l}\) is defined as follows:
where \(\varphi_{j}^{l} \left( {z_{\alpha } ,z_{\beta } } \right) \in \left[ { - 0.5,0.5} \right]\).
Based on the likelihood-based comparison of IVHFEs, we can conclude from Eq. (7) that:
-
1.
If \(L\left( {\tilde{h}_{\alpha j} \ge \tilde{h}_{\beta j} } \right) > 0.5\), that is, \(\varphi_{j}^{l} \left( {z_{\alpha } ,z_{\beta } } \right) > 0\), then \(z_{\alpha }\) ranks over \(z_{\beta }\) under the \(j\)th criterion, and thus, there is concordance between the likelihood-based ranking orders and the preorders of \(z_{\alpha }\) and \(z_{\beta }\) under the \(l\) th permutation \(P_{l}\) [55].
-
2.
If \(L\left( {\tilde{h}_{\alpha j} \ge \tilde{h}_{\beta j} } \right) = 0.5\), that is, \(\varphi_{j}^{l} \left( {z_{\alpha } ,z_{\beta } } \right) = 0\), then both \(z_{\alpha }\) and \(z_{\beta }\) have the same rank in the likelihood-based ranking and in the \(l\)th permutation, thus there is ex aequo [55].
-
3.
If \(L\left( {\tilde{h}_{\alpha j} \ge \tilde{h}_{\beta j} } \right) < 0.5\), that is, \(\varphi_{j}^{l} \left( {z_{\alpha } ,z_{\beta } } \right) < 0\), then \(z_{\beta }\) ranks over \(z_{\alpha }\); thus, there is discordance between the likelihood-based ranking orders and the preorders of \(z_{\alpha }\) and \(z_{\beta }\) under the \(l\)th permutation \(P_{l}\) [55].
The index \(\varphi_{j}^{l} \left( {z_{\alpha } ,z_{\beta } } \right)\) serves as an evaluation value of the pair of alternatives \(\left( {z_{\alpha } ,z_{\beta } } \right)\) in the \(l\)th permutation with respect to the criterion \(c_{j}\). Obviously, equal importance is assigned to each criterion \(c_{j} \in C\) in the concordance/discordance index \(\varphi_{j}^{l} \left( {z_{\alpha } ,z_{\beta } } \right)\). To incorporate individual subjective preference over the criteria into the MCDM process, the weighted concordance/discordance index (WCDI) \(\varphi^{l} \left( {z_{\alpha } ,z_{\beta } } \right)\) for each pair of alternatives \(\left( {z_{\alpha } ,z_{\beta } } \right)\) (\(z_{\alpha } ,z_{\beta } \in Z\)) with respect to the \(l\)th permutation is defined as
where \(\widetilde{{\left[ {0,1} \right]}} = \left\{ {\left[ {0,1} \right]} \right\}\) is a constant IVHFE and \(\tilde{W}_{j} = \left\{ {\tilde{w}_{j}^{1} ,\tilde{w}_{j}^{2} , \ldots ,\tilde{w}_{j}^{{l_{j} }} } \right\}\) is the interval-valued hesitant fuzzy importance weight of the criterion \(c_{j} \in C\).
Furthermore, the comprehensive concordance/discordance index (CCDI) \(\varphi^{l}\) with respect to the \(l\)th permutation is defined as follows:
Finally, the optimal ranking order of the alternatives is derived via the comparisons of all of the comprehensive concordance/discordance indexes.
To sum up, the proposed likelihood-based interval-valued hesitant fuzzy QUALIFLEX approach, which is used to handle an MCDM problem involving interval-valued hesitant fuzzy importance weights, is composed of the following steps.
Algorithm A
(for MCDM problems involving interval-valued hesitant fuzzy importance weights)
-
Step A.1: Formulate a MCDM problem in which \(Z = \left\{ {z_{1} ,z_{2} , \ldots ,z_{m} } \right\}\) is an alternative set and \(C = \left\{ {c_{1} ,c_{2} , \ldots ,c_{n} } \right\}\) is a criterion set.
-
Step A.2: Use the IVHFEs to establish the importance weight \(\tilde{W}_{j} = \left\{ {\tilde{w}_{j}^{1} ,\tilde{w}_{j}^{2} , \ldots ,\tilde{w}_{j}^{{l_{j} }} } \right\}\) of the criterion \(c_{j} \in C\) and the evaluative rating \(\tilde{h}_{ij} = \left\{ {\tilde{\gamma }_{ij}^{1} ,\tilde{\gamma }_{ij}^{2} , \ldots ,\tilde{\gamma }_{ij}^{{l_{ij} }} } \right\}\) of the alternative \(z_{i} \in Z\) with respect to the criterion \(c_{j} \in C\). Then, construct the interval-valued hesitant fuzzy decision matrix \(\tilde{H} = \left( {\tilde{h}_{ij} } \right)_{m \times m}\) in (4) as well as the interval-valued hesitant fuzzy weight vector of criteria, denoted as \(\tilde{W} = \left\{ {\tilde{W}_{1} ,\tilde{W}_{2} , \ldots ,\tilde{W}_{n} } \right\}\).
-
Step A.3: Set out all of the \(m!\) permutations of the \(m\) alternatives. Let \(P_{l}\) (\(l = 1,2, \ldots ,m!\)) denote the \(l\)th permutation by using Eq. (6).
-
Step A.4: Calculate the likelihood \(L\left( {h_{\alpha j} \ge h_{\beta j} } \right)\) using Eq. (5) for \(c_{j} \in C\) and \(\left( {z_{\alpha } ,z_{\beta } } \right)\), where \(z_{\alpha } ,z_{\beta } \in Z\).
-
Step A.5: Compute the concordance/discordance index \(\varphi_{j}^{l} \left( {z_{\alpha } ,z_{\beta } } \right)\) for each pair of alternative \(\left( {z_{\alpha } ,z_{\beta } } \right)\) in the permutation \(P_{l}\) with respect to the criterion \(c_{j} \in C\) using Eq. (7), where \(l = 1,2, \ldots ,m!\).
-
Step A.6: Calculate the WCDI \(\varphi^{l} \left( {z_{\alpha } ,z_{\beta } } \right)\) for each pair of \(\left( {z_{\alpha } ,z_{\beta } } \right)\) in \(P_{l}\) using Eq. (8), where \(l = 1,2, \ldots ,m!\).
-
Step A.7: Calculate the CCDI \(\varphi^{l}\) for each permutation \(P_{l}\) using Eq. (9), where \(l = 1,2, \ldots ,m!\).
-
Step A.8: Choose the permutation with the greatest \(\varphi^{l}\) value as the optimal ranking order of the alternatives.
4.2 Proposed method involving incomplete preference information
Consider an MCDM problem involving interval-valued hesitant fuzzy evaluative ratings of alternatives and incomplete certain information for the importance weights. With respect to the permutation \(P_{l}\), let \(w_{j}^{l}\) be the non-fuzzy importance weight of criterion \(c_{j} \in C\) satisfying the normalization conditions \(w_{j}^{l} \in \left[ {0,1} \right]\), \(j = 1,2, \ldots ,n\), and \(\sum\nolimits_{j = 1}^{n} {w_{j}^{l} } = 1\). Let \(\varGamma_{0}\) denote a set of all non-fuzzy weight vectors, and
The incomplete information regarding non-fuzzy weights on the criteria can be generally provided by using the following five basic ranking forms [6, 23, 30, 44].
-
1.
A weak ranking:
$$\varGamma_{1} = \left\{ {\left. {\left( {w_{1}^{l} ,w_{2}^{l} , \ldots ,w_{n}^{l} } \right) \in \varGamma_{0} } \right|w_{{j_{1} }}^{l} \ge w_{{j_{2} }}^{l} \;{\text{for}}\;{\text{all}}\;j_{1} \in \varUpsilon_{1} \;{\text{and}}\;j_{2} \in \varLambda_{1} } \right\}$$(11)where \(\varUpsilon_{1}\) and \(\varLambda_{1}\) are two disjoint subsets of the subscript index set \(N = \left\{ {1,2, \ldots ,n} \right\}\) of all criteria.
-
2.
A strict ranking:
$$\varGamma_{2} = \left\{ {\left. {\left( {w_{1}^{l} ,w_{2}^{l} , \ldots ,w_{n}^{l} } \right) \in \varGamma_{0} } \right|w_{{j_{1} }}^{l} - w_{{j_{2} }}^{l} \ge \delta^{\prime}_{{j_{1} j_{2} }} \;{\text{for}}\;{\text{all}}\;j_{1} \in \varUpsilon_{2} {\kern 1pt} \;{\text{and}}\;j_{2} \in \varLambda_{2} } \right\}$$(12)where \(\delta^{\prime}_{{j_{1} j_{2} }}\) is a constant that satisfies the condition \(\delta^{\prime}_{{j_{1} j_{2} }} > 0\), and \(\varUpsilon_{2} {\kern 1pt}\) and \(\varLambda_{2}\) are two disjoint subsets of \(N\).
-
3.
A ranking of differences (or strength of preference):
$$\varGamma_{3} = \left\{ {\left. {\left( {w_{1}^{l} ,w_{2}^{l} , \ldots ,w_{n}^{l} } \right) \in \varGamma_{0} } \right|w_{{j_{1} }}^{l} - w_{{j_{2} }}^{l} \ge w_{{j_{2} }}^{l} - w_{{j_{3} }}^{l} \;{\text{for}}\;{\text{all}}\;j_{1} \in \varUpsilon_{3} ,j_{2} {\kern 1pt} \in \varLambda_{3} ,\;{\text{and}}\;j_{3} \in \varOmega_{3} } \right\}$$(13)where \(\varUpsilon_{3} {\kern 1pt}\), \(\varLambda_{3}\), and \(\varOmega_{3}\) are three disjoint subsets of \(N\).
-
4.
An interval bound:
$$\varGamma_{4} = \left\{ {\left. {\left( {w_{1}^{l} ,w_{2}^{l} , \ldots ,w_{n}^{l} } \right) \in \varGamma_{0} } \right|\delta_{{j_{1} }} + \varepsilon_{{j_{1} }} \ge w_{{j_{1} }}^{l} \ge \delta_{{j_{1} }} \;{\text{for}}\;{\text{all}}\;j_{1} \in \varUpsilon_{4} } \right\}$$(14)where \(\delta_{{j_{1} }} \ge 0\) and \(\varepsilon_{{j_{1} }} {\kern 1pt} \ge 0\) are constants that satisfy the condition \(0 \le \delta_{{j_{1} }} \le \delta_{{j_{1} }} + \varepsilon_{{j_{1} }} \le 1{\kern 1pt}\), and \(\varUpsilon_{4}\) is a subset of \(N\).
-
5.
A ratio bound (or a ranking with multiples):
$$\varGamma_{5} = \left\{ {\left. {\left( {w_{1}^{l} ,w_{2}^{l} , \ldots ,w_{n}^{l} } \right) \in \varGamma_{0} } \right|w_{{j_{1} }}^{l} \ge \delta_{{j_{1} j_{2} }}^{\prime \prime } \cdot w_{{j_{2} }}^{l} \;{\text{for}}\;{\text{all}}\;j_{1} \in \varUpsilon_{5} \;{\text{and}}\;j_{2} \in \varLambda_{5} } \right\}$$(15)where \(\delta_{{j_{1} j_{2} }}^{{\prime \prime }}\) is a constant that satisfies the condition \(0 \le \delta_{{j_{1} j_{2} }}^{{\prime \prime }} \le 1\), and \(\varUpsilon_{5} {\kern 1pt}\) and \(\varLambda_{5}\) are two disjoint subsets of \(N\).
Let \(\varGamma\) denote a set of the incompletely known information regarding the non-fuzzy weights on the criteria, and
Combining \(\varGamma\) and \(\varphi_{j}^{l} \left( {z_{\alpha } ,z_{\beta } } \right)\), the ordinary WCDI \(\varphi^{l} \left( {z_{\alpha } ,z_{\beta } } \right)\) for each pair of alternatives \(\left( {z_{\alpha } ,z_{\beta } } \right)\) (\(z_{\alpha } ,z_{\beta } \in Z\)) with respect to the permutation \(P_{l}\) is expressed as the following:
where \(\left( {w_{1}^{l} ,w_{2}^{l} , \ldots ,w_{n}^{l} } \right) \in\Gamma\).
Moreover, the ordinary CCDI \(\varphi^{l}\) for the permutation \(P_{l}\) is
For each permutation \(P_{l}\) (\(l = 1,2, \ldots ,m!\)), the optimal weight vector \(\bar{w}^{l} = \left( {\bar{w}_{1}^{l} ,\bar{w}_{2}^{l} , \ldots ,\bar{w}_{n}^{l} } \right)\) of the criteria is derived by solving the following model [6]:
for each \(l = 1,2, \ldots ,m!\).
Then, we can obtain an optimal objective CCDI \(\bar{\varphi }^{l}\) for each \(l = 1,2, \ldots ,m!\) and choose the permutation with the maximum value \(\bar{\varphi }^{l}\), from which the optimal ranking order of the alternatives can be derived.
If conflicting preference existed in the incompletely known information regarding the non-fuzzy weights, it would be impossible for us to obtain the criteria weights from the conditions in \(\varGamma\). In this case, Chen [6] introduced several nonnegative deviation variables \(\left( {\xi_{{({\text{i}})j_{1} j_{2} }}^{ - } ,\xi_{{({\text{ii}})j_{1} j_{2} }}^{ - } ,\xi_{{({\text{iii}})j_{1} j_{2} j_{3} }}^{ - } ,\xi_{{({\text{iv}})j_{1} }}^{ - } ,\xi_{{({\text{iv}})j_{1} }}^{ + } ,\xi_{{({\text{v}})j_{1} j_{2} }}^{ - } } \right)\) to construct a relaxed set \(\varGamma^{{\prime }}\), which is shown as follows:
Combining \(\varphi^{l}\) and the non-fuzzy weights in the relaxed set \(\varGamma^{{\prime }}\), Chen [6] established the following bi-objective model for solving the MCDM problem with incomplete and conflicting weights information:
for each \(l = 1,2, \ldots ,m\). The application of the max–min operator [57] can transform the above model into a single-objective nonlinear programming model [6], which is shown as follows:
The solution of the above model (27) yields the optimal weight vector \(\bar{w}^{l} = \left( {\bar{w}_{1}^{l} ,\bar{w}_{2}^{l} , \ldots ,\bar{w}_{n}^{l} } \right)\), and the optimal deviation values \(\xi_{{\left( {\text{i}} \right)j_{1} j_{2} }}^{ - } ,\xi_{{\left( {\text{ii}} \right)j_{1} j_{2} }}^{ - } ,\xi_{{\left( {\text{iii}} \right)j_{1} j_{2} j_{3} }}^{ - } ,\xi_{{\left( {\text{iv}} \right)j_{1} }}^{ - } ,\xi_{{\left( {\text{iv}} \right)j_{1} }}^{ + } ,\) and \(\xi_{{\left( {\text{v}} \right)j_{1} j_{2} }}^{ - }\) (\(j_{1} ,j_{2} ,j_{3} \in N\)) for each \(l = 1,2, \ldots ,m\). Then, we acquire the CCDI \(\bar{I}^{l}\) for each permutation \(P_{l}\). After comparing all of the \(\bar{\varphi }^{l}\) values for all permutations \(P_{l}\), the optimal ranking order of the alternatives can be obtained.
Similar to Algorithm A, a likelihood-based interval-valued hesitant fuzzy QUALIFLEX method, which is developed for handling the MCDM problem involving the non-fuzzy importance weights, consists of the following steps.
Algorithm B
(for MCDM problems involving incomplete information)
-
Step B.1: See Step A.1 of Algorithm A.
-
Step B.2: Establish the interval-valued hesitant fuzzy decision matrix \(\tilde{H} = \left( {\tilde{h}_{ij} } \right)_{m \times m}\) in Eq. (4), where \(\tilde{h}_{ij}\) is the evaluative rating of alternative \(z_{i} \in Z\) with respect to criterion \(c_{j} \in C\). Express the weight information of the criteria in \(C\) by means of a weak order, a strict order, a difference order, an interval bound or a ratio bound. Construct the set \(\varGamma\) in Eq. (16) from the known information.
-
Steps B.3–B.5: see Steps A.3–A.5 of Algorithm A.
-
Step B.6: Calculate the ordinary CCDI \(\varphi^{l}\) for each permutation \(P_{l}\) using Eq. (18), where \(l = 1,2, \ldots ,m!\). Then, use (19) to build a linear programming model for incomplete and consistent weight information, or use (27) to build a relaxed nonlinear programming model for incomplete and inconsistent weight information with respect to each permutation \(P_{l}\), where \(l = 1,2, \ldots ,m!\).
-
Step B.7: Derive the optimal weight vector \(\bar{w}^{l}\) and the optimal CCDI \(\bar{\varphi }^{l}\) for each permutation \(P_{l}\) by solving (19) or (27).
-
Step B.8: Choose the permutation with the greatest value of \(\bar{\varphi }^{l}\) as the optimal ranking order of the alternatives.
5 Illustrative applications and comparative analysis
In what follows, we adapt a green supplier selection problem from Zhang and Xu [55] to verify the applicability of Algorithms A and B. In addition, a comparative analysis is carried out to illustrate the advantages of the proposed methods over other interval-valued hesitant fuzzy MCDM methods.
5.1 Decision context
Based on environmental criteria at an automobile manufacturing company [22, 37], Zhang and Xu [55] have introduced a green supplier selection problem (see subsection 5.1 on page 879 in [55] for more details). In this problem, suppose that there are four possible green suppliers: \(z_{1}\), \(z_{2}\), \(z_{3}\) and \(z_{4}\). Nine major criteria are used to evaluate these four possible suppliers, including pollution production (\(c_{1}\)), resource consumption (\(c_{2}\)), eco-design (\(c_{3}\)), green image (\(c_{4}\)), environmental management system (\(c_{5}\)), commitment to GSCM from managers (\(c_{6}\)), use of environmentally friendly technology (\(c_{7}\)), use of environmentally friendly materials (\(c_{8}\)) and staff environmental training (\(c_{9}\)).
5.2 Illustration of Algorithm A
In this subsection, Algorithm A is used to choose a best one from four potential suppliers.
In Step A.1, the set of the alternatives is denoted by \(Z = \left\{ {z_{1} ,z_{2} ,z_{3} ,z_{4} } \right\}\) and the set of the criteria is denoted by \(C = \left\{ {c_{1} ,c_{2} ,c_{3} ,c_{4} ,c_{5} ,c_{6} ,c_{7} ,c_{8} ,c_{9} } \right\}\).
In Step A.2, the evaluative ratings \(\tilde{h}_{ij}\) (for each \(z_{i} \in Z\) and \(c_{j} \in C\)) and the importance weights \(\tilde{W}_{j}\) (for each \(c_{j} \in C\)) are furnished in Table 1.
In the following, we explain where the IVHFSs in Table 1 come from. In order to obtain a more reasonable decision result, a decision organization is invited to evaluate the performance of the four potential suppliers and the weights of the nine criteria. Take \(\tilde{h}_{11}\) as an example. Suppose that some of the decision-makers provide an interval \([ 0. 4 , { 0} . 6 ]\) as the evaluation for the alternative \(z_{1}\) under the criterion \(c_{1}\), some provide an evaluation of \([ 0. 1 , { 0} . 3 ]\) for the alternative \(z_{1}\) under the criterion \(c_{1}\), and the others provide an evaluation of \([ 0. 1 , { 0} . 2 ]\) for the alternative \(z_{1}\) under the criterion \(c_{1}\); the decision-makers in the decision organization cannot persuade one another to change their opinions. Moreover, in the practical setting of group decision-making, anonymity is needed to protect the privacy of the decision-makers or to ensure that noninterference opinions are accumulated. Thus, in this situation, it is natural to maintain and set out all of those possible original evaluations for the alternative \(z_{1}\) under the criterion \(c_{1}\) provided by the decision-makers, which is represented as an IVHFE \(\tilde{h}_{11} = \left\{ { [ 0. 4 , { 0} . 6 ] , { [0} . 1 , { 0} . 3 ] , { [0} . 1 , { 0} . 2 ]} \right\}\). Through such a procedure, we can obtain the IVHFE evaluative ratings of the suppliers with respect to the criteria and the IVHFE weights of criteria, as shown in Table 1.
In what follows, we use the proposed likelihood-based IVHF-QUALIFLEX method to obtain the optimal ranking order of the four green suppliers.
In Step A.3, there is a total of 24 (=4!) permutations of the ranking order of the alternatives:
In Step A.4, we compute the likelihood \(L\left( {h_{\alpha j} \ge h_{\beta j} } \right)\). The computation results of the likelihoods for all the interval-valued hesitant fuzzy preference relations are given in Table 2.
In Step A.5, the CDI \(\varphi_{j}^{l} \left( {z_{\alpha } ,z_{\beta } } \right)\) can be calculated by using Eq. (7). Taking the second permutation \(P_{2}\) as an example, the computation results of \(P_{2}\) are listed in Table 3.
In Step A.6, we utilize Eq. (8) to calculate the values of \(\varphi_{j}^{l} \left( {z_{\alpha } ,z_{\beta } } \right) \cdot L\left( {\tilde{W}_{j} \ge \widetilde{{\left[ {0,1} \right]}}} \right)\) and \(\varphi^{l} \left( {z_{\alpha } ,z_{\beta } } \right)\) for each pair of \(\left( {z_{\alpha } ,z_{\beta } } \right)\) in permutation \(P_{l}\). Considering the second permutation \(P_{2}\), for example, the results of \(P_{2}\) are listed in Table 4.
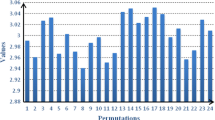
In Step A.7, the CCDI \(\varphi^{l}\) is calculated using Eq. (9) for each \(P_{l}\), as follows:
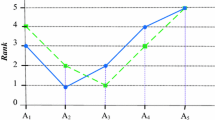
In Step A.8, because \(\varphi^{11} = 1. 7 2 1 8\) gives the largest value, the best permutation is \(P_{11} = \left( {z_{2} ,z_{4} ,z_{1} ,z_{3} } \right)\), implying that the optimal ranking order of the four suppliers is \(z_{2} \succ z_{4} \succ z_{1} \succ z_{3}\). Therefore, the supplier \(z_{2}\) is the optimal alternative.
5.3 Illustration of Algorithm B for incomplete information
In this subsection, let us reconsider the green supplier selection problem provided in Sect. 5.1. Step B.1 has been completed in Sect. 5.2.
In Step B.2, the interval-valued hesitant fuzzy decision matrix has been constructed in Sect. 5.2. Assume that the authorities provide the importance weights of criteria with incompletely known non-fuzzy values. Let \(\varGamma_{0} = \left\{ {\left. {\left( {w_{1}^{l} ,w_{2}^{l} , \ldots ,w_{9}^{l} } \right)} \right|w_{j}^{l} \in \left[ {0,1} \right],{\kern 1pt} \quad j = 1,2, \ldots ,9,{\kern 1pt} \sum\nolimits_{j = 1}^{9} {w_{j}^{l} } = 1} \right\}\) and let the known information on the criterion weights be represented by the following:
It follows from Eq. (16) that the set \(\varGamma\) is determined as follows:
Steps B.3–B.5 have been finished in Sect. 5.2.
In Step B.6, by employing Eq. (18), we calculate the CCDI for each permutation, as indicated in Table 5. For example, consider \(\varphi^{2}\) for the second permutation \(P_{2} = \left( {z_{1} ,z_{2} ,z_{4} ,z_{3} } \right)\) as follows:
Because the incompletely known information regarding the non-fuzzy weights does not conflict, the model (19) is applied to establish the model for each permutation \(P_{l}\). For instance, the model for the permutation \(P_{2}\) is constructed as follows:
In Step B.7, we solve the model (19) for each permutation \(P_{l}\) and then obtain the optimal weight vector \(\bar{w}^{l}\) and the optimal CCDI \(\bar{\varphi }^{l}\), as shown in Table 6.
In Step B.8, it directly follows from Table 6 that \(\bar{\varphi }^{11} = 1. 7 5 6 5\) is the maximum CCDI, and thus, the optimal ranking order of the green suppliers is determined as \(P_{11} = \left( {z_{2} ,z_{4} ,z_{1} ,z_{3} } \right)\), where the optimal weight vector is \(\bar{w}^{11} = \left( { 0. 1 3, 0 , 0 , 0. 0 8,0, 0,0{\kern 1pt} ,0, 0. 7 9} \right)\). Furthermore, the optimal green supplier is \(z_{2}\), the same as that derived by Algorithm A, implying the validity of Algorithms A and B.
5.4 Illustration of Algorithm B for conflicting information
In this subsection, we add the condition of \(w_{8}^{l} - w_{7}^{l} \ge 0.02\) to the set \(\varGamma_{2}\) in the above example. Accordingly, the sets \(\varGamma_{2}\) and \(\varGamma\) are updated as follows:
Obviously, the condition of \(w_{7}^{l} \ge w_{8}^{l}\) in \(\varGamma_{1}\) is in conflict with the condition of \(w_{8}^{l} - w_{7}^{l} \ge 0.02\) in \(\varGamma_{2}^{{({\text{new}})}}\), implying that the weight information in \(\varGamma^{{({\text{new}})}}\) is partially conflicting. Because a conflicting preference exists in the incompletely known information regarding the non-fuzzy weights, we apply the model (27) to establish the relaxed nonlinear programming model for each permutation \(P_{l}\). We relax the conditions in \(\varGamma^{{({\text{new}})}}\) to \(\varGamma^{{\prime }}\), as follows:
where \(\xi_{{\left( {\text{i}} \right)23}}^{ - }\), \(\xi_{{\left( {\text{i}} \right)78}}^{ - }\), \(\xi_{{\left( {\text{ii}} \right)95}}^{ - }\), \(\xi_{{\left( {\text{ii}} \right)87}}^{ - }\), \(\xi_{{\left( {\text{iii}} \right)635}}^{ - }\), \(\xi_{{\left( {\text{iv}} \right)1}}^{ - }\), \(\xi_{{\left( {\text{iv}} \right)1}}^{ + }\), \(\xi_{{\left( {\text{iv}} \right)4}}^{ - }\), \(\xi_{{\left( {\text{iv}} \right)4}}^{ + }\), \(\xi_{{\left( {\text{v}} \right)13}}^{ - }\) and \(\xi_{{\left( {\text{v}} \right)68}}^{ - }\) are nonnegative deviation variables.
For example, the nonlinear programming model for the permutation \(P_{2}\) can be built as follows.
By using the optimization modeling software Lingo 11, we can solve the above nonlinear programming model and obtain the optimal objective value \(\bar{\lambda } = - 0. 0 2\), the optimal weight vector \(\bar{w}^{2} = \left( { 0. 1 7 4 7 , 0. 0 9 4 3 , 0. 0 4 4 9 , 0. 1 1 3 8 , 0. 0 7 4 6 , 0. 0 8 2 1 , 0. 0 5 4 3 , 0. 0 6 2 8 , 0. 2 9 8 6} \right)\), the optimal deviation values \(\xi_{{\left( {\text{i}} \right)78}}^{ - } = 0. 0 0 8 6\), \(\xi_{{\left( {\text{ii}} \right)87}}^{ - } = 0. 0 1 1 4\), \(\xi_{{\left( {\text{i}} \right)23}}^{ - } = \xi_{{\left( {\text{ii}} \right)95}}^{ - } = \xi_{{\left( {\text{iii}} \right)635}}^{ - } = \xi_{{\left( {\text{iv}} \right)1}}^{ - } = \xi_{{\left( {\text{iv}} \right)1}}^{ + } = \xi_{{\left( {\text{iv}} \right)4}}^{ - } = \xi_{{\left( {\text{iv}} \right)4}}^{ + } = \xi_{{\left( {\text{v}} \right)13}}^{ - } = \xi_{{\left( {\text{v}} \right)68}}^{ - } = 0\), and the corresponding CCDI \(\bar{\varphi }^{2} = - 0. 0 2\). When all the \(\bar{\varphi }^{l}\) values are determined, we can find that \(\bar{\varphi }^{12} = - 0. 0 1 9 9 9 9 9 9\) is the maximum value. Thus, the optimal ranking of the four potential suppliers under inconsistent weight information is \(P_{12} = \left( {z_{2} ,z_{4} ,z_{3} ,z_{1} } \right)\), which again implies that \(z_{2}\) is determined as the best supplier.
5.5 Comparative analysis and discussion
In the following, we carry out a comparative analysis with other related methods to verify the proposed IVHF-QUALIFLEX methods.
5.5.1 Comparison with the aggregation operators-based approaches
In the aggregation operators-based approaches [11, 24, 45, 46, 53, 54], some interval-valued hesitant fuzzy aggregation operators were developed for aggregating the individual IVHFEs into the overall IVHFEs. Then, the scores of the overall IVHFEs were calculated, based on which the optimal ranking order of the alternatives were determined. To facilitate a comparison with our Algorithm A, we consider here the same green supplier selection problem in Sect. 5.2 by using Zhang and Wu’s method [54], which consists of the following steps:
Step 1
Use the interval-valued hesitant fuzzy weighted averaging (IVHFWA) operator
to fuse all of the performance values \(\tilde{h}_{ij}\) (\(j = 1,2, \ldots ,9\)) in the ith line of \(\tilde{H}\) and derive the overall performance value \(\tilde{h}_{i}\) (\(i = 1,2,3,4\)) of each alternative \(z_{i}\) (\(i = 1,2,3,4\)), which are not shown here due to space considerations. The dimensions of \(\tilde{h}_{i}\) (\(i = 1,2,3,4\)) are shown as follows:
Step 2
According to Definition 6 in [11], we calculate the scores \(s\left( {\tilde{h}_{i} } \right)\) (\(i = 1,2,3,4\)) of \(\tilde{h}_{i}\) (\(i = 1,2,3,4\)) as follows:
Step 3
According to the comparison methods in [42, 49], the ranking order of the four scores is determined as \(s\left( {\tilde{h}_{2} } \right) > s\left( {\tilde{h}_{1} } \right) > s\left( {\tilde{h}_{4} } \right) > s\left( {\tilde{h}_{3} } \right)\). According to Definition 6 in [11], we can rank the four alternatives \(z_{i}\) (\(i = 1,2,3,4\)) as \(z_{2} \succ z_{1} \succ z_{4} \succ z_{3}\). Thus, the best alternative is again \(z_{2}\).
Obviously, the ranking order of the four suppliers \(z_{i}\) (\(i = 1,2,3,4\)) obtained by using Algorithm A is slightly different from that of Zhang and Wu [54]. A comparison analysis shows that our Algorithm A has some distinct advantages over the aggregation operators-based approaches [11, 24, 45, 46, 53, 54]; these are summarized as follows:
-
1.
From Eq. (28), the IVHFWA operator must perform the addition or multiplicative operations on all of the elements of the input IVHFEs. As a result, the dimension of the derived overall IVHFEs could q increase rapidly as such aggregations are conducted, which could increase the complexity of the calculations. As shown in Step 1 above, the dimensions \(l_{{\tilde{h}_{i} }}\) (\(i = 1,2,3,4\)) of the overall performance values \(\tilde{h}_{i}\) (\(i = 1,2,3,4\)) obtained by using Zhang and Wu’s method [54] is much larger, which increases the computational complexity and could cause a loss of decision information. In contrast, Algorithm A does not need to perform such an aggregation but directly addresses the input IVHFEs; therefore, it does not increase the dimensions of the derived overall IVHFEs and preserves the original decision data to the greatest extent.
-
2.
The aggregation operators-based approaches are suitable for an MCDM problem with a small number of criteria because of the simple solution procedure. However, these approaches become inappropriate for addressing an MCDM problem with a large number of criteria because the number of operations and the magnitudes of the results will increase exponentially with the increase in the number of criteria. In contrast, our algorithm A can handle an MCDM problem with a large number of criteria because of the simple solution steps and the low computational efforts.
-
3.
The aggregation operators-based approaches [11, 24, 45, 46, 53, 54] can only manage the MCDM problems in which the evaluative ratings of the alternative take the form of IVHFEs and the weights of the criteria take the form of crisp numbers. In contrast, the proposed Algorithm A can address MCDM problems in which both the evaluative ratings of the alternatives and the weights of the criteria are given in the form of IVHFEs.
5.5.2 Comparison with the TOPSIS and the maximizing deviation method-based approach
Based on TOPSIS and the maximizing deviation method, Xu and Zhang [50] developed an approach to address the MCDM problems in which the performance ratings take the form of the IVHFEs and the criteria weights take the form of crisp numbers with incomplete and consistent information. Here, we investigate the same example used in Sect. 5.3 with Xu and Zhang’s method, which is presented as follows.
Let \(\tilde{H} = \left( {\tilde{h}_{ij} } \right)_{4 \times 9}\) be the interval-valued hesitant fuzzy decision matrix given in Table 1. In this example, the decision-makers are assumed to be pessimistic and thus the interval-valued hesitant fuzzy decision matrix in Table 1 is transformed into the new one, as shown in Table 7.
In order to derive the best alternative(s), we then proceed to use Xu and Zhang’s method, which includes the following steps:
Step 1
Suppose that the partly known information regarding the criteria weights is given as
Use the model (M-4) in [44] to establish the following single-objective programming model:
The solution to the above model produces the optimal weight vector \(w = \left( { 0. 1 3, 0. 6 4,0, 0. 0 8 ,0,0,0, 0. 1 5} \right)^{T}\).
Step 2
Use Eq. (33) and Eq. (34) in [50] to obtain the interval-valued hesitant fuzzy positive ideal solution (IVHFPIS) \(\tilde{z}^{ + }\) and the interval-valued hesitant fuzzy negative ideal solution (IVHFNIS) \(\tilde{z}^{ - }\), respectively:
Step 3
Use Eq. (35) and Eq. (36) in [50] to compute the distance measures \(\tilde{d}_{i}^{ + }\) and \(\tilde{d}_{i}^{ - }\) of each alternative \(z_{i}\) (\(i = 1,2,3,4\)):
Step 4
Use Eq. (37) in [50] to compute the relative closeness coefficient \(\tilde{C}_{i}\) of each alternative \(z_{i}\) with respect to the IVHFPIS \(\tilde{z}^{ + }\):
Step 5
Based on the relative closeness coefficients \(\tilde{C}_{i}\) (\(i = 1,2,3,4\)), the alternatives \(z_{i}\) (\(i = 1,2,3,4\)) can be ranked as \(z_{2} \succ z_{3} \succ z_{4} \succ z_{1}\), which is slightly different from the result derived by Algorithm B; there are two inverse rank orderings between \(z_{1}\) and \(z_{3}\) as well as between \(z_{3}\) and \(z_{4}\), but the rankings for \(z_{2}\) are the same; that is, the alternative \(z_{2}\) ranks in first place. Thus, both approaches give the priority to \(z_{2}\).
The following comparison analysis shows that the proposed algorithm B has many advantages over Xu and Zhang’s methodology for interval-valued hesitant fuzzy decision-makings.
-
1.
Xu and Zhang’s method calculates the deviation between each actual alternative and an IVHFPIS (IVHFNIS) under the condition that all IVHFEs must be arranged in ascending order and be of equal length. This is not in accordance with real cases, because it is impossible to make sure that all IVHFEs have equal length. If the two IVHFEs being compared have different lengths, then the value of the shorter IVHFE must be increased until both are equal. According to Xu and Zhang [50], there are many different techniques to extend the shorter IVHFE to the same length as the longer one. The most representative techniques are the pessimistic principle and the optimistic principle. For the pessimistic principle, the shorter IVHFE is extended by adding the minimum value to it until it has the same length as the other IVHFE, while for the optimistic principle, the maximum value of the shorter IVHFE should be added until the shorter IVHFE has the same length as the longer one. In the above example, we used the former case. However, in such cases, different methods of extension can produce different results. Moreover, it should also be noted that filling artificial values into an IVHFE would change the information in the original IVHFE. Thus, such an approach is less well justified theoretically and less reliable practically. In the proposed Algorithm B, we do not need the IVHFEs to have the same length, that is to say, it is unnecessary to add a specific value to the shorter of the two until they are both of equivalent length. This can prevent loss of data and distortion of the preference information initially provided, resulting in final outcomes that more closely correspond to those in actual decision-making processes.
-
2.
Xu and Zhang [50] ’s method is inappropriate for addressing the situation in which a conflicting preference exists in the incompletely known information regarding the non-fuzzy weights. In contrast, the proposed Algorithm B is usable for the situation in which incomplete and inconsistent information exist in the criterion importance.
5.5.3 Comparison with the existing QUALIFLEX approaches under different decision contexts
The IT2TrF-QUALIFLEX method, originally developed by Chen et al. [7] and Wang et al. [41] by extending the classical QUALIFLEX method to the IT2TrF environment, uses IT2TrFNs to represent the evaluative ratings of alternatives and the weights of criteria. The IVIF-QUALIFLEX method, originally proposed by Chen [6] by extending the classical QUALIFLEX method to the IVIF environment, uses IVIFNs to represent the evaluative ratings of alternatives and uses crisp numbers to represent the weights of criteria. The HF-QUALIFLEX method, originally proposed by Zhang and Xu [55] by extending the classical QUALIFLEX method to the hesitant fuzzy environment, uses HFEs to represent the evaluative ratings of alternatives and the weights of criteria. It is noted that all of these methods mainly accommodate the IT2TrFNs, IVIFNs and HFEs decision contexts and cannot address IVHFE decision data in MCDM problems. Compared with these QUALIFLEX methods, the prominent advantages of the proposed methods are that they can accommodate the performance ratings expressed by IVHFEs effectively and the criteria weights in the form of IVHFEs or crisp numbers.
6 Concluding remarks
Based on a likelihood-based comparison approach, this paper has developed an IVHF-QUALIFLEX method for addressing MCDM problems that contain the IVHFE evaluative ratings of the alternatives and the IVHFE criterion weights and has also developed an IVHF-QUALIFLEX method for addressing MCDM problems that contain the IVHFE evaluative ratings of the alternatives and non-fuzzy criterion weights with incomplete information. A numerical problem has been provided to illustrate the feasibility and applicability of the proposed methods, and then, a comparison analysis has been conducted to verify the effectiveness and practicality of the proposed methods. The comparative analysis shows that the proposed methods have the following advantages over the existing interval-valued hesitant fuzzy MCDM methods in the literature. (1) The proposed methods do not need to perform aggregation operations, but deal directly with the input IVHFEs, whereby they do not increase the dimensions of the derived overall IVHFEs and can preserve the original decision information as much as possible. (2) The proposed methods do not need the input IVHFEs to have the same length; that is, it is unnecessary to add a specific value to the shorter of the two until they are both of equivalent length. This prevents loss of data and distortion of the preference information initially provided, resulting in final outcomes that more closely correspond to those in actual decision-making processes. (3) The proposed methods can handle MCDM problems in which both the evaluative ratings of alternatives and the weights of criteria are represented by IVHFEs. (4) The proposed methods can deal with the incomplete and inconsistent importance information. (5) The proposed methods are preferable for use in solving MCDM problems where the number of criteria is significantly greater than the number of alternatives.
References
Atanassov K (1986) Intuitionistic fuzzy sets. Fuzzy Sets Syst 20(1):87–96
Atanassov K (1989) More on intuitionistic fuzzy sets. Fuzzy Sets Syst 33:37–46
Atanassov KT, Gargov G (1989) Interval-valued intuitionistic fuzzy sets. Fuzzy Sets Syst 31(3):343–349
Benayoun R, Roy B, Sussman N (1966) Manual de Reference du Program ELECTRE. Note de Synthese et Formation, Direction Scientifique SEMA, No. 25, Paris, 823 France
Chen TY (2013) Data construction process and qualiflex-based method for multiple-criteria group decision making with interval-valued intuitionistic fuzzy sets. Int J Inf Technol Decis Mak 12:425–467
Chen TY (2014) Interval-valued intuitionistic fuzzy QUALIFLEX method with a likelihood-based comparison approach for multiple criteria decision analysis. Inf Sci 261:149–169
Chen TY, Chang CH, Lu JFR (2013) The extended QUALIFLEX method for multiple criteria decision analysis based on interval type-2 fuzzy sets and applications to medical decision making. Eur J Oper Res 226:615–625
Chen TY, Tsui CW (2012) Intuitionistic fuzzy QUALIFLEX method for optimistic and pessimistic decision making. Adv Inf Sci Serv Sci 4(14):219–226
Chen TY, Wang JC (2009) Interval-valued fuzzy permutation method and experimental analysis on cardinal and ordinal evaluations. J Comput Syst Sci 75(7):371–387
Chen TY, Wang JC, Tsui CW (2007) Decision model with permutation methods based on intuitionistic fuzzy sets. In: Proceedings of the 8th Asia Pacific industrial engineering and management system and 2007 Chinese Institute of Industrial Engineers Conference (APIEMS and CIIE 2007), pp 243–250
Chen N, Xu ZS, Xia MM (2013) Interval-valued hesitant preference relations and their applications to group decision making. Knowl-Based Syst 37:528–540
Chen N, Xu ZS, Xia MM (2013) Correlation coefficients of hesitant fuzzy sets and their applications to clustering analysis. Appl Math Model 37(4):2197–2211
Dyer JS, Fishburn PC, Steuer RE, Wallenius J, Zionts S (1992) Multiple criteria decision making, multiattribute utility theory: the next ten years. Manag Sci 38:645–654
Dubois D, Prade H (1980) Fuzzy sets and systems: theory and applications. Academic Press, New York
Facchinetti G, Ricci RG, Muzzioli S (1998) Note on ranking fuzzy triangular numbers. Int J Intell Syst 13:613–622
Farhadinia B (2013) Information measures for hesitant fuzzy sets and interval-valued hesitant fuzzy sets. Inf Sci 240:129–144
Farhadinia B (2014) Correlation for dual hesitant fuzzy sets and dual interval-valued hesitant fuzzy sets. Int J Intell Syst 29:184–205
Griffith DA, Paelinck JHP (2011) Qualireg, a qualitative regression method. Adv Geogr Inf Sci 1(2):227–233
Hinloopen E, Nijkamp P, Rietveld P (2004) Integration of ordinal and cardinal information in multiple criteria ranking with imperfect compensation. Eur J Oper Res 158(2):317–338
Hokkanen J, Lahdelma R, Salminen P (2000) Multicriteria decision support in a technology competition for cleaning polluted soil in Helsinki. J Environ Manag 60(4):339–348
Hwang CL, Yoon K (1981) Multiple attribute decision making: methods and applications. Springer, Berlin
Lahdelma R, Miettinen K, Salminen P (2003) Ordinal criteria in stochastic multicriteria acceptability analysis (SMAA). Eur J Oper Res 147(1):117–127
Li DF (2011) Closeness coefficient based nonlinear programming method for interval-valued intuitionistic fuzzy multiattribute decision making with incomplete preference information. Appl Soft Comput 11(4):3402–3418
Li LG, Peng DH (2014) Interval-valued hesitant fuzzy Hamacher synergetic weighted aggregation operators and their application to shale gas areas selection. Math Probl Eng 2014:1–25
Martel JM, Matarazzo B (2005) Other outranking approaches. In: Figueira J, Greco S, Ehrgott M (eds) Multiple criteria decision analysis: state of the art surveys. Springer, New York, pp 197–262
Meng FY, Wang C, Chen XH, Zhang Q (2016) Correlation coefficients of interval-valued hesitant fuzzy sets and their application based on the Shapley function. Int J Intell Syst 31(1):17–43
Paelinck JHP (1976) Qualitative multiple criteria analysis, environmental protection and multiregional development. Pap Reg Sci Assoc 36(1):59–74
Paelinck JHP (1977) Qualitative multicriteria analysis: an application to airport location. Environ Plan 9(8):883–895
Paelinck JHP (1978) QUALIFLEX: a flexible multiple criteria method. Econ Lett 1(3):193–197
Park JH, Park IY, Kwun YC, Tan X (2011) Extension of the TOPSIS method for decision making problems under interval-valued intuitionistic fuzzy environment. Appl Math Model 35(5):2544–2556
Peng DH, Wang TD, Gao CY, Wang H (2014) Continuous hesitant fuzzy aggregation operators and their application to decision making under interval-valued hesitant fuzzy setting. Sci World J 2014:1–20
Quirós P, Alonso P, Bustince H, Díaz I, Montes S (2015) An entropy measure definition for finite interval-valued hesitant fuzzy sets. Knowl-Based Syst 84:121–133
Rebai A, Aouni B, Martel J-M (2006) A multi-attribute method for choosing among potential alternatives with ordinal evaluation. Eur J Oper Res 174(1):360–373
Roy B (1968) Classement et Choix en Presence de Points de vue Multiples (la method Electre). Revue Francaise d’Informatique et de Recherche Operationnelle 8:57–75
Roy B (1991) The outranking approach and the foundations of ELECTRE methods. Theory Decis 31:49–73
Sarabando P, Dias LC (2010) Simple procedures of choice in multicriteria problems without precise information about the alternatives’ values. Comput Oper Res 37(12):2239–2247
Shen L, Olfat L, Govindan K, Khodaverdi R, Diabat A (2013) A fuzzy multi criteria approach for evaluating green supplier’s performance in green supply chain with linguistic preferences. Resour Conserv Recycl 74:170–179
Stewart TJ (1992) A critical survey on the status of multiple criteria decision making theory and practice. Omega 20:569–586
Torra V (2010) Hesitant fuzzy sets. International Journal of Intelligent Systems 25:529–539
Torra V, Narukawa Y (2009) On hesitant fuzzy sets and decision. In: The 18th IEEE international conference on fuzzy systems, Jeju Island, Korea, 707, pp 1378–1382
Wang JC, Tsao CY, Chen TY (2015) A likelihood-based QUALIFLEX method with interval type-2 fuzzy sets for multiple criteria decision analysis. Soft Comput 19(8):2225–2243
Wang YM, Yang JB, Xu DL (2005) A two-stage logarithmic goal programming method for generating weights from interval comparison matrices. Fuzzy Sets Syst 152:475–498
Wei GW, Lin R, Wang HJ (2014) Distance and similarity measures for hesitant interval-valued fuzzy sets. J Intell Fuzzy Syst 27(1):19–36
Wei GW, Wang HJ, Lin R (2011) Application of correlation coefficient to interval-valued intuitionistic fuzzy multiple attribute decision-making with incomplete weight information. Knowl Inf Syst 26(2):337–349
Wei GW, Zhao XF (2013) Induced hesitant interval-valued fuzzy Einstein aggregation operators and their application to multiple attribute decision making. J Intell Fuzzy Syst 24(4):789–803
Wei GW, Zhao XF, Lin R (2013) Some hesitant interval-valued fuzzy aggregation operators and their applications to multiple attribute decision making. Knowl-Based Syst 46:43–53
Xia MM, Xu ZS (2011) Hesitant fuzzy information aggregation in decision making. Int J Approx Reason 52(3):395–407
Xu ZS, Chen J (2008) Some models for deriving the priority weights from interval fuzzy preference relations. Eur J Oper Res 184:266–280
Xu ZS, Da QL (2002) The uncertain OWA operator. Int J Intell Syst 17:569–575
Xu ZS, Zhang XL (2013) Hesitant fuzzy multi-attribute decision making based on TOPSIS with incomplete weight information. Knowl-Based Syst 52:53–64
Zadeh LA (1965) Fuzzy sets. Inf Control 8(3):338–353
Zadeh LA (1975) The concept of a linguistic variable and its application to approximate reasoning–I. Inf Sci 8:199–249
Zhang ZM, Wang C, Tian DZ, Li K (2014) Induced generalized hesitant fuzzy operators and their application to multiple attribute group decision making. Comput Ind Eng 67:116–138
Zhang ZM, Wu C (2014) Some interval-valued hesitant fuzzy aggregation operators based on Archimedean t-norm and t-conorm with their application in multi-criteria decision making. J Intell Fuzzy Syst 27(6):2737–2748
Zhang XL, Xu ZS (2015) Hesitant fuzzy QUALIFLEX approach with a signed distance-based comparison method for multiple criteria decision analysis. Expert Syst Appl 42(2):873–884
Zhu QH, Sarkis J (2004) Relationships between operational practices and performance among early adopters of green supply chain management practices in Chinese manufacturing enterprises. J Oper Manag 22:265–289
Zimmermann HJ, Zysno P (1980) Latent connectives in human decision making. Fuzzy Sets Syst 4(1):37–51
Acknowledgments
The author thanks the anonymous referees for their valuable suggestions in improving this paper. This work is supported by the National Natural Science Foundation of China (Grant No. 61375075) and the Natural Science Foundation of Hebei Province of China (Grant No. F2012201020).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Zhang, Z. Multi-criteria decision-making using interval-valued hesitant fuzzy QUALIFLEX methods based on a likelihood-based comparison approach. Neural Comput & Applic 28, 1835–1854 (2017). https://doi.org/10.1007/s00521-015-2156-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00521-015-2156-9