1 Introduction

Learning high-level representations of signals for related tasks remains a critical problem in machine learning. Recently, deep architectures have emerged as important tools for learning useful representation. Theoretical results strongly suggest the benefits of deep architectures; however, the numerous parameters in deep learning architectures make their practical application difficult. Learning algorithms such as deep belief networks [11], also known as deep learning, have been proposed to narrow this gap, which makes deep architectures more practical. In recent years, deep learning has played a significant role in the field of machine learning. Deep learning algorithms include pretraining and fine-tuning procedures. Unsupervised pretraining trains the network to an acceptable initial starting point. Then, the entire network is fine-tuned, usually in a supervised manner, relative to the initialization point and the supervised target to obtain optimal parameters for the task. Combining unsupervised pretraining and supervised fine-tuning often results in better generalization than only fine-tuning from a randomly initialized position. In the pretraining procedure, each layer is organized as an auto-encoder [6] that receives patterns from the output of the previous layer and reconstructs them. During the pretraining procedure, auto-encoders can be not only trained, respectively, but also combined into a symmetrical deep neural network that can be trained simultaneously. During the fine-tuning procedure, encoders are stacked and decoders are discarded. Then, a supervised layer such as a logistic regression layer or a softmax regression layer is added. The parameters for supervised fine-tuning are initialized using the weights trained in the pretraining procedure.

There are numerous auto-encoder variants. For example, sparse auto-encoders [12, 18] add a sparse penalty term to the cost function, weight decay auto-encoders add a weight decay term to the overall cost function, denoising auto-encoders (DAEs) [25] use corrupted input data to reconstruct the original data, and contractive auto-encoders (CAEs) [22] penalize the partial derivation of a representation with respect to the input data. All of these auto-encoder variants can improve learning ability and the networks generalization performance and consequently enhance the effectiveness of the learned representations. Using effective representations as input for a supervised task, such as classification, results in better performance, e.g., lower misclassification rates. Classification performance does not depend directly on the choice of classifier; classification results would nearly be the same if the learned representations were sufficient [6, 11]. Therefore, good quality representation is important.

What are the principles of good representation? On the one hand, the representation should retain the information on the input data such that it remains consistent with the underlying data distribution. The ability to capture the salient structure of the input data distribution is a fundamental and intrinsic principle of basic auto-encoders, sparse auto-encoders, and auto-encoders that use a weight decay term. On the other hand, the representation should be robust to the variance of the input pattern, i.e., the representation should ignore small variations in input patterns. Robustness against input pattern variations is demonstrated by DAEs and CAEs. Auto-encoders discover more robust representation as the layers of the network increase [5], which has also been observed empirically [14].

The auto-encoders mentioned above, i.e., traditional auto-encoders, have symmetrical structures. In some auto-encoders, the weights of corresponding layers are set to be symmetrical. In this paper, we investigate the relation between the number of encoder and decoder layers and show that symmetrical structure and parameters are not necessary for learning good representation. We propose an unsymmetrical auto-encoder (UAE) for unsupervised feature learning and pretraining. UAEs have different numbers of layers of encoders and decoders, and UAEs are not symmetrical. We have assessed the performance of the proposed UAE using benchmark datasets. The experimental results show that the performance of UAEs is superior to that of other auto-encoders.

2 Auto-encoders

An auto-encoder [4] is a neural network used for unsupervised learning [15, 16] of efficient features. A typical auto-encoder has one input layer, one output layer, and one hidden layer. The output of the hidden layer can be used as the representation of the input data. The aim of an auto-encoder is to learn a set of better features by mapping given data to the representation space. Typically, the identification or selection of better, i.e., more efficient, features is performed to reduce dimensionality and improve discrimination in classification tasks. An auto-encoder is a special case of a multilayer perceptron where the output layer is trained to reconstruct the input from the representation. Mapping from input to representation is referred to as encoding, and reconstruction from representation to the auto-encoder output is referred to as decoding. More precisely, input data are denoted by \(x\in \mathbb {R}^{n}\), representation is denoted by \(y\in \mathbb {R}^{m}\), and its reconstruction is denoted by \(\hat{x}\in \mathbb {R}^{n}\). The auto-encoder is given as follows:

$$\begin{aligned} \left\{ \begin{aligned} y&= F\left( x;\theta ^e\right) \\ \hat{x}&= {G}\left( y;\theta ^d\right) , \end{aligned} \right. \end{aligned}$$
(1)

where \({F}: \mathbb {R}^{n} \rightarrow \mathbb {R}^{m}\) is the encoder and \({G}: \mathbb {R}^{m} \rightarrow \mathbb {R}^{n}\) is the decoder. \(\theta ^e\) are the parameters for the encoder, and \(\theta ^d\) are the parameters for the decoder. We denote the parameters of the auto-encoder as \(\theta =\theta ^e\cup \theta ^d\). The reconstruction \(\hat{x}\) is a deterministic function of input sample x defined as follows:

$$\begin{aligned} \hat{x} = {G} \circ {F} \left( x;\theta \right) . \end{aligned}$$
(2)

Then, the performance of the auto-encoder can be measured by the reconstruction error. The cost function can be formulated as follows:

$$\begin{aligned} {J}\left( \theta ;X\right) = \frac{1}{N}\sum _{x\in X}L({G}\circ {F}\left( x;\theta \right) ,x). \end{aligned}$$
(3)

Here, N is the number of data in a set of samples X. L denotes a measurement of difference. In most cases, we use square Euclidean distance by which \(L\left( \hat{x},x\right) =\frac{1}{2}\left\| \hat{x} - x\right\| ^{2}\). By minimizing the cost function, we obtain the optimal parameters \(\theta\) for the auto-encoder.

Traditional auto-encoders use a symmetrical setting as follows:

$$\begin{aligned} \left\{ \begin{aligned} {F}&= \underbrace{F_1 \circ F_2 \circ \cdots \circ F_{M}}_{M} \\ {G}&= \underbrace{G_1 \circ G_2 \circ \cdots \circ G_{M}}_{M}. \end{aligned} \right. \end{aligned}$$
(4)

Here, M is the number of auto-encoders, and \(F_{i}\left( x,\theta ^e_i\right)\) and \(G_{i}\left( x,\theta ^d_i\right)\) are neuron layers by which \(f\left( w_{i}x + b_{i}\right)\). \(\theta _{i}=\left\{ w_{i},b_{i}\right\} \subset \theta\) are the parameters for the layer, and f denotes the activation function. In common cases, especially when we pretrain a classifier network, the following auto-encoders with only one layer are used:

$$\begin{aligned} \left\{ \begin{aligned} y&= f\left( w^e_1x + b^e_1\right) \\ \hat{x}&= f\left( w^d_1x + b^d_1\right) . \end{aligned} \right. \end{aligned}$$
(5)

When the activation function is linear and there are fewer hidden nodes than input units, we can obtain a result that is similar to that of principal component analysis [1]. The learned weights are the principle components of the input space. Using more units in the hidden layer than in the input layer with a linear activation function leads to a trivial solution by which the weight is an identical matrix. Commonly, we consider a case using a sigmoid activation function \(f(s)=\frac{1}{1+e^{-s}}\) and more hidden units than input units.

To avoid learning a trivial solution, over-fitting, and other unfavorable results, researchers have introduced many useful auto-encoder variants.

2.1 Sparse auto-encoder (AE+Sparse)

Potentially, we can simply learn an identity function if we use the cost function in 3 to train the network. The representations will no longer be determined uniquely by the input data using more units in the hidden layer than in the input layer with a nonlinear activation function. Among such representations, one with the most zero components is interesting by adding sparsity constraints to the cost Eq. 5. Sparsity constraints are shown to yield features that are (for some) more invariant to geometric transformations of images [9, 20, 21]. Cost function of sparse auto-encoders has the following form:

$$\begin{aligned} {J}_{\mathrm{AE}+\mathrm{Sparse}}\left( \theta ;X\right) ={J}\left( \theta ;X\right) + \lambda S(y), \end{aligned}$$
(6)

where S(y) measures the sparsity of y and \(\lambda\) is a hyper-parameter to balance the penalty.

2.2 Weight decay auto-encoder (AE+WD)

It is shown that if we want to improve the generalization ability of a neural network, we should consider the balance between the information in the training examples and the complexity of the network [3, 23, 24]. A way always used to decrease the complexity is to limit the growth of the weights through some type of weight decay [17]. Commonly, the cost function of auto-encoders with weight decay has the following form:

$$\begin{aligned} {J}_{\mathrm{AE}+\mathrm{WD}}\left( \theta ;X\right) ={J}\left( \theta ;X\right) + \lambda \sum _{w\in \theta }\frac{1}{2}\left\| w\right\| _F^2. \end{aligned}$$
(7)

Here, \(\lambda\) is a hyper-parameter that controls how strongly large weights are penalized, and \(\Vert \cdot \Vert _F\) is the Frobenius norm. It is known that weight decay of this form can improve generalization [10].

2.3 Denoising auto-encoder

A DAE maps a corrupted example back to an uncorrupted example [26]. It minimizes the reconstruction error between the output and the uncorrupted example. Thus, the network can learn a robust representation. Its cost function has the following form:

$$\begin{aligned} {J}_{\mathrm{DAE}}\left( \theta ;X\right) = \frac{1}{N}\sum _{x\in X}L\left( {G}\circ {F}(x^\prime ;\theta ),x\right) . \end{aligned}$$
(8)

Here, \(x^\prime\) denotes corrupted x. In this context, it is assumed that the input data with high dimension lay in an underlying low-dimensional manifold. During training, DAEs learn a stochastic operator p(x|X) mapping the corrupted X back to its uncorrupted version. Corrupted examples are more likely to be outside and distant from the manifold than uncorrupted examples. The mapping learns from the examples encompassing corrupted and uncorrupted data to the manifold by the corrupted examples; thus, it enlarges the learning territory and increases learning ability.

2.4 Contractive auto-encoder

A CAE [22] uses a training criterion that not only reconstructs the input data but also encourages the learned representation y to be as invariant as possible to the input data x. The criterion is used to minimize the sum of a reconstruction error with a Frobenius norm of its Jacobian matrix, which is the derivation of each hidden unit output with respect to each input. The cost function of CAEs has the form:

$$\begin{aligned} {J}_{\mathrm{CAE}}\left( \theta ;X\right) = {J}\left( \theta ;X\right) + \lambda \left\| \frac{\partial a_e}{\partial X}\right\| _F^2. \end{aligned}$$
(9)

When we minimize \({J}_{\mathrm{CAE}}\), the second term will be very small; thus, \(w^{e}\) will tend to zero and \(w^{d}\) will tend to infinity to satisfy the first term. To prevent this trivial solution, we typically employ a tied weight, i.e., \(w^{d}\) is forced to the transpose of \(w^{e}\). However, \(b^d\) and \(b^e\) are initialized and trained, respectively.

3 Unsymmetrical auto-encoder

We generalize the concept of auto-encoders and propose the UAE. The UAE demonstrates the following unsymmetrical structure:

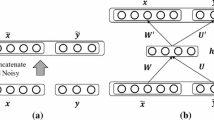
$$\begin{aligned} \left\{ \begin{aligned} {F}&= \underbrace{F_1 \circ F_2 \circ \cdots \circ F_{M}}_{M} \\ {G}&= \underbrace{G_1 \circ G_2 \circ \cdots \circ G_{M^{\prime }}}_{M^{\prime }}, \end{aligned} \right. \end{aligned}$$
(10)

where the encoder and decoder have different numbers of layers. Figure 1 illustrates the architecture of a UAE that differs from conventional auto-encoders.

Fig. 1
figure 1

Architecture for unsymmetrical auto-encoder

Full size image

The proposed UAE is a multilayer neural network with more than one hidden layer. It contains many encoders that are used to learn the multiple-level representation, and many decoders are used to better reconstruct the input data. Generally, a n-layer UAE, including one output layer and \(n-1\) hidden layers, with parameters \(\theta =\{\theta ^i |i \in \{1, 2, 3\cdots n\}\}\), where \(\theta ^i=\{w^i, b^i\}\), can be formulated as follows:

$$\left\{ {\begin{array}{*{20}l} {z^{i} = w^{i} a^{{i - 1}} + b^{i} } \hfill \\ {a^{i} = f^{i} (z^{i} )} \hfill \\ {a^{0} = x.} \hfill \\ \end{array} } \right.$$
(11)

Here, x denotes the input data, i denotes layer \(l_i\), and \(a^n\) denotes the reconstruction of the input data. UAEs try to minimize the following cost function:

$$\begin{aligned} {J}_{\mathrm{UAE}}\left( \theta ;X\right) = \frac{1}{N}\sum _{x\in X}L\left( a^n,a^0\right) . \end{aligned}$$
(12)

Typically, there are two ways to perform pretraining with auto-encoders. Here, a total of Q auto-encoders are assumed. The first pretraining method is to train the first auto-encoder and then use the output of the hidden layer of the first auto-encoder as the input of the second auto-encoder to train the second auto-encoder. This procedure is then repeated to train Q auto-encoders. This method is illustrated in Fig. 2. The second method to train auto-encoders is to stack all auto-encoders to formulate a 2Q + 1-layer neural network. The number of units of the first and last layer equals the dimension of the input data. The number of units in the second layer equals that of the \(2Q+1\)-th layer and so on. Then, we train all Q auto-encoders. The latter procedure is illustrated in Fig. 3.

Fig. 2
figure 2

First way to train auto-encoders

Full size image
Fig. 3
figure 3

Second way to train auto-encoders

Full size image

The auto-encoders mentioned above (AE+Sparse, AE+WD, DAE, and CAE) are symmetrical, i.e., the number of encoders is equal to the number of decoders; however, with UAEs, the numbers of encoders and decoders are not equal. This is motivated by shadow neural networks with more units, which have ability comparable to deep neural networks with fewer units. With the second training procedure, we reduce the layers between the second and \(Q+1\)-th layer to k that is less than Q with more units in these k layers, which remains the same ability of encoding and decoding. However, the number of layers is less than the Q auto-encoders we use. These neural networks become UAEs. Due to gradient vanishing, we cannot use too many layers in UAEs. We assume that the maximum number of layers is \(2P+1\). Using symmetrical auto-encoders, we use only P auto-encoders. However, if we use UAEs, we can use k decoders (\(k>p\)) and \(2P-k\) encoders with more units. Such UAEs have the ability of k auto-encoders. We use k decoders to ensure that we can minimize the reconstruction error. The complexity of the proposed UAEs will be less than that of symmetrical auto-encoders under the condition of the same variant of auto-encoder as introduced in Sect. 3. Moreover, we can obtain improved representation if we use the same number of layers as symmetrical auto-encoders.

3.1 Explanation of UAE

Why does the proposed UAE learn better representations? The reason is very intuitive. The UAE has more units in fewer layers of encoders, which allows it to find more abstract representations. In addition, it has sufficient decoders to reconstruct the input patterns. All of the auto-encoders discussed in Sect. 2 have one hidden layer. With abstract and robust encoded representation of data, a single decoder can be used in the same manner as traditional auto-encoders; thus, the reconstruction is rarely applied. If we can reconstruct with only a single layer, the representation would be no more robust. Another important observation is that if the number of units in one encoder is equal to that of its corresponding decoder, the number of encoders must be the same as that of the decoders for rational reconstruction.

The UAE architecture learns robust representation through more layers of the encoder and demonstrates greater ability to reconstruct the input data using multiple decoder layers. This conforms to the principle of good representation, which benefits from more flexible unsymmetrical structure. Quantitative and qualitative evidence will be presented in Sect. 4.

3.2 Number of layers in UAE

It is commonly known that the representation will be better when the network is sufficiently deep. However, until recently, practical limitations in learning algorithms, e.g., gradient vanishing, have prevented us from building a very deep auto-encoder.

Suppose the number of units of the input and output layers is m. The number of units of layer \(i=1, 2, 3, n-1\) is \(m_i\). \(U^i_j\) denotes the j-th unit in layer i. We select one path from \(U^n_p\) to \(U^{n-k}_q(k \in \{1, 2, 3, n-1\})\) randomly. The selected unit flowing through the path in layer i is denoted as \(S^i\). \(W^i_{jk}\) denotes the weight on the connection from unit j of layer i to unit k of layer \(i-1\).

We use mean square error. The error signal of \(U^n_p\) flowing to \(U^{n-k}_q\) is illustrated in Fig. 4.

$$\begin{aligned} \delta ^n_p = \dot{f}^n\left( z^n_p\right) \left( X_p - a^n_p\right) , \end{aligned}$$
(13)

\(\delta ^n_p\) denotes the error of unit p in layer n and \(\dot{f}^n(\cdot )\) denotes the derivative of function \(f^n(\cdot )\).

$$\begin{aligned} \frac{\partial \delta ^{n-k}_q}{\partial \delta ^n_p}= \prod _{l=0}^{k-1}W^{n-l}_{S^{n-l}S^{n-l-1}}\dot{f}^{n-l-1}\left( z^{n-l-1}_S\right) . \end{aligned}$$
(14)

If \(\left| W^{n-l}_{S^{n-l}S^{n-l-1}}\dot{f}^{n-l-1}\left( z^{n-l-1}_S\right) \right| > 1\), \(\frac{\partial \delta ^{n-k}_q}{\partial \delta ^n_p}\) will increase exponentially with k. In other words, the error increases exponentially when the error signals arrive at unit \(U^{n-k}_q\). This leads to oscillating weights and unstable learning.

If \(\left| W^{n-l}_{S^{n-l}S^{n-l-1}}\dot{f}^{n-l-1}\left( z^{n-l-1}_S\right) \right| < 1\), \(\frac{\partial \delta ^{n-k}_q}{\partial \delta ^n_p}\) will decrease exponentially with k. In other words, the error vanishes and nothing can be learned in the lower layers of this network.

When we use a logistic sigmoid function, the maximal value is 0.25. To avoid oscillation, \(|W^{n-l}_{S^{n-l}S^{n-l-1}}|\) must be \(\le\)4. If we use a network that is too deep, the top layers cannot learn anything important. This is a trade-off between the values used to initialize the weights and the depth of the network. Typically, we initialize the weights between \(-1\) and 1. When the depth is >6, the error will be approximately \(10^{-4}\). If we use a small learning rate (e.g., \({\le}10^{-1}\)), the error would be even less. If the depth is >6 with the initializing weights, it will be not significant. For further analysis of error flow, see [2, 7, 19].

Fig. 4
figure 4

Error flows in UAE

Full size image

3.3 Training with UAE

Basic auto-encoders have been used as building blocks for training deep neural networks [6]. After training a single auto-encoder, its representation will be used as the input to the next auto-encoder. We then train this auto-encoder continually. The trained auto-encoders are stacked, and an additional supervised layer is added to build a multilayer neural network. Weights that have been trained in the auto-encoders are used to initialize this multilayer neural network. Finally, a supervised criterion is employed to optimize the network. This greedy layer-wise procedure has been shown to yield significantly better local minima than random initialization of deep neural networks, thereby achieving better generalization for numerous tasks.

The procedure for training a deep network with the UAE is similar. We use the output of the encoder as the input of the next UAE for unsupervised learning. After training several UAEs, we stack them and add a supervised layer to fine-tune the whole network to obtain the best parameters for a particular task.

4 Experiments and results

We performed experiments with the proposed UAE algorithm on the same benchmark classification problems used in [22]: CIFAR-bw, which is a grayscale version of the CIFAR-10 image-classification task [13], MNIST, and MNIST variations. The variations of the MNIST problem contain rotation, addition background comprising random pixels, addition background made from patches extracted from a set of images, and combinations of these variations.

The MNIST variations benchmark also contains a subset of the original MNIST problem. Each MNIST variation problem was divided into a training set with 10,000 examples, a validation set with 2000 examples, and a test set with 50, 000 examples.Footnote 1 For all datasets, the input was normalized between 0 and 1. All experiments were performed in MATLAB with a graphics processing unit (GPU)Footnote 2.

4.1 Visualization for UAE

First, we used the MNIST dataset to train a UAE and visualized the features that it learned in the hidden layer. In this experiment, we initialized the UAE with four hidden layers of size \(\{2000, 1000, 400, 200\}\). We set the encoder only in the first hidden layer and added a sparsity constraint to this layer. We also added a weight decay penalty to the weights of all layers. We optimized the cost function using L-BFGS to reconstruct the input data to train the UAE. When the optimization of the cost function reaches convergence, we use the activation maximization method [8] with the trained weights to look for the input \(X^*\) that can maximally activate the units of the output of the first hidden layer. Then, we use \(X^*\) to visualize the learned features in the first hidden layer. Figure 5 shows the visualization results of the UAE in the first hidden layer and the visualization of the third layer of the stacked denoising auto-encoder (SDAE) reported in [8].

Fig. 5
figure 5

Activation maximization applied on MNIST. On the left side visualization of 16 units from the first hidden layers of a UAE. On the right side one of the solutions to optimization problem for units in the third layer of the SDAE

Full size image

On the one hand, these learned features in the first layer in the UAE and in the third layer in SDAE seem interpretable; however, they are quite complex. A common understanding arising from investigations of the V1 and V2 areas of the human brain is that features are edges in the first hidden layer and corners in the second hidden layer. Some of the units have characteristics that we would associate with the so-called complex cells. On the other hand, the UAE learns a robust and better representation. The features the UAE learned in the first hidden layer are as good as those learned by SDAE in the third hidden layer.

4.2 Classification performance

We used a sigmoid activation function for both encoder and decoder, cross-entropy for binary classification, and the log of softmax for multiclass problems in UAE which was trained by minimizing the cost function on the training set. First, we used the auto-encoders to perform unsupervised learning to extract features layer by layer. Then, the weights and the biases of the encoder were used to train supervised learning as the initialization.

In all cases, we used stochastic gradient descent with mini-batches of size 100 for both unsupervised and supervised training criterion. Due to the hyper-parameters in each auto-encoder, we used grid search on the validation set to select the best model according to its performance with the lowest reconstruction error on the validation set. Among all auto-encoders, the range of units in the hidden layer was [500, 2000], and the range of the constant learning rate was \(\{0.0001, 0.001, 0.01, 0.1\}\). In the weight decay auto-encoder, the range of weight decay was 0 to \(10^{-5}\). In the sparse auto-encoder, we selected the expectable sparsity parameter in the range [0.1, 0.5], and the corresponding range of the weight coefficient was [0.1, 10]. In the DAE, we selected masking noise, and the fraction v was in the range 0–0.8. In the CAE, the weight coefficient was in the range of \(10^{-1}\) to \(10^{-5}\).

For all experiments, we used early stopping based on the classification error of the model on the validation set. Note that the maximum epoch was 1000. The best score over the compared models on the same benchmark was highlighted with bold font.

The results obtained using one auto-encoder with MNIST and CIFAR-bw datasets are reported in Table 1. In these experiments, we trained an auto-encoder with different variants. Then, we constructed a three-layer network for classification using the parameters obtained by the trained auto-encoder.

Table 1 We use one auto-encoder for pretraining and then fine-tune with an additional softmax layer
Full size table

We also trained a deep neural network. In this experiment, we trained and stacked three auto-encoders for each variant. At the trail of it, we added one supervised layer to perform fine-tuning. The results are reported in Table 2.

Table 2 We use three auto-encoders for pretraining and then fine-tune with an additional softmax layer
Full size table

5 Conclusion

UAEs are auto-encoders with different numbers of encoders and decoders. The experimental results quantitatively and qualitatively demonstrate that the proposed UAE can learn a comparable or even superior representation for better classification. From an architectural perspective, the proposed UAE also contains generic auto-encoders; namely, symmetrical auto-encoders are a special case of unsymmetrical auto-encoders. In addition, UAEs use regularization terms that have always been used in symmetrical auto-encoders, such as sparsity constraints, weight decay, and contractive terms. Relative to better representation, there is a trade-off between reconstruction and robustness. Generic auto-encoders are more close to better reconstruction, although there are several types of explicit regularization terms that can improve the robustness of the learned representation. UAEs obtain better reconstruction using more decoders than encoders. In addition, UAEs learn robust representation using more units in the encoder layers.