Intrusive tumor growth inspired optimization algorithm for data clustering

Abstract

Inspired by the invasive tumor growth mechanism, this paper proposes a new meta-heuristic algorithm. A population of tumor cells can be divided into three subpopulations as proliferative cells, quiescent cells, and dying cells according to the nutrient concentration they get. Different cells have different behaviors and interactions among them for competition. In the tumor growing process, an invasive cell is born around a proliferative cell for the higher nutrient concentration and a necrotic cell occurs around a dying cell for the lower nutrient concentration, which presents the balance between life and death. To evaluate the performance of the intrusive tumor growth optimization algorithm (ITGO), we compared it to the many well-known heuristic algorithms by the Wilcoxon’s signed-rank test with Bonferroni–Holm correction method and the Friedman’s test. At the end, it is applied to solve the data clustering problem, which is a NP-hard problem. The experimental results show that the proposed ITGO algorithm outperforms other traditional heuristic algorithms for several benchmark datasets.

1 Introduction

Nature-inspired meta-heuristic algorithms are powerful and effective in solving optimization problems [1, 2], which have now been used in many fields such as computer science [3], data mining [4], medicine and biology [5], economy [6], and engineering [7]. Over the last few decades, many nature-inspired meta-heuristic algorithms have emerged. For instance, genetic algorithm (GA) [8] which works on the principle of the Darwinian theory of the survival of the fittest by genetic mutation, crossover, and selection operators; differential evolution (DE) [9] which is similar to GA with specialized crossover and selection method; ant colony optimization (ACO) [10] which was inspired by the foraging behavior of the ant for the food; particle swarm optimization (PSO) [11, 12] which was inspired by the foraging behavior of the birds; teaching learning-based optimization (TLBO) which was inspired by the effect of the influence of a teacher on the output of learners in a class [13]; cuckoo search algorithm (CSA) [14] which was inspired by the cuckoo brood parasitism behavior; gravitational search algorithm (GSA) [15], the searcher agents are a collection of masses which interact with each other based on the Newtonian gravity and the laws of motion. Black hole approach (BH), which was inspired by the BH phenomenon [16]; Krill Herd algorithm (KH) [17], which was inspired by the herding behavior of krill individuals; artificial bee colony (ABC) algorithm, which simulates the foraging behavior of bees for multimodal and multi-dimensional numerical optimization problems [18]; biogeography-based optimization (BBO) was initially developed in [19], which can be seen as an evolutionary algorithm (EA) motivated by the optimality perspective of natural biogeography; artificial cooperative search algorithm (ACS) [20], which was inspired of mutualism and cooperation-based biological interaction of two eusocial superorganisms living in the same habitat; Grey wolf optimizer (GWO) [21], which mimics the leadership hierarchy and hunting mechanism of gray wolves in nature; and invasive weed optimization (IWO) [22], which was inspired from colonizing weeds.

This paper presents a new optimization method and its application to data clustering, which is inspired by the invasive tumor growth mechanism. A tumor is a cluster of abnormal cells in body. The deep investigation and study show that tumor is a complex system. Tumor cells can be divided into the main three types: proliferative cells, quiescent cells, and dying cells, which grow for the nutrient (oxygen and glucose etc.). The adequate nutrient makes the invasive cell born around the proliferative cell, while the lower nutrient make the dying cell convert into necrotic cell. Different cells run with different behaviors by cooperation. A proliferative cell grows with a levy flight behavior to obtain more nutrients, and a quiescent cell grows by the leading of a proliferative cell and the interaction among themselves. For dying cell, they can obtain more nutrients by the leading of a proliferative cell and a quiescent cell. The more interactions and behaviors ensure that our proposed algorithm can easily jump out of the local optimum.

The rest of the paper is organized as follows: In Sect. 2, the clustering problem is discussed. A brief explanation of the tumor growth modeling is given in Sect. 3. In Sect. 4, we introduce our proposed invasive tumor growth model and algorithm. The performance of the proposed algorithm is tested with several benchmark functions such as CEC 2005 and CEC 2008 and applied to the data clustering for the benchmark datasets, which are compared with many well-known algorithms in Sect. 5. Parameter tuning is discussed in Sect. 6.  Section 7, we discuss the proposed algorithm (ITGO); finally, Sect. 8 includes a summary and the conclusion of this work.

2 Cluster analysis

Data clustering is an important and popular method in data mining techniques, which has been widely used in many fields such as pattern recognition, document clustering, image processing, marketing, costumer analysis, and biology. Clustering can be seen as a classification process without supervision, in which, a set of data objects is grouped into some clusters. Especially, the data of a cluster must have the great similarity, and the data of different clusters must have high dissimilarity.

Strictly speaking, clustering problem is to determine a partition $G = \left\{ {C_{1} ,C_{2} , \ldots ,C_{k} } \right\},\,\forall k\;C_{k} \ne {\O }\;{\text{and}}\;\forall h \ne k,C_{h} \cap C_{k} = {\O }$ such that objects belong to the same cluster are as similar as possible, while objects belong to the different clusters are as dissimilar as possible. One object can only belong to one cluster. To achieve this, a mathematical model can be described as follows [23]:

$${\text{Min}}\;\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{k} {w_{ij} ||X_{i} - C_{j} ||} }$$

(1)

$$0 < \sum\limits_{i = 1}^{n} {w_{ij} } < n,\quad j = 1,2, \ldots ,k$$

(2)

$$\sum\limits_{j = 1}^{k} {w_{ij} } = 1,\quad i = 1,2, \ldots ,n$$

(3)

$$w_{ij} \in \left\{ {0,1} \right\}$$

(4)

$$w_{ij} \in [0,1]$$

(5)

where n is the number of objects and k is the number of clusters, X _i denotes the object i, C _j denotes the cluster center j. $||X_{i} - C_{j} ||$ is the euclidean distance between the object X _i , and the cluster center C _j . $w_{ij}$ denotes the degree of membership. Using formula (1), (2), (3), and (4), the model was called ‘hard partition,’ while using formula (1), (2), (3) and (5), it can be called ‘soft partition,’ or called as fuzzy clustering. It was proven that the clustering problem is NP problem [24].

There are many clustering algorithms in the literature. The classical clustering algorithms are hierarchical algorithm and partitional algorithm [25, 26]. Among all these algorithms, K-means algorithm was the most well known because of its simplicity and efficiency. However, it suffers from some problems. For instance, the number of the initial cluster centers needs to be defined, and the initial cluster center are chosen randomly so that the algorithm is easy to fall into the local optimal solution. To overcome the weakness of the K-means, many heuristic methods have been used, such as DE algorithm [27], GSA [28, 29], PSO algorithm [30], firefly algorithm [31], ACO [32], big bang–big crunch algorithm [33], honey bee mating optimization [34], and TLBO [35].

3 Modeling of invasive tumor growth

Tumor is a cluster of abnormal cells which grows around some tissues. It is a generally accepted view that genome level changes in cells turn a normal cell into a tumor cell. Usually, the cell growth is controlled by the deactivation of growth pathway and activation of programmed cell death pathway in a normal tissue. When both of these regulatory mechanisms fail with an overproduction of growth factors and inhibition of programmed cell death, tumor occurs [36, 37]. From the point of view of the system science, the tumor can be considered as a complex linear dynamic system. The tumor cells proliferate and invade into surrounding tissue as seen in Fig. 1. The main experimental observations show that tumor cells proliferate when they are in a high nutrient (oxygen and glucose etc.) level, the tumor cells trigger cell death (apoptosis) in low nutrient levels, and in intermediate nutrient levels, the tumor cells stay quiescent [38]. In order to apprehend the mechanism of tumor growth, many mathematical models have been established [38–41]. All these models can be divided into two categories: (1) continuum mathematical models that use space averaging and thus consist of partial differential equations and (2) discrete cell population models that consider processes that occur on the single-cell scale and introduce cell–cell interaction using cellular automata-type computational machinery. For many continuum mathematical models, heat conduction equation was used to present the diffusion of nutrient concentration for the tumor cells. The equation [39] is as follows:

$$\frac{\partial n}{\partial t} = D_{n} \nabla^{2} n + \sigma e - \varphi c - \lambda n$$

(6)

where n, D _n , σ, φ, and λ are the nutrient concentration, diffusion coefficient, production, consumption, and natural decay rates of the nutrient, respectively. To survive and grow, a tumor cell consumes nutrients at a certain rate, and if the nutrient concentration around it in the microenvironment is lower than the specified value, it will become a quiescent cell or dying cell or apoptosis (dead). Moreover, for the discrete cell population models, in order to simulate the process of the tumor growth, they consider the influence of the interactions between tumor cells and their microenvironment, including their surrounding cells, as well as the extracellular matrix (ECM), chemical signals, metabolic substrates such as oxygen and glucose. More of these models can really simulate the process of the tumor growth including the space and time, which makes it more easier to understand the mechanism of the tumor growth.

Fig. 1

GBM multi-cellular tumor spheroid (MTS) gel assay showing dendritic invasive branches. a The invasive branches centrifugal evolve from the central MTS. The linear size of central MTS is approximately 400 mm. b The invasive branches are composed of chains of invasive cells. The images are adapted from Ref. [40]

Summarized from the models of tumor growth [39–41], tumor cells have the following characteristics:

• 1. Tumor can be regarded as a isotropic sphere, and a concentric spatial layered structure consists of an outer rim of proliferative cells, an intermediate layer of viable, but dormant, quiescent cells, and an inner necrotic core.

• 2. In order to survive and grow, tumor cells must get enough nutrients, and the tumor cells have the invasive ability.

• 3. Tumor cells will move toward the direction of higher nutrient concentrations.

• 4. There is a complex interaction between tumor cells.

• 5. They have a random walk of motivation.

• 6. When nutrient concentration is lower than a certain value, the proliferative cells may turn into quiescent cells; while nutrient concentration is lower than the minimum value, the quiescent cells turn into dying cells, or even apoptosis.

• 7. Nutrient concentration corresponds to different types of tumor cells.

4 Intrusive tumor growth optimization algorithm (ITGO)

4.1 Modeling of Intrusive tumor growth

As mentioned above, two kind of mathematical models were used to simulate the tumor growth: continuum mathematical models and discrete cell population models. Continuum mathematical models present the diffusion of nutrient concentration for the tumor, and discrete cell population models present the interactions of cells in tumor. However, these models were used only to simulate the processes of tumor growth. How to create a new model to solve the optimization problem should be studied deeply. According to the principle of the Darwinian theory of the survival of the fittest, tumor cells must compete for the nutrient to be survival. If a tumor cell cannot get adequate nutrients, it may be dead. Different tumor cells get the different nutrient by competition, which influences their growing ways. As we all know, tumor is not an individual but a complex system, so competition and interaction for all the tumor cells must be needed. Then a model of intrusive tumor growth optimization can be established. Different from the previous mathematical models, to implement the evolution process of tumor growth for solving optimization problems, five kinds of cells were considered: invasive cell, proliferative cell, quiescent cell, dying cell, and necrotic cell, depending on the nutrient supply they get.

Figure 2 shows the tumor cell’s competition and interaction. In our model, invasive cells and proliferative cells locate at the outer layer of the tumor, where they can get best nutrients and grow fast, and invasive cells are the daughters of proliferative cells by mutation; quiescent cells locate at the middle layer of the tumor, and they can get general nutrients and grow relatively slow. For competition, they must obtain enough nutrients by leading of proliferative cells; dying cells are located at the inner layer of the tumor, due to the least nutrient concentration, they can grow slowly or may develop into necrotic cells (dead cells). For competition, they obtain nutrient by leading of proliferative cell and quiescent cells; necrotic cells locate at the core of the tumor; they are dead, and they cannot grow or move. Figure 3 shows the diffusion of nutrient, and different colors from dark red to light pink present the diffusion of nutrient from the outer layer to the inner layer of tumor. Different nutrient concentration I, P, Q, D, and N corresponds to different kind of cells: Invasive cell (Icell), proliferative cell (Pcell), Quiescent cell (Qcell), Dying cell (Dcell), and Necrotic cell (Ncell). In addition, necrotic cells have been dead, so they do not move and there are no interactions for them.

Fig. 2

The optimization model of invasive tumor growth

Fig. 3

Diffusion of Nutrient concentration

In our model, tumor growth is a complex system using the interaction among proliferative cells, quiescent cells, dying cells, and invasive cells, which compete for survival. Different cells have different behaviors.

• 1. The growth of proliferative cells

The proliferative cell locates at the outer layer of the tumor with the highest nutrient concentration, so it is a ‘leader role.’ For the other kind of cells, all the proliferative cells are leaders. It is to say, tumor has many leaders, which grow by the stronger invasive behaviors (seen as Fig. 1). A remarkable characteristic of proliferative cells is that they move short distance, occasionally moves long distance. To achieve this goal, we use the Levy distribution. Formula is as following:

$$Pcell_{i,j} (t + 1) = Pcell_{i,j} (t) + \alpha \cdot Levy(s)$$

(7)

$Pcell_{i,j}$ presents the position of proliferative cell, $Levy(s)$ presents the intrusive behavior of the proliferative cell, and α is the control size of step.

$$\alpha = rand \cdot \left( \frac{t}{T} \right)$$

(8)

where t is the current iterative number, and T is the total iterative number.

Levy distribution usually appears in a simplified form, as follows:

$$Levy(s)\sim |s|^{ - 1 - \upsilon } ,\quad (1 < \upsilon \le 2)$$

(9)

Broadly speaking, Levy flight is a random walk, and the step size obeys Levy distributions and walk direction obeys uniform distribution. To perform the Levy distributions, we use the Levy distribution characterized with Mantegna law [42, 43] to select the step length vector. In Mantegna law, the step size is designed as follows:

$$step = \frac{u}{{|v|^{1/\omega } }}$$

(10)

where u, v obeys normal distribution, i.e.,

$$u\sim N(0,\sigma_{u}^{2} ),\quad v\sim N(0,\sigma_{v}^{2} )$$

(11)

$$\sigma_{v} = \left\{ {\frac{{\Gamma (1 + \omega )\sin (\pi \omega /2)}}{{\Gamma \left[ {(1 + \omega )/2} \right]\omega 2^{(\omega - 1)/2} }}} \right\}^{1/\omega }$$

(12)

$\omega$ is a constant.

In the search process of the proliferative cell, $Levy(s)$ presents the search in different regions, and control size of step α achieves the balance of exploration and exploitation. In the early search stage, when $\frac{t}{T} \le 0.5,\,\alpha$ obtains a more small value, each proliferative cell visits those regions of a search space within the neighborhood of previously visited points, and it can be seen as an exploitation, while in the late search stage, when $\frac{t}{T} > 0.5,\,\alpha$ perhaps obtains a more large value, each proliferative cell visits entirely new regions of a search space, and it can be seen as an exploration.

• 2. The growth of quiescent cells

The quiescent cells are the general but most members of the tumor, which locate at the middle layer. Due to the low nutrient they get, they grow relatively slow. For competition, the quiescent cells move toward the higher nutrient concentration, guided by proliferative cells, and they interact with each others.

$$sQcell_{i,j} (t + 1) = \left\{ {\begin{array}{ll} {Qcell_{i,j} (t) + \beta \cdot (hPcell_{p,j} (t) - Qcell_{i,j} (t)) + \beta \cdot ((Qcell_{x,j} (t) - Qcell_{x,j} (t))),} &\quad {rand < 0.5} \\ {Qcell_{i,j} (t) + \beta \cdot (cPcell_{p,j} (t) - Qcell_{i,j} (t)) + \beta \cdot ((Qcell_{x,j} (t) - Qcell_{y,j} (t))),} &\quad {rand > 0.5} \\ \end{array} } \right.$$

(13)

$$\beta = rand(0,1) \cdot normal(0,1) \cdot step$$

(14)

$$Qcell_{i,j} (t + 1) = \left\{ {\begin{array}{ll} {Qcell_{i,j} (t),} &\quad {rand < e^{{\left( {\frac{t}{T} - 1} \right)}} } \\ {sQcell_{i,j} (t + 1),} &\quad {else} \\ \end{array} } \right.$$

(15)

Here, $hPcell_{p,j} (t)$ is the historical best position of proliferative cell, and $cPcell_{p,j} (t)$ is the current position of proliferative cell. $Qcell_{i,j} (t)$ is the old position of quiescent cell, and $sQcell_{i,j} (t + 1)$ is the current position of quiescent cell. The step presents the step size of Levy flight such as formula (10); β presents the growing speed; p is an integer, presents a proliferative cell selected randomly from the group of proliferative cell; x and y are integers, present two quiescent cells selected randomly from the group of quiescent cells, and $x \ne y$, x and y are two quiescent cells near the i quiescent cell. Formula (15) presents the mutation of quiescent cell.

In the search process of quiescent cells, we consider the balance of exploration and exploitation, too. Though quiescent cell population is the main body of the tumor, many cells should search including exploration and exploitation. In formula (13), we can see that, each quiescent cell is guided by the historical best position of proliferative cell $hPcell_{p,j} (t)$ and the current position of proliferative cell $cPcell_{p,j} (t)$ alternately, which means that each quiescent cell search in a large region to find a best position, it can be seen as an exploration; while the two neighbor’s operation ensures the quiescent cell visits in the neighbor regions, it can be seen as an exploitation.

• 3. The growth of dying cells

The dying cells locate at the inner layer of the tumor with the least nutrient, so it is easy to be converted into necrotic cell (dead). Luckily, other cells of them can grow for competition. In dying cell region, nutrient concentration is very low, so these cells move toward the direction of quiescent cells and proliferative cells with a higher nutrient concentration. Formula is as following:

$$Dcell_{i,j} (t + 1) = Dcell_{i,j} (t) + \gamma \cdot (hPcell_{p,j} (t) - Dcell_{i,j} (t)) + \gamma \cdot ((Qcell_{x,j} (t) - Dcell_{i,j} (t)))$$

(16)

$Dcell_{i,j} (t)$ presents the position of the old dying cell, $Dcell_{i,j} (t + 1)$ presents the position of the current dying cell, $Qcell_{i,j} (t)$ presents the position of quiescent cell, $hPcell_{p,j} (t)$ presents the position of proliferative cell (the historical best position); p is an integer that presents a proliferative cell selected randomly from the group of proliferative cells; x is an integer that presents a quiescent cell selected randomly from the group of quiescent cells. When $\gamma = rand[ - 1,1].$, Formula (16) shows that $hPcell_{p,j} (t)$ and $Qcell_{x,j} (t)$ guide $Dcell_{i,j} (t)$ to move for growth.

In the search process of the dying cells, formula (16) means that each dying cell is guided by the proliferative cell and the quiescent cell, and it can be seen as an exploration. Since each dying cell visits a new regions according the position of the proliferative cell and the quiescent cell, two leaders (proliferative cell and the quiescent cell) were chosen in different populations randomly, which can enhance the diversity of our algorithm.

• 4. The growth of invasive cells

As mentioned above, invasive cells locate at the outer layer of the tumor. They are the most active ones, born by the proliferative cells. When an invasive cell is born, a dying cell with the least nutrient will be dead. The balance of life and death will always be the evolution of the tumor.

Formula (17) presents a new cell which is born randomly in the tumor, and formula (18) shows that a mutant daughter of a historical best proliferative cell is born, which is an invasive cell $Icell_{i,j} (t + 1).$ Formula (19) presents that a dying cell is apoptosis and replaced by the invasive cell $Icell_{i,j} (t + 1).$

$$newCell_{i,j} (t) = Random(i,D),D \in [D\;\hbox{min} ,D\;\hbox{max} ]$$

(17)

$$Icell_{i,j} (t + 1) = hPcell_{p,j} (t) + \eta \cdot (newCell_{i,j} (t) - hPcell_{p,j} (t))$$

(18)

$$Dcell_{i,j} (t + 1) = Icell_{i,j} (t + 1)$$

(19)

Here, $\eta \in rand[0,1]$ presents the growing speed.

In the search process of invasive cells, an exploration is achieved. Formula (17), (18) means that an invasive cell visits a more larger search region nearby the proliferative cell. Especially, for the multimodal problems, in the late search process, many proliferative cells maybe obtained from different local optimum. So invasive cell ensures that they can jump out the local optimum and find the best position; it is to say, they can enhance the exploration ability of our algorithm. In addition, formula (19) means that some bad solution (dying cell) can be replaced by the best solution (invasive cell).

• 5. Random walk of cells

Each cell in tumor has a cycle of life. When a cell is not affected by other chemotaxis within the specified cycle of life, the cell performs a random walk as formula (20). Here, $newCell_{i,j} (t)$ presents a new cell using formula (17).

$$Cell(t + 1)_{i,j} (t + 1) = Cell_{i,j} (t) + \lambda \cdot \left( {\frac{{newCell_{i,j} (t)}}{{||newCell_{i,1:D} (t)||}}} \right)$$

(20)

where $||newCell_{i,j:D} (t)||$ is an Euclidean norm. $\lambda \in rand[ - 1,1]$.

At here, the random walk can be seen as an exploitation. $\frac{{newCell_{i,j} (t)}}{{||newCell_{i,1:D} (t)||}}$ represents a small value in the search region. So the random walk can be seen as a small fluctuation for all the tumor cells. It is to say that each tumor cell can visit its neighbor region.

4.2 Intrusive tumor growth algorithms

We implement an invasive tumor growth optimization algorithm according to the mechanism of tumor growth. There are the main five steps in our algorithm: proliferative cell growth, quiescent cell growth, dying cell growth, invasive cell growth and the random walk of all the tumor cells. Details shows as Fig. 4. In Fig. 4, step 1–2 implements the initialization like other meta-heuristic algorithms. Step 3–4 creates the three subpopulations: proliferative cell subpopulation, quiescent cell subpopulation, and dying cell subpopulation. Firstly, proliferative cell growth is implemented as the step 5. For $rand < \frac{t}{T}$, t is the number of the current iteration, and T is the number of total iteration. It means that proliferative cell grows using a higher probability with a liner function. This easily helps proliferative cell to jump out of the local optimum. Formula (7)–(12) enhances the searching ability of proliferative cell by Levy flight. Secondly, quiescent cell growth is implemented as the step 7. Many ‘leaders’ (proliferative cells) are chosen randomly to guide the quiescent cell for the best search direction. Historical position and current position of proliferative cell are used alternately, which enhances the diversity of the algorithm. Third, dying cell growth is implemented as step 9. The proliferative cell and the quiescent cell are chosen randomly to lead the dying cell for the better search. Fourth, invasive cell growth is implemented as step 11. It achieves the balance of the life and death of tumor. The old solution (position of the dying cell) can be replaced by a better solution (the position of the invasive cell), which can enhance the search speed of the algorithm. Fifth, random walk is used for all the tumor cells as step 6, 8, 10. θ is a threshold value, generally, it is an integer. It controls the random walk frequency. The random walk method can help the algorithm jump out of the local optimum.

Fig. 4

Invasive tumor growth algorithm

5 Experiments analysis

In order to solve the data clustering problem, object function shown as formula (1) was used as fitness function of meta-heuristic algorithms. The data clustering problem can be seen to find the best centers for all the clusters. For our algorithm, the position of each tumor cell (solution) is encoded by a link of the centers of all the clusters.

Our experiments are divided into two categories: (1) We choose the benchmark functions for comparison with other algorithms to verify the performance of our proposed algorithm. (2) To verify the performance of our algorithm, we use six benchmark datasets to compare our algorithm with other algorithms for data clustering.

5.1 Comparison of CEC 2005 and CEC 2008

We choose the CEC 2005 [44] and CEC 2008 [45] dataset to verify the performance of the proposed algorithm (ITGO), which are compared with the well-known algorithm such as PSO, DE, GSA, CLPSO, cPSO, rcGA, and TLBO. We choose 15 functions from CEC 2005 with low dimension and five functions from CEC 2008 with high dimension. F1–F4, F16, and F17 are unimodal functions and F5–F15, F18, F19, and F20 are multimodal functions. These functions are shifted or rotated or separable or non-separable or both. So, the 20 functions we choose can reflect the reality problem better. Details are shown in Table 1. Figure 5 shows F11 and F14 function, which are multimodal.

Table 1 Details of CEC2005 and CEC2008

Fig. 5

Benchmark problems. a F11 rotated hybrid comp. Fn 1, b F14 rotated hybrid comp. Fn 4

For purposes of avoiding any negative effects of the structure of the initial population during the tests, the benchmark problems are solved 20 times by using a different initial population each time. Population size is 30 for all the algorithms. The data such as the mean, standard deviation obtained as a result of the tests have been saved for detailed statistical analysis.

For these algorithms, parameter settings are as followings:

• 1. PSO, c1 = c2 = 2 and inertia factor (w) is decreasing linearly from 0.9 to 0.2 [46].

• 2. DE, F = 0.5, CR = 0.5 [9].

• 3. GSA, Rpower = 2, Rnorm = 2, ElitistCheck = 1 as in [15].

• 4. CLPSO [47], $c = 1.49335,\,m = 0,\,p_{c} = 0.5 \cdot \left( {e^{t} - e^{t(1)} } \right)/\left( {e^{{t(p_{s} )}} - e^{t(1)} } \right),t = 0.5 \cdot \left( {0:\frac{1}{{p_{s} - 1}}:1} \right)$ as in the Matlab code given in [48].

• 5. cPSO, $Np = 300,\,\varphi_{1} = - 0.2,\,\varphi_{2} = - 0.007,\,\varphi_{3} = 3.74,\,\gamma_{1} = 1,\,\gamma_{2} = 1$ as in [49].

• 6. rcGA, $Np = 300$ [50].

• 7. TLBO with no parameter [13]. Matlab Code provided by author in [51].

• 8. ITGO, c = 8, d = 8, $beta = 1.5$. C is the cycle size of the cell; d is the number of neighbors in quiescent cells; $beta$ is the parameter of Levy flight.

The tests of all algorithms are rooted on a uniform standard:

• 1. For CEC2005, dimension is 10, population size is 30, MAX_FES (total fitness evaluations number) = 1e5 [44]

• 2. For CEC2008, dimension is 100, population size is 30, MAX_FES = 5e5 [45]

• 3. Pre-determined stopping criteria: If the absolute error obtained by the algorithm is smaller than err = 1e−8, then stop.

The Wilcoxon’s signed-rank test with Bonferroni–Holm correction method and the Friedman’s test [52] were used to compare ITGO with other algorithms. When using Wilcoxon’s test in our experimental study, the first step is to compute the R+ and R− related to the comparisons between ITGO and the rest of algorithms, then p values can be computed. The null hypothesis H0 was used for the Wilcoxon’s signed-rank tests for purposes of this paper. The statistical significance value used to test H0 hypothesis is τ = 0.05. The Bonferroni–Holm procedure adjusts the value of τ in a step-down manner. Let $p_{1} ,p_{2} , \ldots ,p_{k - 1}$ be the ordered p values (from smallest to largest), so that $p_{1} \le p_{2} \le , \ldots , \le p_{k - 1} ,$ and let $H_{1} ,H_{2} , \ldots ,H_{k - 1}$ be the corresponding hypotheses. The Bonferroni–Holm procedure rejects H ₁ to H _i−1 if i is the smallest integer such that $p_{i} > \alpha /(k - 1).$ In addition, Friedman’s test was used for a multiple comparisons test that aims to detect significant differences between the behaviors of two or more algorithms. At the end, average ranks are used to comparison.

In Tables 2 and 3, we compare ITGO to the well-known algorithm including PSO, DE, GSA, CLPSO, cPSO, rcGA, and TLBO by the means and standard of the error value. Bold font means the winner. Table 4 shows the comparison results by Wilcoxon’s signed-rank test; ‘+’ means the algorithm is winner, ‘=’ means the two algorithms are equal, and ‘−’ means the algorithm is lost. The statistical results show the winner number, equation number, and lost number as follows:

Table 2 Comparison with ITGO and PSO, DE, and GSA

Table 3 Comparison with ITGO and CLPSO, cPSO, QIGSA, rcGA, and TLBO

Table 4 Comparison results by Wilcoxon’s signed-rank test

• ITGO versus PSO:20/0/0

• ITGO versus DE: 17/0/3

• ITGO versus GSA:16/0/4

• ITGO versus CLPSO:18/1/1

• ITGO versus cPSO:20/0/0

• ITGO versus rcGA:16/0/4

• ITGO versus TLBO:15/0/5

We can see that ITGO algorithm has best performance than other algorithms. Table 5 shows the comparison results by Wilcoxon’s signed-rank test with Bonferroni–Holm correction. For ITGO vs PSO, cPSO, DE, CLPSO, TLBO, GSA and rcGA, the p values are 8.85e−5, 8.85e−5, 2.53e−4, 2.54e−4, 4.63e−4, 8.91e−4, 1.01e−3, and 2.49e−3,  which are less than α/i values. So the hypothesis H0 was rejected. In other words, ITGO algorithm has better performance than other algorithm. Tables 6 and 7 show the comparison results by Friedman test. Average ranks show that ITGO is better than other algorithms.

Table 5 Comparison with ITGO and other algorithms using Wilcoxon’s signed-rank test and Bonferroni–Holm correction (means)

Table 6 Average ranks of eight algorithms by Friedman test (means)

Table 7 Results of Friedman test for eight algorithms by CEC 2005 and CEC 2008

In order to understand the characteristic of our algorithm, we analyze the experimental results deeply. For F1–F4 functions, they are unimodal functions. These functions are used to verify the local search ability of algorithms. From Tables 2 and 3, we can see that the performance of rcGA is better than others for F1 function, and TLBO has better performance than others for F2, F3, and F4. Though ITGO is not the best one, its performance is better than PSO, GSA, CLPSO, and cPSO for F1 and better than PSO, DE, GSA, CLPSO, cPSO, and rcGA for F2 and F3. Sometimes, one algorithm has so fast convergence speed for unimodal problems, and it is not a good thing, because it is perhaps easy to fall into the local optimum for multimodal problems. So good algorithms must consider it. F5–F15 functions are multimodal problems. These functions are used to verify the global search ability of algorithms. From Table 2, we can see that the performance of ITGO is better than PSO, DE and GSA for F5, F9, F10, F13, F14, and F15, while the performance of ITGO is better than CLPSO, cPSO, rcGA, and TLBO for F7, F8, F9, F12, F13, and F14. The results show that ITGO has powerful global search ability than many other algorithms for multimodal problems. Especially, F1–F15 functions only verify the performance of ITGO in low dimension (dimension = 10), so we verify the performance of ITGO for F16–F20 functions in high dimension (dimension = 100). From Tables 2 and 3, we can see that the performance of ITGO algorithm outperforms PSO, DE, GSA, CLPSO, CPSO, rcGA, and TLBO in high dimension including unimodal and multimodal functions. It is to say that our algorithm can solve more large complex problems.

5.2 Comparison with ITGO and improved PSO versions

In this test, we choose the 11 benchmark functions from the paper [44, 53]. Population size and maximum iteration number are set to 30 and 10,000 according to the suggestion of paper [53]. The benchmark functions are multimodal functions except for F1 and F6 function. In addition, F1–F5 are standard benchmark functions, F6–F9 are shifted functions, and F10–F11 are shifted rotated functions. Details can be seen in paper [53].

In Table 8, we compare ITGO to the currently improved algorithms including PSO-w [53], PSO-cf [53, 54, 55], UPSO [56], CLPSO [47], SG-PSO [53], and SP-PSO [53] by the means of the error value. Bold font means the winner. Table 9 shows the comparison results by Wilcoxon’s signed-rank test with Bonferroni–Holm correction. For ITGO versus PSO-w, PSO-cf, UPSO, CLPSO, SG-PSO, and SP-PSO, the p values are 0.003, 0.003, 0.003, 0.005, 0.005, and 0.016, which are less than α/i values. So the hypothesis H0 was rejected. In other words, ITGO algorithm has better performance than other algorithm. Tables 10 and 11 show the comparison results by Friedman test. Average ranks show that ITGO is better than other algorithms. Especially, from the results of Table 8, we can also see that the performance of ITGO is better than PSO-w, PSO-cf, UPSO, CLPSO, SG-PSO, and SP-PSO for F3, F4, F6, F7, F8, and F11 including standard or shifted or shifted rotated functions. It is to say that our algorithms can solve many different complex problems.

Table 8 Comparison with ITGO and other improved PSO version

Table 9 Comparison with ITGO and other improved PSO versions using Wilcoxon’s signed-rank test and Bonferroni–Holm correction (means)

Table 10 Average ranks of seven algorithms for data clustering dataset by Friedman test (means)

Table 11 Results of Friedman test for seven algorithms

5.3 Comparison for data clustering

We choose six benchmark datasets with different dimensions from the repository of the machine learning databases [57], namely, iris, wine, glass, Wisconsin breast cancer, vowel, and contraceptive method choice (CMC). This dataset has been used to solve the data clustering problem widely in other algorithms [16, 33–35].

The iris dataset contains three categories, where each category refers to a type of iris plant. In the iris dataset, there are four attributes, which are sepal length in cm, sepal width in cm, petal length in cm, and petal width in cm.

The wine dataset contains chemical analyses of wines derived from three different cultivars, with 13 attributes, namely, alcohol, malic acid, ash, alkalinity of ash, magnesium, total phenols, flavonoids, non-flavonoid phenols, proanthocyanins, color intensity, hue, OD280/OD315 of diluted wines, and praline.

The glass identification dataset contains six different types of glass, which are, float-processed building windows, non-float-processed building windows, float-processed vehicle windows, containers, tableware, and headlamps. There are nine attributes, namely, refractive index, sodium, magnesium, aluminum, silicon, potassium, calcium, barium, and iron.

The Wisconsin breast cancer dataset consists of two categories in the data: malignant and benign. There are nine features: clump thickness, cell size uniformity, cell shape uniformity, marginal adhesion, single epithelial cell size, bare nuclei, bland chromatin, normal nucleoli, and mitoses.

The vowel dataset consists of 871 patterns (rows). There are six overlapping vowel classes (Indian Telugu vowel) and three input features (formant frequencies).

The CMC dataset is a subset of the 1987 National Indonesia Contraceptive Prevalence Survey. The objects are married women who either were not pregnant or did not know if they were at the time of interview. The problem involves predicting the choice of the current contraceptive method of a woman based on her demographic and socioeconomic characteristics.

Table 12 summarizes the main characteristics of the used six datasets. The performance of the ITGO algorithm is compared against well-known and the most recent algorithms reported in the literature, including K-means [26], K-medoid, DE [9], GSA [28], and the TLBO [35]. In order to evaluate and compare the performance of the algorithms, criteria can been defined as follows: The distance between each data object and the center of each cluster can be found according to the formula (1). The smaller the sum of intra-cluster distances, the higher the quality of the clustering. So, the sum of intra-cluster distances is the evaluation values in our work, namely, fitness value for meta-heuristic algorithms. Each algorithm is run for 20 times independently, and the min, max value, means, standard, median for the fitness are used to comparison. In addition, box plots are used to verify the performance of the algorithms. Box plots can be very convenient to compare the performance of algorithms in graphical form. In a typical case, endpoint I of the box is on the quarter point, the length of the box is the distance of the quarter point 3 plus quarter point 1, median number marks with line, two dotted lines in the box (called a beard) extends to the maximum and minimum values, and discrete points can also be displayed in box.

Table 12 Details of six datasets

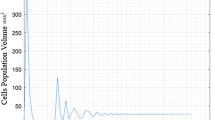
Table 13 shows the fitness values obtained by algorithms. For iris datasets, ITGO is better than K-medoid, K-means, DE, GSA, and TLBO according to the max, means and standard value. ITGO equals GSA by min and median value, and smaller than our algorithms. For wine datasets, ITGO is better than K-medoid, K-means, DE, GSA, and TLBO according to the max, means, standard value, and medians. For glass datasets, ITGO is better than other algorithms by the min and max value except for the means, SD, and median. For cancer and vowel datasets, ITGO is better than other algorithms by the min, max, means SD, and median value. For CMC dataset, ITGO is better than other algorithms, too. To verify the robustness, box plots are used in Fig. 6. The number 1, 2, 3, 4, 5, and 6 of the horizontal ordinate corresponds to the K-medoid, K-means, TLBO, DE, GSA, and ITGO algorithms. We can see that ITGO algorithm is superior to K-medoid, K-means, TLBO, DE, and GSA for the five datasets, except for the glass dataset. For glass dataset, ITGO algorithm is still better than TLBO, DE, and GSA algorithms. At the end, Fig. 7 shows the best results of ITGO algorithm for data clustering of the six datasets in three-dimensional space. Three features are chosen randomly from the six datasets. Tables 17, 18, 19, 20, 21, and 22 show the best center of clusters for the six datasets. Tables 14, 15, and 16 show the comparison results of ITGO for K-medoid, K-means, TLBO, DE and GSA using Wilcoxon signed-rank test and Bonferroni-Holm correction and Friedman test, which indicates that the performance of ITGO is better than other algorithms. In addition, the Fig. 8 shows the trajectory and the convergence curve of the first particle, in which changes of the first search agent in its first dimension can be observed. It can be seen that there are abrupt changes in the initial steps of iterations which are decreased gradually over the course of iterations. According to van den Bergh and Engelbrecht [58], this behavior can guarantee that a SI algorithm eventually convergences to a point in search space.

Fig. 6

Comparison results of five algorithms by box plot

Fig. 7

Results of data clustering by ITGO. a Iris, b wine, c glass, d cancer, e vowel, f CMC

Table 13 The sum of intra-cluster distances obtained by algorithms on different datasets

Table 14 Comparison with ITGO and other algorithms for data clustering dataset using Wilcoxon signed-rank test and Bonferroni–Holm correction (means)

Table 15 Average ranks of six algorithms for data clustering dataset by Friedman test (means)

Fig. 8

Trajectory of one of the search agents in one of the dimension as well as the convergence curves

Table 16 Results of Friedman test for six algorithms

Table 17 The best cluster center of Iris dataset obtained by ITGO

Table 18 The best cluster center of wine dataset obtained by ITGO

Table 19 The best cluster center of glass dataset obtained by ITGO

Table 20 The best cluster center of Wisconsin breast cancer dataset obtained by ITGO

Table 21 The best cluster center of vowel dataset obtained by ITGO

Table 22 The best cluster center of CMC dataset obtained by ITGO

5.4 The computation complexity of ITGO algorithms

In this section, we use the method proposed in [59] for the computational complexity. The computational complexity of the proposed method depends on the number of iterations, the number of cells (particles), the number of fitness evaluations, the repartition of tumor, the mechanism of proliferative cell growth, the mechanism of quiescent cell growth, the mechanism of dying cell growth, the mechanism of invasive cell growth, and the random walk mechanism. So, the overall computational complexity is as follows:

$$O\left( {ITGO} \right) = O\left( {T*\left( {O\left( {repartition} \right) + O\left( {proliferative \, cell} \right) + O\left( {quiescent \, cell} \right) + O\left( {dying \, cell} \right) + \, O\left( {invasive \, cell} \right) \, + O\left( {random \, walk} \right)} \right)} \right)$$

where T is the maximum number of iterations. The computational complexity of the repartition of tumor cells is of O(p * p) in the worst. p is the number of population size. We utilized quicksort to the repartition of tumor cells, and the computational complexity of the repartition is of O(p * logp) in the best case. The computational complexity of proliferative cell growth is of O(npFes) in the implementation where npFes is the number of fitness evaluations for the proliferative cell. Note that the npFes belong to [0, Max_num], Max_num is the number of the proliferative cell. Because the proliferative cell operator is used due to the probability $rand < \frac{t}{T}$, t is the current number of iteration and T is the max number of iteration. The computational complexity of quiescent cell growth is of O(qpFes+qp*qp) in the implementation where qp is the number of the implemented quiescent cell and qpFes is the number of fitness evaluations for quiescent cell. To choose the best two neighbors of quiescent cell, sort operator should be used. We utilized quicksort to the quiescent cell growth, the computational complexity is of O(qpFes+qp * log(qp)) in the best case. The computational complexity of dying cell growth is of O(dpFes) in the implementation where dpFes is the number of fitness evaluations for dying cell. The computational complexity of invasive cell growth is of O(qpFes/2) in the implementation where qpFes/2 is the number of fitness evaluations for invasive cell. Since half of the dying cells are replaced by the invasive cells, the computational complexity of random walk is of O(rwFes) in the implementation where rwFes is the number of fitness evaluations by random walk. Therefore, the final computational complexity of the proposed algorithm is as follows:

$$O\left( {ITGO} \right) = O\left( {T*\left( {O\left( {p*logp + O\left( {npFes} \right) + O\left( {qpFes + qp*log\left( {qp} \right)} \right)} \right) + O\left( {dpFes} \right) + O\left( {dpFes/2} \right)} \right) \, + O\left( {rwFes}\right)}\right))$$

where T is the maximum number of iterations, p is the population size, npFes is the number of fitness evaluations for the proliferative cell, qpFes is the number of fitness evaluations for the quiescent cell, qp is the number of quiescent cell, dpFes is the number of fitness evaluations for the dying cell, and rwFes is the number of fitness evaluations by the random walk.

6 Parameter tuning

Three parameters were used in ITGO, namely, beta, c, and d. Nevertheless, a complete evaluation on all possible combinations of these parameters is impractical. The parameter tuning strategy, as reported in [60, 61], is used to find an appropriate parameter combination of ITGO for the good performances. Two multimodal functions (F8 and F15) are chosen and beta ranges in [0.8, 1.8], c ranges in [1, 10], whereas d ranges in [3, 12]. We first initialize the parameter combination of [beta, c, d] as the mean values of their respective lower and upper boundary values, i.e., [1.3, 5, 8], c and d are integer. Based on this initial combination, we adjust the parameters one at a time. We first vary parameter beta from 0.8 to 1.8 with c and d are fixed. Then we choose the best beta value due to the best fitness value. In the next step, we fix the beta and d value, adjust c from 1 to 10. At the end, we vary parameter d value from 3 to 12 as so on.

From Tables 23 and 24, the simulation results show that beta value should be chosen as 1.5, or 1.6 or 1.7 for function 8 and 1.5 for function 15. Therefore, we set beta value as 1.5. We use new beta value and fixed d value to adjust c value from 1 to 10. From Tables 25 and 26, we can see that c should be chosen as 4 or 8 or 9 for function 8 and 7 or 8 for function 15. So, we set c value as 8, because when c = 8, the function 8 and function 15 can obtain better fitness value, too. At the end, we set the beta value as 1.5 and c value as 8, adjust d value from 3 to 12. From Tables 27 and 28, we can see that d value should be chosen as 8 for function 8 and 4 or 8 or 9 for function 15. So we set d value as 8. Then the parameter tuning process is completed. The experimental findings suggest that we can set the parameter combination [beat, c, d] as [1.5, 8, 8] in the performance evaluation.

Table 23 Results of beta parameter for shifted rotated Ackley’s Function in CEC2005

Table 24 Results of beta parameter for hybrid composition function 1 in CEC2005

Table 25 Results of c parameter for shifted rotated Ackley’s Function in CEC2005

Table 26 Results of c parameter for hybrid composition function 1 in CEC2005

Table 27 Results of d parameter for shifted rotated Ackley’s function in CEC2005

Table 28 Results of d parameter for hybrid composition function 1 in CEC2005

7 Discussions

In this section, we discuss some aspects of the proposed algorithm (ITGO). Though, some operations are similar to the operations of particle swarm optimization, such as the operation of the quiescent cell and dying cell and some operations are similar to the DE or rcGA, because the cross operation is used; it is different from them. Firstly, there are many ‘leaders’ (chosen randomly from the proliferative cell group) which guide other agents; secondly, the cross operation is different from DE or rcGA. In addition, there are many new operations such as the invasive behavior of the proliferative cell with the Levy distribution, the random walk operations, and the search of invasive cell. Especially, we achieved the interaction of the different subpopulations, which can enhance the diversity of the proposed algorithm. In addition, the analysis of the experimental results shows that the proposed algorithms has fast convergence speed for many multimodal or high dimension problems. Standard value shows the stability of our algorithm. It is shown that our algorithm is convenient and efficient to solve the data clustering problems. Then we analyze the computation complexity, the proposed algorithm is ranked third, maybe due to other computation such as the levy distribution and the neighbor numbers of quiescent cell. Though, there are some disadvantages of the proposed algorithm such as the complexity of realization and parameter tuning, there are many advantages such as, fast convergence speed, better stability, and better search ability.

8 Conclusion

In this paper, we proposed a new meta-heuristic algorithm called ‘ITGO’ for data cluttering. According to the mechanism of tumor growth, tumor cells can be divided into five types, namely: invasive cell, proliferative cell, quiescent cell, dying cell, and necrotic cell. In order to implement the invasive tumor growth optimization, five different behaviors occur in tumor for different cells: invasive cell growth, proliferative cell growth, quiescent cell growth, dying cell growth, and random walk. Necrotic cell has been dead, so it does not grow. Many interactions among invasive cell, proliferative cell, quiescent cell and dying cell enhance the search ability of our algorithm. Then, we use CEC 2005 and CEC 2008 benchmark functions to verify the performance of our algorithm, compared with the well-known algorithms including PSO, DE, GSA, CLPSO, cPSO, PSO-w, PSO-cf, UPSO, SG-PSO, SP-PSO rcGA, and TLBO by the Wilcoxon’s signed-rank test with Bonferroni–Holm correction method and the Friedman’s test. At the end, six benchmark datasets are chosen to verify the performance of our algorithm for data clustering, compared with K-means, DE, GSA, and TLBO. Experimental results show that ITGO algorithm can not only be used to solve data clustering problem better, but also be used to solve other optimization problems, which can be widely used in other engineering and science fields. In future, many improvements in ITGO can be started due to the disadvantages of it, such as the better operations and better parameter tuning method.