1 Introduction

A brain–computer interface (BCI) provides a direct communication pathway between the brain and an external device that is independent from any muscular signals. Thus, BCIs enable users with severe motor disabilities to use their brain signals for communication and control [1–3]. Most BCIs use electroencephalography (EEG) to measure brain signals due to its low cost and high temporal resolution [4]. Among EEG-based BCIs, the detection of motor imagery has attracted increased attention in recent years, which is neuro-physiologically based on the detection of changes in sensorimotor rhythms called event-related desynchronization (ERD) or synchronization (ERS) during motor imagery [4–6].

Recently, it was shown that motor imagery-based BCI is effective in restoring upper extremities motor function in stroke [7–10]. To benefit from BCI in the stroke rehabilitation, the accurate and reliable detection of ERD/ERS patterns is important. However, detecting ERD/ERS patterns is generally impeded by poor spatial specifications of EEG due to the volume conduction [11] and different sources of noise and artifacts [12]. Moreover, the discriminative spatio-spectral characteristics of motor imagery vary from one person to another [13]. Thus, extracting discriminative spatio-spectral features is a challenging issue for EEG-based BCIs. Nevertheless, the common spatial patterns (CSP) algorithm has been shown to be effective in discriminating two classes of motor imagery tasks [12, 14]. Despite its effectiveness and widespread use, the CSP is highly sensitive to noise and artifacts [15], and its performance greatly depends on the operational frequency band [12].

To address the sensitivity to noise and artifacts of the CSP algorithm, regularization algorithms were introduced to robustify it [16–19]. In [19], it was shown that regularizing the CSP objective function generally outperformed regularizing the estimates of the covariance matrices. Recently, the sparse common spatial patterns (SCSP) algorithm was proposed by inducing sparsity in the CSP spatial filters [20, 21]. The proposed SCSP algorithm optimizes the spatial filters to emphasize on the regions that have high variances between the classes, and attenuates the regions with low or irregular variances, which can be due to noise or artifacts. Stationary CSP (sCSP) is another algorithm which regularized CSP by penalizing the variations between covariance matrices [36]. In [36], it is shown that sCSP outperforms several existing regularized CSP algorithms.

To address the dependency on the operational frequency band of the CSP algorithm, several spatio-spectral algorithms were introduced. Common spatio-spectral patterns (CSSP) optimized a first-order finite impulse response (FIR) temporal filter with the CSP algorithm [22]. To improve the flexibility of CSSP, common sparse spectral spatial patterns (CSSSP) were then proposed by simultaneous optimization of an arbitrary FIR filter within the CSP analysis [23]. Subsequently, the spectrally weighted common spatial patterns (SPEC-CSP) algorithm [24] and the iterative spatio-spectral patterns learning (ISSPL) [25] algorithm were proposed to further improve CSSP [25]. Recently, the filter bank common spatial patterns (FBCSP) algorithm [26] was proposed that combined a filter bank framework with CSP to select the most discriminative features using a mutual information-based criterion [27]. The FBCSP algorithm was used as the basis of all the winning algorithms in the EEG category of the BCI competition IV.

However, to the best of the authors knowledge, the issues of the sensitivity to noise and artifacts and the dependency on the operational frequency band of the CSP algorithm have not been simultaneously addressed yet. To address these two issues simultaneously, this paper proposes a novel sparse spatio-spectral filtering algorithm optimized by a mutual information-based approach. The proposed OSSSF algorithm decomposes EEG data into an array of pass bands and subsequently performs the sparse CSP optimization in each band. In the proposed algorithm, the optimal regularization parameters are directly selected using a new mutual information-based approach, instead of using the cross-validation approach that is computationally intractable in a filter bank framework (for more explanation, see Sect. 2.2)

In order to evaluate the performance of the proposed algorithm, two datasets are used: the publicly available dataset IVa from BCI competition III [28] and the data collected from 11 stroke patients [9]. The classification accuracies of the proposed OSSSF algorithm are also compared with four existing algorithms, namely CSP [12], sCSP [36], SCSP [20] and FBCSP [27].

The remainder of this paper is organized as follows: Sect. 2 describes the proposed method. The applied datasets and the performed experiments are explained in Sect. 3, Sect. 4 presents the experimental results and finally, Sect. 5 concludes the paper.

2 Methodology

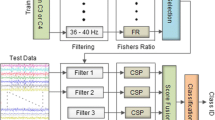
The architecture of the proposed optimized sparse spatio-spectral filters (OSSSF) is illustrated in Fig. 1. It consecutively performs spectral filtering and sparse spatial filtering to extract and select the most discriminative features for motor imagery classification. The proposed methodology comprises the following steps:

  • Step 1-Spectral filtering: This step uses a filter bank that decomposes the EEG data using nine equal bandwidth filters, namely 4−8, 8−12,…, 36−40 Hz as proposed in [26, 27]. These frequency ranges cover most of the manually or heuristically selected settings used in the literature.

  • Step 2-Sparse spatial filtering: In this step, the EEG data from each frequency band are spatially filtered using optimal sparse CSP filters. Let \({\bf X}_{\bf b} \in {\bf R}^{N_{\rm c} \times S}\) denote a single-trial EEG data from the bth band-pass filter, where N c and S denote the number of channels and the number of measurement samples, respectively. A linear projection transforms X b to the spatially filtered Z b as

    $${\bf Z}_{\bf b}={\bf W}^{*}_{\bf b}{\bf X}_{\bf b},$$
    (1)

    where each row of the transformation matrix \({\bf W} ^{*}_{\bf b} \in {\bf R}^{2m \times N_{\rm c}}\) indicates one of the 2m optimal sparse spatial filters. The details on finding the optimal sparse spatial filters corresponding to each frequency band are explained in Sects. 2.1 and 2.2.

  • Step 3-Feature extraction: The sparse spatio-spectrally filtered EEG data are used to determine the features associated with each frequency range. Based on the Ramoser formula [29], the features of the kth EEG trial from the bth band-pass filter are given by

    $${\bf v}_{b,k}={\rm log}({\rm diag} ({\bf Z}_{b,k}{\bf Z}^{\rm T}_{b,k})/{\rm trace} [{\bf Z}_{b,k}{\bf Z}^{\rm T}_{b,k}]),$$
    (2)

    where \({\bf v}_{b,k} \in {\bf R}^{1\times 2m};\) diag(.) returns the diagonal elements of the square matrix; trace[.] returns the sum of the diagonal elements of the square matrix; and the superscript T denotes the transpose operator. Since nine frequency bands are used, the feature vector for the kth trial is formed as

    $${\bf V}_{k}=[{\bf v}_{1,k}, {\bf v}_{2,k}, \ldots, {\bf v}_{9,k}],$$
    (3)

    where \({\bf V}_{k} \in {\bf R}^{1\times 18m}\).

  • Step 4-Feature selection: The last step selects the most discriminative features of the feature vector V. Various feature selection algorithms can be used in this step. The study presented in [26] showed that the mutual information-based best individual feature (MIBIF) algorithm [27] yielded better 10 × 10-fold cross-validation results than other considered feature selection algorithms. Moreover, the study showed that selecting four pairs of the best individual features using MIBIF yielded a higher averaged accuracy compared to the different numbers of selected features [26]. Thus, in this work, the MIBIF algorithm is used to select four pairs of features.

Fig. 1
figure 1

Architecture of the proposed OSSSF algorithm

Full size image

2.1 Sparse spatial filters

The second step of the proposed algorithm performs sparse spatial filtering using the optimized SCSP filters. This subsection describes details of the SCSP filters, and the next subsection describes the proposed mutual information-based approach to find the optimum SCSP filters.

The CSP algorithm [12, 14] is an effective technique in discriminating two classes of EEG data. The CSP algorithm linearly transforms the band-pass filtered EEG data to a spatially filtered space, such that the variance of one class is maximized while the variance of the other class is minimized. The CSP transformation matrix corresponding to the bth band-pass filter, W b, is generally computed by solving the eigenvalue decomposition problem:

$${\bf C}_{b,1}{\bf W}_{b} = \left({\bf C}_{b,1} + {\bf C}_{b,2} \right){\bf W}_{b}{\bf D},$$
(4)

where C b,1 and C b,2 are, respectively, the average covariance matrices of the band-passed EEG data of each class; D is the diagonal matrix that contains the eigenvalues of (C b,1 + C b,2)−1 C b,1. Usually, only the first and the last m rows of W b are used as the most discriminative filters to perform spatial filtering [12].

Despite the popularity and efficiency of the CSP algorithm, the CSP algorithm which is based on the covariance matrices of EEG trials can be distorted by artifacts and noise [15]. This issue motivated an approach that involves sparsifying the CSP spatial filters to emphasize on the regions with high variances between the classes and to attenuate the regions with low or irregular variances. To sparsify the CSP spatial filters of the bth band, first the CSP algorithm is reformulated as an optimization problem proposed in our previous work [21]:

$$\begin{aligned} &\underset{{\bf w}_{b,i}}{\hbox{min}}\sum_{i=1}^{i=m} {\bf w}_{b,i}{\bf C}_{b,2}{\bf w}_{b,i}^{\rm T} + \sum_{i=m+1}^{i=2m} {\bf w}_{b,i}{\bf C}_{b,1}{\bf w}_{b,i}^{\rm T}\\ &\quad\hbox{Subject to:}\;\;\;{\bf w}_{b,i}({\bf C}_{b,1} + {\bf C}_{b,2}){\bf w}_{b,i}^{\rm T}= 1\;\;\;\;\;i= \{1,2,{\ldots}, 2m\}\\ &\quad{\bf w}_{b,i}({\bf C}_{b,1} + {\bf C}_{b,2}){\bf w}_{b,j}^{\rm T}= 0\;\;\;\;\;i,j =\{1,2,{\ldots}, 2m\}\;\;\;\;\;i\neq j, \end{aligned}$$
(5)

where the unknown weights \({\bf w}_{b,i} \in {\bf R}^{1 \times N_{\rm c}} , i=\{1,..,2m\},\) respectively, denote the first and the last m rows of the CSP projection matrix from the bth band-pass filter. In this optimization, the constraints keep the covariance matrices of the both projected classes diagonal and uncorrelated.

Sparsity can be induced in the CSP algorithm by adding an l 0 norm regularization term into the optimization problem given in (5). \(\|{\bf x}\|_0,\) the l 0 norm of x, is the measure giving the number of nonzero elements of x. However, solving a problem with the l 0 norm is combinatorial in nature and thus computationally prohibitive. Furthermore, since an infinitesimal value is treated the same as a large value, the presence of noise in the data may render the l 0 norm completely ineffective in inducing sparsity [30]. Therefore, instead of the l 0-norm, the approximation below is used to measure the sparsity [21]:

$$\|{\bf x}\|_0\longrightarrow\frac{\|{\bf x}\|_1}{\|{\bf x}\|_2},$$
(6)

where \(\|{\bf x}\|_k=(\sum_{i=1}^{n}|{\bf x}_i|^{k})^{1/k}\) for k equal to either 1 or 2, and n denotes the total number of elements of the vector x. For the sparsest possible vector whereby, only a single element is nonzero \(\frac{\|{\bf x}\|_1}{\|{\bf x}\|_2}\) equals to one, whereas for a vector with all equal nonzero elements \(\frac{\|{\bf x}\|_1}{\|{\bf x}\|_2}\) equals to √n. The proposed SCSP algorithm is then formulated as:

$$\begin{aligned} &\underset{{\bf w}_{b,i}}{\hbox{min}}\;\;\;( 1 - r )\left( \sum_{i=1}^{i=m}{\bf w}_{b,i}{\bf C}_{b,2}{\bf w}_{b,i}^{\rm T} + \sum_{i=m+1}^{i=2m}{\bf w}_{b,i}{\bf C}_{b,1}{\bf w}_{b,i}^{\rm T}\right) + r \sum_{i=1}^{i=2m} \frac{\|{\bf w}_{b,i}\|_1}{\|{\bf w}_{b,i}\|_2}\\ &\hbox{Subject to:}\;\;\;{\bf w}_{b,i}({\bf C}_{b,1} + {\bf C}_{b,2}){\bf w}_{b,i}^{\rm T}= 1\;\;\;\;\;i= \{1,2,{\ldots},2m\}\\ &{\bf w}_{b,i}({\bf C}_{b,1} + {\bf C}_{b,2}){\bf w}_{b,j}^{\rm T}= 0\;\;\;\;\;i,j =\{1,2,{\ldots},2m\}\;\;\;\;\;i\neq j, \end{aligned}$$
(7)

where r (0 ≤ r ≤ 1) is a regularization parameter that controls the sparsity and the classification accuracy. When r = 0, the solution is essentially the same as the CSP algorithm.

The SCSP algorithm is a nonlinear optimization problem, and due to the equality constraints, it is a nonconvex optimization problem. It is solved using several methods such as sequential quadratic programming (SQP) and augmented Lagrangian methods [31]. In this study, for r ≠ 0, spatial filters obtained from the CSP algorithm are used as the initial point.

2.2 Optimizing sparse spatial filters using mutual information

Choosing a suitable value for the regularization parameter r in (7) is a challenging issue in the proposed algorithm. A larger value of r results in more sparse spatial filters, but may decrease the accuracy because some useful information is lost. Therefore, optimal r values should be chosen in a way to yield more efficient features.

The existing regularized CSP algorithms generally use the cross-validation method on the train data to automatically select the optimal regularization parameters [19]. Thus, a set of candidates is considered for the regularization parameter. For each candidate, the corresponding regularized CSP filters are calculated and then evaluated using m × n-fold cross-validation on the train data. Finally, the candidate yielding the highest average m × n-fold cross-validation accuracy is selected as the regularization parameter. However, performing m × n-fold cross-validation for a set of different regularization parameters is computationally intensive. Particularly, in the proposed filter bank framework, the problem is more pronounced due to the use of a separate SCSP for each band, since the value of the regularization parameter may differ from band to band. As an illustration, if five different r values (candidates) were to be evaluated for each SCSP of the nine frequency bands, the m × n-fold cross-validation should be performed for 59 different combinations. Thus, selecting the optimal regularization parameters using the cross-validation approach is computationally intractable in a filter bank framework.

To address this issue of computationally intractable approach, this paper proposes a mutual information-based algorithm to directly select the r values from a predefined set. Mutual information is a nonlinear measure of statistical dependence based on information theory [32]. Indeed, in this work, the r value is optimized by maximizing the mutual information between the feature vectors obtained from the sparse spatio-spectral filters and the corresponding class labels. Based on the proposed algorithm, the optimal r value and consequently the optimal SCSP filters from the bth band-pass filter are found as follows:

  1. 1.

    For each r value from a predefined set \(\mathcal{R}, r \in \mathcal{R} = \{r_{1},r_{2},{\ldots},r_{n}\},\) obtain the corresponding sparse spatial filters \({w}^{r}_{b,i}, i = \{1,{\ldots},2m\},\) from the bth band by solving (7).

  2. 2.

    Initialize the set of features \({\overline{\bf F}}_b = [{\bf F}_{b,r_{1}} ,{\bf F}_{b,r_{2}},{\ldots}, {\bf F}_{b,r_{n}}]\) as given in (2) from the training data, where \({\bf F}_{b,r_{j}}\in{\bf R}^{n_{\rm t} \times 2m}\) denotes the features obtained from SCSP filters when r = r j , and n t denotes the total number of training trials. In this work, the ith column vector of F b,r j is presented as f b,r j, i .

  3. 3.

    Compute the mutual information of each feature vector f b,r,i with the class label \(\varOmega = \{1,2\}.\) The mutual information of \({\bf f}_{b,r,i}, I\left({\bf f}_{b,r,i} ;\Upomega\right)\;\forall\;\; [\;r\in \mathcal{R}=\{r_{1},r_{2},\ldots,r_{n}\}, i=\{1,2,\ldots,2m\}],\) can be computed using [33]:

    $$I \left({\bf f}_{b,r,i} ;\varOmega \right)=H \left(\varOmega\right)-H \left(\varOmega|{\bf f}_{b,r,i} \right),$$
    (8)

    where \(H \left(\varOmega \right)\) is the entropy of the class label defined as:

    $$H \left(\varOmega \right)=-\sum_{\Upomega=1}^{2}P \left(\varOmega \right)\log _{2} P \left(\varOmega \right);$$
    (9)

    and the conditional entropy is

    $$\begin{aligned} H \left(\varOmega |{\bf f}_{b,r,i}\right) &=-\sum _{\varOmega =1}^{2}P\left(\varOmega |{\bf f}_{b,r,i} \right)\log _{2} P\left(\varOmega |{\bf f}_{b,r,i} \right)\\ &= - \sum_{\varOmega =1}^{2} \sum _{k=1}^{n_t} P \left(\varOmega |f_{b,r,i,k}\right)\log _{2} P \left(\varOmega |f_{b,r,i,k}\right), \end{aligned}$$
    (10)

    where f b,r,i,k is the ith feature value of the kth trial from F b,r , and P is the probability function. The conditional probability \(P \left(\varOmega |f_{b,r,i,k} \right)\) can be computed using Bayes rule given in (11) and (12).

    $$P \left(\Upomega|f_{b,r,i,k}\right)=(P \left(f_{b,r,i,k}|\varOmega \right)P \left(\varOmega \right))/P \left(f_{b,r,i,k}\right),$$
    (11)
    $$P \left(f_{b,r,i,k}\right)=\sum _{\varOmega =1}^{2}P \left(f_{b,r,i,k}|\varOmega \right) P \left(\varOmega \right).$$
    (12)

    The conditional probability \(P(f_{b,r,i,k}|\Upomega)\) can be estimated using the Parzen window algorithm [27], given by

    $$\hat{p}\left(f_{b,r,i,k} |\varOmega \right)=\frac{1}{n_{\varOmega } } \sum _{t\in I_{\Upomega}}\phi \left(f_{b,r,i,k}-f_{b,r,i,t} ,h\right),$$
    (13)

    where \(n_\Upomega\) is the number of trials in the training data belonging to class \(\Upomega; I_\Upomega\) is the set of indices of the training trials belonging to class \(\Upomega; f_{b,r,i,t}\) is the ith feature value of the tth trial from F b,r , and ϕ is a smoothing kernel function with a smoothing parameter h. The proposed algorithm employs the univariate Gaussian kernel given by

    $$\phi \left(y,h\right)=\frac{1}{\sqrt{2\pi } } e^{-\left(\frac{y^{2} }{2h^{2} } \right)},$$
    (14)

    and normal optimal smoothing strategy [34] given by

    $$h^{opt} =\left(\frac{4}{3n_\Upomega} \right)^{\frac{1}{5}} \sigma,$$
    (15)

    where σ denotes the standard deviation of y from (14).

  4. 4.

    Find the feature with the highest mutual information. The r value corresponding to this feature is selected as the optimal regularization parameter for SCSP from the bth frequency band. Mathematically, this step is performed as follows:

    $$I \left({\bf f}_{b,r^{*}_{b},i^{*}} ;\varOmega \right) ={\mathop{\mathop{\max}\limits_{i=\{1,2,{\ldots},2m\}}}\limits_{r\in {\mathcal{R}}=\{r_{1},r_{2},{\ldots},r_{n}\}}} I \left({\bf f}_{b,r,i} ;\varOmega \right),$$
    (16)

    where r * b denotes the optimal regularization parameter constructing the optimal SCSP filters from the bth frequency band (i.e., W * b ).

The relevance of computing mutual information to select the optimal r value is as follows: The mutual information \(I \left({\bf f}_{b,r,i} ;\varOmega \right)\) evaluates the reduction in uncertainty given by the feature vector f b,r,i . If the mutual information between the feature vector f b,r,i and the class labels \(\Upomega\) is large (small), it means that f b,r,i and \(\Upomega\) are closely (not closely) related [33]. Maximizing the objective function (16) results in selecting the optimal r value that yields the feature with the highest relevance with respect to the class labels. Note that the proposed method to select the optimal regularization parameter is not limited to the SCSP algorithm, but applicable for all regularized CSP algorithms that require automatic selection of regularized parameters.

The relevance of computing mutual information to select the optimal r value is as follows: The mutual information \(I \left({\bf f}_{b,r,i} ;\varOmega \right)\) evaluates the reduction in uncertainty given by the feature vector f b,r,i . If the mutual information between the feature vector f b,r,i and the class labels \(\Upomega\) is large (small), it means that f b,r,i and \(\Upomega\) are closely (not closely) related [33]. Maximizing the objective function (16) results in selecting the optimal r value that yields the feature with the highest relevance with respect to the class labels. Note that the proposed method to select the optimal regularization parameter is not limited to the SCSP algorithm, but applicable for all regularized CSP algorithms that require automatic selection of regularized parameters.

2.3 Feature extraction

Based on the optimal regularization value selected for each SCSP, the third step of the proposed OSSSF algorithm extracts the features from the bth band as \({\bf F}_{b,r^{*}_{b}}=[{\bf f}_{b,r^{*}_{b},1},{\bf f}_{b,r^{*}_{b},2},{\ldots},{\bf f}_{b,r^{*}_{b},2m}]\) where \({\bf F}_{b,r^{*}_{b}} \in {\bf R}^{n_{\rm t} \times 2m};\) n t and 2m denote the total number of the training trials and the sparse spatial filters, respectively. Since there are nine frequency bands, all the extracted features can be presented as \({\bf V}=[{\bf F}_{1,r^{*}_{1}},{\bf F}_{2,r^{*}_{2}},{\ldots},{\bf F}_{9,r^{*}_{9}}]\) where \({\bf V} \in {\bf R}^{n_{\rm t} \times18m}\).

2.4 MIBIF feature selection

The forth step of the OSSSF algorithm selects discriminative features from the features V using the MIBIF algorithm. The MIBIF sorts all the 18m extracted features in descending order of mutual information computed in step 2 and selects the first k features. Mathematically, this step is performed as follows till |S| = k

$$\begin{aligned} {\bf V}&={\bf V}\backslash {\bf f}_{b,r^{*}_{b},i}, {\bf S}={\bf S}\cup {\bf f}_{b,r^{*}_{b},i}|\\ I\left({\bf f}_{b,r^{*}_{b},i} ;\varOmega \right)&={\mathop{\mathop{\max }\limits_{i=1\ldots (2m)}}_{b=1\ldots 9}} I\left({\bf f}_{b,r^{*}_{b},i} ;\varOmega \right), \end{aligned}$$
(17)

where S is the set of the selected features; \ denotes set theoretic difference; ∪ denotes set union; and | denotes given the condition. The parameter k in the MIBIF algorithm denotes the number of best individual features to select. Based on the results presented in Sect. 4, k = 4 is used in this work.

3 Experiments

3.1 Data description

In this study, the EEG data of 16 subjects from two datasets were used. These two datasets are described as follows:

  1. 1.

    Dataset IVa [28] from BCI competition III [35]: This publicly available dataset comprised EEG data from five healthy subjects recorded using 118 channels. During the recording session, the subjects were instructed to perform one of two motor imagery tasks: right hand or foot. A total of 280 trials were available for each subject, where 168, 224, 84, 56 and 28 trials formed the training sets for subjects aa, al, av, aw and ay, respectively. Subsequently, the remaining trials formed the test sets. Since the objective of this work is not investigating the performance of the OSSSF algorithm on a small training set, the number of training trials was increased to 140 for subjects aw and ay

  2. 2.

    Neuro-rehabilitation dataset [9]: This dataset contained 25 channels EEG data from 11 hemiparetic stroke patients who used motor imagery-based BCI with robotic feedback neuro-rehabilitation (refer NCT00955838 in ClinincalTrials.gov). In this study, the data collected from the calibration phase of this dataset were used. This phase comprised 80 motor imagery trials of stroke-affected hand and 80 trials of the rest condition. Each trial lasted approximately 12 s. For each trial, the subject was first prepared with a visual cue for 2 s on the screen, and another visual cue then instructed the subject to perform either the motor imagery task or the rest for 4 s, followed by 6 s of resting.

3.2 Data processing

The performance of the proposed OSSSF algorithm was compared with three existing feature extraction algorithms, namely CSP, SCSP and FBCSP. The SCSP algorithm with two different approaches in selecting the optimal regularization parameters were considered: SCSP-CV, which uses the tenfold cross-validation approach, and SCSP-MI, which uses the proposed mutual information approach.

The EEG data from 0.5 to 2.5 s after the visual cue were used in all the above-mentioned algorithms. For the CSP algorithm, the EEG signals were band-pass filtered using 8–35 Hz elliptic filters, since this frequency band included the range of frequencies that are mainly involved in performing motor imagery. Subsequently, the CSP filters were used to compute the features. For the sCSP and SCSP algorithms, the EEG signals were also band-pass filtered using 8–35 Hz elliptic filters. Next, the spatially filtered signals obtained by sCSP and SCSP were used to compute the features accordingly. For the FBCSP algorithm, the EEG data were band-pass filtered using nine Chebyshev Type II filters. Thereafter, CSP was performed in each band, and a reduced set of features from all the bands was selected using the MIBIF algorithm [27]. For the OSSSF algorithm, the EEG data were band-pass filtered using nine Chebyshev Type II filters, and the subsequent steps described in Sect. 2 were applied.

It is noted that in this study, for each applied (s/S) CSP, m = 2 pairs of the filters were used, and for all the mentioned algorithms, the Naïve Bayesian Parzen window classifier [27] was employed in the classification step. For the proposed OSSSF (s/SCSP) algorithms, 20 different candidates of r, \(r\in R=\{0.01,0.02, {\ldots}, 0.19, 0.2\},\) were evaluated using the train data, and those yielding the highest mutual information with the class labels (the highest cross-validation accuracy) were selected as the optimal r values. In case that none of the r values yielded the higher mutual information with the class labels (higher cross-validation accuracy) compared with the standard CSP filters, the CSP features were used rather than the OSSSF (s/SCSP) features (i.e., r = 0). In the sCSP algorithm, the number of trials in each epoch was selected from the set of {1, 5, 10} using cross-validation as suggested by [36].

4 Results and discussion

In the proposed algorithm, in each frequency band, the regularization value r that yielded the highest mutual information between the best feature and the class labels is selected as the optimal r value. However, in the cross-validation algorithm, the optimal regularization value is the one resulting in the highest cross-validation accuracy.

Figure 2 illustrates how the mutual information between the best features and the class labels, as well as the tenfold cross-validation accuracy, changes by varying the r value for two subjects. This figure shows that the use of small values of r increased the mutual information and the tenfold cross-validation accuracy by attenuating noisy and redundant EEG signals, while further increase in the r value reduced both the mutual information and the cross-validation accuracy. Interestingly, for subject av, both the mutual information-based algorithm and the cross-validation algorithm yielded the same optimal r value (see Fig. 2a). For subject aa, although the two algorithms yielded different optimal r values, the difference between the cross-validation accuracies of the optimal r values is very small (see Fig. 2b). According to Fig. 2, evaluating a small set of r values suffices to find the optimal r values.

Fig. 2
figure 2

Effects of varying regularization value on the mutual information of the best features, as well as the tenfold cross-validation accuracy for: a Subject av, and b Subject aa. The train data filtered from 8 to 35 Hz were used in this figure. r* indicates the optimal regularization value

Full size image

As described in the Sect. 2.1, selecting the optimal regularization parameters of the OSSSF algorithm using the cross-validation method is computationally intractable, due to the use of a separate SCSP for each frequency band. Therefore, the proposed mutual information-based approach which is computationally tractable is used to select the optimal regularization parameters of the proposed OSSSF algorithm.

As mentioned in Sect. 2.4, in the fourth step of the proposed OSSSF algorithm, the MIBIF feature selection algorithm is used to select the most discriminative features among the features extracted from all the nine bands. The proposed OSSSF algorithm was evaluated using different number of selected features by performing fivefold cross-validation on the train data of dataset IVa [28] from BCI competition III. Figure 3 shows the average classification accuracies of the proposed OSSSF algorithm using different number of features selected by MIBIF. This figure shows that selecting four pairs of the features yielded on average the highest classification accuracy. According to these results, in the remaining of this paper, the OSSSF algorithm with four pairs of the features was used.

Fig. 3
figure 3

Average fivefold cross-validation accuracy of the proposed OSSSF algorithm using different number of features, on the train data of the dataset IVa BCI competition III

Full size image

Table 1 presents the classification accuracies on the test data from the dataset IVa obtained using different algorithms. The SCSP algorithms using the tenfold cross-validation and the mutual information-based approach to select the regularization parameters are respectively abbreviated as SCSP-CV and SCSP-MI. Table 1 shows that the SCSP-MI algorithm substantially outperformed the CSP algorithm in terms of the classification accuracy by an average of 1.93 %. Hence, the results show that the proposed mutual information-based approach truly finds a regularization parameter leading to more discriminative spatial filters. The results also show that SCSP-CV performed slightly better than sCSP and SCSP-MI and yielded an average improvement of 2.4 % in the classification accuracy compared to the CSP algorithm. However, there is no statistically significant difference between the SCSP-MI and the SCSP-CV results, and the sCSP results and SCSP-CV results (p > 0.05).

Table 1 Test classification accuracies of dataset IVa from BCI III, obtained by CSP, sCSP, SCSP-CV, SCSP-MI, FBCSP and the proposed OSSSF
Full size table

Importantly, using an Intel Quad 2.83 GHz CPU and the package fmincon in MATLAB 7.5, the SCSP-CV algorithm took an average of 5339.9 s to select the optimal regularization parameters among 20 different small r values. In contrast, the SCSP-MI algorithm only took an average of 505.36 s under the same conditions. The elapsed computational times and the obtained classification accuracies illustrated that the proposed mutual information-based approach is able to select the optimal regularization parameter of the SCSP algorithm effectively and efficiently.

Table 1 also shows that the FBCSP algorithm improved the CSP results by an average of 3.49 %. Although FBCSP averagely outperformed SCSPs, SCSPs resulted in higher classification accuracies for subject ay. Taking the advantages of both SCSP and FBCSP, the proposed OSSSF algorithm further improved the results and outperformed CSP, sCSP, SCSP-MI, SCSP-CV and FBCSP by an average of 5.18, 3.14 2.78, 3.25 and 1.69 %, respectively.

Regarding the computation time, the most time consuming part of the OSSSF algorithms is finding the regularization parameters. Although the computation time has been considerably reduced using the proposed mutual information-based algorithm, it may be still challenging to train the model using the OSSSF algorithms in few minutes break between the calibration and test sessions. However, using parallel computing can make this issue feasible.

Figure 4 illustrates the operational frequency bands selected by the FBCSP and the proposed OSSSF algorithms for the five subjects from the BCI competition III dataset IVa. Comparing this figure and the classification accuracies given in Table 1, the results show that the selected frequency bands for subjects aa and av are similar for both FBCSP and OSSSF. However, OSSSF yielded higher classification accuracy in these subjects by optimizing the CSP spatial filters of the selected frequency bands. The results also show that the selected frequency bands of the subjects aw and ay are different in FBCSP and OSSSF. Indeed, in these two subjects, the proposed OSSSF algorithm improved the classification accuracy by optimizing the spatial filters and also by selecting more optimal frequency bands due to attenuating noisy EEG signals.

Fig. 4
figure 4

Selected operational frequency bands using the FBCSP and the proposed OSSSF algorithms

Full size image

Table 2 compares the average tenfold cross-validation accuracies of 11 stroke patients from the neuro-rehabilitation dataset obtained using the OSSSF algorithm against the CSP, sCSP, SCSP-CV, SCSP-MI and FBCSP algorithms.

Table 2 Tenfold cross-validation accuracies of neuro-rehabilitation dataset obtained by CSP, sCSP, SCSP-CV, SCSP-MI, FBCSP and the proposed OSSSF
Full size table

The results showed that the proposed OSSSF algorithm outperformed the other algorithms by an average of 12.6, 4.94, 4.1, 4.5 and 2.3 %, respectively. Compared to the dataset IVa, the performance difference between OSSSF and CSP in the neuro-rehabilitation dataset was more salient. This can be due to the fact that the neuro-rehabilitation dataset was more contaminated by noise and artifact-corrupted trials. Thus, the OSSSF algorithm could considerably improve the performance by increasing the signal to noise ratio.

In terms of the statistical significance, a Friedman test [37] was applied. We used the Friedman test, since it is a nonparametric equivalent of the repeated-measure ANOVA [37]. Statistical analysis on all the results presented in the Tables 1 and 2 showed that the regularized spatial and spatio-spectral filters used in this paper had significant effects on the classification performance at the 1 % level (p = 2 × 10−7). Post hoc multiple comparisons revealed that sCSP, SCSP-CV, SCSP-MI, FBCSP and the proposed OSSSF algorithms were significantly more efficient than the CSP algorithm. Moreover, the proposed OSSSF algorithm was significantly more efficient than sCSP and SCSP-MI, while among the sCSP, SCSP-MI, SCSP-CV and FBCSP algorithms none of them performed significantly more efficient than the other.

The limitation of the proposed algorithm is when the train set is very small. Our investigation showed that the FBCSP algorithm and the proposed OSSSF algorithm were unsuccessful in classifying trials with a small training size (e.g., <20 trials per class). This may be due to overfitting. Thus, when the number of train trials is too small, we suggest using the SCSP algorithm with a fixed frequency band rather than the OSSSF algorithm.

The proposed OSSSF algorithm reduces the adverse effects of some intra-session nonstationarities by attenuating irrelevant channels as well as selecting the most discriminative frequency bands. However, the variations in the data are not considered directly in the OSSSF optimization problem. Moreover, since the OSSSF algorithm only uses the train data, the trained model may not be able to capture some of session-to-session nonstationarities that are not seen in the train data. Thus, the OSSSF results can be further improved by jointly using adaptive algorithms such as [38] to better deal with nonstationarities.

5 Conclusion

This paper proposed a novel optimized sparse spatio-spectral filtering algorithm (OSSSF) to simultaneously address the dependency on operational frequency bands and the sensitivity to noise and artifacts of the CSP algorithm. The proposed OSSSF algorithm optimizes the sparse spatial filters over multi-band frequency filters to find the best combination of the sparse CSP features extracted from different frequency bands. The SCSP filters of the proposed algorithm are directly optimized using a new mutual information-based approach instead of using the cross-validation approach that is computationally intractable in a filter bank framework. The experimental results on five healthy subjects from the publicly available BCI competition III dataset IVa, as well as 11 stroke patients performing neuro-rehabilitation, demonstrated that the proposed OSSSF algorithm outperformed the existing algorithms called CSP, sCSP, SCSP and FBCSP. Furthermore, the results showed that compared to the cross-validation method, the proposed mutual information-based approach is able to efficiently and effectively optimize the regularization parameters of the sparse CSP spatial filters with substantially reduced computational time. More importantly, the proposed new mutual information-based approach is not limited to the SCSP algorithm, but it is applicable for all general regularized CSP algorithms that require automatic selection of optimal regularization parameters.