A linear hybrid methodology for improving accuracy of time series forecasting

Abstract

Modeling and forecasting of time series data are integral parts of many scientific and engineering applications. Increasing precision of the performed forecasts is highly desirable but a difficult task, facing a number of mathematical as well as decision-making challenges. This paper presents a novel approach for linearly combining multiple models in order to improve time series forecasting accuracy. Our approach is based on the assumption that each future observation of a time series is a linear combination of the arithmetic mean and median of the forecasts from all participated models together with a random noise. The proposed ensemble is constructed with five different forecasting models and is tested on six real-world time series. Obtained results demonstrate that the forecasting accuracies are significantly improved through our combination mechanism. A nonparametric statistical analysis is also carried out to show the superior forecasting performances of the proposed ensemble scheme over the individual models as well as a number of other forecast combination techniques.

1 Introduction

Many natural as well as synthetic phenomena can be expressed in terms of time series which are sequential collections of observations measured over successive times. Analysis and forecasting of time series data have fundamental importance in various scientific and engineering applications. As such, improving forecasting accuracies is a matter of constant attentions of researchers [1]. Various linear and nonlinear forecasting models are the outcomes of extensive works in this area during the past three decades [1–3]. However, due to the stochastic nature of a time series, it is evident that no single model alone can capture all the intrinsic details of the associated data-generating process [4]. Hence, it is quite risky and inappropriate to rely upon only one of the available models for forecasting future data. On the other hand, combining forecasts from conceptually different models is a reliable approach of decreasing the model selection risk while at the same time improving overall forecasting precisions. Moreover, the accuracies obtained through combining forecasts are often better than any individual model in isolation [4–6].

Intrigued by their strengths and benefits, many forecast combination algorithms have been developed during the last two decades. At present, selection of the most promising combination scheme for a particular application is itself a nontrivial task [5]. Here, it is worth mentioning that a combination of multiple forecasts attempts to enhance the forecasting precisions at the expense of increased computational complexity. Obviously, a balanced trade-off between the accuracy improvement and associated computational cost is highly desirable from an ideal combination scheme. An extensive body of the literature has shown that simple methods for combining often provide much better accuracies than more complicated and sophisticated techniques [6, 7]. Thus, for combining forecasts, one should use straightforward tools and avoid intricacies.

The simple average in which all component forecasts are weighted equally is so far the most elementary, yet widely popular combination method. Together with being easy to understand, implement, and interpret, it is also computationally inexpensive. A well-known fact is that unequal or judgmental weighting often suffers from miscalculations, biasness, and estimation errors [8]. From this viewpoint, a simple average is quite robust as it does not require any estimation of combining weights or other parameters. Moreover, several research evidences in the literature have shown that the naïve simple average in many occasions produced remarkably better forecasting results than various other intricate combination tools [1, 6, 7]. Due to these salient features, simple averages have been extensively used for combining time series forecasts. However, they are highly sensitive to extreme values, and so sometimes, there are considerable extent of variation and instability among the obtained forecasts [7, 8]. As a remedial measure, numerous studies have suggested the use of the median which is far less sensitive to extreme values than the simple average. But there are varied results regarding forecasting superiority of the simple average and median. The former produced better accuracies in the work of Stock and Watson [9], worse in the works of Larreche and Moinpour [10] and Agnew [11], and about the same in the work of McNees [12]. From these studies, it is not possible to rationally differentiate between the performances of these two statistical averages. But evidently, both simple average and median can achieve significantly improved forecasting accuracies that too at a very few computational costs.

In this paper, we propose a novel linear ensemble method that attempts to take advantage of the strengths of both simple average and median for combining time series forecasts. Our proposed method is based on the assumption that each future observation of a time series is a linear combination of the arithmetic mean and median of the individual forecasts, together with a random noise. Five different forecasting models are combined through the proposed mechanism that is then tested on six real-world time series datasets. A nonparametric statistical analysis is also carried out to compare the accuracies of our ensemble scheme with those of the individual models as well as other benchmark forecast combination techniques.

The rest of the paper is organized as follows. Section 2 describes the related works on combining time series forecasts. The details of our proposed combination scheme are described in Sect. 3. Section 4 presents a concise discussion on the five individual forecasting models, which are used to build up the proposed ensemble. The empirical results are reported in Sect. 5, and finally, Sect. 6 concludes this paper.

2 Related works

Combining multiple methods in scientific applications has a long history that dates back to early eighteenth century [6]. The notable use of models combining for time series forecasting started in late 1960s with important contributions from Crane and Crotty [13], Zarnowitz [14], and Reid [15]. However, the seminal work of Bates and Granger [16] was the first to introduce a general analytical model for effectively combining multiple forecasts. Till then, several forecast combination mechanisms have been developed in the literature.

The constrained Ordinary Least Square (OLS) method is one of the earlier tools for linear combination of forecasts. It determines the combining weights through solving a Quadratic Programming Problem (QPP) that minimizes the Sum of Squared Error (SSE) error between the original and forecasted datasets with the restriction that the weights are nonnegative and unbiased [17–19]. An alternative is the Least Square Regression (LSR) method [1, 4, 5, 19] that does not impose any restriction on the combining weights and often provides better forecasting accuracies than the constrained OLS method.

A familiar fact is that the weights of a linear combination of forecasts can be optimized with the knowledge of the covariance matrix of one-step-ahead forecast errors. As the covariance matrix is unknown in advance, Newbold and Granger [20] suggested five procedures for estimating the weights from the known data and these are commonly known as the differential weighting schemes. Winkler and Makridakis [21] performed an extensive empirical analysis of these five methods and found that two of them provided better forecasting results than the others.

In order to cope with the dynamic nature of a time series, a forecast combination algorithm should be able to recursively update the weights with additions of new data values. As such, a number of recursive combination schemes have also been developed in the literature, which include the Recursive Least Square (RLS) technique and its variants, such as the Dynamic RLS, Covariance Addition RLS (RLS-CA), Kalman filter (KF), etc. [22]. These algorithms are often reported to be more efficient than the fixed weighting methods [1, 6, 22].

The Outperformance method by Bunn [23] is another effective linear combination technique that is based on the Bayesian probabilistic approach. It determines how likely a component model outperforms the others. This method assigns subjective weight to a component model on the basis of the number of times it performed best in the past [5, 23].

Implicit combinations of two or more forecasting models are also developed by time series researchers. One such benchmark technique, due to Zhang [24], adopts a hybridization of autoregressive integrated moving average (ARIMA) [2, 3, 24] and artificial neural network (ANN) models [2, 4, 24]. In this hybrid mechanism, the linear correlation structure of the time series is modeled through ARIMA, and then, the remaining residuals, which contain only nonlinear part, are modeled through ANN. With three real-world datasets, Zhang [24] showed that his hybrid scheme provided reasonably improved accuracies and also outperformed each component model. Recently, Khashei and Bijari [25, 26] further explored this approach, thereby suggesting a similar but slightly modified and more robust combination method.

Forecast combinations through nonlinear techniques are analyzed as well in the time series literature, but to a limited extent. This is mainly due to the lack of recognized studies which document success of such schemes [5]. Adhikari and Agrawal [27] recently developed a nonlinear-weighted-ensemble technique that considers both the individual forecasts as well as the correlation among pairs of forecasts. Their scheme was able to provide reasonably enhanced forecasting accuracies for three popular time series datasets.

In spite of several improved techniques, the robustness and efficiency of elementary statistical combination methods are always appreciated in the literature [1]. Many empirical evidences show that the naïve simple average notably outperformed more complex ensemble schemes [7, 28]. A robust alternative to the simple average is the trimmed mean in which forecasts are averaged by excluding an equal percentage of highest and lowest forecasts [5, 7, 8]. In a recent comprehensive study, Jose and Winkler [7] have found that trimmed means were able to provide slightly more accurate results than the simple averages and reduced the risk of high errors. But hitherto, there is no rigorous method for selecting the exact amount of trimming. The median (i.e., the ultimate trimming) has also been studied as an alternative to the simple average with varied results [7–12]. Thus, it seems to be advantageous to adequately combine both simple average and median.

3 The proposed combination method

3.1 Formulation of the proposed combination method

Let, ${\mathbf{Y}} = [y_{1} ,y_{2} , \ldots ,y_{N} ]^{\text{T}} \in {\mathbb{R}}^{N}$ be the actual testing dataset of a time series, which is forecasted using n different models, and ${\hat{\mathbf{Y}}}^{\left( i \right)} = \left[ {\hat{y}_{1}^{\left( i \right)} ,\hat{y}_{2}^{\left( i \right)} , \ldots ,\hat{y}_{N}^{\left( i \right)} } \right]^{\text{T}}$ be the ith forecast of Y (i = 1, 2,…, n). Let, u _j and v _j , respectively, be the mean and median of $\left\{ {\hat{y}_{j}^{\left( 1 \right)} ,\hat{y}_{j}^{\left( 2 \right)} , \ldots ,\hat{y}_{j}^{\left( n \right)} } \right\},\quad j = 1,2, \ldots ,N$. Then, the proposed combined forecast of Y is defined as ${\hat{\mathbf{Y}}} = [\hat{y}_{1} ,\hat{y}_{2} , \ldots ,\hat{y}_{N} ]^{\text{T}}$, where

$$\hat{y}_{j} = \left\{ {\begin{array}{*{20}c} {v_{j} ,\quad {\text{for}}\quad \alpha = 0} \hfill \\ {u_{j} ,\quad {\text{for}}\quad \alpha = 1} \hfill \\ {\alpha u_{j} + (1 - \alpha )v_{j} + \varepsilon_{j} ,\quad {\text{for}}\quad 0 < \alpha < 1} \hfill \\ \end{array} } \right.$$

(1)

$$\varepsilon_{j} \sim N(0,\sigma^{2} )\quad \forall j = 1,2, \ldots ,N.$$

In Eq. 1, $\{ \varepsilon_{j} |j = 1,2, \ldots ,N\}$ is assumed to be a white noise process, i.e., a sequence of independent, identically distributed (i.i.d.) random variables, which follow the typical normal distribution with zero mean and a constant variance σ ². These white noise terms are introduced as the trade-offs between the accuracy improvement and proper combination of the two averages. The parameter α manages the contributions of the two averages in the final combined forecast. The median is more dominating for 0 ≤ α < 0.5, whereas the simple average is more dominating for 0.5 < α ≤ 1. The proposed ensemble scheme can be written in the vector form as follows:

$$\begin{aligned} & {\hat{\mathbf{Y}}} = \alpha {\mathbf{U}} + (1 - \alpha ){\mathbf{V}} + {\mathbf{\rm E}} \\ & 0 \le \alpha \le 1 \\ \end{aligned}$$

(2)

where ${\mathbf{U}} = [u_{1} ,u_{2} , \ldots ,u_{N} ]^{\text{T}} ,{\mathbf{V}} = [v_{1} ,v_{2} , \ldots ,v_{N} ]^{\text{T}}$ are, respectively, the vectors of means and medians, and ${\mathbf{E}} = [\varepsilon_{1} ,\varepsilon_{2} , \ldots ,\varepsilon_{N} ]^{\text{T}}$ is the vector of the white noise terms.

3.2 Selections of the tuning parameters

Our proposed scheme combines the simple average and median of individual forecasts in an unbiased manner. The success of the scheme solely depends on the suitable selection of the parameters α and σ. Here, we suggest effective techniques for selecting these parameters.

For selecting α, first, we consider one of the two ranges: 0 ≤ α < 0.5 (median dominating) and 0.5 < α ≤ 1 (mean dominating). In either of these ranges, we vary α in an arithmetic progression with a certain step size (i.e., common difference) s. The desired value of α is then taken to be the mean of its values in this particular range and is denoted as α ^*. The precise mathematical formulation of α ^* is given as follows:

$$\alpha^{*} = \frac{1}{{N_{s} }}\sum\limits_{i = 1}^{{N_{s} }} {[l + (i - 1)s]}$$

(3)

where $N_{s} = \left\lceil {\frac{0.5}{s}} \right\rceil$ and l = 0, 0.5 in the ranges 0 ≤ α < 0.5 and 0.5 < α ≤ 1, respectively.

It is obvious that smaller values of the step size s ensure better estimation of the final combined forecast. The value s = 0.01 is used for all empirical works in this paper.

The nature of the white noise terms has a crucial impact on the success of our combination scheme, and so the noise variance σ ² must have to be chosen with utmost care. The value of σ ² is closely related to the deviation between the simple average and median of the forecasts. Keeping this fact in mind, we suggest choosing σ ² as the variance of the difference between the mean and median vectors, i.e.,

$$\sigma^{2} = \text{var} \left( {{\mathbf{U}} - {\mathbf{V}}} \right)$$

(4)

Equation 4 provides a rational as well as robust method for selecting the noise variance in our combination scheme. After choosing the two tuning parameters α and σ through Eqs. 3 and 4, the combined forecast vector is given by

$${\hat{\mathbf{Y}}} = \alpha^{*} {\mathbf{U}} + (1 - \alpha^{*} ){\mathbf{V}} + {\mathbf{\rm E}}$$

(5)

The requisite steps of our combination method are concisely summarized in Algorithm 1.

Algorithm 1 The proposed linear combination of multiple forecasts

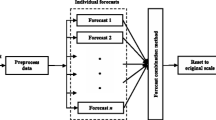
A schematic depiction of our proposed combination method is presented in Fig. 1.

Fig. 1

The proposed forecast combination mechanism

3.3 Salient features of our proposed combination mechanism

• 1. The primary advantage of the proposed scheme is that it reduces the overall forecasting error in more precise manner than various other ensemble mechanisms. In our method, a large extent of error is already reduced through simple average and median of the individual forecasts. Then, combining these averages results in further reduction in the forecasting error. Hence, the proposed methodology is evidently better than directly combining the forecasts from the individual models.

• 2. The proposed method benefits from the forecasting skills of diverse constituent models, unlike some others, which combines only a few particular ones. For example, Zhang [24] suggested a hybridization of two models, viz. ARIMA and ANN. Similarly, Tseng et al. [29] suggested the ensemble scheme SARIMABP which combines seasonal ARIMA (SARIMA) and backpropagation ANN (BP-ANN) models for seasonal time series forecasting. However, in many situations, our linear ensemble method can be apparently more accurate as it combines a large number of competing forecasting models.

• 3. Considering a wide pool of available forecast combination schemes, nowadays, a major challenge faced by the time series research community is to select the most appropriate method of combining forecasts. Our proposed mechanism improves the forecasting accuracy as well as diminishes the model selection risk to a great extent. The formulation of our method suggests that it apparently performs much better than both simple average and median. As such, the proposed scheme provides a potentially good choice in the domain of time series forecast combination.

• 4. Our proposed scheme is notably simple and much more computationally efficient than various existing combination methods. This is due to the fact that many sophisticated methods, e.g., RLS, dynamic RLS, NRLS, outperformance, etc., require repeated in-sample applications of the constituent forecasting models, thus entailing large amount of computational times. On the contrary, our proposed method applies the component models only once and, hence, saves a lot of associated computations.

4 The component forecasting models

The effectiveness of a forecast combination mechanism depends a lot on the constituent models. Several studies document that for a good combination scheme, the component forecasting models are essentially to be as diverse and competent as possible [4, 8, 21]. Armstrong [8] in his extensive study on combining forecasts further emphasized on using four to five constituent models for achieving maximum combined accuracy. Based on these studies and recommendations, here, we use the following five diverse forecasting models to build up our proposed ensemble:

• The Autoregressive Integrated Moving Average (ARIMA) [2, 3].

• The Support Vector Machine (SVM) [30].

• The iterated Feedforward Artificial Neural Network (FANN) [2, 25, 32, 33].

• The iterated Elman ANN (EANN) [5, 34].

• The direct EANN [5, 34].

In the forthcoming subsections, we concisely describe these five forecasting techniques.

4.1 The ARIMA model

ARIMA models are the most extensively used statistical techniques for time series forecasting. These are developed in the benchmark work of Box and Jenkins [3] and are also commonly known as the Box-Jenkins models. The underlying hypothesis of these models is that the associated time series is generated from a linear combination of predefined numbers of past observations and random error terms. A typical ARIMA model is mathematically given by

$$\phi (L)(1 - L)^{d} y_{t} = \theta (L)\varepsilon_{t}$$

(6)

where,

$$\phi (L) = 1 - \sum\limits_{i = 1}^{p} {\phi_{i} L^{i} } ,\quad \theta (L) = 1 + \sum\limits_{j = 1}^{q} {\theta_{j} L^{j} } ,\quad Ly_{t} = y_{t - 1} .$$

The parameters p, d, and q are, respectively, the number of autoregressive, degree of differencing, and moving average terms; y _t is the actual time series observation, and ε _t is a white noise term. The white noise terms are basically i.i.d. normal variables with zero mean and a constant variance. It is customary to refer the model, represented through Eq. 6 as the ARIMA (p, d, q) model. This model effectively converts a nonstationary time series to a stationary one through a series of ordinary differencing processes. A single differencing is enough for most applications. The appropriate ARIMA model parameters are usually determined through the well-known Box-Jenkins three-step iterative model building methodology [3, 24].

The ARIMA (0, 1, 0), i.e., y _t  − y _t−1 = ε _t is in particular known as the random walk (RW) model and is commonly used for modeling nonstationary data [24]. Box and Jenkins [3] further generalized the basic ARIMA model to forecast seasonal time series, as well, and this extended model is referred as the seasonal ARIMA (SARIMA). A SARIMA (p, d, q) × (P, D, Q)^s model adopts an additional seasonal differencing process to remove the effect of seasonality from the dataset. Like ARIMA (p, d, q), the parameters (p, P), (q, Q), and (d, D) of a SARIMA model represent the autoregressive, moving average, and differencing terms, respectively, and s denote the period of seasonality.

4.2 The SVM model

SVM is a relatively recent statistical learning theory, originally developed by Vapnik [30]. It is based on the principle of Structural Risk Minimization (SRM) whose objective is to find a decision rule with good generalization ability through selecting some special-training data points, viz. the support vectors [30, 31]. Time series forecasting is a branch of support vector regression (SVR) problems in which an optimal separating hyperplane is constructed to correctly classify real-valued outputs. But the explicit knowledge of this mapping is avoided through the use of a kernel function that satisfies the Mercer’s condition [31].

Given a training dataset of N points $\left\{ {{\mathbf{x}}_{i} ,y_{i} } \right\}_{i = 1}^{N}$ with ${\mathbf{x}}_{i} \in {\mathbb{R}}^{n} ,y_{i} \in {\mathbb{R}}$, the goal of SVM is to approximate the unknown data-generating function in the following form:

$$f({\mathbf{x}},{\mathbf{w}}) = {\mathbf{w}} \cdot \varphi ({\mathbf{x}}) + b$$

(7)

where w is the weight vector, x is the input vector, φ is the nonlinear mapping to a higher dimensional feature space, and b is the bias term.

Using Vapnik’s ε-insensitive loss function, given in Eq. 8, the SVM regression is converted to a quadratic programming problem (QPP) to minimize the empirical risk, as defined in Eq. 9.

$$L_{\varepsilon } \left( {y,f\left( {{\mathbf{x}},{\mathbf{w}}} \right)} \right)\, = \left\{ \begin{gathered} 0,\quad{\text{if }}\left| {y - f\left( {{\mathbf{x}},{\mathbf{w}}} \right)} \right| \le \in \, \hfill \\ \left| {y - f\left( {{\mathbf{x}},{\mathbf{w}}} \right)} \right| - \in, \quad {\text{ otherwise}} \hfill \\ \end{gathered} \right.$$

(8)

$$J\left( {{\mathbf{w}},\xi_{i} ,\xi_{i}^{*} } \right) = \frac{1}{2}\left\| {\mathbf{w}} \right\|^{2} + C\sum\limits_{i = 1}^{N} {\left( {\xi_{i} + \xi_{i}^{*} } \right)} \,.$$

(9)

In Eq. 9, C is the positive regularization constant that assigns a penalty to misfit, and $\xi_{i} ,\,\,\xi_{i}^{*}$ are the nonnegative slack variables.

After solving the associated QPP, the optimal decision hyperplane is given by

$$y({\mathbf{x}}) = \sum\limits_{i = 1}^{{N_{s} }} {(\alpha_{i} - \alpha_{i}^{*} )K({\mathbf{x}},{\mathbf{x}}_{i} ) + b_{\text{opt}} } .$$

(10)

where N _s is the number of support vectors, $\alpha_{i}$ and $\alpha_{i}^{*}$ (i = 1, 2,…, N _s ) are the Lagrange multipliers, b _opt is the optimal bias, and K(x, x _i ) is the kernel function.

From several choices for the SVM kernel function, the Radial Basis Function (RBF) kernel [31], defined as K(x, y) = exp(–||x–y||²/2σ ²), σ being a tuning parameter is used in this paper. While fitting the SVM models, the associated hyperparameters C and σ are determined through precisely following the grid-search technique, as recommended and utilized by Chapelle [35].

4.3 The FANN model

Initially inspired from the biological structure of human brain, ANNs gradually achieved great success and recognition in versatile domains, including time series forecasting. The major advantage of ANNs is their nonlinear, flexible, and model-free nature [4, 25, 33]. ANNs have the remarkable ability of adaptively recognizing relationship in input data, learning from experience and then utilizing the gained previous knowledge to predict unseen future patterns. Unlike other nonlinear statistical models, ANNs do not require any information about the intrinsic data-generating process. Moreover, an ANN can always be designed that can approximate any nonlinear continuous function as closely as desired. Due to this reason, ANNs are referred to as the universal function approximators [24, 33].

The most common ANN architecture, used in time series forecasting, is the multilayer perceptron (MLP). An MLP is a feedforward architecture of an input, one or more hidden and an output layer in such a way that each layer consists of several interconnecting nodes, which transmits processed information to the next layer. It is also known as an FANN model. An FANN with a single hidden layer is often sufficient for practical time series forecasting applications, and so FANNs with single hidden layers are considered in this paper. There are two extensively popular approaches for multi-periodic forecasts through FANNs, viz. iterative and direct [5, 32]. An iterative approach consists of one neuron in the output layer, and the value of the next period is forecasted using the current predicted value as one of the inputs. On the contrary, the number of output neurons in a direct approach is precisely equal to the forecasting horizon, i.e., the number of future observations to be forecasted. In short-term forecasting, the direct method is usually more accurate than its iterative counterpart, but there is no firm conclusion in this regard [32]. The network structures for iterative and direct FANN forecasting methods are shown in Fig. 2a, b respectively.

Fig. 2

The FANN architectures for the following: a iterative forecasting, b direct forecasting

4.4 The EANN model

Relatively recently, EANNs attracted notable attention of time series forecasting community. An EANN has a recurrent network structure that differs from a common feedforward ANN through inclusion of an extra context layer and feedback connections [34]. The context layer is continuously fed back by the outputs from the hidden layer, and as such it acts as a reservoir of past information. This recurrence imparts robustness and dynamism to the network so that it can perform temporal nonlinear mappings. The architecture of an EANN model is shown in Fig. 3.

Fig. 3

Architecture of an EANN model

EANNs generally provide better forecasting accuracies than FANNs due to the introduction of additional memory units. But they require more network weights, especially the hidden nodes in order to properly model the associated temporal relationship. However, there is no rigorous guideline in the literature for selecting the optimal structure of an EANN model [5]. In this paper, we set the number of hidden nodes as 25 and the training algorithm as traingdx [36] for all EANN models.

5 Empirical results and discussions

Six real-world time series from different domains are used in order to empirically examine the performances of our proposed ensemble scheme. These are collected from the Time Series Data Library (TSDL) [37], a publicly available online repository of a wide variety of time series datasets. Table 1 presents the descriptions of these six time series, and Fig. 4 depicts their corresponding time plots. The horizontal and vertical axis of each time plot, respectively, represents the indices and actual values of successive observations. Here, we are considering short-term forecasting, and so the size of the testing dataset for each time series is kept reasonably small.

Table 1 Descriptions of the time series datasets

Fig. 4

Time plots of the following: a LYNX, b SNSPOT, c RGNP, d BIRTHS, e AP, f UE

All experiments are performed on MATLAB. The default neural network toolbox [36] is used for the FANN and EANN models. The forecasting accuracies are evaluated through the mean-squared error (MSE) and the symmetric mean absolute percentage error (SMAPE), which are defined as follows:

$${\text{MSE = }}\frac{1}{N}\sum\limits_{t = 1}^{N} {(y_{t} - \hat{y}_{t} )^{2} }$$

(11)

$${\text{SMAPE = }}\frac{1}{N}\sum\limits_{t = 1}^{N} {\frac{{\left| {y_{t} - \hat{y}_{t} } \right|}}{{{{(y_{t} + \hat{y}_{t} )} \mathord{\left/ {\vphantom {{(y_{t} + \hat{y}_{t} )} 2}} \right. \kern-0pt} 2}}} \times 100}$$

(12)

where $y_{t}$ and $\hat{y}_{t}$ are, respectively, the actual and forecasted values, and N is size of the testing set.

MSE and SMAPE are relative error measures and both provide a reasonably good idea about the forecasting ability of a fitted model. For better forecasting performance, the values of both these error statistics are desired to be as small as possible. The information about the determined optimal forecasting models for all the six datasets is presented in Table 2.

Table 2 The appropriate forecasting models for the six time series datasets

Five other linear combination schemes are considered for comparing with our proposed method. The obtained forecasting results of the individual models and linear combination methods for all six time series are, respectively, presented in Tables 3 and 4. The best forecasting accuracies, i.e., the least error measures in each of these tables, are shown in bold. Following previous works [24], the logarithms to the base 10 of the LYNX data are used in the present analysis. Also, the MSE values for the AP dataset are given in transformed scale (original MSE = MSE × 10⁴).

Table 3 Forecasting results of the individual models

Table 4 Forecasting results of the combination methods

The following important observations are evident from Tables 3 and 4:

• 1. The obtained forecasting accuracies notably vary among the individual models, and no single model alone could achieve the best forecasting results for all datasets.

• 2. In terms of MSE, the simple average and the median outperformed the best individual models for three and four datasets, respectively. In terms of SMAPE, both of them outperformed the best individual model for four datasets.

• 3. Our proposed schemes, viz. Proposed-I and Proposed-II outperformed all individual forecasting models as well as linear combination methods in terms of both MSE and SMAPE.

• 4. Among themselves, the Proposed-I scheme achieved least MSE and SMAPE values for three and five datasets, respectively, whereas the Proposed-II scheme achieved least MSE and SMAPE values for three and one datasets, respectively.

We present the two bar diagrams in Fig. 5 for visual depictions of the forecasting performances of different methods for all six time series.

Fig. 5

Bar diagrams showing the performances of all fitted models on the basis of the following: a MSE, b SMAPE

We have transformed the error measures for some datasets in order to uniformly depict them in Fig. 5a, b. In Fig. 5a, the MSE values for SNSPOT and RGNP are divided by 10,000, and those for BIRTHS and UE are divided by 1,000 and 100, respectively. Similarly, in Fig. 5b, the SMAPE values for the SNSPOT data are divided by 10. Figure 5a, b clearly show that the two forms of our proposed scheme, viz. Proposed-I and Proposed-II achieved least MSE and SMAPE values throughout.

We further show the percentage reductions in MSE and SMAPE of the best individual models through our proposed schemes in Fig. 6a, b, respectively. From these figures, it can be seen that except SNSPOT, for all other datasets, our proposed schemes reduced the forecasting errors of the best individual models to considerably large extents. Only for SNSPOT, the amounts of error reductions are small, which can be credited to the reasonably good performances of the corresponding best individual models for this dataset.

Fig. 6

Percentage improvements over the best individual model in terms of the following: a MSE, b SMAPE

The diagrams of the actual observations and their forecasts through the proposed combination scheme for all six time series are shown in Fig. 7. The closeness among the actual and forecasted observations for each dataset is clearly visible in all the six plots of Fig. 7.

Fig. 7

Diagrams of actual and forecasted observations for the time series: a LYNX, b SNSPOT, c RGNP, d BIRTHS, e AP, f UE

We have carried out the nonparametric Friedman test for a statistical analysis of the obtained forecasting results. This test evaluates the null hypothesis (H₀) that all the forecasting methods are equally effective in terms of MSE or SMAPE against the alternative hypothesis (H₁) that all of them are not equally effective [38]. The obtained Friedman test results are as follows:

• For forecasting MSE, the Friedman’s χ ² statistic is 46.92 and p = 0.0000022.

• For forecasting SMAPE, the Friedman’s χ ² statistic is 46.69 and p = 0.0000024.

Here, p represents the probability that the null hypothesis is true. From the sufficiently small values of p, we reject the null hypotheses with 95 % confidence level and conclude that the forecasting methods differ significantly in terms of both MSE and SMAPE.

The Friedman test results are depicted in Fig. 8a, b. In these figures, the mean rank of a forecasting method is pointed by a circle, and the horizontal bar across each circle is the critical difference. The performances of two methods differ significantly if their mean ranks differ by at least the critical difference, i.e., if their horizontal bars are nonoverlapping.

Fig. 8

Friedman test result in terms of the following: a MSE, b SMAPE

From Fig. 8a, b, it can be seen that the individual forecasting methods do not differ significantly among themselves, but many of them are significantly outperformed by our combination schemes in terms of both obtained MSE and SMAPE values.

6 Conclusions

Time series analysis and forecasting have major applications in various scientific and industrial domains. Improvement of forecasting accuracy has been constantly drawing the attentions of researchers during the last two decades. Extensive works in this area have shown that combining forecasts from multiple models substantially improves the overall accuracies. Moreover, in many occasions, the simple combinations performed considerably better than more complicated and sophisticated methods. In this paper, we propose a linear combination scheme that takes advantage of the strengths of both simple average and median for combining forecasts. The proposed method assumes that each future observation of a time series is a linear combination of arithmetic mean and median of the individual forecasts together with a random noise. Two approaches are suggested for estimating the tuning parameter α that manages the relative weights between simple average and median. Empirical analysis is conducted with six real-world time series datasets and five forecasting models. The obtained results clearly demonstrate that both forms of our proposed ensemble scheme significantly outperformed each of the five individual models and a number of other common linear forecast combination techniques. These findings are further justified through a nonparametric statistical test.