1 Introduction

The determination of flow by using the past measurements is required in design, plan, project, construction, maintenance, especially management of water resources, and determination of natural disasters such as flood and drought. So the studies of hydrological modeling based on the flow data measured in the past are becoming increasingly important. The completion of missing flow data is important in case if there is a degradation of the measurement device and the land conditions are not established at the measurement station. The forecasting of the missing flow measurements with appropriate models, improving of the model performance, and obtaining of the better forecasting results provide convenience in terms of both economically and usage. Therefore, the hydrological time series models are commonly used for flow forecasting in recent years such as stochastic models and data-driven techniques. The stochastic models firstly proposed by Box and Jenkins [1] have been preferred in especially forecasting of stream flow [6]. Kişi [20] used artificial neural networks (ANN) to predict monthly flow and compared with autoregressive models (AR). He stated the ANN predictions in general are better than those found with AR(4). Yürekli and Öztürk [41] determined alternative autoregressive moving average process (ARMA) models by using the graphs of autocorrelation function (ACF) and partial autocorrelation function (PACF) for streamflow of Kelkit Stream. The plots of the ACF show that ARMA (1,0) with a constant is the best model by considering Schwarz Bayesian criterion (SBC) and error estimates. Wu and Chau [40] investigated ARMA, K-nearest neighbors (KNN), and ANN and phase space reconstruction-based artificial neural networks (ANN–PSR) models to determine the optimal approach of predicting monthly streamflow time series. They compared these models by 1-month-ahead forecast. They determined that the KNN model performs the best among the four models, but only exhibits weak superiority to ARMA.

The data-driven techniques having capability of analyzing long-time series have been preferred by many researchers in hydrology. Of data-driven techniques, artificial neural networks and the adaptive neural-based fuzzy inference system which are computer systems developed with the aim of automatically performing capabilities have been investigated for problems in the water researches and meteorology studies such as solar radiation [9, 29], evaporation [19, 35], wind speed [28] and rainfall estimation [5, 26, 31], and river flow [8, 16, 22]. Lin and Chen [25] used the radial basis function network (RBFN) to construct a rainfall–runoff model for the parametric estimation of the network. The result shows that the RBFN can be successfully applied to build the relation of rainfall and runoff. Keskin and Taylan [18] developed flow prediction model, based on the adaptive neural-based fuzzy inference system (ANFIS) and ANN. The results show the ANFIS model is better than ANN model. The ANFIS model and its principles first proposed by Jang [17] have been successfully applied to many problems [30]. Chang and Chang [3] studied the intelligent control of a real-time reservoir operation model and found that given sufficient information to construct the fuzzy rules, the ANFIS helps to ensure more efficient reservoir operation than the classical models based on rule curve. Terzi et al. [37] proposed an alternative model for Penman evaporation estimation from a water surface by using ANFIS and showed that the ANFIS model can be used to estimate daily Penman evaporation for Lake Eğirdir.

Gene expression programming (GEP) was invented by Ferreira [10] and is the natural development of genetic algorithms and genetic programming. The researchers have investigated the applicability of GEP to problems in the field of water resources engineering [4, 13, 36]. Makkeasorn et al. [27] applied genetic programming (GP) and artificial neural networks (ANNs) to short-term streamflow forecasting with global climate change implications. Savic et al. [34] developed rainfall–runoff model using GP and ANNs. Güven and Aytek [15] presented GEP to the modeling stage–discharge relationship. Whigham and Crapper [39] described the application of a grammatically based GP system to discover rainfall–runoff relationships for two vastly different catchments. Chang et al. [2] applied fuzzy theory and genetic algorithm (GA) to interpolate precipitation. Zhang et al. [42] investigated the use of GA in a sediment transport model. Reddy and Ghimire [32] used M5 model tree (MT) and GEP to predict suspended sediment loads. They stated that MT gives good performance as compared the model results to sediment rating curve and multiple linear regression.

The objectives of this study are to investigate data-driven techniques for forecasting monthly flow which include GEP, ANN (RBFN and FFNN), and ANFIS techniques and to compare their performances with AR modeling which is one of the traditional time series modeling techniques. This task is intended to be accomplished in Kızılırmak River, Turkey. These techniques are tried to forecast monthly flow values (F t ) using the previous 1-month (F t−1), 2-month (F t−2), and 3-month (F t−3) flow values. The correlation coefficient (R) and the root-mean-square error (RMSE) performance criteria are employed to validate all developed models.

2 The modeling techniques

A brief overview of the GEP, ANN, ANFIS, and AR modeling techniques used in forecasting monthly flow was presented here.

2.1 Gene expression programming (GEP)

Gene expression programming (GEP) is, like genetic algorithms (GAs) and genetic programming (GP), a genetic algorithm as it uses populations of individuals, selects them according to fitness, and introduces genetic variation using one or more genetic operators. The fundamental difference between the three algorithms resides in the nature of the individuals: In GAs, the individuals are linear strings of fixed length (chromosomes); in GP, the individuals are nonlinear entities of different sizes and shapes (parse trees); and in GEP, the individuals are encoded as linear strings of fixed length (the genome or chromosomes) which are afterward expressed as nonlinear entities of different sizes and shapes (i.e., simple diagram representations or expression trees) [10].

There are five major preparatory steps of genetic programming paradigm to solve a problem.

  1. 1.

    To identify the set of terminals to be used in the individual computer programs in the population, the terminals can be viewed as the input to the computer program being sought by GP. In turn, the output of the computer program consists of the value(s) returned by the program.

  2. 2.

    To determine a set of functions. The function set is arithmetic operators (*, /, −, +), mathematical functions (sin, cos, log), logical expressions (IF–THEN–ELSEs), and Boolean operators (AND, OR, NOT) or any other user-defined function. The terminals and the functions are the ingredients from which the individual computer programs in the population are composed.

  3. 3.

    To identify a way of evaluating how good a given computer program is at solving the problem at hand.

  4. 4.

    To select the values of certain parameters to control the runs. This step involves control parameters which are the values of the numerical parameters and qualitative variables for controlling the run.

  5. 5.

    To specify the criterion for designating a result and the criterion for terminating a run [21].

The fundamental steps of the gene expression programming are schematically represented in Fig. 1. The process begins with the random generation of the chromosomes of a certain number of individuals. Then, these chromosomes are expressed, and the fitness of each individual is evaluated against a set of fitness cases. The individuals are then selected according to their fitness to reproduce with modification, leaving progeny with new traits. These new individuals are, in their turn, subjected to the same developmental process: expression of the genomes, confrontation of the selection environment, selection, and reproduction with modification. The process is repeated for a certain number of generations or until a good solution has been found [12].

Fig. 1
figure 1

The flowchart of gene expression programming [12]

Full size image

The individuals of gene expression programming are encoded in linear chromosomes which are expressed or translated into expression trees (branched entities). Thus, in GEP, the genotype (the linear chromosomes) and the phenotype (the expression trees) are different entities (both structurally and functionally) that, nevertheless, work together forming an indivisible whole. In contrast to its analogous cellular gene expression, GEP is rather simple. The main players in GEP are only two: the chromosomes and the expression trees (ETs), being the latter the expression of the genetic information encoded in the chromosomes [14].

In nature, the phenotype has multiple levels of complexity, the most complex being the organism itself. But tRNAs, proteins, ribosomes, cells, and so forth are also products of expression, and all of them are ultimately encoded in the genome. In all cases, however, the expression of the genetic information starts with transcription (the synthesis of RNA) and, for protein genes, proceeds with translation (the synthesis of proteins). In GEP, from the simplest individual to the most complex, the expression of genetic information starts with translation, the transfer of information from a gene into an ET. In contrast to nature, the expression of the genetic information in GEP is very simple. Worth emphasizing is the fact that in GEP, there is no need for transcription: The message in the gene is directly translated into an ET [10]. As the translation which is the process of information decoding (from the chromosomes to the expression trees), it includes code and rules. The genetic code of GEP is very simple: a one-to-one relationship between the symbols of the chromosome and the functions or terminals they represent in the trees. The rules are also very simple: They determine the spatial organization of the functions and terminals in the expression trees and the type of interaction between sub-expression trees. Therefore, there are two languages in GEP: the language of the genes and the language of expression trees. However, thanks to the simple rules that determine the structure of expression trees and their interactions, it is possible to infer immediately the expression tree given the sequence of a gene and vice versa. This bilingual and unequivocal system is called Karva language. For example, the mathematical expression:

$$\frac{a*b}{c} + \sqrt {d - e}$$
(1)

It can also be represented as an expression tree in Fig. 2 where Q represents the square root function.

Fig. 2
figure 2

An example of expression trees

Full size image

This kind of diagram representation is what is called the phenotype of GEP chromosomes, and the genotype can be easily inferred from the phenotype as follows:

$$\begin{gathered} 0123456789 \hfill \\ + /Q*c - abde \hfill \\ \end{gathered}$$
(2)

which is the straightforward reading of the expression tree from left to right and from top to bottom. The expression 2 is an open reading frames, starting at ‘+’ (position 0) and terminating at ‘e’ (position 9). This expression is from Karva notation [11].

2.2 Artificial neural networks (ANN)

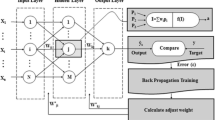
Neural networks are composed of simple elements operating in parallel. These elements are inspired by biological nervous systems. As in nature, the network function is determined largely by the connections between elements. A neural network can be trained to perform a particular function by adjusting the values of the connections (weights) between the elements. Commonly neural networks are adjusted, or trained, so that a particular input leads to a specific target output. Such a situation is shown in Fig. 3. Here, the network is adjusted, based on a comparison of the output and the target, until the sum of square differences between the target and output values becomes the minimum. Typically, many such input/target output pairs are used to train a network. Batch training of a network proceeds by making weight and bias changes based on an entire set (batch) of input vectors. Incremental training changes the weights and biases of a network as needed after presentation of each individual input vector. Neural networks have been trained to perform complex functions in various fields of application including pattern recognition, identification, classification, speech, vision, and control systems. Today, neural networks can be trained to solve problems that are difficult for conventional computers or human beings [7].

Fig. 3
figure 3

Basic principle of artificial neural networks

Full size image

2.2.1 Feed-forward neural networks (FFNN)

Feed-forward ANNs comprise a system of neurons, which are arranged in layers. Between the input and output layers, there may be one or more hidden layers. The neurons in each layer are connected to the neurons in a subsequent layer by a weight w, which may be adjusted during training. A data pattern comprising the values x i presented at the input layer i is propagated forward through the network toward the first hidden layer j. Each hidden neuron receives the weighted outputs w ij x ij from the neurons in the previous layer. These are summed to produce a net value, which is then transformed to an output value upon the application of an activation function [16].

2.2.2 Radial basis function networks (RBFN)

A radial basis function network is a two-layer network whose output neurons form a linear combination of the basis functions computed by the hidden neurons. The basis functions in the hidden layer produce a localized response to the input. That is, each hidden neuron has a localized receptive field. The basis function can be viewed as the activation function in the hidden layer. The network employs a radial basis function such as the Gaussian function, which is the most popular hidden layer function. The others are thin-plate-spline, multiquadric, inverse quadratic, inverse multiquadric function, and polyharmonic spline. The basis function used in this study is a Gaussian function [23].

2.3 Adaptive neural-based fuzzy inference system (ANFIS)

Various fuzzy inference system (FIS) types are studied in the literature, and each one is characterized by consequent parameters. In this section, a brief description of ANFIS model principles is presented. The reader is referred to Chang and Chang [3] for more detail.

Fundamentally, ANFIS is a graphical network representation of Sugeno-type fuzzy systems, endowed by neural learning capabilities. The network is comprised of nodes and with specific functions, or duties, collected in layers with specific functions [38].

In order to illustrate ANFIS’s representational strength, the neural fuzzy control systems are considered based on the Tagaki–Sugeno–Kang (TSK) fuzzy rules, whose consequent parts are linear combinations of their preconditions. The TSK fuzzy rules are in the following forms:

$$R^{j} :{\text{IF}}\,x_{1} \;{\text{is}}\;A_{1}^{j} \;{\text{AND}}\;x_{2} \;{\text{is}}\;A_{2}^{j} \;{\text{AND}} \cdots {\text{AND}}\;x_{n} \;{\text{is}}\;A_{n}^{j} ,$$
$${\text{THEN}}\;y = f_{j} = a_{0}^{j} + a_{1}^{j} x_{1} + a_{2}^{j} x_{2} + \cdots + a_{n}^{j} x_{n}$$
(3)

where x i ’s (i = 1, 2, …, n) are input variables, y is the output variable (solar radiation measurements), A j i are linguistic terms of the precondition part with membership functions μA j 1 (x i ) (j = 1, 2, …, n), and a j 1 ЄR are coefficients of linear equations f i (x 1, x 2, …, x n ). To simplify the discussion, it is necessary to focus on a specific neuro-fuzzy Controller (NFC) of the type called an adaptive neural-based fuzzy inference system (ANFIS).

Let us assume that the fuzzy control system under consideration consists of two inputs x 1 and x 2 and one output y and that the rule base contains two TSK fuzzy rules as follows:

$$R^{1} :{\text{IF}}\;x_{1} \;{\text{is}}\;A_{1}^{1} \;{\text{AND}}\;x_{2} \;{\text{is}}\;A_{2}^{1} \;,\quad {\text{THEN}}\;y = f_{1} = a_{0}^{1} + a_{1}^{1} x_{1} + a_{2}^{1} x_{2}$$
(4)
$$R^{2} :{\text{IF}}\;x_{1} \;{\text{is}}\;A_{1}^{2} \;{\text{AND}}\;x_{2} \;{\text{is}}\;A_{2}^{2} \;,\quad {\text{THEN}}\;y = f_{2} = a_{0}^{2} + a_{1}^{2} x_{1} + a_{2}^{2} x_{2}$$
(5)

In TSK fuzzy system, for given input values x 1 and x 2, the inferred output y* is calculated by the following formula [24]:

$$y^{*} = \left( {\mu_{1} f_{1} + \mu_{2} f} \right)_{2} /\left( {\mu_{1} + \mu_{2} } \right)$$
(6)

where μ j are firing strengths of R j, j = 1, 2, given by the equation below,

$$\mu_{j} = \mu_{{A_{1}^{j} }} (x_{1} ) + \mu_{{A_{2}^{j} }} (x_{2} ),\quad \, j = 1,2$$
(7)

2.4 Autoregressive modeling (AR)

Time series models have been extensively used in hydrology and water resources since the early 1960’s, for modeling annual and periodic hydrologic time series. The application of these models has been attractive in hydrology mainly because the autoregressive form has an intuitive type of time dependence (the value of variable at the present time depends on the values at previous times), and they are the simplest models to use [33].

The autoregressive model (AR) may be generally written as

$$y_{t} = \mu + \varphi_{1} \left( {y_{t - 1} - \mu } \right) + \cdots + \varphi_{p} \left( {y_{t - p} - \mu } \right) + \varepsilon_{t}$$
(8)

where y t is the time-dependent series (variable) and ε t is the time-independent (uncorrelated) series which is independent of y t , and it is also normally distributed with mean zero and \(\sigma_{\varepsilon }^{2}\). The coefficients φ 1, …, φ p are called the autoregression coefficients. The parameter set of the model of Eq. (8) is \(\left\{ {\mu , \sigma^{2} , \varphi_{1} , \ldots ,\varphi_{p} , \sigma_{\varepsilon }^{2} } \right\}\), and it must be specified or estimated from data.

Autoregressive models with periodic parameters are those models in which part or all of their parameters vary within the year or they are periodic. These models are often referred to as periodic AR models. The time series used in hydrological studies are generally annual or monthly [33].

It is assumed that AR models are stationary and follow the normal distribution. However, it is possible to eliminate such assumptions with the data-driven models. Also, the use of data-driven methods can be easier in terms of the processing time according to the AR modeling.

3 Study region and data

The length of the Kızılırmak River which is the longest river in Turkey is 1,355 km. The area of the watershed is 78,646 km2. The yearly average flow and rainfall are about 184 m3/s and 446.1 mm, respectively. The data used to develop model include the monthly mean flow observations between 1955 and 1995, i.e., a total of 480 months in this study. The monthly mean flow data were obtained for Yamula (1501) station of the Kızılırmak River from the General Directorate of Electrical Power Resources Survey and Development Administration. The location of the station is shown in Fig. 4. In the modeling, the training data set consisted of the years 1955–1987. The trained models were used to run a set of test data for year 1988–1995.

Fig. 4
figure 4

The location of the Yamula (1501) station

Full size image

4 Application and results

In this study, the previous 1-month (F (t−1)), 2-month (F (t−2)), and 3-month (F (t−3)) mean flow values of Kızılırmak River were used in developing models. The models were developed by using AR, GEP, FFNN, RBFN, and ANFIS techniques.

In AR modeling, monthly mean flow data set is periodic series due to shorter time interval than annual data set. Internal dependence increases because statistical characteristics in periodic series are different for another day of same process. First, the series must be fitted to normal distribution and then standardized for removing periodicity of monthly mean flow data set. It was controlled according to skewness whether or not flow values are fit to normal distribution. It was seen that flow values are not fit to normal distribution. Then, the logarithmic transformation function was applied to flow values. The transformed flow values were given in Fig. 5. As shown in Fig. 5, there is a periodicity for logarithmic flow values. The moment values (periodic mean (μ τ ), periodic standard deviation (σ τ ) and skewness) of flow data and transform function were determined and given in Table 1.

Fig. 5
figure 5

Transformed flow values

Full size image
Table 1 The moment values of the flow data
Full size table

The standard normal series was obtained by applying standardization process to historical time series. The autocorrelation function (ACF) and partial autocorrelation function (PACF) of standard normal series were obtained. The upper and lower limits were determined for 95 % confidence interval (Fig. 6). It was shown that y t series is a dependent series according to autocorrelation values.

Fig. 6
figure 6

The 95 % confidence interval a autocorrelation and b partial autocorrelation values

Full size image

Then, autocorrelation coefficient (δk) was calculated, and residual series was determined according to this value (Table 2). AR(1), AR(2), and AR(3) models were tested, and it was concluded that AR(2) is most appropriate model for autocorrelation values. The autocorrelation values of models were given in Fig. 7. As shown in Fig. 7, there is an agreement between autocorrelation values of AR(2) model and historical series. It was controlled that the AR(2) model provided stationarity condition in using Eq. (9).

$$u^{p} - \varphi_{1} u^{p - 1} - \varphi_{2} u^{p - 2} - \cdots - \varphi_{p} = 0$$
(9)
Table 2 Autocorrelation coefficients of AR models
Full size table
Fig. 7
figure 7

The relationship ACFs of historical and AR(1), AR(2), and AR(3) models

Full size image

Variance of residual series \(\sigma_{\varepsilon }^{2}\) was obtained according to Eq. (10),

$$\sigma_{\varepsilon }^{2} = \frac{{N\sigma^{2} }}{(N - p)}(1 - \mathop \sum \limits_{j = 1}^{p} \varphi_{j} r_{j} )$$
(10)

where N is number of data; p is model parameter; and φ is autoregression coefficient. The Akaike’s information criterion (AIC) was used to investigate fitness of the selected model degree. AICs of AR(1), AR(2), and AR(3) models were calculated as 0.624, 0.623, and 0.705, respectively. It was confirmed that the AR(2) model having the smallest AIC is appropriate.

The synthetic series was generated for AR(2) model. Initially, the 25 random series were produced. The synthetic series were obtained by using AR(2) model and residual of the historical data. Hence, the mean, standard deviation, and ACF of the synthetic series with in 95 % confidence interval were calculated and compared with historical series (Figs. 8, 9, 10). As shown these figures, there is agreement between the historical and synthetic series. It was observed that the statistics of the synthetic series is within 95 % confidence interval for the selected AR(2) model. This situation indicates suitability of AR(2) model for predicting flow.

Fig. 8
figure 8

The mean values for synthetic series generated by AR(2)

Full size image
Fig. 9
figure 9

Standard deviations for synthetic series generated by AR(2)

Full size image
Fig. 10
figure 10

The correlogram of historical and synthetic series generated by AR(2)

Full size image

In GEP, there are five major steps, and the first is to choose the fitness function. For this study, the R-square-based fitness function was selected. This kind of fitness function is very useful as it is usually interested in finding a model with a high value of R-square. The second step is to choose the set of terminals T and the set of functions F. The terminal set consisted, obviously, of the independent variable, giving T = {F (t−1), F (t−2), F (t−3), where F is the monthly mean flow data of Kızılırmak River}. The various arithmetic operators were used, F = {+, −, *, /, power, √, ex, ln(x), log(x), 10x} in this study. The third step is to choose the structural organization of chromosomes, namely the length of the head and the number of genes: The length of the head equals to 8, and the number of genes per chromosome equals to 3 in this study. The fourth step is to choose the kind of linking function. In this problem, the sub-expression trees were linked by addition. And finally, the fifth major step in preparing to use gene expression programming is to choose the set of genetic operators and their rates. The genetic operators developed to introduce genetic diversity in GP populations always produce valid expression trees. Variation in the population is introduced by applying one or more genetic operators, i.e., crossover, mutation, and rotation to selected chromosomes. The genetic operators used in this study were given in Table 3.

Table 3 Parameters of the GEP models
Full size table

In ANN modeling, feed-forward neural networks (FFNN) and radial basis function network (RBFN) were used for forecasting monthly flow. Prior to execution of the model, standardization was done according to the following expression such that all data values fall between 0 and 1.

$$F = (F_{i} - F_{\hbox{min} } )/(F_{\hbox{max} } - F_{\hbox{min} } )$$
(11)

where F is the standardized value of the F i , F max, and F min are the maximum and minimum values in all observation sequence [35]. In RBFN, the models were developed to forecast monthly flow using the same input combinations. The various spread constants were tested for each RBFN model. In FFNN, FFNN(i, j, k) indicates a network architecture with i, j, and k neurons in input, hidden, and output layers, respectively. Herein, i runs 1, 2, and 3; j assume values of 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, and 12, whereas k = 1 is adopted in order to decide about the best FFNN model alternative. The numbers of neuron in hidden layer were determined using a trial-and error-method by considering the performance criteria for testing data set. The hyperbolic tangent sigmoid, logarithmic sigmoid, and linear activation functions were tried for hidden and output layers in modeling. The appropriate activation function was determined as the tangent sigmoid function after trial-and-error. The stopping criterion was employed 1,000 epochs for training, because the variation of error was too small after this epoch. The learning rate and momentum are the parameters that affect the speed of the convergence of the back-propagation algorithm. A learning rate of 0.001 and momentum 0.1 were fixed for selected network after training, and the model selection was completed for training set. The trained networks were used to run testing set.

In ANFIS modeling, each variable may have several values (in terms of rules), and each rule includes several parameters of membership functions. For instance, if each variable has three rules and each rule includes three parameters, then there are 45 [5 (variables) × 3 (rules) × 3 (parameters)] parameters needed to be determined in layer 2. The sole reason for having three memberships for each variable is due to the reduction in the number of rule base alternatives. Also, the ANFIS trains these membership functions according to data in layer 3, these rules will generate 35 nodes, and there are 1,458 (35 × 6) parameters undetermined within the defuzzification process in layer 5. In this study, to establish the rule base relationship between the input and output variables, subtractive fuzzy clustering was used. In this study, hybrid and back-propagation optimization methods were tested, and the highest R and the lowest RMSE values were obtained by using back-propagation method.

In this paper, the same training and testing sets are used for comparing of all the above-developed models. The correlation coefficient (R) and the root-mean-square error (RMSE) performance criteria are employed to evaluate the performances of the developed models. These criteria are given for three input combinations (1) F (t−1), (2) F (t−1), F (t−2), and (3) F (t−1), F (t−2), F (t−3) in Tables 4, 5, and 6, respectively.

Table 4 The R and RMSE values of the developed models using F (t−1) parameter
Full size table
Table 5 The R and RMSE values of the developed models using F (t−1) and F (t−2) parameters
Full size table
Table 6 The R and RMSE values of the developed models using F (t−1), F (t−2), and F (t−3) parameters
Full size table

It can be observed from Tables 4, 5, and 6 that AR modeling performed the best R values within AR, GEP, FFNN, RBFN, and ANFIS techniques for training and testing sets. The GEP and ANFIS models have higher performance than other data-driven models developed in this study. In processing of AR modeling given above, there is not good agreement between the AR(3) model and historical flow series, and it was shown that RMSE criterion of AR(3) model is 55.243 for testing set. The AR(2) model has the best agreement with historical series compared to AR(1) and AR(3) models, and the highest R (0.842) and lowest RMSE (34.601) criteria for testing set. Also, this situation was generally supported by GEP, FFNN, RBFN, and ANFIS models developed by using F (t−1) and F (t−2) parameters. The results of the AR(2) model were plotted against monthly flow measurements for training and testing sets in Fig. 11. The results of the all models developed by using F (t−1), F (t−2) parameters together with the monthly flow measurements for testing set were presented in Fig. 12. As seen from Fig. 12, the AR(2) model provided much closer values to the observed flow values than the other models.

Fig. 11
figure 11

The scatter diagrams between the AR(2) model versus monthly flow measurements for a training set and b testing set

Full size image
Fig. 12
figure 12

Time series of forecasted and measured monthly flow values for testing set

Full size image

5 Conclusions

This study investigated the ability of AR modeling and GEP, FFNN, RBFN, and ANFIS data-driven techniques to forecast monthly mean flow values. The proposed methods were applied to Kızılırmak River, in Turkey which is used in irrigation, in power generation, and as drinking water. The various models were developed by using lagged monthly mean flow values obtained from Yamula (1501) station of Kızılırmak River. The comparison results indicated that AR models gave better performance than the data-driven models. This is because the AR model is a univariate model. It was shown that the AR(2) model had the best correlation coefficient in the AR models. The GEP and ANFIS models obtained better results than the other data-driven models except AR(2). The performance of the developed models suggested that the flow could be forecasted using AR approaches. Finally, AR(2) model can be used for forecasting flow in which measurement system has failed or to forecast missing monthly flow data in hydrological modeling studies. Also, it is important to underline the high computing speed gained by data-driven approaches in comparison with stochastic models. The performance of the data-driven models can be improved by using flow data of another station and rainfall data as input parameters in future studies.