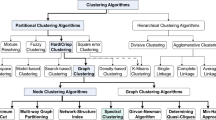
Abstract
Spectral clustering is a clustering method based on algebraic graph theory. It has aroused extensive attention of academia in recent years, due to its solid theoretical foundation, as well as the good performance of clustering. This paper introduces the basic concepts of graph theory and reviews main matrix representations of the graph, then compares the objective functions of typical graph cut methods and explores the nature of spectral clustering algorithm. We also summarize the latest research achievements of spectral clustering and discuss several key issues in spectral clustering, such as how to construct similarity matrix and Laplacian matrix, how to select eigenvectors, how to determine cluster number, and the applications of spectral clustering. At last, we propose several valuable research directions in light of the deficiencies of spectral clustering algorithms.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Clustering is an important research field in data mining. The purpose of clustering is to divide a dataset into natural groups so that data points in the same group are similar while data points in different groups are dissimilar to each other [56]. Traditional clustering methods, such as k-means algorithm [30, 41], FCM algorithm [21], and EM algorithm [13], are simple, but lack the ability to handle complex data structures. When the sample space is non-convex, these algorithms are easy to fall into local optimum [29].
In recent years, spectral clustering has aroused more and more attention of academia, due to its good clustering performance and solid theoretical foundation [47]. Spectral clustering does not make any assumptions on the global structure of the data. It can converge to global optimum and performs well for the sample space of arbitrary shape, especially suitable for non-convex dataset [16]. The idea of spectral clustering is based on spectral graph theory. It treats data clustering problem as a graph partitioning problem and constructs an undirected weighted graph with each point in the dataset being a vertex and the similarity value between any two points being the weight of the edge connecting the two vertices [8]. Then, we can decompose the graph into connected components by certain graph cut method and call those components as clusters.
There are a variety of traditional graph cut methods, such as minimum cut, ratio cut, normalized cut and min/max cut. The optimal clustering results can be obtained by minimizing or maximizing the objective function of the graph cut methods. However, for various graph cut methods, seeking the optimal solution of the objective function is often NP-hard. With the help of spectral method, the original problem can be solved in polynomial time by relaxing the original discrete optimization problem to the real domain [17]. In graph partitioning, a point can be considered part belonging to subset A and part belonging to subset B, rather than strictly belonging to one cluster. It can be proved that the classification information of vertices is contained in the eigenvalues and eigenvectors of graph Laplacian matrix. And we can get good clustering results, if we make full use of the classification information during the clustering process [35]. Spectral clustering can get the relaxation solution of graph cut objective function, which is an approximate optimal solution.
The earliest study on spectral clustering began in 1973. Donath and Hoffman put forward that graph partitioning can be built based on the eigenvectors of adjacency matrix [18]. In the same year, Fiedler proved that the bipartition of a graph is closely related to the second eigenvector of Laplacian matrix [23]. He suggested using this eigenvector to conduct graph partitioning. Hagen and Kahng found the relations among clustering, graph partitioning and the eigenvectors of similarity matrix, and constructed a practical algorithm first [25]. They proposed ratio cut method in 1992. In 2000, Shi and Malik proposed normalized cut [55]. This method not only considers the external connections between clusters, but also considers the internal connections within a cluster, so it can produce balanced clustering results. Then, Ding et al. [14] proposed min/max cut; Ng et al. [51] proposed classic NJW algorithm. These algorithms are based on matrix spectral theory to classify data points, so they are called spectral clustering. Since 2000, spectral clustering has gradually become a research hotspot of data mining. At present, spectral clustering has been successfully applied to many fields, such as computer vision [42, 76], integrated circuit design [2], load balancing [20, 27], biological information [33, 52], and text classification [69], etc. Spectral clustering algorithms provide a new idea to solve the problem of clustering and can effectively deal with many practical problems, so their research has great scientific value and application potential.
This paper is organized as follows: Sect. 2 introduces the basic concepts of algebraic graph theory, compares the objective functions of typical graph cut methods, and explores the nature of spectral clustering algorithm; Sect. 3 summarizes the latest research achievements of spectral clustering and discusses several key issues in spectral clustering, such as how to construct similarity matrix and Laplacian matrix, how to select eigenvectors, how to determine cluster number, and the applications of spectral clustering; finally, several valuable research directions are proposed, in light of the deficiencies of spectral clustering algorithms.
2 Basic concepts of spectral clustering
2.1 Algebraic graph theory
Graph theory originated in the famous problem of Konigsberg Seven Bridges, which is an important branch of mathematics. It is the study of theories and methods about graphs. Algebraic graph theory is a cross-field combining graph theory, linear algebra, and matrix computation theory. As one of the branches of the graph theory, the research of algebraic graph theory began in the 1850s, aiming to use algebraic methods to study the graph, convert graph characteristics into algebraic characteristics, and then use the algebraic characteristics and algebraic methods to deduce the theorems about graphs [19]. In fact, the main content of algebraic graph theory is spectrum. Here, spectrum represents the eigenvalues and their multiplicities of matrix. The earliest research on algebraic graph theory is made by Fiedler [23]. He derived the algebraic criterion about the connectivity of graph. Whether a graph is connected or not can be judged by the second smallest eigenvalue of Laplacian matrix. Later, the eigenvector corresponding to the second smallest eigenvalue is named Fiedler vector, which contains the instruction information about dividing a graph into two parts.
Adjacency matrix (denoted as A) and Laplacian matrix (denoted as L) are commonly used representations for graph. The adjacency matrix of weighted graph uses real numbers to reflect the different relations between vertices. Laplacian matrix L = D − A, where D is a diagonal matrix, the diagonal values equal to the absolute row sums of A, and the non-diagonal elements are 0. Most spectral clustering algorithms are based on the spectrum of Laplacian matrix to split graphs. There are two kinds of Laplacian matrixes: un-normalized Laplacian matrix (L) and normalized Laplacian matrix. Normalized Laplacian matrix includes symmetric form (denoted as L s ) and random walk form (denoted as L r ). Their expressions are shown in Table 1.
Mohar introduced some characteristics of un-normalized Laplacian matrix [46]. Shi and Malik studied the characteristics of normalized Laplacian matrix [55]. The spectrum of Laplacian matrix provides very useful information for graph partitioning. Based on Fiedler vector, we can divide a graph into two parts; based on multiple main eigenvectors, we can divide a graph into k parts. Luxburg made a comprehensive summary about the characteristics of Laplacian matrix [60]. Whether we should use un-normalized Laplacian matrix or normalized Laplacian matrix is still under discussion. Ng et al. [51] provided the evidence that normalized Laplacian matrix is more suitable for spectral clustering, which means that the performance of normalized spectral clustering is better than un-normalized spectral clustering. Higham Kibble pointed out that under certain conditions, un-normalized spectral clustering can produce better clustering results [28]. While, Luxburg et al. [40] proved that from the view of statistical consistency theory, normalized Laplacian matrix is superior to un-normalized Laplacian matrix.
Table 1 also shows the expression of probability transition matrix (denoted as P). Probability transition matrix is essentially the normalized form of similarity matrix. Since the row sum of normalized similarity matrix is 1, the elements in P can be understood as the Markov transition probability. The larger the transition probability between two nodes, the possibility that they belong to the same cluster is greater. The spectrum of probability transition matrix also contains the necessary information to split a graph, but it is slightly different from the spectrum of Laplacian matrix. In probability transition matrix, the eigenvector corresponding to the second largest eigenvalue can indicate the bipartition of a graph, and multiple eigenvectors corresponding to the main eigenvalues can indicate the multi-partition of a graph [43].
Another novel matrix is modularity matrix (denoted as B), which comes from the study of community structure in complex networks [48, 49, 34]. It has a clear physical meaning, and its expression is shown in Table 1. In the expression, d represents the column vector, whose elements are the degree of nodes; m represents the total weight of graph edges; the elements of B is the difference between the actual edge number and the desired edge number of pairwise nodes, which also represents the extent that actual edge number beyond desired edge number. Therefore, this matrix leads directly to an objective function that the optimal partition should make the edges of communities (corresponding to “clusters”) as dense as possible, preferably beyond expected. As for matrix characteristics, modularity matrix and Laplacian matrix have some similarities, such as row sum (column sum) is 0 and 0 is the eigenvalue. But they also have an obvious difference that modularity matrix is not a positive semi-definite matrix, so, some of its eigenvalues may be negative. As for graph partitioning, the bipartition of a network is based on the eigenvector of the largest eigenvalue, and the multi-partition of a network is based on multiple main eigenvectors.
2.2 Graph cut methods
Spectral clustering uses the similarity graph to deal with the problem of clustering. Its final purpose is to find a partition of the graph such that the edges between different groups have very low weights, which means that points in different clusters are dissimilar from each other; and the edges within a group have high weights, which means that points within the same cluster are similar to each other. The prototype of graph cut clustering is minimum spanning tree (MST) method [59, 72]. MST clustering method is proposed by Zahn [72]. This algorithm builds the minimum spanning tree by the adjacency matrix of graph, and then removes the edges with large weights from the minimum spanning tree to get a set of connected components. This method is successful in detecting clearly separated clusters, but if the density of nodes is changed, its performance will deteriorate. Another disadvantage is Zahn’s research is under the circumstance that the cluster structure (such as separating cluster, contact cluster, density cluster, etc.) is known in advance.
Cutting a graph means to divide a graph into multiple connected components by removing certain edges, and the sum of weight of the removed edges is called cut. Bames first proposed minimum cut clustering criteria [6]. Its basic idea is seeking the minimum cut while dividing a graph into k connected sub-graphs. Then Alpert and Yao put forward the spectral method to solve the minimum cut criteria, which laid an important foundation for the later development of spectral clustering [3]. Wu and Leahy applied minimum cut to image segmentation and based on the maximum network flow theory to calculate the minimum cut [66]. Minimum cut clustering is successful in some applications of image segmentation, but the biggest problem is it may lead to serious uneven split, such as “solitary point” or “small cluster”. In order to solve this problem, Wei and Cheng proposed ratio cut [65], Sarkar and Soundararajan proposed average cut [54], Shi and Malik proposed normalized cut [55], Ding et al. [14] proposed Min/Max cut. The expressions of their objective functions are shown in Table 2. These optimization objectives are able to produce more balanced split.
Take graph bipartition for example. Assume V is a given set of data points. A represents a subset of V, and B represents V/A. For illustrative purposes, we define the following four terms:
-
1.
\( {\text{Cut}}(A,B) = \sum\nolimits_{i \in A,j \in B} {w_{ij} } \) denotes the sum of connection weights between cluster A and B.
-
2.
\( {\text{Cut}}(A,A) = \sum\nolimits_{i \in A,j \in A} {w_{ij} } \) denotes the sum of connection weights within cluster A.
-
3.
\( {\text{Vol}}(A) = \sum\nolimits_{i \in A} {d_{i} } \) denotes the total degrees of the vertices in cluster A.
-
4.
\( \left| A \right| = n_{A} \) denotes the number of vertices in cluster A, which is used to describe the size of cluster A.
The study of complex networks has caused great attention in the past decade. Complex networks possess a rich, multi-scale structure reflecting the dynamical and functional organization of the systems they model [44]. Newman systematically studied the spectral algorithm for community structure in non-weighted network, weighted network, as well as directed network [34, 48, 50]. He uses modularity function to detect communities. Modularity criterion is a novel idea. Take non-weighted graph for example: only if the real proportion of edges in communities is greater than the “expected” proportion, the split is considered to be reasonable. The “expected” edge number is derived from a random graph model, which is based on the configuration model. This is obviously different from the starting point of traditional graph cut clustering methods. The modularity function is shown in Table 2, where Q represents modularity, m represents the number of edges contained in the graph, k i represents the degree of node i (k j is similar), v i and v j is −1 or 1. v i ≠ v j indicate node i and j belong to different communities; v i = v j indicate node i and j belong to the same community.
Minimizing ratio cut, average cut, normalized cut, and maximizing modularity are all NP discrete optimization problems. Fortunately, spectral method can provide a loose solution within polynomial time for these optimization problems. Here, “loose” means relax the discrete optimization problem to the real number field, and then using some heuristic approach to re-convert it to a discrete solution. The essence of graph partitioning can be summarized as the minimization or maximization problem of matrix trace. To complete the minimizing or maximizing tasks need to rely on spectral clustering algorithm.
Usually most spectral clustering algorithms are formed of the following three stages: preprocessing, spectral representation and clustering [26]. First construct the graph and similarity matrix to represent the dataset; then form the associated Laplacian matrix, compute eigenvalues and eigenvectors of the Laplacian matrix, and map each point to a lower-dimensional representation, based on one or more eigenvectors; at last, assign points to two or more classes, based on the new representation. In order to partition a dataset or graph into k (k > 2) clusters, there are two basic approaches: recursive 2-way partitioning and k-way partitioning. The comparison of these two methods is shown in Table 3.
3 The latest development of spectral clustering
Spectral clustering is a large family of grouping methods, and its research is very active in machine learning and data mining, because of the universality, efficiency, and theoretical support of spectral analysis. Next, we will discuss the latest development of spectral clustering from the following aspects: “construct similarity matrix”, “form Laplacian matrix”, “select eigenvectors”, “the number of clusters” and “the applications of spectral clustering”.
3.1 Construct similarity matrix
The key to spectral clustering is to select a good distance measurement, which can well describe the intrinsic structure of data points. Data in the same groups should have high similarity and follow space consistency. Similarity measurement is crucial to the performance of spectral clustering [62]. The Gaussian kernel function is usually adopted as the similarity measure. However, with a fixed scaling parameter σ, the similarity between two data points is only determined by their Euclidean distance and is not adaptive to their surroundings. While dealing with complex dataset, the similarity simply based on Euclidean distance cannot reflect the data distribution accurately and in turn resulting in the poor performance of spectral clustering.
Zhang et al. [74] propose a local density adaptive similarity measure—CNN (Common-Near-Neighbor), which uses the local density between two data points to scale the Gaussian kernel function. CNN method is based on the following observation: if two points are distributed in the same cluster, they are in the same region which has a relatively high density. It has an effect of amplifying intra-cluster similarity thus making the affinity matrix clearly block diagonal. Experimental results show that the spectral clustering algorithm with local density adaptive similarity measure outperforms the traditional spectral clustering algorithm, the path-based spectral clustering algorithm and the self-tuning spectral clustering algorithm.
Yang et al. [70] develop a density sensitive distance measure. This measure defines the adjustable line segment length, which can adjust the distance in regions with different density. It squeezes the distances in high density regions while widen them in low density regions. By the distance measure, they design a new similarity function for spectral clustering. Compared with the spectral clustering based on conventional Euclidean distance or Gaussian kernel function, the proposed algorithm with density sensitive similarity measure can obtain desirable clusters with high performance on both synthetic and real life datasets.
Wang et al. [64] present spectral multi-manifold clustering (SMMC), based on the analysis that spectral clustering is able to work well when the similarity values of the points belonging to different clusters are relatively low. In their model, the data are assumed to lie on or close to multiple smooth low-dimensional manifolds, where some data manifolds are separated but some are intersecting. Then, local geometric information of the sampled data is incorporated to construct a suitable similarity matrix. Finally, spectral method is applied to this similarity matrix to group the data. SMMC achieves good performance over a broad range of parameter settings and is able to handle intersections, but its robustness remains to be improved.
In order to better describe the data distribution, Zhang and You propose a random walk based approach to process the Gaussian kernel similarity matrix [75]. In this method, the pairwise similarity between two data points is not only related to the two points, but also related to their neighbors. Li and Guo develop a new affinity matrix generation method using neighbor relation propagation principle [36]. The affinity matrix generated can increase the similarity of point pairs that should be in same cluster and can well detect the structure of data. Blekas and Lagaris introduce Newtonian spectral clustering based on Newton’s equations of motion [7]. They build an underlying interaction model for trajectory analysis and employ Newtonian preprocessing to gain valuable affinity information, which can be used to enrich the affinity matrix.
3.2 Form Laplacian matrix
After the similarity matrix is constructed, the next step is forming the corresponding Laplacian matrix according to different graph cut methods. There are three forms of traditional Laplacian matrix, which are, respectively, suitable for different clustering conditions. The selection of graph cut methods and the establishment of Laplacian matrix both have an important impact on the performance of spectral clustering algorithms.
As a natural nonlinear generalization of graph Laplacian, p-Laplacian has recently been applied to two-class cases. Luo et al. [39] propose full eigenvector analysis of p-Laplacian and obtain a natural global embedding for multi-class clustering problems, instead of using greedy search strategy implemented by previous researchers. An efficient gradient descend optimization approach is introduced to obtain the p-Laplacian embedding space, which is guaranteed to converge to feasible local solutions. Empirical results suggest that the greedy search method often fails in many real-world applications with non-trivial data structures, but this approach consistently gets robust clustering results and preserves the local smooth manifold structures of real-world data in the embedding space.
Yang et al. [71] propose a new image clustering algorithm, referred to as clustering using local discriminant models and global integration (LDMGI). A new Laplacian matrix is learnt in LDMGI by exploiting both manifold structure and local discriminant information. This algorithm constructs a local clique for each data point sampled from a nonlinear manifold, and uses a local discriminant model to evaluate the clustering performance of samples within the local clique. Then a unified objective function is proposed to globally integrate the local models of all the local cliques. Compared with Normalized cut, LDMGI is more robust to algorithmic parameter and is more appealing for the real image clustering applications, in which the algorithmic parameters are generally not available for tuning.
Most graph Laplacians are base on the Euclidean distance, which does not necessarily reflect the inherent distribution of the data. So Xie et al. [68] propose a method to directly optimize the normalized graph Laplacian by using pairwise constraints. The learned graph is consistent with equivalence and non-equivalence pairwise relationships, which can better represent the similarity between samples. Meanwhile, this approach automatically determines the scaling parameter during the optimization. The learned normalized Laplacian matrix can be directly applied in spectral clustering and semi-supervised learning algorithms.
Frederix and Van Barel use linear algebra techniques to solve the eigenvalue problem of a graph Laplacian and propose a novel sparse spectral clustering method [24]. This method exploits the structure of the Laplacian to construct an approximation, not in terms of a low-rank approximation but in terms of capturing the structure of the matrix. With this approximation, the size of the eigenvalue problem can be reduced. Chen and Feng present a novel k-way spectral clustering algorithm called discriminant cut (Dcut) [10]. It normalizes the similarity matrix with the corresponding regularized Laplacian matrix. Dcut can reveal the internal relationships among data and produce exciting clustering results.
3.3 Select eigenvectors
The eigenvalues and eigenvectors of Laplacian matrix can be obtained by eigen-decomposition. An analysis of the characteristics of eigenspace is carried out which shows that: (a) not every eigenvector of a Laplacian matrix is informative and relevant for clustering; (b) eigenvector selection is critical because using uninformative/irrelevant eigenvectors could lead to poor clustering results; (c) the corresponding eigenvalues cannot be used to select relevant eigenvectors given a realistic dataset. NJW algorithm partitions data using the largest k eigenvectors of the normalized Laplacian matrix derived from the dataset. However, some experiments demonstrate that the top k eigenvectors cannot always detect the structure of the data for real pattern recognition problems. So it is necessary to find a better way to select eigenvectors for spectral clustering.
Xiang and Gong propose the concept of “eigenvector relevance”, which differs from previous approaches in that only informative/relevant eigenvectors are employed for determining the number of clusters and performing clustering [67]. The key element of their algorithm is a simple but effective relevance learning method, which measures the relevance of an eigenvector according to how well it can separate the dataset into different clusters. Experimental results show that this algorithm is able to estimate the cluster number correctly and reveal natural grouping of the input data/patterns even given sparse and noisy data.
Zhao et al. [77] propose an eigenvector selection method based on entropy ranking for spectral clustering (ESBER). In this method, first all the eigenvectors are ranked according to their importance on clustering, and then a suitable eigenvector combination is obtained from the ranking list. There are two strategies to select eigenvectors in the ranking list of eigenvectors: one is directly adopting the first k eigenvectors in the ranking list, which are the most important eigenvectors among all the eigenvectors, different to the largest k eigenvectors of NJW method; the other strategy is to search a suitable eigenvector combination among the first k m (k m > k) eigenvectors in the ranking list, which can reflect the structure of the original data. ESBER method is more robust than NJW method and can obtain satisfying clustering results in most cases.
Rebagliati and Verri find a fundamental working hypothesis of NJW algorithm, that the optimal partition of k clusters can be obtained from the largest k eigenvectors of matrix L sym, only if the gap between the k-th and the k + 1-th eigenvalue of L sym is sufficiently large. If the gap is small, a perturbation may swap the corresponding eigenvectors and the results can be very different from the optimal ones. So they suggest a weaker working hypothesis: the optimal partition of k clusters can be obtained from a k-dimensional subspace of the first m (m > k) eigenvectors, where m is a parameter chosen by the user [53]. The bound of m is based upon the gap between the m + 1-th and the k-th eigenvalue and ensures stability of the solution. This algorithm is robust to small changes of the eigenvalues, and gives satisfying results on real-world graphs by selecting correct k-dimensional subspaces of the linear span of the first m eigenvectors.
3.4 The number of clusters
In most spectral clustering algorithms, the number of clusters must be manually set and it is very sensitive to initialization. How to accurately estimate the number of clusters is one of the major challenges faced by spectral clustering. Some existing approaches attempt to get the optimal cluster number by minimizing some distance-based dissimilarity measure within clusters.
Wang proposes a novel selection criterion, whose key idea is to select the number of clusters as the one maximizing the clustering stability [61]. Since maximizing the clustering stability is equivalent to minimizing the clustering instability, they develop an estimation scheme for the clustering instability based on modified cross-validation. The idea of this scheme is to split the data into two training datasets and one validation dataset, where the two training datasets are used to construct two clustering and the validation dataset is used to measure the clustering instability. This selection criterion is applicable to all kinds of clustering algorithms, including distance-based or non-distance-based algorithms. However, the data splitting reduces the sizes of training datasets, so the effectiveness of the cross-validation method is remained to be further studied.
The concept of clustering stability can measure the robustness of any given clustering algorithm. Inspired by Wang’s method [61], Fang and Wang develop a new estimation scheme for clustering instability based on the bootstrap, in which the number of clusters is selected so that the corresponding estimated clustering instability is minimized [22]. The implementation of the bootstrap method is straightforward, and it has a number of advantages. First, the bootstrap samples are of the same size as that of the original data, so the bootstrap method is more efficient. Second, the bootstrap estimate of the clustering instability is the nonparametric maximum likelihood estimate (MLE). Third, the bootstrap method can provide the instability path of a clustering algorithm for any given number of clusters.
Tepper et al. [57] introduce a perceptually driven clustering method, in which the number of clusters is automatically determined by setting parameter ε that controls the average number of false detections. The detection thresholds are well adapted to accept/reject non-clustered data and can help find the right number of clusters. This method only takes into account inter-point distances and has no random steps. Besides, it is independent from the original data dimensionality, which means that its running time is not affected by an increase in dimensionality. The combination of this method with normalized cuts performs well on both synthetic and real-world datasets and the detected clusters are perceptually significant.
3.5 The applications of spectral clustering
Nowadays, spectral clustering has been successfully applied to many areas, such as data analysis, speech separation, video indexing, character recognition, image processing, etc. In such applications, the number of data points to cluster can be enormous. Indeed, a small 256 × 256 gray level image leads to a dataset of 65,536 points, while 4 s of speech sampled at 5 kH leads to more than 20,000 spectrogram samples. In addition, real-world datasets often contain a lot of outliers and noise points with complex data structures [38]. All these issues should be carefully considered when dealing with the specific clustering problems.
Bach and Jordan use spectral clustering to solve the problem of speech separation and present a blind separation algorithm, which separates speech mixtures from a single microphone without requiring models of specific speakers [5]. It works within a time–frequency representation (a spectrogram), and exploits the sparsity of speech signals in this representation. That is, although two speakers might speak simultaneously, there is relatively little overlap in the time–frequency plane if the speakers are different. Thus, speech separation can be formulated as a problem in segmentation in the time–frequency plane. Bach et al. have successfully demixed speech signals from two speakers using this approach.
Video indexing requires the efficient segmentation of video into scenes. A scene can be regarded as a series of semantically correlated shots. The visual content of each shot can be represented by one or multiple frames, called key-frames. Chasanis et al. [9] develop a new approach for video scene segmentation. To cluster the shots into groups, they propose an improved spectral clustering method that both estimates the number of clusters and employs the fast global k-means algorithm in the clustering stage after the eigenvector computation of the similarity matrix. The shot similarity is computed based only on visual features and a label is assigned to each shot according to the group that it belongs to. Then, a sequence alignment algorithm is applied to detect when the pattern of shot labels changes, providing the final scene segmentation result. This scene detection method can efficiently summarize the content of each shot and detect most of the scene boundaries accurately, while preserving a good tradeoff between recall and precision.
Zeng et al. [73] apply spectral clustering to recognize handwritten numerals and obtain satisfying results. They first select the Zernike moment features of handwritten numerals based on the principles that the distinction degree of inside-cluster features is small and the dividing of the features between clusters is huge; then construct the similarity matrix between handwritten numerals by the similarity measure based on Grey relational analysis and make transitivity transformation to the similarity matrix for better block symmetry after reformation; finally make spectrum decomposition to the Laplacian matrix derived from the reformed similarity matrix, and recognize the handwritten numerals with the eigenvectors corresponding to the second minimal eigenvalue of Laplacian matrix as the spectral features. This algorithm is robust to outliers and its recognition is also very effective.
Spectral clustering has been broadly used in image segmentation. Liu et al. [37] take into account the spatial information of the pixels in image and propose a novel non-local spatial spectral clustering algorithm, which is robust to noise and other imaging artifacts. Nowadays, High-Definition (HD) images are widely used in television broadcasting and movies. Segmenting these high resolution images presents a grand challenge because of significant computational demands. Wang and Dong develop a multi-level low-rank approximation-based spectral clustering method, which can effectively segment high resolution images [63]. They also develop a fast sampling strategy to select sufficient data samples, leading to accurate approximation and segmentation. In order to deal with large images, Tung et al. [58] propose an enabling scalable spectral clustering algorithm, which combines a blockwise segmentation strategy with stochastic ensemble consensus. The purpose of using stochastic ensemble consensus is to integrate both global and local image characteristics in determining the pixel classifications.
Ding et al. [15] focus on controlled islanding problem and use spectral clustering to find a suitable islanding solution for preventing the initiation of wide area blackouts. The objective function used in this controlled islanding algorithm is the minimal power-flow disruption. It is demonstrated that this algorithm is computationally efficient when solving the controlled islanding problem, particularly in the case of a large power system. Adefioye et al. [1] develop a multi-view spectral clustering algorithm for chemical compound clustering. The tensor-based spectral methods provide chemically appropriate and statistically significant results when attempting to cluster compounds from multiple data sources. Experiments show that compounds of extremely different chemotypes clustering together, which can help reveal the internal relations of these compounds.
4 Conclusion and prospect
Spectral clustering is an elegant and powerful approach for clustering, which has been widely used in many fields. Especially in the graph and network areas, a lot of personalized improved algorithms have emerged. Why spectral clustering attracts so many researchers, there are three most important reasons: firstly, it has a solid theoretical foundation—algebraic graph theory; secondly, for complex cluster structure, it can get a global loose solution; thirdly, it can solve the problem within a polynomial time. However, as a novel clustering method, spectral clustering is still in the development stage, and there are many problems worthy of further study.
-
1.
Semi-supervised spectral clustering
Traditional spectral clustering is an unsupervised learning that does not take into account the clustering intention of the user. User intention is actually a priori knowledge, also known as the supervised information. The clustering algorithm guided by supervised information is called semi-supervised clustering. Limited priori knowledge can be easily obtained from samples in practice, such as the pairwise constraints of samples. A large number of studies have shown that making full use of priori knowledge in the process of searching clusters can significantly improve the performance of the clustering algorithm [11, 32]. Therefore, it will be very meaningful to combine priori knowledge with spectral clustering and carry out the research of semi-supervised spectral clustering.
-
2.
Fuzzy spectral clustering
Most of the existing spectral clustering algorithms are hard partition methods. They strictly divide each object into a class and the class of an object is either this or that, which belongs to the scope of classical set theory. In fact, most objects do not have strict properties. These objects are intermediary in forms and classes, suitable for soft division [45]. The classical set theory often cannot completely solve the classification problems of ambiguity. Fuzzy set theory proposed by Zadeh, provides a powerful tool for this soft division. Applying fuzzy set theory to spectral clustering and studying effective fuzzy spectral clustering algorithms are also very significant.
-
3.
Kernel spectral clustering
Spectral clustering algorithms are mostly based on some similarity measure to classify the samples, so that similar samples are gathered into the same cluster, while dissimilar samples are separated into different clusters. Thus, the clustering process is mainly dependent on the characteristic difference between the samples. If the distribution of samples is very complex, conventional methods may not be able to get ideal clustering results. Using kernel methods can enlarge the useful features of samples by mapping them to a high dimensional feature space, so that the samples are easier to clustering, and the convergence speed of the algorithm will be accelerated [4]. Therefore, when dealing with complex clustering problems, the combination of kernel methods and spectral techniques can be considered as a valuable research direction.
-
4.
Clustering of large datasets
Spectral clustering algorithms involve the calculation of eigenvalues and eigenvectors. The underlying eigen-decomposition takes cubic time and quadratic space with regard to the dataset size [12]. These can be reduced by the Nystrom method which samples only a subset of columns from the matrix. However, the manipulation and storage of these sampled columns can still be expensive when the dataset is large. Time and space complexity has become an obstacle for the generalization of spectral clustering in practical applications. So, it is worthy of deep study to explore an effective method to reduce the computation complexity of spectral clustering algorithms, and make them suitable for massive learning problems.
-
5.
Spectral clustering ensemble
Traditional spectral clustering algorithms are sensitive to the scaling parameter and have inherent randomness. In order to overcome these problems, clustering ensemble strategy can be introduced to spectral clustering [31]. Because it is possible to get better clusters by searching the combination of multiple clustering results. Clustering ensemble can make full use of the results of learning algorithms under different conditions and find the cluster combinations that cannot be obtained by a single clustering algorithm. Thus, the spectral clustering ensemble algorithm is able to improve the quality and stability of the clustering results, with strong robustness to noise, outliers, and sample changes.
References
Adefioye AA, Liu XH, Moor BD (2013) Multi-view spectral clustering and its chemical application. Int J Comput Biol Drug Des 6(1–2):32–49
Alpert CJ, Kahng AB (1995) Multi-way partitioning via geometric embeddings, orderings and dynamic programming. IEEE Trans Comput-Aaid Des Integr Circuits Syst 14(11):1342–1358
Alpert CJ, Yao SZ (1995) Spectral partitioning: the more eigenvectors, the better. In: Proceedings of the 32nd annual ACM/IEEE design automation conference. ACM, New York, pp 195–200
Alzate C, Suykens JAK (2012) Hierarchical kernel spectral clustering. Neural Netw 35:21–30
Bach FR, Jordan MI (2006) Learning spectral clustering, with application to speech separation. J Mach Learn Res 7:1963–2001
Bames ER (1982) An algorithm for partitioning the nodes of a graph. SIAM J Algebraic Discrete Methods 17(5):541–550
Blekas K, Lagaris IE (2013) A spectral clustering approach based on Newton’s equations of motion. Int J Intell Syst 28(4):394–410
Cai XY, Dai GZ, Yang LB (2008) Survey on spectral clustering algorithms. Comput Sci 35(7):14–18
Chasanis VT, Likas AC, Galatsanos NP (2009) Scene detection in videos using shot clustering and sequence alignment. IEEE Trans Multimed 11(1):89–100
Chen WF, Feng GC (2012) Spectral clustering with discriminant cuts. Knowl-Based Syst 28:27–37
Chen WF, Feng GC (2012) Spectral clustering: a semi-supervised approach. Neurocomputing 77(1):229–242
Chen WY, Song YQ, Bai HJ et al (2011) Parallel spectral clustering in distributed systems. IEEE Trans Patt Anal Mach Intell 33(3):568–586
Dempster AP, Laird NM, Rubin DB (1977) Maximum likelihood from incomplete data via the EM algorithm. J R Stat Soc Ser B Stat Methodol 39(1):1–38
Ding CHQ, He X, Zha H et al (2001) A min-max cut algorithm for graph partitioning and data clustering. In: Proceedings of IEEE international conference on data mining (ICDM’ 2001), pp 107–114
Ding L, Gonzalez-Longatt FM, Wall P, Terzija V (2013) Two-step spectral clustering controlled islanding algorithm. IEEE Trans Power Syst 28(1):75–84
Ding SF, Jia HJ, Zhang LW et al (2012) Research of semi-supervised spectral clustering algorithm based on pairwise constraints. Neural Comput Appl. doi:10.1007/s00521-012-1207-8
Ding SF, Qi BJ, Jia HJ et al (2013) Research of semi-supervised spectral clustering based on constraints expansion. Neural Comput Appl 22(Suppl 1):S405–S410
Donath WE, Hoffman AJ (1973) Lower bounds for the partitioning of graph. IBM J Res Dev 17(5):420–425
Dong XW, Frossard P, Vandergheynst P, Nefedov N (2012) Clustering with multi-layer graphs: a spectral perspective. IEEE Trans Sig Process 60(11):5820–5831
Driessche RV, Roose D (1995) An improved spectral bisection algorithm and its application to dynamic load balancing. Parallel Comput 21(1):29–48
Dunn JC (1974) Well-separated clusters and the optimal fuzzy partitions. J Cybern 4(1):95–104
Fang YX, Wang JH (2012) Selection of the number of clusters via the bootstrap method. Comput Stat Data Anal 56(3):468–477
Fiedler M (1973) Algebraic connectivity of graphs. Czechoslov Math J 23(2):298–305
Frederix K, Van Barel M (2013) Sparse spectral clustering method based on the incomplete Cholesky decomposition. J Comput Appl Math 237(1):145–161
Hagen L, Kahng AB (1992) New spectral methods for radio cut partitioning and clustering. IEEE Trans Comput-aid Des Integr Circuits Syst 11(9):1074–1085
Hamad D, Biela P (2008) Introduction to spectral clustering. In: 3rd International conference on information and communication technologies: from theory to applications, 1–5, pp 490–495
Hendrickson B, Leland R (1995) An improved spectral graph partitioning algorithm for mapping parallel computations. SIAM J Sci Comput 16(2):452–459
Higham DJ, Kibble M (2004) A unified view of spectral clustering. In: University of Strathclyde Mathematics Research Report 02
Huang Z (1997) A fast clustering algorithm to cluster very large categorical data sets in data mining. In: Proceedings of the SIGMOD workshop on research issues on data mining and knowledge discovery. Tucson, pp 146–151
Huang Z (1998) Extensions to the k-means algorithm for clustering large data sets with categorical values. Data Min Knowl Discov 2(3):283–304
Jia JH, Xiao X, Liu BX, Jiao LC (2011) Bagging-based spectral clustering ensemble selection. Patt Recogn Lett 32(10):1456–1467
Jiao LC, Shang FH, Wang F, Liu YY (2012) Fast semi-supervised clustering with enhanced spectral embedding. Patt Recogn 45(12):4358–4369
Kluger Y, Basri R, Chang JT et al (2003) Spectral biclustering of microarray data: coclustering genes and conditions. Genome Res 13(4):703–716
Leicht EA, Newman MEJ (2008) Community structure in directed networks. Phys Rev Lett 100(11):118703
Li JY, Zhou JG, Guan JH et al (2011) A survey of clustering algorithms based on spectra of graphs. CAAI Trans Intell Syst 6(5):405–414
Li XY, Guo LJ (2012) Constructing affinity matrix in spectral clustering based on neighbor propagation. Neurocomputing 97:125–130
Liu HQ, Jiao LC, Zhao F (2010) Non-local spatial spectral clustering for image segmentation. Neurocomputing 74(1–3):461–471
Liu HQ, Zhao F, Jiao LC (2012) Fuzzy spectral clustering with robust spatial information for image segmentation. Appl Soft Comput 12(11):3636–3647
Luo DJ, Huang H, Ding C, Nie FP (2010) On the eigenvectors of p-Laplacian. Mach Learn 81(1):37–51
Luxburg U, Belkin M, Bousquet O (2008) Consistency of spectral clustering. Ann Stat 36(2):555–586
MacQueen J (1967) Some methods for classification and analysis of multivariate observations. In: Proceedings of 5th Berkeley symposium on mathematical statistics, 1, pp 281–297
Malik J, Belongie S, Leung T et al (2001) Contour and texture analysis for image segmentation. Int J Comput Vis 43(1):7–27
Meila M, Shi JB (2001) Learning segmentation by random walks. Advances in neural information processing systems. MIT Press, Cambridge, pp 873–879
Michoel T, Nachtergaele B (2012) Alignment and integration of complex networks by hypergraph-based spectral clustering. Phys Rev E 86(5):056111
Mirkin B, Nascimento S (2012) Additive spectral method for fuzzy cluster analysis of similarity data including community structure and affinity matrices. Inf Sci 183(1):16–34
Mohar B (1997) Some applications of Laplace eigenvalues of graphs. Graph Symmetry Algebraic Methods Appl 497(22):227–275
Nascimento MCV, de Carvalho ACPLF (2011) Spectral methods for graph clustering: a survey. Eur J Oper Res 211(2):221–231
Newman MEJ (2004) Analysis of weighted networks. Phys Rev E 70(5):056131
Newman MEJ (2006) Finding community structure in networks using the eigenvectors of matrices. Phys Rev E 74(3):036104
Newman MEJ (2006) Modularity and community structure in networks. Proc Nat Acad Sci US 103(23):8577–8582
Ng AY, Jordan MI, Weiss Y (2002) On spectral clustering: analysis and an algorithm. Adv Neural Inf Process Syst 14:849–856
Paccanaro A, Chennubhotla C, Casbon JA (2006) Spectral clustering of protein sequences. Nucl Acids Res 34(5):1571–1580
Rebagliati N, Verri A (2011) Spectral clustering with more than K eigenvectors. Neurocomputing 74(9):1391–1401
Sarkar S, Soundararajan P (2000) Supervised learning of large perceptual organization: graph spectral partitioning and learning automata. IEEE Trans Patt Anal Mach Intell 22(5):504–525
Shi J, Malik J (2000) Normalized cuts and image segmentation. IEEE Trans Patt Anal Mach Intell 22(8):888–905
Sun JG, Liu J, Zhao LY (2008) Clustering algorithms research. J Softw 19(1):48–61
Tepper M, Muse P, Almansa A, Mejail M (2011) Automatically finding clusters in normalized cuts. Patt Recogn 44(7):1372–1386
Tung F, Wong A, Clausi DA (2010) Enabling scalable spectral clustering for image segmentation. Patt Recogn 43(12):4069–4076
Urquhart R (1982) Graph theoretical clustering based on limited neighborhood sets. Pattern Recogn 15(3):173–187
von Luxburg U (2007) A tutorial on spectral clustering. Stat Comput 17(4):395–416
Wang JH (2010) Consistent selection of the number of clusters via cross validation. Biometrika 97(4):893–904
Wang L, Bo LF, Jiao LC (2007) Density-sensitive spectral clustering. Acta Electronica Sinica 35(8):1577–1581
Wang LJ, Dong M (2012) Multi-level low-rank approximation-based spectral clustering for image segmentation. Patt Recogn Lett 33(16):2206–2215
Wang Y, Jiang Y, Wu Y, Zhou ZH (2011) Spectral clustering on multiple manifolds. IEEE Trans Neural Netw 22(7):1149–1161
Wei YC, Cheng CK (1989) Toward efficient hierarchical designs by ratio cut partitioning. In: IEEE international conference on CAD. New York, pp 298–301
Wu Z, Leahy R (1993) An optimal graph theoretic approach to data clustering: theory and its application to image segmentation. IEEE Trans Patt Anal Mach Intell 15(11):1101–1113
Xiang T, Gong S (2008) Spectral clustering with eigenvector selection. Patt Recogn 41(3):1012–1029
Xie B, Wang M, Tao DC (2011) Toward the optimization of normalized graph Laplacian. IEEE Trans Neural Netw 22(4):660–666
Xie YK, Zhou YQ, Huang XJ (2009) A spectral clustering based conference resolution method. J Chin Inf Process 23(3):10–16
Yang P, Zhu QS, Huang B (2011) Spectral clustering with density sensitive similarity function. Knowl-Based Syst 24(5):621–628
Yang Y, Xu D, Nie FP, Yan SC, Zhuang YT (2010) Image clustering using local discriminant models and global integration. IEEE Trans Image Process 19(10):2761–2773
Zahn CT (1971) Graph-theoretic methods for detecting and describing gestalt clusters. IEEE Trans Comput 20(1):68–86
Zeng S, Sang N, Tong XJ (2011) Hand-written numeral recognition based on spectrum clustering. In: MIPPR 2011: pattern recognition and computer vision, Proceedings of SPIE, p 8004
Zhang XC, Li JW, Yu H (2011) Local density adaptive similarity measurement for spectral clustering. Patt Recogn Lett 32(2):352–358
Zhang XC, You QZ (2011) An improved spectral clustering algorithm based on random walk. Frontiers Comput Sci China 5(3):268–278
Zhang XR, Jiao LC, Liu F (2008) Spectral clustering ensemble applied to SAR image segmentation. IEEE Trans Geosci Rem Sens 46(7):2126–2136
Zhao F, Jiao LC, Liu HQ et al (2010) Spectral clustering with eigenvector selection based on entropy ranking. Neurocomputing 73(10–12):1704–1717
Acknowledgments
This work is supported by the National Key Basic Research Program of China (No.2013CB329502), and the Fundamental Research Funds for the Central Universities (No.2013XK10).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Jia, H., Ding, S., Xu, X. et al. The latest research progress on spectral clustering. Neural Comput & Applic 24, 1477–1486 (2014). https://doi.org/10.1007/s00521-013-1439-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00521-013-1439-2