Application of differential transform method on nonlinear integro-differential equations with proportional delay

Abstract

In this work, we applied the differential transform method, by presenting and proving some theorems, to solve the nonlinear integro-differential equation with proportional delays. This technique provides a sequence of functions which converges to the exact solution of the problem. In order to show the power and the robustness of the method and to illustrate the pertinent features of related theorems, some examples are presented.

1 Introduction

Delay integro-differential equations (DIDEs) are often used to model of some problems with aftereffect in mechanics and the related scientific fields. Many typical examples such as stress–strain states of materials, motion of rigid bodies, aeroauto-elasticity problems and models of polymer crystallization can be found in Kolmanovskii and Myshkis’s [1] monograph and the references there in.

In this paper, we consider the following nonlinear integro-differential equations with proportional delay [2–9]:

$$ {c} f\left(t,u(p_0t),u'(p_1t),\ldots,u^{(n)}(p_nt),\int\limits_{0}^{rt}{\boldsymbol {\rm K}} {\rm d}s\right)=0,\quad t\geq 0, $$

(1)

where K = K(t, s, u(q ₀ s), u′(q ₁ s), …, u ^(m)(q _m s)), is the kernel function, $u\in \mathbb{R}$ is an unknown function, f, K, are given functions with appropriate domains of definition, p _i , q _j , r ∈ (0, 1), for i = 0, 1, …, n, j = 0, 1, …, m, and m < n.

In recent years, the differential transform method (DTM) has been developed for solving ordinary and partial differential equations. It is a semi-numerical/analytic technique that formalizes the Taylor series in a totally different manner. It was first introduced by Zhou [10] in a study about electrical circuits. The DTM obtains an analytical solution in the form of a polynomial. It is different from the traditional high-order Taylor series method, which requires symbolic competition of the necessary derivatives of the data functions. The Taylor series method is computationally taken long time for large orders. With this method, it is possible to obtain highly accurate results or exact solutions for differential equations. The differential transform is an iterative procedure for obtaining analytic Taylor series solutions of differential equations. DTM has been successfully applied to solve many nonlinear problems arising in engineering, physics, mechanics, biology, etc. Abazari et al. [11] are also employed DTM on some PDEs and their coupled version in and applied it to solve the second-order IVP and BVP of Matrix Differential Models [12].

Recently, Abazari et al., [13] employed RDTM to study the partial differential equation with proportional delay, and [14] applied RDTM on simulation of generalized Hirota–Satsuma coupled KdV equation. The purpose of this research is to employ DTM, mentioned in [13], to apply for Eq. (1).

2 Differential transform method

An arbitrary function u(t) can be expanded in Taylor series about a point t = t ₀ as

$$ u(t)=\sum_{k=0}^{\infty}\frac{(t-t_0)^k}{k!}\left[\frac{{\rm d}^ku(t)} {{\rm d}t^k}\right]_{t=t_0}. $$

(2)

If U(k) is defined as

$$ U(k)=\frac{1}{k!}\left[\frac{{\rm d}^ku(t)}{{\rm d}t^k}\right]_{t=t_0}, $$

(3)

where k = 0, 1, …, ∞, then Eq. (2) is reduced to

$$ u(t)=\sum_{k=0}^{\infty}U(k)(t-t_0)^k. $$

(4)

The U(k), defined in Eq. (4), is called the differential transform of function u(t). The following theorems that can be deduced from Eqs. (3) and (4) are given below.

Theorem 1

Assume that W(k), U(k) and V(k)  are the differential transforms of the functions w(t), u(t) and v(t), respectively, then

• (a) If w(t) = u(t) ± v(t), then W(k) = U(k) ± V(k).

• (b) If w(t) = λ u(t), then W(k) = λ U(k).

• (c) If $w(t)=\frac{{\rm d}^mu(t)}{{\rm d}t^m},$ then $W(k)=\frac{(k+m)!}{k!}U(k+m).$

• (d) If w(t) = u(t)v(t), then $W(k)=\sum\nolimits_{{\ell}=0}^kU({\ell})V(k-{\ell}).$

• (e) If w(x) = t ^m then $W(k)=\delta(k-m)= \left\{\begin{array}{*{20}c} 1 \hfill & {k = m,} \hfill \\ 0 \hfill & {{\text{otherwise}}} \hfill \\ \end{array}\right.$

Proof

See ([10], and their references). $\square$

3 Applications of differential transform method on Eq. (1)

In this section, we extend the one-dimensional transform method for approximating the Eq. (1). First, using the concept of differential transform method, we formulate the following Lemma.

Lemma 1

Assume that W(k) and U(k) are the differential transforms of the functions w(t) and u(t), respectively, and q, r,  ∈ (0, 1), then

• (a) If w(t) = u(qt), then W(k) = q ^k U(k).

• (b) If $w(t)=\frac{{\rm d}^m}{{\rm d}t^m}u(qt),$ then $W(k)=\frac{(k+m)!}{k!}q^{k+m}U(k+m).$

• (c) If $w(t) = \int_{0}^{{rt}} {u(qs){\text{d}}s}$, then $W(k)=\frac{1}{k}r^kq^{k-1}U(k-1), k=1,2,\ldots .$

Proof

• (a) From the Eq. (3), we get

  $$ \frac{{\rm d}^k}{{\rm d}t^k}w(t)=\frac{{\rm d}^k}{{\rm d}t^k}[u(qt)] =q^k\frac{{\rm d}^k}{{\rm d}\tilde{t}^k}u(\tilde{t}), $$

  where $\tilde{t}=qt,$ therefore

  $$ \left[\frac{{\rm d}^k}{{\rm d}t^k}w(t)\right]_{t=0}=q^k\left[\frac{{\rm d}^k} {{\rm d}\tilde{t}^k}u(\tilde{t})\right]_{t=t_0}=q^kk!U(k), $$

  hence by (3)

  $$ W(k)=\frac{1}{k!}\left[\frac{{\rm d}^kw(t)}{{\rm d}t^k}\right]_{t=0} =\frac{1}{k!}q^kk!U(k)=q^kU(k), $$

  where k = 0, 1, …, ∞.

• (b) From part (a), we get

  $$ \begin{aligned} \left[\frac{{\rm d}^k}{{\rm d}t^k}w(t)\right]_{t=0}&=q^{k+m} \left[\frac{{\rm d}^{k+m}}{{\rm d}\tilde{t}^{k+m}}u(\tilde{t})\right]_{t=0} \\ &= (k+m)!q^{k+m}U(k+m),\\ \end{aligned} $$

  then

  $$ W(k)=\frac{1}{k!}\left[\frac{{\rm d}^kw(t)}{{\rm d}t^k}\right]_{t=0} =\frac{(k+m)!}{k!}q^{k+m}U(k+m). $$

• (c) We get $\frac{{\rm d}^k}{{\rm d}t^k}w(t)=r\frac{{\rm d}^{k-1}}{{\rm d}t^{k-1}}u(rqt),$ then

  $$ \begin{aligned} \left[\frac{{\rm d}^k}{{\rm d}t^k}w(t)\right]_{t=0}&=r(k-1)!(rq)^{k-1}U(k-1) \\ &=(k-1)!r^kq^{k-1}U(k-1)\\ \end{aligned} $$

  hence, by (3), and for k = 1, 2, …, N we have

  $$ W(k)=\frac{1}{k!}\left[\frac{{\rm d}^k}{{\rm d}t^k}w(t)\right]_{t=0} =\frac{1}{k}r^kq^{k-1}U(k-1) $$

and therefore, the proof is completed. $\square$

By Lemma 1, we easily obtain the following Theorems.

Theorem 2

Assume that W(k), U ₁(k) and U ₂(k) are the differential transforms of the functions w(t), u ₁(t) and u ₂(t), respectively, and q ₁, q ₁ ∈ (0, 1),  then

• (2-a) If w(t) = u ₁(q ₁ t)u ₂(q ₂ t), then for $k=0,1,2,\ldots,N$

  $$ W(k)=\sum_{\ell=0}^kq_1^{\ell}q_2^{k-\ell}U_1(\ell)U_2(k-\ell). $$

• (2-b) If $w(t)=\int_{0}^{rt}u_1(q_1s)u_2(q_2s){\rm d}s,$ then for $k=1,2,\ldots,N$

  $$ W(k)=\frac{1}{k}\sum_{\ell=0}^{k-1}r^kq_1^{\ell}q_2^{k-\ell-1} U_1(\ell)U_2(k-\ell-1). $$

• (2-c) If $w(t)=u(p t)\int_{0}^{rt}v_1(q_1s)v_2(q_2s){\rm d}s,$ then for $k=1,2,\ldots,N$

  $$ W(k)=\sum_{\ell=0}^{k-1}\sum_{s=0}^{k-\ell-1}\frac{1}{k-\ell} r^{k-\ell}p^{\ell} q_1^{s} q_2^{k-\ell-s-1}U(\ell)V_1(s)V_2(k-\ell-s-1). $$

Proof

• (2-a) From the Lemma 1, and Leibnitz formula, we get

  $$ \begin{aligned} \frac{{\rm d}^kw(t)}{{\rm d}t^k}&=\frac{{\rm d}^k}{{\rm d}t^k}\left[u_1(q_1t)u_2(q_2t)\right] \\ &=\sum_{\ell=0}^k {\left( {\begin{array}{*{20}c} k \\ \ell \\ \end{array} } \right)}q_1^{\ell}\frac{{\rm d}^{\ell}}{{\rm d}\tilde{t}^{\ell}} u_1(\tilde{t})q_2^{k-\ell}\frac{{\rm d}^{k-\ell}} {{\rm d}\hat{t}^{k-\ell}}u_2(\hat{t}), \end{aligned} $$

  where $\hat{t}=q_1t,$ and $\tilde{t}=q_1t,$ therefore,

  $$ \begin{aligned} \left[\frac{{\rm d}^kw(t)}{{\rm d}t^k}\right]_{t=0}& =\sum_{\ell=0}^k {\left( {\begin{array}{*{20}c} k \\ \ell \\ \end{array} } \right)}\left[q_1^{\ell}\ell!U_1(\ell)\right] \left[q_2^{k-\ell}(k-\ell)!U_2(k-\ell)\right] \\ &=\sum_{\ell=0}^k k!q_1^{\ell}q_2^{k-\ell}U_1(\ell)U_2(k-\ell), \end{aligned} $$

  then, from Eq. (3), we get

  $$ W(k)=\frac{1}{k!}\left[\frac{{\rm d}^kw(t)}{{\rm d}t^k}\right]_{t=0}=\sum_{\ell=0}^k q_1^{\ell}q_2^{k-\ell}U_1(\ell)U_2(k-\ell). $$

  where $k=0,1,\ldots,\infty.$

• (2-b) Similar to previous parts, we get

  $$ \begin{aligned} \frac{{\rm d}^k}{{\rm d}t^k}w(t)&=r\frac{{\rm d}^{k-1}}{{\rm d}t^{k-1}} [u_1(rq_1t)u_1(rq_1t)]\\ &=r\sum_{\ell=0}^{k-1}{\left( {\begin{array}{*{20}c} k-1 \\ \ell \\ \end{array} } \right)}(rq_1)^{\ell}\frac{{\rm d}^{\ell}}{{\rm d}\hat{t}^{\ell}}u_1 (\hat{t}) (rq_2)^{k-\ell-1}\frac{{\rm d}^{k-\ell-1}} {{\rm d}\check{t}^{k-\ell-1}}u_2(\check{t}), \end{aligned} $$

  then

  $$ \begin{aligned} \left[\frac{{\rm d}^k}{{\rm d}t^k}w(t)\right]_{t=0} =r\sum_{\ell=0}^{k-1}{\left( {\begin{array}{*{20}c} k-1 \\ \ell \\ \end{array} } \right)}(rq_1)^{\ell}\ell!U_1(\ell) (rq_2)^{k-\ell-1}(k-\ell-1)!U_2(k-\ell-1). \end{aligned} $$

  hence by Eq. (3), and for $k=1,2,\ldots,N,$ we obtain

  $$ \begin{aligned} W(k)&=\frac{1}{k!}\left[\frac{{\rm d}^k}{{\rm d}t^k}w(t)\right]_{t=0} \\ &=\frac{1}{k}\sum_{\ell=0}^{k-1}r^kq_1^{\ell} q_2^{k-\ell-1}U_1(\ell)U_2(k-\ell-1).\\ \end{aligned} $$

• (2-c) Let $y(t)=\int_{0}^{rt}v_1(q_1s)v_2(q_2s){\rm d}s,$ then from previous parts, we get

  $$ \begin{aligned} \frac{{\rm d}^k}{{\rm d}t^k}w(t)&=\frac{{\rm d}^{k}}{{\rm d}t^{k}}\left[u(p t)y(t)\right] \\ &=\sum_{\ell=0}^{k}{\left( {\begin{array}{*{20}c} k \\ \ell \\ \end{array} } \right)}p^{\ell}\frac{{\rm d}^{\ell}}{{\rm d}\hat{t}^{\ell}} u(\hat{t}) \frac{{\rm d}^{k-\ell}}{{\rm d}t^{k-\ell}}y(t)\\ \end{aligned} $$

  where $\hat{t}=pt,$ and

  $$ \begin{aligned} \frac{{\rm d}^{k-\ell}}{{\rm d}t^{k-\ell}}y(t)&= r\frac{{\rm d}^{k-\ell-1}} {{\rm d}t^{k-\ell-1}}\left[v_1(rq_1t)v_2(rq_2t)\right] \\ &= r\sum_{s=0}^{k-\ell-1}{\left( {\begin{array}{*{20}c} k-l-1 \\ s \\ \end{array} } \right)} (rq_1)^s\frac{{\rm d}^s}{{\rm d}\tilde{t}^s}v_1(\tilde{t}) (rq_2)^{k-\ell-s-1}\frac{{\rm d}^{k-\ell-s-1}}{{\rm d}\check{t}^{k-\ell-s-1}} v_2(\check{t})\\ \end{aligned} $$

  where $\tilde{t}=rq_1\tilde{t}$ and $\check{t}=rqt,$ then

  $$ \begin{aligned} \left[\frac{{\rm d}^k}{{\rm d}t^k}w(t)\right]_{t=0}&=\sum_{\ell=0}^{k} \sum_{s=0}^{k-\ell-1} {\left( {\begin{array}{*{20}l} k \\ \ell \\ \end{array} } \right)} {\left( {\begin{array}{*{20}l} k-l-1 \\ s \\ \end{array} } \right)} \left[r^{k-\ell}p^{\ell} q_1^{s} q_2^{k-\ell-s-1}\ell! s! (k-\ell-s-1)! \right.\\ \left. U(\ell)V_1(s)V_2(k-\ell-s-1)\right].\\ \end{aligned} $$

  but for $\ell=k$, we have

  $$ \left[\frac{{\rm d}^{k-\ell}}{{\rm d}t^{k-\ell}}y(t)\right]_{t=0}=0, $$

  then by Eq. (3), for $k=1,2,\ldots,N$ we obtained

  $$ \begin{aligned} W(k)=\sum_{\ell=0}^{k-1}\sum_{s=0}^{k-\ell-1}\frac{1}{k-\ell} r^{k-\ell}p^{\ell} q_1^{s} q_2^{k-\ell-s-1}U(\ell)V_1(s)V_2(k-\ell-s-1). \end{aligned} $$

and therefore, the proof completed. $\square$

Theorem 3

Assume that W(k), U ₁(k) and U ₂(k) are the differential transforms of the functions w(t), u ₁(t) and u ₂(t), respectively, and $q_1,q_1\in(0,1),$ then

• (3-a) If $w(t)=\frac{{\rm d}^n}{{\rm d}t^n}u_1(q_1t)\frac{{\rm d}^m}{{\rm d}t^m}u_2(q_2t),$ then for $k=0,1,2,\ldots,N$

  $$ W(k)=\sum_{\ell=0}^kq_1^{\ell+n}q_2^{k-\ell+m}\frac{(\ell+n)! (k-\ell+m)!}{\ell!(k-\ell)!}U_1(\ell+n)U_2(k-\ell+m). $$

• (3-b) If $w(t)=\int_{0}^{rt}\frac{{\rm d}^n}{{\rm d}t^n}u_1(q_1s)\frac{{\rm d}^m}{{\rm d}t^m}u_2(q_2s){\rm d}s,$ then for $k=1,2,\ldots,N$

  $$ W(k)=\!\frac{1}{k}\sum_{\ell=0}^{k-1}\frac{(\ell\!+\!n)! (k\!-\!\ell\!+\!m\!-\!1)!}{\ell!(k\!-\!\ell\!-\!1)!} r^{k+n+m}q_1^{\ell+n}q_2^{k-\ell+m-1}U_1(\ell\!+\!n)U_2 (k\!-\!\ell\!+\!m\!-\!1). $$

• (3-c) If $w(t)=\frac{{\rm d}^\lambda}{{\rm d}t^\lambda}u(p t)\int_{0}^{rt}\frac{{\rm d}^n}{{\rm d}t^n}v_1(q_1s)\frac{{\rm d}^m}{{\rm d}t^m}v_2(q_2s){\rm d}s,$ then for $k=1,2,\ldots,N$

  $$ \begin{aligned} W(k)&=\sum_{\ell=0}^{k-1}\sum_{s=0}^{k-\ell-1} \left[\frac{1}{k-\ell}\frac{(\ell+\lambda)!(s+n)!(k-\ell-s+m-1)!} {\ell!s!(k-\ell-s-1)!} \right.\\ &\quad \left. p^{\ell+\lambda} r^{k-\ell+n+m} q_1^{s+n} q_2^{k-\ell-s+m-1}U(\ell\!+\!\lambda)V_1(s\!+\!n) V_2(k\!-\!\ell\!-\!s\!+\!m\!-\!1)\right]. \end{aligned} $$

Proof

• (3-a) From the Lemma 1, and Leibnitz formula, we get

  $$ \begin{aligned} \frac{{\rm d}^k}{{\rm d}t^k}w(t)&=\frac{{\rm d}^k}{{\rm d}t^k}\left[\frac{{\rm d}^n}{{\rm d}t^n}u_1(q_1t) \frac{{\rm d}^m}{{\rm d}t^m}u_2(q_2t)\right]\\ &=\sum_{\ell=0}^k {\left( {\begin{array}{*{20}c} k \\ \ell \\ \end{array} } \right)}q_1^{\ell+n}\frac{{\rm d}^{\ell+n}} {{\rm d}\tilde{t}^{\ell+n}} u_1(\tilde{t})q_2^{k-\ell+m}\frac{{\rm d}^{k-\ell+m}} {{\rm d}\hat{t}^{k-\ell+m}}u_2(\hat{t}), \end{aligned} $$

  where $\tilde{t}=q_1t,$ and $\hat{t}=q_2t,$ therefore

  $$ \begin{aligned} \left[\frac{{\rm d}^k}{{\rm d}t^k}w(t)\right]_{t=0}&=\sum_{\ell=0}^k {\left( {\begin{array}{*{20}c} k \\ \ell \\ \end{array} } \right)}\left[q_1^{\ell+n}(\ell+n)!U_1(\ell+n)\right] \left[q_2^{k-\ell+m}(k-\ell+m)!U_2(k-\ell+m)\right]\\ &=\sum_{\ell=0}^k \frac{k!(\ell+n)!(k-\ell+m)!}{\ell!(k-\ell)!} q_1^{\ell+n}q_2^{k-\ell+m}U_1(\ell+n)U_2(k-\ell+m), \end{aligned} $$

  then from Eq. (3), we obtained

  $$ W(k)=\sum_{\ell=0}^kq_1^{\ell+n}q_2^{k-\ell+m}\frac{(\ell+m)! (k-\ell+m)!}{\ell!(k-\ell)!}U_1(\ell+n)U_2(k-\ell+m). $$

• (3-b) Similar to previous parts, we get

  $$ \begin{aligned} \frac{{\rm d}^k}{{\rm d}t^k}w(t)&=r\frac{{\rm d}^{k-1}}{{\rm d}t^{k-1}}\left[\frac{{\rm d}^n} {{\rm d}t^n}u_1(rq_1t)\frac{{\rm d}^m}{{\rm d}t^m}u_2(rq_2t)\right]\\ &=r\sum_{\ell=0}^{k-1}{\left( {\begin{array}{*{20}c} k-1 \\ \ell \\ \end{array} } \right)}(rq_1)^{\ell+n} \frac{{\rm d}^{\ell+n}}{{\rm d}\hat{t}^{\ell+n}}u_1(\hat{t}) (rq_2)^{k-\ell+m-1}\frac{{\rm d}^{k-\ell+m-1}}{{\rm d}\check{t}^{k-\ell+m-1}} u_2(\check{t}), \end{aligned} $$

  then

  $$ \begin{aligned} \left[\frac{{\rm d}^k}{{\rm d}t^k}w(t)\right]_{t=0}\!=\!r\sum_{\ell=0}^{k-1} {\left( {\begin{array}{*{20}c} k-1 \\ \ell \\ \end{array} } \right)}(rq_1)^{\ell+n}(\ell\!+\!n)!U_1(\ell\!+\!n)\\ (rq_2)^{k-\ell+m-1}(k\!-\!\ell\!+\!m\!-\!1)!U_2(k\!-\!\ell\!+\!m\! -\!1).\\ \end{aligned} $$

  hence by Eq. (3), and for $k=1,2,\ldots,N$ we have

  $$ \begin{aligned} W(k)\!=\!\frac{1}{k}\sum_{\ell=0}^{k-1}\frac{(\ell\!+\!n)! (k\!-\!\ell\!+\!m\!-\!1)!}{\ell!(k\!-\!\ell\!-\!1)!} r^{k+n+m}q_1^{\ell+n}q_2^{k-\ell+m-1}U_1(\ell\!+\!n)U_2(k\!-\!\ell\!+\!m\!-\!1). \end{aligned} $$

• (3-c) Let $y(t)=\int_{0}^{rt}\frac{{\rm d}^n}{{\rm d}t^n}v_1(q_1s)\frac{{\rm d}^m}{{\rm d}t^m}v_2(q_2s){\rm d}s,$ then from previous parts, we get

  $$ \begin{aligned} \frac{{\rm d}^k}{{\rm d}t^k}w(t)=\frac{{\rm d}^{k}}{{\rm d}t^{k}}\left[\frac{{\rm d}^{\lambda}u(p t)}{{\rm d}t^{\lambda}}y(t)\right] =\sum_{\ell=0}^{k}{\left( {\begin{array}{*{20}c} k \\ \ell \\ \end{array} } \right)}p^{\ell+\lambda}\frac{{\rm d} ^{\ell+\lambda}}{{\rm d}\hat{t}^{\ell+\lambda}}u(\hat{t}) \frac{{\rm d}^{k-\ell}}{{\rm d}t^{k-\ell}}y(t) \end{aligned} $$

  where $\hat{t}=p t,$ and

  $$ \begin{aligned} \frac{{\rm d}^{k-\ell}}{{\rm d}t^{k-\ell}}y(t)&= r\frac{{\rm d}^{k-\ell-1}}{{\rm d}t^{k-\ell-1}} \left[\frac{{\rm d}^n}{{\rm d}t^n}v_1(rq_1t)\frac{{\rm d}^m}{{\rm d}t^m}v_2(rq_2t)\right] \\ &= r\sum_{s=0}^{k-\ell-1}{\left( {\begin{array}{*{20}c} k-l-1 \\ s \\ \end{array} } \right)}(rq_1)^{s+n}\frac{{\rm d}^{s+n}} {{\rm d}\tilde{t}^{s+n}}v_1(\tilde{t}) (rq_2)^{k-\ell-s+m-1} \frac{d^{k-\ell-s+m-1}}{{\rm d}\check{t}^{k-\ell-s+m-1}}v_2(\check{t})\\ \end{aligned} $$

  where $\tilde{t}=rq_1\tilde{t}$ and $\check{t}=rqt,$ then

  $$ \begin{aligned} \frac{{\rm d}^k}{{\rm d}t^k}w(t)&=\sum_{\ell=0}^{k}\sum_{s=0}^{k-\ell-1} {\left( {\begin{array}{*{20}c} k \\ \ell \\ \end{array} } \right)}{\left( {\begin{array}{*{20}c} k-l-1 \\ s \\ \end{array} } \right)} \left[p^{\ell+\lambda} r^{k-\ell+n+m} q_1^{s+n} q_2^{k-\ell-s+m-1}\right. \\ &\left.\frac{{\rm d}^{\ell+\lambda}}{{\rm d}t^{\ell+\lambda}}u(\hat{t})\frac{{\rm d}^{s+n}} {{\rm d}\tilde{t}^{s+n}}v_1(\tilde{t}) \frac{d^{k-\ell-s+m-1}}{{\rm d}\check{t}^{k-\ell-s+m-1}}v_2(\check{t})\right]. \end{aligned} $$
  $$ \begin{aligned} \left[\frac{{\rm d}^k}{{\rm d}t^k}w(t)\right]_{t=0}&=\sum_{\ell=0}^{k}\sum_{s=0}^{k-\ell-1} {\left( {\begin{array}{*{20}c} k \\ \ell \\ \end{array} } \right)}{\left( {\begin{array}{*{20}c} k-l-1 \\ s \\ \end{array} } \right)} \left[p^{\ell+\lambda} r^{k-\ell+n+m} q_1^{s+n} q_2^{k-\ell-s+m-1}\right. \\ \left.(\ell\!+\!\lambda)!U(\ell\!+\!\lambda)(s\!+\!n)!V_1(s\!+\!n) (k\!-\!\ell\!-\!s\!+\!m\!-\!1)!V_2(k\!-\!\ell\!-\!s\!+\!m\!-\!1)\right].\\ \end{aligned} $$

  but for $\ell=k$, we have

  $$ \left[\frac{{\rm d}^{k-\ell}}{{\rm d}t^{k-\ell}}y(t)\right]_{t=0}=0, $$

  then by Eq. (3), for $k=1,2,\ldots,N$ we obtained

  $$ \begin{aligned} W(k)&=\sum_{\ell=0}^{k-1}\sum_{s=0}^{k-\ell-1} \left[\frac{1}{k-\ell}\frac{(\ell+\lambda)!(s+n)!(k-\ell-s+m-1)!} {\ell!s!(k-\ell-s-1)!}\right.\\ \left. p^{\ell+\lambda} r^{k-\ell+n+m} q_1^{s+n} q_2^{k-\ell-s+m-1}U(\ell\!+\!\lambda)V_1(s\!+\!n) V_2(k\!-\!\ell\!-\!s\!+\!m\!-\!1)\right].\\ \end{aligned} $$

and therefore, the proof completed. $\square$

4 Numerical examples

In this section, we give the following prototype examples to clarify the accuracy of the presented method. These examples are chosen such that there exist exact solutions for them.

Example 1

In the first example, consider the following nonlinear first-order integro-differential equation with proportional delay

$$ u'(t)-u\left(\frac{t}{2}\right)-\frac{1}{2}u\left(\frac{t}{2}\right)\int\limits_{0}^{\frac{t}{3}}u(s) u\left(\frac{s}{2}\right){\rm d}s=0, $$

(5)

subject to initial condition u(0) = 1. Substituted t = 0, in Eq. (5), we get u′(0) − 1 = 0, then u′(0) = 1.

Using differential transform method, the differential transform version of Eq. (5), for $k=1,2,\ldots,N$ will be

$$ \begin{aligned} &(k+1)U(k+1)-\left(\frac{1}{2}\right)^kU(k)\\ & \quad - \frac{1}{2}\sum_{{\ell}=0}^{k-1}\sum_{s=0}^{k-\ell-1}\frac{1}{k-\ell} \left(\frac{1}{3}\right)^{k-\ell} \left(\frac{1}{2}\right)^{k-s-1}U(\ell)U(s)U(k\!-\!\ell\!-\!s\!-\!1)=0, \end{aligned} $$

(6)

and the differential transform version of initial conditions u(0) = u′(0) = 1 will be

$$ U(0)=U(1)=1, $$

(7)

where U(k) is the differential transform of u(t).

Using Eq. (6), by taking N = 5, the following system is obtained:

$$ \begin{aligned} &2U(2)-1= 0, \\ &3U(3)-\frac{1}{4}U(2)-\frac{3}{8}= 0, \\ &4U(4)-\frac{1}{8}U(3)-\frac{4}{27}U(2)-\frac{31}{432} = 0\\ &5U(5)-\frac{1}{16}U(4)-\frac{13}{192}U(3)-\frac{5}{108}U(2) -\frac{1}{216}= 0, \\ &6U(6)-\frac{1}{32}U(5)-\frac{211}{6480}U(4) -\frac{197}{10368}U(3)-\frac{79}{12960}U(2)^2-\frac{7}{1728}U(2)=0,\\ \end{aligned} $$

(8)

Solving the above system and using the inverse transformation rule (3), we get the following series solution

$$ U_6(t)=1+t+\frac{1}{2}t^2+\frac{1}{6}t^3+\frac{1}{24}t^4 +\frac{1}{120}t^5+\frac{1}{720}t^6. $$

Note that when N > 5 by solving the obtained system, we get the following series solution

$$ U_N(t)=1+t+\frac{1}{2!}t^2+\frac{1}{3!}t^3+\frac{1}{4!}t^4+ \cdots +\frac{1}{N!}t^N. $$

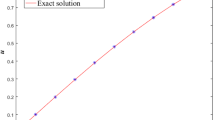
The closed form of above series solution is u(t) = e ^t, which is the exact solution of Eq. (5). Table 1 shows the numerical results of this example.

Table 1 Absolute errors of Example 1 at some points and for different value of N

Example 2

In this example, consider the following nonlinear second-order integro-differential equation with proportional delay

$$ u''\left(\frac{t}{2}\right)\int\limits_{0}^{\frac{t}{2}}u(s)u'(s){\rm d}s -\frac{1}{4}u' \left(\frac{t}{2}\right)-\frac{1}{8}u(t)u \left(\frac{t}{2}\right)=0, $$

(9)

subject to initial condition u(0) = 1, and u′(0) =  − 1.

From Theorem (2) and Theorem (3), the differential transformed version of Eq. (9) is

$$ \begin{aligned} &\sum_{\ell=0}^{k-1}\sum_{s=0}^{k-\ell-1}\frac{(\ell+2)!(k-\ell-s)}{(k-\ell)\ell!} \left(\frac{1}{2}\right)^{k+2}U(\ell+2)U(s)U(k-\ell-\!s)\\ & \quad -\frac{1}{4}\left(\frac{1}{2}\right)^{k+1}(k+1)U(k+1)-\frac{1}{8} \sum_{\ell=0}^{k}\left(\frac{1}{2}\right)^{k-\ell}U(\ell)U(k-\ell)=0, \end{aligned} $$

(10)

where U(k) is the differential transform of u(t), and the transformed version of initial conditions u(0) = 0 and u′(0) = 1 are

$$ U(0)=0,\quad U(1)=-1, $$

(11)

Using Eqs. (10), and (11), and by taking N = 4, the following system for k = 1, 2, 3, 4 is obtained:

$$ \begin{aligned} &\frac{3}{2}U(2)-\frac{3}{4}= 0, \\ &\frac{15}{8}U(3)+\frac{3}{8}U(2)-\frac{1}{2}U(2)^2+\frac{1}{4} = 0, \frac{7}{4}U(4)+\frac{3}{16}U(3)-\frac{3}{8}U(2)-U(2)U(3) +\frac{1}{4}U(2)^2 = 0\\ &\frac{45}{32}U(5)+\frac{5}{32}U(4)-\frac{5}{16}U(3) +\frac{1}{8}U(2)^2-\frac{7}{8}U(2)U(4) +\frac{1}{2}U(2)U(3)-\frac{1}{16}U(2)^3-\frac{3}{8}U(3)^2 = 0, \\ \end{aligned} $$

(12)

Solving the above system and using the inverse transformation rule (3), we get the following series solution

$$ U_5(t)=1-t+\frac{1}{2}t^2-\frac{1}{6}t^3+\frac{1}{24}t^4 -\frac{1}{120}t^5, $$

Note that for N > 4, the closed form of above solution is u(t) = e ^−t, which is the exact solution of Eq. (9). The numerical results of this example are shown in Table 2.

Table 2 Absolute errors of Example 2 at some points and for different value of N

Example 3

Consider the following nonlinear third-order integro-differential equation with proportional delay

$$ u'''\left(\frac{t}{2}\right)+u''\left(\frac{t}{2}\right)u'(t)-\frac{1}{2}u(t) \int\limits_{0}^{\frac{t}{2}}u\left(\frac{s}{2}\right)u'\left(\frac{s}{2}\right){\rm d}s=f(t), $$

(13)

subject to initial conditions

$$ u(0)=0, u'(0)=2, u''(0)=0. $$

(14)

where $f(t)=-\frac{3}{8}e^{t/2}+\frac{5}{8}e^{-t/2}+\frac{1}{2}e^t -\frac{1}{2}e^{-t}.$ Similar to previous examples, the differential transformed version of Eq. (13) for $k=0,1,2,\ldots,N$ will be

$$ \begin{aligned} &\left(\frac{1}{2}\right)^{k+3}\frac{(k+3)!}{k!}U(k+3)+\sum_{\ell=0}^{k} \left(\frac{1}{2}\right)^{\ell+2}\frac{(\ell+2)!(k-\ell+1)!}{\ell!(k-\ell)!} \quad U(\ell+2)U(k-\ell+1)\\ &-\frac{1}{2}\sum_{\ell=0}^{k-1}\sum_{s=0}^{k-\ell-1} \frac{k-\ell-s}{k-\ell}\left(\frac{1}{2}\right)^{2k-2\ell+1}U(\ell)U(s)U(k-\ell-s)\\ &=\frac{1}{2k!}\left(-\frac{3}{4}\left(\frac{1}{2}\right)^k +\frac{5}{4}(-\frac{1}{2})^k-(-1)^k+1\right), \end{aligned} $$

(15)

and the differential transform version of initial conditions is

$$ U(0)=0,\quad U(1)=2,\quad U(2)=0. $$

(16)

respectively, where U(k) is the differential transform of u(t).

Using Eq. (15), by taking N = 4, the following system is obtained:

$$ \begin{aligned} &\frac{3}{4}U(3)+\frac{1}{2}U(2)U(1)=\frac{1}{4}, \\ &\frac{3}{4}U(4)+U^2(2)+\frac{3}{4}U(3)U(1)-\frac{1}{16}U^3(0)U(1) =\frac{1}{2}, \\ &\frac{15}{8}U(5)+3U(2)U(3)+\frac{3}{4}U(1)U(4) +\left(\frac{1}{2}\right)^6U^2(0)U(2)-5\left(\frac{1}{2}\right)^6U(0)U^2(1) =\frac{1}{32}\\ &\frac{15}{8}U(6)+\frac{5}{2}U(2)U(4)+\frac{9}{4}U^3(3) +5\left(\frac{1}{2}\right)^3U(1)U(5)-\left(\frac{1}{2}\right)^8U^3(0)U(3)-21\left(\frac{1}{2}\right)^8U(0)U(1)U(2)-\left(\frac{1}{2}\right)^7U^3(1)= \frac{7}{48},\\ \end{aligned} $$

(17)

Solving the above system by utilizing the (16) and using the inverse transformation rule (3), we get the following series solution

$$ U_6(t)=2t+\frac{1}{3}t^3+\frac{1}{60}t^5. $$

Note that for N > 4, the closed form of above series solution is u(t) = e ^t − e ^−t, which is the exact solution of Eq. (13). Table 3 also shows the numerical results of this example.

Table 3 Absolute errors of Example 3 at some points and for different value of N

5 Conclusions

In this work, we have shown that the differential transformation method can be used successfully for solving the nonlinear integro-differential equations with proportional delay. Some theorems are introduced with their proofs, and as application, some prototype examples are carried out. The present method reduces the computational difficulties of the other methods, and all the calculations can be made simple manipulations. The accuracy of the obtained solution can be improved by taking more terms in the solution. In many cases, the series solutions obtained with DTM can be written in exact closed form. So it may be easily applied by researchers and engineers familiar with the Taylor expansion.