1 Introduction

Wind is a safe, clean, and nature-friendly type of energy. Thus, many countries are interested to invest on the wind energy. The worldwide total installed capacity has reached more than 238 GW by the end of 2011. This represents an increase of 21 %, with an increase in the size of the annual global market of just over 6 %. Today, about 75 countries worldwide have commercial wind power installations, with 22 of them already passing the 1 GW level [1]. However, the main disadvantage of wind is due to the fast changes in wind’s speed and direction. Hence, the wind power varies depending on the environmental factors, which causes the need for accurate on-line identification of the optimal operating point [2].

Wind energy conversion systems (WECSs), as an example of wind turbines, can work by fixed speed and variable speed using the power electronic converters. The variable-speed type is more desirable because of its ability to achieve maximum efficiency at all wind speeds [3]. The variable-speed wind turbines mostly use doubly fed induction generator (DFIG) with half (small) converters. However, the wind turbines with full converters are mostly based on synchronous generators [4]. In the structures based on DFIG, the converter is small since only a fraction of the output power from generator goes through it. These structures, owing to the small converters, minimize the production cost and power losses in converter. However, the fully rated converters are commonly used for gearless structures that are able to give smoother power output and can operate in full frequency-range variation. However, in comparison with DFIG, due to using large converters, the production cost and power losses in converter will be dramatically increased [5].

The main operational region for wind turbines according to wind speed is divided into partial load and full load. In the partial-load region, which is between the wind speed V cut-in (approximately 3 m/s) and V rated (approximately 12 m/s), the objective is to capture the maximum power from the wind. This is done by controlling generator speed using the generator torque and thus the rotor current through DFIG converter. In the full-load region, which is between the wind speeds V rated and V cut-out (approximately 25 m/s), the objective is to tune the pitch angles to keep the generator power in its nominal value [6]. In this paper, our focus is on the partial-load region, and thus the objective is to capture the maximum wind power.

The output power of a WECS is maximized if the rotor is driven at an optimal rotational speed for a particular wind speed. To achieve this, the maximum power point tracking (MPPT) controllers are usually employed. Knowledge of the turbine dynamics and instantaneous measurements of the wind speed and rotor speed are required in implementation of an MPPT controller. To obtain the optimal operating point, rotor-generator characteristics should be known, and these are different from one system to another. The MPPT control of WECSs becomes difficult due to fluctuation in wind speed and rotor inertia [7].

Most of the implementations of MPPT controllers are model-based methods. In the model-based methods, the approximate knowledge about the mathematical model of the plant should be known in advance for designing the controller. However, due to the different kinds of uncertainties, this is a difficult task in practical applications, especially for large-scale systems like wind turbines. However, the model-free methods do not need mathematical model, and design of the controller is based on input–output data from the real system. Thus, by using model-free methods, we can cope with nonlinearities and uncertainties at the same time.

Based on the comparison made in [8] between the performance of different MPPT algorithms on the basis of various speed profiles and ability to achieve the maximum energy yield, the optimal torque control has been found to be the best MPPT method for the wind energy systems due to its simplicity.

In this paper, an optimal proportional-integral (PI) controller is proposed to maximize the captured wind power. The proposed method is based on particle swarm optimization (PSO) algorithm and fuzzy logic theory. The PSO is used to regulate the fuzzy membership functions for the partial-load region according to different wind speeds and considering the objective of maximizing the captured power. Then, the PI gains are derived for each wind speed using the optimized fuzzy system similar to a gain-scheduling controller. The proposed PI controller guarantees the optimal tip speed ratio (TSR) tracking.

This paper is organized as follows: Related work is reviewed in Sect. 2. Section 3 describes the problem definition and preliminaries. For this purpose, the wind turbine model, which is a variable-speed 5-MW wind turbine, is presented. It should be noted that the mathematical model only is used for simulation purposes and the proposed controller design procedure does not need the mathematical model. In addition, the foundations of PSO algorithm and fuzzy logic systems (FLSs) are briefly described in Sect. 3. The proposed control strategy is presented in Sect. 4. In Sect. 5, the proposed method is applied to a 5-MW wind turbine model and the performance results are compared with two recent stated methods. Finally, Sect. 6 concludes the main advantages of the proposed method.

2 Related work

In recent years, several researches have been conducted on the methods to capture maximum wind power in partial-load region. For example, Liao et al. [9] have shown that by assuming that the input power to the drive train is equal to the output power from it, the smooth torque signal is derived. However, in turbulent winds, the large rotor inertia prevents it from changing speed fast enough to follow the wind. Thus, the rotor speed will be smaller than the optimal value. Hence, the power coefficient will be declined, which consequently decreases the captured power. However, the above method considering the friction effects for a drive-train model was expanded in [10] to reduce the steady-state error.

To achieve maximum output power of a WECS, several control methods have been proposed such as PI control [11], robust control based on H ∞ [12], linear quadratic Gaussian (LQG) control [11], optimal control [13], sliding mode control (SMC) [14], state feedback control [15], predictive control [16], fuzzy control [7, 17–20], adaptive control [21], artificial neural network (ANN)-based control [18], and different hybrid approaches such as combination of fuzzy model and genetic algorithm (GA) and recursive least-squares (RLS) optimization methods [22, 23], combination of fuzzy ANN and PSO algorithm [24–26], hybrid of classic control and evolutionary strategy algorithm [27], hybrid of ANN and fuzzy inference system (FIS) [2, 18], combination of PI and SMC [28], integration of model predictive control (MPC) and evolutionary computation [29], and embedding fuzzy controller into model reference adaptive control framework [30].

As examples of classic control approaches in this field, Van der Hoven wind model is considered in the frequency domain, and LQG and PI controllers have been designed in [11] for high and low frequencies, respectively. Vihriälä et al. [13] have attempted to track optimal generator speed with the approach of using the feedforward aerodynamic torque controller. Beltran et al. [14] have reduced the steady-state error of tracking the optimal speed by using a high-order sliding mode controller as a nonlinear method. Boukhezzar and Siguerdidjane [15] have used nonlinear static and dynamic state feedback controllers for this purpose. Bououden et al. [16] have proposed a fuzzy model-based multivariable predictive control (FMMPC) for wind turbine generator. They have combined the linear matrix inequalities (LMI) technique with predictive approach to design a FMMPC law by solving a convex optimization problem subject to LMI conditions.

As samples of soft computing–based methods, Narayana et al. [7] have proposed an adaptive filter with a fuzzy MPPT controller for small-scale WECSs. In addition, an FIS and a radial basis function (RBF) neural network have been used for dynamic modeling of wind turbine rotor in [18].

As samples of hybrid approaches in this field, Calderaro et al. [22] have presented a data-driven design methodology able to generate a Takagi–Sugeno–Kang (TSK) fuzzy model for maximum energy extraction from the variable-speed wind turbines. In order to obtain the TSK model, fuzzy clustering methods for partitioning the input–output space, combined with GA and RLS optimization methods, have been used for model parameter adaptation. Lin et al. [26] have employed a recurrent fuzzy neural network (RFNN) controller in which PSO algorithm has been adopted to adapt the learning rates in the back-propagation process. Lin and Hong [25] have proposed a Wilcoxon RBF network with hill-climb searching (HCS) MPPT strategy for a permanent magnet synchronous generator (PMSG) with a variable-speed wind turbine. Kusiak and Zheng [27] have developed an evolutionary computation approach for optimization of power factor and power output of wind turbines by optimal control settings. Sargolzaei and Kianifar [18] have used an adaptive neuro-fuzzy inference system (ANFIS) for dynamic modeling of wind turbine rotor and compared this system with FIS and RBF neural network. Meharrar et al. [2] have combined Sugeno fuzzy model and neural network for MPPT in a variable-speed wind generator.

3 Problem definition and preliminaries

The model of wind turbine, the definition of problem, and foundations of the PSO algorithm and fuzzy logic systems are briefly described in this section.

3.1 Wind turbine model

The schematic of a wind turbine system can be seen in Fig. 1. The available power of the wind based on the radius of the rotor is determined as follows:

$$ P_{v} = 0.5A\rho v^{3} $$
(1)

where A is the swept area by blades, v is the actual wind speed, and ρ is the air density.

Fig. 1
figure 1

Schematic of wind turbine system

Full size image

Generally, a turbine can capture only a fraction of this power. This fraction is called power coefficient or Betz limit called C p . The C p is a function of pitch angle (β) and TSR (λ) defined as follows:

$$ \lambda = \frac{{w_{r} \times R}}{v} $$
(2)

where w r is the rotor angular speed, and R is the radius of the rotor. For instance, the C p for 5-MW wind turbine is depicted in Fig. 2. Thus, the power captured by turbine can be stated as follows:

$$ P_{a} = 0.5A\rho v^{3} C_{p} (\lambda ,\beta ) $$
(3)
Fig. 2
figure 2

C p for a 5-MW wind turbine [15]

Full size image

So, the aerodynamic torque can be obtained as:

$$ T_{a} = \frac{{P_{a} }}{{w_{r} }} $$
(4)

The collection of low-speed shaft, gearbox, and high-speed shaft is called drive train. In this paper, a two-mass model is considered for drive train [15] (as depicted in Fig. 3) with parameters stated in Table 1.

Fig. 3
figure 3

Drive-train two-mass model

Full size image
Table 1 5-MW wind turbine mechanical parameters [15]
Full size table

The model of the drive train can be stated by the following equations (Fig. 3):

$$ J_{r} \dot{w}_{r} = T_{a} - T_{ls} - K_{r} w_{r} $$
(5)
$$ T_{ls} = K_{ls} (\theta_{r} - \theta_{ls} ) + B_{ls} (w_{r} - w_{ls} ) $$
(6)
$$ J_{g} \dot{w}_{g} = T_{hs} - K_{g} w_{g} - T_{g} $$
(7)

where θ r , θ ls , and w ls are rotor-side angular deviation, gearbox-side angular deviation, and the speed of low-speed shaft, respectively. Meanwhile, T a , T ls , T hs , and T g are aerodynamic, low-speed shaft, high-speed shaft, and generator torques, respectively. It should be noted that w g is the generator speed.

Considering the gearbox ratio as:

$$ \eta = \frac{{T_{ls} }}{{T_{hs} }} = \frac{{w_{g} }}{{w_{ls} }} = \frac{{\theta_{g} }}{{\theta_{ls} }} $$
(8)

with θ g as the generator angular deviation, by using (5–7) and (8) we have:

$$ \begin{aligned} \dot{T}_{ls} & = \left( {K_{ls} - \frac{{B_{ls} K_{r} }}{{J_{r} }}} \right)w_{r} + \frac{1}{\eta }\left( {\frac{{B_{ls} K_{g} }}{{J_{g} }} - K_{ls} } \right)w_{g} - B_{ls} \left( {\frac{{J_{r} + \eta^{2} J_{g} }}{{\eta^{2} J_{g} J_{r} }}} \right)T_{ls} \\ & \quad + \frac{{B_{ls} T_{a} }}{{J_{r} }} + \frac{{B_{ls} T_{g} }}{{\eta J_{g} }} \\ \end{aligned} $$
(9)

3.2 Problem definition

In the partial-load region, the objective is to track C p(max) to capture the maximum power. It can be seen from Fig. 2 that C p(max) is given at β = 0 and λ = λ opt, which in Fig. 2 is 7.55. By setting the blades to be orthogonal on the wind direction, the β = 0 is fulfilled. However, in order to keep λ at λ opt, the rotor speed should be tuned by a controller.

To solve this problem, two common methods have been used [10, 13]. In [10], the conventional MPPT (CMPPT) calculates the electromagnetic torque as follows:

$$ T_{{g({\text{opt}})}} = K_{\text{opt}} w_{g}^{2} - Kw_{g} $$
(10)

where

$$ K_{\text{opt}} = \frac{{\rho \pi R^{5} C_{p(\max )} }}{{2\lambda^{3} \eta^{3} }},\quad K = \left( {K_{g} + \frac{{K_{r} }}{{\eta^{2} }}} \right). $$
(11)

In other strategy [13], by extending \( X = [w_{r} \,w_{g} \,T_{ls} ] \) to \( X_{e} = [\hat{w}_{r} \,\hat{w}_{g} \,\hat{T}_{ls} \,\hat{T}_{a} ] \) and using Kalman filter to estimate X e , T g(opt) is obtained as follows:

$$ T_{{g({\text{opt}})}} = \frac{{\hat{T}_{a} }}{\eta } - \left( {\frac{{K_{r} }}{{\eta^{2} }} + K_{g} } \right)\hat{w}_{g} - \frac{{K_{c} }}{{\eta^{2} }}\left( {w_{{g({\text{ref}})}} - \hat{w}_{g} } \right) $$
(12)

where

$$ w_{{g({\text{ref}})}} = \sqrt {\frac{{\hat{T}_{a} }}{{\eta K_{\text{opt}} }}} . $$
(13)

Moreover, K c is a parameter chosen by the designer to reduce steady-state error. This method is called aerodynamic torque feedforward (ATF) controller. The performance of the proposed method in this paper is compared by the ones in [10] and [13] described above.

3.3 PSO algorithm

The particle swarm optimization (PSO) algorithm is a biologically inspired algorithm motivated by social analogy. PSO provides a population-based search procedure, in which individuals, called particles, change their position (state) with time. In a PSO system, particles fly around in a multidimensional search space. During flight, each particle adjusts its position according to its own experience and neighboring particle, making use of the best position encountered by itself and its neighbor. In PSO algorithm, each particle has a velocity and a position as follows [31]:

$$ v_{i} (k + 1) = v_{i} (k) + \gamma_{1i} (P_{i} - x_{i} (k)) + \gamma_{2i} (G - x_{i} (k)) $$
(14)
$$ x_{i} (k + 1) = x_{i} (k) + v_{i} (k + 1) $$
(15)

where i is the particle index, k is the discrete time index, v i is the velocity of ith particle, x i is position of ith particle, P i is the best position found by ith particle (personal best), G is the best position found by swarm (global best), and γ 1i and γ 2i are random numbers in the interval [0,1] applied to ith particle. In our simulations, the following equation is used for velocity [32]:

$$ v_{i} (k + 1) = \varphi (k)v_{i} (k) + \alpha_{1} \left[ {\gamma_{1i} (P_{i} - x_{i} (k))} \right] + \alpha_{2} \left[ {\gamma_{2i} (G - x_{i} (k))} \right] $$
(16)

in which φ(k) is the inertia function, and α 1 and α 2 are the acceleration constants. In this paper, linear decreasing strategy has been used, in which an initially large inertia weight (i.e., 0.9) is linearly decreased to a small value (i.e., 0.1) as follows:

$$ \varphi (k) = \left[ {\varphi (0) - \varphi (N_{T} )} \right]\frac{{(N_{T} - k)}}{{N_{T} }} + \varphi (N_{T} ) $$
(17)

where N T is the maximum number of time steps for which the algorithm is executed, φ(0) is the initial inertia weight, and φ(N T ) is the final inertia weight. The steps of PSO algorithm are as follows:

Step 1 (Initialization): Initialize swarm and randomize the position and velocity of each particle (x i , v i ; i = 1, …, M).

Step 2 (Fitness function evaluation): Compute the fitness function of each particle (y(i) = fitness(x i )).

Step 3 (Initialization of the best personal and global positions): Initialize each P i and G as P i0 = y i and G = min(P i0); i = 1, …, M.

Step 4 (Velocity and position update): Update the velocity of particle using dynamic inertia weight (Eqs. 16, 17) and control it by velocity clamping as follows:

$$ v_{i} (k + 1) = \left\{ {\begin{array}{*{20}c} {v_{i} (k + 1)} \hfill & {{\text{if}}\;v_{i} (k + 1) < V_{\max } } \hfill \\ {V_{\max } } \hfill & {{\text{if}}\;v_{i} (k + 1) \ge V_{\max } } \hfill \\ \end{array} } \right. \, $$
(18)

Update the position of particle (Eq. 15).

Step 5 (Update of the best personal and global positions): Update P i and G based on the new value of fitness function as y i,new = fitness(x i,new), P i  = y i,new, and G = min(P i ).

Step 6 (Test): If the stop conditions are not satisfied, go to Step 4. Otherwise, stop and return G as the best solution.

3.4 Fuzzy logic system (FLS)

Fuzzy logic was first introduced by Lotfi A. Zadeh in 1965 [33]. A fuzzy system is based on fuzzy logic, which has reasoning similar to human’s reasoning. The fuzzy system is a particular form of nonlinear mapping depicted in Fig. 4.

Fig. 4
figure 4

Schematic of a FLS

Full size image

The fuzzifier maps a numerical input to a fuzzy set, and the defuzzifier maps a fuzzy set to a numerical output. The fuzzy inference engine based on fuzzy IF–THEN rules in fuzzy rule base maps the input fuzzy set to the output fuzzy set. Most often, singleton fuzzifier, center average defuzzifier, and product inference engine are used. The design of FLS does not require complicated mathematical calculations, the FLS can be easily generalized and developed, and they can cope well with uncertainties and nonlinearities. However, all of these advantages are achieved, if the membership functions are well tuned. Unfortunately, there is not a unique method to tune the membership functions. However, this goal can be achieved using intelligent optimization methods [34].

4 Proposed method

The objective in this paper is to propose an optimal PI controller, which for any wind-speed profile can capture the maximum power. The proposed method has two stages (Figs. 5, 6): In the first stage, the PSO algorithm is applied to derive a pair of PI gains for some wind speeds (Fig. 5). In the second stage, the data derived in the first stage are used to tune the membership functions of a one-input two-output fuzzy system. This fuzzy system is used to give the optimal PI gains in each wind speed (Fig. 6).

Fig. 5
figure 5

Block diagram of the proposed controller in stage 1: preparing optimal data for training FLS (an off-line procedure)

Full size image
Fig. 6
figure 6

Block diagram of the proposed controller in stage 2: using the trained FLS by the data derived in stage 1 to control wind turbines for any wind-speed profile

Full size image

Figure 7 shows the desired λ and C p versus wind speed in both partial- and full-load operational regions. Here, the focus is on partial-load region. It can be seen from Fig. 7 that at the beginning λ is chosen larger than the optimal value, since the abrupt change in the generator speed causes a bump in torque signal and thus may lead the generator into the motoring mode.

Fig. 7
figure 7

λ and C p curves for WT model

Full size image

The wind speed is assumed in the interval [3,11.3] in the partial-load region. Since the measurement of w r is with considerable noise in practice, we use the measured w g to derive w r with desirable accuracy as w r  = w g /η. The following cost function is used for PSO algorithm:

$$ C = \int\limits_{0}^{T} {\left| {\frac{{w_{g} (t)}}{\eta } - \frac{{v(t) \times \lambda_{\text{opt}} }}{R}} \right|{\text{d}}t} $$
(19)

where T denotes the total simulation time and should be selected by the designer, and w r(opt) is derived using (3) as follows:

$$ w_{{r({\text{opt}})}} = \frac{{v\lambda_{\text{opt}} }}{R} $$
(20)

The optimal PI gains for some wind speeds are obtained using the PSO algorithm.

In the second stage, depicted in Fig. 6, the data derived by PSO are used to make the fuzzy logic system called FLS. The input membership functions of the FLS, as shown in Fig. 8, are chosen Gaussian with centers at wind speeds [3, 3.5, 4, 4.5, 5, 6, 7, 8, 9, 10, 10.8, 11.3]. The output membership functions can be any type of membership functions with centers at optimal Kp’s and Ki’s for different wind speeds. Using singleton fuzzifier, center average defuzzifier and product inference engine, the optimal Kp and Ki are obtained from the fuzzy system for each wind-speed profile in the partial-load region.

Fig. 8
figure 8

FLS input membership functions

Full size image

In order to decrease the torque fluctuations that are usually caused by fast variations in wind speed a low-pass filter (LPF) is used to filter the optimal rotor speed. This is because, due to (2) and considering a constant TSR, the fast variations in wind speed causes fast variations in optimal rotor speed, which thus leads to torque fluctuations. Thus, the optimal rotor speed is filtered using the following second-order low-pass filter (LPF):

$$ H(s) = \frac{1}{{\alpha^{2} s^{2} + 2\alpha s + 1}} $$
(21)

where s is the Laplace variable. In order to avoid the attenuation of the filtered optimal rotor speed from the original optimal rotor speed, α should be chosen small enough. In this paper, it is chosen as 0.01. This gives a smoother optimal rotor speed, thus a smoother torque signal.

5 Simulation results and comparisons

In this section, the proposed controller is applied to a 5-MW wind turbine model. In our simulations, the parameters of PSO algorithm are set as shown in Table 2.

Table 2 PSO parameters setting
Full size table

The cost values (based on Eq. 19) and the derived gains for different wind speeds are reported in Table 3. Since the starting and the ending of wind-speed interval are more important, the step size for them is chosen smaller.

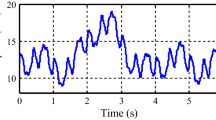
Table 3 Optimization results by PSO
Full size table

Figure 9 shows the wind-speed profile for this simulation. It should be noted this is an arbitrary wind-speed profile and one can choose any other profiles; this is due to the independency of the proposed method to wind-speed profiles.

Fig. 9
figure 9

Wind-speed profile

Full size image

Figure 10 shows the power coefficient for different methods. It should be noted that C p(max) = 0.482 for the wind turbine in this simulation.

Fig. 10
figure 10

Power coefficient for different methods: proposed method (magenta, continuous line), CMPPT (green, dashed line), and ATF (blue, dotted line) (color figure online)

Full size image

The rotor speed for different methods is shown in Fig. 11. It can be seen from Figs. 10 and 11 that the proposed method in average is able to track the optimal power coefficient better than the conventional methods and thus is able to track the desired rotor speed better.

Fig. 11
figure 11

Generator speed for different methods: proposed method (magenta, continuous line), CMPPT (green, dashed line), and ATF (blue, dotted line) (color figure online)

Full size image

The torque signal and the captured power are shown in Figs. 12 and 13, respectively. It can be seen that the proposed torque signal has acceptable fluctuations in comparison with the conventional methods. Meanwhile, to compare the captured power for different methods, the following criterion is used:

$$ J = \frac{1}{T}\int\limits_{0}^{T} {\Uppsi (t){\text{d}}t} $$
(22)

where Ψ(t) can be P(t) or C p (t), that is, output power or power coefficient, respectively. Obviously, the method that gives a bigger number for J (bigger P out(avg) or C p(avg)) has captured the larger power.

Fig. 12
figure 12

Generator torque for different methods: proposed method (magenta, continuous line), CMPPT (green, dashed line), and ATF (blue, dotted line) (color figure online)

Full size image
Fig. 13
figure 13

Generator power for different methods: proposed method (magenta, continuous line), CMPPT (green, dashed line), and ATF (blue, dotted line) (color figure online)

Full size image

Also, the performance of the proposed controller is compared with the commonly used strategies mentioned before (CMPPT and ATF). Table 4 demonstrates the results. It shows that the proposed method has a better power capturing performance in comparison with the other methods. It can be stated that the proposed method is able to capture effective power in partial load while giving acceptable fluctuations in torque signal.

Table 4 Comparison of different methods in terms of captured power and power coefficient
Full size table

6 Conclusions

In this paper, an optimal PI torque controller has been proposed for wind turbines to capture the maximum power in the partial-load region. The proposed controller uses the PSO technique to derive the optimal PI gains for some wind speeds in the partial-load region. Then, a fuzzy system as a decision maker, by using the derived information by PSO algorithm, has been proposed to give the PI gain for any wind speed. Moreover, to cope with fluctuations in torque signal caused by the wind-speed variations, an LPF filter has been used. The simulation results have shown the superiority of proposed method in comparison with the commonly used methods in capturing maximum power.