1 Introduction

Many real-world datasets are imbalanced, in which most of the instances belong to one class and far fewer instances belong to another one, yet usually more interesting class, such as fraud detection, risk management, medical diagnosis, bioinformatic, text classification and information retrieval [1]. In the case of binary classification, imbalanced dataset means that the number of negative samples is much larger than that of positive ones. The classification for imbalanced datasets is a quite pervasive and ubiquitous problem, so it has received a lot of attentions in the machine learning community. This interest gave rise to two important workshops held in 2000 and 2003 at the AAAI [2] and ICML [3] conferences, respectively. A follow-up workshop, PAKDD, was conducted in 2009 [4]. Despite the fact that many workshops have already been held to discuss about the topic, a large number of practitioners plagued by the problem are still working in isolation [5, 6].

One of the main challenges of imbalance problem is that the small classes are often more useful, but standard classifiers tend to be overwhelmed by the large classes and ignore the small ones. To handle the problem, the main idea is to rebalance the data distribution and deflect the decision boundary; so far, a number of approaches have been proposed. Generally, the common methods can be divided into two main directions: at the data level, resampling approaches such as undersampling and oversampling; at the algorithms level, algorithm-based approaches such as cost-sensitive learning, one-class learning and ensemble learning [6].

Undersampling [7] is the simplest way to rebalance a dataset by under-sampling the majority class to match the size of the minority class. Obviously, this method can potentially remove certain important samples and results in information loss for the majority class. In contrast, oversampling duplicates minority instances in the hope of reducing class imbalance, but it can easily lead to over-fitting and introduce an additional computational task if the dataset is already large. SMOTE algorithm [8], as one of the successful oversampling methods, is expected to alleviate the over-fitting problem by adding the “new” minority instances. However, just because of this, it may introduce excessive noise.

Algorithm-based approaches are designed to modify the classifiers based on their inherent characteristics in order to adapt them to the datasets. Cost-sensitive learning seems to be the best approach of this kind by assigning distinct costs to the training instances. Usually, this strategy gives higher learning cost to the samples in the minority class and this scheme is generally merged into the common formulation of classification algorithms. Consequently, various experimental studies of this type have been performed using different kinds of classifiers [9–11]. One-class learning is another strategy for imbalance problem, the advantage of which is that discarding the distractive majorities, the “space” where minority data resides could be better determined [12, 13]. But there is a disadvantage of one-class learning: the classifier may over-fit the training minority class.

On the basis of statistical learning theory, support vector machine (SVM) was proposed as computationally powerful tools for supervised learning including both classification and regression [14, 15]. SVM have established themselves as a successful approach for various machine learning tasks. But as for the extremely imbalanced datasets, the decision boundary of SVM obtained from the training data is largely biased toward the minority class. Many researchers have studied and proposed plenty of effective techniques to adjust the decision boundary [16, 17]. Ensemble learning strategies are also employed to construct new algorithms to improve SVM’s performance for the imbalance learning problem [18].

In this paper, we propose a new algorithm, namely ensemble support vector machine with segmentation (SeEn–SVM), for the classification of imbalanced datasets. In particular, vector quantization (VQ) algorithm is used to segment the majority class and hence generate some small datasets that are of less imbalance than original one, and two different weighted functions are proposed to integrate all the results of basic classifiers. The goal of the SeEn–SVM algorithm is to improve prediction accuracy of the minority class, which is more interesting for people. Of course, it will be void if the algorithm decrease specificity too much.

The rest of the paper is organized as follows. In Sect. 2, we provide the background of SVM, ensemble learning as well as VQ principle. The proposed ensemble framework is presented in Sect. 3. In Sect. 4, we report the experiment results, and Conclusion is given in Sect. 5.

2 Background

2.1 Support vector machine (SVM)

Generally, support vector machine is used for classification. The essential idea of SVM is to search a linear separating hyperplane that maximizes the distance between two classes of data to create a classifier.

For a binary classification problem, the training dataset consists of samples \( x_{i} \in \Re^{n} ,\quad i = 1,\; \ldots ,\;l \) with corresponding class values \( y_{i} \in \{ - 1,1\} ,\quad i = 1,\; \ldots ,\;l \). The formulation is a linear soft margin algorithm, which is used to solve the following optimization problem:

$$ \begin{array}{llll} {\mathop {\min }\limits_{w,b} } \hfill & \frac{1}{2} {\left\| w \right\|^{2} + C\sum\limits_{i = 1}^{l} {\xi_{i} } } \hfill \\ {{\text{s}} . {\text{t}} .} \hfill & {y_{i} \left( {\left( {w \cdot x_{i} } \right) + b} \right) \ge 1 - \xi_{i} ,\quad i = 1,\; \ldots ,\;l} \hfill \\ {} \hfill & {\xi_{i} \ge 0,\quad i = 1,\; \ldots ,\;l} \hfill \\ \end{array} $$
(1)

where the predefined parameter C is a trade-off between training accuracy and generalization, \( \xi_{i} \) is the slack variable, \( w \in \Re^{n} \) is a weight vector that defines a direction perpendicular to the hyperplane of the decision function, while b is a bias that moves the hyperplane parallel to itself. The decision function is presented as follows:

$$ f(x) = \text{sgn} ((w \cdot x) + b) $$
(2)

The solution of this optimization problem is given by solving the corresponding dual problem with introduced Lagrange multiplier α

$$ \begin{array}{llll} {\mathop {\min }\limits_{\alpha } } \hfill & \frac{1}{2} {\sum\limits_{i = 1}^{l} {\sum\limits_{j = 1}^{l} {y_{i} y_{j} \left( {x_{i} \cdot x_{j} } \right)\alpha_{i} \alpha_{j} } } - \sum\limits_{j = 1}^{l} {\alpha_{j} } } \hfill \\ {{\text{s}} . {\text{t}} .} \hfill & {\sum\limits_{i = 1}^{l} {y_{i} \alpha_{i} = 0} } \hfill \\ {} \hfill & {0 \le \alpha_{i} \le C,\quad i = 1,\; \ldots ,\;l} \hfill \\ \end{array} $$
(3)

Generally, the solution α* of the dual problem is sparse, and the corresponding decision hyperplane depends only on few “support vectors.”

$$ f\left( x \right) = \text{sgn} \left( {\left( {w^{*} \cdot x} \right) + b^{*} } \right) = \text{sgn} \left( {\sum\limits_{i = 1}^{l} {\alpha_{i}^{*} y_{i} \left( {x_{i} \cdot x} \right) + b^{*} } } \right) $$
(4)

Actually, not every problem is classified linearly; SVM firstly maps n dimensional input data into a higher dimensional feature space via a nonlinear function \( \Upphi ( \cdot ) \). Using the “kernel trick,” a kernel function \( K(x_{i} ,\;x_{j} ) \) is used to substitute the dot product of mapping function \( (\Upphi (x_{i} ),\;\Upphi (x_{j} )) \). Thus, the explicit computing of \( \Upphi ( \cdot ) \) can be avoided, and the decision function is obtained as follows:

$$ f\left( x \right) = \text{sgn} \left( {\sum\limits_{i = 1}^{l} {\alpha_{i}^{*} y_{i} K\left( {x_{i} \cdot x} \right) + b^{*} } } \right) $$
(5)

2.2 Ensemble learning

Ensemble learning is a machine learning paradigm where multiple learners are trained to solve the same problem. In contrast to individual classifier, ensemble methods try to construct a set of base classifiers and then classify new samples by combining their outputs in some way. It has been accepted widely that ensemble classification has promising capabilities in improving classification accuracy. Obviously, there exist two steps in constructing ensemble scheme: the first step is to generate a number of base classifiers and the second is to aggregate the base classifiers by weighted or unweighted voting typically.

To obtain a good ensemble, the base learners should be as more accurate as possible, and as more diverse as possible [19]. In other words, the generalization performance of ensemble classifiers depends on the accuracy and diversity trade-off of the base classifiers. In practice, the diversity of the base learners can be introduced from different channels, such as subsampling the training samples, manipulating the attributes, manipulating the outputs, injecting randomness into learning algorithms or even using multiple mechanisms simultaneously. The employment of different base learner generation processes and/or different combination schemes leads to different ensemble methods [20].

2.3 Vector quantization (VQ)

Vector quantization, also called “block quantization” or “pattern matching quantization,” is often used in lossy data compression [21]. Given a training dataset consisting of l vectors, \( T = \left\{ {x_{1} ,\;x_{2} ,\; \ldots ,\;x_{l} } \right\} \), the vector quantizer maps T into a finite set of vectors \( {\it{Code}} = \left\{ {c_{1} ,\;c_{2} ,\; \ldots ,\;c_{M} } \right\} \), each vector \( c_{i} ,\left( {i = 1,\;2,\; \ldots ,\;M} \right) \) is called a codevector, and the set of all the codevectors is called a codebook. Then the whole region is partitioned by the codevectors into a set of subregions, so-called “Voronoi Region,” \( V = \left\{ {V_{1} ,\;V_{2} ,\; \ldots ,\;V_{M} } \right\} \), and it is defined by:

$$ V_{i} = \left\{ {x \in T:\left\| {x - c_{i} } \right\| \le \left\| {x - c_{j} } \right\|,\;\forall j \ne i} \right\},\quad i = 1,\; \ldots ,\;M $$
(6)
$$ \mathop \cup \limits_{i = 1}^{M} V_{i} = T,\quad \mathop \cap \limits_{i = 1}^{M} V_{i} = \Phi $$
(7)

Vectors within a region V i are represented by their codevector \( \varphi \left( {x_{k} } \right) = c_{i} , \) if \( x_{k} \in V_{i} \). Figure 1 shows the division of VQ.

Fig. 1
figure 1

Division of vector quantization

Full size image

To find Code and V is to minimize the average distortion which can be given by:

$$ D = \frac{1}{\text{Mn}}\sum\limits_{i = 1}^{l} {\left\| {x_{i} - \varphi \left( {x_{i} } \right)} \right\|^{2} } $$
(8)

where n is the dimension of training vectors [22].

3 Proposed algorithm: SeEn–SVM

In this paper, we present a new method that focuses on improving classification performance for imbalanced datasets by using an ensemble of SVM integrated with VQ technique. The detailed procedure of the proposed method is given in the following subsections.

3.1 The basic idea of SeEn–SVM

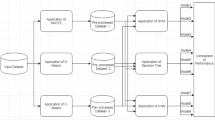
There are three main steps in our proposed algorithm, which includes segmentation, training and aggregation. An overview of the procedure is given in Fig. 2.

Fig. 2
figure 2

Procedure of SeEn–SVM

Full size image
  1. (1)

    First, as mentioned in introduction, undersampling and oversampling have their drawbacks and might result in information loss and over-fitting, respectively. So we start rebalancing the datasets by segmenting the majority (negative) class; similar to clustering, the idea of VQ technique is applied to divide the majority class into K small data subsets, and the similarity of the data in same subset is much higher than that in two different subsets. Meanwhile, the size of each dataset is allowed to be different and is not necessary to be the same with the size of minority class. What needs us to determine is the number of small data subsets. In SeEn–SVM algorithm, a detailed strategy is constructed for this.

  2. (2)

    Then, by combining minority class with each segmented small subset, K less imbalanced training datasets are generated. Subsequently, SVM is used as base learner to train every modified version of the data and K base classifiers can be obtained. Owing to the negative classes in every new training data are distinct completely, the major differences exist among diverse classifiers. This plays an important role in improving generalization ability of an ensemble.

  3. (3)

    Finally, after training, we need to aggregate all independent base classifiers into an appropriate combination manner. Instead of majority voting and other combining methods generally used, we formulate two types of functions to determine the weight for every base classifier according to the distance between negative dataset and positive dataset in each training process. For a new test sample, the final prediction is produced by all of the base classifiers.

3.2 Algorithm of SeEn–SVM

Given the minority (positive) training set P and the majority (negative) training set N, there will be two related important problems when implementing our proposed SeEn–SVM: the first is how many small negative subsets should be generated from N; the second is how to formulate the weighting functions that aggregate all independent base classifiers into an appropriate combination manner. The algorithm of SeEn–SVM is shown in Table 1.

Table 1 SeEn–SVM algorithm
Full size table

Step 2 of learning process displays a concrete strategy for choosing an appropriate M, which consists of two aspects:

  1. (1)

    It is known that SVM may perform well while the imbalance ratio is moderate and some observations have demonstrated that SVM could be robust and self-adjusting, so when \( {{m_{1} } \mathord{\left/ {\vphantom {{m_{1} } {m_{2} }}} \right. \kern-\nulldelimiterspace} {m_{2} }} > 1:5 \), that means the ratio between the number of positive samples and negative samples could not be too large to influence their performance. Hence, let M = 1, which is equivalent to do nothing for negative training data, and only SVM is utilized to train the original dataset D.

  2. (2)

    However, due to extremely skewed data distribution, SVM modeled on the original training dataset is prone to classify most of the samples to be negative. When \( {{m_{1} } \mathord{\left/ {\vphantom {{m_{1} } {m_{2} }}} \right. \kern-\nulldelimiterspace} {m_{2} }} \le 1:5 \), that means the imbalance ratio is larger than the first case, and this may lead to a high false negative rate, so we let \( M = 2^{{n_{0} }} \), where n 0 can be equal to any positive integer, which is subjected to \( \mathop {\min }\limits_{n} \left| {q - 2^{n} } \right|,\quad (n = 1,\;2 \ldots ) \). In this situation, at least one division should be done to the negative class.

Of course, M is not only the number of negative subsets but also the number of component members used in ensemble process to achieve a good performance. In order to be more reasonable and feasible, after n 0 is computed, M can be chosen among \( 2^{{n_{0} - 1}} \), \( 2^{{n_{0} }} \) and \( 2^{{n_{0} + 1}} \). Because n 0 is only related to imbalance ratio, but except for this, the size and distribution of data may also influence the performance of classifiers, the capability of SeEn–SVM algorithm would be limited if only \( M = 2^{{n_{0} }} \) is considered.

SVM assumes that only SVs are informative to classification and other samples can be considered redundant. For imbalanced classification, SVM would be less affected by the negative instances that lie far away from the learned boundary even if there are many of them. In addition, some of the negative SVs may not be the most informative or even noisy. The goal of SeEn–SVM algorithm manages to cope with this problem. Step 9 of the learning process in Table 1 shows the formulation of the weighted function, which decides the importance of the i-th (\( i = 1,\; \ldots ,\;M \)) base classifier. It is clear that the closer the distance between the codevector of the i-th negative dataset and the codevector of positive dataset, the lager the weight value of the i-th classifier is. And this does not satisfy the linear relationship but the exponential relationship. This strategy can increase the number of SVs especially the negative SVs that are far away from the real decision boundary and hence alleviate the boundary skewness.

3.3 Improvement of SeEn–SVM

For a large and imbalanced dataset, there may be many redundant or noisy negative samples, even there are some positive samples in the negative class and we do not know which ones are false. This phenomenon is common in bioinformatics problems, such as gene function prediction [23], alternative splicing sites identification [24] and horizontal gene transfer detection [25] and so on. It is a well-known fact that the false negative samples may distribute closed to true positive data samples. In this sense, step 9 of learning process in algorithm might be reformulated as follows:

$$ v_{i}^{*} = \exp \left[ { - {{\left| {d_{i} - d_{m} } \right|} \mathord{\left/ {\vphantom {{\left| {d_{i} - d_{m} } \right|} {\left( {d_{\max } + d_{m} - d_{i} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {d_{\max } + d_{m} - d_{i} } \right)}}} \right],\quad i = 1,\; \ldots ,\;M $$
(9)

where d m and d max are the median and maximum of M values \( d_{i} ,(i = 1,\;2,\; \ldots ,\;M) \) that represent the distances between the codevectors of negative subsets and the codevector of positive dataset, respectively. \( v_{i}^{*} \) is different form \( v_{i} \) by putting the highest weight to the classifier \( g_{i} (x) \) whose negative dataset is in the “middle” of original negative dataset not to the closest one from the positive dataset. For the rest classifiers, the farther the distance from the positive dataset, the smaller weight the value is. Because negative subset closer to the positive dataset is more useful than farther ones in classification despite some noisy points, the closer subsets’ weights would be larger than the farther ones’. Thus, it is hoped to improve the generalization performance of SeEn–SVM algorithm.

4 Experiments and results

In this section, six UCI imbalanced datasets are used in our experimental study to test our proposed method, namely Glass (7), Segment (1), Abalone (7), Satalog (4), Letter (4) and letter (1). The numbers in the parentheses indicate which classes are selected as minority (positive) class, and all others are used as majority (negative) class.

These datasets are often appeared in related works about imbalanced research. The basic information about these datasets is summarized in Table 2 including the size of every dataset, the number of features, and the number of positive samples and negative samples in each dataset. These datasets are seriously selected to vary in data size (from several hundreds to tens of thousands) and imbalance ratio, the first two datasets are mildly imbalanced, while the rest ones are highly imbalanced as less than 10 % samples are positive.

Table 2 Characteristics of datasets used in this paper
Full size table

In order to evaluate the classifiers on imbalanced datasets, we use G-mean instead of prediction accuracy to measure the performance of algorithm since it combines the values of both sensitivity and specificity. Because overall accuracy is not sufficient any more in evaluating the classifier with highly skewed dataset, sensitivity and specificity are then usually adopted to monitor classification performance on two classes separately and they are defined as

$$ {\text{sensitivity}} = \frac{{\# {\text{true}}\_{\text{positive}}}}{{\# {\text{true}}\_{\text{positive}} + \# {\text{false}}\_{\text{negative}}}} $$
(10)
$$ {\text{specificity}} = \frac{{\# {\text{true}}\_{\text{negative}}}}{{\# {\text{true}}\_{\text{negative}} + \# {\text{false}}\_{\text{positive}}}} $$
(11)

Based on these two metrics, G-mean metric suggested by Kubat et al. [26] is defined as follows:

$$ {\text{G}}{\text{-mean}} = \sqrt {{\text{sensitivity}} \cdot {\text{specificity}}} $$
(12)

G-mean metric indicates balanced classification ability between positive class accuracy and negative class accuracy by taking the geometric mean of sensitivity and specificity, and obviously, if a classifier is highly biased toward one class, the G-mean value would be low. Hence, G-mean metric is used to compare the classification performance of models with imbalanced datasets in our experiments.

In the following, SeEn–SVM algorithm is compared with four other popular methods, which are SVM, undersampling, SMOTE and cost-sensitive learning. In our experiments, we use 10-fold cross-validation to train our classifier since it provides more realistic results. Each dataset in Table 2 is trained respectively by all methods, while finding the optimal parameters the final 10-fold cross-validation results can be obtained. SVM is implemented in LIBSVM [27], and SeEn–SVM is implemented by writing procedure in Matlab, but the results of other three methods on different datasets are referred to different literatures as shown in Table 3. Our G-mean measure is gained by running the experiment 10 times with different training and test datasets; besides the measurement of G-mean, the standard error of the G-mean is also given to our classifier. Table 3 also illustrates the comparison of the G-mean value by our method and the rest ones.

Table 3 G-mean values of five methods on six datasets
Full size table

In executing SeEn–SVM algorithm, for every dataset, radial basis functions (RBF) are used as kernel functions, and we choose the same cost parameter C in every component SVM. But for SeEn–SVM algorithm, the segmentation number M and weighted function should be determined. In last column of Table 3, the results of selected M and weighted function are given in brackets; ν or \( v_{i}^{*} \) represents which weighted function is used in decision-making process.

Table 3 shows obviously that the performance of SeEn–SVM algorithm is better than the previously proposed methods, and the G-mean value of SeEn–SVM is higher than that of other methods on most of the experiment datasets. There are only two datasets on which SeEn–SVM does not perform best, but the G-mean value of SeEn–SVM is much close to the best result. The last line of Table 3 displays the average G-mean values over all datasets of each methods, the result of SeEn–SVM is higher overwhelmingly than other methods, and the standard errors show that SeEn–SVM is stabile too. Figure 3 gives the bar graph of compared methods’ results, which shows the results gained by all of the methods more visually, and the relative improvements can be gotten from the bar graph.

Fig. 3
figure 3

Bar graph of compared methods’ results

Full size image

Table 4 displays the sensitivity and specificity of SVM and SeEn–SVM algorithm on all datasets. Note that SVM has almost perfect specificity, but poor sensitivity because it tends to classify all samples as negative. Any proposed algorithm for imbalanced datasets sacrifices inevitably some specificity in order to improve the sensitivity and SeEn–SVM has no exception. But SeEn–SVM decreases specificity in a less extent and simultaneously increases sensitivity greatly.

Table 4 Sensitivity and specificity values of SVM and SeEn–SVM on six datasets
Full size table

5 Conclusions

This paper introduces a novel approach for learning from imbalanced datasets through making an ensemble of SVM classifiers with VQ techniques. Although SVM has shown an outstanding performance in many research areas and it can adjust itself well to some degree of data imbalance, the performance of SVM can still be influenced by data imbalance.

To cope with the problem associated with imbalanced datasets, SeEn–SVM segments the original negative data into some small subsets firstly and then trains M new small training datasets to learn base classifiers by SVM, and finally makes decision by aggregating all the base learners with appropriate weighted function. Through theoretical analysis and empirical studies, we demonstrate this algorithm effective and applicable. In the experiment studies, the new algorithm was applied to six UCI datasets, and the results confirmed its better performance than previously proposed methods for imbalance problem.