Swallow swarm optimization algorithm: a new method to optimization

Abstract

This paper presents an exposition of a new method of swarm intelligence–based algorithm for optimization. Modeling swallow swarm movement and their other behavior, this optimization method represents a new optimization method. There are three kinds of particles in this method: explorer particles, aimless particles, and leader particles. Each particle has a personal feature but all of them have a central colony of flying. Each particle exhibits an intelligent behavior and, perpetually, explores its surroundings with an adaptive radius. The situations of neighbor particles, local leader, and public leader are considered, and a move is made then. Swallow swarm optimization algorithm has proved high efficiency, such as fast move in flat areas (areas that there is no hope to find food and, derivation is equal to zero), not getting stuck in local extremum points, high convergence speed, and intelligent participation in the different groups of particles. SSO algorithm has been tested by 19 benchmark functions. It achieved good results in multimodal, rotated and shifted functions. Results of this method have been compared to standard PSO, FSO algorithm, and ten different kinds of PSO.

1 Introduction

Swarm intelligence (SI) [1] as observed in natural swarms is the result of actions that individual in the swarm perform exploiting local information. Usually, the swarm behavior serves to accomplish certain complex colony-level goals. Examples include group foraging by ants, division of labor among scouts and recruits in honeybee swarms, evading predators by fish schools, flocking of birds, and group-hunting as observed in canids, herons, and several cetaceans.

The decentralized decision-making mechanisms found in the above examples, and others in the natural world, offer an insight on how to design distributed algorithms that solve complex problems related to diverse fields, such as optimization, multi-agent decision making, and collective robotics. Ant colony optimization technique [2–4], particle swarm optimization algorithm [5–7], artificial fish swarm optimization algorithm [8–10], and glowworm swarm optimization algorithm [11–14] and several swarms based collective robotic algorithms, etc are different methods of swarm intelligence [15–17].

In this paper, we present a novel algorithm called swallow swarm optimization (SSO) for the simultaneous computation of multimodal functions. The algorithm shares some common features with particle swarm optimization (PSO) with fish swarm optimization (FSO), but with several significant differences. Swallows own high swarm intelligence. Their flying speed is high, and they are able to fly long distances in order to migrate from one point to another. They fly in great colonies. Flying collectively, they mislead hunters in dangerous positions. Swallow swarm life has many particular features that are more complicated and bewildering in comparison with fish schools and ant colonies. Consequently, it has been appointed as the subject of research and algorithm simulation.

The second section is about the method. Third section is about the benchmark function. Forth section is about experimental results and examining the diverse states of PSO and FSO and then comparing them to proposed method.

2 Method

Using swarm intelligence in optimization problems has become prevalent in recent decades. Methods like PSO, GA, ACO, FSO, GSO and many compound methods which by combining these methods are trying to refine the diverse engineering problems more and more. Some examples of what have been done which are combinations of different methods of SI are shown in Table 1. Certainly, fuzzy logic plays an important role in optimization [18].

Table 1 Review to compound methods of new optimization

2.1 PSO and its developments

2.1.1 PSO structure

The initial ideas on particle swarms of Kennedy (a social psychologist) and Eberhart (an electrical engineer) were basically aimed at producing computational intelligence by exploiting simple analogs of social interaction, rather than purely individual cognitive abilities. The first simulations [5] were influenced by Heppner and Grenander’s work [19] and involved analogs of bird flocks searching for corn. These soon developed [5, 20, 21] into a powerful optimization method—PSO [22].

In PSO, a swarm of particles are represented as potential solutions, and each particle i is associated with two vectors, that is, the velocity vector $V_{i} = \left[ {v_{i}^{1} ,v_{i}^{2} , \ldots ,v_{i}^{D} } \right]$ and the position vector $X_{i} = \left[ {x_{i}^{1} ,x_{i}^{2} , \ldots ,x_{i}^{D} } \right]$ where D stands for the dimensions of the solution space. The velocity and the position of each particle are initialized by random vectors within the corresponding ranges. During the evolutionary process, the velocity and position of particle i on dimension d are updated as:

$$ v_{i}^{d} = wv_{i}^{d} + c_{1} rand_{1}^{d} \left( {p{\text{Best}}_{i}^{d} - x_{i}^{d} } \right) + c_{2} rand_{2}^{d} \left( {n{\text{Best}}^{d} - x_{i}^{d} } \right) $$

(1)

$$ x_{i}^{d} = x_{i}^{d} + v_{i}^{d} $$

(2)

where w is the inertia weight [23], c ₁ and c ₂ are the acceleration coefficients [20], and $rand_{1}^{d}$ and $rand_{2}^{d}$ are two uniformly distributed random numbers independently generated within [0, 1] for the dth dimension [5]. In (1), pBest _i is the position with the best fitness found so far for the ith particle, and nBest is the best position in the neighborhood. In the literature, instead of using nBest, gBest may be used in the global-version PSO, whereas lBest may be used in the local-version PSO (LPSO). An user-specified parameter $V_{\max }^{d} \in \Re^{ + }$ is applied to clamp the maximum velocity of each particle on the dth dimension. Thus, if the magnitude of the updated velocity $\left| {v_{i}^{d} } \right|$ exceeds $V_{\max }^{d}$, then $v_{i}^{d}$ is assigned the value $sign\left( {v_{i}^{d} } \right)V_{\max }^{d}$.

2.1.2 New developments of the PSO

Given its simple concept and efficiency, the PSO has become a popular optimizer and has widely been applied in practical problem solving. Thus, theoretical studies and performance improvements of the algorithm have become important and attractive. Convergence analysis and stability studies have been reported by Clerc and Kennedy [24], Trelea [25], Yasuda et al. [26], Kadirkamanathan et al. [27], and van den Bergh and Engelbrecht [28].

The inertia weight w in (1) was introduced by Shi and Eberhart [23]. They proposed a w linearly decreasing with the iterative generations as:

$$ w = w_{\max } - (w_{\max } - w_{\min } )g/G $$

(3)

where g is the generation index representing the current number of evolutionary generations and G is a predefined maximum number of generations. Here, the maximal and minimal weights w _max and w _min are usually set to 0.9 and 0.4, respectively [23, 29]. In addition, a fuzzy adaptive w was proposed in [30], and a random version setting w to 0.5 + random (0, 1)/2 was experimented in [31] for dynamic system optimization. As this random w has an expectation of 0.75, it has a similar idea as Clerc’s constriction factor [32, 33]. The constriction factor has been introduced into PSO for analyzing the convergence behavior, that is, by modifying (1) to

$$ v_{i}^{d} = \chi \left[ {v_{i}^{d} + c_{1} rand_{1}^{d} \left( {p{\text{Best}}_{i}^{d} - x_{i}^{d} } \right) + c_{2} rand_{2}^{d} \left( {n{\text{Best}}^{d} - x_{i}^{d} } \right)} \right] $$

(4)

where the constriction factor

$$ \chi = \frac{2}{{\left| {2 - \phi - \sqrt {\phi^{2} - 4\phi } } \right|}} $$

(5)

is set to 0.729 with

$$ \phi = c_{1} + c_{2} = 4.1 $$

(6)

where c1 and c2 are both set to 2.05 [33]; mathematically, the constriction factor is equivalent to the inertia weight, as Eberhart and Shi pointed out in [34]. Besides the inertia weight and the constriction factor, the acceleration coefficients c1 and c2 are also important parameters in PSO. In Kennedy’s two extreme cases [35], that is, the “social-only” model and the “cognitive-only” model, experiments have shown that both acceleration coefficients are essential to the success of PSO. Kennedy and Eberhart suggested a fixed value of 2.0, and this configuration has been adopted by many other researchers. Suganthan [36] showed that using ad hoc values of c1 and c2 rather than a fixed value of 2.0 for different problems could yield better performance. Ratnaweera et al. [37] proposed a PSO algorithm with linearly time-varying acceleration coefficients (HPSO-TVAC), where a larger c1 and a smaller c2 were set at the beginning and were gradually reversed during the search. Among these three methods, the HPSO-TVAC shows the best overall performance [37]. This may be due to the time-varying c1 and c2 that can balance the global and local search abilities, which implies that adaptation of c1 and c2 can be promising in enhancing the PSO performance. Hence, this paper will further investigate the effects of c1 and c2 and develop an optimal adaptation strategy according to ESE.

Another active research trend in PSO is hybrid PSO, which combines PSO with other evolutionary paradigms. Angeline [38] first introduced into PSO a selection operation similar to that in a genetic algorithm (GA). Hybridization of GA and PSO has been used in [39] for recurrent artificial neural network design. In addition to the normal GA operators, for example, selection [38], crossover [40], and mutation [41], other techniques such as local search [42] and differential evolution [43] have been used to combine with PSO. Cooperative approach [44], self-organizing hierarchical technique [45], deflection, stretching, and repulsion techniques [46] have also been hybridized with traditional PSO to enhance performance. Inspired by biology, some researchers introduced niche [47, 48] and speciation [49] techniques into PSO to prevent the swarm from crowding too closely and to locate as many optimal solutions as possible and adaptive particle swarm optimization (APSO) that features better search efficiency than classical particle swarm optimization [50]. The orthogonal PSO (OPSO) reported in [41] uses an “intelligent move mechanism” (IMM) operation to generate two temporary positions, H and R, for each particle X, according to the cognitive learning and social learning components, respectively. Then, OED is performed on H and R to obtain the best position X* for the next move, and then, the particle velocity is obtained by calculating the difference between the new position X* and the current position X. Such an IMM was also used in [51] to orthogonally combine the cognitive learning and social learning components to form the next position, and the velocity was determined by the difference between the new position and the current position. The OED in [52] was used to help generate the initial population evenly. Different from previous work and to go steps further, in this paper, we use the OED to form an orthogonal learning strategy, which discovers and preserves useful information in the personal best and the neighborhood best positions in order to construct a promising and efficient exemplar. This exemplar is used to guide the particle to fly toward the global optimal region. The OL (orthogonal learning) strategy is a generic operator and can be applied to any kind of topology structure. If the OL is used for the GPSO, then P _n is P _g . If it is used for the LPSO, then P _n is P _l . For either a global or a local version, when constructing the vector of P _o , if P _i is the same as P _n (e.g., for the globally best particle, P _i and P _g are identical vectors), the OED (orthogonal experimental design) makes no contribution. In such a case, OLPSO will randomly select another particle P _r and then construct P _o by using the information of P _i and P _r through the OED. Two OLPSO versions that based on a global topology (OLPSO-G) and a local topology (OLPSO-L) are simulated [53].

In addition to research on parameter control and auxiliary techniques, PSO topological structures are also widely studied. The LPSO with a ring topological structure and the von Neumann topological structure PSO (VPSO) have been proposed by Kennedy and Mendes [54, 55] to enhance the performance in solving multimodal problems. Further, dynamically changing neighborhood structures have been proposed by Suganthan [36], Hu and Eberhart [56], and Liang and Suganthan [57] to avoid the deficiencies of fixed neighborhoods. Moreover, in the “fully informed particle swarm” (FIPS) algorithm [58], the information of the entire neighborhood is used to guide the particles. The CLPSO in [59] lets the particle use different pBests to update its flying on different dimensions for improved performance in multimodal applications.

2.2 Artificial fish swarm algorithm (AFSA)

A new evolutionary computation technique, artificial fish swarm algorithm (AFSA), was first proposed in 2002 [60]. The idea of AFSA is based on the simulation of the simplified natural social behavior of fish schooling and the swarming theory. AFSA possess similar attractive features of genetic algorithm (GA) such as independence from gradient information of the objective function, the ability to solve complex non-linear high-dimensional problems. Furthermore, they can achieve faster convergence speed and require few parameters to be adjusted. The AFSA does not possess the crossover and mutation processes used in GA, so it could be performed more easily. AFSA is also an optimizer based on population. The system is initialized firstly in a set of randomly generated potential solutions and then performs the search for the optimum one iteratively [61].

Artificial fish (AF) is a fictitious entity of true fish, which is used to carry on the analysis and explanation of problem, and can be realized by using animal ecology concept. With the aid of the object-oriented analytical method, we can regard the artificial fish as an entity encapsulated with one’s own data and a series of behaviors, which can accept amazing information of environment by sense organs, and do stimulant reaction by the control of tail and fin. The environment in which the artificial fish lives is mainly the solution space and the states of other artificial fish. Its next behavior depends on its current state and its environmental state (including the quality of the question solutions at present and the states of other companions), and it influences the environment via its own activities and other companions’ activities [62].

The AF realizes external perception by its vision shown in Fig. 1. X is the current state of an AF, Visual is the visual distance, and X _v is the visual position at some moment. If the state at the visual position is better than the current state, it goes forward a step in this direction and arrives the X _next state; otherwise, it continues an inspecting tour in the vision. The greater number of inspecting tour the AF does, the more knowledge about overall states of the vision the AF obtains. Certainly, it does not need to travel throughout complex or infinite states, which is helpful to find the global optimum by allowing certain local optimum with some uncertainty.

Fig. 1

Vision concept of the artificial fish

Let X = (x ₁, x ₂, …, x _n ) and $X_{v} = \left( {x_{1}^{v} ,x_{2}^{v} , \ldots ,x_{n}^{v} } \right)$, then this process can be expressed as follows:

$$ x_{i}^{v} = x_{i} + Visual.rand(),\quad i \in (0,n] $$

(7)

$$ X_{next} = X + \frac{{X_{v} - X}}{{\left\| {X_{v} - X} \right\|}}.Step.rand(). $$

(8)

where Rand() produces random numbers between 0 and 1, Step is the step length, x _i is the optimizing variable, and n is the number of variables. The AF model includes two parts (variables and functions). The variable X is the current position of the AF, Step is the moving step length, Visual represents the visual distance, try_number is the try number, and δ is the crowd factor (0 < δ < 1). The functions include the behaviors of the AF: AF_Prey, AF_Swarm, AF_Follow, AF_Move, AF_Leap, and AF_Evaluate.

2.2.1 The basic functions of AFSA

Fish usually stay in the place with a lot of food, so we simulate the behaviors of fish based on this characteristic to find the global optimum, which is the basic idea of the AFSA. The basic behaviors of AF are defined [9, 10] as follows for maximum:

(1) AF_Prey: This is a basic biological behavior that tends to the food; generally, the fish perceives the concentration of food in water to determine the movement by vision or sense and then chooses the tendency. Behavior description: Let X _i be the AF current state and select a state X _j randomly in its visual distance, and Y is the food concentration (objective function value); the greater Visual is, the more easily the AF finds the global extreme value and converges.

$$ X_{j} = X_{i} + Visual.rand() $$

(9)

If Y _i  < Y _j in the maximum problem, it goes forward a step in this direction;

$$ X_{i}^{(t + 1)} = X_{i}^{(t)} + \frac{{X_{j} - X_{i}^{(t)} }}{{\left\| {X_{j} - X_{i}^{(t)} } \right\|}}.Step.rand(). $$

(10)

Otherwise, select a state X j randomly again and judge whether it satisfies the forward condition. If it cannot satisfy after try_number times, it moves a step randomly. When the try_number is small in AF_Prey, the AF can swim randomly, which makes it flee from the local extreme value field.

$$ X_{i}^{(t + 1)} = X_{i}^{(t)} + Visual.rand() $$

(11)

(2) AF_Swarm: The fish will assemble in groups naturally in the moving process, which is a kind of living habits in order to guarantee the existence of the colony and avoid dangers. Behavior description: Let X i be the AF current state, X c be the center position, and n _f be the number of its companions in the current neighborhood (d _ij  < Visual), and n is total fish number. If Y _c  > Y _i and $\frac{{n_{f} }}{n} < \delta$, which means that the companion center has more food (higher fitness function value) and is not very crowded, it goes forward a step to the companion center;

$$ X^{(t + 1)}_{i} = X_{i}^{(t)} + \frac{{X_{c} - X_{i}^{(t)} }}{{\left\| {X_{c} - X_{i}^{(t)} } \right\|}}.Step.rand(). $$

(12)

Otherwise, executes the preying behavior. The crowd factor limits the scale of swarms, and more AF only cluster at the optimal area, which ensures that AF move to optimum in a wide field.

(3) AF_Follow: In the moving process of the fish swarm, when a single fish or several ones find food, the neighborhood partners will trail and reach the food quickly. Behavior description: Let Xi be the AF current state, and it explores the companion Xj in the neighborhood (d _ij  < Visual), which has the greatest Y _j . If Y _j  > Y _i and $\frac{{n_{f} }}{n} < \delta$, which means that the companion X _j state has higher food concentration (higher fitness function value) and the surroundings are not very crowded, it goes forward a step to the companion X _j ,

$$ X_{i}^{(t + 1)} = X_{i}^{(t)} + \frac{{X_{j} - X_{i}^{(t)} }}{{\left\| {X_{j} - X_{i}^{(t)} } \right\|}}.Step.rand(). $$

(13)

Otherwise, executes the preying behavior.

(4) AF_Move: Fish swim randomly in water; in fact, they are seeking food or companions in larger ranges.

Behavior description: Chooses a state at random in the vision; then it moves toward this state; in fact, it is a default behavior of AF_Prey.

$$ X_{i}^{(t + 1)} = X_{i}^{(t)} + Visual.rand() $$

(14)

(5) AF_Leap: Fish stop somewhere in water, every AF’s behavior result will gradually be the same, the difference in objective values (food concentration, FC) becomes smaller within some iterations, it might fall into local extremum, change the parameters randomly to the still states for leaping out current state.

Behavior description: If the objective function is almost the same or difference in the objective functions is smaller than a proportion during the given (m–n) iterations, choose some fish randomly in the whole fish swarm and set parameters randomly to the selected AF. The β is a parameter or a function that can make some fish to have other abnormal actions (values), and eps is a smaller constant.

$$ {\text{if}}(BestFC(m) - BestFC(n)) < eps $$

$$ X_{some}^{(t + 1)} = X_{some}^{(t)} + \beta .Visual.rand() $$

(15)

The detail behavior pseudo-code can be seen in [63]. AF_Swarm makes few fish confined in local extreme values move in the direction of a few fish tending to global extreme value, which results in AF fleeing from the local extreme values. AF_Follow accelerates AF moving to better states and, at the same time, accelerates AF moving to the global extreme value field from the local extreme values.

2.3 Swallow swarm optimization (SSO)

2.3.1 Swallows natural life

There are eight different breeds of swallows. They have social life, migrate together, and find appropriate places for resting, breeding, and feeding. Swarm moving (swarm intelligence) keeps them immune against the attacks of other birds. A pair of swallows has to search a wide area in order to find food, while in collective living as soon as one swallow finds food, other birds of the group fly toward that area and enjoy it. Swallows are very intelligent birds. They fly quickly, and there is a strong interaction between members of groups [64]. They apply different sounds in different situations (warning, asking help, inviting to food, being ready to breeding) that the number of these sounds is more than other birds’ and even signal of swallow’s sound is used as a special model in signal processing [65]. Figure 2 is a swallow tree.

Fig. 2

Tree male swallow photograph by Steve Berliner [88]

Many creatures have a social life and live in groups, including birds. A variety of birds in the small and large colonies have a social life, and each one has certain characteristics and social behaviors. By investigating these behaviors and getting inspired by them, various optimization algorithms have been presented, such as PSO. These swallows have unique characteristics and social behaviors that have attracted our attention.

Swallow is an insect-eating bird; 83 species of swallows have been so far identified [66]. Due to its high compatibility with the environment, this bird lives almost everywhere on Earth. This bird has special characteristics that make it distinct from the other birds. So many studies have been conducted on the life of various species of swallows and remarkable results have been obtained, which will be further discussed:

2.3.1.1 Immigration

“Swallows” annually travel 17,000 km and migrate from a continent to another continent. Swallows migrate in very large groups of even hundred thousand [67]. The very social life in large groups indicates high swarm intelligence of these birds.

2.3.1.2 High-speed flying

Swallows keep a record of speed among the other migrants, so that they travel 4,000 km per 24 h, that is, with a speed of 170 km/h per hour. This feature can be very effective in the particles’ convergence speed and in solving the optimization problems in the least time.

2.3.1.3 Skilled hunters

Swallows have adapted to hunting insects on the wing by developing a slender streamlined body and long-pointed wings, which allow great maneuverability and endurance, as well as frequent periods of gliding. Their body shape allows for very efficient flight, which costs 50–75 % less for swallows than equivalent passerines of the same size. Swallows usually forage at around 30–40 km/h. Swallows are excellent flyers and use these skills to feed and attract a mate.

The swallows generally forage for prey that is on the wing, but they will on occasion snap prey off branches or on the ground. The flight may be fast and involve a rapid succession of turns and banks when actively chasing fast-moving prey; less agile prey may be caught with a slower more leisurely flight that includes flying in circles and bursts of flapping mixed with gliding. Where several species of swallow feed together, they will be separated into different niches based on height off the ground: some species feeding closer to the ground and others feeding at higher levels. Similar separation occurs where feeding overlaps with swifts. Niche separation may also occur with the size of prey chosen.

2.3.1.4 Different calls

Swallows are able to produce many different calls or songs, which are used to express excitement, to communicate with others of the same species, during courtship, or as an alarm when a predator is in the area. The songs of males are related to the body condition of the bird and are presumably used by females to judge the physical condition and suitability for mating of males. Begging calls are used by the young when soliciting food from their parents. The typical song of swallows is a simple, sometimes musical twittering [68].

Swallows are regularly correlated through various sounds, and if one of them does not find the food source, it immediately calls the other birds in the colony. These special sounds help them to have a better social life.

2.3.1.5 Information centers

Cliff swallow colonies function as “information centers” in which individuals unsuccessful at finding food locate other individuals that have found food and follow them to a food source [69]. Advantages associated with information sharing on the whereabouts of food are substantial and probably represent a major reason why cliff swallows live in colonies. He also discovered that cliff swallows represent one of the few birds (and indeed non-human vertebrates) that actively communicate the presence of food to others by giving distinct signals (calls) used only in that context [70]. The evolution of such information sharing is perplexing, because the typical beneficiaries of calling are individuals unrelated to the caller.

2.3.1.6 Floating swallow

When migrating, a few swallows always fly out of the colony and in the first glance; it might look like that they disturb the colony order. But these swallows that are generally young (newly matured) play an important role in the colony. First, the swallows have the chance to find food outside the internal areas of the colony and call the other swallows as soon as they find food. Second, if a hunting bird intends to attack the swallows, these floating swallows quickly notice and inform the other members of the colony. These swallows fly between the colonies and can change their colonies. This behavior has been used in this study. These particles can increase the chance to find the optimum points, and if the other particles converge on a local optimum by mistake, these particles strengthen the chance to find better points by their random and independent movement. In this paper, these particles have been called aimless particle.

2.3.1.7 The interest in social life

Swallows are one of the most important species of birds that prefer living in colonies to individual life. Sometimes, thousands of swallows can be seen as a colony in the sky. However, large colonies are composed of several smaller colonies. The number of birds in the group has a critical role in more successful reproduction, fighting predators, and a better search for food [71, 72]. There is a factor in the group life of swallows called social stimulation, which is an important influence [72]. Swallows’ colony size can have a direct impact on the hormones level in their bodies. The larger the colony is, the higher the hormone levels will be and the more successful swallows’ life and reproduction will be [73]. During 1,000 years of evolution, this bird has obtained a high swarm intelligence and has a successful social life.

2.3.1.8 Leaders

Each colony is divided into several subcolonies that have side-by-side nests and live in a site. Each colony has a leader that is commonly an experienced bird. If the suitability of the group leader is reduced for any reason, another bird immediately supersedes it. Swallows always follow the leader, provided they have the necessary competencies. In this study, two types of leaders are used: Local leaders that conduct the internal colonies and show a local optimum point and Head Leader that is responsible for the leadership of the entire colony and shows the public optimum point.

2.3.1.9 Escaping from predators

Because of their small body, swallows are good prey for most birds. Two of their strategies are synchronous flying and namely safety in numbers. Swallows’ intelligent behaviors against hunting birds are very interesting. Swallows can be highly adaptable to the different environments. These adaptive behaviors have been intelligent and can be well seen in feeding and nest-building architecture. Swallows are very successful in search of food and have specific strategies for finding food which are very complex [74]. Many behaviors of the swallows have remained unknown, and it is very difficult to implement all behaviors of this bird to produce a working collective intelligence algorithm, because the desired algorithm will have a high time complexity and will not have the necessary optimality, due to the high complexity of these behaviors. In this paper, only the behaviors of 8, 6, 2, and 1 have been used and good results have been obtained.

2.3.2 Algorithm SSO

Major idea of this new optimization algorithm is inspired by swallow swarm. There are three kinds of particles in this algorithm:

• 1. Explorer particle (e _i )

• 2. Aimless particle (o _i )

• 3. Leader particle (l _i )

These particles move parallel to each other and always are in interaction. Each particle in colony (each colony can be consisted of some subcolonies) is responsible for something that through doing it guides the colony toward a better situation.

2.3.2.1 Explorer particle

These particles encompass the major population of colony. Their primary responsibility is to explore in problem space. With just arriving at an extreme point (swallow), using a special sound guides the group toward there, and if this place is the best one in problem space, this particle plays role as a Head Leader (HL _i ). But if the particle is in a good (not the best) situation in comparison with its neighboring particles, it is chosen as a local leader LL _i ; otherwise, each particle e _i regarding $V_{{{\text{HL}}_{i} }}$ (velocity vector of particle toward HL), $V_{{{\text{LL}}_{i} }}$ (velocity vector of particle toward LL), and competence of resultant of these two vector makes a random move. Figure 3 shows how a particle moves in problem space.

Fig. 3

Kinds of particles and how explorer particles move

$$ V_{{{\text{HL}}_{i + 1} }} = V_{{{\text{HL}}_{i} }} + \alpha_{\text{HL}} rand ( )(e_{\text{best}} - e_{i} ) + \beta_{\text{HL}} rand ( )({\text{HL}}_{i} - e_{i} ) $$

(16)

$$ \alpha_{\text{HL}} = \{ {\text{if}}(e_{i} = 0||e_{\text{best}} = 0) \to 1.5\} $$

(17)

$$ \alpha_{\text{HL}} = \left\{ {\begin{array}{*{20}c} {{\text{if}}(e_{i} < e_{\text{best}} )\& \& (e_{i} < {\text{HL}}_{i} ) \to } \hfill & {\frac{{rand().e_{i} }}{{e_{i} \cdot e_{\text{best}} }}} \hfill & {e_{i} ,e_{\text{best}} \ne 0} \hfill \\ {{\text{if}}(e_{i} < e_{\text{best}} )\& \& (e_{i} > {\text{HL}}_{i} ) \to } \hfill & {\frac{{2rand() \cdot e_{\text{best}} }}{{1/(2.e_{i} )}}} \hfill & {e_{i} \ne 0} \hfill \\ {{\text{if}}(e_{i} > e_{\text{best}} ) \to } \hfill & {\frac{{e_{\text{best}} }}{1/(2.rand())}} \hfill & {} \hfill \\ \end{array} } \right. $$

(18)

$$ \beta_{\text{HL}} = \{ {\text{if}}(e_{i} = 0||e_{\text{best}} = 0) \to 1.5\} $$

(19)

$$ \beta_{\text{HL}} = \left\{ {\begin{array}{*{20}c} {{\text{if}}(e_{i} < e_{\text{best}} )\& \& (e_{i} < {\text{HL}}_{i} ) \to } \hfill & {\frac{{rand().e_{i} }}{{e_{i} \cdot {\text{HL}}_{i} }}} \hfill & {e_{i} ,{\text{HL}}_{i} \ne 0} \hfill \\ {{\text{if}}(e_{i} < e_{\text{best}} )\& \& (e_{i} > {\text{HL}}_{i} ) \to } \hfill & {\frac{{2rand() \cdot {\text{HL}}_{i} }}{{1/(2.e_{i} )}}} \hfill & {e_{i} \ne 0} \hfill \\ {{\text{if}}(e_{i} > e_{\text{best}} ) \to } \hfill & {\frac{{{\text{HL}}_{i} }}{1/(2.rand())}} \hfill & {} \hfill \\ \end{array} } \right. $$

(20)

Vector $V_{{{\text{HL}}_{i} }}$ has a significant effect on explorer particle behavior. e _i is the particle current position in problem space. e _best is the best position that particle remembers from the beginning up to now. HL _i is a leader particle that has the best possible response in current position. α_HL and β_HL are the control of acceleration coefficients that are defined adaptively. These two parameters change during the particle movements, and this change depends on the particle’s position. If the particle is a minimum point (minimizing problem) and is in a better position than the e _best and HL _i , probability of being a global minimum for that particle should be considered and control coefficients estimate a small amount to decrease the particle movement to the least. If the particle is in a better situation than e _best but is in worse situation than HL _i , it should move toward HL _i with an average amount. If the particle position is worse than e _best, consequently it is worse than HL _i too, so it can move toward HL _i with a larger amount. Remember that the vector of $V_{{{\text{LL}}_{i} }}$ affects this movement.

$$ V_{{{\text{LL}}_{i + 1} }} = V_{{{\text{LL}}_{i} }} + \alpha_{\text{LL}} rand ( )(e_{\text{best}} - e_{i} ) + \beta_{\text{LL}} rand()({\text{LL}}_{i} - e_{i} ) $$

(21)

$$ \alpha_{\text{LL}} = \{ {\text{if}}(e_{i} = 0||e_{\text{best}} = 0) \to 2\} $$

(22)

$$ \alpha_{\text{LL}} = \left\{ {\begin{array}{*{20}c} {{\text{if}}(e_{i} < e_{\text{best}} )\& \& (e_{i} < LL_{i} ) \to } \hfill & {\frac{{rand().e_{i} }}{{e_{i} \cdot e_{\text{best}} }}} \hfill & {e_{i} ,e_{\text{best}} \ne 0} \hfill \\ {{\text{if}}(e_{i} < e_{\text{best}} )\& \& (e_{i} > LL_{i} ) \to } \hfill & {\frac{{2rand() \cdot e_{\text{best}} }}{{1/(2.e_{i} )}}} \hfill & {e_{i} \ne 0} \hfill \\ {{\text{if}}(e_{i} > e_{\text{best}} ) \to } \hfill & {\frac{{e_{\text{best}} }}{1/(2.rand())}} \hfill & {} \hfill \\ \end{array} } \right. $$

(23)

$$ \beta_{\text{LL}} = \{ {\text{if}}(e_{i} = 0||e_{\text{best}} = 0) \to 2\} $$

(24)

$$ \beta_{\text{LL}} = \left\{ {\begin{array}{*{20}c} {{\text{if}}(e_{i} < e_{\text{best}} )\& \& (e_{i} < {\text{LL}}_{i} ) \to } \hfill & {\frac{{rand().e_{i} }}{{e_{i} \cdot {\text{LL}}_{i} }}} \hfill & {e_{i} ,{\text{LL}}_{i} \ne 0} \hfill \\ {{\text{if}}(e_{i} < e_{\text{best}} )\& \& (e_{i} > {\text{LL}}_{i} ) \to } \hfill & {\frac{{2rand() \cdot {\text{LL}}_{i} }}{{1/(2.e_{i} )}}} \hfill & {e_{i} \ne 0} \hfill \\ {{\text{if}}(e_{i} > e_{\text{best}} ) \to } \hfill & {\frac{{{\text{LL}}_{i} }}{1/(2.rand())}} \hfill & {} \hfill \\ \end{array} } \right. $$

(25)

$$ V_{i + 1} = V_{{{\text{HL}}_{i + 1} }} + V_{{{\text{LL}}_{i + 1} }} $$

(26)

$$ e_{i + 1} = e_{i} + V_{i + 1} $$

(27)

Every particle e _i utilizes nearest particle LL _i in order to compute the vector of $V_{{{\text{LL}}_{i} }}$.

2.3.2.2 Aimless particle

These particles in the beginning of exploring the situation do not have a good position in comparison with other particles, and the amount of their f(o _i ) is bad. These particles, after being recognized, are differentiated from explorer particles e _i , so a new responsibility in group is defined for them (o _i ). Their duty is an exploratory and random search. They start moving randomly and do not have anything to do with the position of HL _i and LL _i . They are swallows that explore remote areas as the scout of colony and inform the group if they find a good point. In a lot of optimization problems because of inappropriate distribution of particles in position space, the optimum response is kept hidden from the group’s eyes and the group converges in a local optimum. This is the greatest difficulty with optimization problems (early convergence in local optimum pints). Particles o _i , apparently, may have an aimless and useless behavior but examine the probability of neglecting the global optimum response and go around the diverse surrounding points with their long jumps and examine the situation of optimization. The particle o _i compares its position with the local optimum points LL _i and HL _i .

If this particle finds an optimum point while it is searching, it will replace its position with the nearest explorer particle e _i and then keep searching.

$$ o_{i + 1} = o_{i} + \left[ {rand(\{ - 1,1\} )*\frac{{rand(\min_{s} ,\max_{s} )}}{1 + rand()}} \right] $$

(28)

New position of each particle of o _i is equal to its previous position plus a random amount between the minimum and the maximum of position space, divided by an amount between one and two. The division answer is added to or subtracted from the previous position of particle o _i randomly.

For example, the range of the function Rosenbrock has been defined between (−50, 50). If the function rand (min, max) produces a random number (25) and the function rand() produces 0.5, the fraction result would be 12.5. Now this amount may be added to or subtracted from the position of o _i . This will increase the chance of examining the different areas of environment.

2.3.2.3 Leader particle

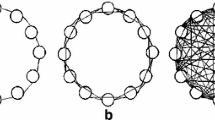
There are particles in SSO algorithm named Leader. These particles have the best amount of f(l _i ) in the beginning of position space searching. Their place and their amount may change in each level. There is just one leader particle in PSO method (g_best), while in this new method there may be n _l leader particle. These particles may be distributed or gathered in space. The best leader is named Leader Head, which is recognized as the major leader in colony, also there are some particles named Local Leader. They are candidates for quite good answers which we preserve. In real world of swallows, each thousands member colony is divided into a number of subcolonies. These subcolonies have a local leader; though, this leadership may be changed repeatedly by other wiser and stronger swallows. In the population of swallows, leader is a bird which is in a better location which is near to food and a resting place. The duty of this leader is to guide other members of colony to this area. This issue is simulated in SSO algorithm. In each repetition, leader particles whether head or local may be changed or an aimless particle may discover an area that is the best response of problem up to then; consequently, this swallows acts as a leader. Figure 4 shows an example of swallow swarm flying.

Fig. 4

Swallow swarm flying. Circles are subcolonies, and triangles are local leaders (choosing that swallow is surely a hard job but that swallow is generally in the center of subcolony and there is a high density around it. Never forget that this swallow may be changed every second. Squares are aimless swallows o _i

Real boundaries between subcolonies may never be marked because swallow movements happen in high speed and high dynamic. The diagram of swallows and their numbers changes according to the size of subcolonies.

All of these three particles (e _i , o _i , and l _i ) interact with each other continuously, and each particle (swallow) can play each of these three roles. During searching period, these particles may frequently change their role but primary goal (finding optimum point) is such a more important task.

2.3.2.4 Pseudocode SSO

Programming the SSO algorithm is easy. In this research, MATLAB software is used for above simulation (Figs. 5, 6).

Fig. 5

Swallow swarm flying

Fig. 6

Swallow swarm flying and food searching

Swallow swarm optimization algorithm:

 

1. Initialize population (random all particle e i )

2. Iter = 1

3. While (iter < max_iter)

4. For every particle (e i ) Calculate f(e i )

5. Sort f(e 1, e 2, …, e n ))→min to max

6. All particles e i  = f(e i )

7. HL = e min

8. For (j = 2 to j < m) LL i  = e j

9. For (j = 1 to j < b) o j  = e n−j+1

10. i = 1

11. While (k < iter)

12. While (j < N)

13. if (e best > e i ) e best = e i

14. While (i < N)

15. Search (nearest LL i to e i )

16. αHL = {if(e i  = 0||e best = 0)→1.5}

17.$\alpha_{\text{HL}} = \left\{ {\begin{array}{*{20}c} {{\text{if}}(e_{i} < e_{\text{best}} )\& \& (e_{i} < {\text{HL}}_{i} ) \to } \hfill & {\frac{{rand().e_{i} }}{{e_{i} \cdot e_{\text{best}} }}} \hfill & {e_{i} ,e_{\text{best}} \ne 0} \hfill \\ {{\text{if}}(e_{i} < e_{\text{best}} )\& \& (e_{i} > {\text{HL}}_{i} ) \to } \hfill & {\frac{{2rand() \cdot e_{\text{best}} }}{{1/(2.e_{i} )}}} \hfill & {e_{i} \ne 0} \hfill \\ {{\text{if}}(e_{i} > e_{\text{best}} ) \to } \hfill & {\frac{{e_{\text{best}} }}{1/(2.rand())}} \hfill & {} \hfill \\ \end{array} } \right.$

18. βHL = {if(e i  = 0||e best = 0)→1.5}

19. $\beta_{\text{HL}} = \left\{ {\begin{array}{*{20}c} {{\text{if}}(e_{i} < e_{\text{best}} )\& \& (e_{i} < {\text{HL}}_{i} ) \to } \hfill & {\frac{{rand().e_{i} }}{{e_{i} \cdot {\text{HL}}_{i} }}} \hfill & {e_{i} ,{\text{HL}}_{i} \ne 0} \hfill \\ {{\text{if}}(e_{i} < e_{\text{best}} )\& \& (e_{i} > {\text{HL}}_{i} ) \to } \hfill & {\frac{{2rand() \cdot {\text{HL}}_{i} }}{{1/(2.e_{i} )}}} \hfill & {e_{i} \ne 0} \hfill \\ {{\text{if}}(e_{i} > e_{\text{best}} ) \to } \hfill & {\frac{{{\text{HL}}_{i} }}{1/(2.rand())}} \hfill & {} \hfill \\ \end{array} } \right.$

20. $V_{{{\text{HL}}_{i + 1} }} = V_{{{\text{HL}}_{i} }} + \alpha_{\text{HL}} rand()(e_{\text{best}} - e_{i} ) + \beta_{\text{HL}} rand()({\text{HL}}_{i} - e_{i} )$

21. αLL = {if(e i  = 0||e best = 0)→2}

22. $\alpha_{\text{LL}} = \left\{ {\begin{array}{*{20}c} {{\text{if}}(e_{i} < e_{\text{best}} )\& \& (e_{i} < {\text{LL}}_{i} ) \to } \hfill & {\frac{{rand().e_{i} }}{{e_{i} \cdot e_{\text{best}} }}} \hfill & {e_{i} ,e_{\text{best}} \ne 0} \hfill \\ {{\text{if}}(e_{i} < e_{\text{best}} )\& \& (e_{i} > {\text{LL}}_{i} ) \to } \hfill & {\frac{{2rand() \cdot e_{\text{best}} }}{{1/(2.e_{i} )}}} \hfill & {e_{i} \ne 0} \hfill \\ {{\text{if}}(e_{i} > e_{\text{best}} ) \to } \hfill & {\frac{{e_{\text{best}} }}{1/(2.rand())}} \hfill & {} \hfill \\ \end{array} } \right.$

23. βLL = {if(e i  = 0||e best = 0)→2}

24. $\beta_{\text{LL}} = \left\{ {\begin{array}{*{20}c} {{\text{if}}(e_{i} < e_{\text{best}} )\& \& (e_{i} < {\text{LL}}_{i} ) \to } \hfill & {\frac{{rand().e_{i} }}{{e_{i} \cdot {\text{LL}}_{i} }}} \hfill & {e_{i} ,{\text{LL}}_{i} \ne 0} \hfill \\ {{\text{if}}(e_{i} < e_{\text{best}} )\& \& (e_{i} > {\text{LL}}_{i} ) \to } \hfill & {\frac{{2rand() \cdot {\text{LL}}_{i} }}{{1/(2.e_{i} )}}} \hfill & {e_{i} \ne 0} \hfill \\ {{\text{if}}(e_{i} > e_{\text{best}} ) \to } \hfill & {\frac{{{\text{LL}}_{i} }}{1/(2.rand())}} \hfill & {} \hfill \\ \end{array} } \right.$

25. $V_{{{\text{LL}}_{i + 1} }} = V_{{{\text{LL}}_{i} }} + \alpha_{\text{LL}} rand()(e_{\text{best}} - e_{i} ) + \beta_{\text{LL}} rand ( )({\text{LL}}_{i} - e_{i} )$

26. $V_{i + 1} = V_{{{\text{HL}}_{i + 1} }} + V_{{{\text{LL}}_{i + 1} }}$

27. e i+1 = e i  + V i+1

28. $o_{i + 1} = o_{i} + rand(\{ - 1,1\} )*\frac{{rand(\min_{s} ,\max_{s} )}}{1 + rand()}$

29. if ($f(o_{i + 1} ) > f({\text{HL}}_{i} )$) e nearest = O i+1 → go to 30

30. While (k o  ≤ b)

31. While (l ≤ n l )

32. if $(f(o_{{k_{o} }} ) > f({\text{LL}}_{l} ))$

33. e nearest = O i+1

34. Loop//i < N

35. Loop//iter < max_iter

36. End.

e _i is that f(e _i ) in above algorithm (Table 2).

Table 2 Parameters of SSO algorithm

3 Benchmark functions

To test the ability of the proposed algorithm and to compare it to conventional Variant PSO and FSO, some benchmarks are considered. Each of these functions tests the optimization algorithm in special conditions. So, weakness points of the optimization algorithm will be obvious. These functions are described in Table 3 and Fig. 7.

Table 3 Benchmarks that are used to test the ability of the proposed algorithm

Fig. 7

Benchmark tests and its view in 2-dimensional axes

The first problem is the sphere function, and it is easy to solve. The second problem is the Rosenbrock function. It can be treated as a multimodal problem. It has a narrow valley from the perceived local optima to the global optimum. In the experiments below, we find that the algorithms that perform well on sphere function perform well on Rosenbrock function too. Ackley’s function has one narrow global optimum basin and many minor local optima. It is probably the easiest problem among the six as its local optima are shallow. Griewank’s function has a $\prod\nolimits_{i = 1}^{D} {\cos (x_{i} /\sqrt i )}$ component causing linkages among variables, thereby making it difficult to reach the global optimum. An interesting phenomenon of Griewank’s function is that it is more difficult for lower dimensions than for higher dimensions [75].

Rastrigin’s function is a complex multimodal problem with a large number of local optima. When attempting to solve Rastrigin’s function, algorithms may easily fall into a local optimum. Hence, an algorithm capable of maintaining a larger diversity is likely to yield better results. Non-continuous Rastrigin’s function is constructed based on the Rastrigin’s function and has the same number of local optima as the continuous Rastrigin’s function. The complexity of Schwefel’s function is due to its deep local optima being far from the global optimum. It will be hard to find the global optimum if many particles fall into one of the deep local optima.

To rotate a function, first an orthogonal matrix M should be generated. The original variable is left multiplied by the orthogonal matrix M to get the new rotated variable y = M*x, and this variable y is used to calculate the fitness value f.

$$ {\text{if}}\,M = \left[ {\begin{array}{*{20}c} {m_{11} } & {m_{12} } & \ldots & {m_{1D} } \\ {m_{21} } & {m_{22} } & \ldots & {m_{2D} } \\ \ldots & \ldots & \ldots & \ldots \\ {m_{D1} } & {m_{D2} } & \ldots & {m_{DD} } \\ \end{array} } \right]x = [x_{1} ,x_{2} , \ldots ,x_{D} ]^{T} {\text{and}}\,y = [y_{1} ,y_{2} , \ldots ,y_{D} ]^{T} $$

(29)

$$ {\text{then}}\quad y_{i} = m_{i1} x_{1} + m_{i2} x_{2} + \cdots + m_{iD} x_{D} \quad i = 1,2, \ldots ,D $$

(30)

When one dimension in x vector is changed, all dimensions in vector y will be affected. Hence, the rotated function cannot be solved by just D one-dimensional searches. The orthogonal rotation matrix does not affect the shape of the functions. In this paper, we used Salomon’s method to generate the orthogonal matrix [76].

In rotated Schwefel’s function, in order to keep the global optimum in the search range after rotation, noting that the original global optimum of Schwefel’s function is at [420.96, 420.96,…, 420.96], y′ = M * (x − 420.96) and y = y′ + 420.96 are used instead of y = M * x. Since Schwefel’s function has better solutions out of the search range [500, −500]^D, when |y _i | > 500, z _i  = 0.001(y _i  − 500)², that is, z _i is set in portion to the square distance between y _i and the bound.

4 Experiments

A number of benchmarks have been used to test the proposed algorithm. Choosing each of these functions for testing had a particular reason, for instance Ackley function is used to aimless particles testing. These particles are expected to find one of the minimum areas with their random movements and guide the group toward there. Each of these functions has particular features that generally have been applied in numerous articles to examine the optimization methods. The SSO method with different iterations of particles and different iterations has been tested by every function of bench and then has been compared to FSO and PSO.

In SSO algorithm, first amount of parameters are try_number = 3, S = 3, δ = 16, visual _min = 0.001, dimension = 30, and step_min = 0.0002. Proposed idea besides standard FSO and standard PSO simulated in the MATLAB software and then functions of section three have been used to test the accuracy of the method performance. Goal of this simulation is to compare the performance of these three methods in speed of convergence and escaping from minimum local points. First, the Ackley function is applied to test. Table 4 shows the results of performance of two optimization methods (PSO and FSO) and the proposed method (SSO).

Table 4 Comparing the performance results between two optimization methods (PSO and FSO) and proposed method (SSO) in the function Ackley

Regarding the Table 4, proposed method (SSO) does not have good performance when the number of particles is low, and in comparison with other two methods, it does not achieve good results. But by increasing the number of particles, performance of proposed method begins being refined and shows a better performance than PSO’s and FSO’s. This is a fact that when there are a few swallows in a colony, there is not a big success. This shows why swallows choose bigger colonies to live in and to migrate in (Fig. 8).

Fig. 8

Comparing the performance of SSO to the FSO and PSO. In the function Ackley with 5 particles and 300 repetition

It is seen clearly in Fig. 9 when exploring particles’ number is high, the convergence speed of the SSO method heightens, and in iterations that are more than 100, the process of finding the global minimum point is satisfying. FSO has a better convergence speed than PSO, but unfortunately both methods got stuck in a local minimum point in the function Ackley and they have not optimized after 600 repetitions. Another point that is seen in Fig. 9 is that in iterations less than 50, the proposed method (SSO) has a same performance as the FSO.

Fig. 9

Comparing the performance of SSO with the FSO and PSO in the function Ackley with 50 particles and 1,000 repetition

Function Sphere is a good function to test every optimization method because it is a simple structure one with a global minimum equal to zero. Generally, different optimization methods perform quite well in this function. Table 5 compares the proposed method with PSO and FSO.

Table 5 Comparison between SSO, PSO, and FSO in the function Sphere

Performance of the proposed method stays the same in comparison with FSO when there are 100 particles and 1,000 unchanging iterations. This is correct for 50 particles too. But when the number of particles decreases and comes to 30, the SSO performs a better performance, and if the number of particles keeps on decreasing and comes to (5, 10), the SSO performs a better performance again comparing to other two methods. But a steep decrease in the number of particles (2, 3) changes the result. Then, FSO and PSO make a better performance, respectively (Fig. 10).

Fig. 10

Comparison between SSO, PSO, and FSO in the function Sphere with 100 particles and 1,000 repetitions

Performance of three optimization methods with a low number of particles (2) and 1,000 iterations is shown in Fig. 11. The FSO and PSO had a quite good performance and could find small minimum amounts. Since the proposed method is heavily relied on swarm intelligence knowledge, when the population is small, it confronts a fundamental deficiency. Actually, this problem is not a weak point of the SSO but it is its particular feature. The number of particles should not be less than a distinct amount in order to have a good performance. However, in iterations less than 200, this method has a better performance comparing to FSO and PSO, and in iterations 400–600, it is better than PSO again but in iterations more than 600 has not found optimum response and got stuck in local minimum points.

Fig. 11

Comparison between SSO and PSO, FSO in the function Sphere with 2 particles and 1,000 repetitions

Function Griewank has a complex structure. It is like a hedgehog full of ups and downs and a collection of local extremum points. It is a hard function for testing the optimization methods. Searching would be stopped, falling down one of the local optimum points. Performance of the SSO in this function is good. Table 6 shows the result of comparing three considered methods with each other.

Table 6 Comparison between SSO and PSO, FSO in the function Griewank

The SSO has shown a good performance in the function Griewank. Because of the interaction between the particles e _i and aimless movements of particles o _i , the probability of finding the minimum points is well examined. This method comparing to PSO has a better performance with a less number of particles in function Griewank (Fig. 12).

Fig. 12

Comparison between SSO and PSO, FSO in the function Griewank with 10 particles and 1,000 repetitions

Convergence speed in SSO is more than other two methods. Step-like movements in diagram of SSO performance exhibit how it escapes from local minimum points in order to find a better optimum point (Fig. 13).

Fig. 13

Comparison between SSO and PSO, FSO in the function Griewank with 2 particles and 1,000 iterations

SSO with two particles in function Griewank has a good performance. It shows more proper behavior comparing to other two methods in the iterations less than 100, but in iterations more than 100, FSO escapes better from local minimum points.

Rastrigin is a hard and difficult function. It, like Griewank, has many local minimum points and, different from Griewank, its apexes (peaks) are too higher and too deeper (Table 7).

Table 7 Comparison between SSO and PSO, FSO in the function Rastrigin

Performance of PSO has not been good at all in this function. PSO gets stuck very quickly in one of the local minimum points and cannot find a more proper response. FSO’s behavior is better and more intelligently has found more optimum points comparing to PSO. The performance of the SSO is much better than that of other two methods and in all cases with any number of particles has survived from local minimum points (Fig. 14).

Fig. 14

Comparison between SSO, PSO, and FSO in the function Rastrigin with 30 particles and 1,000 repetitions

Function Rosenbrock has a complex and particular structure. This function has different areas that distract any optimization method. This special function is used in this research to observe the performance of proposed method. Table 8 shows the comparison between proposed method and other two methods.

Table 8 Between SSO, PSO, and FSO in the function Rosenbrock

As shown in Table 8, the PSO represents inappropriate responses. But FSO with 100 particles has a quite good response. The SSO has been able to pass different areas of this function and recognizes different minimum points. Appointing some local leaders and using aimless particles o _i have been a great help to intensify the feasibility of finding the minimum points.

Performance of the three methods is shown in Fig. 15. All the three methods have had a quite good performance in iterations less than 200 and a descending movement toward minimum points. In iterations between 200 and 400, the PSO has not optimized but other two methods especially PSO have behaved well. In iterations between 400 and 600, the PSO has not optimized again but the FSO has had a small optimization and the SSO has found better minimum points again. In iterations between 600 and 800, the PSO suddenly performs a good movement and jumps over a local minimum point but other two methods have not had any noticeable optimization. At the end (iterations between 800 and 1,000), the three methods have not had any noticeable optimization. Totally, the SSO method has had a very good function and in lower numbers of iterations, has found optimum points with high convergence speed.

Fig. 15

Comparison between SSO, PSO, and FSO in the function Rosenbrock with 10 particles and 1,000 repetitions

Perm is a hard function. Its outline is like a flatfish keeping its wings up and has a curving back. In this function, particle distribution in goal space is so crucial in order to let the particles have the chance of finding the global optimum point. Table 9 shows the results of these three methods’ performance.

Table 9 Comparison between SSO, PSO, and FSO in the function perm

The SSO has a quite good performance in this function. Its responses are close to FSO’s. But what is really clear is that its results are better than PSO’s (Fig. 16).

Fig. 16

Comparison between SSO, PSO, and FSO in the function Perm with 10 particles and 1,000 repetitions

Convergence speed in the function Perm is very good. In iterations less than 200, it has been able to achieve considerable minimum points. Common aspect between these three methods is in iterations more than 400. All three methods have got stuck in local minimum points and could not release themselves up to the end. The FSO did not have a good commencement. It means that in iterations less than 100, it had a bad behavior comparing to the PSO. But in iterations more than 100, it has found proper minimum points.

Global best has been used for comparing the proposed method to other optimization methods up to now; however, this topology is bad for multimodal functions [77].

Local best PSO, or lbest PSO, uses a ring social network topology where smaller neighborhoods are defined for each particle. The social component reflects the information exchanged within the neighborhood of the particle, reflecting local knowledge of the environment. With reference to the velocity equation, the social contribution to particle velocity is proportional to the distance between a particle and the best position found by the neighborhood of particles [78].

In this comparison, the number of particles 20, the number of iterations 1000, the size of neighborhood 2, ring topology, and the parameters c ₁ = c ₂ = 1.5, ω = 0.73 have been used for lbest PSO. try_number = 3, S = 3, δ = 16, visual _min = 0.001, dimension = 30, and step visual _min = 0.002 have been used for FSO. Comparison of the proposed method to the other two methods PSO and FSO with the size of neighborhood 2 is shown in Table 10.

Table 10 Comparison between SSO and PSO, FSO in the local best

According to the results of the Table 10, the SSO method, considering the Ibest, is better than the other two methods FSO and PSO. The reason why it is better is local searching of function Sphere as well as having a local leader, which causes the particles not to converge prematurely and not to get stuck in local optimum points. The SSO has found more optimum points in multimodal functions and has achieved better results. A considering thing about the SSO is that the results of local best have been improved in comparison with the global best. This is an attribute of the SSO. Besides, the results of the FSO have been noticeable.

Certainly, it is not claimed in this research that the SSO is the best optimization method since this is a new method and should be optimized by other researchers as the PSO has been optimized by other researchers and, now, there are different kinds of this good optimization method. Many methods of PSO algorithm have been innovated. Table 11 shows different methods of PSO.

Table 11 Shows different methods of PSO

It is represented that the comparison among the performance of new optimization method SSO and a number of current optimization methods. This is done to assess the significance of the SSO among other current methods. To do it, these methods should be tested in same software and hardware. Applied software is MATLAB version 7.0.4 (R14) service pack2. Current hardware is Celeron 2.26-GHz CPU, 256-MB memory, and Windows XP2 operating system. The number of particles is 20 and the number of iterations is 1,000. Table 12 shows the performance of the methods of Table 11 and the SSO method.

Table 12 Comparison between SSO and optimization several methods

According to the results of Table 12, in the Sphere function, the proposed method achieved the best result and the total optimum point. The APSO with a proper result is placed second, and the DMS-PSO with a rather good result is placed third. In the Rosenbrock function, the proposed method, the OLPSO-L, and the APSO are placed first to third, respectively. Table 13 shows the ranking of different methods in every benchmark function.

Table 13 The ranking of different methods in every benchmark function

The best performance in the sphere function was achieved by SSO and after that APSO. GPSO, DMS-PSO, and OLPSO-G have achieved almost the same results, but the speed of convergence of OLPSO-G is more. In the iterations less than 100, the speed of convergence of APSO is high, but SSO has had a better convergence after the iteration of 200. In all PSO methods except for SSO, getting trapped in local optima points is visible (Fig. 17).

Fig. 17

Convergence performance of the eleven different PSOs and SSO on the six test functions. a Sphere, b Ackley, c Griewank, d N_Rastrigin, e Quadric noise, f Quadric

Various behaviors of the eleven PSO methods are seen in the Ackley function, and the best result is achieved by OLPSO-L, and OLPSO-G, FIPS, and DMS-PSO have achieved almost the same results. HPSO and OPSO proved to have gotten trapped in local optima points and to obtain the worst results. In the iterations less than 250, SSO had the fastest convergence among the other methods, but the particles were trapped in local optima and could not escape from this point until the iteration of 600. In the iteration of 600, the particles escaped from the local optima point and reached a better result, but in the iteration of 700, they got trapped in the other local optima again and failed to provide better results up to the end of iterations. However, some good methods such as APSO have also similar behaviors toward SSO, but they have shown better performance.

The best performance in the Griewank function has been achieved by OLPSO-L, CLPSO and SSO, respectively. The other methods have nearly identical performance, and getting trapped in local optima points is a serious problem in all of them and has been unable to achieve good results. In the iterations less than 300, the speed of convergence of SSO is better than that of the other PSO methods.

The best results in the non-continuous Rastrigin function were obtained by SSO. The speed of convergence and escaping from local optima points in the low iterations can be seen well by the SSO. The function is one of the difficult functions for the various PSO methods. The APSO and OLPSO-G methods could also achieve good results.

The best result in the Quadric function was obtained by SSO, and after that, APSO, OLPSO-G, and HPSO, respectively, achieved relatively good results. SSO has presented a very good behavior in this function, and the role of particles is seen well here. These particles prevent the other particles from getting trapped in the local optima points, and the chance to find some better points will be always investigated in Fig. 18.

Fig. 18

Convergence performance of the eleven different PSOs and SSO on the six test functions. g Rastrigin, h Rosenbrock, k Schwefel’s P2.22, l Schwefel, m Rotated Rastrigin, n Rotated Griewank

The best result in the Rosenbrock function was obtained by SSO; however, in the initial iterations (less than 100), FIPS has managed to reach a good optima point very quickly.

Between 100 and 400 iterations, the performance of APSO has been better than that of the other methods, but unfortunately it has been trapped in a local optima point and has been able to be optimized. After iteration of 400, SSO has managed to escape from a local optima point and present the best performance.

SSO has had the best performance in the rotated Griewank function. APSO, FIPS, and OLPSO-L methods have also achieved acceptable results. In the iterations less than 250, APSO has converged faster than SSO and has had better performance, but after the iteration of 250, SSO method has managed to become more efficient.

Now, a general comparison between the different methods of PSO and the proposed method is made. Table 14 shows a comparison of the results of different methods in 6 unimodal functions, 7 multimodal functions, and 6 rotated and shifted functions.

Table 14 The ranking of different methods in three groups of benchmark functions

According to the results of the Table 14, in unimodal functions, the OLPSO_L, the proposed method, and the OLPSO_L are placed first to third, respectively. In the multimodal functions, the proposed method, the APSO, and the OLPSO_G are placed first to third, respectively. In the rotated and shifted functions, the proposed method, the OLPSO_L, and the OLPSO_G are placed first to third, respectively.

5 Conclusion

In this paper, the method of SSO is a new optimization method that is inspired by the PSO and FSO methods. This method has represented a new optimization method with examining the swallow swarms and their behavioral features. In this method, the particles can have three distinct duties during the searching period: explorer particles, aimless particles, and leader particles. Every particle shows a different behavior regarding its position. They interact with each other continuously. This new method has particular features such as high convergence speed in different functions and not getting stuck in local minimum points. If a particle gets stuck in one of these points, assistance offered by local leader particles and/or aimless particles give hope to it to flee. Different optimization methods such as FSO and kinds of PSO were performed in MATLAB. Different benchmark functions have been used. These methods have been compared to SSO and have been tested. In some functions, the SSO has represented a more optimized response comparing to the other methods, and in some functions and positions, it is rated in second place or third place. It is not claimed in this research that the SSO is the best optimization method but it can be applied in different engineering problems for optimizing the functions and problems. Regarding the results achieved, it can be claimed that it is one of the best optimization methods in swarm intelligence. This method should be examined and refined by other researchers. Using fuzzy logic for increasing the flexibility of this method is a part of future activities.