1 Introduction

The stability of recurrent neural networks has attracted considerable attention due to its potential applications in classification, parallel computing, associative memory, signal and image processing, and especially in solving some difficult optimization problems. In practice, significant time delays, such as constant time delays, time-varying delays, especially, continuously distributed delays, are ubiquitous both in neural processing and in signal transmission. For example, in the modeling of biological neural networks, it is necessary to take account of time delays due to the finite processing speed of information. Time delays may lead to bifurcation, oscillation, divergence or instability which may be harmful to a system [1, 2]. The stability of neural networks with delays has been studied in [2–24] and references therein.

In addition to the delay effects, a neural system is usually affected by external perturbations. Synaptic transmission is a noisy process brought on by random fluctuations from the release of neurotransmitters and other probabilistic causes [9]. Therefore, it is significant to consider stochastic effects to the stability property of the delayed recurrent neural networks.

Moreover, both in biological and artificial neural networks, diffusion effects cannot be avoided when electrons are moving in asymmetric electromagnetic fields. Hence, it is essential to consider the state variables varying with time and space. The neural networks with diffusion terms can commonly be expressed by partial differential equations [10–15] have considered the stability of neural networks with diffusion terms, in which boundary conditions are all the Neumann boundary conditions.

The neural networks model with Dirichlet boundary conditions has been considered in [16, 21], but it concentrated on deterministic systems and did not take random perturbation into consideration. To the best of our knowledge, few authors have considered global exponential stability in the mean square of stochastic reaction–diffusion recurrent neural networks with continuously distributed delays and Dirichlet boundary conditions. Motivated by these, the stability of stochastic reaction–diffusion neural networks with both continuously distributed delays and Dirichlet boundary conditions is studied in this paper. We use a similar method as in [21], but deal with a more general case in which stochastic perturbations are concerned. The influence of diffusion, continuously distributed delays upon the stability of the concerned system is also discussed. New conditions ensuring the globally exponential stability in the mean square are presented by using of Lyapunov method, inequality techniques and stochastic analysis. These conditions show that the stability is independent of the magnitude of delays, but is dependent of the magnitude of noise and diffusion effects. Therefore, under the sufficient conditions, diffusion and noisy fluctuations are important to the system. The proposed results extend those in the earlier literature and easier to verify.

This paper is constructed as follows. In Sect. 2, our mathematical model of the stochastic reaction–diffusion recurrent neural networks with continuously distributed delays and Dirichlet boundary conditions is presented and some preliminaries are given. Our main results are given in Sect. 3 . In Sect. 4, some examples are provided to illustrate the effectiveness of the obtained results. Our conclusions are drawn in Sect. 5.

2 Model description and preliminaries

Consider the following stochastic reaction–diffusion delayed recurrent neural networks with the Dirichlet boundary conditions:

$$ \begin{aligned} \hbox{d}u_i(t,x)&=\sum_{k=1}^m\frac{{\partial}}{{\partial x_k}}\left(D_{ik}\frac{{\partial u_i}}{{\partial x_k}}\right)\hbox{d}t+\left[-b_iu_i(t,x)+\sum_{j=1}^nc_{ij}f_j(u_j(t,x))\right.\\ &\quad+\left.\sum_{j=1}^nd_{ij}\int\limits_{-\infty}^tK_{ij}(t-s)g_j(u_j(s,x))\hbox{d}s+J_i\right]\hbox{d}t+\sum_{j=1}^n\sigma_{ij}(u_j(t,x))\hbox{d}w_j(t),\\ \end{aligned} $$
$$ \begin{array}{lll} u_i(t,x)=0,&(t,x)\in [0, +\infty)\times \partial X,&\\ u_i(t,x)=\phi_i(t,x),&(t,x)\in (-\infty,0]\times X ,&i=1,2,\ldots, n.\\ \end{array} $$
(1)

In the above model,

  1. (i)

    n ≥ 2 is the number of neurons in the networks; \(x=(x_1,x_2,\ldots,x_m)^T \in X \subset R^m\) and X = {x = (x1, x2,…,x m )T||x i | < l i  = 1,2,…,m} is a bounded compact set with smooth boundary ∂X and mesX > 0 in space Rm;

  2. (ii)

    u(t,x) = (u1(t,x),u2(t,x),…,u n (t,x))T ∈ Rn and u i (t,x) is the state of the ith neuron at time t and in space x;

  3. (iii)

    smooth function D ik  > 0 represents the transmission diffusion operator along the ith unit; b i  > 0 represents the rate with which the ith unit will reset its potential to the resting state in isolation when disconnected from the networks and external inputs; c ij ,d ij denote the strength of jth unit on the ith unit at time t and in space x;

  4. (iv)

    f j (u j (t,x)) and g j (u j (t,x)) denote the activation function of the jth unit at time t and in space x; ϕ(t,x) = (ϕ1(t,x),ϕ2(t,x),…,ϕ n (t,x))T and ϕ i (t,x) are continuous function;

  5. (v)

    w(t) = (w1(t),…,w n (t))T is a n-dimensional Brownian motion defined on a complete probability space \((\Omega,{{\mathcal{F}}},P)\) with a natural filtration \(\{{{\mathcal{F}}}_t\}_{t{\ge} 0} \) generated by the standard Brownian motion {w(s):0 ≤ s ≤ t}.

  6. (vi)

    The delay kernels K ij :[0, +∞)→ [0, +∞) (i,j = 1,2,…,n) are real-valued nonnegative continuous functions and satisfy the following conditions

    1. (a)

      ∫ ∞0 K ij (s)ds = 1,

    2. (b)

      ∫ ∞0 sK ij (s)ds < ∞,

    3. (c)

      There exists a positive μ such that ∫ ∞0 seμs K ij (s)ds < ∞.

Let C[(−∞,0] × X,R n] denote the Banach space of continuous functions which map (−∞,0] × X into R n with norm \(\|\phi\|=\sup_{-\infty<{\theta\leq}0}|\phi(\theta)|. |\cdot|\) is the Euclidean norm in R n. x t  = {x(t + θ) :−∞ < θ ≤ 0} for t ≥ 0. Denote by \(C=C^b_{{{\mathcal{F}}}_0}[(-\infty,0]\times X,R^n]\) the family of all bounded \({{\mathcal{F}}}_0\) measurable, random variables ϕ, satisfying \(\|\phi\|_{L^p}^p=\sup_{-\infty<\theta\leq 0}E\|\phi(s)\|^p<\infty,\) where E stands for the mathematical expectation with respect to the given probability measure P. For ϕ ∈ C, define the norm

$$\|\phi\|^2=\hbox{sup}_{-\infty < t\leq 0}\left\{\sum_{i=1}^n\|\phi_i(t)\|^2_2 \right\},\quad \|\phi_i(t)\|_2^2=\int\limits_X|\phi_i(t,x)|^2\hbox{d}x. $$

Let L 2(X) be the space of real Lebesgue measurable function on X. It is a Banach space for the L 2-norm

$$\|u_i(t)\|_2=\left[\int\limits_X|u_i(t,x)|^2\hbox{d}x\right]^\frac{{1}}{2},$$

where u(t,x) = (u 1(t,x),u 2(t,x),…,u n (t,x))T ∈ R n. Define

$$\|u(t)\|=\left[\sum_{i=1}^n\|u_i(t)\|^2_2\right]^\frac{{1}}{2}.$$

Throughout this paper, for system (1), we have the following assumptions:

  1. (A1)

    f j , g j and σ ij are Lipschitz continuous with Lipschitz constants F j  > 0,G j  > 0 and L ij  > 0, respectively, for i,j = 1,2,…,n.

  2. (A2)

    B−C+F−D+G is a nonsingular M-matrix, where

    F = diag(F1,…,F n ), G = diag(G1,…,G n );

    B = diag(b1,…,b n ), C+  = (|c ij |)n × n, D+ = (|d ij |)n × n;

    If there is no noise in system (1), it turns out to be the following deterministic system.

    $$ \begin{aligned} \hbox{d}u_i(t,x)&=\sum_{k=1}^m\frac{{\partial}}{{\partial x_k}}\left(D_{ik}\frac{{\partial u_i}}{{\partial x_k}}\right)\hbox{d}t+\left[-b_iu_i(t,x)+\sum_{j=1}^nc_{ij}f_j(u_j(t,x))\right.\\&\quad+\left.\sum_{j=1}^nd_{ij}\int\limits_{-\infty}^tK_{ij}(t-s)g_j(u_j(s,x))\hbox{d}s+J_i\right]\hbox{d}t, \quad x\in X. \end{aligned} $$
    (2)

    Let

    $$ \begin{aligned}H_i(u_i)&=-b_iu_i+\sum_{j=1}^nc_{ij}f_j(u_j)\\&\quad+\sum_{j=1}^nd_{ij}\int\limits_{-\infty}^tK_{ij}(t-s)g_j(u_j)\hbox{d}s+J_i\quad i=1,2,\ldots,n \end{aligned} $$

    then it is known that the solution of H i (u i ) = 0 (i = 1,2,…,n) are equilibrium point of system (2).

    Since

    $$ \begin{aligned}H_i(u_i)&=-b_iu_i+\sum_{j=i}^nc_{ij}f_j(u_j)+\sum_{j=1}^nd_{ij}g_j(u_j)\int\limits_{-\infty}^tK_{ij}(t-s)\hbox{d}s+J_i\\&=-b_iu_i+\sum_{j=1}^nc_{ij}f_j(u_j)+\sum_{j=1}^nd_{ij}g_j(u_j)+J_i,\qquad i=1,2,\ldots,n \end{aligned} $$

    from hypothesis (A1) and (A2) (see [24]), we know that system (2) has one unique equilibrium point u * = (u *1 ,u *2 ,…,u * n )T. Suppose

  3. (A3)

    σ ij (u * i ) = 0 for i,j = 1,2,…,n.

Then u * = (u *1 ,…,u * n )T is an equilibrium point of system (1) provided that system (1) satisfies (A1)–(A3).

We end this section by introducing the definition of globally exponential stability in the mean square and a useful lemma.

Definition 1

For every \(\phi \in C=C^b_{{{\mathcal{F}}}_0}[(-\infty,0]\times X,R^n],\) the equilibrium solution of system (1) is said to be globally exponentially stable in the mean square if there exists positive scalars α > 0 and β > 0 such that

$$ E\|x(t,\phi)\|^2\leq\alpha \hbox{e}^{-\beta t}E\|\phi\|^2. $$

Lemma 1

[16] Let X be a cube |x i | < l i (i = 1,2,…,m) and let h(x) be a real-valued function belonging to C 1(X) which vanish on the boundary ∂X of X, i.e., h(x)|∂X  = 0. Then

$$ \int\limits_Xh^2(x)\hbox{d}x\leq l_i^2\int\limits_X\left|\frac{{\partial h}}{{\partial x_i}}\right|^2\hbox{d}x.$$

3 Main results

In this section, we will employ the Ito formula and martingale theory to present a sufficient condition for the globally exponential stability in the mean square of stochastic reaction–diffusion recurrent neural networks with continuously distributed delays and Dirichlet boundary conditions defined by Eq. 1. The usual continuously distributed delayed RNNs without diffusion or stochastic perturbation are included as special cases of equation (1).

Theorem 1

The stochastic reaction–diffusion delayed recurrent neural network (1) with Dirichlet boundary condition is globally exponentially stable in mean square if there exist constantsr i  > 0, β ij  > 0, (i = 1,2,…,n, j = 1,2,…,n), such that

$$ \begin{aligned}-2r_ib_i&-\sum_{k=1}^m\frac{{2D_{ik}r_i}}{{l_k^2}}+\sum_{j=1}^nr_iF_j|c_{ij}|+\sum_{j=1}^nr_jF_i|c_{ji}|+r_i\sum_{j=1}^n\beta_{ij}^{-1}|d_{ij}|\\&+\sum_{j=1}^nr_jG_i^2\beta_{ji}|d_{ji}|+\sum_{j=1}^nr_jL_{ji}^2<0, \end{aligned} $$
(3)

in which F i ,G i and L ij , (i = 1,2,…,n, j = 1,2,…,n) are Lipschitz constants.

Proof

If condition (3) holds, we can always find a small positive number γ > 0 such that for i = 1,2,…,n

$$ \begin{aligned}-2r_ib_i&-\sum_{k=1}^m\frac{{2D_{ik}r_i}}{{l_k^2}}+\sum_{j=1}^nr_iF_j|c_{ij}|+\sum_{j=1}^nr_jF_i|c_{ji}|+r_i\sum_{j=1}^n\beta_{ij}^{-1}|d_{ij}|\\&+\sum_{j=1}^nr_jL^2_{ji}+\sum_{j=1}^nr_jG_i^2\beta_{ji}|d_{ji}|\int\limits_0^{\infty}K_{ji}(s)\hbox{e}^{\epsilon s}\hbox{d}s +\gamma < 0. \end{aligned} $$

Let us consider functions

$$ \begin{aligned}p_i(y_i)&=r_iy_i-2r_ib_i-\sum_{k=1}^m\frac{{2D_{ik}r_i}}{{l_k^2}}+\sum_{j=1}^nr_iF_j|c_{ij}|+\sum_{j=1}^nr_jF_i|c_{ji}|\\&\quad+r_i\sum_{j=1}^n\beta_{ij}^{-1}|d_{ij}|+\sum_{j=1}^nr_jG_i^2\beta_{ji}|d_{ji}|\int\limits_0^{+\infty}K_{ji}(s)\times\hbox{e}^{2y_is}+\sum_{j=1}^nr_jL_{ji}^2, \end{aligned} $$
(4)

From (4) and (A2), we have p i (0) < −γ < 0 and p i (y i ) is continuous for y i  ∈ [0, +∞). In addition, p i (y i )→ +∞ as y i → +∞. Thus there exists constant ε i  ∈ (0, +∞) such that

$$ \begin{aligned}p_i(\epsilon_i)&=r_i\epsilon_i-2r_ib_i-\sum_{k=1}^m\frac{{2D_{ik}r_i}}{{l_k^2}}+\sum_{j=1}^nr_iF_j|c_{ij}|+\sum_{j=1}^nr_jF_i|c_{ji}|\\&\quad+r_i\sum_{j=1}^n\beta_{ij}^{-1}|d_{ij}|+\sum_{j=1}^nr_jG_i^2\beta_{ji}|d_{ji}|\int\limits_0^{+\infty}K_{ji}(s)\times\hbox{e}^{2\epsilon_is}+\sum_{j=1}^nr_jL_{ji}^2=0, \end{aligned}$$

for i ∈ 1,2,…,n.

By choosing ε = min1 ≤ i ≤  n{ε i } > 0, we have

$$ \begin{aligned}p_i(\epsilon)&=r_i\epsilon-2r_ib_i-\sum_{k=1}^m\frac{{2D_{ik}r_i}}{{l_k^2}}+\sum_{j=1}^nr_iF_j|c_{ij}|+\sum_{j=1}^nr_jF_i|c_{ji}|\\&\quad+r_i\sum_{j=1}^n\beta_{ij}^{-1}|d_{ij}|+\sum_{j=1}^nr_jG_i^2\beta_{ji}|d_{ji}|\int\limits_0^{+\infty}K_{ji}(s)\times\hbox{e}^{2\epsilon s}+\sum_{j=1}^nr_jL_{ji}^2\leq 0 \end{aligned}$$
(5)

for i ∈ 1,2,…,n.

Let u * = (u *1 ,…,u * n )T be an equilibrium point of system (1) and let z i  = u i −u * i , then Eq. 1 is equivalent to

$$ \begin{aligned} \hbox{d}z_i(t)&=\sum_{k=1}^m\frac{{\partial}}{{\partial x_k}}\left(D_{ik}\frac{{\partial z_i(t)}}{{\partial x_k}}\right)\hbox{d}t+\left\{-b_iz_i(t,x)+\sum_{j=1}^nc_{ij}\tilde{f}_j(z_j(t,x))\right.\\&\quad+\left.\sum_{j=1}^nd_{ij}\int\limits_{-\infty}^tK_{ij}(t-s)\tilde{g}_j(z_j(s,x))\hbox{d}s\right\}\hbox{d}t+\sum_{j=1}^n\sigma_{ij}(u_j(t,x))\hbox{d}w_j(t),\quad x\in X,\end{aligned} $$
(6)

where

$$\tilde{f}_j(z_j(t,x))=f_j(z_j(t,x)+u_j^*)-f_j(u_j^*), $$
$$\tilde{g}_j(z_j(s,x)=g_j(z_j(s,x)+u^*_j)-g_j(u_j^*). $$

For system (6), we construct the following Lyapunov functional:

$$ V(t)=V_1(t)+V_2(t)$$

with

$$V_1(t)=\int\limits_X\sum_{i=1}^nr_i|z_i(t,x)|^2{\hbox{e}^{\epsilon t}}\hbox{d}x,$$

and

$$V_2(t)=\int\limits_X\sum_{i=1}^nr_i\left[\sum_{j=1}^n|\beta_{ij}d_{ij}|\int\limits_0^{+\infty}K_{ij}(s)\int\limits_{t-s}^t|\tilde{g}_j(z_j(\rho,x))|^2\hbox{e}^{\epsilon (\rho+s)}\hbox{d}\rho \hbox{d}s \right]\hbox{d}x. $$

Applying Ito formula to V 1(t) and V 2(t), respectively, we obtain

$$ \begin{aligned} \hbox{d}V_1(s)&=\int\limits_X \left\{\epsilon \hbox{e}^{\epsilon s}\sum_{i=1}^nr_i|z_i(s,x)|^2\hbox{d}s\right.+2{\hbox{e}^{\epsilon s}}\sum_{i=1}^nr_iz_i(s,x)\left[\sum_{k=1}^m\frac{{\partial}}{{\partial x_k}}\left(D_{ik}\frac{{\partial z_i}}{{\partial x_k}}\right) \right.\\ &\quad\left.-b_iz_i(s,x)+\sum_{j=1}^nc_{ij}\tilde{f}_j(z_j(s,x))+\sum_{j=1}^nd_{ij}\int\limits_{-\infty}^sK_{ij}(s-\rho)[g_j(u_j(\rho,x))-g_j(u_j^*)]\hbox{d}\rho \right] \hbox{d}s\\ &\quad+2{\hbox{e}^{\epsilon s}}\sum_{i=1}^nr_iz_i(s,x)\sum_{j=1}^n\sigma_{ij}(u_j(s,x))\hbox{d}w_j(s)+\hbox{e}^{\epsilon s}\left.\sum_{i=1}^nr_i\sum_{j=1}^n\sigma_{ij}^2(u_j(s,x))\hbox{d}s\right\}\hbox{d}x, \end{aligned} $$
(7)

and

$$ \begin{aligned} \hbox{d}V_2(s)&=\int\limits_X\sum_{i=1}^nr_i\left[\sum_{j=1}^n|\beta_{ij}d_{ij}|\int\limits_0^{\infty}K_{ij}(\rho)|g_j(z_j(s,x)+u^*_j)-g_j(u^*_j)|^2\hbox{e}^{\epsilon (s+\rho)}\hbox{d}\rho \hbox{d}s \right]\hbox{d}x\\&\quad-\int\limits_X\sum_{i=1}^nr_i\left[\sum_{j=1}^n|\beta_{ij}d_{ij}|\int\limits_0^{\infty}K_{ij}(\rho)|g_j(z_j(s-\rho,x)+u^*_j)-g_j(u^*_j)|^2\hbox{e}^{\epsilon s}\hbox{d}\rho \hbox{d}s \right ] \hbox{d}x.\end{aligned}$$
(8)

Since

$$ \begin{aligned} &2{\hbox{e}^{\epsilon s}}\sum_{i=1}^nr_iz_i(s,x)\sum_{j=1}^nd_{ij}\int\limits_{-\infty}^sK_{ij}(s-\rho)\left[g_j\left(z_j(\rho,x)+u_j^*\right)-g_j\left(u_j^*\right)\right]\hbox{d}\rho\\& \leq \hbox{e}^{\epsilon s}\sum_{i=1}^nr_i\sum_{j=1}^n|d_{ij}|\beta_{ij}^{-1}\int\limits_{-\infty}^sK_{ij}(s-\rho)|z_i(s,x)|^2\hbox{d}\rho\\&\quad+\hbox{e}^{\epsilon s}\sum_{i=1}^nr_i\sum_{j=1}^n|d_{ij}|\beta_{ij}\int\limits_{-\infty}^sK_{ij}(s-\rho)\left|g_j\left(z_j(\rho,x)+u_j^*\right)-g_j\left(u_j^*\right)\right|^2\hbox{d}\rho\\&=\hbox{e}^{\epsilon s}\sum_{i=1}^nr_i\sum_{j=1}^n|d_{ij}|\beta_{ij}^{-1}\int\limits_{-\infty}^sK_{ij}(s-\rho)|z_i(s,x)|^2\hbox{d}\rho\\&\quad+\hbox{e}^{\epsilon s}\sum_{i=1}^nr_i\sum_{j=1}^n|d_{ij}|\beta_{ij}\int\limits_0^{\infty}K_{ij}(\rho)\left|g_j\left(z_j(s-\rho,x)+u_j^*\right)-g_j\left(u_j^*\right)\right|^2\hbox{d}\rho,\end{aligned} $$
(9)

substituting (9) into (7) and combining with (8), we have

$$ \begin{aligned}V(t)&=V(0)+\int\limits_0^t \hbox{d}V(s)=V(0)+\int\limits_0^t\hbox{d}V_1(s)+\int\limits_0^t\hbox{d}V_2(s)\\&\leq \int\limits_0^t\int\limits_X\left\{\epsilon \hbox{e}^{\epsilon s}\sum_{i=1}^nr_i|z_i(s,x)|^2\right.+2\hbox{e}^{\epsilon s}\sum_{i=1}^nr_iz_i(s,x)\left[\sum_{k=1}^m\frac{{\partial}}{{\partial x_k}}\left(D_{ik}\frac{{\partial z_i}}{{\partial x_k}}\right)\right]\\&\quad-2\hbox{e}^{\epsilon s}\sum_{i=1}^nr_iz_i(s,x)b_iz_i(s,x) +2\hbox{e}^{\epsilon s}\sum_{i=1}^nr_i|z_i(s,x)|\sum_{j=1}^nc_{ij}F_j|z_j(s,x)|\\&\quad+\hbox{e}^{\epsilon s}\sum_{i=1}^nr_i\sum_{j=1}^n|d_{ij}|\beta_{ij}^{-1}\int\limits_{-\infty}^sK_{ij}(s-\rho)|z_i(s,x)|^2\hbox{d}\rho\\&\quad+\hbox{e}^{\epsilon s}\sum_{i=1}^nr_i\sum_{j=1}^n|d_{ij}|\beta_{ij}\int\limits_0^{\infty}K_{ij}(\rho)\left|g_j\left(z_j(s-\rho,x)+u_j^*\right)-g_j\left(u_j^*\right)\right|^2\hbox{d}\rho\\&\quad+\sum_{i=1}^nr_i\left[\sum_{j=1}^n|\beta_{ij}d_{ij}|\int\limits_0^{\infty}K_{ij}(\rho)\left|g_j\left(z_j(s,x)+u^*_j\right)-g_j\left(u^*_j\right)\right|^2\hbox{e}^{\epsilon (s+\rho)}\hbox{d}\rho \right]\\ &\quad\left.-\sum_{i=1}^nr_i\left[\sum_{j=1}^n|\beta_{ij}d_{ij}|\int\limits_0^{\infty}K_{ij}(\rho)\left|g_j\left(z_j(s-\rho,x)+u^*_j\right)-g_j\left(u^*_j\right)\right|^2\hbox{e}^{\epsilon s}\hbox{d}\rho \right ] \right\}\hbox{d}x \hbox{d}s\\&\quad+\int\limits_0^t\int\limits_X\sum_{i=1}^nr_i\left\{\hbox{e}^{\epsilon s}\sum_{j=1}^nL_{ij}^2|z_j(s,x)|^2\hbox{d}x\hbox{d}s+2\hbox{e}^{\epsilon s} z_i(s,x)\sum_{j=1}^n\sigma_{ij}(u_j(s,x))\hbox{d}x\hbox{d}w_j(s)\right\}.\end{aligned} $$
(10)

From the Dirichlet boundary conditions and Lemma 1, we have

$$ \begin{aligned}\int\limits_X&\sum_{i=1}^nr_iz_i(t,x)\sum_{k=1}^m\frac{{\partial}}{{\partial x_k}}\left(D_{ik}\frac{{\partial z_i(t,x)}}{{\partial x_k}}\right)\hbox{d}x=-\sum_{i=1}^nr_i\sum_{k=1}^m\int\limits_XD_{ik}\left(\frac{{\partial z_i(t,x)}}{{\partial x_k}}\right)^2\hbox{d}x\\ & \leq-\sum_{i=1}^nr_i\sum_{k=1}^m\int\limits_X\frac{{D_{ik}}}{{l^2_k}}|z_i(t,x)|^2\hbox{d}x.\end{aligned} $$

Since \(\int_0^t\int_X 2\hbox{e}^{\epsilon s}\sum_{i=1}^nr_iz_i(s,x)\sum_{j=1}^n\sigma_{ij}(u_j(s,x))\hbox{d}x\hbox{d}w_j(s)\) is a martingale [20], we have

$$E\int\limits_0^t\int\limits_X 2\hbox{e}^{\epsilon s}\sum_{i=1}^nr_iz_i(s,x)\sum_{j=1}^n\sigma_{ij}(u_j(s,x))\hbox{d}x\hbox{d}w_j(s)=0.$$

Therefore, taking expectation on both sides of (10), we obtain

$$ \begin{aligned} EV(t)&\leq EV(0)+E\int\limits_0^t \hbox{e}^{\epsilon s}\int\limits_X\sum_{i=1}^n\left[\epsilon r_i-\sum_{k=1}^m\frac{{2D_{ik}r_i}}{{l_k^2}}-2r_ib_i\right.\\&\quad+\sum_{j=1}^nr_iF_j|c_{ij}|+\sum_{j=1}^nr_jF_i|c_{ji}|+r_i\sum_{j=1}^n|d_{ij}|\beta_{ij}^{-1}\int\limits_{-\infty}^sK_{ij}(s-\rho)|z_i(s,x)|^2\hbox{d}\rho\\&\quad\left.+\sum_{j=1}^nr_jL^2_{ji}+\sum_{j=1}^nr_jG_i^2|\beta_{ji}d_{ji}|\int\limits_0^{\infty}K_{ji}(\rho)\hbox{e}^{\epsilon \rho}\hbox{d}\rho\right]|z_i(s,x)|^2\hbox{d}x\hbox{d}s\\&= EV(0)+\int\limits_X\sum_{i=1}^n\left[\epsilon r_i-\sum_{k=1}^m\frac{{2D_{ik}r_i}}{{l_k^2}}-2r_ib_i+\sum_{j=1}^nr_iF_j|c_{ij}|\right.\\&\quad+\sum_{j=1}^nr_jF_i|c_{ji}|+ r_i\sum_{j=1}^n|d_{ij}|\beta_{ij}^{-1} +\sum_{j=1}^nr_jL^2_{ji}\\ &\quad\left.+\sum_{j=1}^nr_jG_i^2|\beta_{ji}d_{ji}|\int\limits_0^{\infty}K_{ji}(\rho)\hbox{e}^{\epsilon \rho}\hbox{d}\rho \right]E\int\limits_0^t \hbox{e}^{\epsilon s}|z_i(s,x)|^2\hbox{d}s\hbox{d}x.\end{aligned} $$

It follows from (5) that

$$ EV(t)\leq EV(0) \quad t\ge 0. $$
(11)

Since

$$ \begin{aligned}EV(0)&=\int\limits_X\left[\sum_{i=1}^nr_iE|z_i(0,x)|^2+\sum_{i=1}^nr_i\sum_{j=1}^n|\beta_{ij}d_{ij}|\right.\\& \quad\left. \times E\int\limits_0^{\infty}K_{ij}(s)\int\limits_{-s}^0\left|g_j\left(z_j(s,x)+u^*_j\right)-g_j\left(u^*_j\right)\right|^2\hbox{e}^{\epsilon (s+\rho)}\hbox{d}\rho \hbox{d}s\right] \hbox{d}x\\ & \leq \int\limits_X\left[\sum_{i=1}^n\max_{1\leq i\leq n}\{r_i\}|z_i(0,x)|^2\right.\\ &\quad\left.+\sum_{i=1}^n{r_i}\sum_{j=1}^n\beta_{ij}|d_{ij}|G_j^2E\int\limits_0^{\infty}K_{ij}(s)\int\limits_{-s}^0 \hbox{e}^{\epsilon (s+\rho)}\hbox{d}\rho |z_j(s,x)|^2 \hbox{d}s\right]\hbox{d}x\\ & \leq \max_{1\leq i\leq n}\{r_i\}\left(1+\max_{1\leq i\leq n}\left\{\sum_{j=1}^n\beta_{ji}|d_{ji}|G^2_i\int\limits_0^{\infty}s\hbox{e}^{\epsilon s}K_{ji}(s)\hbox{d}s \right\}\right)E\|\phi\|^2, \end{aligned} $$
(12)

and

$$ EV(t) \ge\int\limits_X\sum_{i=1}^nr_iE|z_i(t,x)|^2\hbox{e}^{\epsilon t}\hbox{d}x \ge \hbox{e}^{\epsilon t}\min_{1\leq i\leq n}\{r_i\}E\|z(t)\|^2,\quad t>0,$$
(13)

combining (12) and (13) with (11), we have

$$ E\|z(t)\|^2\leq \alpha E\|\phi\|^2\hbox{e}^{-\epsilon t},$$

where

$$ \alpha=\frac{{\max_{1\leq i\leq n}\{r_i\}\left(1+\max_{1\leq i\leq n}\left\{\sum_{j=1}^n\beta_{ji}|d_{ji}|G^2_i\int_0^{\infty}s\hbox{e}^{\epsilon s}K_{ji}(s)\hbox{d}s \right\}\right)}}{{\min_{1\leq i\leq n}{\{r_i\}}}} >1 $$

is a constant. This complete the proof.

In Theorem 1, if we take D ik  = 0, i = 1,…,n,k = 1,…,m, system (1) turns out to be the following stochastic recurrent neural networks with continuously distributed delays.

$$ \begin{aligned} \hbox{d}u_i(t)&=\left[-b_iu_i(t,x)+\sum_{j=1}^nc_{ij}f_j(u_j(t,x))+\sum_{j=1}^nd_{ij}\int\limits_{-\infty}^tK_{ij}(t-s)g_j(u_j(s,x))+J_i\right]\hbox{d}t\\&\quad+\sum_{j=1}^n\sigma_{ij}(u_j(t,x))\hbox{d}w_j(t), \qquad t\in [0,+\infty)\end{aligned}$$
(14)
$$ u_i(t)=\phi_i(t), t\in(-\infty,0], \quad i=1,\ldots,n, $$

Corollary 1

Under assumptions (A1)–(A3), if there exist constantsr i  > 0, β ij  > 0, (i = 1,2,…,n,j = 1,2,…,n) such that

$$ \begin{aligned} &-2r_ib_i+\sum_{j=1}^nr_iF_j|c_{ij}|+\sum_{j=1}^nr_jF_i|c_{ji}|+r_i\sum_{j=1}^n\beta_{ij}^{-1}|d_{ij}|\\&+\sum_{j=1}^nr_jG_i^2\beta_{ji}|d_{ji}|+\sum_{j=1}^nr_jL_{ji}^2<0. \end{aligned} $$

Then for all \(\phi \in C=C^b_{{{\mathcal{F}}}_0}[(-\infty,0],R^n],\) the equilibrium solution of system (14) is globally exponentially stable in the mean square.

For system (1), when σ ij  = 0, i,j, = 1,2,…,n, it turns out to be the deterministic recurrent neural networks (2). So we have

Corollary 2

Under assumptions (A1)–(A2), if there exist constantsr i  > 0, β ij  > 0, (i = 1,2,…,n,j = 1,2,…,n), such that

$$ \begin{aligned}&-2r_ib_i-\sum_{k=1}^m\frac{{2D_{ik}r_i}}{{l_k^2}}+\sum_{j=1}^nr_iF_j|c_{ij}|+\sum_{j=1}^nr_jF_i|c_{ji}|\\&+r_i\sum_{j=1}^n\beta_{ij}^{-1}|d_{ij}|+\sum_{j=1}^nr_jG_i^2|\beta_{ji}d_{ji}|<0. \end{aligned} $$
(15)

Then for all \(\phi \in C=C^b_{{{\mathcal{F}}}_0}[(-\infty,0],R^n],\) the equilibrium point of system (2) is globally exponentially stable.

Proof

If there is no stochastic perturbation, the solution of system (2) is deterministic. By Cauchy inequality and Theorem 1, we have \(\|z(t)\|=E\|z(t)\| \leq(E\|z(t)\|^2)^\frac{{1}}{2} \leq \alpha^\frac{{1}}{2}(E\|\phi\|^2)^\frac{{1}}{2}\hbox{e}^{-\frac{{\epsilon}}{{2}}t},\) for all t ≥ 0.

Thus system (2) is globally exponentially stable, which is the result of [21].

Remark 1

We extend [21] to systems with stochastic perturbation.

Remark 2

Noting \((E|x(t)|^{\hat{p}})^{1/\hat{p}}\leq (E|x(t)|^p)^{1/p}\) for \(0 < \hat{p}< p,\) we see that the pth moment exponential stability implies the \(\hat{p}\) th moment exponential stability (see [19]). Therefore for system (1), the globally exponential stability in the mean square implies the mean value exponential stability of an equilibrium solution.

Remark 3

Global exponential stability is the term used for the deterministic system. For the effect of stochastic forces to the stability property of continuously distributed delayed RNNs (1), we usually study the almost sure exponential stability, mean square exponential stability and mean value exponential stability of their equilibrium solution. Generally speaking, the pth moment exponential stability and the almost sure stability do not imply each other and additional conditions are required in order to deduce one from the other (see [19])

Remark 4

In [18], the activation functions are bounded. However, in corollary 1, the stability conditions are obtained without assuming the boundedness, monotonicity and differentiability of the activation functions nor symmetry of synaptic interconnection weights. Hence the proposed results are easier to verify.

4 An example

In this section, we present a numerical example to demonstrate the effectiveness of the proposed results.

Example 1

Consider the following stochastic reaction–diffusion delayed recurrent neural networks:

$$ \left\{\begin{array}{l}\hbox{d} u_i(t,x)=\left[\sum\limits_{k=1}^2\frac{\partial}{\partial x_k}\left(D_{ik}\frac{\partial u_i}{\partial x_k}\right)-b_iu_i(t,x)+\sum\limits_{j=1}^2c_{ij}f_j(u_j(t,x))\right.\\\quad\quad\quad \left.+\sum\limits_{j=1}^2d_{ij}\int_{-\infty}^tK_{ij}(t-s)g_j(u_j(s,x))+J_i\right]\hbox{d}t+\sum\limits_{j=1}^2\sigma_{ij}(u_j(t,x))\hbox{d}w_j(t),\\\begin{array}{ll}&(t,x)\in [0,+\infty)\times X\\u_i(t,x)=0,&(t,x)\in [-\tau,+\infty)\times \partial X,\\u_i(t,x)=\phi_i(t,x),&(t,x)\in [-\tau,0]\times X, \quad\quad i=1,2.\end{array}\end{array}\right. $$
(16)

where X = {x|x i | < 1, i = 1,2} and D 11 = 0.5, D 12 = 0.5, D 21 = 0.3, D 22 = 0.7, b 1 = 0.5, b 2 = 0.4, c 11 = 0.5, c 12 = 0.4, c 21 = 0.3, c 22 = 0.2, d 11 = 0.1, d 12 = 0.2, d 21 = 0.3, d 22 = 0.5, L 11 = L 12 = L 21 = L 22 = 0.4, J = (J 1,J 2)T is the constant input vector. K ij (t) = te−t, i,j = 1,2,g j (x) = arctan(x) , f j (x) = 0.5(|x + 1| − |x − 1|), (j = 1,2). Obviously, f j (·) and g j (·) satisfy Lipschitz condition with F j  = G j  = 1. By simple calculation , we get

$$ B-C^+F-D^+G= \left({\begin{array}{ll} {- 0.1} & {- 0.6}\\ {-0.6} & {-0.3}\\\end{array}} \right).$$

Choosing r 1 = r 2 = 1, β11 = 1, β12 = 1, β21 = 1, and β22 = 1, we have

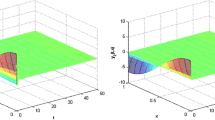
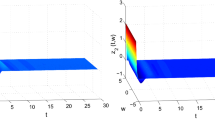
$$ \begin{aligned}-2r_1b_1&-\sum_{k=1}^2\frac{{2D_{1k}r_1}}{{l^2_k}}+\sum_{j=1}^2r_1F_j|c_{1j}|+\sum_{j=1}^2r_jF_1|c_{j1}|+\sum_{j=1}^2r_1\beta_{1j}^{-1}|d_{1j}|\\&+\sum_{j=1}^2r_jG_1^2|\beta_{j1}d_{j1}|+\sum_{j=1}^2L_{j1}^2=-0.28<0,\\&-2r_2b_2-\sum_{k=1}^2\frac{{2D_{2k}r_2}}{{l^2_k}}+\sum_{j=1}^2r_2F_j|c_{2j}|+\sum_{j=1}^2r_jF_2|c_{j2}|+\sum_{j=1}^2r_1\beta_{2j}^{-1}|d_{2j}|\\&+\sum_{j=1}^2r_jG_2^2|\beta_{j2}d_{j2}|+\sum_{j=1}^2L_{j2}^2=-0.38<0. \end{aligned} $$

Hence, it follows from Theorem 1 that system (16) is globally exponentially stable in the mean square. Figure 1 gives the numerical results of Example 1.

Fig. 1
figure 1

Numerical results of Example 1

Full size image

Example 2

Consider a stochastic reaction–diffusion recurrent neural network with continuously distributed delays:

$$ \begin{aligned} &d\left({\begin{array}{ll} {u_{1} (t,x)}\\ {u_{2} (t,x)}\\\end{array}}\right)=\left( {\begin{array}{ll} {D_{{11}}\frac{{\partial u_{1} }}{{\partial x_{1} }}} & {D_{{12}}\frac{{\partial u_{1} }}{{\partial x_{2} }}}\\{D_{{21}}\frac{{\partial u_{2} }}{{\partial x_{1} }}} & {D_{{22}}\frac{{\partial u_{2} }}{{\partial x2}}}\\ \end{array}}\right)\left( {\begin{array}{ll} {\frac{\partial}{{\partial x_{1}}}}\\ {\frac{\partial }{{\partial x_{2}}}}\\\end{array}}\right)\hbox{d}t\\ -& \left({\begin{array}{ll} {16} & 0\\ 0& 9\\ \end{array}} \right)\left( {\begin{array}{ll} {u_{1} }\\{u_{2} }\\ \end{array}} \right)\hbox{d}t + \left({\begin{array}{ll} 1 & 2\\ 3 & 1\\ \end{array}} \right)\left({\begin{array}{ll}{\arctan u_{1}}\\ {\arctan u_{2}}\\ \end{array}}\right)\hbox{d}t\\-&\left({\begin{array}{ll} {-3} & 1\\ 2 & {-2}\\ \end{array}}\right)\left( {\begin{array}{ll} {\int\limits_{{- \infty }}^{t}{K(t - s)} \cdot \tanh (u_{1} )\hbox{d}s}\\ {\int\limits_{{-\infty}}^{t}{K(t - s)} \cdot \tanh (u_{2})\hbox{d}s}\\ \end{array} } \right)\hbox{d}t\\&\left({\begin{array}{ll} {- 4u_{1} } & {u_{1} }\\ {u_{2} } &{u_{2} }\\ \end{array} } \right)\left( {\begin{array}{ll} {\hbox{d}w_{1} (t)}\\ {\hbox{d}w_{2} (t)}\\ \end{array}} \right)\\\end{aligned}$$
(17)

where \(\tanh(x)=\frac{{\hbox{e}^x-\hbox{e}^{-x}}}{{\hbox{e}^x+\hbox{e}^{-x}}}, \quad K(t)=\hbox{e}^{-t} \) and X = {x||x i | < 1, i = 1,2}.

It is obvious that F j  = G j  = 1, j = 1,2 and

$$ B-C^+F-D^+G=\left( \begin{array}{ll} {4}& {-3}\\ {-5} &{5}\\ \end{array} \right) $$

which is a nonsingular M-matrix. Choosing r 1 = r 2 = 1, β11 = 1, β12 = 1, β21 = 1, and β22 = 1, we have

$$ \begin{aligned} &-2r_1b_1-\sum_{k=1}^2\frac{{2D_{1k}r_1}}{{l^2_k}}+\sum_{j=1}^2r_1F_j|c_{1j}| +\sum_{j=1}^2r_jF_1|c_{j1}|+\sum_{j=1}^2r_1\beta_{1j}^{-1}|d_{1j}|\\ &+\sum_{j=1}^2r_jG_1^2|\beta_{j1}d_{j1}|+\sum_{j=1}^2L_{j1}^2=-1< 0,\\ \end{aligned} $$

and

$$ \begin{aligned} &-2r_2b_2-\sum_{k=1}^2\frac{{2D_{2k}r_2}}{{l^2_k}}+\sum_{j=1}^2r_2F_j|c_{2j}| +\sum_{j=1}^2r_jF_2|c_{j2}|+\sum_{j=1}^2r_1\beta_{2j}^{-1}|d_{2j}|\\ &+\sum_{j=1}^2r_jG_2^2|\beta_{j2}d_{j2}|+\sum_{j=1}^2L_{j2}^2=-1< 0. \end{aligned} $$

It follows from Theorem 1 that system (17) is globally exponentially stable in the mean square.

5 Conclusions

As is pointed out in Sect. 1, stochastic perturbation and diffusion do exist in a neural network, due to random fluctuations and asymmetry of the field. Thus it is necessary and rewarding to study stochastic effects to the stability property of reaction–diffusion neural networks. In this paper, some new conditions ensuring the global exponential stability in the mean square of the considered system are derived, by using of Lyapunov method, inequality techniques and stochastic analysis. Notice that, these obtained results show that, the stability conditions on system (1) are independent of the magnitude of delays, but are dependent of the magnitude of noise and diffusion effect. Therefore, in the above content, globally exponential stability in the mean square holds, regardless of system delays. The proposed results extend those in the earlier literature and are easier to verify. Our methods are also suitable to the more general stochastic reaction–diffusion neural networks with time delays.