1 Introduction

Our proposed model is to use the statistical-based probabilistic neural network (PNN) as our choice of neural network for pattern classification purposes. The PNN was introduced in 1990 by Specht [1] and puts the statistical kernel estimator [2] into the framework of radial basis function networks [3]. We will use the expectation–maximization (EM) method to train the PNN for the simple fact that it can help cut down the number of neurons in the network. The proposed model can be used for condition-based monitoring, which has garnered more attention nowadays and clearly deserves it because of increased efficiency and reduced time consumption. That is why more focus is given on the creation of a more error tolerant, accurate, and fast diagnosis model.

Expecting random sensor failures that take vibration signals from key locations on a piece of machinery is very sensible, because no machinery can guarantee to work indefinitely without errors occurring. Mishaps do occur and these faulty sensors will no longer provide feedback to the model thus creating input vectors with missing values in them. Simply discarding those incomplete input vectors is not plausible, because it takes time to replace the faulty sensors. Hence, a better solution will be through imputation. The method used to solve missing data problem is the regularized EM method [5]. Regularized EM can also handle rank-deficient datasets, which means the number of features is greater than the available sample size.

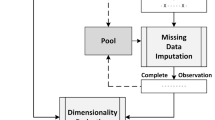
The EM method used to train the network has its perks, but also brings to focus its problems. In general, it is hard to initialize, and the quality of the final solution depends on the quality of the initial solution [4]. Initialization has to be randomly done by the user for the number of clusters required. This is done through trial and error method and it is stochastic. Therefore, to build an autonomous and deterministic neural network, we chose to use Global k-means to help automatically find the optimum number of clusters based on minimizing the clustering error. In an overview, our model uses regularized EM first to impute any missing values if any. Then the complete data set is fed into Global k-means to find out the number of clusters to be used. The result from Global k-means is fed into the EM algorithm, which is used for training the PNN.

In Sect. 2, PNN is briefly discussed followed by Sect. 3, where the E-step and M-step of the EM method is showed together with the flaws of EM. In Sect. 4, two methods of cluster determination, which is Global k-means and its variant, fast Global k-means, will be discussed in brief. Then, in Sect. 5, regularized EM brings about the solution for the data imputation problem. Experiments on medical benchmark and Westland data sets are presented in Sect. 6 to compare results between Global k-means and random initialization, Global k-means and fast Global k-means, tests on data imputation using regularized EM and finally some tests on Westland dataset. Section 7 will conclude the paper (Fig. 1).

Fig. 1
figure 1

Proposed model—PNN with data imputation capabilities

Full size image

2 Probabilistic neural network

Probabilistic neural network was introduced by Donald Specht in a series of two papers, namely “Probabilistic neural networks for classification, mapping, or associative memory” in 1988 [6] and “Probabilistic neural networks” in 1990 [1]. This statistical-based neural network that uses Bayes theory and Parzen estimators can be utilized to solve pattern classification problems. The basic idea behind Bayes theory is that it will make use of relative likelihood of events and also a priori information, which in our case would be interclass mixing coefficients. As for Parzen estimators, it is a classical probability density function estimator.

Let us assume the data set, X, will be partitioned into K number of subsets (classes), where X = X 1 ∪ X 2 ∪ … ∪ X K and each subset has N k number of sample size, and it would also mean ∑ K k=1 N k  = N, where N is the size of our sample. This four-layered, feed forward, supervised learning neural network as shown in Fig. 2 reserves the first layer as input neurons and accepts d-dimensional input vectors. Each dimension of the input vector is passed to its corresponding input neuron.

Fig. 2
figure 2

Probabilistic neural network

Full size image

As for the second layer of the PNN, Gaussian basis functions (GBFs) are estimated here. It takes the form of

$$ \rho_{m,k} \left( X \right) = \frac{1}{{\left( {2\Uppi \sigma_{m,k}^{2} } \right)^{{\frac{d}{2}}} }}\exp - \left( {\frac{{\left\| {X - \upsilon_{m,k} } \right\|^{2} }}{{2\sigma_{m,k}^{2} }}} \right) $$
(1)

and this specifies the GBF for mth cluster in the kth class, where σ 2 m,k is the variance, υ m,k is the cluster centroid, and d represents the dimension of the input vector. The third layer of the PNN is where the class conditional probability density function is estimated,

$$ f_{k} (X) = \sum\nolimits_{m = 1}^{{M_{k} }} {\beta_{m,k} \rho_{m,k} (X)} , $$
(2)

where M k is the number of clusters for class k and β m,k is the intraclass mixing coefficient,

$$ \sum\nolimits_{m = 1}^{{M_{k} }} {\beta_{m,k} = 1} . $$
(3)

On top of all that, we have a fourth layer, which will be used as a decision layer to choose the class with the highest probability. An interclass mixing coefficient, α k , will be used to increase the accuracy of the result. With α k being a value obtained by the inverse of its sample size, N k , it is clear that the summation of α k shall be bound to 1. o k will depict the probability of the input vector being class k,

$$ o_{k} = \alpha_{k} f_{k} (x) , $$
(4)
$$ {\text{decision}} = \arg (\max O_{k} ). $$
(5)

The advantage PNN has is that it interprets the network’s structure in probability density functions, due to its statistical nature. On the downside, PNN’s number of nodes can be extremely huge if the training dataset is large. This is because one neuron is created for each training pattern. This makes the PNN infeasible for large datasets. Therefore, another training method that does not commit every training pattern as a node in the neural network should be used. For this purpose, we have selected the EM method.

3 Learning algorithm

In the learning algorithm, two parameters of the model are adjusted to obtain better results in classification. In each E-step and M-step, the mean and variance parameter is constantly tweaked until the log posterior likelihood function has minimal change. To calculate the new mean and variance values, EM deploys a weight parameter, which is also adjusted after each step.

3.1 Expectation–maximization

Expectation–maximization (EM) [7] by Dempster et al. in 1977 is a powerful iterative procedure, which converges to an ML estimate. Basically, the EM consists of two steps, namely the E-step and the M-step. Both steps will be iterated until the change in the log posterior likelihood function is minimal,

$$ \log L_{f} = \sum\nolimits_{k = 1}^{K} {\log f_{k} } (X). $$
(6)

In the E-step, the missing/hidden data is estimated, given the observed data and the current parameter estimate. It will use the PDF estimated in the second layer of the PNN as defined in (1) together with intraclass mixing coefficient to estimate the weight parameter,

$$ W_{m,k} = \frac{{\beta_{m,k} \rho_{m,k} (X)}}{{\sum\nolimits_{i = 1}^{{M_{k} }} {\beta_{i,k} \rho_{i,k} (X)} }}. $$
(7)

Next comes the M-step that uses the data estimated in the E-step and the weight parameter, W m,k , to form a likelihood function and determine the ML estimate of the parameter. It calculates the new values for the cluster centroid, υ m,k , the variance, σ 2 m,k , and the intraclass mixing coefficients, β m,k , using the weight calculated from the E-step. The equations for the parameter updates are as given below:

$$ \upsilon_{m,k} = \frac{{\sum\nolimits_{n = 1}^{{N_{k} }} {W_{m,k} (X)X} }}{{\sum\nolimits_{n = 1}^{{N_{k} }} {W_{m,k} (X)} }}, $$
(8)
$$ \sigma_{m,k}^{2} = \frac{{\sum\nolimits_{n = 1}^{{N_{k} }} {W_{m,k} (X)\left\| {X - \upsilon_{m,k} } \right\|^{2} } }}{{d\sum\nolimits_{n = 1}^{{N_{k} }} {W{}_{m,k}} (X)}}, $$
(9)
$$ \beta_{m,k} = \frac{1}{{N_{k} }}\sum\nolimits_{n = 1}^{{N_{k} }} {W_{m,k} (X)} . $$
(10)

The EM algorithm is guaranteed to converge to an ML estimate [8, 9] and the convergence rate of the EM algorithm is usually quite fast [10]. EM also produces lesser neurons than the traditional PNN by Donald Specht. Another advantage is that it does not require computations of gradients or Hessians, thus reducing the computational complexity of the network. Though EM is a good choice for a training method, it is not autonomous. This is attributed to the fact that EM requires initialization in the form of a number of clusters to be expected of the neural network. The initialization quality severely affects the final outcome of the network. To aid in this matter, Global k-means will be chosen as a precursor to find out how many clusters are needed for a certain dataset in view, before being fed into the EM-trained PNN.

4 Cluster initialization

Part of the problems faced by the model is determining the number of clusters needed prior to learning. This is usually done by the user through trial and error. Also the usage of random initialization does not provide deterministic results. Global k-means and Fast Global k-means can overcome these problems.

4.1 Global k-means

Introduced by Likas et al. in the paper entitled “The Global k-means clustering algorithm” in 2003, the concept of clustering with Global k-means is partitioning the given dataset into M clusters so that a clustering criterion is optimized. The common clustering criterion is the sum of squared Euclidean distances between each data point and the cluster centroid:

$$ E(M_{1} , \ldots ,M_{k} ) = \sum\nolimits_{i = 1}^{{N_{k} }} {\sum\nolimits_{m = 1}^{{M_{k} }} {\left\| {X_{i} - \upsilon_{m} } \right\|^{2} } } . $$
(11)

Global k-means deploy the k-means algorithm to find locally optimal solutions by trying to keep the clustering error to the minimum. This algorithm starts by placing the cluster center arbitrarily and continues by moving at each step the cluster center with the aim to minimize the clustering error. The down side to this algorithm is that it is sensitive to the initial position of the cluster centers. To overcome this, k-means can be scheduled to run several times and each time with a different starting point. The gist of Global k-means is that instead of trying to find all cluster centers at once, it proceeds in an incremental way. Incremental in the sense that one cluster center is found at a time.

Assume a K-cluster problem is to be solved; the algorithm starts by solving for a one-cluster problem and the placement of the cluster center in this instance would equal the centroid of the given dataset. The next step would be to add another cluster at its optimal solution given the first cluster center has already been found. To do this, N executions of k-means algorithm will be executed with the initial positions of the cluster centers being the first cluster, which was found when solving for a one-clustering problem and the second cluster’s starting position will be at x n where 1 ≤ n ≤ N. The final answer for a two-cluster problem will be the best solution from the N executions of k-means algorithm. Let (c 1(k),…,c k (k)) denote the final solution for a k-clustering problem. We solve this through iteration, which means one-clustering problem then two-clustering problem until (k − 1) clustering problem. The solution of k-clustering problem can be solved by performing N executions of k-means algorithm with starting positions of (c 1(k − 1),…,c (k−1)(k − 1),X n ). A simple pseudo code of it will be

With the final solution, (c 1(k),…,c k (k)), Global k-means has actually found solutions of all k-cluster problem where k = 1,…,K without needing any further computations. This assumption seems very natural: we expect that the solution of the k-clustering problem to be reachable (through local search) from the solution of (k − 1)-clustering problem, once the additional center is placed at an appropriate position within the data set [11]. Alas, the downside is that the computational time of Global k-means can be rather long.

4.2 Fast Global k-means

Using this method will help reduce the computational time taken by the Global k-means algorithm. The core difference is that fast Global k-means does not perform N executions of k-means algorithm with starting positions of (c 1(k − 1),…,c (k−1)(k − 1),X n ). Instead, what the algorithm does is to calculate the upper bound, E n  ≤ E − b n , on the resulting error, E n , for every instances of X n . We define E as the error value of (k − 1)-clustering problem and b n as

$$ b_{n} = \sum\nolimits_{j = 1}^{N} {\max (d_{k - 1}^{j} - \left\| {x_{n} - x_{j} } \right\|^{2} ,0)} $$
(12)

and d j k−1 is the squared Euclidean distance between x j and the cluster centroid, which it belongs to. After obtaining the value of b n , select the x i that maximizes b n and make it the new cluster centroid that will be added. This is because by maximizing the value of b n , we are at the same time minimizing the E n value, which as stated is our error. The new cluster centroid, x n , will allocate all data points, which are having a smaller squared Euclidean distance from x n rather than from their previous cluster centroid, d j k−1 . In view of that, the reduced clustering error for all those reassigned data points is d j k−1  − ‖x n  − x j ‖2. Then we execute the k-means algorithm to find the solution for k-clustering problem. Since the k-means algorithm is guaranteed to decrease the clustering error at each step, E − b n upper bounds the error measure that will be obtained if we run the algorithm until convergence after inserting the new center at x n (this is the error measure used in the Global k-means algorithm) [11].

5 Data imputation for missing features

As discussed earlier, faulty sensors do happen and merely discarding input vectors can affect the condition-based monitoring. Therefore, a plausible solution is to impute the missing values and continue on with the classification using the imputed input vector.

5.1 Regularized EM

With an estimated mean and covariance matrix, the missing values in a dataset can be imputed with their conditional expectation values given the available values in the dataset. The regularized EM algorithm’s regularized regression parameters will be computed using a method called ridge regression or also known as Tikhonov regularization. In ridge regression, a continuous regularization parameter controls the degree of regularization imposed on the regression coefficients [5]. This regularization parameter is determined by generalized crossvalidation (GCV) so that it minimizes the expected mean-squared error of the imputed values. In the conventional EM algorithm, it is assumed that the missing values in the dataset are missing at random and this assumption also carries to the regularized EM algorithm.

We will briefly discuss the conventional EM algorithm first. In the execution of the EM, the estimated mean and covariance matrix are iterated in three steps. Firstly, for each record with missing values, the regression parameters of the variables with missing values on the variables with available values are computed from the estimates of the mean and of the covariance matrix. Secondly, the missing values in a record are filled in with their conditional expectation values given the available values and the estimate of the mean and of the covariance matrix, the conditional expectation values being the product of the available values and the estimated regression coefficients. Thirdly, the mean and the covariance matrix are re-estimated, the mean as the sample mean of the completed dataset and the covariance matrix as the sum of the sample covariance matrix of the completed dataset and the contributions of the conditional covariance matrices of the imputation errors in the records with imputed values [5, 12]. Let us say we have a dataset X, where it contains n number of records and p number of variables. The conventional EM assumes that n exceeds p so that sample covariance is positive definite. Using the incomplete dataset, the estimates for mean, μ, and the covariance matrix, Σ, will be calculated. For a given record x = X i with missing values, let x a consists of p a variables for which the values are available in the given record and x m consist of the remaining p m variables for which the values are missing. Let μ be split into μ a and μ m , where μ a is the mean value of the variables for which the values are available in the given record and μ m is the mean value of the variables for which the values are missing. For each record with missing values, x = X i , where i = 1,…,n, the relationship between p a and p m is modeled by linear regression model

$$ x_{m} = \mu_{m} + \left( {x_{a} - \mu_{a} } \right){\text{B}} + e, $$
(13)

where B is the matrix of regression coefficient and the residual e is random vector with mean zero and unknown covariance matrix C. Assume μ t and Σt represent the mean and covariance matrix for the tth iteration. Σi contains Σ aa and Σ mm , where Σ aa is the covariance of the variables for which the values are available in a given record and Σ mm is the covariance of the variables for which the values are missing. With the estimated cross covariance, Σ am  = Σ T ma , the regression coefficient is

$$ B = \Upsigma_{aa}^{ - 1} \Upsigma_{am} . $$
(14)

By substituting B, an estimate of the residual covariance matrix is

$$ C = \Upsigma_{mm} - \Upsigma_{ma} \Upsigma_{aa}^{ - 1} \Upsigma_{am} . $$
(15)

After the missing values in all records are imputed, the new estimate of the mean of the records would be

$$ \mu^{i + 1} = \frac{1}{n}\sum\limits_{i = 1}^{n} {X_{i} .} $$
(16)

The new estimate of the covariance matrix would in turn be

$$ \Upsigma^{i + 1} = \frac{1}{{\tilde{n}}}\sum\limits_{i = 1}^{n} {(S_{i}^{t} - (\mu^{t + 1} )^{T} \mu^{t + 1} ),} $$
(17)

where S t i is the conditional expectation, which comprises three parts x T a x a , x T a x m , and x T m x m  + C. \( \tilde{n} \) is the number of degrees of freedom of the sample covariance matrix of the completed dataset. The iterations of the EM are stopped when the estimates of μ t, Σt, and the imputed values x m stop changing appreciably. Regularized EM is similar to conventional EM, just that it replaces the Σ −1 aa with (Σ aa  + h 2 D)−1, where D is diagonal matrix consisting of diagonal elements from the covariance matrix, Σ aa , and h is the regularization parameter. The regularization parameter is determined by minimizing the generalized crossvalidation function

$$ G(h) = \frac{{\tilde{n}^{2} }}{{T^{2} (h)}}{\text{tr}}C_{h} , $$
(18)

where

$$ T(h) = {\text{tr}}(I - X_{a} X_{a}^{\tau } ), $$
(19)
$$ X_{a}^{\tau } = (X_{a}^{T} X_{a} + \tilde{n}h^{2} I)^{ - 1} X_{a}^{T} , $$
(20)

in which X τ a is the pseudoinverse of the data matrix X a .

6 Experimental results

6.1 General description

First, a test is conducted using EM-based PNN with two types of initialization, random and Global k-means. The medical benchmark datasets together with the Iris dataset was used for this purpose. Then a test between EM-based PNN with initialization from Global k-means and fast Global k-means was done to observe the improved computational time and also the difference in classification performance. The medical benchmark datasets were used. This was followed by imputing datasets with missing values using regularized EM. The Iris and Pima datasets were used. Missing values were simulated from 0 to 50% missing values and were done completely random. Next were tests done on the Westland vibration dataset. Firstly, classification of Westland using EM-based PNN with Global k-means was done. Then, Westland was tested for data imputation for missing values from 0 to 50% using regularized EM.

6.2 Comparative tests between randomly initialized and Global k-means

A comparative study was done on the effects of using Global k-means to initialize the values of the parameters in EM and without that initialization. The Iris dataset [13] and the medical datasets, consisting of data from cancer, dermatology, hepato, heart, and Pima were used.

The Iris dataset consists of 150 samples and four input features. It was tested on the PNN trained by EM algorithm with randomly initialized cluster centroids and EM with Global k-means initialization. Both the methods were executed in heteroscedastic PNN and in homoscedastic PNN. A tenfold validation was used. Iris dataset was set as a 10-clustering problem for Global k-means and then the number of cluster centroids was returned based on minimizing the squared Euclidean distance between each data point in a cluster and its centroid. This was then used to set the cluster parameter for random initialization to help it get a better result and assume under similar conditions as Global k-means.

The mean accuracy of the homoscedastic with random initialization is 96.29%, while the heteroscedastic version reports 95.36% accuracy, but in both cases, they were outdone by the accuracy of the EM with Global k-means initialization, whose mean accuracy was 97.86 and 95.71%, respectively, for homoscedastic and heteroscedastic PNN. Although random initialization was fed with the number of clusters needed, by Global k-means, Global k-means still had the better classification rate (Table 1).

Table 1 Correct classification rate for Iris dataset
Full size table

Cancer dataset contains 569 samples with a 30 dimension size, dermatology dataset contains 358 samples with a 34 dimension size, and hepato dataset contains 536 samples with a nine dimension size. Heart dataset contains 270 samples with a 13 dimension size and two output labels, which are “0” for absence of heart disease and “1” for presence of heart disease. Pima data set is available from machines learning database at UCI [14]. Pima dataset contains 768 samples with an eight dimension size and has two classes, which are diabetes-positive and diabetes-negative. A tenfold validation was employed. When tested using all the above datasets, Global k-means was set with a higher than required clustering problem to solve and in every case it returns a lower number of clusters, which is optimum to the clustering criterion. This was then fed into the EM with random initialization.

The medical datasets showed improved performance by the EM with Global k-means initialization in both homoscedastic and heteroscedastic PNN over the results using random initialization (Tables 2, 3). Although in practice both were fed with the same number of clusters required, in most cases of the datasets, even the maximum accuracy from the EM with random initialization is not higher than the mean of EM with initialization from Global k-means.

Table 2 Correct classification rates for the medical datasets by using homoscedastic PNN
Full size table
Table 3 Correct classification rates for the medical datasets by using heteroscedastic PNN
Full size table

6.3 Comparative tests between Global k-means and fast Global k-means

To minimize the computational time without sacrificing the classification performance, we opted for the fast Global k-means method. A comparison between Global k-means and fast Global k-means using both heteroscedastic and homoscedastic EM-trained PNNs is shown in the following. Tests were conducted on the medical datasets and using a tenfold validation. Global k-means and fast Global k-means were set to solve a higher clustering problem than required.

As the results in Table 4 and Fig. 3 shows, fast Global k-means provide a comparable accuracy for correct classification rate on the benchmark medical datasets. On top of that, it still manages to accomplish its purpose, which was to cut down the computational time, and Table 5 clearly supports this matter.

Table 4 Comparison of correct classification rates
Full size table
Fig. 3
figure 3

Comparison of correct classification rates

Full size image
Table 5 Comparison of execution times in seconds
Full size table

6.4 Tests on data imputation

Next, we compare results of missing data imputation of varying percentage with the original completed dataset using Iris (Table 6; Fig. 4) and Pima datasets (Table 7; Fig. 5). A tenfold validation was employed on heteroscedastic and homoscedastic PNN using EM and Global k-means.

Table 6 Correct classification rates for Iris
Full size table
Fig. 4
figure 4

Classification results for Iris dataset

Full size image
Table 7 Correct classification rate for Pima
Full size table
Fig. 5
figure 5

Classification results for Pima dataset

Full size image

The method imputes the missing values that were randomly created from the completed Iris and Pima datasets. Both datasets were created with missing value percentages from 10 to 50%. By using the proposed method to preprocess the data before being accepted into the neural network for training, we can see that the performance degradation is acceptable.

6.5 Westland vibration dataset

A real world case study was done to test the EM-trained PNN with initialization parameters obtained from the execution of Global k-means using the popular benchmark dataset Westland [15]. This dataset consists of vibration time-series data, which is gathered from an aft main power transmission of a US Navy CH-46E helicopter by placing eight accelerometers at the known fault-sensitive locations of the helicopter gearbox. The data was recorded for various faults including a no-defect case (Table 8).

Table 8 Westland helicopter gearbox data description
Full size table

This dataset consists of nine torque levels, but for our experiment purposes, only the 100% torque level on Sensors 1–4 is used. As the number of features from this dataset is quite substantial, feature reduction was needed. Wavelet packet feature extraction [16] was used to reduce the dimension of the input vectors without sacrificing too much of the classification performance.

Wavelet packets, a generalization of wavelet bases, are alternative bases that are formed by taking linear combinations of the usual wavelet functions [17, 18]. These bases inherit properties such as orthonormality and time–frequency localization from their corresponding wavelet functions [16]. Wavelet packet functions can be defined as

$$ W_{j,k}^{n} (t) = 2^{j/2} W^{n} (2^{j} t - k), $$
(21)

where n is the modulation or oscillation parameter, j is the index scale, and k is the translation.

For a function f, the wavelet packet coefficients can be calculated as given below

$$ w_{j,n,k} = \left\langle {f,W_{j,k}^{n} } \right\rangle = \int {f(t)W_{j,k}^{n} (t){\text{d}}t} . $$
(22)

Decomposition of the vibration signal is done using wavelet packet transform (WPT) to extract out the time–frequency-dependant information. For each vibration signal segment, full decomposition is done up to the seventh level. This will produce a group of 2r+1 − 2 sets of coefficients, where r is the resolution level. Therefore, in our case, it shall produce a group of 254 sets of coefficients, where each set corresponds to a wavelet packet node. For the coefficients of every wavelet packet node, the wavelet packet node energy e j,n is computed and this acts as the extracted feature:

$$ e_{j,n} = \sum\limits_{k} {w_{j,n,k}^{2} } . $$
(23)

Then apply a statistical-based feature selection criterion to help identify the features that provide the most discrimination amongst the classes of Westland. The Fisher’s criterion was used [19]. As a result, the number of features for Westland was reduced to eight and this modified dataset was fed into our model to test for data imputation using regularized EM. A tenfold validation was used.

The performance obtained by the proposed system on the eight-feature, 776-sample Westland dataset strengthens the positive performance that was marked in testing done on medical benchmark datasets. Westland was also tested for data imputation with missing values ranging from 0 to 50%, but only using Sensors 1–4 (Tables 9, 10, 11, 12, 13; Figs. 6, 7, 8, 9). Tests were conducted on heteroscedastic and homoscedastic PNNs using tenfold validation. Missing values were randomly produced.

Table 9 Correct classification rates for Westland using homoscedastic and heteroscedastic PNNs
Full size table
Table 10 Correct classification rates for Sensor 1
Full size table
Table 11 Correct classification rates for Sensor 2
Full size table
Table 12 Correct classification rates for Sensor 3
Full size table
Table 13 Correct classification rates for Sensor 4
Full size table
Fig. 6
figure 6

Correct classification rates for Sensor 1

Full size image
Fig. 7
figure 7

Correct classification rates for Sensor 2

Full size image
Fig. 8
figure 8

Correct classification rates for Sensor 3

Full size image
Fig. 9
figure 9

Correct classification rates for Sensor 4

Full size image

Much like the imputation tests done on Iris and Pima datasets, the degradation of classification performance for Sensors 1–4 of Westland dataset is acceptable. The loss of classification rate does not plummet when dealing with higher missing value percentages. This shows that using regularized EM as a means of data imputation in cases, where discarding datasets with missing values is too costly, is a viable option to implement into our model.

7 Conclusions

Though using EM to train the PNN model is an excellent method, it can still be improved. To make our model autonomous, the Global k-means algorithm was used prior to EM to find the number of clusters based on minimizing the clustering error. Comparative results indicated that even when set with the same number of clusters as Global k-means, EM with random initialization still had a poorer performance. This shows that EM with Global k-means initialization makes a good autonomous and deterministic PNN. We further tried to improve the model by doing comparative tests between fast Global k-means and Global k-means to observe the correct classification rates and the computational times. The results were favorable to fast Global k-means as it managed to provide relatively close accuracies but with much improved computational times. Regularized EM was then used as a preprocessing step to overcome the missing data problem that can simply be caused by faulty sensors. Results for both Iris and Pima showed acceptable degradation of classification rate for 0% up until 50% missing data. Then, implementation of Global k-means and regularized EM was further tested with the reduced eight-feature version of Westland dataset. It was done on data from Sensors 1–4 and the results from the tests were promising. Regularized EM imbues flexibility as the proposed model is able to handle missing data through imputation and not just discarding imperfect input vectors. The model presented in this paper is a suitable diagnosis model that can be used in the business industry to monitor the condition of assets such as machines and to classify them into their fault modes based on the input vectors received from sensors placed on the machines.