Efficient vector quantization using genetic algorithm

Abstract

This paper proposes a new codebook generation algorithm for image data compression using a combined scheme of principal component analysis (PCA) and genetic algorithm (GA). The combined scheme makes full use of the near global optimal searching ability of GA and the computation complexity reduction of PCA to compute the codebook. The experimental results show that our algorithm outperforms the popular LBG algorithm in terms of computational efficiency and image compression performance.

1 Introduction

Genetic algorithm (GA) [1, 2] is a stochastic search method for solving optimization problems. It is so named as the scheme is based on the mechanics of natural selection and genetics. Research interests in heuristic search algorithms with underpinnings in natural and physical processes began in the 1970s, when Holland [3] first proposed GA. GA generates a sequence of populations using a selection mechanism and applies crossover and mutation as search mechanisms. GA has demonstrated considerable success in providing good solutions to many complex optimization problems [4], such as capital budgeting, vehicle routing problem, critical path problem, parallel machine scheduling, redundancy optimization, open inventory network etc. The advantage of GA is due to its ability to obtain a global optimal solution fairly in a multidimensional search landscape, which has several locally optimal solutions as well.

GA is a powerful tool for the codebook generation of vector quantization in image compression, since the codebook generation process is in essence, a multidimensional optimization problem. With the growth of e-commerce, there are increasing needs for the transmission of multimedia data through the wired and wireless networks to cater for applications such as digital broadcasting and video conferencing. The demand for a high communication bandwidth always exceeds the capacity of growth of network infrastructure. In this connection, techniques that aim to reduce communication bandwidth or storage requirements for multimedia data have always been an important research area. Image compression is a technique that aims to reduce bit-rates of transmited digital images across channels with a limited capacity.

There are two types of image compression techniques, namely, lossless and lossy image compression [5]. Lossless compression removes as much redundancy from the source image as possible, and guarantees that the original information will be perfectly recovered from the compressed data. Despite this excellent feature, the compression ratio has a relatively low range from two to ten. This technique is useful for applications which tolerate no loss in information such as medical image transmissions. For lossy compression, a much higher compression ratio can be achieved by sacrificing some accuracy of the recovered image. The reconstructed image contains distortion, which may or may not be visually apparent. Unlike lossless technologies, a relatively high compression ratio can be achieved. In fact, many lossy compression technologies can provide very good recognizable images with compression ratios of 30 or higher. Among the various kinds of lossy compression methods, vector quantization (VQ) is one of the most popular and widely used method.

Vector quantization is basically a clustering method, grouping similar vectors (blocks) into one class. The vectors are obtained from image data by extracting non-overlapping square blocks of size n × n (such as 4×4). The pixels in each block are arranged in a line-by-line order. VQ can be considered as mapping of features. It maps input vectors into a set of codewords. Similar vectors are mapped to the same class or codeword in the codebook. VQ provides many attractive features for image and speech coding applications with high compression ratios [6–10]. One important feature of VQ is the ease of control of the compression ratio and amount of loss through the variation of number of bits used for quantization. Another important advantage of VQ image compression is its fast decompression by table lookup technologies.

The process of image compression using VQ can be divided into three phases: codebook generation, encoding, and decoding. In the codebook generation stage, a set of precomputed codewords is generated based on a set of training image vectors. The main objective is to find the most representative set of codewords that will produce the least distorted image after compression. To compress the image, the encoder generates the address of the codeword, which is closest to the input image vector. To decompress, the decoder uses this address to regenerate the image vector. Codebook generation is the key factor that will affect the performance of the whole image compression process. Research efforts in codebook design have been concentrated in two directions:

• To generate a representative codebook.

• To reduce the computational complexity of codebook generation.

Many algorithms for optimal codebook design have been proposed [6, 11–17]. Among them, the most popular one was developed by Linde et al. [6] and is referred to as the LBG algorithm. It is basically a direct iterative process that generates a set of representative codewords which minimizes the overall distortion of the training vectors. This codeword generation process is computation intensive and the distortion rate is affected by the selection of the initial codewords and may end up in suboptimal codebooks. Let the number of training vectors be M and the number of codewords be N, the codebook design problem can be formulated as a classification problem of dividing M training vectors into N clusters which is a NP-hard problem. For large M and N, a traditional search algorithm such as the LBG method can hardly find the global optimal classification.

GA [4, 18] is an efficient and near global optimum search method based on the ideas of natural selection and genetics. During the search process, it can automatically achieve and accumulate knowledge about the search space and adaptively control the search process to approach the global optimal solution. However, in most cases, the convergence speed of GA is slow because of its poor local optimum search ability. GA has been applied to codebook generation in recent years. Delport et al. [19] proposed a partition-based GA codebook design algorithm, whose coding string is the codebook indices of the training data. However, previous GA-based codebook design algorithms have the shortcoming of long search-time. Chang et al. [20] proposed a fast search algorithm using principal component analysis (PCA) in the VQ encoding phase, which can significantly speed up the codebook search. Wu [21] also proposed, using PCA and dynamic programming algorithm for designing codebook, to reduce the computational complexity.

In our research, we propose a scheme that combines and makes use of the virtues of GA and PCA for the efficient generation of codebooks with optimal image compression performance. GA can adaptively search for a global optimal solution while the PCA algorithm can reduce the computational complexity. The scheme starts by sorting the training vectors using PCA to reduce the computational complexity, and then makes full use of the near global optimal searching ability of GA to compute the codebook. The rest of the paper is organized as follows. In Sect. 2, we describe the fundamental concepts of VQ, PCA, and GA, which are the basis of our algorithm. The combined scheme of VQ using PCA and GA is presented in Sect. 3. The experimental results are presented in Sect. 4. Finally, we conclude the paper in Sect. 5.

2 The VQ, PCA and GA algorithms

2.1 Vector quantization

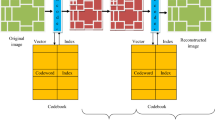
In the codebook generation phase, some representative images are selected as training images. These training images are decomposed into a set of training vectors (or blocks). The dimensionality of each training vector is pre-defined as k. The VQ algorithm uses these training vectors to generate a codebook. The VQ process is depicted in Fig. 1.

Fig. 1

Vector quantization

Vector quantization is a mapping Q of a k-dimensional Euclidean space $\Re ^k$ into a finite subset C of $\Re ^k ,$ where C={c₁,...,c _N } is the codebook with size N and each codeword c _i =(c_i1 ,... ,c _ik ) in C is k-dimensional. The quantizer is completely described by the codebook C together with the partitioned set consisting of subspaces of $\Re ^k ,$ S={s₁,...,s _N }, and the mapping function:

$$ Q(X) = c_i \quad {\text{if}}\;X \in s_i . $$

(1)

The elements of the partitioned set S satisfy the conditions $\cup _{i = 1}^N s_i = \Re ^k ,$ and $s_i \cap s_j = \emptyset$ if i≠ j.

To encode an image, the VQ encoder first divides the image into a set of vectors according to the pre-defined dimension. Then, an appropriate codeword c _i is selected for each vector X=(x₁,...,x _k ) such that the distortion between X and c _i is the smallest. If the squared Euclidean distortion measure is used, the output of the encoder is the index i of the codeword c _i such that

$$ i = \arg \,\mathop {\min }\limits_p \sum\limits_{j = 1}^k {\left( {x_j - c_{pj} } \right)^2 .} $$

(2)

Codebook generation is the key problem in VQ in that the codebook generated has a profound effect on the image compression performance. The image compression performance is measured both in terms of the image compression ratio and the degree of distortion. In VQ, a high image compression ratio is achieved by choosing a codebook with relatively fewer codewords than all possible image vectors. To minimize the degree of distortion of the compressed image, it is necessary to generate the most representative codewords based on the large amount of training vectors. To this end, seeking an algorithm that is able to produce an optimal codebook with a suitable number of codewords is the central topic of many studies in VQ. Among the proposed algorithms for optimal codebook design, the LBG algorithm [6] is the most popular one and is always used by researchers in VQ as the “standard” codebook design algorithm for benchmarking. The LBG algorithm is described as follows:

• Step 1. Initialization. Given

  N :

  number of codebook levels

  ɛ≥ 0:

  distortion threshold

  A ₀ :

  an initial N-level codebook

  S={X _j : j=1,...,M}:

  a set of training vectors of dimension k

  m :

  =

  0

  D ₋₁ :

  =∞

• Step 2. Given A _m ={c _i : i=1,...,N}. Find the partition p(A _m )={s _i : i=1,...,N} of the training vectors sequence such that X _j ∈s _i if d(X _j ,c _i )≤ d(X _j ,c _p ) for all p. The distortion function is defined by

  $$ d\left( {X_j ,c} \right) = \sum\limits_{i = 1}^k {\left( {x_{ji} - c_i } \right)^2 .} $$

• Step 3. Compute the total distortion of all training vectors

  $$ D_m = \sum\limits_{j = 1}^M {\mathop {\min }\limits_{c \in A_m } d\left( {X_j ,c} \right).} $$

  If ((D_{m -1}−D _m )/D _m ) ≤ ɛ, halt with A _m being the final codebook.

• Step 4. Compute A_m+1={c _i : i=1,...,N} where c _i is the centroid of the training vectors belonging to the partition s _i . Replace m by m+1 and go to step 1.

As we can see, there are two shortcomings of the LBG codebook generation algorithm:

• 1. Inefficiency due to the heavy computations in the full codeword search in step 2 and the calculation of the distortion function D _m in step 3.

• 2. The result is affected by the selection of the initial codebook A₀, which often leads to the generation of a suboptimal final codebook.

In the following subsection, we will describe the PCA that can be used to avoid the heavy computations in the full codeword search and the distortion function which are based on the Euclidean distances.

2.2 Principal component analysis

The basic idea of PCA is to project vectors in a high dimensional Euclidean space into a subspace where the variance among the original vectors can be maximally retained. The projected subspace of dimension one is called the principal axis of the vectors.

Given a set of M vectors, S={X _i : i=1,...,M} and each vector X _i =(x_i1,...,x _ik ) is in the k-dimensional Euclidean space. The principal axis of the set of vectors is given by the unit vector

$$ V = \left( {v_1 , \ldots ,v_k } \right), $$

such that the sum of projection of all the M vectors onto V, i.e. $\sum\nolimits_{i = 1}^M {X_i^{\text{T}} V}$ is the maximum among all possible V in ℜ^k.

The algorithm to find the principal axis of the M vectors {X _i : i=1,...,M} is stated as follows [22]:

• Step 1. Construct a matrix A=(x _ij )_M*k.

• Step 2. Construct the normalized matrix $\hat A = \left( {\hat x_{ij} } \right)_{M*k} ,$ where

  $$ \hat x_{ij} = \frac{{x_{ij} }} {{\sqrt {\sum\nolimits_{j = 1}^k {x_{ij}^2 } } }}. $$

• Step 3. Compute the covariance matrix $\hat A^{\text{T}} \hat A.$

• Step 4. Compute the largest eigenvalue λ_max and the corresponding eigenvector V_max of the covariance matrix $\hat A^{\text{T}} \hat A.$

V_max is the principal axis of the M vectors. The use of PCA and the principal axis of the training vectors to reduce the computations for Euclidean distances in codebook generation will be shown in the next section.

2.3 Genetic algorithm

It has been shown that the LBG algorithm will result in suboptimal codebook generation. This is due to the termination of the algorithmic steps when the codebook falls into a local optimal solution instead of the global optimal solution. GA [4, 18] is a stochastic search method for optimization problems based on the mechanics of natural selection and natural genetics. GA has demonstrated its success in providing good solutions to many complex optimization problems. The advantage of GA is its ability to obtain the global optimal solution, hence it is a powerful technique that can be applied in codebook design.

GA starts with an initial set of random-generated chromosomes called a population where each chromosome encodes a solution of an optimization problem. All chromosomes are evaluated by an evaluation function which is some measure of fitness. A selection process based on the fitness values will form a new population. A cycle from one population to the next is called a generation. In each new generation, all chromosomes will be updated by the crossover and mutation operations. Then, the selection process selects chromosomes to form a new population. After performing a given number of cycles, or when other termination criteria are satisfied, we denote the best chromosome as a solution, which is regarded as the optimal solution of the optimization problem. In our algorithm, we use GA to compute the near global optimal classification of the sorted training vectors, which are the results of PCA.

3 The new codebook design algorithm

It has been shown that one of the shortcomings of the LBG algorithm is the heavy Euclidean distance computation in the training vectors partition step and the total distortion function calculation step. To avoid these heavy Euclidean distance computations, the optimization of the N-partition of the M training vectors is done by cutting against the principal axis of the training vectors set S={X _i : i=1,...,M}. The principal axis V is obtained by the PCA algorithm. Then, all the M training vectors are sorted by their projections on V, i.e establishing the order that

$$ X_i \leqslant X_j \Leftrightarrow X_i^{\text{T}} V \leqslant X_j^{\text{T}} V. $$

This constitutes a mapping R : S → {1,...,M}, with R(X)=i means the projected value X^′TV′ ranks i in the sorted list of the total M projections. Now, we define a finite set

$$ P_M^{(N - 1)} \equiv \left\{ {p|0 < p_1 < \ldots < p_{N - 1} < M} \right\} \subset \aleph ^{N - 1} , $$

where ℵ is the set of all natural numbers. Then, any p∈P ^(N-1) _M corresponds to a N-partition of the training vector set $S(0,M] = \left\{ {X\left| {0 < R(X) \leqslant M} \right.} \right\}$ into subsets

$$ S\left( {p_{i - 1,} p_i } \right] = \left\{ {X|p_{i - 1} < R(X) \leq p_i } \right\},\quad p_0 = 0,{\enspace} p_N = M,{\enspace} 1 \leq i \leq N. $$

This algorithm simplifies the original N-partition of the M training vectors of k-dimension to N parallel cells bounded by N−1 cutting halfplanes normal to the principal axis of S.

The original problem of the codebook design is to find the optimal N-partition of the M training vector set with a minimal total distortion function. With the PCA conversion, this has been simplified to a problem of finding the optimal (N−1)-partition cut against the principal axis. Then, the codewords are the centroids of the vectors corresponding to each partition. Further, we will make use of GA to perform the optimization to avoid suboptimal solutions. The GA algorithm of finding the optimal (N−1)-partition cut is described as follows:

Initialization

To ensure that an optimal solution can be obtained in a reasonable runtime, an initial population consists of a considerable amount of chromosomes ((N−1)-partition cut) is necessary. To start the algorithm, an integer pop_size is defined as the number of chromosomes. From the set P ^N-1 _M , pop_size chromosomes are selected randomly, denoted by $A_1 , \ldots ,A_{pop\_size} .$

Evaluation function

In GA, the selection of chromosomes to reproduce is determined by a probability assigned to each chromosome A _l . This probability is proportional to its fitness relative to other chromosomes in the population, i.e. chromosomes with higher fitness will have more chance to produce offsprings by the selection process. In the context of VQ, the fitness of a chromosome is evaluated by an evaluation function E(A _l ) ,which measures the performance of the codebook derived from that chromosome. This evaluation function, in essence, computes the overall distortion and is defined as:

$$ E\left( {A_l } \right) = \sum\limits_{l \leqslant i \leqslant N} {\sum\limits_{X \in S\left( {p_{i - 1} ,p_i } \right]} {\left\| {X,c_{il} } \right\|_2^2 } } , $$

where c _il is the i^th codeword in the codebook derived from A _l . To reduce the computational complexity, instead of computing the Euclidean distance between all X in the vector set and c _il , we use the following approximation:

$$ E\left( {A_l } \right) = \sum\limits_{l \leqslant i \leqslant N} {\left( {\left\| {X_{p_{i - 1} + 1} ,c_{il} } \right\|_2^2 + \left\| {X_{p_i } ,c_{il} } \right\|_2^2 } \right)} \times \frac{{p_i - p_{i - 1} }} {2}. $$

To obtain an optimal codebook, we need to determine the best classification of the training vector set that it has the least overall distortion. Hence, the fitness function F(A _l ) for selection is defined as the inverse of the evaluation function, i.e. F(A _l ) =1/E(A _l ). Based on the value of the fitness function for each chromosome, the population of chromosomes $A_1 , \ldots ,A_{{\text{pop}}\_{\text{size}}}$ can be rearranged from high fitness to low fitness.

Selection

The selection process is basically a “spinning the roulette wheel” process. The roulette wheel is spun pop_size times and each time a chromosome from the rearranged population $A_1 , \ldots ,A_{pop\_size}$ is selected. As we have stated, the chromosome with a higher fitness should have a higher probability to be selected. This is achieved by the following steps:

• Step 1. Define a ranking function for each chromosome

  $$ {\text{eval}}\left( {A_i } \right) = a\left( {1 - a} \right)^{(i - 1)} ,\quad i = 1, \ldots ,pop\_size, $$

  where a ∈(0,1) is a predefined parameter.

• Step 2. Based on this ranking function, calculate the cumulative probability q _i for each chromosome A _i . q _i is given by

  $$ \begin{aligned} q_0 & = 0, \\ q_i & = \sum\limits_{j = 1}^i {{\text{eval}}\left( {A_j } \right),} \quad i = 1, \ldots ,pop\_size. \\ \end{aligned} $$

• Step 3. Generate a random real number r in $\left( {0,q_{pop\_size} } \right].$

• Step 4. Select the i^th chromosome A _i such that q_i-1 < r ≤ q _i . Repeat step 3 and step 4 until pop_size copies of chromosomes are obtained.

These pop_size copies of selected chromosomes $\hat A_1 , \ldots ,\hat A_{pop\_size}$ are the mother chromosomes for the reproduction of the next generation.

Crossover

The crossover process will produce a new generation of population based on the set of mother chromosomes $\hat A_1 , \ldots ,\hat A_{{\text{pop}}\_{\text{size}}}$ resulting from the selection process. We define P _c ∈[0, 1] as the probability of the crossover. Hence, the expected number of mother chromosomes that will undergo the crossover is P _c *pop_size. To pick the parents for crossover, we perform the following action:

$$ \begin{array}{*{20}c} {{\text{For }}i = 1\;{\text{to}}\;pop\_size} \\ {\quad {\text{generate}}\;{\text{a}}\;{\text{random}}\;{\text{number}}\;r \in \left[ {0,1} \right];} \\ {\quad {\text{if}}\;r < P_c \;{\text{put}}\;\hat A_i \;{\text{in}}\;{\text{a}}\;{\text{parent}}\;{\text{list}}} \\ {\quad {\text{else}}\;{\text{put}}\;\hat A_i \;{\text{in}}\;{\text{a}}\;{\text{non - - parent}}\;{\text{list}}} \\ {{\text{end}}.} \\ \end{array} $$

We denote the parent list as $\tilde A_1 ,\tilde A_2 , \ldots$ and the non-parent list as $\bar A_1 ,\bar A_2 , \ldots .$ If there are odd number of members in the parent list, the last member will be switched to the non-parent list. With an even number of members in the parent list, we group the members into pairs $\left( {\tilde A_1 ,\tilde A_2 } \right),\left( {\tilde A_3 ,\tilde A_4 } \right), \ldots .$ A random number c ∈(0,1) is generated and applied to the crossover operation to each parent pair to produce two children given by:

$$ \begin{aligned} X = & c*\tilde A_1 + \left( {1 - c} \right)*\tilde A_2 , \\ Y = & \left( {1 - c} \right)*\tilde A_1 + c*\tilde A_2 . \\ \end{aligned} $$

Since c is real, the resulting elements in the children are converted to natural number by rounding. A new generation of population is produced by combining the children produced by the parent pairs and the non-parent chromosomes.

Mutation

In GA, to avoid the solution being bounded by a local optimum, a mutation process is applied to the chromosomes in the new generation. We define P _m ∈[0, 1] as the probability of mutation. Hence, the expected number of chromosomes that will undergo mutation is P _m *pop_size. Similar to the picking of chromosomes for crossover, chromosomes are picked for mutation based on P _m . For each chromosome picked, denoted by A=(a₁,...,a_N-1), two mutation position n₁ and n₂ are randomly chosen where 1≤ n₁ < n₂ ≤ N−1. For i=n₁ to n₂, change a _i to a random number between 1 and M−1 which does not equal any of the existing genes. After all the genes in and between the two mutation positions are changed, the genes in A are rearranged in ascending order to form a new mutated chromosome A′.

Termination

Two termination criteria are used. Either the process is executed to produce a fixed number of generations and the best solution among all these generations is chosen, or the process is terminated if no further improvement in the best solution is observed in four consecutive generations.

4 Experimental results

To illustrate the computational efficiency and image compression performance of the new codebook design algorithm, two famous 512 × 512 gray-scale images, “Lena” and “Peppers” are used. The image “Lena” is used to generate codebooks of different sizes with dimension 16 (4 × 4) and the image “Peppers” is used to test the performance of the codebooks generated. We use the LBG algorithm as a reference for comparison. Both algorithms are implemented in Visual C++ and executed on a Pentium IV PC. In the new codebook design algorithm, the following parameter values are used:

$$ \begin{aligned} pop\_size = & 30; \\ a = & 0.05; \\ P_c = & 0.3; \\ P_m = & 0.2; \\ {\text{Number}}\;{\text{of}}\;{\text{generations}} = & 100 \\ \end{aligned} $$

For the LBG algorithm, the distortion threshold ɛ is set to 0.001. For the comparison of image compression performance, the image quality is evaluated by the peak signal to noise ratio (PSNR) function [5], which is defined as:

$$ {\text{PSNR}} = 10\log _{10} \,\frac{{255^2 }} {{{\text{MSE}}}} $$

where MSE is the mean-square error for an m × m gray-scale image and is defined as:

$$ {\text{MSE}} = \left( {\frac{1} {m}} \right)^2 \sum\limits_{i = 1}^m {\sum\limits_{j = 1}^m {\left( {x_{ij} - \bar x_{ij} } \right)^2 } .} $$

x _ij denotes the original pixel value and $\bar x_{ij}$ denotes the compressed pixel value.

The performance (in terms of PSNR) and the CPU time for different codebook size of the two algorithms are depicted in Figs. 2, 3, 4. The codebook size is measured by bit/codeword where for a codebook of N codewords, the bit/codeword is defined as bit/codeword=log₂N. Figure 2 compares LBG and our algorithm based on the image Lena from which the training vector set is extracted. We can see that for codebooks of size less than 64, our algorithm outperforms LBG by 0.06–1.69 dB. Figure 3 compares LBG with our algorithm based on the image Peppers, which does not contain the training vector set. Similarly, for codebooks of size less than 64, our algorithm outperforms LBG by 0.09–3.50 dB. For codebooks with size larger than 64, the performance of LBG is better for both images. Figure 4 compares the CPU times of our algorithm with LBG for generation of codebooks of different size. It indicates that the time for generating codebooks needed by LBG increases with the codebook size, while the time needed by our algorithm remains fairly consistent regardless of the codebook size.

Fig. 2

PSNR comparisons for the image Lena

Fig. 3

PSNR comparisons for the image Peppers

Fig. 4

CPU time comparisons

The comparisons of the visual quality of the image compression using both algorithms are presented in Figs. 5, 6, 7, 8. In Fig. 5, the test image Lena was compressed and recovered using LBG and our algorithm with 32 codewords. In Fig. 6, the test image Peppers was compressed and recovered using both algorithm with also 32 codewords. It can be seen clearly that the image quality of the recovered images using our algorithm is better than LBG for both test images. However, we can see from Figs. 7, 8 that the image quality of the recovered images using LBG is better if 256 codewords are used in compression.

Fig. 5

Comparisons of Lena by LBG and our algorithm for the codebook with 32 codewords. a The original image of Lena. b Lena recovered by LBG, PSNR=26.88 dB. c Lena recovered by our algorithm, PSNR=27.64 dB

Fig. 6

Comparisons of Peppers by LBG and our algorithm for the codebook with 32 codewords. a The original image of Peppers. b Peppers recovered by LBG, PSNR=24.68 dB. c Peppers recovered by our algorithm, PSNR=25.77 dB

Fig. 7

Comparisons of Lena by LBG and our algorithm for the codebook with 256 codewords. a The original image of Lena. b Lena recovered by LBG, PSNR=30.18 dB. c Lena recovered by our algorithm, PSNR=28.98 dB

Fig. 8

Comparisons of Peppers by LBG and our algorithm for the codebook with 256 codewords. a The original image of Peppers. b Peppers recovered by LBG, PSNR=28.58 dB. c Peppers recovered by our algorithm, PSNR=27.10 dB

5 Conclusion

A new codebook generation algorithm for image compression is presented. This new algorithm combines the principal component analysis (PCA) and genetic algorithm (GA) in order to efficiently search for an optimal codebook based on the training image. The PCA is used to sort the training vectors to reduce computational complexity while the near global optimal searching ability of GA is used to generate a codebook with optimal distortion ratio. Experimental results demonstrated that our new algorithm can generate near global optimal codebook (in comparison with the widely used LBG method) with codeword size not more than 64. In terms of computational efficiency, the combined algorithm outperforms the LBG algorithm significantly in that the computation time required remains almost constant with varying codeword sizes. With these characteristics, this new combined algorithm is very suitable for image compression where a high compression ratio is needed.