1 Introduction

Intelligent systems including neural networks (NNs), fuzzy logic (FL), and wavelet techniques utilize the concepts of biological systems and human cognitive capabilities. They possess learning, adaptation, and classification capabilities that hold out the hope of improved modeling and control for today’s complex systems. In this study, we present improved model design through three sorts of intelligent modeler which will be used in intelligent controllers; those based on dynamic neural networks (DNNs), those based on dynamic fuzzy networks (DFNs), and those based on dynamic wavelet networks (DWNs). DNNs capture the dynamic parallel processing and learning capabilities of biological nervous systems; DFNs, in addition to those properties, capture the decision-making capabilities of human linguistic and cognitive systems; and DWNs give a better approximation to signals and other transient or localized phenomena, both in time and frequency, and also capture the dynamic parallel processing and learning capabilities.

This study brings DNNs, DFNs, and DWNs together with dynamical model and control systems. Intelligent systems modeling (or identification) and control achieve automation via the emulation of biological intelligence. Intelligent systems modeling and control contain a wide area of technologies, such as the proportional-integral-derivative (PID) control, optimal control theory, system identification, artificial intelligence (AI) such as NNs, FL, wavelets, etc., and heuristics. In many physical and engineering systems, non-linearity properties are enough to prevent the well known application of linear control theory. There are many methods to solve different kinds of non-linear optimal control problem [5, 6, 16, 25, 26, 57]. One of the difficult problems encountered is optimal control for non-linear systems. An important aspect of any control system is its implementation on actual industrial systems. The major complication introduced during the modeling of a non-linear dynamical system with intelligent systems (which are DNNs, DFNs, and DWNs in this study) is which principles should be considered to obtain the accurate “model equivalence” of a known model of a non-linear dynamical system? Neural, fuzzy, and wavelet modeling and control have emerged as the most important branches in the last decade. They achieved successes in their application to many engineering systems in the real world [21, 23, 41, 58, 73, 75]. One of the goals of AI is focused on developing computational approaches to intelligent behavior [14]. As a final analysis, the role model is the human brain and NNs, the human mind and fuzzy networks (FNs), and the localized signals and wavelet networks (WNs), which are three of the oversimplified models of it [23].

Recently, NNs, FNs, and WNs have been paid more attention in the identification and control of unknown non-linear systems, owing to their massive parallelism, fast adaptation properties, and locality capturing and learning capabilities. But, until now, the most widely used NNs, FNs, and WNs systems are algebraic systems, despite the immense popularity of the algebraic neural, fuzzy, and wavelet systems (or feedforward networks) that are usually implemented for the approximation of a non-linear function [13, 23, 50, 52, 69, 73, 75].

In this study, the modeling principles of a non-linear system with DNNs, DFNs, and DWNs with unconstrained connectivity and with dynamic neural, fuzzy, or wavelet processing units, called “neurons”, “feurons”, or “wavelons”, have been given. The dynamic networks modeling problem is considered as a non-linear optimization with dynamic equality constraints and DNNs, DFNs, and DWNs, as compared with each other, are used for modeling with learning, generalization, and encapsulating capabilities.

The application of NNs, FNs, and WNs to dynamic system modeling and control has been constrained by the non-dynamic nature of popular network architectures. All algebraic (feedforward) NNs, FNs, and WNs suffer from some drawbacks. In non-linear system modeling, a taped-delay lines approach is required, resulting in the number of rules increasing exponentially, the number of parameters in the rules getting large (this is called as “the curse of dimensionality”), a long computational time, easily being affected by external noise, and difficulty in obtaining an independent system simulator [32, 45, 52, 54]. The major drawbacks in these architectures are the curse of dimensionality, such as the requirement of too many parameters in NNs, the use of large rule bases in FL, the large number of wavelets, and the long training times, etc. An important problem for neural and fuzzy system applications is how to deal with the neuron and layer number, and this rule explosion problem. The same problems also exist in algebraic (feedforward) wavelet networks. Many of the problems as stated above can be overcome with DNNs, DFNs, and DWNs [1–4, 17, 18, 21, 28, 30, 31, 33, 45].

In previous research, to overcome the drawbacks, some alternative approaches have been developed. The recurrent neural network (RNN) structure is developed for this purpose [33, 53, 56, 68]. The most important model is the fuzzy Takagi–Sugeno model. The original idea of the Takagi–Sugeno model comes from fuzzy identification. The linear dynamic fuzzy model is used for non-linear system modeling [63, 64]. The Takagi–Sugeno model incorporates an idea that local dynamics (linear dynamics) of a non-linear system can be represented by different linear dynamic models [8, 66, 67]. On the wavelet front, some important developments have been made in the last decade [2, 12, 40, 45, 65, 71, 73].

In this study, alternatively, we used dynamic networks (for DNNs, DFNs, and DWNs)—these have a quasi-linear dynamic nature—containing dynamic elements such as integrators (or delayers in discrete time) in their processing units, which promise to overcome those drawbacks and may also allow for the incorporation of both heuristics (this includes neuron number from test and experience, if–then rules from people experience, and wavelons number from test and experience) and hard knowledge to exploit the best characteristics of the dynamical systems [1–4, 28, 30, 31, 45, 52, 69, 72].

The most important complication when dynamics are incorporated into the networks (algebraic networks) model is related to supervised training algorithms. The training algorithms are used to obtain appropriate network weights, time constants, and membership and wavelet function parameters of the wavelet and fuzzy systems. In only algebraic/feedforward neural, fuzzy, and wavelet networks, identification of its parameters is easy to compute [13, 39, 45, 50, 52, 69]. In dynamic networks, the gradient calculation with respect to networks weights (or parameters) are more complicated [59]. The gradient calculation structure in dynamic systems has been developed in systems, control, identification, and optimal control theory [5, 16, 34, 38, 72]. These approaches have been successfully applied in identification, modeling, and control applications [1–4, 27–31, 45, 53].

Intelligent systems cover a wide range of technologies related to hard sciences, such as modeling and control theory, and soft sciences, such as AI. Figure 1 shows a general diagram of intelligent modeling and control history.

Fig. 1
figure 1

Schematic diagram of intelligent modeling and control

Full size image

In Sect. 2, we present the structure of the DNN, DFN, and DWN we used, together with illustrative examples. The non-linear optimization problem based on the adjoint sensitivity approach is discussed in Sect. 3. Simulation results are given in Sect. 4 for modeling a system with a non-linear discrete event process using a fully connected neuron DNN, DFN, and DWN.

2 General dynamic network architecture

During the last few years, the non-linear dynamic system modeling of processes by neural and fuzzy networks has been extensively studied. NNs, FNs, and WNs have learning, approximation, and generalization properties. We present the dynamic type of networks. In fact, FNs and WNs are NNs with a special structure. NN and FN systems belong to a larger class of systems called “non-linear network structures” [37] that have some properties of extreme importance for feedback control systems. These networks are universal approximators [11, 19, 20, 51, 70], and WNs are also alternative universal approximators [12, 40, 74]. Non-linear dynamic models of processes with NNs, FNs with taped-delay lines, and recurrency have been often used [13, 32, 33, 39, 50, 52–54, 56, 68, 69], but WNs during the last few years have been even more widely used [45, 65, 71].

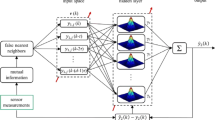
Dynamic network models has been used in the meaning of a network. The DNN, DFN, and DWN models we used have unconstrained connectivity and have dynamic elements in the neuro (neuron of DNN), feuro (neuron of DFN), and wavelo (neuron of DWN) processing units. A schematic diagram for the dynamic networks with three neurons is shown in Fig. 2. N i can be a neuron in a DNN, a feuron in a DFN, or a wavelon in a DWN. In general, there are L input signals which can be time-varying, n dynamic units, n bias terms, and M output signals. The units have dynamics associated with them and they receive the input from themselves, the bias term, and from all other units. The output of a unit y i is an activation function h(x i ) of a state variable x i associated with the unit. The output of the overall network is a linear weighted sum of the unit outputs. The bias term b i is added to the unit inputs. p ij is the input connection weights from the jth input to the ith neuron (or feuron or wavelon), w ij is the interconnection weight from the jth neuron (or feuron or wavelon) to the ith neuron (or feuron or wavelon) and q ij is the output connection weight from the jth neuron (or feuron or wavelon) to the ith output. T i is the dynamic constant of the ith neuron (or feuron or wavelon) and b i is the bias (or polarization) term of the ith neuron (or feuron or wavelon).

Fig. 2
figure 2

Schematic diagram of a DNN, DFN, or DWN with three neurons/feurons/wavelons

Full size image

The DNNs we describe here can be contrasted with the mathematical representations of neural systems found in the literature [1, 3, 4, 17, 18]. They take a popular form: standard algebraic neural network systems with external dynamics [15, 53]. In this study, a logarithmic sigmoid function is used as the activation function in the DNN:

$$ h_{i} {\left( {x_{i} ,\gamma _{i} ,\beta _{i} } \right)} = \frac{1} {{1 + \exp - {\left( {\gamma _{i} x_{i} + \beta _{i} } \right)}}} $$
(1)

The processing unit in the DFN is the feuron [4, 46–48]. The feuron represents a single dynamic neuron with a fuzzy activation function. A DFN schematic diagram is as in Fig. 2. The dynamic feuron resembles the biological neuron model. This model fires if the inputs of the feurons are excited enough. The firing procedure is done through lag dynamics, such as Hopfield dynamics. The fuzzy activation function h behaves as biological neurons which have receptive field units in the visual cortex, in part of the cerebral cortex, and in the outer parts of the brain [17, 18, 52]. We have chosen the Gaussian function (this is known as the membership function in fuzzy logic literature) for the receptive field function (that is the part of fuzzy activation functions) as below:

$$ R_{{ij}} {\left( {x_{i} } \right)} = \exp {\left( { - \frac{1} {2}{\left( {\frac{{x_{i} - c_{{ij}} }} {{\sigma _{{ij}} }}} \right)}^{2} } \right)} $$
(2)

where c ij is the center and σ ij is the spread of the jth receptive field unit of the its ith feuron. The standard fuzzy system that has been used is the singleton fuzzifier, product inference engine with Gaussian membership function and center average defuzzifier. The ith activation function with the standard fuzzy system can be written as:

$$ h_{i} {\left( {x_{i} } \right)} = \frac{{{\sum\nolimits_{j = 1}^{R_{i} } {a_{{ij}} \mu _{j} {\left( {x_{i} } \right)}} }}} {{{\sum\nolimits_{j = 1}^{R_{i} } {\mu _{j} {\left( {x_{i} } \right)}} }}} = \frac{{{\sum\nolimits_{j = 1}^{R_{i} } {a_{{ij}} \exp {\left( { - \frac{1} {2}{\left( {\frac{{x_{i} - c_{{ij}} }} {{\sigma _{{ij}} }}} \right)}^{2} } \right)}} }}} {{{\sum\nolimits_{j = 1}^{R_{i} } {\exp {\left( { - \frac{1} {2}{\left( {\frac{{x_{i} - c_{{ij}} }} {{\sigma _{{ij}} }}} \right)}^{2} } \right)}} }}} $$
(3)

The upper and lower membership functions of the universe of discourse can be considered by hard constraints (x iL and x iU ) as below:

$$ \begin{aligned} & \mu _{1} {\left( {x_{i} } \right)} = 1\quad {\text{if}}\;x_{i} \leqslant x_{{iL}} \;{\text{and}} \\ & \mu _{{R_{i} }} {\left( {x_{i} } \right)} = 1\quad {\text{if}}\;x_{i} \geqslant x_{{iU}} \\ \end{aligned} $$
(4)

where R is number of fuzzy rules, a ij are the output membership function centers and μ j (x i ) is the premise membership function of the jth rule. The feurons’ fuzzification structure is a single input/single output (SISO) algebraic fuzzy system. The dynamic fuzzy networks we describe here can be contrasted with the mathematical representations of fuzzy and neural systems found in the literature. They take a popular form: standard algebraic neural network systems with external dynamics [15, 53, 69]. Another form is functional fuzzy systems, which are based on Takagi–Sugeno systems [49, 63, 64]. The standard algebraic and functional fuzzy systems necessitate the large number of rules that cause the important problem of “the curse of dimensionality.” On the contrary, the DFN has a fewer number of parameters and simpler units.

In DWNs, wavelet neurons (wavelons) input over a lag dynamic transport to output via a wavelet activation function. Wavelets are usually explained as basis functions which are compact (closed and bounded), orthogonal (or orthonormal), and have time–frequency localization properties. But, to provide all of those properties is very difficult. Basis functions are called “activation functions” in ANN literature, and can be a global or local feature in time. Global basis functions are active for the wide values of inputs and the receptive field of the basis function is approximately constant far from the center (i.e., logarithmic sigmoid function). But, the local basis functions are only active near the center; the value tends to zero far from the center.

If the global basis function is used in a network, all activation functions interact with each other and each node, and they cover a wide input interval. This causes the large number of parameters to adjust and necessitates a long computation time. In addition, for wide input intervals, much more extrapolation error occurs. The most important disadvantage of orthonormal compact basis functions is that they can not obtained in the closed analytical form.

To remove all those disadvantages, the local basis functions can be used. The local basis functions are only active for certain inputs. In addition, the generalization errors decrease [36]. In this study, only the local basis functions have been used. The most important local function is Gaussian:

$$ \phi {\left( x \right)} = \exp {\left( { - \frac{{x^{2} }} {2}} \right)},\quad x \in R $$
(5)

where ϕ∈L2(R). For the more general case:

$$ \phi {\left( {\frac{{x - \mu }} {\sigma }} \right)} = \exp {\left( { - \frac{1} {2}{\left( {\frac{{x - \mu }} {\sigma }} \right)}^{2} } \right)},\quad x \in R $$
(6)

where μ is the center or translation and σ is the standard deviation or dilation. The localization of the Gaussian function in time is shown in Fig. 3a . However, the Gaussian function is not local in frequency, as shown in Fig. 3b. The locality features in both time and frequency is a very important concept for the representation of the signals. Therefore, the mission of the wavelet functions is comprehensive.

Fig. 3
figure 3

a Gaussian (solid line) and wavelet (dashed line) basis functions. b The Fourier transform of the Gaussian (solid line) and wavelet (dashed line) basis functions

Full size image

The locality in time and frequency can be explained as follows:

  • If a function is described in a bounded interval and has a very small value outside the boundary, then that function is local in time. The local function in time can be shifted by changing its center.

  • If the frequency spectrum of the local function in time is described in a bounded frequency interval and has very small value outside the boundary, and also can be shifted by changing its dilation, then that function is local in frequency.

A deficiency of Gaussian-based ANNs is that they do not have localization capabilities in frequency. As shown in Fig. 3b, the Gaussian function is not local in frequency. Therefore, it is very difficult to use Gaussian-based functions in some applications [60]. To overcome these problems, there is a very effective way to use wavelet functions with time–frequency localization properties [7]. The time and frequency envelope of the Mexican Hat function (second derivative of the Gaussian function) is shown in Fig. 3. In some studies, the first derivative of the Gaussian function has been used [40, 45]. However, the locality properties of the second derivative of the Gaussian function are clearer. A non-orthonormal Mexican Hat basis function can be easily written in the analytical form and its Fourier transform can be found [65], thus:

$$ \phi {\left( {x_{i} } \right)} = {\left( {1 - x^{2}_{i} } \right)}\exp {\left( { - \frac{{x^{2}_{i} }} {2}} \right)},\quad x \in R $$
(7)
$$ \phi {\left( \omega \right)} = {\sqrt {2\pi } }\omega ^{2} \exp {\left( { - \frac{{\omega ^{2} }} {2}} \right)},\quad \omega \in R $$
(8)

where ω is a real frequency. The last equation can be generalized as follows:

$$ \phi {\left( {\frac{{x_{i} - \mu _{i} }} {{\sigma _{i} }}} \right)} = {\left( {1 - {\left( {\frac{{x_{i} - \mu _{i} }} {{\sigma _{i} }}} \right)}^{2} } \right)}\exp {\left( { - \frac{1} {2}{\left( {\frac{{x_{i} - \mu _{i} }} {{\sigma _{i} }}} \right)}^{2} } \right)} $$
(9)

where μ i and σ i are the translation (center) and dilation (standard deviation) parameters, respectively. Wavelet functions have efficient time–frequency localization properties, as shown from the frequency spectrum [40]. As shown in Fig. 4, if the dilation parameter is changed, the support region width of the wavelet function changes, but the number of cycles does not change. That is, the peak number does not change; however, when the dilation parameter decreases, the peak point of the spectrum shifts to a higher frequency. Therefore, all frequency spectrums can be obtained by changing the dilation. In this study, Eq. 7 has been used as a mother (main) wavelet [65]. An N-dimensional mother wavelet can be given in the separable structure with the product rule as follows [7, 40, 45, 74, 75]:

$$ \Phi _{i} {\left( x \right)} = {\prod\limits_{j = 1}^N {\phi _{j} {\left( {\frac{{x_{j} - \mu _{{ij}} }} {{\sigma _{{ij}} }}} \right)}} } $$
(10)

where x i ∈RN is the input and N is the input number. A function y=f(x) can be represented with wavelets obtained from the mother wavelet, [7, 40, 45] as below:

$$ y_{i} = h_{i} {\left( x \right)} = {\sum\limits_{j = 1}^{N_{{\text{w}}} } {c_{{ij}} \Phi _{j} {\left( x \right)}} } + a_{{i0}} + {\sum\limits_{j = 1}^N {a_{{ik}} x_{k} } } $$
(11)

where c ij are the coefficients of the mother wavelets, Nw is the number of wavelets, ai0 is a mean or bias term, and a ik are the linear term coefficients of this approach.

Fig. 4a, b
figure 4

Illustration of the dilation parameter effect. a Mexican Hat wavelet function. b Its Fourier transform

Full size image

The wavelet function in this structure will be used in the DWN given in Fig. 2. The structure used in [1, 3, 4, 28, 30, 31, 46–48] has been adapted to this network. The wavelets in Eqs. 10 and 11 will be used as the activation functions in the network. Each activation function has a single input/single output (SISO), and can be re-expressed as:

$$ \Phi _{i} {\left( {x_{i} } \right)} = \phi _{i} {\left( {\frac{{x_{i} - \mu _{{ij}} }} {{\sigma _{{ij}} }}} \right)} $$
(12)
$$ y_{i} = h_{i} {\left( {x_{i} } \right)} = {\sum\limits_{j = 1}^{N_{{\text{w}}} } {c_{{ij}} \phi _{i} {\left( {\frac{{x_{i} - \mu _{{ij}} }} {{\sigma _{{ij}} }}} \right)}} } + a_{{i0}} + a_{{i1}} x_{i} $$
(13)
$$ \phi _{i} {\left( {\frac{{x_{i} - \mu _{{ij}} }} {{\sigma _{{ij}} }}} \right)} = {\left( {1 - {\left( {\frac{{x_{i} - \mu _{{ij}} }} {{\sigma _{{ij}} }}} \right)}^{2} } \right)}\exp {\left( { - \frac{1} {2}{\left( {\frac{{x_{i} - \mu _{{ij}} }} {{\sigma _{{ij}} }}} \right)}^{2} } \right)} $$
(14)

The mathematical expression of the DWN can be written like that of the DNN and DFN [1–4, 28, 30, 31, 46–48].

In all of these theoretical aspects, the more general and open computational model of DNNs, DFNs, and DWNs is shown in Fig. 5.

Fig. 5
figure 5

General mathematical computational model diagram of DNNs, DFNs, and DWNs

Full size image

The computational model of DNNs, DFNs, and DWNs is given in the following equations:

$$ z_{i} = {\sum\limits_{j = 1}^n {q_{{ij}} y_{j} } },\quad i = 1,2, \ldots M $$
(15)
$$ y_{i} = h{\left( {x_{i} ,\pi _{i} } \right)},\quad i = 1,2, \ldots ,n $$
(16)
$$ \ifmmode\expandafter\dot\else\expandafter\.\fi{x}_{i} = f_{i} {\left( {x_{i} ,p} \right)} = \frac{1} {{T_{i} }}{\left[ { - x_{i} + {\sum\limits_{j = 1}^n {w_{{ij}} y_{j} } } + {\sum\limits_{j = 1}^L {p_{{ij}} u_{j} } } + b_{i} } \right]};\quad x_{i} {\left( 0 \right)} = x_{{i0}} ,\quad i = 1,2, \ldots ,n $$
(17)

where q ij are the weights of the outputs of networks, w, p, q, and b are the interconnection parameters of the dynamic networks, T is the time constant, and π is the parameter of the activation function which are the neuron, feuron, or wavelon parameters, as given above. The initial conditions on the state variables x i (0) must be specified. This model is similar to those in the literature [1–4, 18, 24, 43, 46–48, 56, 62].

2.1 Illustrative examples for the dynamical behavior of DNNs, DFNs, and DWNs

These models (DNN, DFN, DWN) approximate physical dynamic non-linear systems. In this section, some examples are given in which the DNNs, DFNs, and DWNs converge to an attractor or limit cycle, oscillate, or end in a chaotic fashion. The problem of training trajectories by means of continuous recurrent neural networks whose feedforward parts are as a multilayer perceptron has been studied [35]. The DNN, DFN, and DWN open diagram with two inputs/two outputs and two neurons, feurons, or wavelons is shown in Fig. 6.

Fig. 6
figure 6

The state diagram of DNN/DFN/DWN with two neurons/feurons/wavelons and two inputs/two outputs

Full size image

Given a set of parameters, initial conditions, and input trajectories, the output set of Eqs. 16 and 17 can be numerically integrated from t=0 to the final time tf. This will produce trajectories over time for the state variables x i . We have used a 5-degree Runga–Kutta method [9, 44]. The integration step size has to be commensurate with the temporal scale of dynamics, determined by the time constants T i . In our work, we have specified a lower bound on T i and have used a fixed integration time step of some fraction (e.g., 1/10) of this bound.

2.1.1 DNNs, DFNs, and DWNs as a chaotic system

Consider the Lorenz system [25, 32] for the training of DNNs, DFNs, and DWNs. The interconnection and some neurons’, feurons’ membership (here, we used five memberships in a feuron), and wavelons’ (with three-mother wavelet) parameters of the networks found by the training algorithm are given below:

$$ \begin{aligned} & w = {\left[ {\begin{array}{*{20}c} {{1.5}} & {{3.5}} & {{ - 3.5}} \\ {{ - 3.5}} & {{1.2}} & {{ - 5}} \\ {{ - 3.5}} & {5} & {1} \\ \end{array} } \right]},\;p = {\left[ {\begin{array}{*{20}c} {0} \\ {0} \\ {0} \\ \end{array} } \right]},\;q = {\left[ {\begin{array}{*{20}c} {1} \\ {1} \\ {1} \\ \end{array} } \right]},\;b = {\left[ {\begin{array}{*{20}c} {0} \\ {0} \\ {0} \\ \end{array} } \right]},\;T = {\left[ {\begin{array}{*{20}c} {1} & {0} & {0} \\ {0} & {1} & {0} \\ {0} & {0} & {1} \\ \end{array} } \right]}\;{\text{for}}\;{\text{DNN,}}\;{\text{DFN,}}\;{\text{DWN}} \\ & {\text{additionally}}\;{\text{for}}\;{\text{DFN:}}\;\sigma = \;{\left[ {\begin{array}{*{20}c} {{0.522}} & {{0.226}} & {{0.032}} & {{0.963}} & {{1.433}} \\ {{0.362}} & {{0.536}} & {{0.039}} & {{0.336}} & {{0.454}} \\ {{0.375}} & {{0.102}} & {{0.005}} & {{1.313}} & {{0.745}} \\ \end{array} } \right]}{\text{,}}\;a = {\left[ {\begin{array}{*{20}c} {{ - 0.548}} & {{2.232}} & {{ - 2.322}} & {{0.983}} & {{ - 0.926}} \\ {{ - 2.243}} & {{1.541}} & {{ - 1.145}} & {{0.879}} & {{ - 1.135}} \\ {{ - 1.432}} & {{1.123}} & {{ - 1.029}} & {{1.125}} & {{ - 1.155}} \\ \end{array} } \right]} \\ & {\text{additionally}}\;{\text{for}}\;{\text{DWN:}}\;c = \;{\left[ {\begin{array}{*{20}c} {{ - 0.872}} & {{ - 1.209}} & {{ - 1.102}} \\ {{ - 1.431}} & {{ - 1.098}} & {{ - 1.011}} \\ {{ - 1.671}} & {{ - 0.907}} & {{ - 1.006}} \\ \end{array} } \right]}{\text{,}}\;\mu = {\left[ {\begin{array}{*{20}c} {{0.059}} & {{ - 1.113}} & {{ - 2.537}} \\ {{ - 0.287}} & {{0.098}} & {{ - 1.786}} \\ {{ - 0.265}} & {{ - 1.203}} & {{ - 2.976}} \\ \end{array} } \right]} \\ \end{aligned} $$

The initial conditions were x i (0)=−6, −10, −4, (i=1, 2, 3). All of the dynamic networks successfully realized a chaotic system, which only shows x1−x3 as a state space combination of DNN, DFN, and DWN. Figure 7 also shows the state x1 error trajectories between DNN/DFN/DWN and the actual Lorenz attractor trajectories. The error is very small up to approximately 18 s. After that, the error increases and the overlap rate is high. Overall, the overlap rate is satisfactory. When these portraits are compared with the real Lorenz system, the DWN portrait is nearest to the Lorenz portrait with the DFN being next in terms of good performance and, lastly, is the DNN. All networks were trained with the same iterations. Trajectory tracking performance is excellent in this application for all networks.

Fig. 7a–f
figure 7

The state space trajectories of a DNN, b DFN, and c DWN as a chaotic system and error trajectories of state x1 for d DNN, e DFN, and f DWN

Full size image

2.1.2 DNN, DFN, and DWN as an oscillator example

In this application, an oscillator system in [25] is modeled with two neurons/feurons/wavelons in a DNN/DFN/DWN. The interconnection and some neurons’, feurons’ membership (we used five memberships in a feuron), and wavelons’ (with three-mother wavelet) parameters of networks are shown below:

$$ \begin{aligned} & w = {\left[ {\begin{array}{*{20}c} {0} & {{ - 1}} \\ {1} & {1} \\ \end{array} } \right]},\;p = {\left[ {\begin{array}{*{20}c} {0} \\ {0} \\ \end{array} } \right]},\;q = {\left[ {\begin{array}{*{20}c} {1} \\ {1} \\ \end{array} } \right]},\;b = {\left[ {\begin{array}{*{20}c} {0} \\ {0} \\ \end{array} } \right]},\;T = {\left[ {\begin{array}{*{20}c} {1} & {0} \\ {0} & {1} \\ \end{array} } \right]}\;{\text{for}}\;{\text{DNN,}}\;{\text{DFN,}}\;{\text{DWN}} \\ & {\text{additionally}}\;{\text{for}}\;{\text{DNN:}}\;\gamma = \;{\left[ {\begin{array}{*{20}c} {{0.786}} \\ {{0.812}} \\ \end{array} } \right]} \\ & {\text{additionally}}\;{\text{for}}\;{\text{DFN:}}\;\sigma = \;{\left[ {\begin{array}{*{20}c} {{0.594}} & {{1.005}} & {{0.129}} & {{0.865}} & {{1.131}} \\ {{0.683}} & {{1.118}} & {{0.122}} & {{0.924}} & {{2.129}} \\ \end{array} } \right]} \\ & {\text{additionally}}\;{\text{for}}\;{\text{DWN:}}\;c = \;{\left[ {\begin{array}{*{20}c} {{ - 0.872}} & {{ - 1.209}} \\ {{ - 1.431}} & {{ - 1.098}} \\ \end{array} } \right]}{\text{,}}\;\mu = {\left[ {\begin{array}{*{20}c} {{0.059}} & {{ - 1.113}} \\ {{ - 0.287}} & {{0.098}} \\ \end{array} } \right]} \\ \end{aligned} $$

The DNN/DFN/DWN converge to an oscillation situation for several initial conditions (x i (0), i=1, 2) (see Fig. 8). As can be seen, all the dynamic networks capture the oscillator system’s behavior adequately.

Fig. 8a–c
figure 8

The state space trajectories of a DNN, b DFN, and c DWN as an oscillatory system

Full size image

In all of the above illustrative examples, the DNN, DFN, and DWN successfully capture the behavior of a non-linear physical dynamic system.

3 Parameter identification based on adjoint sensitivity analysis for dynamic network training

The DNN, DFN, and DWN training is used to encapsulate a given set of trajectories by adjusting network parameters. In this section, adjusting the parameters of the dynamic networks is presented for trajectory tracking. This is done by minimizing the cost function (error function). The gradient-based algorithms have been used for this problem. The cost gradients with respect to network parameters are required for the algorithm. The dynamic networks’ general schematic diagram is shown in Fig. 9. Our focus in this paper has been the adjoint sensitivity analysis for calculating the cost gradients with respect to all networks parameters. The common network parameters are w, p, q, b, T; γ and β for DNN also; c, σ, and a for DFN also; and c, μ, σ, and a for DWN also. Note that some DFN and DWN parameters are different but the same notation was used.

Fig. 9
figure 9

Dynamic network training block diagram

Full size image

A performance index (PI) or cost structure is selected in the simple quadratic form as follows:

$$ E = \frac{1} {2}{\int\limits_0^{t_{{\text{f}}} } {{\left[ {z{\left( t \right)} - z^{d} {\left( t \right)}} \right]}^{{\text{T}}} {\left[ {z{\left( t \right)} - z^{d} {\left( t \right)}} \right]}{\text{d}}t} } $$
(18)

where e(t)=z(t)−z d(t) is the error function. z(t) is the response of the DNN, DFN, and DWN models (output), and zd(t) is the desired (target) system response. We want to compute the cost sensitivities with respect to the various parameters:

$$ \frac{{\partial E}} {{\partial w}},\frac{{\partial E}} {{\partial p}},\frac{{\partial E}} {{\partial q}},\frac{{\partial E}} {{\partial T}},\frac{{\partial E}} {{\partial b}},\frac{{\partial E}} {{\partial c}},\frac{{\partial E}} {{\partial \sigma }},\frac{{\partial E}} {{\partial a}},\frac{{\partial E}} {{\partial \mu }} $$
(19)

The output weight gradients can be easily obtained by differentiating Eqs. 18 and 15:

$$ \frac{{\partial E}} {{\partial q_{{ij}} }} = {\int\limits_0^{t_{{\text{f}}} } {{\left[ {z_{i} {\left( t \right)} - z^{d}_{i} {\left( t \right)}} \right]}\frac{{\partial z_{i} }} {{\partial q_{{ij}} }}{\text{d}}t} } = {\int\limits_0^{t_{{\text{f}}} } {e_{i} {\left( t \right)}y_{j} {\text{d}}t} } $$
(20)

One approach to solving the constrained dynamic optimization problem is based on the use of the calculus of variations, which is called the “adjoint” method for sensitivity computation [1, 3–5, 27–31, 34]. The number of differential equations to be solved only depends on the neuron/feuron/wavelon number, and does not depend on network parameters. A new dynamical system defined with adjoint state variables λ i is obtained as follows:

$$ - \ifmmode\expandafter\dot\else\expandafter\.\fi{\lambda }_{i} = - \frac{1} {{T_{i} }}\lambda _{i} + \frac{1} {{T_{i} }}{\sum\limits_j {w_{{ij}} {y}\ifmmode{'}\else$'$\fi_{j} \lambda _{j} } } + e_{i} {\left( t \right)}{\sum\limits_j {q_{{ij}} {y}\ifmmode{'}\else$'$\fi_{j} } },\quad \lambda _{j} {\left( {t_{{\text{f}}} } \right)} = 0 $$
(21)
$$ {y}\ifmmode{'}\else$'$\fi_{j} = \frac{{\partial h_{j} {\left( {x_{j} } \right)}}} {{\partial x_{j} }} = \left\{ {\begin{array}{*{20}l} {{\gamma _{j} h_{j} {\left( {1 - h_{j} } \right)}} \hfill} & {{{\text{for}}\;{\text{DNN}}} \hfill} \\ {{\frac{{{\sum\nolimits_{k = 1}^{R_{j} } {{\left( {h_{j} - a_{{jk}} } \right)}\exp {\left( { - \frac{1} {2}{\left( {\frac{{x_{j} - c_{{jk}} }} {{\sigma _{{jk}} }}} \right)}^{2} } \right)}{\left( {\frac{{x_{j} - c_{{jk}} }} {{\sigma ^{2}_{{jk}} }}} \right)}} }}} {{{\sum\nolimits_{k = 1}^{R_{j} } {\exp {\left( { - \frac{1} {2}{\left( {\frac{{x_{j} - c_{{jk}} }} {{\sigma _{{jk}} }}} \right)}^{2} } \right)}} }}}} \hfill} & {{{\text{for}}\;{\text{DFN}}} \hfill} \\ {{ - {\sum\limits_{k = 1}^{N_{{\text{w}}} } {c_{{jk}} {\left( {3\phi _{j} + 2{\left( {\frac{{x_{j} - \mu _{j} }} {{\sigma ^{2}_{{jk}} }}} \right)}^{2} } \right)}{\left( {\frac{{x_{j} - \mu _{j} }} {{\sigma ^{2}_{{jk}} }}} \right)}} } + a_{{j1}} } \hfill} & {{{\text{for}}\;{\text{DWN}}} \hfill} \\ \end{array} } \right. $$
(22)

The size of the adjoint vector is n and is independent of the network parameters. There are n quadratures for computing the sensitivities. The integration of the differential equations must be performed backwards in time, from tf to 0. We have used the 5th-order Runga–Kutta–Butcher integration rule [9, 44]. Let p be a vector containing all network parameters. Then, the cost gradients with respect to the parameters are given by the following quadratures:

$$ \frac{{\partial E}} {{\partial p}} = {\int\limits_0^{t_{{\text{f}}} } {{\left( {\frac{{\partial f}} {{\partial p}}} \right)}^{{\text{T}}} \lambda {\text{d}}t} } $$
(23)

Some of the cost gradients as in [1–4, 30, 46–48] are as follows:

$$ \frac{{\partial E}} {{\partial w_{{ij}} }} = {\int\limits_0^{t_{{\text{f}}} } {\frac{{\lambda _{i} y_{j} }} {{T_{i} }}{\text{d}}t} },\;\frac{{\partial E}} {{\partial b_{i} }} = {\int\limits_0^{t_{{\text{f}}} } {\frac{{\lambda _{i} }} {{T_{i} }}{\text{d}}t} } $$
(24)
$$ \frac{{\partial E}} {{\partial T_{i} }} = {\int\limits_0^{t_{{\text{f}}} } {\frac{{\lambda _{i} }} {{T^{2}_{i} }}{\left[ { - x_{i} + {\sum\limits_{j = 1}^n {w_{{ij}} y_{j} } } + {\sum\limits_{j = 1}^l {p_{{ij}} u_{j} } } + b_{i} } \right]}{\text{d}}t} } $$
(25)
$$ \frac{{\partial E}} {{\partial \gamma _{i} }} = {\int\limits_0^{t_{{\text{f}}} } {{\left( {{\sum\limits_i {\frac{{\lambda _{i} }} {{T_{i} }}w_{{ij}} } }} \right)}x_{j} h_{j} {\left( {1 - h_{j} } \right)}{\text{d}}t} } $$
(26)
$$ \begin{aligned} & \frac{{\partial E}} {{\partial c_{{ik}} }} = {\int\limits_0^{t_{{\text{f}}} } {{\left( {{\sum\limits_i {\frac{{\lambda _{i} }} {{T_{i} }}w_{{ij}} \frac{{a_{{ik}} - f_{i} }} {{{\sum\nolimits_{k = 1}^R {\exp {\left( { - \frac{1} {2}{\left( {\frac{{x_{i} - c_{{ik}} }} {{\sigma _{{ik}} }}} \right)}^{2} } \right)}} }}}} }\exp {\left( { - \frac{1} {2}{\left( {\frac{{x_{i} - c_{{ik}} }} {{\sigma _{{ik}} }}} \right)}^{2} } \right)}{\left( {\frac{{x_{i} - c_{{ik}} }} {{\sigma ^{2}_{{ik}} }}} \right)}} \right)}{\text{d}}t} } \\ & k = 1,2, \ldots R_{i} \;{\text{for}}\;{\text{DFN}} \\ \end{aligned} $$
(27)
$$ \frac{{\partial J}} {{\partial c_{{ij}} }} = {\int\limits_0^{t_{{\text{f}}} } {{\left( {{\sum\limits_k {\frac{{\lambda _{k} }} {{T_{k} }}w_{{ki}} \phi _{i} {\left( {\frac{{x_{i} - \mu _{{ij}} }} {{\sigma _{{ij}} }}} \right)}} }} \right)}{\text{d}}t\;} }{\text{for}}\;{\text{DWN}} $$
(28)

All other gradients can be easily derived. Detailed results can be found in the literature [1, 3, 46, 47]. We assume that, at each iteration, the gradients of the performance index with respect to all networks parameters, \( g = \frac{{\partial E}} {{\partial p}} \), is computed. Here, we describe an algorithm we have used for updating parameter values based on this gradient information:

$$ p^{{k + 1}} = p^{k} + \tau ^{k} d^{k} ,\quad d^{k} = - H^{k} g^{k}_{p} $$
(29)

where d is the search direction, τ is the optimal step size along the search direction, g is the cost gradient with respect to the parameter, and \( H \cong {\left( {\nabla _{{pp}} J} \right)}^{{ - 1}} \) is the inverse of the approximate Hessian matrix. The Broyden-Fletcher-Golfarb-Shanno gradient method has been used for updating network weights. This method is faster than the simple gradient method and more robust than the simple conjugate gradient approach [1, 3, 4, 10, 16, 30, 46, 47, 55, 61]. This method provides the history of the parameter and gradient changes, yielding approximately second-order information.

The adjoint way of computing performance index sensitivities is efficient in the number of differential equations that need to be solved, but the intermediate computations within the time interval do not produce information that is meaningful in the original networks (DNN, DFN, DWN). Whereas the forward sensitivity method produces trajectories of the state and response sensitivities, the adjoint method produces trajectories of adjoint variables.

For algorithms requiring the exact Hessian, a computationally efficient approach is available using both the adjoint and forward response sensitivities [27, 29]. Thus, by performing both the forward and adjoint sensitivity analyses, an exact Newton method in the function space can be implemented at a substantially lower cost than that involved in the “forward” computation of exact second-order sensitivities.

4 Simulation results

As an application, a non-linear piecewise-continuous scalar function (discrete event system) [74] has been considered in the dynamic structure (passing through 1 s−1) by adding a control function and this function is the one to be modeled with DNN, DFN, and DWN. For this, the f(x) function is substituted into the \( \ifmmode\expandafter\dot\else\expandafter\.\fi{x} = f{\left( {x,u} \right)},\;x{\left( {t_{0} } \right)} = x_{0} ,\;0 \leqslant t \leqslant t_{{\text{f}}} \) expression as below:

$$ \ifmmode\expandafter\dot\else\expandafter\.\fi{x} = f{\left( {x,u} \right)} = \left\{ {\begin{array}{*{20}l} {{ - 2.186x - 12.864 + u} \hfill} & {{ - 10 \leqslant x < - 2} \hfill} \\ {{4.246x + u} \hfill} & {{ - 2 \leqslant x < 0} \hfill} \\ {{10\exp {\left( { - 0.05x - 0.5} \right)} \times \sin {\left( {{\left( {0.03x + 0.7} \right)}x} \right)} + u} \hfill} & {{0 \leqslant x < 10} \hfill} \\ \end{array} } \right. $$
(30)

The modeling structure is shown in Fig. 10a. The unit step gain functions k i (x) (i=1, 2, 3) used are given in Fig. 10b.

Fig. 10
figure 10

a Modeling diagram of discrete event system. b The unit step gain functions

Full size image

This process has been trained by a DWN with a wavelon in the time interval t∈[0, 10]. The control function to be applied to the system input that was selected so that there was an adequate amount of oscillation of the system is shown in Fig. 11a. The initial condition was taken to be x0=−0.4. At the beginning of the training, some modeling parameters were set to p ij =1 and T i =1, but the others were started randomly. After the training, the output of the DNN, DFN, and DWN are as in Fig. 11a–c, respectively. The right-hand side of Eq. 17 for u(t)=0 (that is, \( \ifmmode\expandafter\hat\else\expandafter\^\fi{f}{\left( x \right)}, \) the static side of DNN, DFN, and DWN) has been successfully fitted to the real function f(x) given by right-hand side of Eq. 30 for u(t)=0 (see Fig. 12a–c). As can be seen, the joint point at x=−2 was successfully modeled with DNN, DFN, and DWN. When one carefully looks at Figs. 11 and 12, the DWN approximation is better than the others, but DNN and DFN also are successful approximators.

Fig. 11a–f
figure 11

The modeled process with DNN, DFN, and DWN. a Control input (dashed-dotted line), DNN output (dashed line), and process output (solid line). b DFN output (dashed line) and process output (solid line). c DWN output (dashed line) and process output (solid line), Error trajectories for d DNN, e DFN, and f DWN

Full size image
Fig. 12a–c
figure 12

Static function approximation performance of DNN, DFN, and DWN. a DNN approximation \( \ifmmode\expandafter\hat\else\expandafter\^\fi{f}{\left( x \right)} \) (dashed line) and real function f(x) (solid line). b DFN approximation \( \ifmmode\expandafter\hat\else\expandafter\^\fi{f}{\left( x \right)} \) (dashed line) and real function f(x) (solid line). c DWN approximation \( \ifmmode\expandafter\hat\else\expandafter\^\fi{f}{\left( x \right)} \) (dashed line) and real function f(x) (solid line)

Full size image

5 Conclusions and future works

In this work, we presented three intelligent methods to be used in modeling, control, and the other applications. Any non-linear physical dynamic system can be captured by dynamic neural networks (DNNs), dynamic fuzzy networks (DFNs), and dynamic wavelet networks (DWNs). Simulation results show that the dynamic network structure can grown more accurately by neuro/fuzzy/wavelet approximators.

All of the results presented here were obtained with the help of a trained DNN, DFN, and DWN, which generated the model response policy close to the target process. In the illustrative examples, the dynamic networks used have some non-linear dynamic system behavior, such as chaotic, oscillator, etc.

In the simulations presented, we used a non-linear system with a discrete event system. All three networks were successfully used for modeling the target process. According to the modeling and training speed performance, better results have been obtained from DWNs, but DFNs and DNNs have also produced satisfactory results. The exact Hessian-based optimization algorithm for application to DNN, DFN, and DWN is a valuable approximation to speed up training time. In addition, the local and orthogonal wavelet usage in these areas can increase the training speed for DWNs.