1 Introduction

Clustering analysis can be used to explore the structure of data to understand the characteristics of that data for many practical issues. Therefore, clustering analysis has been applied in many different fields such as customer segmentation in marketing (Kuo et al. 2002), bill of material clustering in manufacturing industries (Agard and Penz 2009), and characteristic clustering in various fields (Kahali et al. 2019; Kannan et al. 2017; Milligan and Sokol 1980). Many different clustering algorithms have been proposed to date, including the K-means algorithm (MacQueen 1967), the fuzzy c-means (FCM) algorithm (Bezdek 1981; Dunn 1973), the fuzzy K-prototype algorithm (Ji et al. 2012), and so on. Each algorithm has its own pros and cons, making each appropriate for application in certain cases.

The FCM algorithm is one of the most popular cluster analysis methods. In most databases, an uncertainty commonly exists. To deal with uncertainty and hesitation, fuzzy sets and intuitionistic fuzzy sets (IFS) were proposed by Zadeh (1965) and Atanassov (1986), respectively. IFS deal with the uncertainty and hesitation which commonly occur in human thinking. Thus, the intuitionistic fuzzy c-means (IFCM) algorithm was proposed and extended for clustering interval-valued datasets (Xu and Wu 2010). The IFCM algorithm has been proven to achieve better performance than the FCM algorithm (Chaira 2011; Lin 2014).

In addition, the possibilistic fuzzy c-means (PFCM) algorithm is also an improvement of the FCM algorithm, which simultaneously calculates memberships and possibilities (Pal et al. 2005). The PFCM algorithm overcomes the problems of noise and coincident clusters. The algorithm is interesting and provides a good solution. However, the PFCM algorithm still has a drawback of sensitivity to the initialization. Moreover, the PFCM classifies the unlabeled dataset according to feature vectors without take into account the qualitative information. Therefore, it may lead to an incorrect assignment of membership (typicality) values to their clusters during the clustering process (Verma and Agrawal 2015).

Motivated by the contributions of the IFS, and the potential of the PFCM algorithm, this study proposes a possibilistic intuitionistic fuzzy c-means (PIFCM) algorithm, which combines both IFS and possibility concepts, to address the improper assignment of membership and typicality values to their clusters.

To improve clustering results and overcome the drawback of initialization sensitivity, multi-objective fuzzy clustering algorithms, which combine meta-heuristic algorithms and the proposed PIFCM algorithm, are also developed to consider multi-objective functions simultaneously. Numerous multi-objective fuzzy clustering algorithms have been proposed. Nguyen and Kuo (2019) combined Non-Dominated Sorting Particle Swarm Optimization to fuzzy clustering for categorical data in which global cluster compactness and fuzzy separation are the two objective functions. Kuo et al. (2022) proposed a framework of sequential clustering and classification that combined deep learning technique and multi-objective sine–cosine algorithm to explore the structure of data. Belhor et al. (2023) combined the Strength Pareto Evolutionary Algorithm (SPEA2) and Non-dominated Sorting Genetic Algorithm (NSGA-II) with k-means clustering and applied it to the routing and scheduling of home health care. Besides, multiple multi-objective fuzzy clustering algorithm have been developed and applied for image segmentation (Singh et al. 2022; Singh and Muchahari 2023; Zhao et al. 2022a, 2022b).

In this study, three metaheuristic algorithms are employed, i.e., genetic algorithm (GA), particle swarm optimization (PSO) algorithm, and gradient evolution (GE) algorithm. GA is a heuristic search algorithm inspired by the theory of evolutionary genetics. Generally, GA is used to generate high-quality solutions to optimization and search problems by mutation, crossover and selection processes. Similarly, PSO algorithms are also an evolutionary method that try to look for an optimal solution by moving all the particles in a population around a search space. At every move, the position and velocity of the particles are updated. The best-known position of each step is found. The particles will move toward the best solutions. Correspondingly, GE is a new meta-heuristic optimization algorithm inspired by the gradient-based search technique. GE algorithm consists of three operators, namely vector updating, jumping, and refreshing, which are updated based on a gradient theorem. GE provides a promising result compared with those of other meta-heuristic methods such as PSO or differential evolution (Kuo and Zulvia 2015).

The proposed algorithms integrate several meta-heuristic approaches with the PIFCM algorithm. Herein, three meta-heuristic algorithms, i.e., GA, PSO, and GE are employed. First, the PIFCM algorithm is implemented. Thereafter, the clustering result (the cluster centroids) is used as the initial population of the meta-heuristic algorithms. Moreover, multi-objective optimization, which uses global cluster compactness (π), and 2) fuzzy separation (Sep) as two objective functions, is applied to balance the clustering result. Thus, these combinations form three multi-objective evolutionary methods with the PIFCM algorithms, i.e., multi-objective genetic algorithm-based PIFCM (MOGA–PIFCM), multi-objective particle swarm optimization-based PIFCM (MOPSO–PIFCM), and multi-objective gradient evolution-based PIFCM (MOGE–PIFCM). The proposed algorithms are expected to improve the quality of clustering performance.

The remainder of this paper is organized as follows. Section 2 presents the related literature survey. Section 3 describes the proposed clustering algorithm, while the model evaluation results are illustrated in Sect. 4. Finally, concluding remakes are made in Sect. 5.

2 Literature review

This section provides some concepts related to data clustering, which include several clustering algorithms. Moreover, some metaheuristic approaches for both single-objective optimization and multi-objective optimization are also reviewed.

2.1 Fuzzy c-means algorithm

Fuzzy sets are like sets whose elements have degrees of membership, and were proposed to deal with vagueness and uncertainty (Zadeh 1965). The fuzzy set theory allows one piece of data to belong to two or more clusters. This represents the similarity of a point shared with each cluster with a membership function whose values are between zero and one (Dunn 1973; Tan 2006; Zadeh 1965).

FCM is one of the most popular clustering algorithms. The FCM algorithm was developed by Dunn (1973) to detect well-separated clusters, and was improved by Bezdek (1981) to solve the clustering problem. The algorithm can be described as follows. Given a dataset of n data instancces \(X=\{{x}_{1}, {x}_{2}, \dots , {x}_{n}\}\) and c clusters \(V=\{{v}_{1}, {v}_{2}, \dots , {v}_{c}\}\), the FCM algorithm partitions X into c fuzzy clusters, forming a fuzzy partition in data instances. A fuzzy partition can be conveniently represented as a matrix U = \({[{u}_{ij}]}_{n \times c}\) whose elements \({u}_{ij}\in [\mathrm{0,1}]\) are the membership degree of data instances \({x}_{i}\) in cluster\({v}_{j}\). The sum of \({u}_{ij}\) for a data instance \({x}_{i}\) on c clusters should be equal 1. These two constraints are presented in the following equations:

$$0\le {u}_{ij}\le 1 i=\mathrm{1,2},\dots ,n j=\mathrm{1,2},\dots ,c,$$
(1)
$$\sum _{j=1}^{c}{u}_{ij}=1 i=\mathrm{1,2},\dots n.$$
(2)

The FCM minimizes the distance-based objective function which is defined as follows:

$$J= \sum_{i=1}^{n}\sum_{j=1}^{c}{\left[{u}_{ij}\right]}^{m} \times {{d}_{ij}}^{2}({x}_{i},{v}_{j}),$$
(3)

where m is a weighting exponent \((m\in [1,+\infty )\) that control the influence of membership degree, \({d}_{ij}({x}_{i},{v}_{j})\) is the Euclidean distance between \({x}_{i}\) and cluster center\({v}_{j}\). Suppose that the given dataset contains \(p\) attributes. A data instance \({x}_{i}\) and a cluster center \({v}_{j}\) are presented as \({x}_{i}=\left\{{x}_{1i}, {x}_{2i}, \dots , {x}_{pi}\right\}\) and \({v}_{j}=\left\{{v}_{1j}, {v}_{2j}, \dots , {v}_{pj}\right\},\) respectively. The distance \({d}_{ij}({x}_{i},{v}_{j})\) is calculated as follows:

$${d}_{ij}({x}_{i},{v}_{j})= \sqrt{\sum_{a=1}^{p}{({x}_{ia}-{v}_{ja})}^{2},}$$
(4)

where \({x}_{ia}\) is the \(a\)th attribute value of data instance \({x}_{i}\), and \({v}_{ja}\) is the \(a\)th attribute value of cluster center \({v}_{j}\), \(a=1, 2, \dots , p.\)

To minimize J, membership \({u}_{ij}\) and the centers of cluster \({v}_{j}\) are updated as:

$${{u}_{ij}}^{(t+1)} = \frac{1}{\sum_{k=1}^{c}{\left(\frac{{d}_{ij}({x}_{i},{v}_{j})}{{d}_{ij}({x}_{i},{v}_{k})}\right)}^{\frac{2}{m-1}}}\; \mathrm{and}$$
(5)
$${v}_{j}=\frac{{\sum }_{i=1}^{n}{\left[{u}_{ij}\right]}^{m}{x}_{i}}{{\sum }_{i=1}^{n}{\left[{u}_{ij}\right]}^{m}} j=\mathrm{1,2},\dots ,c.$$
(6)

This iteration will stop when \(\left|{J}^{(t+1)}-{J}^{\left(t\right)}\right|\le \varepsilon \), where \(\varepsilon \) is a termination condition, whereas t is the iteration step.

The FCM algorithm does, however, have some drawbacks, i.e., its sensitivity to the initialization, and its sensitivity to noise and outlier data.

2.2 Intuitionistic fuzzy c-means algorithm

This section describes intuitionistic fuzzy theory and the intuitionistic fuzzy c-means (IFCM) algorithm.

2.2.1 Intuitionistic fuzzy theory

Intuitionistic fuzzy set (IFS) theory was proposed by Atanassov (1986) to handle uncertainty. Intuitionistic fuzzy sets extend Zadeh’s fuzzy sets and consider both membership and non-membership.

An IFS, A, in a fixed set, E, is an objective of the expression. The model of intuitionistic fuzzy sets is defined by Atanassov (1989) as:

$$A=\left\{x,{u}_{A}\left(x\right), {v}_{A}(x)|x\in E\right\},$$
(7)

where the function \({u}_{A}\left(x\right)\to \left[\mathrm{0,1}\right]\, \text{ denotes the membership}, \text{ and }\, {v}_{A}(x)\to \left[\mathrm{0,1}\right]\) denotes the non-membership degree of the element in set A.

When \({u}_{A}\left(x\right)+{v}_{A}\left(x\right)=1\) for every \(x\in E\), then the IFS becomes a fuzzy set. For all IFS, Atanassov also considers a hesitation degree, \({\pi }_{A}\left(x\right)\). Therefore, the IFS function is defined as:

$${\pi }_{A}\left(x\right)=1- {u}_{A}\left(x\right)-{v}_{A}\left(x\right), 0\le { \pi }_{A}\left(x\right) \le 1.$$
(8)

With regard to intuitionistic fuzzy sets, Yager proposed an intuitionistic fuzzy generator by defining the complement of an intuitionistic fuzzy set (Burillo and Bustince 1996). Hence, an intuitionistic fuzzy complement with Yager-generating functions can be written as:

$$ N\left( x \right) = \left( {1 - x^{\alpha } } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \alpha }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\alpha $}}}} ,\alpha > 0\quad where\quad N\left( 0 \right) = 1\quad and\quad N\left( 1 \right) = 0, $$
(9)

where α is the parameter in Yager-generating functions, for each value of parameter α ∈ (0,∞).

With the help of Yager’s intuitionistic fuzzy compliment, the intuitionistic fuzzy set becomes:

$$ A = \left\{ {x,u_{A} \left( x \right),{ }\left( {1 - u_{A} \left( x \right)^{\alpha } } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \alpha }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\alpha $}}}} |x \in E} \right\} $$
(10)

and the hesitation degree is:

$$ \pi_{A} \left( x \right) = 1 - { }u_{A} \left( x \right) - \left( {1 - u_{A} \left( x \right)^{\alpha } } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \alpha }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\alpha $}}}} . $$
(11)

2.2.2 Intuitionistic fuzzy c-means algorithm

To integrate intuitionistic fuzzy theory into a conventional FCM algorithm, the intuitionistic fuzzy membership values are obtained as:

$${{u}_{ij}}^{*}={u}_{ij}+{\pi }_{ij},$$
(12)

where \({{u}_{ij}}^{*}({u}_{ij})\) denotes the intuitionistic (conventional) fuzzy membership degree of the data point i in cluster j.

The cluster center of the IFCM is updated as:

$${{v}_{j}}^{*}=\frac{{\sum }_{i=1}^{n}\left[{{u}_{ij}}^{*}\right]{x}_{i}}{{\sum }_{i=1}^{n}\left[{{u}_{ij}}^{*}\right]} j=\mathrm{1,2},\dots ,c.$$
(13)

Using Eq. (13), the cluster center and the degree of membership matrix are updated simultaneously. The IFCM optimizes the objective function by continuously updating the membership functions and centers of clusters until stopping criteria \(\varepsilon \) is satisfied.

The IFCM algorithm can deal with uncertainty and vagueness; however, it cannot solve the problems of clustering noise and outlier data.

2.3 Possibilistic fuzzy c-means algorithm

Possibilistic fuzzy c-means (PFCM) is an improvement of FCM which calculates memberships and possibilities simultaneously (Pal et al. 2005). PFCM can overcome the sensitivity to noise and outlier data of the FCM algorithm. Moreover, the drawback of coincident cluster problems is also solved in the PFCM algorithm. PFCM has a parameter which controls the influence of outliers on centroids. Therefore, the clustering results are expected to be more compact. PFCM introduces the typicality of data \({x}_{i}\) with respect to cluster \({v}_{j}\), notated by \({t}_{ij}\). The objective function of PFCM is defined in the following equation as:

$$J= \sum_{i=1}^{n}\sum_{j=1}^{c}\left(a{u}_{ij}^{m}+{bt}_{ij}^{\eta }\right) {{d}_{ij}({x}_{i},{v}_{j})}^{2}.$$
(14)

Here, \({t}_{ij}\) and \({v}_{j}\) are calculated based on Eqs. (15) and (16), respectively, as follows:

$${t}_{ij}=\frac{1}{1+{\left(\frac{b}{{\gamma }_{j}}d{\left({x}_{i},{v}_{j}\right)}^{2}\right)}^{\frac{1}{(\eta -1)}}} \mathrm{ and}$$
(15)
$${v}_{j}=\frac{{\sum }_{i=1}^{n}\left({au}_{ij}^{m}+{bt}_{ij}^{\eta }\right){x}_{i}}{{\sum }_{i=1}^{n}\left({au}_{ij}^{m}+{bt}_{ij}^{\eta }\right)}.$$
(16)

The sum of all of a cluster center’s \({t}_{ij}\) vlaues should be 1:

$$0\le {t}_{ij}\le 1 i=\mathrm{1,2},\dots ,n j=\mathrm{1,2},\dots ,c,$$
(17)
$$\sum_{i=1}^{n}{t}_{ij}=1 j=\mathrm{1,2},\dots c,$$
(18)

where a and b are parameters defining the relative importance of fuzzy membership and typicality values. If a > b, then the centroids have a higher influence than the membership values. Therefore, to reduce the effect of the outliers, the value of b should be higher than a. \(\eta \) is a real number that governs the influence of typicality values, and \(\eta \)>1. In addition, \({\gamma }_{j}\)>0 is defined as:

$${\gamma }_{j}=K\frac{{\sum }_{i=1}^{n}{u}_{ij}^{m}\times {{d}_{ij}({x}_{i},{v}_{j})}^{2}}{{\sum }_{i=1}^{n}{u}_{ij}^{m}},$$
(19)

where K > 0, and the most common is K = 1.

The PFCM algorithm has been applied in many areas. Verma and Agrawal (2015) proposed an algorithm integrating Atanassov’s IFS and the PFCM algorithm, used in the segmentation of human brain images. Emary et al. combined a cuckoo search algorithm with the PFCM algorithm for retinal vessel segmentation (Emary et al. 2014). Ji et al. (Ji et al. 2011) proposed a modified PFCM algorithm which employed the novel adaptive method to deal with intensity inhomogeneities and noise for brain magnetic resonance (MR) image segmentation. Similarly, Aparajeeta et al. also extended the PFCM algorithm for MR image segmentation with a bias field (Ji et al. 2011). Sarkar et al. developed a Rough Possibilistic Type-2 Fuzzy C-Means clustering to cluster MR images with overlapping areas (Sarkar et al. 2016). Recently, Memon et al. combined PFCM with kernel function and local information for image segmentation (Memon et al. 2019). Chen et al. (2021) improved the PFCM performance by considering weight component to assign membership and typicality. Wu and Zhang (2022) proposed an iterative weighted PFCM that not only adopted the principle of maximum entropy construct a new objective function and redesigned the weight coefficient but also determined the optimal number of clusters. Wu and Peng (2023) combined PFCM with type-2 fuzzy set to enhance the initilization and noise sensitivity of the original PFCM. Besides, the PFCM is also integrated with instance-level infomation, i.e., labeled patterns, to become semi-supervised clustering (Antoine et al. 2022).

The PFCM algorithm can achieve good performance in many real-world applications. However, the combination of evolutionary methods with conventional clustering algorithms always provides better performance. Thus, the next sub-section will review some meta-heuristic algorithms that are used in the proposed methods.

2.4 Multi-objective optimization algorithm

Multi-objective optimization deals with more than one objective function. In many real-world cases, several objectives must be optimized simultaneously. In considering multi-objective optimization, it is difficult to compare one solution with another. Therefore, a domination term is applied. Suppose that there are two solutions, \({x}_{1}\) and \({x}_{2}\). Solution \({x}_{1}\) dominates \({x}_{2}\) if \({x}_{1}\) has a better objective value for at least one of the objective functions and is not worse with respect to the remaining objective functions. A non-dominated solution which has no solution can be found that dominates it. These non-dominated solutions are recorded in Pareto optimal solutions. The goal of multi-objective optimization is to find the entire Pareto front. The non-dominated and Pareto optimality are shown in Fig. 1. The two objectives F1 and F2 are minimized simultaneously. Solutions X1, X2, X3, X4, X5, and X6 are not dominated by any other solution. Therefore, the set represents the Pareto optimal set.

Fig. 1
figure 1

Non-domination and Pareto optimality

Full size image

2.4.1 Multi-objective genetic algorithm

Genetic algorithm (GA) is an optimization technique that simulates the phenomenon of natural selection, described by Charles Darwin. The basic theory of GA was proposed by Holland (1975). In GA, the characteristics of the population are expressed using genotypes, and are called chromosomes. Each chromosome represents a potential solution to a problem. GA has three main steps: (1) selection, (2) crossover, and (3) mutation.

Deb et al. (2002) proposed a fast and elitist multi-objective GA (NSGA-II) which not only contains non-dominated sorting, but also uses elitism to accelerate convergence. NSGA-II uses the fast non-dominated sorting process to compare each solution. The parent and offspring are merged and compared to find all non-dominated solutions. If identical non-dominated fronts are produced, then values are compared to pick a better solution as the next parent using crowding distance.

The non-dominated sorting process for selecting elitist offspring is illustrated in Fig. 2.

Fig. 2
figure 2

The non-dominated sorting process for selecting elitist offspring

Full size image

2.4.2 Multi-objective particle swarm optimization algorithm

PSO is a heuristic technique proposed by Eberhart and Kennedy (1995). In the PSO algorithm, potential solutions are called particles, and each particle corresponds to a fitness value. Each particle has its velocity and position, and these are corrected by individual and group search experience.

In PSO, particles’ velocities are dynamically adjusted according to their historical behaviors, and the function is evaluated with the new coordinate for every iteration.

For multi-objective applications, Li (2003) proposed the non-dominated sorting particle swarm optimizer (NSPSO). The NSPSO compares all personal best solutions of all particles and their offspring in the population to find all dominant solutions. If two first non-dominated fronts are produced, then values are compared to pick a better solution as the next particle using crowding distance.

2.4.3 Multi-objective gradient evolution algorithm

The gradient evolution (GE) algorithm was proposed by Kuo and Zulvia (2015). It was developed from the Newton–Raphson algorithm. The GE algorithm consists of three operators, namely vector updating, jumping, and refreshing. Vector updating is the main operator in the GE algorithm, and is responsible for exploitation. The function used in vector updating was inspired by the updating rule in the Newton–Raphson algorithm. Vector updating is continued by vector jumping, which performs wider exploration.

The vector updating rule controls the vector movement to reach a better position. It consists of two parts. The first part is a gradient-based updating rule, and the second part is the acceleration factor. To expand the exploration, a random number \({r}_{g}\) is added to the updating rule. The updating rule by GradientMove is:

$$ {\text{Gradient Move}} = { }\left( {r_{g} \cdot \frac{{\Delta x_{ij}^{t} }}{2}} \right){ } \cdot \left( {\frac{{x_{ij}^{W} - x_{ij}^{B} }}{{x_{ij}^{W} - 2x_{ij}^{t} + x_{ij}^{B} }}} \right),{ }\forall {\text{j}} = 1, \ldots ,{\text{D}}, $$
(20)
$$ \Delta x_{ij}^{t} = \left( {\frac{{\left| {x_{ij}^{t} - x_{ij}^{B} } \right| + \left| {x_{ij}^{W} - x_{ij}^{t} } \right|}}{2}} \right),\forall j = 1, \ldots ,D, $$
(21)

where \({X}_{i}^{B}\) is a neighbor of vector i that has better fitness, and \({X}_{i}^{W}\) is a neighbor of vector i that has worse fitness.

The acceleration factor Acc is also embedded to accelerate the convergence of each vector. The Acc, defined in Eq. (22), is also multiplied by a random number \({r}_{a}\)~N (0, 1). This ensures that each vector has a different step size:

$$Acc={r}_{a}\cdot \left({y}_{j}-{x}_{ij}^{t}\right), \forall \mathrm{j}=1,\dots ,\mathrm{D},$$
(22)

where Y is the best vector.

Finally, vector updating is written as:

$${u}_{ij}^{t}={x}_{ij}^{t}-\mathrm{ Gradient Move}+\mathrm{Acc},$$
(23)
$$ u_{ij}^{t} = x_{ij}^{t} - { }\left( {r_{g} \cdot \frac{{\Delta x_{ij}^{t} }}{2}} \right){ } \cdot \left( {\frac{{x_{ij}^{W} - x_{ij}^{B} }}{{x_{ij}^{W} - 2x_{ij}^{t} + x_{ij}^{B} }}} \right) + r_{a} \cdot \left( {y_{j} - x_{ij}^{t} } \right),{ }\forall {\text{j}} = 1, \ldots ,{\text{D}}, $$
(24)

where \({U}_{i}^{t}\) is the vector transition.

Because this process involves better and worse vectors, it requires an additional procedure for best and worst vectors. If \({X}_{i}^{t}\) is the best vector \({B}^{t}\), then \({x}_{ij}^{B}\) is replaced with \({b}_{j}\), as defined in Eq. (25):

$$ b_{j} = x_{ij}^{t} - \Delta x_{ij}^{t} , \forall {\text{j}} = 1, \ldots ,{\text{D and}} $$
(25)
$$ \Delta x_{ij}^{t} = \left( {\frac{{{\upgamma } + \left| {x_{ij}^{W} - x_{ij}^{t} } \right|}}{2}} \right),{ }\forall {\text{j}} = 1, \ldots ,{\text{D}}. $$
(26)

Similarly, if the worst vector is \({W}^{t}\), then \({x}_{ij}^{W}\) is replaced with \({w}_{j}\), as defined in Eq. (27):

$$ w_{j} = x_{ij}^{t} + \Delta x_{ij}^{t} , \forall {\text{j}} = 1, \ldots ,{\text{D and}} $$
(27)
$$ \Delta x_{ij}^{t} = { }\left( {\frac{{\left| {x_{ij}^{t} - x_{ij}^{B} } \right| + {\upgamma }}}{2}} \right),{ }\forall {\text{j}} = 1, \ldots ,{\text{D}}, $$
(28)

where \(\upgamma \) is a pre-defined parameter, and is defined as the initial step size. Therefore, it is a static or dynamic number, which decreases as the number of iterations increases.

Vector jumping can avoid local optima. The GE algorithm sets a jumping rate \({J}_{r}\) to determine whether a vector jumps or not. Vector jumping is defined as the following equation:

$$ u_{ij}^{t} = - u_{ij}^{t} + r_{m} \cdot \left( {u_{ij}^{t} - x_{kj}^{t} } \right), \forall {\text{j}} = 1, \ldots ,{\text{D}}, $$
(29)

where \({x}_{kj}^{t}\) is any random neighbor vector, \(\forall \mathrm{i}\ne k\), and \({r}_{m}\) is a random number within [0,1].

Vector refreshing is performed on a vector which is stuck in a position. The GE also records the updating history of vector i, which is rotated by \({s}_{i}\in \left[\mathrm{0,1}\right]\). If \({s}_{i}\) is less than the refreshing rate, vector i must be regenerated, and the newly generated vector, \({s}_{i}\), is set to one. \({s}_{i}\) is reduced by the following equation:

$${s}_{i}={s}_{i}-{\varepsilon \cdot s}_{i},$$
(30)

where \(\varepsilon \) is the reduction rate.

Kuo and Zulvia (2020) proposed a GE-based K-means algorithm which considers two objectives. It tries to minimize dissimilarity within the cluster, and maximize cluster separateness.

3 Methodology

This section introduces the proposed multi-objective clustering algorithms and the possibilistic intuitionistic fuzzy c-means (PIFCM) algorithm.

3.1 Objective functions

The proposed methods consider two objective functions: (1) global cluster compactness (π), and (2) fuzzy separation (Sep) (Yang et al. 2015), which will be optimized simultaneously. Given the information of n data points and c clusters, the global compactness π of a solution represented by the cluster centers is defined as:

$$\uppi =\sum_{j=1}^{c}\frac{{\sum }_{i=1}^{n}{u}_{ij}^{m}{d}_{ij}({x}_{i, }{v}_{j})}{{\sum }_{j=1}^{n}{u}_{ij}}.$$
(31)

In Eq. (31), the term \({\sum }_{i=1}^{n}{u}_{ij}^{m}{d}_{ij}({x}_{i, }{v}_{j})\) and \({\sum }_{j=1}^{n}{u}_{ij}\) are represented for the variation \({\sigma }_{j}\) and the fuzzy cardinality \({n}_{j}\) of the \({j}^{th}\) cluster, respectively (Mukhopadhyay et al. 2009). Herein, \({u}_{ij}\) is the membership degree of data instance \({x}_{i}\) to cluster \(j\), and \({d}_{ij}({x}_{i, }{v}_{j})\) is the distance between \({x}_{i}\) and cluster center \({v}_{j}\), which is defined in Sect. 2.1. For each cluster, the cluster compactness is the ratio of \({\sigma }_{j}/{n}_{j}\). Thus, the global compactness is calculated as a summation of cluster compactness for all clusters. A good partition is indicated by a low global cluster compactness.

To calculate the fuzzy separation, the cluster center \({v}_{j}\) is considered as the center of a fuzzy set that contains the remaining cluster centers \({v}_{k}\) in which \(\left\{{v}_{k}|1\le k\le c, k\ne j\right\}.\) The membership degree of each cluster center \({v}_{k}\) to \({v}_{j},j\ne k\) is calculated as follows:

$${\mu }_{jk}={\left({ \sum _{l=1,l\ne k}^{c}\left(\frac{{d}_{kj}({{v}_{k},v}_{j})}{{d}_{kl}({{v}_{k},v}_{l})}\right)}^{\frac{1}{m-1}}\right)}^{-1}, j\ne k.$$
(32)

Subsequently, the fuzzy separation Sep is a distance-based measure between the cluster centers which is defined by the product of membership degree and distance of each cluster center \({v}_{k}\) to \({v}_{j}\):

$$Sep=\sum_{j=1}^{c}\sum _{k=1, j\ne k}^{c}{\mu }_{jk}^{m}{d}_{jk}({{v}_{j},v}_{k}).$$
(33)

To obtain compact clusters, the measure π must be as small as possible or minimized. Conversely, to obtain well-separated clusters, Sep should be as large as possible or maximized.

3.2 Possibilistic intuitionistic fuzzy c-means algorithm

This study proposes the PIFCM algorithm which integrates the advantages of the FCM, possibilistic c-means (PCM) algorithms, and the IFS. Thereafter, the PIFCM is combined to the multi-objective meta-heuristic algorithms to improve the clustering results. The steps of PIFCM are described below.

Step 1: Initialize the parameters. Set \(T=0\). Set up number of clusters \(c\), membership degree m, possibilistic \(\eta \), \({\gamma }_{j}\), tolerance \(\varepsilon \), Yager index \(\alpha \), and possibilistic parameters \(a\mathrm{ and }b\), and generate initial membership functions U and \(t\).

Step 2: Calculate hesitation degree \({\pi }_{ij}\) by Eq. (11), and \({{u}_{ij}}^{*}\) by Eq. (12).

Step 3: Calculate \({{v}_{j}}^{*}\) by Eq. (16), where \({u}_{ij}\) is replaced by \({{u}_{ij}}^{*}\).

Step 4: Calculate \({J}^{(T)}\) by Eq. (14).

Step 5: Update \({{{t}_{ij}}^{*}}^{(T+1)}\) by Eq. (15).

Step 6: Update \({{{u}_{ij}}^{*}}^{(T+1)}\) by Eq. (5).

Step 7: Update \({{v}_{j}}^{*(T+1)}\) by Eq. (16).

Step 8: Calculate \({J}^{(T+1)}\) by Eq. (14).

Step 9: Compare \({J}^{(T)}\) and \({J}^{(T+1)}\). If \(\left|{J}^{(T+1)}-{J}^{\left(T\right)}\right|\le \varepsilon \), then stop; otherwise, increase T by one and return to Step 5.

3.3 Multi-objective meta-heuristic algorithm-based PIFCM algorithm

PIFCM is probably not robust because the dimension dataset is large. Thus, to improve the accuracy, this study proposes meta-heuristic algorithm-based PIFCM algorithm. The main idea is to provide the meta-heuristic algorithm with a set of better initial centroids so that it can obtain good clustering results. Moreover, this study considers two objective functions as the cluster validity measurements to provide a better clustering result.

3.3.1 Multi-objective genetic algorithm-based PIFCM algorithm

This sub-section describes MOGA–PIFCM. As in GA, the MOGA–PIFCM procedure includes population initialization, fitness computation, selection, crossover, mutation, and termination criteria. In this study, the MOGA–PIFCM uses the clustering result of PIFCM to generate the initial chromosomes. Herein, each chromosome represents a set of alternative centroids. Figure 3 illustrates the solution representation. It shows that a chromosome consists of D \(\times \) K bits, where D represents the number of attributes, and K represents the number of centroids.

Fig. 3
figure 3

Solution representation

Full size image

The selection strategy process is based on the roulette wheel method (Zhao et al. 1996). Selection of parents is in accordance with the probability distribution of the fitness values. The selected chromosomes are put into the mating pool for further genetic operations. This study uses the method introduced by Krishna and Murty (1999). The probability of roulette wheel selection is defined as the following equation:

$${P}_{i}=\frac{{f}_{i}}{\sum_{j=1}^{N}{f}_{j}},$$
(34)

where the \({P}_{i}\) is the selection probability of chromosome i \(\left(1\le i\le N\right)\), \({f}_{i}\) and \({f}_{j}\) are the fitness of chromosome i and chromosome j \(\left(1\le j\le N\right)\), respectively.

The well-known rank-based evaluation function is used to evaluate the fitness functions (Gan et al. 2009):

$${f}_{i}=\beta {(1-\beta )}^{{r}_{i}-1},$$
(35)

where the \({r}_{i}\) is the rank of chromosome i, and \(\beta \in \left[\mathrm{0,1}\right]\) is a parameter which is the selective pressure of the algorithm.

In the crossover procedure, this study generates two new chromosomes using the following function (Michielssen et al. 1992):

$${X}^{\mathrm{new}}=\alpha X+\left(1-\alpha \right)Y \mathrm{and}$$
(36)
$${Y}^{\mathrm{new}}=\beta X+(1-\beta )X,$$
(37)

where \({X}^{\mathrm{new}}\) and \({Y}^{\mathrm{new}}\) are the genes of offspring after the crossover process, \(\alpha \) and \(\beta \) is a random number between 0 and 1, and \(X\) and \(Y\) are the genes of parents which are selected from all of the chromosomes.

In the mutation procedure, this study applies a function to change the genes of chromosomes. The function is represented as follows (Sumathi et al. 2008):

$${X}^{\mathrm{new}}=X+s\times r\times a, \mathrm{and}$$
(38)
$$a={2}^{-uk},$$
(39)

where \({X}^{\mathrm{new}}\) is the genes of offspring after the mutation process, s \(\in \{-\mathrm{1,1}\}\) is uniform at random, r is mutation range and the standard is 10%, u is a random number between 0 and 1, and k \(\in \left\{\mathrm{4,5},\dots .20\right\}\) is mutation precision.

The MOGA–PIFCM procedure can be described as follows:

Step 1:Set up parameters of GA including population size, crossover rate, mutation rate and cluster number.

Step 2: Initialization: Initial chromosomes are derived from PIFCM.

Step 3: Compute the two objective values as fitness functions.

Step 4: Apply non-dominated sorting to rank the current chromosomes.

Step 5: Use roulette wheel selection to select N chromosomes.

Step 6: Randomly select two chromosomes to be parent chromosomes, and check the probability of crossover to decide whether the crossover process must be applied.

Step 7: Check the probability of mutation to determine whether mutation should take place.

Step 8: Compute the two objective values as fitness functions.

Step 9: Implement non-dominated sorting for offspring and parent chromosomes.

Step 10: Select good chromosomes using crowding distance.

Step 11: Stop if the termination criterion is satisfied; otherwise, return to Step 5.

Step 12: Select the optimal solution from the set of non-dominated solutions.

3.3.2 Multi-objective particle swarm optimization-based PIFCM algorithm

Van der Merwe and Engelbrecht (2003) proposed two methods using a PSO algorithm for cluster analysis. The first method is the PSO clustering algorithm (PSOC), and the second method is the PSO-based K-means clustering algorithm (PSOKC). In this study, MOPSO–PIFCM is a hybrid of PSOC which combines the multi-objective optimization algorithm and PIFCM.

In this study, MOPSO–PIFCM uses the clustering result of PIFCM to set the initial particles, and uses inertia weight to control the influence of the previous velocity. The solution representation of each particle is the same as that used in the GA.

For inertia weight, this study equilibrates the global search ability and local search ability. When the inertia weight is large, PSO tends to exploitation, and is similar to global search methods. When inertia weight is smaller, PSO tends to exploration, and can find the best value in the local area. This is also similar to local search methods.

Initially, a large inertia weight is used to ferform an overall search. Then, it is reduced as the number of iterations increases to achieve convergence (Shi and Eberhart 1998). The inertia weight is as follows (Li et al. 2011):

$${w}_{t}=\frac{{t}^{\mathrm{max}}-t}{{t}^{\mathrm{max}}}\times \left({w}^{\mathrm{max}}-{w}^{\mathrm{min}}\right)+{w}^{\mathrm{min}},$$
(40)

where \({w}_{t}\) is the inertia weight of the number of iterations t, \({t}^{\mathrm{max}}\) is the maximum of number of iterations t, \({w}^{\mathrm{max}}\) is the maximum inertia weight, and \({w}^{\mathrm{min}}\) is the minimum inertia weight.

In this study, the MOPSO–PIFCM uses position and velocity adjustment to obtain the optimal solution. The velocity and position of a particle are updated as follows:

$${v}_{i}^{t+1}={w}_{t}\times {v}_{i}^{t}+{c}_{1}\times {r}_{1 }\times \left({\mathrm{pBest}}_{i}-{x}_{i}^{t}\right)+{c}_{2}\times {r}_{2 }\times \left(\mathrm{gBest}-{x}_{i}^{t}\right) \mathrm{and}$$
(41)
$${x}_{i}^{t+1}={x}_{i}^{t}+{v}_{i}^{t+1},$$
(42)

where \({r}_{1}\) and \({r}_{2}\) are two random numbers uniformly distributed between 0 and 1, and \({c}_{1}\) and archive as a repository for non-dominated solutions and choosing members of the archive to direct further search. The elite archive accepts a new position of a particle if it is non-dominated by all the stored solutions. All dominated members of the archive are deleted.

The selection of pBest simply replaces the previous best experience with the current position if the former does not dominate the latter. This is implemented using the archive members that dominate the fewest particles in the current iteration as the gBest (Mostaghim and Teich 2003).

The MOPSO–PIFCM procedure is as follows:

Step 1:Set up parameters including population size, maximum velocity, inertia weight, two learning factors, and cluster number \(c\).

Step 2: Set up the initial particles, from PIFCM.

Step 3: Compute the two objective values as fitness functions.

Step 4: Implement non-dominated sorting.

Step 5: Find pBest and gBest.

Step 6: Calculate inertia weight.

Step 7: Update the position and velocity of each particle by Eqs. (41) and (42).

Step 8: Compute the two objective values as fitness functions.

Step 9: Implement non-dominated sorting including new particles and pBest.

Step 10: Generate elitist particles.

Step 11: Stop if the termination criterion is satisfied; otherwise, return to Step 5.

Step 12: Select the optimal solution.

3.3.3 Multi-objective gradient evolution-based PIFCM algorithm

In this study, the proposed MOGE–PIFCM improves the conventional GE algorithm and combines PIFCM. The improvements of the GE algorithm include the modification of vector updating to be applied to multi-objective problems, and the crowding distance to manage the diversity of the solutions in the archive. Similarly, this study also considers two objective functions as the cluster validity measurements.

PIFCM is responsible for providing a good initial solution for MOGE–PIFCM. The solution representation of each vector is the same as that used in GA. To deal with more than one objective, an archive management strategy is applied, which uses a crowding distance concept to maintain a good spread of solutions.

The MOGE–PIFCM procedure is as follows:

Step 1:Set up parameters including population size, jumping rate, refreshing rate, and cluster number \(c\).

Step 2: Set up the initial vectors, from PIFCM.

Step 3: Compute the two objective values as fitness functions.

Step 4: Perform non-dominated sorting.

Step 5: Find the best vector and worst vector, and record the best vector.

Step 6: Calculate the vector updating by Eq. (24).

Step 7: Calculate the vector jumping by Eq. (29).

Step 8: Calculate the vector refreshing.

Step 9: Compute the two objective values as fitness functions.

Step 10: Implement non-dominated sorting including new vectors and old vectors.

Step 11: Generate elitist vectors.

Step 12: Stop if the termination criterion is satisfied; otherwise, return to Step 5.

Step 13: Select the optimal solution.

3.4 Selecting the optimal solution

In multi-objective optimization problems, the solution in the Pareto front usually contains multiple options which do not dominate each other. The final solution is usually picked up randomly from the set of non-dominated solutions, since these solutions are considered equal. This study adopts a method for selecting the optimal solution from Pareto non-inferior solutions, proposed by Wang et al. (2017). The performance-price ratio is used as a reference to construct the average variability with adjacent non-inferior solutions corresponding to the objective function values.

The average variability is the average value of the slopes of the lines connecting any point except endpoints with two adjacent points. Let \({{k}_{1}}^{(m)}\) and \({{k}_{2}}^{(m)}\) be the average variability of the two objective values \({{f}_{1}}^{(m)}\) and \({{f}_{2}}^{(m)}\) of Pareto non-inferior solution \({x}^{(m)}\), respectively. The average variability is defined as:

$${{k}_{1}}^{(m)}=\frac{1}{2}\left(\frac{{{f}_{2}}^{(m)}-{{f}_{2}}^{(m-1)}}{{{f}_{1}}^{(m)}-{{f}_{1}}^{(m-1)}}+\frac{{{f}_{2}}^{(m+1)}-{{f}_{2}}^{(m)}}{{{f}_{1}}^{(m+1)}-{{f}_{1}}^{(m)}}\right) , m = 2, 3\dots (M-1)\mathrm{ and}$$
(43)
$${{k}_{2}}^{(m)}=\frac{1}{2}\left(\frac{{{f}_{1}}^{(m)}-{{f}_{1}}^{(m-1)}}{{{f}_{2}}^{(m)}-{{f}_{2}}^{(m-1)}}+\frac{{{f}_{1}}^{(m+1)}-{{f}_{1}}^{(m)}}{{{f}_{2}}^{(m+1)}-{{f}_{2}}^{(m)}}\right), m = 2, 3\dots \left(M-1\right).$$
(44)

The average variability of the endpoints in the Pareto front is defined as:

$${{k}_{1}}^{(1)}=\frac{{{f}_{2}}^{(2)}-{{f}_{2}}^{(1)}}{{{f}_{1}}^{(2)}-{{f}_{1}}^{(1)}},$$
(45)
$${{k}_{2}}^{(1)}=\frac{{{f}_{1}}^{(2)}-{{f}_{1}}^{(1)}}{{{f}_{2}}^{(2)}-{{f}_{2}}^{(1)}},$$
(46)
$${{k}_{1}}^{(M)}=\frac{{{f}_{2}}^{(M)}-{{f}_{2}}^{(M-1)}}{{{f}_{1}}^{(M)}-{{f}_{1}}^{(M-1)}} ,\mathrm{ and}$$
(47)
$${{k}_{2}}^{(M)}=\frac{{{f}_{1}}^{(M)}-{{f}_{1}}^{(M-1)}}{{{f}_{2}}^{(M)}-{{f}_{2}}^{(M-1)}}.$$
(48)

Then, the sensitivity ratio, which is similar to the performance-price, ratio is obtained, and a quantitative method is developed to evaluate Pareto non-inferior solutions. The sensitivity ratio reflects the sensitivity degree of average variability in the objective function values. The sensitivity ratio is defined as:

$${{\delta }_{1}}^{(m)}=\frac{{{k}_{1}}^{(m)}}{{{f}_{1}}^{(m)}}, m = 1, 2\dots M\; \mathrm{and}$$
(49)
$${{\delta }_{2}}^{(m)}=\frac{{{k}_{2}}^{(m)}}{{{f}_{2}}^{(m)}}, m = 1, 2\dots M.$$
(50)

For comparison, the sensitivity ratio must be non-dimensionalized. It is defined as:

$${{\varepsilon }_{1}}^{(m)}=\frac{{{\delta }_{1}}^{(m)}}{{\sum }_{i=1}^{M}{{\delta }_{1}}^{(i)}} , m = 1, 2\dots M \, \mathrm{and}$$
(51)
$${{\varepsilon }_{2}}^{(m)}=\frac{{{\delta }_{2}}^{(m)}}{{\sum }_{i=1}^{M}{{\delta }_{2}}^{(i)}} , m = 1, 2\dots M.$$
(52)

Finally, the solution corresponding to \({(\Delta \varepsilon )}_{min}\) is the unbiased and good solution which is simultaneously most suitable for \({{f}_{1}}^{(m)}\) and \({{f}_{2}}^{(m)}\). The \({(\Delta \varepsilon )}_{min}\) is defined as:

$${(\Delta \varepsilon )}_{min}=\mathrm{min}\left\{{\Delta \varepsilon }^{1},{\Delta \varepsilon }^{2}\dots {\Delta \varepsilon }^{M}\right\} \, \mathrm{and}$$
(53)
$${\Delta \varepsilon }^{(m)}=\left|{{\varepsilon }_{1}}^{(m)}-{{\varepsilon }_{2}}^{(m)}\right| , m = 1, 2\dots M.$$
(54)

4 Experimental results

This section presents the results of experiments conducted in this study to evaluate the performance of the proposed clustering algorithms. Fifteen datasets from the UCI machine learning repository were used to test the functions of the proposed algorithms.

4.1 Datasets

This research used fifteen datasets including Ukm, Wine, Wbc, Tae, Vehicle, Pima, Iris, Breast, Liver, Banknote, Audit, Fertility, Seed, Haberman, and Vertebral to validate the clustering performance. In addition, the Wbc, Wine, and Pima datasets have outliers. Of these three datasets, Wbc has 239 noise points (35%), Wine has 10 noise points (5.6%), and Pima has 268 noise points (34.9%). Table 1 shows the details of each dataset.

Table 1 The parameters of datasets
Full size table

4.2 Performance measurement

To compare clustering results, this study used two clustering validation indices as the performance measurement. The first index is the clustering accuracy, which depends on the correct cluster (Graves and Pedrycz, 2010).

The second index is the Adjusted Rand Index (ARI) which is a popular measure for comparing clustering results (Hubert and Arabie 1985; Rand 1971; Vinh et al. 2010). Given a set of n objects S, suppose U = {\({u}_{1}, {u}_{2},\dots , {u}_{c}\)} and V = {\({v}_{1}, {v}_{2},\dots , {v}_{c}\)} represent two different partitions of the objects in S. Let \({n}_{ij}\) be the count in both the predicted cluster \({u}_{i}\) and the correct cluster \({v}_{j}\). The notations are described in the contingency table (Table 2).

Table 2 Contingency table
Full size table

The ARI is computed as follows:

$$ ARI = \frac{{{{\sum\nolimits_{ij} {\left( {\begin{array}{*{20}c} {n_{ij} } \\ 2 \\ \end{array} } \right) - \left[ {\sum\nolimits_{i} {\left( {\begin{array}{*{20}c} {a_{i} } \\ 2 \\ \end{array} } \right)\sum\nolimits_{j} {\left( {\begin{array}{*{20}c} {b_{j} } \\ 2 \\ \end{array} } \right)} } } \right]} } \mathord{\left/ {\vphantom {{\sum\nolimits_{ij} {\left( {\begin{array}{*{20}c} {n_{ij} } \\ 2 \\ \end{array} } \right) - \left[ {\sum\nolimits_{i} {\left( {\begin{array}{*{20}c} {a_{i} } \\ 2 \\ \end{array} } \right)\sum\nolimits_{j} {\left( {\begin{array}{*{20}c} {b_{j} } \\ 2 \\ \end{array} } \right)} } } \right]} } {\left( {\begin{array}{*{20}c} n \\ 2 \\ \end{array} } \right)}}} \right. \kern-0pt} {\left( {\begin{array}{*{20}c} n \\ 2 \\ \end{array} } \right)}}}}{{{{\frac{1}{2}\left[ {\sum\nolimits_{i} {\left( {\begin{array}{*{20}c} {a_{i} } \\ 2 \\ \end{array} } \right) + \sum\nolimits_{j} {\left( {\begin{array}{*{20}c} {b_{j} } \\ 2 \\ \end{array} } \right)} } } \right] - \left[ {\sum\nolimits_{i} {\left( {\begin{array}{*{20}c} {a_{i} } \\ 2 \\ \end{array} } \right)\sum\nolimits_{j} {\left( {\begin{array}{*{20}c} {b_{j} } \\ 2 \\ \end{array} } \right)} } } \right]} \mathord{\left/ {\vphantom {{\frac{1}{2}\left[ {\sum\nolimits_{i} {\left( {\begin{array}{*{20}c} {a_{i} } \\ 2 \\ \end{array} } \right) + \sum\nolimits_{j} {\left( {\begin{array}{*{20}c} {b_{j} } \\ 2 \\ \end{array} } \right)} } } \right] - \left[ {\sum\nolimits_{i} {\left( {\begin{array}{*{20}c} {a_{i} } \\ 2 \\ \end{array} } \right)\sum\nolimits_{j} {\left( {\begin{array}{*{20}c} {b_{j} } \\ 2 \\ \end{array} } \right)} } } \right]} {\left( {\begin{array}{*{20}c} n \\ 2 \\ \end{array} } \right)}}} \right. \kern-0pt} {\left( {\begin{array}{*{20}c} n \\ 2 \\ \end{array} } \right)}}}}. $$
(55)

The two selected validation indices belong to the group of the external indices. The external validation indices measure the similarity between the clustering result obtained by the proposed algorithms and the true class labels. ARI and accuracy are not an exception. However, the ARI are calculated based on the pair-counting measures in the contingency table, while the accuracy is computed by the sum of all the objects of one-to-one mapping between the obtained clusters and true labels. ARI and accuracy have been used simultaneously for clustering evaluation in many studies (Cao et al. 2017, 2013; Chen et al. 2016; Chen and Huang 2019).

4.3 Parameter settings

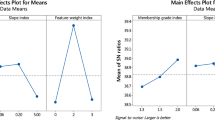
The parameters should be pre-determined before the computational experiment is conducted because different parameters will influence the experiment results. First, the level of each parameter was determined based on previous studies. Thereafter, this study used the Taguchi method to determine the parameters for the PIFCM algorithm and the multi-objective meta-heuristic algorithms (Kackar 1985; Taguchi 1986). Every algorithm was run 30 times, and the number of iterations was set as 100. The other parameters were determined using Taguchi methods for each dataset.

The α in the Yager-generating function was set as 2 (Lin 2014) to calculate the hesitation degree. Four parameters must be determined for the PIFCM algorithm, namely the relative importance of the fuzzy membership a, relative importance of typicality values b, influence of membership grades m and influence of typicality values \(\eta \). The relative importance of fuzzy membership and typicality values were constrained to a + b = 1. Thus, b = 1-a and the relative importance of fuzzy membership were set as 0.2, 0.5, and 0.8. Table 3 shows the three different levels of factors for the PIFCM algorithms.

Table 3 Parameters setup for the PIFCM algorithm
Full size table

In GA, the population size, crossover rate, and mutation rate must be determined. According to previous work, this study determined three different levels of factors (Michielssen et al. 1992).

Four parameters must be determined for the PSO algorithm, namely the number of particles (n), learning factor 1 (c1), learning factor 2 (c2), and inertia weight (W). The values for c1 and c2 were 0.5 and 1.495, and 2 (Jiang et al. 2014; Kuo et al. 2012). The maximum inertia weight was set as 0.9, and reduced until it reached 0.4, according to a previous study (Shi 2001).

For the GE algorithm, the number of vectors, jumping rate and refreshing rate must be determined. Table 4 summarizes all the parameters se tup for multi-objective-based clustering algorithms. The parameters of the proposed algorithms were determined by Taguchi method. The L9(33) orthogonal array was used to analyze the parameters in this study.

Table 4 Parameters setup for all metaheuristic-based PIFCM clustering algorithms
Full size table

The Taguchi method using the Minitab 17 package can show the best combination of parameters for the proposed algorithms. Tables 5 and 6 show the best combination of parameters for each dataset.

Table 5 The parameters of PIFCM for all datasets
Full size table
Table 6 The parameters of meta-heuristic-based PIFCM algorithms for all datasets
Full size table

4.4 Computational results

Since each algorithm is a heuristic, each run will give a different result. Therefore, running the algorithm multiple times will yield a better chance of finding a good result. The average result is adopted after multiple runs. In this study, each algorithm was run 30 times for each dataset, and the average accuracy and the ARI as the performance measurement were then calculated. Three proposed multi-objective algorithms were compared with other existing algorithms. Table 7 shows the results in terms of accuracy for each dataset, while Table 8 shows the results in terms of ARI.

Table 7 The computation results in terms of accuracy
Full size table
Table 8 The computation results in terms of ARI
Full size table

According to the results, the three proposed multi-objective algorithms based on PIFCM exhibited better performances than those of the other clustering algorithms on most of the tested datasets. For instance, the three proposed multi-objective algorithms obtained better results on 12 (Ukm, Wine, Wbc, Tae, Vehicle, Pima, Liver, Audit, Fertility, Seed, Haberman, and Vertebral) of the 15 tested datasets in terms of all performance validation indices.

For outlier datasets, the MOGE–PIFCM achieved better results for the Wine and Pima datasets, while the MOPSO–PIFCM and MOGA–PIFCM achieved better results for the Wbc dataset, with respect to accuracy comparison. Compared with the MOGE–PIFCM and IFCM performances with outlier datasets, the MOGE–PIFCM always achieved better results than the IFCM. This is reasonable, since hybridizing evolutionary methods (GA, PSO, and GE) with PIFCM can remove the drawback caused by initialization of PIFCM, and enhance the clusteirng result. Of the three algorithms, i.e., MOGE, MOGA, and MOPSO, the combination of MOGE with PIFCM achieved the best results due to its advantage of vector jumping, which can handle outliers. Therefore, the MOGE–PIFCM algorithm can address the outlier problem.

Because GA was originally proposed for binary coding, and was later modified for continuous coding certain objectives (π or Sep) often easily dominate the results. Therefore, GA is affected by continuous code, which causes it to generate unstable results.

Next, the performances of multi-objective-based PIFCM and single-objective-based PIFCM algorithms were compared. MOGA–PIFCM and GA–PIFCM were compared first. The accuracy values of the all the tested datasets showed that there is no significant difference between these GA-based algorithms. Because GA was originally proposed for binary coding and was later modified for continuous coding, the GA–PIFCM algorithm with single objective (π or Sep) often easily dominates the results.Thus MOGA–PIFCM algorithm is affected by continuous coding, which causes it to generate unstable results.

In the comparison between the MOPSO–PIFCM and PSO–PIFCM algorithms, the MOPSO–PIFCM produced better results in eleven datasets (Ukm, Wbc, Tae, Vehicle, Iris, Breast, Liver, Audit, Fertility, Seed, and Vertebral) in terms of accuracy. Compared with GE–PIFCM, the MOGE–PIFCM achieves better results in ten datasets in terms of accuracy (Ukm, Wine, Wbc, Tae, Vehicle, Pima, Breast, Banknote, Audit, and Fertility). For the five remaining datasets, there was not much difffence between MOGE and GE-based PIFCM algorithms. It can be concluded that the clustering results of both MOPSO–PIFCM and MOGE–PIFCM algorithms are better than those of single objective PSO–PIFCM and GE–PIFCM, respectively. The multi-objective-based algorithms achieve this because they can balance the cluster compactness and fuzzy seperation to enhance the clustering result. Moreover, employing the proposed technique to select the optimal solution in the Pareto front contributes to improving the obtained results. In addition, it can be recognized that the MOGE–PIFCM algorithm is the best in terms of accuracy with a dominant result in seven datasets (Ukm, Wbc, Wine, Tae, Vehicle, Pima, and Audit).

The experiment results also show that the comparison results in terms of ARI are similar to those of comparison in terms of accuracy. The three proposed multi-objective-based PIFCM algorithms had the highest ARI value for seven datasets. The MOGE–PIFCM was also the best clustering algorithm in this experiment, achieving the best results for nine of the fifteen datasets.

Next, computational times were compared, as shown in Table 9. According to the comparison, the meta-heuristic-based PIFCM algorithms require more time than the IFCM and PIFCM algorithms. This is reasonable because the meta-heuristic-based PIFCM algorithms use the clustering result of PIFCM to generate the initial clusters. However, the computational time required by the meta-heuristic-based PIFCM algorithms is acceptable since the computational time of most datasets is less than two minutes. Only one dataset, Vehicle, which contains 846 instances and 18 attributes, requires more comptation time. In addition, because the GE algorithm has more complex updating rules, it requires more time. Thus, the MOGE–PIFCM requires the greatest anount of time of all the compared algorithms. To reduce the required computational time, it may be feasible to conduct feature selection. In addition, from the current computational result, it seems that most meta-heuristics can improve clustering performance. Thus, choosing an easier meta-heuristic is a viable alternative.

Table 9 The computational time (in second)
Full size table

4.5 Statistical hypothesis

In this study, to prove whether the proposed clustering algorithms are significantly superior to other clustering algorithms or not, a statistical hypothesis was conducted. The t test was, and the significance level α was set at 0.05. All statistical hypotheses were implemented on Minitab 17. The procedure of the statistic test is as follows. First, the two-sides test, in which the null hypothesis is “A = B”, is conducted. If there is no evidence to reject the null hypothesis in the first test, the testing procedure is terminated. Then, it can be concluded that there is no significant difference between the two compared algorithms. If the null hypothesis in the first test is rejected, the second test is performed to determine whether “A < B” or “A > B”. This procedure is implemented for all the tested datasets.

Table 10 shows the comparison results of single objectives and multiple objectives for all datasets. The symbol + means that the proposed algorithm performs better. Similarly, the symbol = means that there is no significant difference between the two compared algorithms, while the symbol – signifies that the proposed algorithm performs worse.

Table 10 The comparison results of single objective and multiple objectives
Full size table

According to Table 10, the MOGA–PIFCM is significantly better than GA-PIFCM(π) for seven datasets, and there is no difference between MOGA–PIFCM and GA–PIFCM(π) for eight datasets. Compared with GA–PIFCM(Sep), MOGA–PIFCM obtains better results for three datasets, and worse results for three datasets, while there is no difference for the remaining datasets. Thus, it can be concluded that MOGA–PIFCM has better performance than GA–PIFCM(π). However, there is no significant difference between MOGA–PIFCM and GA–PIFCM(Sep).

The proposed MOPSO–PIFCM yields better results for seven datasets compared with PSO–PIFCM(π), and ten datasets compared with PSO–PIFCM(Sep). There are two datasets for which MOPSO–PIFCM obtains worse results comparedg with PSO–PIFCM(π). For the remaining datasets, there is no difference between MOPSO–PIFCM and other algorithms. Thus, it can be concluded that MOPSO–PIFCM has a better performance than the single-objective PSO algorithm.

Compared with GE–PIFCM(π), MOGE–PIFCM has better performance for six datasets, and only one dataset yields a worse result. For the remaining datasets, there is no difference between MOGE–PIFCM and GE–PIFCM(π) perormance. GE–PIFCM(Sep) achieves better results for ten datasets, equal results for three datasets, and worse results for two datasets. This is sufficent evidence that MOGE–PIFCM is better than a single-objective GE algorithm. The three proposed multi-objective algorithms, therefore, all demonstrate better performance than the other compared algorithms.

5 Conclusions

This study proposed a PIFCM algorithm, which combines IFS and PFCM algorithms. Meta-heuristic algorithms were employed to improve clustering performance and avoid local optimal solutions of the PIFCM algorithm. Three multi-objective meta-heuristic algorithms, namely MOGA, MOPSO, and MOGE, were integrated with the PIFCM algorithm. For multi-objective optimization problems, selecting an optimal solution in the Pareto front is also important. Thus, this study also employed a new technique to select the clustering result for the three proposed multi-objective-based algorithms. The clustering performance of the proposed algorithms was verified using fifteen datasets from the UCI machine learning repository. To implement the proposed algorithms, parameters were determined by Taguchi method. This study applied the Taguchi method to find the optimal combination of parameters for each algorithm on each tested dataset. To evaluate the clustering results, accuracy and ARI were selected as two cluster validation indices. In addition, the results of the proposed multi-objective meta-heuristic-based PIFCM algorithms were compared with those of a conventional IFCM algorithm, a PIFCM algorithm, and its single-objective clustering algorithms. The experiment results showed that the proposed multi-objective-based PIFCM algorithms achieved better performance than the single-objective-based PIFCM algorithms in terms of both accuracy and ARI. In addition, a comparison between the three proposed multi-objective algorithms was made. The clustering result of the MOGE–PIFCM algorithm was better than those of the MOGA–PIFCM and MOPSO–PIFCM algorithms in most of the tested datasets.

However, in this study, the parameter \(\alpha \) in the Yager-generating functions was applied based on previous studies. In the future research, this parameter will be optimized by the meta-heuristic algorithms to improve the accuracy of the clustering results. In addition, all problems in this study were continuous. Thus, future work will extend the results of this study for binary and discrete problems, since many real problems involve discrete and binary variables. Finally, the proposed algorithms will also be tested for high dimensional data in the future research.