1 Introduction

For the analysis and design of slope stability or the safety of tunneling or embankments, the long-term settlement calculation of these infrastructures is vital in order to control the post construction settlement within an allowed range (Shen et al. 2014; Meng et al. 2018; Yang et al. 2019; Zhang et al. 2020; Zhu et al. 2020). Currently, the most widely used methods to calculate the long-term settlement of soft clays is the standard or advanced elastic viscoplastic models (Yin et al. 2010, 2015; Tan et al. 2018). However, the determination of viscosity parameters requires a lot of time for researchers and engineers, which made it difficult to be used in practice.

Creep index \(C_{\alpha }\) is one of the key parameters when using the standard or advanced elastic viscoplastic models to calculate the long-term settlement of soft clays (Karstunen and Yin 2010; Yin et al. 2017). Although the creep index is not an intrinsic property of intact clays, it can provide a help for understanding the creep behaviors of remoulded clays (Zhang et al. 2020). Therefore, it is very important to determine the creep index quickly and accurately.

Previous studies have proved that the microstructure of soft clays has an important effect on its creep property, and the calculation formula of creep index is usually determined by regression analysis technology based on experimental data (Yin et al. 2009, 2014a; b). For example, Nakase et al. (1988) developed an empirical model involving the plasticity index \(I_{p}\) and the creep index \(C_{\alpha }\); Zeng et al. (2012) proposed an empirical model describing the relationships between the creep index \(C_{\alpha }\) and the void ratio at liquid limit \(e_{L}\) and the void ratio e; Yin et al. (2015) proposed an elastic-viscoplastic model of natural soft clay, which takes nonlinear creep into account; Zhu et al. (2016) further proposed an empirical model considering both the plasticity index \(I_{p}\) and liquid limit \(w_{L}\). However, the models proposed by Nakase et al. (1988), Zeng et al. (2012), Yin (1999), Yin et al. (2015) and Zhu et al. (2016) have fewer influencing factors and lower prediction accuracy. It cannot provide a very accurate reference for the determination of creep index \(C_{\alpha }\).

In recent years, artificial intelligence (AI) methods have been widely used in the field of geotechnical engineering (Sharma et al. 2021; Jong et al. 2021; Zhang et al. 2021). For example, Gordan et al. (2016) investigated the seismic slope stability by using the hybrid model of artificial neural networks (ANNs) and particle swarm optimization (PSO). Koopialipoor et al. (2019) predicted the safety factor (SF) of slopes by using the PSO-ANN model. Fattahi (2017) evaluated the slope stability using the adaptive neuro-fuzzy inference system (ANFIS) model. Previous studies have shown that the predictive performance of empirical models is far inferior to that of models proposed based on AI techniques; however, AI techniques may face some issues like trapping in local minima (Xiong et al. 2004; Sun et al. 2016; Zhang et al. 2016). The gene expression programming (GEP) was first proposed by Ferreira (2001, 2006) to solve some problems in genetic programming (GP). The biggest difference between the two is GEP’s use of linear fixed length expression tree (ET), which is the key to GEP’s ability to solve relatively complex problems with high performance (Jafari and Mahini 2017; Murad et al. 2019).

Considering the lack of prediction accuracy of existing models and the advantages of AI technologies, the main purpose of this study is to propose a new creep index model based on GEP technique. The biggest difference between GEP technique and most regression technologies is that when establishing the functional relationship between creep index and various parameters, GEP technology only needs to consider the possible parameters in the relationship, and does not need to specify predefined functions. The main contributions of this study can be clarified as follows:

  1. (1)

    To the best of our knowledge, this study is the first method using GEP technology to predict the creep index of soft clays in the literature;

  2. (2)

    In this paper, the influence of different parameter combinations on the prediction accuracy of the model is studied, and seven GEP models are proposed according to the results of seven combinations;

  3. (3)

    Compared with the literature models, the GEP model established in this paper considers more influencing factors for prediction of the creep index of soft clays;

  4. (4)

    Compared with other ML-based models (i.e., back propagation (BP) neural network and random forest (RF)), GEP model has relatively simple calculation formula and high prediction accuracy, which is conducive to popularization and application. In addition, in order to facilitate the application of GEP model in engineering, we developed a convenient graphical user interface.

The rest of the paper is organized as follows: Database is presented in Sect. 2. Methodologies are explained in Sect. 3. Results and discussion are presented in Sect. 4. Finally, conclusions are introduced in Sect. 5.

2 Database

The choice of input variables is vital to the accurate prediction of creep index \(C_{\alpha }\). In this study, four physical parameters (i.e., liquid limit \(w_{L}\), void ratio \(e\), plasticity index \(I_{p}\) and clay content \(CI\)) of soft clays were taken as the input variables and the creep index \(C_{\alpha }\) as the output variable. A total of 151 sets of data points collected from the literature (Shen et al. 2014; Meng et al. 2018; Tan et al. 2018; Yang et al. 2019; Zhu et al. 2020) were used to establish the GEP model. Figure 1 and Tables 1 and 2 show the frequency distribution histogram of the four input parameters, the statistical results of the database and the Pearson correlation analysis results between different parameters, respectively. As observed from Fig. 1 and Table 1, these parameters have a wide range of values, which is enough to make the proposed GEP model have better generalization and application. The 151 sets of data were randomly divided into two parts: training set (120 groups) and test set (31 groups), which were used for model establishment and evaluation, respectively.

Fig. 1
figure 1

Histograms of the four input parameters

Full size image

3 Methodology

3.1 GEP

GEP, a machine learning algorithm based on genetic algorithm (GA) and genetic programming (GP), was first proposed by Ferreira (2001). Generally speaking, GEP is mainly composed of five parts: termination condition, fitness function, terminal set, control parameters and function set. In GEP, a genome or chromosome may contain one or more genes, and a gene can be divided into a head containing terminals and functions (e.g., variables, mathematical operators and functions) and a tail containing only terminals (e.g., variables and constants). In this study, GeneXproTools5.0 software was used to establish the GEP model. The main steps of GEP establishment are summarized as follows:

  1. (1)

    Selecting an appropriate fitness function is conducive to the successful solution of the problem. In this study, the following equation was used as the fitness value:

    $$ f_{i} = 1000\left[ {1 + \sqrt {\frac{1}{m}\sum\limits_{j = 1}^{m} {\left( {Y_{i,j} - X_{i} } \right)^{2} } } } \right]^{ - 1} $$
    (1)

where \(f_{i}\) represents the fitness value and it ranges between 0 and 1000 (ideally, the fitness value is 1000); m represents the total number of chromosomes; \(Y_{i,j}\) and \(X_{i}\) represent the value predicted by the individual chromosome \(i\) for fitness case \(j\) and the monitored value for fitness case \(i\), respectively.

  1. (2)

    The sets of functions F and terminals T need to be selected. Obviously, the set of functions F consists of all the function symbols that may appear in the formula, thus giving F = {Inv, X2, 3Rt, *, /, +, −, exp, Ln}. The set of terminals T consists of input and output parameters, thus giving T = {\(w_{L}\),\(e\),\(I_{p}\),\(CI\),\(C_{\alpha }\)}.

  2. (3)

    In this study, the optimal value of each parameter in the GEP model is determined by the trial-and-error strategy, and the selected parameters are listed in Table 3.

  3. (4)

    Select the type of linking function. In the GEP model, there are many linking functions. (e.g., multiplication (×), subtraction (−), addition (+), division (/), Min, Max, CL2D {0,1}, CL2A {− 1,1}, CL3A {− 1,0,1}, CL3B {− 1,0,1}, CL3C {− 1,0,1} and AMin2 {0,1}). In this study, the linking functions of addition (+) and multiplication (×) are selected because they can provide better results than other linking functions.

  4. (5)

    Select the genetic operators. In this study, the selection of genetic operators is mainly based on the research results of Ferreira (2006), and the selected genetic operators are listed in Table 3.

Figure 2 illustrates the flowchart of GEP model.

Fig. 2
figure 2

Flowchart of GEP (Ferreira 2006)

Full size image

3.2 Empirical formulas

According to Zhang et al. (2020), some available empirical formulas are listed as follows:

  1. (1)

    Developed by Nakase et al. (1998):

    $$ C_{\alpha } = 0.00168 + 0.00033I_{p} $$
    (2)
  2. (2)

    Developed by Yin (1999):

    $$ C_{\alpha } = 0.000369I_{p} - 0.00055 $$
    (3)
  3. (3)

    Developed by Zeng et al. (2012):

    $$ C_{\alpha } = \left( { - 0.0067 + 0.0115e_{L} - 0.0016\left( {e_{L} } \right)^{2} } \right)\left( {1 + e} \right) $$
    (4)
  4. (4)

    Developed by Zhu et al. (2016):

    $$ C_{\alpha } = \left( {0.0007w_{L} - 0.0223} \right)\left( {\frac{{w_{L} }}{w}} \right)^{{0.23031 - 0.014978w_{L} }} $$
    (5)
  5. (5)

    Developed by Zhu et al. (2020):

    $$ C_{\alpha } = \left( { - 0.0274 + 0.0011w_{L} - 0.00048I_{p} } \right)\left( {\frac{w}{{w_{L} }}} \right)^{{0.7872 - 0.0369w_{L} + 0.0619I_{p} }} $$
    (6)

3.3 RF

RF, first proposed by Breiman (2001), is a supervised ML algorithm composed of decision trees. The following is a brief introduction to the RF algorithm.

The training data is drawn randomly from the distribution of the random vector S and T and assuming that \({\text{h}}_{1} \left( {\text{x}} \right)\),\({\text{h}}_{2} \left( {\text{x}} \right)\),\(\ldots\),\({\text{h}}_{k} \left( {\text{x}} \right)\) are ensemble of classifiers, then the margin function \(mg\left( {S{,}T} \right)\) can be expressed as (Breiman 2001):

$$ mg\left( {S{,}T} \right) = I\left( {{\text{h}}_{k} \left( S \right) = T} \right)v_{k} a - \mathop {\max }\limits_{{j \ne {\text{Y}}}} I\left( {{\text{h}}_{k} \left( S \right) = j} \right)v_{k} a $$
(7)

where \(I\left( \cdot \right)\) denotes the indicator function. It should be noted that the confidence in the classification is proportional to the margin.

The calculation formula of generalization error \(G_{{\text{e}}}\) is given as follows (Breiman 2001):

$$ G_{{\text{e}}} = G_{S,T} \left( {mg\left( {S,T} \right) < 0} \right) $$
(8)

where the subscripts S,T indicate that the probability is over the S,T space. More details of RF can be found in Breiman (2001).

3.4 BP

The BP neural network is generally composed of three layers of neurons, which are (1) the output layer, (2) the hidden layer, and (3) the input layer. The gradient descent algorithm is commonly used to train BP neural network by adjusting the weights to minimize the total error between the actual output and the target output. More details of BP neural network can be found in Xue (2017).

3.5 Evaluation of the proposed creep index models

In order to evaluate the prediction performance of each creep index model, three statistical indices, namely, the root mean squared error (RMSE), mean absolute percentage error (MAPE) and mean absolute error (MAE) are used in this study, and the calculation formulas are as follows:

$$ {\text{RMSE}} = \sqrt {\frac{{\sum\limits_{i = 1}^{n} {\left( {O_{i} - P_{i} } \right)^{2} } }}{n}} $$
(9)
$$ {\text{MAPE}} = \frac{1}{n}\sum\limits_{i = 1}^{n} {\left| {\frac{{O_{i} - P_{i} }}{{P_{i} }}} \right|} $$
(10)
$$ {\text{MAE}} = \frac{1}{n}\sum\limits_{i = 1}^{n} {\left| {O_{i} - P_{i} } \right|} $$
(11)

where \(O_{i}\) and \(P_{i}\) represent the actual and predicted results, respectively. n is the total number of data (n = 151). Obviously, the lower values of these three indicators, the better the prediction performance.

4 Results and discussion

In this study, different combinations of four input variables were used to obtain seven GEP models for predicting the creep index \(C_{\alpha }\) of soft clays. The optimal parameters of the first GEP model are listed in Table 3. Because the setting parameters of the other six GEP models are fine-tuned on this basis, they are not listed separately in this study.

4.1 Combination of \(CI - e\)

The expression tree of the first established GEP model consists of five sub-expression trees, as shown in Fig. 3. In Fig. 3, the constants of the first sub-expression tree (gene) \(c_{6}\) and \(c_{9}\) are 10.69 and -9.365, respectively. The constant of the third sub-expression tree \(c_{2}\) is 2.566, and the constants of the fourth sub-expression tree (gene) \(c_{6}\) and \(c_{8}\) are -0.899 and 4.90, respectively. The linking function of this model is multiplication ( ×), and the expression of the model can be written as:

$$ C_{a} = \frac{{\left( {\sqrt {CI} + CI + e \cdot CI + 2.566} \right)\left[ {\sin \left( {\frac{\sin CI + CI}{{CI}}} \right)} \right]^{ - 1} }}{{\left( {\sin CI + CI + 98.415} \right)\left( {2\sin CI + CI + e} \right)\left( {e - \tan CI - 4.409} \right)}} $$
(12)
Fig. 3
figure 3

Expression tree language (5 sub-expression trees) of the first model

Full size image

4.2 Combination of \(CI - I_{p} - e\)

The expression tree of the second established GEP model consists of two sub-expression trees, as shown in Fig. 4. In Fig. 4, the constants of the first sub-expression tree \(c_{6}\) and \(c_{7}\) are 1.17 and − 9.67, respectively. The constants of the second sub-expression tree \(c_{3}\) and \(c_{9}\) are 8.69 and − 16.94, respectively. The linking function of this model is addition ( +), and the expression of the model can be written as:

$$ C_{a} = \frac{{e^{3} }}{93.559 + 109.661e} + \frac{{\left( {CI + 16.934} \right)I_{p} }}{{e^{8.679} CI}} $$
(13)
Fig. 4
figure 4

Expression tree language (2 sub-expression trees) of the second model

Full size image

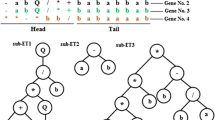
4.3 Combination of \(CI - w_{L} - e\)

The expression tree of the third established GEP model consists of three sub-expression trees, as shown in Fig. 5. In Fig. 5, the constants of the first sub-expression tree \(c_{0}\),\(c_{1}\),\(c_{5}\),\(c_{8}\) and \(c_{9}\) are − 68.312, − 88.91, 87.29, − 59.56 and 75.13, respectively. The constants of the second sub-expression tree \(c_{8}\) and \(c_{9}\) are 50.21 and 35.14, respectively. The constants of the third sub-expression tree \(c_{0}\),\(c_{6}\) and \(c_{9}\) are − 87.24, − 15.48 and 33.71, respectively. The linking function of this model is addition ( +), and the expression of the model can be written as:

$$ C_{a} = \frac{1.663}{{\left( {62.967 - CI} \right)w_{L} }} + 0.173e^{1.33} \left( {e + w_{L} } \right) \times 10^{ - 3} + \frac{{0.015w_{L} - 0.032e}}{{w_{L} }} - 0.012 $$
(14)
Fig. 5
figure 5

Expression tree language (3 sub-expression trees) of the third model

Full size image

4.4 Combination of \(CI - w_{L} - I_{p} - e\)

The expression tree of the fourth established GEP model consists of three sub-expression trees, as shown in Fig. 6. In Fig. 6, the constants of the first sub-expression tree \(c_{0}\) and \(c_{1}\) are − 3.03 and − 32.22, respectively. The constants of the second sub-expression tree \(c_{5}\), \(c_{6}\) and \(c_{7}\) are − 63.03, 79.16 and 35.75, respectively. The constant of the third sub-expression tree \(c_{1}\) is − 6.46. The linking function of this model is addition ( +), and the expression of the model can be written as:

$$ \begin{gathered} C_{a} = \frac{{2ew_{L} + 158.32e + 35.752}}{15892.85 - 4CI} + {\text{Tanh}} \left[ {0.25I_{p} - 0.25e - 1.616 + \frac{1}{{\left( {CI - 6.462} \right)e}}} \right] + \hfill \\ \, {\text{Tanh}} \left( {0.5eCI - 0.25I_{p} - 0.25e - 0.5CI - 30.706} \right) \hfill \\ \end{gathered} $$
(15)
Fig. 6
figure 6

Expression tree language (3 sub-expression trees) of the fourth model

Full size image

4.5 Combination of \(I_{p} - e\)

The expression tree of the fifth established GEP model consists of three sub-expression trees, as shown in Fig. 7. In Fig. 7, the constant of the first sub-expression tree \(c_{6}\) is 7.20. The constants of the second sub-expression tree \(c_{2}\) and \(c_{5}\) are − 20.10 and 98.72, respectively. The constant of the third sub-expression tree \(c_{6}\) is 7.20. The linking function of this model is addition ( +), and the expression of the model can be written as:

$$ C_{a} = 0.193e - \frac{4.91e}{{I_{p} }} + \frac{0.019}{{e^{1.5} I_{p} }} $$
(16)
Fig. 7
figure 7

Expression tree language (3 sub-expression trees) of the fifth model

Full size image

4.6 Combination of \(w_{L} - e\)

The expression tree of the sixth established GEP model consists of three sub-expression trees, as shown in Fig. 8. In Fig. 8, the constants of the first sub-expression tree \(c_{2}\) and \(c_{6}\) are − 52.99 and 72.32, respectively. The constants of the second sub-expression tree \(c_{2}\) and \(c_{6}\) are − 58.88 and 72.32, respectively. The constant of the third sub-expression tree \(c_{6}\) is 72.32. The linking function of this model is addition ( +), and the expression of the model can be written as:

$$ C_{a} = \frac{52.991 - e}{{5230.139w_{L} - 72.32w_{L}^{2} }} - \frac{0.814e}{{w_{L} + e}} + \frac{e}{{1.5e - e^{2} + 36.16}} $$
(17)
Fig. 8
figure 8

Expression tree language (3 sub-expression trees) of the sixth model

Full size image

4.7 Combination of \(w_{L} - I_{p} - e\)

The expression tree of the seventh established GEP model consists of two sub-expression trees, as shown in Fig. 9. In Fig. 9, the constant of the first sub-expression tree \(c_{1}\) is − 71.43. The linking function of this model is addition ( +), and the expression of the model can be written as:

$$ C_{\alpha } = \frac{{ew_{L} }}{{e^{2} w_{L} - 71.433e - 71.433}} + \frac{{e^{4} }}{{4\left( {I_{p} + \frac{{w_{L} }}{e}} \right)^{2} }} $$
(18)
Fig. 9
figure 9

Expression tree language (2 sub-expression trees) of the seventh model

Full size image

4.8 Comparison of different GEP models

The prediction accuracy of these seven GEP models in all data sets, training sets and test sets was compared, as shown in Fig. 10. As observed from Fig. 10, regardless of all data or training or test sets, the RMSE, MAE and MAPE values of the two GEP models (i.e., with combinations \(CI - w_{L} - e\) and \(CI - w_{L} - I_{p} - e\) as input, respectively) are the lowest among these seven models. For example, the RMSE, MAE and MAPE values of the GEP models (with combinations \(CI - w_{L} - e\) and \(CI - w_{L} - I_{p} - e\) as input, respectively) for all data sets are 0.0047, 0.0032 and 0.1783; 0.0045, 0.0029 and 0.1757, respectively, and they are recommended for the prediction of the creep index \(C_{\alpha }\) in engineering practice. In addition, it can be seen from Fig. 10 that different parameter combinations have a significant impact on the prediction accuracy of the model. Therefore, it is necessary to consider the influence of parameter combinations when using GEP or other neural networks to build the model.

Fig. 10
figure 10

Prediction results of different GEP models

Full size image

4.9 Comparison among the proposed models, ML-based models and existing empirical models

The prediction results of the existing five empirical models and two ML-based models (i.e., BP and RF) on all data samples are plotted in Fig. 11. The prediction performance comparisons of the two GEP models and the existing five empirical models and two ML-based models are shown in Table 4. As can be seen from Fig. 11 and Table 4, the RMSE, MAE and MAPE values of the two GEP models are 0.0045, 0.0029 and 0.1757; 0.0047, 0.0032 and 0.1783, respectively. However, the RMSE, MAE and MAPE values of the empirical models of Yin (1999), Nakase et al. (1998), Zeng et al. (2012), Zhu et al. (2020) and Zhu et al. (2016) are 0.0080, 0.0052 and 0.2497; 0.0079, 0.0053 and 0.2857; 0.0098, 0.0080 and 0.4803; 0.0097, 0.0077 and 0.5569; 0.0102, 0.0078 and 0.4801, respectively. The RMSE, MAE and MAPE values of BP and RF models are 0.0049, 0.0037 and 0.2483; 0.0056, 0.0032 and 0.2459, respectively. The above results show that the forecasting performances of the two GEP models developed in this study surpass those of the five empirical models and two ML-based models.

Fig. 11
figure 11

Prediction results of different creep index models

Full size image

4.9.1 Sensitivity analysis of variables

To study whether the two developed GEP models can capture the functional relationship between the creep index \(C_{\alpha }\) and various parameters, and also to compare with the results of sensitivity analysis in Zhang et al. (2020), a parametric study was carried out. As such, in the two developed GEP models, the desired independent variable change within the scope of the database, while the values of other variables are the same as those in Zhang et al. (2020). The variations of input variables against the creep index \(C_{\alpha }\) predicted by the two developed GEP models are shown in Figs. 12 and 13. As can be seen from Figs. 12 and 13, the creep index \(C_{\alpha }\) increases nonlinearly and monotonically with the increases in the clay content \(CI\), void ratio \(e\) and liquid limit \(w_{L}\). In regard to plasticity index \(I_{p}\), the predicted creep index \(C_{\alpha }\) increases initially with an increase in plasticity index \(I_{p}\), and when plasticity index \(I_{p}\) reaches its maximum, the creep index \(C_{\alpha }\) stabilizes as the plasticity index \(I_{p}\) continues to increase. The evolution of the predicted value of creep index \(C_{\alpha }\) with the change of the independent variable is similar at three points, which is similar to the results of the study in Zhang et al. (2020), except that the size of the creep index \(C_{\alpha }\) differs. Nevertheless, from the sensitivity analysis results of Zhang et al. (2020), it can be seen that the prediction performance of the PSO-RF model largely depends on the quality and size of the database used, so it is difficult to obtain a completely smooth correlation between output and input parameters, which merely reflects a general trend (Zhang et al. 2020). Overall, the correlations presented in Figs. 12 and 13 are consistent with the physical explanation, which confirms the reasonableness of the developed GEP model. Therefore, the GEP models developed in this study can accurately reflect the internal mechanism between the creep index \(C_{\alpha }\) and various parameters.

Fig. 12
figure 12

Predicted \(C_{\alpha }\) using GEP model combining \(CI - w_{L} - e\) against a CI b wL c e

Full size image
Fig. 13
figure 13

Predicted \(C_{\alpha }\) using GEP model combining \(CI - w_{L} - I_{p} - e\) against a CI b wL c Ip d e

Full size image

4.9.2 Graphical user interface

In order to promote the application of GEP model (Eq. (15)) in engineering, we developed a convenient graphical user interface (GUI) based on Visual Basic 6.0 software, as shown in Fig. 14. In Fig. 14, the input parameters are on the left and the formula calculation results are on the right.

Fig. 14
figure 14

Graphical user interface

Full size image

5 Conclusions

In this study, different combinations of four input variables were used to predict creep index \(C_{\alpha }\) and seven GEP models were established. The proposed GEP models are evaluated by using five empirical models and two ML-based models (i.e., BP and RF). The following conclusions can be drawn:

  1. (1)

    The two developed GEP models (i.e., with combinations \(CI - w_{L} - I_{p} - e\) and \(CI - w_{L} - e\) as input, respectively) have higher prediction precision than the available five regression models in the literature and two ML-based models (i.e., BP and RF), with the RMSE, MAE and MAPE values of 0.0045, 0.0029 and 0.1757; 0.0047, 0.0032 and 0.1783, respectively.

  2. (2)

    The results of parametric analysis of GEP model show that the creep index \(C_{\alpha }\) increases nonlinearly and monotonically with the increases in the liquid limit \(w_{L}\), clay content \(CI\), and void ratio \(e\). In regard to plasticity index \(I_{p}\), the predicted creep index \(C_{\alpha }\) increases initially with an increase in plasticity index \(I_{p}\), and when plasticity index \(I_{p}\) reaches its maximum, the creep index \(C_{\alpha }\) stabilizes as the plasticity index \(I_{p}\) continues to increase.

  3. (3)

    The GEP models proposed in this study are only suitable for prediction of creep index of soft clays, not for rock-like materials. Therefore, the applicability of the proposed models and the richness of the database need to be further studied. In addition, GEP also has some problems, such as slow convergence rate, premature convergence and easy to fall into local extreme points, which should be studied in further research.

Table 1 Statistics analysis of datasets
Full size table
Table 2 Results of Pearson correlation analysis
Full size table
Table 3 Optimal parameters of the first GEP model
Full size table
Table 4 Prediction performance comparisons of different creep index models
Full size table