1 Introduction

Attribute reduction (also known as feature reduction) (Zhang and Miao 2014) is a very useful data preprocessing technique, which removes noise, irrelevant or misleading features by mining the importance of feature, and obtains the smallest subset of features from the decision system while maintaining the same classification accuracy. In today's era of data explosion, attribute reduction of data can greatly improve the utilization of data, reduce storage space, save resources, and promote the visualization and understanding of data.

Rough Set Theory (RST) (Pawlak 1982) is an effective feature reduction tool proposed by Professor Zdzisław Pawlak in 1982, and has been widely used in many fields such as fault diagnosis (Xu et al.2020), pattern recognition (Sinha and Namdev 2020), and data mining (Singh and Pamula 2020). RST can obtain the key attributes from the data itself without any prior knowledge, so it is suitable for obtaining the key factors that affect the fatigue life of welded joints from the fatigue test data of welded joints, and can obtain the objective and comprehensive evaluation of the influencing factors of the fatigue life of welded joints. In recent years, RST has been applied to the fatigue life analysis of welded joints (Liu et al.2017; Zou et al. 2019a, b), and the evaluation model and fatigue life prediction model of welded joints are constructed. This paper proposes a neighborhood rough set attribute reduction algorithm based on supervised granulation. The possible influence of different classes in decision attribute from the perspectives of neighborhood partition and calculation of conditional entropy could be considered by the algorithm. And the influence of conditional attributes was also considered by introducing mutual information theory. Based on the proposed algorithm, the evaluation model of influencing factors of titanium alloy welded joint was established. The coupling relationship between influencing factors was discussed. The influencing factors of joint fatigue life were quantitatively evaluated, and the set of key influencing factors of fatigue life was obtained.

2 Related works

Besides RST, information theory is also a method to deal with uncertainty problems. Shannon (1948) first proposed the concept of information entropy in 1948. Information entropy provides the quantitative measurement of information. Miao (1997) merged information theory with rough set theory in 1997, and established the relationship between the roughness of knowledge and information entropy. Using the information quantity of knowledge as the measure of attribute importance, Liang et al. (2001) quantified the relationship between knowledge and information quantity in information system. However, the classical rough set model can only deal with discrete data. For continuous data, it needs to be discretized, which will cause data loss. To solve this problem, Hu et al. (2006, 2008) proposed a neighborhood rough set model based on the definitions of \(\delta\) neighborhood and neighborhood relations in metric spaces. Then Hu et al. (2009, 2011) generalizes Shannon’s information entropy to neighborhood information entropy, and proposes a measure of neighborhood mutual information. According to the measurement attribute method, rough set is mainly divided into algebraic view method (Shen et al.2013) and information view method (Wang and Ou.2008). In which algebra view method calculates the weight value of attribute importance of features by calculating the upper and lower approximation of samples. The information view method is based on the idea of information theory. Through the study of the uncertainty of the universe, it calculates the information entropy or conditional information entropy to get the weight, so as to reduce the attributes of the data.

At present, the main research direction of rough set attribute reduction algorithm is divided into the improvement of different types of data and the improvement of different granulation methods. Due to the complexity and diversity of data, many scholars begin to study different types of data, including dynamic data, incomplete data, mixed data, etc. Then incremental reduction, dynamic reduction, multi decision table reduction and parallel reduction are developed. In the view of algebra, Chu et al. (2020) proposed a three-way clustering algorithm based on neighborhood rough sets for incomplete and attribute-related random large sample data; Deng et al. (2021) proposed F-neighbor rough sets and its reducts for dynamic numerical data, combining the advantages of neighbor rough set and F-rough set; Singh et al. (2020) introduced a novel approach for attribute selection in set-valued information system based on tolerance rough set theory. In terms of information view, Zhao and Qin (2014) proposes an extended rough set model based on neighborhood-tolerance relation for incomplete data mixed by categorical and numerical features, and then proposes conditional entropy of neighborhood tolerance; Sang et al. (2021) proposed incremental feature selection approaches based on a fuzzy dominance neighborhood rough set for dynamic interval-valued ordered data; Wan et al. (2021) proposed a new objective evaluation function of the interactive selection of hybrid features and designed a novel interaction feature selection algorithm based on neighborhood conditional mutual information for hybrid data; Chen et al. (2018a, b, c) proposed a variable precision neighborhood rough set attribute reduction heuristic algorithm based on mutual information entropy for incomplete hybrid decision system; Sun et al. (2020) proposed a novel neighborhood multi-granulation rough sets based attribute reduction method using Lebesgue and entropy measure in incomplete neighborhood decision system; Shu et al. (2020) proposed a neighborhood entropy-based incremental feature selection framework by neighborhood rough set model for dynamic hybrid data with mixed-type features. For multi label data, Qian et al. (2020) integrated label distribution learning into multi label feature selection, and proposed a multi-label feature selection algorithm based on label distribution and feature complementarity.

At present, more and more scholars combine rough set theory with granular computing (Zadeh 1997), and realize the transformation and representation of uncertain knowledge by using different granulation mechanisms. It makes the subsequent calculation start from different levels or granularity, and realizes the characterization of neighborhood information system from multiple perspectives. In the view of algebra, Zhang et al.(2019a, b) developed a novel model called local multi-granulation decision-theoretic rough set in an ordered information system; Zhan and Xu (2018) introduced two types of coverings based (optimistic, pessimistic and variable precision) multi granulation rough fuzzy set models respectively by means of neighborhoods and presented an approach to multiple criteria group decision making problem, and then Zhang et al. (2019a, b) proposed two types of multi-granulation rough sets model called the optimistic multi-granulation hesitant fuzzy rough sets and pessimistic multi-granulation hesitant fuzzy rough sets; Tsang et al. (2020) investigated the mechanism of multi-level cognitive concept learning method oriented to data sets with fuzziness; Tan et al. (2019) defined several measurements to compare the granularity of neighborhood granulations, using which the granulation selection with multi granulation rough set is characterized; Jiang et al. (2019) proposed a multi-scale based acclerated stragegy for attribute reduction by means of the changing of radius; Chen et al. (2018c) proposed a three-level structure of granules in the neighborhood system: the neighborhood granule, the neighborhood granule swarm and the neighborhood granule library; Chen et al. (2018a) proposed a multi-radius neighborhood rough set weighted feature extraction method for high-resolution remote sensing image classification; Li et al. (2020) proposed a dynamic granularity selection algorithm by introducing local weighted accuracy and local likelihood ratio to compute the weight of granularity. In terms of information view, Zhao et al. (2015) proposed a new complement information entropy model in fuzzy rough set based on arbitrary fuzzy relation, which takes inner-class and outer-class information into consideration; Zhou et al. (2018,2020) applied the idea of three-layer construction to conditional neighborhood entropy; Zhao and Yang (2019) proposed an incremental attribute reduction algorithm for object constantly increasing in numeric information system; Mou et al. (2020) decomposed high classification- based neighborhood approximation condition-entropy and proposed a class-specific attribute reduct based on the new information measure. Mu et al. (2019) establishes double-granule conditional-entropies based on three-level granular structures by improvements of hierarchical granulation.

The parameter of radius in the neighborhood reduction algorithm plays an important role. Different radius results in different reduction result. If the same radius is used, the influence of samples under different labels cannot be fully considered. To solve this problem, Yang et al. (2019) proposed a pseudo-label neighborhood relation. On this basis, Rao et al. (2020) put forward relevant reduction acceleration strategies; Nevertheless, not only is it a time-consuming process for generating pseudo labels of samples, but also the information provided by pseudo labels may be incorrect which will lead to lower quality of neighborhood rough approximations. Jiang et al. (2020) proposed a supervised neighborhood based on the supervised strategy. By using two neighborhood radii, which successfully reduced the interference between samples with different labels.

The traditional rough set reduction algorithm based on information view fails to consider the influence relationship between different decision attributes when calculating conditional neighborhood entropy, and the traditional radius does not take into account the information provided by decision attributes. In this paper, a two-step reduction algorithm is proposed. We combine the supervised strategy (Jiang et al.2020) with the concept of three-level granulation (Zhou et al.2018) in the first step of reduction, and fully consider the influence of decision attributes from the perspective of determination and measurement calculation. In order to further consider the influence of different conditional attributes and eliminate those attributes that are too similar to each other and have little impact on decision attributes, the feature complementary relationship in reference (Qian et al.2020) is introduced in the second step of reduction. The two-step reduction algorithm is called the neighborhood rough set based on supervised granulation (NRSBSG) attribute reduction algorithm. Then, it is applied for the fatigue life influencing factors’ analysis of titanium alloy welded joints, coupling relationship between the fatigue life influencing factors of titanium alloy welded joints are studied. The implicit relationship between the influencing factors is researched, and the corresponding intelligent model is constructed. The model is tested by using the fatigue experiment data of titanium alloy welded joints. At last, the analysis system of fatigue life influencing factors of welded joints based on NRSBSG is designed and developed.

The rest of this paper is organized as follows. Section 3, describes the theory of neighborhood rough set reduction by defining some concepts, and the proposed NRSBSG is introduced. Section 4, carries out some experiments on the standard UCI datasets and analyzes the results. Section 5, describes details with the design and implementation of the fatigue life influencing factors analysis system. Section 6, concludes the paper and presents further work in this area.

3 Basic concepts

3.1 Preliminary

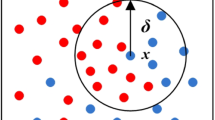
Generally, a neighborhood decision system can be denoted as \(NDS = (U,C,d,f)\), in which U is the set of nonempty samples, C is the set of conditional attributes and d is the decision attribute. \(\forall x \in U\), \(d(x)\) indicates the value of \(x\) over decision attribute. \(IND(d) = \{ (x,y) \in U \times U:d(x) = d(y)\}\) indicates the equivalent relation of decision attribute d,\(U/IND(d) = \{ X_{1} ,X_{2} ,...,X_{q} \}\) indicates the sample division of decision attribute d,and \(X_{q}\) is the q decision class with the same label sample. In this Section, some basic concepts of neighborhood rough set and the proposed NRSBSG are introduced.

3.1.1 Neighborhood relation

Definition 1.

(Hu 2006) Distance function.

Given a decision system NDS, \(U = \{ x_{1} ,x_{2} ,...,x_{i} \}\),\(\forall B \subseteq C\), the conditional attribute collection \(B = \{ c_{1} ,c_{2} ,...,c_{n} \}\),then the distance function of B is:

$$ \Delta _{B} (x,x_{i} ) = \left( {\sum\limits_{{k = 1}}^{n} {\left| {f(x,c_{k} ) - f(x_{i} ,c_{k} )} \right|^{p} } } \right)^{{\frac{1}{p}}} $$
(1)

in which \(f(x,c_{k} )\) denotes the value of sample x with respect to conditional attribute \(c_{k}\). When p = 1, it is Manhattan distance, and when p = 2, it is Euclidean distance. In this paper, we use Manhattan distance as the distance function.

Definition 2.

(Hu 2006) Neighborhood relation.

Given a decision system NDS,\(U = \{ x_{1} ,x_{2} ,...,x_{i} \}\),\(x_{i} \in U\),the neighborhood of \(x_{i}\) can be denoted as:

$$ n_{B}^{\delta } (x_{i} ) = \{ x|\Delta_{B} (x,x_{i} ) < \delta ,x \in U\} $$
(2)

in which conditional attribute collection \(B \subseteq C\),\(B = \{ c_{1} ,c_{2} ,...,c_{n} \}\) indicates the conditional attribute contained in the conditional attribute set B,\(\Delta_{B} (x,x_{i} )\) indicates the distance between sample \(x_{i}\) and x with respect to conditional attribute set B,\(\delta\) is the neighborhood radius. The neighborhood relation can be denoted as follows:

$$ n_{B}^{\delta } = \{ (x,y)|\Delta_{B} (x,y) < \delta ,\forall x,y \in U\} $$
(3)

3.1.2 Neighborhood rough set based on information view

Hu et al. (2009) combined the classical Shannon entropy with neighborhood rough set, studied the correlation measure of neighborhood decision system under the information view, including neighborhood entropy, conditional neighborhood entropy and neighborhood mutual information. It can be directly applied to multi-label data with numerical and discrete characteristics without discretization. The concept is introduced as follows:

Definition 3.

(Hu et al. 2009) Conditional neighborhood entropy.

Given a decision system NDS,\(\forall A,B \subseteq C\),the conditional neighborhood entropy of conditional attribute set A with respect to conditional attribute set B is defined as:

$$ NH_{\delta } (A/B) = - \frac{1}{|U|}\sum\limits_{i = 1}^{|U|} {\log \frac{{|n_{A}^{\delta } (x_{i} ) \cap n_{B}^{\delta } (x_{i} )|}}{{|n_{B}^{\delta } (x_{i} )|}}} $$
(4)

the conditional neighborhood entropy of decision attribute d with respect to the set of conditional attribute B is defined as:

$$ NH_{\delta } (d/B) = - \frac{1}{|U|}\sum\limits_{i = 1}^{|U|} {\log \frac{{|[x_{i} ]_{d} \cap n_{B}^{\delta } (x_{i} )|}}{{|n_{B}^{\delta } (x_{i} )|}}} $$
(5)

where \([x_{i} ]_{d}\) is the decision class corresponding to sample \(x_{i}\).

Definition 4.

(Hu et al. 2009) Neighborhood mutual information.

Given a decision system NDS,\(\forall A,B \subseteq C\),the neighborhood mutual information of conditional attribute set A with respect to conditional attribute set B is defined as:

$$ NH_{\delta } (A;B) = - \frac{1}{|U|}\sum\limits_{i = 1}^{|U|} {\log \frac{{|n_{A}^{\delta } (x_{i} )||n_{B}^{\delta } (x_{i} )|}}{{|U||n_{A}^{\delta } (x_{i} ) \cap n_{B}^{\delta } (x_{i} )|}}} $$
(6)

the neighborhood mutual information of decision attribute d with respect to the set of conditional attribute B is defined as:

$$ NH_{\delta } (d;B) = - \frac{1}{|U|}\sum\limits_{i = 1}^{|U|} {\log \frac{{|[x_{i} ]_{d} ||n_{B}^{\delta } (x_{i} )|}}{{|U||[x_{i} ]_{d} \cap n_{B}^{\delta } (x_{i} )|}}} $$
(7)

If variables B and C are independent of each other, then the value of neighborhood mutual information between B and C is minimum. The value of neighborhood mutual information between B and C is maximum, if B is completely determined by C (Qian et al. 2020).

3.1.3 (Zhou et al. 2018) Conditional neighborhood entropy with granulation monotonicity

Definition 5.

Conditional neighborhood entropy with granulation monotonicity.

Given a decision system NDS, \(\forall x_{i} \in U\),\(\forall B \subseteq C\) and \(U/IND(d) = \{ X_{1} ,X_{2} ,...,X_{q} \}\), the conditional neighborhood entropy with granulation monotonicity is defined as:

$$ \left\{ \begin{aligned}& H_{\delta } (X_{j} /n_{B}^{\delta } (x_{i} )) = - \frac{1}{|U|}\log (\frac{{|n_{B}^{\delta } (x_{i} )|^{2} }}{{|U|^{2} }}\frac{{|X_{j} \cap n_{B}^{\delta } (x_{i} )|}}{{|n_{B}^{\delta } (x_{i} )|}}),\;X_{j} \cap n_{B}^{\delta } (x_{i} ) \ne \emptyset \hfill \\& H_{\delta } (X_{j} /n_{B}^{\delta } (x_{i} )) = - \frac{1}{|U|}\log (\frac{{|n_{B}^{\delta } (x_{i} )|^{2} }}{{|U|^{2} }}\frac{1}{{|n_{B}^{\delta } (x_{i} )|}}),\;X_{j} \cap n_{B}^{\delta } (x_{i} ) = \emptyset \hfill \\ \end{aligned} \right. $$
(8)

3.1.4 Supervision strategy

The traditional neighborhood relation is determined by the distance between two samples and the radius of a single neighborhood. This method may not be able to express whether the samples with different decision attributes are similar and two samples with different labels will fall into the same neighborhood. In order to solve this problem, the neighborhood relationship based on supervisory decision is proposed in document (Jiang et al. 2020). The neighborhood relationship is introduced as follows:

Definition 6.

(Jiang et al. 2020) Supervised neighborhood.

Given a decision system NDS, \(\forall x_{i} \in U\),\(\forall B \subseteq C\),the supervised neighborhood of conditional attribute set B is defined as:

$$ \begin{gathered} n_{B}^{{\delta_{I,} \delta_{O} }} (x_{i} ) = \{ x|x \in U,d(x) = d(x_{i} )\& \Delta_{B} (x,x_{i} ) < \delta_{I} \\ \cup d(x) \ne d(x_{i} )\& \Delta_{B} (x,x_{i} ) < \delta_{O} \} \\ \end{gathered} $$
(9)

in which the intra class radius \(\delta_{I}\) and inter class radius \(\delta_{O}\) should satisfy \(\delta_{O} < \delta_{I}\), which can effectively reduce the impact between different label samples.

3.1.5 Neighborhood rough set based on supervised granulation

Conditional neighborhood entropy with granulation monotonicity takes into account the influence of different decision classes in the calculation of conditional neighborhood entropy. In order to further improve the discriminant performance of neighborhood relations, the supervision strategy is introduced, and the influence relationship between different decision attribute samples is fully considered in the calculation. A neighborhood rough set based on supervised granulation is proposed. The related definitions are introduced as follows:

Definition 7.

Conditional neighborhood entropy and neighborhood mutual information based on supervised granulation.

Given a decision system NDS, \(\forall x_{i} \in U\),\(\delta_{I} ,\delta_{O} \in [0,1]\),\(\forall B \subseteq C\),the decision class of the sample is divided into \(U/IND(d) = \{ {\kern 1pt} X_{1} ,X_{2} ,...,X_{q} \} {\kern 1pt}\),the conditional neighborhood entropy of decision attribute d with respect to conditional attribute set B based on supervised granulation is defined as:

$$ H_{{\delta_{I} ,\delta_{O} }} (d/B) = - \frac{1}{|U|}\sum\limits_{j = 1}^{q} {\sum\limits_{i = 1}^{|U|} {H_{{\delta_{I} ,\delta_{O} }} (X_{j} /n_{B}^{{\delta_{I,} \delta_{O} }} (x_{i} ))} } $$
(10)

The neighborhood mutual information of decision attribute d with respect to conditional attribute set B based on supervised granulation is defined as:

$$ NH_{{_{{\delta_{I} ,\delta_{O} }} }} (d;B) = - \frac{1}{|U|}\sum\limits_{i = 1}^{|U|} {\log \frac{{|[x_{i} ]_{d} ||n_{B}^{{_{{\delta_{I} ,\delta_{O} }} }} (x_{i} )|}}{{|U||[x_{i} ]_{d} \cap n_{B}^{{_{{\delta_{I} ,\delta_{O} }} }} (x_{i} )|}}} $$
(11)

Definition 8.

Attribute reduction.

Given a decision system NDS, \(\forall x_{i} \in U\),\(\delta_{I} ,\delta_{O} \in [0,1]\),\(\forall B \subseteq C\),the decision class of the sample is divided into \(U/IND(d) = \{ {\kern 1pt} X_{1} ,X_{2} ,...,X_{q} \} {\kern 1pt}\) when the following two conditions are satisfied, the conditional attribute set B is the attribute reduction of C relative to decision attribute d.

$$ \left\{ \begin{aligned}& H_{{\delta_{I} ,\delta_{O} }} (d/B) \ne H_{{\delta_{I} ,\delta_{O} }} (d/B - \{ c\} ),\;\forall c \in B \hfill \\& H_{{\delta_{I} ,\delta_{O} }} (d/B) = H_{{\delta_{I} ,\delta_{O} }} (d/C) \hfill \\ \end{aligned} \right. $$
(12)

Definition 9.

Core.

Given a decision system NDS, \(\forall x_{i} \in U\),\(\delta_{I} ,\delta_{O} \in [0,1]\) and \(\forall c \subseteq C\),the decision class of the sample is divided into \(U/IND(d) = \{ {\kern 1pt} X_{1} ,X_{2} ,...,X_{q} \} {\kern 1pt}\). If \(H_{{\delta_{I} ,\delta_{O} }} (d/C) \ne H_{{\delta_{I} ,\delta_{O} }} (d/C - \{ c\} )\), then c is the core attribute of the decision system, all core attributes constitute the core of decision system.

Definition 10.

Significance.

Given a decision system NDS, supposed \(c \in C - B\),then the significance of adding conditional attribute c to conditional attribute set B with respect to decision attribute d is:

$$ sig_{out} (c,B,d) = H_{{\delta_{I} ,\delta_{O} }} (d/B \cup \{ c\} ) - H_{{\delta_{I} ,\delta_{O} }} (d/B) $$
(13)

supposed \(c \in B\), then the significance of deleting conditional attribute c to conditional attribute set B with respect to decision attribute d is:

$$ sig_{in} (c,B,d) = H_{{\delta_{I} ,\delta_{O} }} (d/B) - H_{{\delta_{I} ,\delta_{O} }} (d/B - \{ c\} ) $$
(14)

The proof of the monotonicity of conditional neighborhood entropy can be obtained from (Zhou et al. 2018).

3.2 Attribute reduction algorithm of neighborhood rough set based on supervised granulation

In this paper, the algorithm of attribute reduction of neighborhood rough set based on supervised granulation is formed by combining the conditional neighborhood entropy with granulation monotonicity with the supervised strategy, and then considering the interaction between the conditional attributes by introducing the feature complementary relationship. The workflow of the proposed algorithm is shown in Fig. 1.

Fig. 1
figure 1

Attribute reduction process of neighborhood rough set based on supervised

Full size image

As is shown in Fig. 1, \(\delta_{I} ,\delta_{O}\) are intra class radius and inter class radius respectively, calculated by \(\delta_{I} (c_{i} ) = std(c_{i} )/\lambda\),\(\delta_{O} (c_{i} ) = a * \delta_{I} (c_{i} )\), where \(\delta_{I} (c_{i} )\) indicates the intra class radius of conditional attributes \(c_{i}\),\(\delta_{O} (c_{i} )\) indicates the inter class radius, parameters \(\lambda\) and \(a\) control the size of radius. The size of the inter class radius are determined by the value of a. The value range of a should between [0,1]. The closer it is to 1, the closer the inter class radius is to the intra class radius and the proportion of considering the influence of decision attributes in neighborhood division becomes smaller. No difference in dividing neighborhoods between the five algorithms when the inter class radius is equal to the intra class radius. In order to ensure the intra class radius is greater than the inter class radius. a is taken as 0.5. sig_ctrl and threH are the significance threshold and complementarity threshold respectively, and the value is a positive number slightly greater than 0. The larger the value of sig_ctrl, the less number of the reduction results satisfying the conditions. So, the reduction set will have fewer attribute elements. The larger the value of threH, the more similar attributes will be divided into a reduction set. The reduction set will have more attribute elements.

figure a

In the first step of proposed algorithm, firstly, the attribute importance is taken as the evaluation criterion to find out the redundant attributes in the whole dataset. In this way, the reduct set can be quickly found in a short time. Then,\(H_{{\delta_{I} ,\delta_{O} }} (d/redSet) \ge H_{{\delta_{I} ,\delta_{O} }} (d/C)\) is taken as the evaluation criterion to ensure the integrity of information. From the point of view of information, the amount of information of the reduced set is not less than that of the original data set by supplementing the reduced set. The first step of proposed algorithm corresponds to steps 1,2,3 and 4 in the reduction step. In the second step, reduction results are calculated by the mutual information \(NH_{{\delta_{I} ,\delta_{O} }} (A;B)\) and \(NH_{{\delta_{I} ,\delta_{O} }} (d;B)\). The attributes which are similar to each other and have little influence on the decision attributes in the reduction set are eliminated. The second step of proposed algorithm corresponds to steps 5,6,7 and 8 in the reduction step. For calculation convenience, the average value R(i) of influence between conditional attribute ci and other features is calculated. The detailed calculation steps of the algorithm are shown in ALGORITHM.

3.3 Illustrative example

In order to show the calculation process of the proposed algorithm, eight samples are selected from iris dataset from UCI (http://archive.ics.uci.edu/ml/index.php). The specific data are shown in Table 1. Normalization is conducted at the beginning. The normalization formula is as follows:

$$ f(x_{i} ) = \frac{{x_{i} - x_{\min } }}{{x_{\max } - x_{\min } }} $$
(15)

where \(x_{\max }\) and \(x_{\min }\) are the maximum and minimum values of samples with the same attribute. The normalized data is shown in Table 2.

Table 1 Iris data set
Full size table
Table 2 Normalized iris data set
Full size table

Suppose a = 0.5, \(\lambda\) = 2, neighborhood radius δI(ci) = std(ci)/λ, δO(ci) = a*δI(ci) are calculated, δI(c1) = 0.1930, δO(c1) = 0.0965, δI(c2) = 0.1485, δO(c2) = 0.0743. According to formula (10), the supervised neighborhood of samples in attribute set \(B_{1} = \{ c_{1} \}\),\(B_{2} = \{ c_{2} \}\), \(B_{12} = \{ c_{1} ,c_{2} \}\) are obtained, as is shown in Table 3.

Table 3 Supervised neighborhood
Full size table

The decision class of the sample is \(U/IND(d) = \{ X_{1} ,X_{2} ,X_{3} \}\), in which \(X_{1} = \{ x_{1} ,x_{2} \}\), \(X_{2} = \{ x_{3} ,x_{4} ,x_{5} \}\),\(X_{3} = \{ x_{6} ,x_{7} ,x_{8} \}\). According to formula (10), the corresponding conditional neighborhood entropy is calculated. Calculating of the neighborhood of samples with respect to attribute set \(B_{1}\) is detailed as following. The calculation process with respect to \(B_{2}\) and \(B_{12}\) is similar and will not be repeated.

$$ X_{1} \cap n_{{B_{1} }}^{\delta } (x_{1} ) = \{ x_{1} ,x_{2} \} ,\;X_{2} \cap n_{{B_{1} }}^{\delta } (x_{1} ) = \{ \emptyset \} ,\;X_{3} \cap n_{{B_{1} }}^{\delta } (x_{1} ) = \{ \emptyset \} $$
$$ X_{1} \cap n_{{B_{1} }}^{\delta } (x_{2} ) = \{ x_{1} ,x_{2} \} ,\;X_{2} \cap n_{{B_{1} }}^{\delta } (x_{2} ) = \{ \emptyset \} ,\;X_{3} \cap n_{{B_{1} }}^{\delta } (x_{2} ) = \{ \emptyset \} $$
$$ X_{1} \cap n_{{B_{1} }}^{\delta } (x_{3} ) = \{ \emptyset \} ,\;X_{2} \cap n_{{B_{1} }}^{\delta } (x_{3} ) = \{ x_{3} \} ,\;X_{3} \cap n_{{B_{1} }}^{\delta } (x_{3} ) = \{ \emptyset \} $$
$$ X_{1} \cap n_{{B_{1} }}^{\delta } (x_{4} ) = \{ \emptyset \} ,\;X_{2} \cap n_{{B_{1} }}^{\delta } (x_{4} ) = \{ x_{4} \} ,\;X_{3} \cap n_{{B_{1} }}^{\delta } (x_{4} ) = \{ x_{8} \} $$
$$ X_{1} \cap n_{{B_{1} }}^{\delta } (x_{5} ) = \{ \emptyset \} ,\;X_{2} \cap n_{{B_{1} }}^{\delta } (x_{5} ) = \{ x_{5} \} ,\;X_{3} \cap n_{{B_{1} }}^{\delta } (x_{5} ) = \{ x_{6} ,x_{7} \} $$
$$ X_{1} \cap n_{{B_{1} }}^{\delta } (x_{6} ) = \{ \emptyset \} ,\;X_{2} \cap n_{{B_{1} }}^{\delta } (x_{6} ) = \{ x_{5} \} ,\;X_{3} \cap n_{{B_{1} }}^{\delta } (x_{6} ) = \{ x_{6} ,x_{7} \} $$
$$ X_{1} \cap n_{{B_{1} }}^{\delta } (x_{7} ) = \{ \emptyset \} ,\;X_{2} \cap n_{{B_{1} }}^{\delta } (x_{7} ) = \{ x_{5} \} ,\;X_{3} \cap n_{{B_{1} }}^{\delta } (x_{7} ) = \{ x_{6} ,x_{7} \} ,\;X_{1} \cap n_{{B_{1} }}^{\delta } (x_{8} ) = \{ \emptyset \} ,\;X_{2} \cap n_{{B_{1} }}^{\delta } (x_{8} ) = \{ x_{4} \} ,\;X_{3} \cap n_{{B_{1} }}^{\delta } (x_{8} ) = \{ x_{8} \} $$

The supervised granulation conditional neighborhood entropy of decision class \(X_{1}\) with respect to the conditional attribute set \(B_{1}\) is obtained as follows:

$$ \begin{gathered} H_{{\delta_{I} ,\delta_{O} }} (X_{1} /n_{{B_{1} }}^{{\delta_{I,} \delta_{O} }} (x_{1} )) = - \frac{1}{|U|}\log \;\left( {\frac{{\left| {n_{{B_{1} }}^{\delta } (x_{1} )} \right|^{2} }}{{\left| U \right|^{2} }}\frac{{\left| {X_{1} \cap n_{{B_{1} }}^{\delta } (x_{1} )} \right|}}{{\left| {n_{{B_{1} }}^{\delta } (x_{1} )} \right|}}} \right) \hfill \\ \rm{ } = - \frac{1}{8}\log (\frac{{2^{2} }}{{8^{2} }}\frac{2}{2}) = 0.5 \hfill \\ \end{gathered} $$
$$ H_{{\delta _{I} ,\delta _{O} }} \left( {X_{1} /n_{{B_{1} }}^{{\delta _{{I,}} \delta _{O} }} (x_{2} )} \right) = - \frac{1}{8}\log \left( {\frac{{2^{2} }}{{8^{2} }}\frac{2}{2}} \right) = 0.5 $$
$$ H_{{\delta _{I} ,\delta _{O} }} \left( {X_{1} /n_{{B_{1} }}^{{\delta _{{I,}} \delta _{O} }} (x_{3} )} \right){\text{ = }} - \frac{1}{8}\log \left( {\frac{{1^{2} }}{{8^{2} }}\frac{1}{1}} \right) = 0.75 $$
$$ H_{{\delta _{I} ,\delta _{O} }} \left( {X_{1} /n_{{B_{1} }}^{{\delta _{{I,}} \delta _{O} }} (x_{4} )} \right){\text{ = }} - \frac{1}{8}\log \left( {\frac{{2^{2} }}{{8^{2} }}\frac{1}{2}} \right) = 0.625 $$
$$ H_{{\delta _{I} ,\delta _{O} }} \left( {X_{1} /n_{{B_{1} }}^{{\delta _{{I,}} \delta _{O} }} (x_{5} )} \right){\text{ = }} - \frac{1}{8}\log \left( {\frac{{3^{2} }}{{8^{2} }}\frac{1}{3}} \right) = 0.552 $$
$$ H_{{\delta _{I} ,\delta _{O} }} \left( {X_{1} /n_{{B_{1} }}^{{\delta _{{I,}} \delta _{O} }} (x_{6} )} \right){\text{ = }} - \frac{1}{8}\log \left( {\frac{{3^{2} }}{{8^{2} }}\frac{1}{3}} \right) = 0.552 $$
$$ H_{{\delta _{I} ,\delta _{O} }} \left( {X_{1} /n_{{B_{1} }}^{{\delta _{{I,}} \delta _{O} }} (x_{7} )} \right){\text{ = }} - \frac{1}{8}\log \left( {\frac{{3^{2} }}{{8^{2} }}\frac{1}{3}} \right) = 0.552 $$
$$ H_{{\delta _{I} ,\delta _{O} }} \left( {X_{1} /n_{{B_{1} }}^{{\delta _{{I,}} \delta _{O} }} (x_{8} )} \right){\text{ = }} - \frac{1}{8}\log \left( {\frac{{2^{2} }}{{8^{2} }}\frac{1}{2}} \right) = 0.625 $$

The conditional neighborhood entropy of decision class \(X_{1}\) is:

$$ H_{{\delta_{I} ,\delta_{O} }} (X_{1} /B_{1} ) = \sum\limits_{i = 1}^{|U|} {H_{{\delta_{I} ,\delta_{O} }} (X_{1} /n_{{B_{1} }}^{{\delta_{I,} \delta_{O} }} (x_{i} ))} = 4.656 $$

The conditional neighborhood entropy of decision class \(X_{2}\) and \(X_{3}\) is:

$$ H_{{\delta_{I} ,\delta_{O} }} (X_{2} /B_{1} ) = \sum\limits_{i = 1}^{|U|} {H_{{\delta_{I} ,\delta_{O} }} (X_{2} /n_{{B_{1} }}^{{\delta_{I,} \delta_{O} }} (x_{i} ))} = 4.906\quad \quad H_{{\delta_{I} ,\delta_{O} }} (X_{3} /B_{1} ) = \sum\limits_{i = 1}^{|U|} {H_{{\delta_{I} ,\delta_{O} }} (X_{3} /n_{{B_{1} }}^{{\delta_{I,} \delta_{O} }} (x_{i} ))} = 4.531 $$

Therefore, the conditional neighborhood entropy of the supervised granulation of conditional attribute set \(B_{1}\) with respect to decision attribute d is:

$$ H_{{\delta_{I} ,\delta_{O} }} (d/B_{1} ) = \sum\limits_{j = 1}^{3} {H_{{\delta_{I} ,\delta_{O} }} (X_{j} /B_{1} )} = 14.093 $$

Then, the supervised granulation conditional neighborhood entropy of conditional attribute set \(B_{2}\),\(B_{12}\),\(B_{13}\),\(B_{23}\) and C can be calculated:

$$ H_{{\delta_{I} ,\delta_{O} }} (d/B_{2} ) = 14.873,\;H_{{\delta_{I} ,\delta_{O} }} (d/B_{3} ) = 10.238 $$
$$ H_{{\delta_{I} ,\delta_{O} }} (d/B_{12} ) = 17,\;\;H_{{\delta_{I} ,\delta_{O} }} (d/B_{13} ) = 14.092 $$
$$ H_{{\delta_{I} ,\delta_{O} }} (d/B_{23} ) = 17,\;\;H_{{\delta_{I} ,\delta_{O} }} (d/C) = 17 $$

The significance of attributes \(c_{1}\),\(c_{2}\) and \(c_{3}\) can be calculated by formula (15):

$$ \begin{gathered} sig_{in} (c_{1} ,C,d) = H_{{\delta_{I} ,\delta_{O} }} (d/C) - H_{{\delta_{I} ,\delta_{O} }} (d/C - \{ c_{1} \} ) \hfill \\ \rm{ } = H_{{\delta_{I} ,\delta_{O} }} (d/C) - H_{{\delta_{I} ,\delta_{O} }} (d/B_{23} ) = 0 \hfill \\ sig_{in} (c_{2} ,C,d) = H_{{\delta_{I} ,\delta_{O} }} (d/C) - H_{{\delta_{I} ,\delta_{O} }} (d/C - \{ c_{2} \} ) \hfill \\ \rm{ } = H_{{\delta_{I} ,\delta_{O} }} (d/C) - H_{{\delta_{I} ,\delta_{O} }} (d/B_{13} ) = 2.908 \hfill \\ sig_{in} (c_{3} ,C,d) = H_{{\delta_{I} ,\delta_{O} }} (d/C) - H_{{\delta_{I} ,\delta_{O} }} (d/C - \{ c_{3} \} ) \hfill \\ \rm{ } = H_{{\delta_{I} ,\delta_{O} }} (d/C) - H_{{\delta_{I} ,\delta_{O} }} (d/B_{12} ) = 0 \hfill \\ \end{gathered} $$

According to the above calculation process, the significance of attribute \(c_{1}\) and \(c_{3}\) with respect to d is 0, which is redundant thus could be deleted.

4 Experimental work

Experiments on 10 open UCI data sets are carried out here. The data sets are shown in Table 4.

Table 4 Dataset used in the experiment
Full size table

The effectiveness of the proposed algorithm is verified from two aspects: reduction rate and accuracy of classification. The reduction rate formula is shown in formula (16):

$$ Rate = \frac{|C| - |redSet|}{{|C|}} $$
(16)

where \(|C|\) indicates the number of original attributes,\(|redSet|\) indicates the number of attributes about reduction set.

The accuracy of classification is as following:

$$ Accuracy = \frac{{|U_{a} |}}{|U|} * 100\% $$
(17)

where \(|U_{a} |\) indicates the number of samples correctly classified, \(|U|\) indicates the total number of samples.

To reduce the adverse effects caused by inconsistent sample data, the preprocessed data are limited to [0,1] by normalization. The normalization formula is shown in (18):

$$ f(x_{i} ) = \frac{{x_{i} - x_{\min } }}{{x_{\max } - x_{\min } }} $$
(18)

where \(x_{\max }\) and \(x_{\min }\) are the maximum and minimum values of samples under the same attribute respectively.

Comparative experiments are carried out with the same and different neighborhood parameters respectively. The experiment is carried out on an Ali-cloud server computer: using X86 computing architecture, 16vCPU: AMD EPYC™ ROME 7H12, 64 GB running memory. MATLAB R2018b is used as the development tool.

4.1 Reduction results with same parameters

To verify the performance of NRSBSG algorithm, we compared NRSBSG with FARNeMF (Hu 2008), NRSBCE (Zou et al. 2021), IFSANRSR (Zou et al.2019a) and SNBAR (Jiang et al.2020) on the selected 10 data sets. The parameter a in NRSBSG algorithm and SNBAR algorithm is set to be 0.5. And the intra class radius \(\delta_{I}\) in NRSBSG is 0.1 which is the same as that in the other four algorithms. In IFSANRSR, the number of iterations is 100, and the number of artificial fish is set to be half of the number of conditional attributes, the maximum field of vision is half of the number of artificial fish, and the maximum movement step is 1 less than the maximum field of view. The reduction results and reduction rate of the five algorithms are shown in Table 5. The accuracy of classification and running time are shown in Table 6.

Table 5 Reduction results and reduction rate at \(\delta { = }0.1\)
Full size table
Table 6 Accuracy of classification and running time at \(\delta { = }0.1\)
Full size table

As could be seen from Table 5, the reduction effect of NRSBSG is similar to the other four algorithms in most data sets when \(\delta\) = 0.1. In high-dimensional data sets including Arrhythmia, Parkinson’s disease and Swarm behavior, the average reduction rate of the proposed algorithm is above 0.95. Compared with NRSBCE and IFSANRSR algorithms, it is slightly better than the two algorithms.

As is shown in Table 6, when \(\delta\) = 0.1, the accuracy of classification of the proposed NRSBSG algorithm is 0.9504 and 0.9388 on Wine and Ionosphere data sets which is slightly lower than that of NRSBCE algorithm. It has higher accuracy of classification than the other four algorithms on other datasets. The standard deviation of the accuracy of the five algorithms was about 0.04.

As could be seen from Table 6, the FARNeMF algorithm has the shortest running time of the five on the selected ten data sets. The running time of NRSBSG algorithm is shorter than that of IFSANRSR algorithm. The time complexity of NRSBSG algorithm is O(|U|2·|C|3). The time complexity of NRSBCE algorithm is O(|U|2·|C|2)(Zou et al. 2021). The time complexity of SNBAR algorithm is O(|U|2·|C|2)(Jiang et al.2020). The time complexity of FARNeMF algorithm is O(|U|log|U|·|C|2)(Hu 2008). The time complexity of IFSANRSR algorithm is O(|Iterations|·|Fish|2·|try_number|·|U|2·|C|)(Zou et al.2019a).

From the above, when \(\delta\) = 0.1, NRSBSG algorithm has made a progress in the aspect of accuracy of classification at the cost of running time. At the same time, NRSBSG algorithm has also perform well in the reduction rate of high-dimensional data sets.

4.2 Reduction rate evaluation under different parameters

As we know that different value of radius parameter results in different granularity of knowledge. In order to see the change of reduction rate of the four algorithms with different value of radii parameter, 20 radius parameters are selected. The radius range is from 0.05 to 1.0, and the change step is 0.05. The radius parameters \(\delta_{I}\) is taken as the horizontal axis, and the value of reduction rate as the vertical axis. Figure 2 shows the comparison result of reduction rate.

Fig. 2
figure 2figure 2

Reduction rates of different reduction algorithms in 10 data sets

Full size image

It can be seen from Fig. 2, with the increase of radii, the overall trend of reduction rate is gradually decreasing. Compared with the other three algorithms, the maximum reduction rates of NRSBSG algorithm on Breast, Fertility, Ionosphere and Wine data sets are 0.5556, 0.5556, 0.9697 and 0.8462 respectively. While the maximum reduction rates of other three algorithms are 0.5556, 0.5556, 0.8788 and 0.8462. Which are lower or same than that of NRSBSG algorithm. In high-dimensional data sets including Parkinson’s Disease, Arrhythmia and Swarm behavior, the maximum reduction rates of NRSBSG algorithm are close to the other three algorithms. The maximum reduction rate of NRSBSG algorithm on Conn data set is slightly lower than the other three algorithms. Although the maximum reduction rate of NRSBSG algorithm on Zoo data set is lower than NRSBCE algorithm, but it is higher than FARNeMF algorithm and IFSANRSR algorithm. Therefore, in most cases, the NRSBSG algorithm perform better than the other three algorithms in the reduction rate.

4.3 Evaluation of classification accuracy under different parameters

The accuracy of classification is believed more important for algorithm evaluation criteria. In this paper, the support vector machine is used as a classification tool, and the ten-fold cross validation method is used to verify the accuracy of classification of the proposed NRSBSG algorithm. Based on 10 data sets, 20 different neighborhood radius parameters in the reduction experiment are used. The radius values range from 0.05 to 1.0. The radius parameter is taken as the horizontal axis and the value of classification accuracy is taken as the vertical axis. The comparison results are shown in Fig. 3.

Fig. 3
figure 3figure 3

Accuracy of classification of different reduction algorithms in 10 data sets

Full size image

According to Fig. 3, the best accuracy of classification can be obtained by using different neighborhood radius parameters in different algorithms. On Breast, Fertility, Ionosphere, Wine, Zoo, Conn and Lymphography data sets, the maximum accuracy of classification of NRSBSG algorithm are 0.7478, 0.8964, 0.9687, 0.9850, 0.8253, 0.7648 and 0.7952 respectively which is higher than that of the other three algorithms. In high-dimensional data sets including Arrhythmia, Parkinson’s disease and Swarm behavior, the maximum accuracy of classification of NRSBSG algorithm are 0.6988, 0.8083 and 0.6608 while the maximum accuracy of classification of other three algorithms are 0.6758, 0.7171 and 0.6454. Therefore, the accuracy of classification of NRSBSG algorithm is better than the other three algorithms in most cases.

As could also be seen from Figs. 2 and 3 that the NRSBSG algorithm can obtain higher accuracy of classification and efficiently delete the redundant features from the original data. Compared with the other algorithms, the proposed NRSBSG algorithm mainly carries out attribute reduction from the perspective of information view. Firstly, in the process of dividing the neighborhood, the possible influence among different classes in decision attribute is considered by introducing the supervised strategy. Secondly, in the process of entropy calculation, the possible influence among different classes in decision attribute is considered by using conditional neighborhood entropy with granulation monotonicity. Thirdly, the influence of conditional attributes on each other is also considered in attribute reduction through mutual information. Thus, the possible influence of attributes is fully considered from three aspects in the proposed NRSBSG algorithm. So that NRSBSG algorithm is superior to the other algorithms in classification accuracy. At the same time, with the increase of the categories of decision attributes, the influence between different decision attributes will be more and the influence of decision attributes needs to be considered more. NRSBSG algorithm will perform better than other algorithms at this occasion. However, due to the high time complexity, the running time of NRSBSG algorithm will increase. How to decrease the time complexity of the proposed algorithm and how to determine the appropriate neighborhood radius parameters to achieve high accuracy and reduction rate at the same time should be focused in the future.

5 Application

In order to comprehensively analyze the influencing factors of fatigue life of titanium alloy welded joints and the coupling relationship between the influencing factors, an analysis model of fatigue influencing factors of titanium alloy welded joints is established. The NRSBSG algorithm is applied in attribute reduction of the fatigue decision system of titanium alloy welded joints. The key influencing factors of fatigue life of titanium alloy welded joints are determined. At the same time, the coupling relationship between the influencing factors is analyzed based on mutual information theory.

5.1 Fatigue decision system of titanium alloy welded joints

Fatigue test data of titanium alloy welded joints are collected as introduced in reference (Iwata and Matsuoka 2004) and the fatigue database is established as shown in Table 7. There are 43 samples in the database. The database is used as the experimental basis to analyze the influencing factors of fatigue life of titanium welded joints. In total, there are 6 attributes in the established database. Among which, the character of fatigue life is decision attribute, and the other 5 characters including Nominal Stress Range, Thickness, Stress concentration and Equivalent Structural Stress Range are conditional attributes. In the established fatigue database, except the value of Joint Type is discrete, the values of other attributes are all continuous.

Table 7 Data set of factors affecting fatigue life of Titanium alloy welded joints
Full size table

Let \(S_{1}\)\(=\){Nominal Stress Range \((c_{1} )\),Thickness \((c_{2} )\),Stress Concentration Factor \((c_{3} )\),Joint Type \((c_{4} )\)} and \(S_{2}\)\(=\){Equivalent Structural Stress Range \((c_{1} )\),Thickness \((c_{2} )\),Stress Concentration Factor \((c_{3} )\),Joint Type \((c_{4} )\)}, by taking the “fatigue life” character as decision attribute, two fatigue decision systems of titanium alloy welded joints are established. As is shown in Table 8 and Table 9.

Table 8 Nominal stress decision system
Full size table
Table 9 Equivalent structural stress decision system
Full size table

The proposed reduction algorithm is applied in the fatigue decision system. Several experiments show that when the radius parameter is 1.2, the accuracy of classification is better. So, the radius parameter is set as 1.2. The other parameters are set as a = 0.5, sig_ctrl = 0.01, threH = 0.3. The reduction result of the nominal stress decision system is {Nominal Stress Range, Stress Concentration Factor, Joint type}; The reduction result of the equivalent structural stress decision system is {Equivalent structural stress range, Stress concentration factor, Joint type}.

The weight of the conditional attribute is calculated by formula (18) proposed in (Qian et al.2020). Larger value of weight indicates more influence on the fatigue life of the welded joints. Weight of conditional attributes of the two fatigue decision systems are shown in Table 10 and 11.

$$ \omega_{j} = \frac{{NH_{{\delta_{I} ,\delta_{O} }} (d;c_{j} )}}{{\sum\limits_{i = 1}^{|redSet|} {NH_{{\delta_{I} ,\delta_{O} }} (d;c_{i} )} }} $$
(18)
Table 10 The percentage of the influence of each influencing factor on the fatigue life (nominal stress)
Full size table
Table 11 The percentage of the influence of each influencing factor on the fatigue life (equivalent structural stress)
Full size table

Mutual information between different attributes is computed to measure the different influence degree. The smaller of the value of mutual information, the better independent between the two attributes would be. The mutual information between the conditional attributes is computed as shown in Table 12.

Table 12 The degree of influence between each influencing factor
Full size table

According to Table 10, in the nominal stress decision system, the joint type has the largest influence on the fatigue life of titanium alloy welded joint, which is 0.4123. The nominal stress range is 0.3133, and the stress concentration factor is 0.2744. According to Table 11, in the equivalent structural stress decision system, the influence of equivalent structural stress range is the largest, which is 0.4563. The stress concentration factor and joint type are 0.2173 and 0.3264 respectively. Compared with the nominal stress decision system, the influence of stress concentration factor and joint type in the equivalent structure stress decision system are smaller.

According to Table 12, the influence weight of plate thickness on the stress concentration factor is 0.301. The influence weight of joint type on the stress concentration factor is 0.4071. That indicates the stress concentration factor is more easily affected by the joint type than the plate thickness.

5.2 Design and implementation of the influencing factors analysis system

In this work, influencing factors analysis system of welded joint fatigue life is designed and developed by using the proposed NRSBSG algorithm. The development platform of the system is MATLAB 2018b. The attribute reduction algorithms involved in the system are all written in MATLAB. After requirement analysis, the influencing factors analysis system should include 3 modules, including data selection, coupling relationship analysis and quantitative evaluation of influencing factors.

The data selection function enables users to browse and select the fatigue life test data set of welded joints or other data sets for analysis and comparison. The data selection function interface is shown in Fig. 4.

Fig. 4
figure 4

Data selection interface

Full size image

Coupling relationship analysis function enables users to analyze and evaluate the influence degree of different influencing factors in data set, and can see the histogram of influence degree of other factors on the influencing factors by selecting specific influencing factors. As shown in Fig. 5.

Fig. 5
figure 5

Coupling relationship analysis interface

Full size image

In the quantitative evaluation of influencing factors, the reduction result of the data set is calculated and the influence ratio of the reduction result on the fatigue life is obtained. The interface of algorithm operation results is shown in Fig. 6, and the interface of quantitative evaluation of influencing factors is shown in Fig. 7.

Fig. 6
figure 6

Algorithm running result interface

Full size image
Fig. 7
figure 7

Quantitative evaluation interface

Full size image

6 Conclusion

This paper proposed a neighborhood rough set attribute reduction algorithm NRSBSG, which combines the supervised strategy, three-layer granulation, feature complementary relationship with conditional neighborhood entropy. Experiments on 10 UCI data sets showed that the algorithm improves the reduction rate and accuracy compared with the other three algorithms.

On this basis, a coupling analysis model and quantitative evaluation model of influencing factors of titanium alloy welded joints was proposed. The key factors of titanium alloy welding joints were determined in two stress decision making systems. Through comparative analysis, the effect of equivalent structural stress range on fatigue life of welded joints is greater. It is shown that the equivalent structure stress range can predict the fatigue life of welded joints more accurately. In the coupling relationship of influencing factors, the Stress Concentration Factor is most importantly affected by joint type, which indicates that the influence of joint type should be more considered important when calculating the Stress Concentration Factor.

The design and development of fatigue analysis system in this work provides technical support for fatigue analysis and design of titanium alloy welded joints in industrial production. It reduces the labor intensity of designers, improves the working efficiency, and has great practical value and applicability.

The following topics need to be further studied.

  1. 1.

    The inter class radius of supervision strategy is determined by experts. It can be dynamically and automatedly updated by intelligent algorithms in the future.

  2. 2.

    This paper carries on the analysis experiment on static complete data set. In the future, we can analyze on incomplete data set and dynamic data set.

  3. 3.

    In this paper, the coupling relationship analysis and quantitative evaluation of influencing factors are only from aspects of analysis of the fatigue test data. In the future, it can be comprehensively considered and analyzed from the experimental combined with data analyzing aspect.