1 Introduction

Isogrid structures were initially developed for the aeronautical industry, considerably reducing the mass without significantly compromising the structure’s rigidity. The advancement of additive manufacturing technology contributed to the development of these complex structures, facilitating their applications in other sectors, such as the development of human prostheses. Since then, the subject has gained more visibility in the literature (Francisco et al. 2021).

Most of the studies are dedicated to the fabrication process and manufacture of isogrid structures, aiming at experimental tests. Forcellese et al. (2020) used the 3D printing process to develop lattice panels in polyamide reinforced with carbon fiber. The authors studied how the geometric parameters affected the compressive strength and buckling performance. Li et al. (2019) used the additive technique to build a hierarchical isogrid tube and evaluate its buckling resistance and plastic performance. Ciccarelli et al. (2021) also used 3D print to manufacture six isogrid panels varying the rib width and the rib thickness to investigate the geometric parameters influence in compressive loads. The authors conclude that the increase in rib width leads to an increase in strength.

Li and Fan (2018) manufactured isogrid-stiffened cylinders using carbon fiber to study failure modes. The authors conclude that skin thickness, cell dimension, rib height, rib thickness and end strengthening scheme jointly decide the failure pattern. Bellini et al. (2021) also manufactured an isogrid-stiffened cylinder and compared it, having the same geometry, with another made of titanium alloy. The authors concluded that the composite made has the same stiffness and strength, but is lighter.

Other authors proposed analyzing isogrid structures numerically through the finite element method (FEM). Liang et al. (2020) proposed a numerical thin-walled isogrid-stiffened cylinder and analyzed its structural buckling under imperfections considering reduced-order modeling. The authors concluded that the proposed method presented good results. Junqueira et al. (2019) studied the isogrid performance under compression and torsion efforts. Using numerical and experimental approaches, the authors proved that the proposed model had better performance than conventional prosthetic tubes.

Although the authors listed above have carried out important studies to understand the fabrication and influence of design variables on isogrid structures, none of them have studied their optimization. Few studies have done so in the literature. Akl et al. (2008) developed numerical methods to describe the performance of plates with isogrid stiffeners and optimized the static and dynamic characteristics of the model. Similarly, Jadhav and Mantena (2007) carried out an optimization study to find the geometric parameters that maximize the specific energy absorption. Lakshmi et al. (2013) studied the optimal design for the maximum buckling load of a laminate composite isogrid with dynamically reconfigurable quantum PSO.

Francisco et al. (2020a, b) carried out design optimization studies for carbon fiber-reinforced polymer isogrids with lower limb prosthesis applications. The authors used the Response Surface Methodology to find the equation set that represented the structural complex behavior of isogrid and performed all the optimizations using particle swarm optimization (PSO) and the Lichtenberg algorithm (LA).

These studies considered only one objective in the optimization, which led to obtaining only a single response. A multi-objective problem, in addition to being able to provide a set of solutions through the Pareto Front, allows the decision maker to understand how the objectives behave among themselves, revealing the nature of the optimization problem. Despite this importance and the fact that it has been increasingly used in the literature, only two studies address the problem of optimizing isogrid structures using multi-objective optimization.

Ehsani and Dalir (2020) used the genetic algorithm (GA) to find the optimum architecture to maximize the axial buckling load and minimize the weight of an isogrid plate. The authors used the ϵ-constrained method, which considers only a main objective and converts the others into constraints. The authors used explicit equations and obtained good results. Francisco et al. (2021) were the first to consider the optimization of CFRP isogrid tubes and the first to consider more than two objectives. The authors made a numerical model in FEM and used metamodeling resulting from the response surface methodology (RSM) to represent the complex behaviors of isogrid tubes. The author used the Multi-objective Sunflower Optimization as algorithm optimization.

Only Francisco et al. (2021) found Pareto fronts that represented how the objectives related to each other. However, metamodels are polynomial representations of objectives and, as found by Francisco et al. (2021), deliver responses that have an error when comparing the response of the metamodel with that of the same variables simulated in the FEM. That is, can lead to simplified Pareto fronts and can hide the true behavior of these structures when optimized. This study aims to eliminate this error and find the true Pareto fronts of the most important objectives in the multi-objective optimization of an isogrid tube made of carbon fiber polymer reinforcement (CFRP) for the first time in the literature.

The multi-objective optimization in this paper will consider six different structural responses, i.e., mass, Tsai-Wu failure index, instability coefficient (under compression and torsion efforts), and natural frequency. The objectives will be distributed and compared with other results in the literature through three cases: torsion, compression, and modal performance. The answers to these objectives will be acquired in two different ways, which will be compared in each case: (i) using metamodels from a RSM design, which generates second-order polynomial equations that represent the models with a certain level of confidence; and (ii) considering the direct FEM software responses, interacting with a meta-heuristic during the optimization process, resulting in null error and building a real Pareto front (deep optimization). This is unprecedented in the literature for isogrid structures.

Therefore, each case will have two Pareto fronts that will be compared using inverted general distance (IGD) (Sierra and Coello 2005), spacing (SP) (Schott 1995), and maximum spread (MS) (Zitzler 1999) to check which one has more convergence and coverage. The best PF according to these metrics will be chosen to discuss the non-dominated solutions and obtain the decision variables for the optimized carbon fiber-reinforced polymer (CFRP) isogrid tube.

The multi-objective optimization will be performed by the multi-objective Lichtenberg algorithm (LA) (Pereira et al. 2022), a hybrid physics-based meta-Heuristic inspired in lightening that recently showed superior results not only to multi-objective particle swarm optimization (MOPSO) or non-sorting genetic algorithm-II (NSGA-II), but also against modern algorithms like multi-objective grey wolf optimizer (MOGWO) (Mirjalili et al. 2016) and multi-objective grasshopper optimizer (MOGOA) (Mirjalili et al. 2017).

Therefore, the paper´s contributions are as follows: (i) the multi-objective optimization problem obtaining results through deep optimization for the first time in the literature; (ii) the CFRP isogrid tube true nature presentation and understanding through real Pareto fronts; (iii) the metamodeling use evaluation in this case; and (iv) testing MOLA in this application for the first time in the literature, since recently the algorithm showed superior results to multi-objective particle swarm optimization (MOPSO), non-sorting genetic algorithm-II (NSGA-II), multi-objective grey wolf optimizer (MOGWO), and multi-objective grasshopper optimizer (MOGOA) in a comparison on complex multi-objective test functions (Pereira et al. 2022).

Therefore, the manuscript is organized as follows: Sect. 2 brings the Theoretical Framework, which presents a knowledge-needed summary for the work. Section 3 shows the methodology. Section 4 brings the results and discussions, and Sect. 5 draws the conclusion.

2 Theoretical framework

2.1 Isogrid structures

There are two theories in the literature about the word “isogrid”. Some authors believe that the just structures whose formed equilateral triangles can be called isogrid and “iso” refers to isotropy of the structure within the plane (Kanou et al. 2013). On the other hand, some authors agree that all lattice structure (even those that are not isotropic) must be called isogrids (Huybrechts et al. 1999; Akl et al. 2008). According to Fan et al. (2009), the helical and circular ribs meet point is called nodes. It is created triangular (or another geometric figure) between these points to provide structural stability (Sorrentino et al. 2017; Zheng et al. 2015).

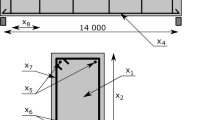
Isogrid structures can be just the rigid ribs or can be the rigid ribs covered with a coating, the first model is used in this paper and is called open. The second is called close. Eight variables can be used to describe the structure, they are as follows: angle between helical ribs (φ), width of circular (δc) and helical (δh) ribs, thickness (h), length (L), diameter (D), distance of circular (αc) and helical (αh) sleepers from the structure axis. The first three are the main ones in the design of the isogrid tube and that is why they are the decision variables in this study. They are represented in Fig. 1.

Fig. 1
figure 1

Geometric parameters of the isogrid tube

Full size image

Two main researchers studied the isogrid structures optimization without using metamodels or FEM. Totaro et al. (2004) used the isogrid geometric parameters as variables in an optimization problem focused in minimize safety factors. The author evaluates a structure subjected to axial load and finds the optimal parameters. Another procedure is used by Vaziliev and Razin (2006) and it will be described here. An optimization based on load normalization factor (p) given by Eq. 1 was proposed. The author compares p with the parameters ps (Eq. 2) and po (Eq. 3) and it can be resulted into three cases that are shown in Table 1.

Table 1 Optimum results for three different cases in isogrid
Full size table
$$p= \frac{4P}{\pi {D}^{2}}$$
(1)
$${p}_{s}= \frac{48{\bar{\sigma }}^{2}}{\pi {E}_{h}}\sqrt{\frac{\bar{\sigma }p}{k{E}_{c}}}$$
(2)
$${p}_{o }= {p}_{s}\sqrt{\frac{1}{2}\sqrt{\frac{2{E}_{h}\overline{p}}{{E }_{c}}+ \sqrt{\frac{2{E}_{h}\overline{p}}{{E }_{c}}-1} }}$$
(3)

The variables shown in Table 1 for calculate the parameters are the ultimate stress of helical ribs under compression efforts (\(\bar{\sigma })\), the young modulus (E), the mass density (ρ) and the local buckling coefficient (k). It implies in axisymmetric global buckling when \(p\le {p}_{s}\) or \({p}_{s} \le p \le {p}_{o}\) and in no axisymmetric global buckling when \({p}_{o} \le p\). The authors found that the optimized mass is given by Eq. 4.

$$M= \pi DLh{\rho }_{h}\left(2{\overline{\delta }}_{h}+ \overline{\rho }{\overline{\delta }}_{c}\right)$$
(4)

The isogrid structure use is justified due its high mechanical performance and low weight. In this work, CFRP material will be used as it is a material that helps in minimizing mass and has high mechanical resistance.

2.2 Response surface method

The explicit equations for the behavior of CFRP isogrid tubes formulation are complex and vary greatly depending on the loading and boundary conditions. However, with the physical structure for experimental evaluation or a FEM software where the structure can be modeled, mathematical and statistical methods can be applied to obtain equations that represent the model. That is, that allows obtaining metamodels. One of these methods is the response surface method (RSM).

Through the elaboration of an experimental matrix using design of experiments (DoE), the responses can be used to create equations based on the second-order fit, as shown in Eq. 5 (Montgomery and Runger 2003):

$$ Y = \beta_{0} + \sum\limits_{i = 1}^{k} {\beta_{i} x_{i} + } \sum\limits_{i = 1}^{k} {\beta_{ii} x_{i}^{2} + \sum\limits_{i < j} {} } \sum {\beta_{ij} x_{i} } x_{j} + \varepsilon $$
(5)

where k is the decision variables number of the problem.

The central composite design (CCD) is used in RSM to generate a complete quadratic model using all decision variables, being 2 k factorial points, 2 k axial points and a central point. According to Montgomery and Runger (2003), the Y metamodel can have a real problem good representation within the experimental region if the problem operator has good knowledge in the region estimation.

The models adjustment is given through the determination coefficient (R2), which represents the variation percentage in the response that is explained by the conceptual model. However, a high R2 value does not necessarily imply a good model, as adding variables to the model will always increase the determination coefficient, regardless the variable added be (or not) statistically significant. Due to this fact, it is chosen to use the R2 adjusted (R2adj), which does not increase whenever a variable is added to the model. If an unnecessary term is added, the value of R2adj decreases. With an adjusted RSM, the process optimization can proceed (Montgomery 2017).

2.3 Lichtenberg algorithm

Meta-heuristics are algorithms capable of combining decision variables and, from the answers, acquire knowledge of the problem and move towards an optimal region. To do so, they do not even need a function definition, as in this work, where the output response evaluation is done by FEM software. Due to the algorithm's ability to learn from decision variables and escape non-optimal regions and local minima, meta-heuristics are considered as an Artificial Intelligence algorithm (Mirjalili, 2016; Pereira et al. 2021c).

These algorithms can deal with multimodal, non-convex problems and with many decision variables. Currently, there are many meta-heuristics dealing with mono-objective problems and, in smaller number, with multi-objective problems. Being based on phenomena found in nature to find precise solutions with lower computational cost, each algorithm has parameters that control its capabilities to improve the solutions already found (exploitation) and to search new regions to find other solutions (exploration) according to its inspiration source.

There is no single algorithm that can be perfect in all applications, according to the no-free-lunch (NFL) theorem. However, the search for new and powerful algorithms is constant since it is a modern tendency for a problem operator to find as many solutions as possible before deciding which one to adopt (Yang 2014; Pereira et al., 2021c).

The Lichtenberg Algorithm is inspired by lightning propagation in resistant media and is the first algorithm in the literature to be based on trajectory and population at the same time. It is inspired by lightning propagation in resistant media, which generates figures with fractal aspects called Lichtenberg figures (Pereira et al. 2021a). The single-objective version has been successfully applied in the identification of cracks (Pereira et al. 2020), damage in composites (Pereira et al. 2021b), and isogrid tubes design optimization using metamodels (Francisco et al. 2020ba). The Multi-objective lichtenberg algorithm (MOLA) was recently published and will be used here (Pereira et al. 2022).

The algorithm uses a Lichtenberg figure to be thrown into the search space with different rotations and sizes in each of the Niter iterations. Three optimizer parameters are used in the Lichtenberg Figure creation: the creation radius (Rc), the number of particles (Np), and the stickiness coefficient (S). The latter controls the density of the Lichtenberg figure created, while the first two are associated with its size.

Then, a number of Pop points are randomly selected in the Lichtenberg figure to be evaluated in the objective functions. Each assessment generates a solution in Search Space and these solutions are compared using the Pareto dominance relationship. In this way, a partial Pareto front is formed and updated at each iteration. The Lichtenberg figure launched in the search space at each iteration has as its central trigger point a randomly selected point from the current Pareto front.

The basic principle of how the algorithm works in the multi-objective version is this. However, the algorithm still has two other parameters. The parameter M controls the Lichtenberg Figures creation during the entire optimization. If M = 0, no Lichtenberg figure is created and an optimized one is loaded. This makes the algorithm deliver final responses in less than 1 s in the mono-objective version. If M = 1, a Lichtenberg Figure is created and used in all iterations. If M = 2, a Lichtenberg figure is created at each iteration. The Lichtenberg Figure process creation takes about 2 min.

The ref parameter, if nonzero, creates a Lichtenberg Figure at a rate ref of the Lichtenberg Figure used in that iteration. Half of Pop is required to be in this smaller Figure, which can improve the algorithm's accuracy/convergence. Figure 2 shows the LA acting in the search space through some iterations and the respective convergence in the objective space. Figure 3 shows a summary of how the algorithm works.

Fig. 2
figure 2

Basic search strategy of MOLA in the design and objective space

Full size image
Fig. 3
figure 3

MOLA flowchart

Full size image

3 Methodology

The isogrid tube optimization depends on the output responses acquisition from the decision variable inputs. In this study, Mechanical ANSYS APDL® is used. A reduced number of experiments can be done to build the metamodel through RSM, which is performed in MINITAB® Software, or the optimizer can be linked directly into FEM for a deep optimization. Both will be used in this paper.

3.1 Numerical modeling using finite element method

Francisco et al. (2020ba) studied an isogrid numerical model and made comparisons with experimental tests to find the best fits. The results found by the authors showed that the numerical approach is in accordance with the experiments. Therefore, in this paper will be used the same shell element with 8 nodes and six degrees of freedom.

The isogrid model proposed is made with CFRP T300/epoxy. This material was analyzed by Madhavi (2009). The author carried out experimental tests for its characterization and the parameters are shown in Table 2. These data were used by Francisco et al. (2020ba, 2021) for a prosthetic tube numerical analysis.

Table 2 Properties of T300 Carbon fiber/epoxy resin (
Full size table

The isogrid tube is formed by 7 sheets of 0.2 mm each, i.e., the total thickness of the model is equal to 1.4 mm. This value was adopted by Junqueira et al. (2019) and shows excellent results in experimental tests. In addition, it is important to highlight that the carbon fibers orientation are shown in Fig. 4. For the numerical analysis, the force and the moment were applied at the end of the structure while the other side is locked as shown in Fig. 5. The loads used in this numerical model are according to the standard that have norms to lower limbs prosthesis structural testing (NBR ISO 10328: 2002). The adopted loads are 4480 N for compression and 7.1 N m for torsion tests.

Fig. 4
figure 4

Fiber orientation used to build the isogrid (Francisco et al. 2021)

Full size image
Fig. 5
figure 5

Boundary conditions applied to the model for a compression test and b torsion cases

Full size image

Having the structure modeled, the main objectives to be analyzed will be the Mass, natural frequency, Tsai–Wu and critical buckling load in the isogrid tube torsional and compression scenarios.

The Tsai-Wu failure criterion (TW) was used in this work to determine the safety factor of the composite orthotropic shells. This criterion takes into consideration the total effort energy to predict failure, i.e., the failure will occur when the index is greater or equal to the unit. Therefore, it is necessary to minimize it and this criterion can be modeled as shown in Eq. 5.

$$ F \, = \, F_{1} \sigma_{1} + F_{11} \sigma_{1}^{2} + F_{2} \sigma_{2} + F_{22} \sigma_{2}^{2} + 2F_{12} \sigma_{1} \sigma_{2} + F_{66} \tau_{12}^{2} $$
(5)

where:

$$ \begin{aligned}{\text{F}}_{{1}} &= \frac{1}{{X_{1T} }} - \frac{1}{{Y_{1C} }};\,{\text{F}}_{{2}} = \frac{1}{{X_{2T} }} - \frac{1}{{Y_{2C} }};\,F_{11} = \frac{1}{{X_{1T} Y_{1C} }} \\ F_{22} &= \frac{1}{{X_{2T} Y_{2C} }} ;F_{66} = \frac{1}{{S_{12}^{2} }}\end{aligned}$$
(6)
$$\begin{aligned} {\text{F}}_{{{12}}} = \frac{1}{{2P^{2} }}\left[ {{1 }{-}P\left( {\frac{1}{{X_{1T} }} - \frac{1}{{Y_{1C} }} + \frac{1}{{X_{2T} }} - \frac{1}{{Y_{2C} }}} \right) - P^{2} \left( {\frac{1}{{X_{1T} Y_{1C} }} + \frac{1}{{X_{2T} Y_{2C} }}} \right)} \right] \end{aligned}$$
(7)

where \({\sigma }_{1}\), \({\sigma }_{2}\), \({\tau }_{12}^{2}\) are the principal stress; X1T, X2T are the tensile strength in fiber direction and transversal fiber direction, respectively; Y1C, Y2C are the compressive strength in fiber direction and transversal fiber direction, respectively; S12 is the shear strength of material.

The critical buckling load (\({C}_{\mathrm{cr}}\)) is another answer analyzed in this work with the maximization intention. It can be associated with an eigenvalue (λ) and the structure stiffness matrix as shown by Eqs. 8 and 9 as follows.

$$ \left( {\left[ {\text{K}} \right]{-}\lambda \left[ {{\text{K}}_{{\text{G}}} } \right]} \right)\{ \theta \} = 0 $$
(8)
$$ C_{cr} = \, \lambda \cdot {\text{ F}}_{{\text{i}}} $$
(9)

where [K] is the global stiffness matrix and [KG] is the isogrid tube global geometric stiffness matrix. In this way, the λ is a multiplier that shows how many times the structure can support the initial load without buckling.

3.2 Response surface design

More than eight input variables can be used in the isogrid tube code in FEM; however, the main ones that control the others are as follows: (i) the angle between helical ribs (φ), ranging from 20 to 50°, (ii) width of the helical crossbeams (δh), ranging from 2 to 6 mm and (iii) width of the circular crossbars (δc), ranging from 2 to 6 mm. These intervals are recommendations found in Francisco et al. (2021) and Junqueira et al. (2019).

Using the CCD with 3 decision variables, 8 factorial, 6 axial and 1 central experiments are generated. Adding 5 central points to assess the problem variability, there are 20 experiments in Table 3. The objectives are as follows: Mass (M), natural frequency (ωn), eigenvalues associated with the critical buckling load for compression (λC) and torsion (λT) and Tsai–Wu for compression (TWC) and torsion (TWT).

Table 3 Experimental matrix of the CFRP isogrid tube metamodeling
Full size table

3.3 Multi-objective optimization of isogrid tubes

For the construction of a visible Pareto front, 3 case studies will be proposed. Each of these cases will be performed with the two methodologies (LA-FEM and LA-RSM) and the generated Pareto fronts will be compared. The one that presents the best result for the three metrics used (IGD, SP, and MS) will be chosen for the isogrid tube optimization discussion.

Case I is a torsion case and aims to minimize the mass and Tsai-Wu and maximize the critical buckling load. The optimization problem can be seen in Eq. 10. Note that the minus sign is used for maximization.

$$ \begin{aligned} &{\text{min}}\,F\left( {\mathbf{X}} \right) = \left\{ {{\mathbf{M}}\left( {\mathbf{X}} \right), \, - {{\varvec{\uplambda}}}_{{\mathbf{T}}} \left( {\mathbf{X}} \right),{\mathbf{TW}}_{{\mathbf{T}}} \left( {\mathbf{X}} \right)} \right\} \hfill \\ &{\text{subject }}\,{\text{to:}} \hfill \\ &\quad20 \le {\boldsymbol{\varphi }} \le \, 50\left[^\circ \right] \hfill \\ &\quad2 \le {{\varvec{\updelta}}}_{{\mathbf{h}}} \le \, 6\left[ {{\text{mm}}} \right] \hfill \\ &\quad2 \le {{\varvec{\updelta}}}_{{\mathbf{c}}} \le \, 6\left[ {{\text{mm}}} \right] \hfill \\ \end{aligned} $$
(10)

Case II is a Compression case. The optimization problem modeling is similar to the previous one and is expressed in Eq. 11:

$$ \begin{aligned} &{\text{min}}F\left( {\mathbf{X}} \right) = \left\{ {{\mathbf{M}}\left( {\mathbf{X}} \right), \, - {{\varvec{\uplambda}}}_{{\mathbf{C}}} \left( {\mathbf{X}} \right),{\mathbf{TW}}_{{\mathbf{C}}} \left( {\mathbf{X}} \right)} \right\} \hfill \\ &{\text{subject }}\,{\text{to:}} \hfill \\ &\quad20 \le {\boldsymbol{\varphi }} \le \, 50\left[^\circ \right] \hfill \\ &\quad2 \le {{\varvec{\updelta}}}_{{\mathbf{h}}} \le \, 6\left[ {{\text{mm}}} \right] \hfill \\ &\quad2 \le {{\varvec{\updelta}}}_{{\mathbf{c}}} \le \, 6\left[ {{\text{mm}}} \right] \hfill \\ \end{aligned} $$
(11)

Case III is about modal performance and is composed of two objectives. It aims to minimize mass and maximize natural frequency. The optimization problem is expressed in Eq. 12.

$$ \begin{aligned} &{\text{min}}\,F\left( {\mathbf{X}} \right) = \{ {\mathbf{M}}\left( {\mathbf{X}} \right), \, - {{\varvec{\upomega}}}_{{\mathbf{n}}} \left( {\mathbf{X}} \right)\} \hfill \\ &{\text{subject}}\,{\text{ to:}} \hfill \\ &\quad 20 \le {\boldsymbol{\varphi }} \le \, 50\left[^\circ \right] \hfill \\&\quad 2 \le {{\varvec{\updelta}}}_{{\mathbf{h}}} \le \, 6\left[ {{\text{mm}}} \right] \hfill \\&\quad 2 \le {{\varvec{\updelta}}}_{{\mathbf{c}}} \le \, 6\left[ {{\text{mm}}} \right] \hfill \\ \end{aligned} $$
(12)

Case IV unites all the six studied objectives for the first time in the literature. The optimization problem is expressed in Eq. 13.

$$ \begin{aligned} &{\text{min}}\,F\left( {\mathbf{X}} \right) = \{ {\mathbf{M}}\left( {\mathbf{X}} \right), \, - {{\varvec{\uplambda}}}_{{\mathbf{C}}} \left( {\mathbf{X}} \right),{\mathbf{TW}}_{{\mathbf{C}}} \left( {\mathbf{X}} \right), \, - {{\varvec{\uplambda}}}_{{\mathbf{T}}} \left( {\mathbf{X}} \right),{\mathbf{TW}}_{{\mathbf{T}}} \left( {\mathbf{X}} \right), \, - {{\varvec{\upomega}}}_{{\mathbf{n}}} \left( {\mathbf{X}} \right) \, )\} \hfill \\ &subject \, to: \hfill \\ &\quad 20 \le {\boldsymbol{\varphi }} \le \, 50\left[^\circ \right] \hfill \\ &\quad 2 \le {{\varvec{\updelta}}}_{{\mathbf{h}}} \le \, 6\left[ {{\text{mm}}} \right] \hfill \\ &\quad 2 \le {{\varvec{\updelta}}}_{{\mathbf{c}}} \le \, 6\left[ {{\text{mm}}} \right] \hfill \\ \end{aligned} $$
(13)

The MOLA parameters for the multi-objective optimization problems in Eqs. 10, 11, 12, and 13 for both methodologies are as follows: Pop = 100; Niter = 100; Rc = 200; Np = 106; S = 1; ref = 0.4; and M = 0. The solutions of these cases do not lead to one solution, but to a solutions set called Pareto front. That is, no other solution can reduce some objective without causing a simultaneous increase in at least one other objective (Chiandussi et al. 2012).

The Pareto fronts generated for each case using the two methodologies will be compared using the inverted generational distance (IGD), Spacing (SP) and maximum spread (MS). These metrics need a reference Pareto front, often called true Pareto front (TPF) to evaluate the methodology or algorithm. As this problem is complex and there is no real Pareto front in the literature to use as reference, a Pareto front resulting from all solutions of all methodologies for each case will be used.

The IGD is a metric that measures the convergence capacity and is expressed by Eq. 13 (Sierra and Coello 2005):

$$ {\text{IGD}} = \frac{{\sqrt {\sum\limits_{I = 1}^{nt} {(d^{\prime}_{i} )^{2} } } }}{n} $$
(14)

where nt is the Pareto optimal solutions number and d’i indicates the Euclidean distance between the i-th true Pareto optimal solution and the closest Pareto optimal solution obtained in the reference set (TPF). If the IGD is null, the solutions obtained are equal to the true Pareto front.

To measure the coverage and quantitatively compare the algorithms, the SP (Schott 2005) and MS (Zitzler 1999) metrics are employed. SP and MS are given in Eqs. 14 and 15, respectively.

$$ {\text{SP}} = \sqrt {\frac{1}{n - 1}\sum\limits_{I = 1}^{n} {(\overline{d} - d_{i} )^{2} } } $$
(15)

where \(\overline{d }\) is the average of all di, n is the number of Pareto optimal solutions obtained, and\({d}_{i}=(\left|{f}_{1}^{i}\left(\overrightarrow{x}\right)-{f}_{1}^{j}\left(\overrightarrow{x}\right)\right|+\left|{f}_{2}^{i}\left(\overrightarrow{x}\right)-{f}_{2}^{j}\left(\overrightarrow{x}\right)\right|)\) for all i, j = 1, 2, 3, …, n.

$$ {\text{MS}} = \sqrt {\sum\limits_{i = 1}^{o} {\max (d(a_{i} ,b_{i} ))} } $$
(16)

where d is a function to calculate the Euclidean distance, ai is the maximum value in the i-th objective, bi is the minimum in the i-th objective, and o is the objectives number.

Note that for IGD and SP, lower values show better results. On the contrary, a higher MS shows a better algorithm and best coverage. With these three metrics, the best methodology for each Case will be chosen.

4 Numerical results and discussion

4.1 Metamodeling

Applying the simulations in Table 3, output variables are shown in Table 4.

Table 4 Results of the experimental matrix of the isogrid tube
Full size table

All metamodels found had an adjusted fit greater than 80%, being considered reasonable. These results are shown in Table 5. The generated metamodels that will be used in the LA-RSM methodology are in Table 6.

Table 5 Table for fit regression model
Full size table
Table 6 Metamodels coefficients generated by the response surface method
Full size table

4.2 Multi-objective optimization

The Pareto fronts generated for the optimization problems in Eqs. 10 to 12 are shown in Fig. 6. It is possible to see the non-dominated solutions and the best solution found using the Technique for Order of preference by similarity to ideal Solution (TOPSIS) (Yoon and Kim 2017) for the LA-FEM and LA-RSM methodologies, i.e., in the Torsion, Compression and Modal performance cases.

Fig. 6
figure 6

Pareto fronts generated for LA-FEM and LA-RSM

Full size image

TOPSIS was the decision-making technique chosen for being one of the most used in the last 5 years, having more than 4500 citations. The method uses the utopia point as positive ideal solution (A +) and the nadir point as negative ideal solution (A−) to calculate a score for each solution in Pareto front. The utopia point is an imaginary point composed of the imaginary minima of each objective, while the Nadir point is exactly the opposite. Using Euclidean distance, it determines which solution is the closest to (A +) and the furthest from (A−). Still, the method can be accompanied by tools for normalization of the search space, so that objectives that have larger ranges are not favored. Also, weights can be used to increase the importance of some objectives (Yoon and Kim 2017; Pereira et al. 2021c; Francisco et al. 2021).

The main motivation for using the two methodologies is to compare the accuracy of the results. In terms of computational cost, each simulation using FEM takes about 40 s. In the LA-RSM methodology, there are 20 experiments, which generates a 13 min simulation time. In the LA-FEM, there are 40 × Pop × Niter experiments, which results in approximately 55 h.

For the LA-RSM in all cases, the Pareto fronts have more consistency and continuity, given the optimization generated by second-order polynomial equations. However, it is possible to observe that the isogrid structure optimization true nature has discontinuous Pareto fronts. Also, even with the same search spaces in both methodologies, the LA-FEM methodology shows solutions with larger critical lambda (Case I) and natural frequencies (Case III) ranges. For this reason, the solution via TOPSIS for LA-FEM ends up being more displaced in relation to LA-RSM.

Three metrics are used to compare these generated Pareto fronts: IGD, SP and MS. The lower the IGD, the closer the analyzed Pareto front approached the true Pareto front. The smaller the SP, the less spaced the solutions are from each other. The larger the MS, the greater the interval between the solutions found. In this way, the smaller the IGD and SP and the larger the MS, the better the Pareto front. As in this problem there is no true Pareto front to be used as a reference, a Pareto front was generated that is composed of the solutions of the two methodologies for each case. These results are shown in Table 7.

Table 7 Statistical comparison of Pareto fronts
Full size table

As expected, given the ease of the optimization problem with second-order polynomial functions, the LA-RSM methodology SP is smaller in all cases. This result can also indicate the presence of discontinuity between the solutions, confirming the non-continuous Pareto front nature in this multi-objective optimization problem. MS indicates how the further away are the extreme solutions found and for all cases, the LA-FEM Methodology was higher (as can also be seen in Fig. 6).

One of the most important metrics is the IGD, as it is the metric that guarantees better solutions when using TOPSIS or a solution closest to the ideal point (Pereira et al., 2021c). In all situations, the LA-FEM presented better values, with the exception of Case II. However, a high discontinuity can be observed in this region, that was not identified by the RSM. The difference in IGD is even greater on the hyper-dimensional Pareto fronts generated in Case IV—a case with six objectives (or dimensions). For this reason, the optimal solutions for this work are those found by LA-FEM.

All the solutions using TOPSIS highlighted in Fig. 6 are in Table 8. As The LA-RSM methodology finds the optimal decision variables from metamodels, when entering them into the FEM for a conference simulation, there may be an error. Then, for this methodology, the Error is calculated and also is presented in Table 8. The difference (Diff) is also calculated for the objectives found between the LA-FEM and LA-RSM methodologies. It is important to emphasize that using only the Diff to assess which solution is better in multi-objective optimization is insufficient.

Table 8 Optimized decision variables for the four multi-objective design optimization cases
Full size table

For Case I, LA-FEM found a solution with 3 times the mass, less than half the TW, and 32.5 times the capacity to support a buckling load. However, a small error is observed using the LA-RSM, since the solution determined by TOPSIS is close to the true Pareto front (LA-FEM), as can be seen in Fig. 6a.

Approximately, half of the TW and 18 times the load capacity for only 16% increase in mass were found by the LA-FEM in the Compression case (Case II). In it, significant errors were identified for the TW and the critical Lambda. It can be seen in Fig. 6b that the solution found by LA-RSM is close to the discontinuous region found by LA-FEM. Still, this was the only case in which the methodology using the metamodel had a higher IGD than the one using the direct link with the FEM. Therefore, this point feasibility may be questionable.

As for modal performance case (Case III), the LA-RSM methodology found an 18.7% smaller mass, but with a natural frequency 32.9% smaller. It can be seen in Fig. 6c that the point found by the LA-RSM is not far from the Pareto front found by the LA-FEM. Thus, it presents a minor error. However, even the two methodologies having the same search space, can be seen a larger solutions number in LA-FEM in higher natural frequencies.

The multi-objective optimization problem becomes more complex with more objectives. As seen, the isogrid tube optimization problem even in small dimensions generated discontinuities and despite being visually difficult, it can be projected that more discontinuities will have for Case IV. This difference is evidenced by the difference in IGD in Table 7. The LA-RSM found a solution with a mass 43.8% smaller; however it obtained a TW greater than 1, which indicates a structure failure. The LA-FEM methodology found safe TW values, and critical lambda values 3 times higher for compression and 8 times higher for torsion.

The results found in this work can be compared Junqueira et al. (2019) and Francisco et al. (2021), as seen in Table 9. Difference 1 is the percentage difference between the results of this study and Junqueira et al. (2019). Difference 2 is for Francisco et al. (2021). There is no comparison for Case IV because this study is the first to do.

Table 9 Comparison of studies on the optimization of isogrid tubes
Full size table

This work significantly improves all the optimization objectives for Case I compared to other works in the literature, finding a smaller mass, a larger critical lambda and a smaller TW for the torsion case. In the case of compression, it also finds a mass and a TW smaller than all the other related studies; however, it has a lower critical λ, even though it has an expressive value of 18.71.

For case 3, this study finds higher natural frequency values, having increased by at least 52.57% the best found in the literature with only 12.8% more mass. Figure 7 shows the isogrid tubes optimized for each Case using the LA-FEM.

Fig. 7
figure 7

Isogrid tubes after deep optimization using TOPSIS

Full size image

5 Conclusion

This work proposes a CFRP isogrid tube deep multi-objective optimization considering six objectives: structural mass, Tsai–Wu failure index, instability coefficient (for compression and torsion efforts), and natural frequency. The objectives are divided into three cases for comparison with the literature: torsion, compression, and modal. The optimizations are considered using the direct link between the multi-objective Lichtenberg algorithm and the finite element method software and using metamodeling through the response surface methodology.

The LA-FEM methodology revealed the Pareto fronts’ real nature for this problem for the first time in the literature and allowed the evaluation of regions where the response surface methodology application is successful or not. Also, even with the same search spaces, the LA-FEM methodology allowed to find a non-dominated solutions range with higher critical lambdas and natural frequencies. Design variables were found with significant improvement compared to the most recent study in the literature. In the torsion case, there was a mass reduction of 48.09%, an increase in the critical lambda of buckling by 2.16%, and a reduction in Tsai-Wu by 90.90%. For compression, mass reduction by 45.69%, critical lambda reduction by 18.40%, and Tsai-Wu reduction by 68.67%. For the modal case, it allowed an increase of up to 52.57% in natural frequency for just a 12.8% increase in mass.

This study not only allowed to find the design variables of a safe and lightweight isogrid tube, as it showed that the Multi-objective Lichtenberg Algorithm was able to find excellent solutions even in problems without explicit equations.