1 Introduction

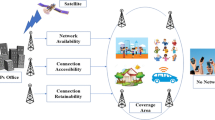
Telecommunication market is the essential and rapidly rising industry across the countries and an emerging factor for the potential of economic growth in different sectors. The innovation of cell phones and the World Wide Web (WWW) have given the momentum to breathtaking business growth. Mobile phones and the internet are précised impulsion to valuable financial development (Hung and Lu 2007). It offers a large quantity of information flows, prompting customer demand for top products and services by diminishing transaction ethics. India is currently the second largest telecommunication sector and third highest internet user in the globe. India is currently margining in both wireless and wire-line market around the world with 1197.87 million telephone subscribers at the last of Dec-18 to 1203.77 million at the last of Jan-19 (TRAI report 2019). The urban subscription raised from 666.28 million to 672.91 million, though, the rural subscription declined from 531.59 million to 530.86 million during the same time phase. As per India’s latest telecom data, the overall Tele-density in India raised from 91.45 to 91.82 at the end of Dec-18 and Jan-19, respectively. The urban Tele-density in the country increased from 159.98 to 161.34, but the rural Tele-density decreased from 59.50 to 59.38 during the same time phase. Out of the total number of telephone subscribers, the portion of urban and rural users was 55.90% and 44.10% respectively, at the end of Jan-19. For escalating the revenue, the TSPs will advance their services because of the healthy competition in the telecom sector. Bharti Airtel, BSNL, Idea, Reliance Communications and Tata DOCOMO are the leading telecom services providers in the Indian telecommunication market. Telecommunication is the fundamental support services necessary for briskly growth and improvement of the biz economy (Nigam et al. 2012). As appropriate, the telecommunication sector has sparked an evolvement in moulding up the process of universal adjustment to seizure the opportunities (Debnath and Shankar 2008).

As the rapid growth of the telecommunication market, researchers have taken a keen interest and applied their various approaches in this area. In a survey (Garg and Gupta 2007) which seeks to evaluate practices for bind the distance between present working levels and the expected possibilities of the Indian telecom market. Yang and Chang (2009) and Resende (2008) applied DEA for determining the proficiency of TSPs in Taiwan and the USA, respectively. One more survey (Shemshadi et al. 2011) results in a proportion of literature analysis, study of respondents from the sector, and insight gained through exploratory interviews and discovers a tool for analysing the class inside the group. Kumar and Kumar (2013) presented a hybrid approach using AHP and TOPSIS approaches to estimate the efficiencies of TSPs in the Delhi region.

Owing to the contribution of multiple factors and lack of precise facts, the selection of TSPs can be observed as a difficult uncertain MCDM concern. Fuzzy sets (FSs) originated by Zadeh (1965), have been fruitfully utilized in several areas and proved its great ability to solve with inaccurate and vague information. Several theories and applications have been widely employed in the existing studies from different perspectives (Wang and Chen 2008; Lee and Chen 2015; Mishra et al. 2016). Numerous researchers have employed the concept of FSs in the analysis of TSPs performances. For instance, Kumar et al. (2015) studied a unified model based on DEA and AHP methods to discuss the comparative efficiency of TSPs within the FSs context. Kumar et al. (2017) used an innovative model using the fuzzy ELECTRE method to evaluate the efficiencies of TSPs in the Delhi region. Using VIKOR and GRA, Li and Zhao (2016) introduced an MCDM model to examine the usefulness of thermal power plants for FSs. Rani et al. (2018) discussed the Shapley information measure-based VIKOR model to tackle the MCDM problem. Rani et al. (2020a) planned a combined methodology with Pythagorean fuzzy SWARA and VIKOR models to assess and select the desirable solar panel. Rani and Mishra (2020a) discussed a single-valued neutrosophic fuzzy MCDM model with SWARA and VIKOR procedures. Mishra et al. (2020c) presented a methodology with SWARA and COPRAS models for considering bioenergy production procedures. Rani et al. (2020b) projected the PF-COPRAS model to consider and select the best pharmacological therapy for T2D patients. Rani and Mishra (2020b) recommended a q-ROF-WASPAS approach for assessing and choosing desirable alternative-fuel technology.

FSs cannot handle the hesitation of experts because it is only characterized by a belongingness degree (BD). To overcome the flaws of FSs, Atanassov (1986) introduced the view of IFSs, which is an enhancement of FSs. IFSs are renowned by belongingness degree (BD), non-belongingness degree (NBD) and hesitancy degree (HD). It describes a competent arithmetical outline for solving problems in which decision experts (DEs) are not sure whether to support a specific decision or not and he/she refrains from the option. Afterwards, different researchers have applied MCDM within IFSs context (Chen and Chang 2015; Chen et al. 2016; Mishra 2016; Rani and Jain 2017, 2019; Mishra et al. 2017; Mishra and Rani 2019; Rani et al. 2019; Mishra et al. 2019a, b; Mishra 2016; Mishra and Rani 2018, 2019; Mishra et al. 2020a, b). Mishra et al. (2018) established a hybrid methodology with divergence measures and ELECTRE approach for IFSs to select the best TSPs. Recently, Kumari et al. (2019) extended Shapley information measure-based TOPSIS method for MCDM issues. Mishra et al. (2019c) discussed the WASPAS approach to assess the performance of TSPs in MP, India under the intuitionistic fuzzy environment. Mishra et al. (2019d) extended the HF-COPRAS model to enlighten the MCDM concerns. Mishra et al. (2020a) discussed the IVIF-COPRAS model to assess the hazardous-waste recycling facility problem. Kumari and Mishra (2020) gave IF-COPRAS model to explain the green supplier assessment problem. Mishra et al. (2020d) extended the EDAS methodology to evaluate the health-care waste disposal procedures for IFSs.

Grey system doctrine (GSD) (Deng 1989) is one of the decision-making frameworks applied to solve the ambiguity, being better in the numerical assessment of structures with an uncertain environment. In GSD, according to the degree of information, a structure with completely known information is said to be a white system, a structure with unknown information is said to be a black system and a structure with partially known information is said to be a grey system. The grey relational analysis (GRA), a fraction of GSD, is an appropriate process to handle the concerns with complex associations between several parameters and variables. Due to its ability, the GRA framework has been broadly applied to tackle the ambiguity on the discrete data and incomplete information (Liu et al. 2011; Rao and Zhao 2009; Wei et al. 2012; Wu and Peng 2016). Next, the GRA framework is one of the very fashionable ways to investigate diverse relationships amongst the multiple attribute circumstances. The key outcomes of this method are that the outcomes are according to the real data, the evaluations are easy and simple, and it provides an appropriate framework to make decisions on the business environment.

Based on the above discussion, we extend the GRA framework under IFSs to express the procedure for a comparative investigation of TSPs in MP (including CG) region. In the extended methodology, the attribute weights are figured out by developed the intuitionistic fuzzy divergence measure. After that, a comparison is presented to rank TSPs. The study will provide in outranking the poor performers. Hence, it may facilitate customers to select the top-ranked TSPs in the MP region. Moreover, it assists the TSPs to advance their performances by benchmarks the top rankers. The key contributions of the present work are as follows:

  • To recognize the factors for measuring the assessment of the telecom sector.

  • An innovative decision-making framework is introduced using GRA and developed divergence measures within the IFSs context.

  • To compute criteria weights, a new divergence measure for IFSs is proposed.

  • To express the usefulness and applicability, a comparison with the VIKOR approach is discussed. Also, a sensitivity analysis is given.

The rest of the paper is arranged as follows: Section 2 presents the fundamental conceptions allied with IFSs. Section 3 recommends novel IF-divergence measure to calculate the parameter weights. Section 4 proposes the extended GRA method under an intuitionistic fuzzy environment and named IF-GRA. Section 5 shows a TSPs selection problem to exemplify the usefulness of the IF-GRA framework. Next, comparison and sensitivity analyses are performed to illustrate the strength of the obtained outcomes. Lastly, Section 6 displays the conclusion of the work.

2 Preliminaries

This section presents elementary ideas related to IFSs and divergence measures.

Definition 2.1 (Atanassov 1986)

Let \( P = \left\{ {p_{1} ,p_{2} , \ldots ,p_{n} } \right\} \) be the finite discourse set. Then, an IFS \( \alpha \) is defined by

$$ \alpha = \left\{ {\left\langle {p_{i} ,\mu_{\alpha } (p_{i} ),\nu_{\alpha } (p_{i} )} \right\rangle :p_{i} \in P} \right\}, $$
(1)

where \( \mu_{\alpha } :P \to [0,\,\,1] \) and \( \nu_{\alpha } :P \to [0,\,\,1] \) are BD and NBD of \( p_{i} \) to \( \alpha \) in \( P, \), respectively, with the constraint

$$ 0 \le \mu_{\alpha } (p_{i} ),\nu_{\alpha } (p_{i} ) \le 1,\;0 \le \mu_{\alpha } (p_{i} ) + \nu_{\alpha } (p_{i} ) \le 1,\forall p_{i} \in P. $$
(2)

Next, the hesitancy degree of an object \( p_{i} \in P \) to \( \alpha \) is specified by

$$ \pi_{\alpha } (p_{i} ) = 1 - \mu_{\alpha } (p_{i} ) - \nu_{\alpha } (p_{i} ),\;0 \le \pi_{\alpha } (p_{i} ) \le 1. $$
(3)

For easiness, Burillo et al. (1994) described the concept of intuitionistic fuzzy number (IFN) and represented by \( \zeta \, = \,\left( {\mu_{\zeta } ,\,\nu_{\zeta } } \right) \) such that \( \mu_{\zeta } ,\,\nu_{\zeta } \, \in \,\left[ {0,\,1} \right] \) and \( 0\, \le \,\mu_{\zeta } + \nu_{\zeta } \le \,1 \).

Definition 2.2 (Xu 2007)

Let \( \zeta_{j} = \left( {\mu_{j} ,\nu_{j} } \right) \in {\text{IFSs}}\left( P \right),\,j = 1\left( 1 \right)n. \) Then, IF-weighted averaging operator (IFWAO) is specified by

$$ {\text{IFWA}}_{\omega } \left( {\zeta_{1} ,\zeta_{2} , \ldots ,\zeta_{n} } \right) = \left[ {1 - \prod\limits_{j = 1}^{n} {\left( {1 - \mu_{j} } \right)^{{\omega_{j} }} } ,\prod\limits_{j = 1}^{n} {\nu_{j}^{{\omega_{j} }} } } \right], $$
(4)

where \( \omega = \left( {\omega_{1} ,\omega_{2} , \ldots ,\omega_{n} } \right)^{T} \) is an important value of \( \zeta_{j} ,\,\,j = 1\left( 1 \right)n, \) with \( \sum\nolimits_{j = 1}^{n} {\omega_{j} = 1} ,\,\omega_{j} \in \left[ {0,1} \right]. \)

At first, Vlachos and Sergiadis (2007) proposed a divergence measure to show the distinction between two IFNs. Further, Montes et al. (2015) presented the axiomatic definition as follows:

Definition 2.3 (Montes et al. 2015)

A function \( J:{\text{IFS}}\left( P \right) \times {\text{IFS}}\left( P \right) \to {\mathbb{R}} \) is called an IF-divergence measure (IF-DM), if it fulfils the given conditions:

  • (D1). \( J\left( {\alpha ,\beta } \right)\, = \,J\left( {\beta ,\alpha } \right), \)

  • (D2). \( J\left( {\alpha ,\,\beta } \right) = \,0 \Leftrightarrow \,\,\alpha = \beta , \)

  • (D3). \( J\left( {\alpha \cap \gamma ,\beta \cap \gamma } \right) \le J\left( {\alpha ,\beta } \right),\forall \gamma \in {\text{IFS}}\left( P \right), \)

  • (D4). \( J\left( {\alpha \cup \gamma ,\beta \cup \gamma } \right) \le J\left( {\alpha ,\beta } \right),\forall \gamma \in {\text{IFS}}\left( P \right). \)

First IF-DM was given by Vlachos & Sergiadis (2007) as

$$ J_{\text{VS}} \left( {\alpha ,\beta } \right) = \sum\limits_{i = 1}^{n} {\left[ {\mu_{\alpha } (p_{i} )\ln \left( {\frac{{\mu_{\alpha } (p_{i} )}}{{\left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}} \right)\left( {\mu_{\alpha } (p_{i} ) + \mu_{\beta } (p_{i} )} \right)}}} \right) + \nu_{\alpha } (p_{i} )\ln \left( {\frac{{\nu_{\alpha } (p_{i} )}}{{\left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}} \right)\left( {\nu_{\alpha } (p_{i} ) + \nu_{\beta } (p_{i} )} \right)}}} \right)} \right]} , $$
(5)

and the symmetric edition of measure (5) is as follows:

$$ J_{\text{VS}}^{\text{sym}} \left( {\alpha ,\beta } \right) = J_{\text{VS}} \left( {\alpha ,\beta } \right) + J_{\text{VS}} \left( {\beta ,\alpha } \right). $$
(6)

3 New IF-Divergence measure

In the modern days, the concept of fuzzy directed divergence measure has been progressively enhanced and has verified its suitability in several disciplines namely engineering, image processing, decision-making, speech recognition, and others. To keep the flexibility and effectiveness of IFSs, a new parametric IF-DM is established for measuring the fuzziness degree of IFSs. Motivated by Ansari et al. (2018), we propose the following divergence measure. Let \( \alpha ,\beta \in {\text{IFSs}}\left( P \right), \) then

$$ \begin{array}{*{20}l} {J\left( {\alpha ,\beta } \right) = \frac{1}{{\left( {2^{{n\,\left( {1 - \tau } \right)}} - 1} \right)}}\left[ {\exp \left\{ {\left( {\tau - 1} \right)\sum\limits_{i = 1}^{n} {\left( {\left( {\frac{{\mu_{\alpha } \left( {p_{i} } \right) + \mu_{\beta } \left( {p_{i} } \right)}}{2}} \right)\ln \left( {\frac{{\mu_{\alpha } \left( {p_{i} } \right) + \mu_{\beta } \left( {p_{i} } \right)}}{{\mu_{\alpha } \left( {p_{i} } \right) + \mu_{\beta } \left( {p_{i} } \right) + \nu_{\alpha } \left( {p_{i} } \right) + \nu_{\beta } \left( {p_{i} } \right)}}} \right)} \right.} } \right.} \right.} \hfill \\ {\quad \quad \quad \quad + \left( {\frac{{\nu_{\alpha } \left( {p_{i} } \right) + \nu_{\beta } \left( {p_{i} } \right)}}{2}} \right)\ln \left( {\frac{{\nu_{\alpha } \left( {p_{i} } \right) + \nu_{\beta } \left( {p_{i} } \right)}}{{\mu_{\alpha } \left( {p_{i} } \right) + \mu_{\beta } \left( {p_{i} } \right) + \nu_{\alpha } \left( {p_{i} } \right) + \nu_{\beta } \left( {p_{i} } \right)}}} \right)\left. {\left. { - \left( {\frac{{\pi_{\alpha } \left( {p_{i} } \right) + \pi_{\beta } \left( {p_{i} } \right)}}{2}} \right)\ln 2} \right)} \right\}} \hfill \\ {\quad \quad \quad \quad \frac{ - 1}{2}\left\{ {\exp \left\{ {\left( {\tau - 1} \right)\sum\limits_{i = 1}^{n} {\left( {\mu_{\alpha } \left( {p_{i} } \right)\ln \left( {\frac{{\mu_{\alpha } \left( {p_{i} } \right)}}{{\mu_{\alpha } \left( {p_{i} } \right) + \nu_{\alpha } \left( {p_{i} } \right)}}} \right)} \right.} \left. { + \nu_{\alpha } \left( {p_{i} } \right)\ln \left( {\frac{{\nu_{\alpha } \left( {p_{i} } \right)}}{{\mu_{\alpha } \left( {p_{i} } \right) + \nu_{\alpha } \left( {p_{i} } \right)}}} \right)\left. { - \pi_{\alpha } \left( {p_{i} } \right)\ln 2} \right)} \right)} \right\}} \right.} \hfill \\ {\left. {\left. {\quad \quad \quad \quad + \exp \left\{ {\left( {\tau - 1} \right)\sum\limits_{i = 1}^{n} {\left( {\mu_{\beta } \left( {p_{i} } \right)\ln \left( {\frac{{\mu_{\beta } \left( {p_{i} } \right)}}{{\mu_{\beta } \left( {p_{i} } \right) + \nu_{\beta } \left( {p_{i} } \right)}}} \right)} \right.} \left. { + \nu_{\beta } \left( {p_{i} } \right)\ln \left( {\frac{{\nu_{\beta } \left( {p_{i} } \right)}}{{\mu_{\beta } \left( {p_{i} } \right) + \nu_{\beta } \left( {p_{i} } \right)}}} \right)\left. { - \pi_{\beta } \left( {p_{i} } \right)\ln 2} \right)} \right)} \right\}} \right\}} \right]} \hfill \\ \end{array} $$
(7)

Theorem 3.1

Let \( \alpha ,\beta ,\gamma \in {\text{IFSs}}\left( P \right), \) the measure \( J\left( {\alpha ,\,\beta } \right), \) given by (7) holds the following postulates:

  • (P1). \( J\left( {\alpha ,\beta } \right) = J\left( {\beta ,\alpha } \right), \)

  • (P2). \( 0 \le J\left( {\alpha ,\beta } \right) \le 1,J\left( {\alpha ,\alpha^{c} } \right) = 1 \Leftrightarrow \alpha \) is a crisp set;

  • (P3). \( J\left( {\alpha ,\beta } \right) = 0 \Leftrightarrow \alpha = \beta , \)

  • (P4). \( J\left( {\alpha ,\beta } \right) = J\left( {\alpha^{c} ,\beta^{c} } \right) \) and \( J\left( {\alpha^{c} ,\beta } \right) = J\left( {\alpha ,\beta^{c} } \right), \)

  • (P5). \( J\left( {\alpha ,\beta } \right) \le J\left( {\alpha ,\gamma } \right) \) and \( J\left( {\beta ,\gamma } \right) \le J\left( {\alpha ,\gamma } \right) \) for \( \alpha \subseteq \beta \subseteq \gamma , \)

  • (P6). \( J\left( {\alpha \cup \beta ,\alpha \cap \beta } \right) = J\left( {\alpha ,\beta } \right), \)

  • (P7). \( J\left( {\alpha \cup \beta ,\gamma } \right) \le J\left( {\alpha ,\gamma } \right) + J\left( {\beta ,\gamma } \right),\forall \gamma \in {\text{IFS}}\left( P \right), \)

  • (P8). \( J\left( {\alpha \cap \beta ,\gamma } \right) \le J\left( {\alpha ,\gamma } \right) + J\left( {\beta ,\gamma } \right),\forall \gamma \in {\text{IFS}}\left( P \right), \)

  • (P9). \( J\left( {\alpha \cap \gamma ,\beta \cap \gamma } \right) \le J\left( {\alpha ,\beta } \right),\forall \gamma \in {\text{IFS}}\left( P \right), \)

  • (P10). \( J\left( {\alpha \cup \gamma ,\beta \cup \gamma } \right) \le J\left( {X,Y} \right),\forall \gamma \in {\text{IFS}}\left( P \right). \)

Proof

The proofs of the properties are omitted.

4 Intuitionistic fuzzy GRA (IF-GRA) approach

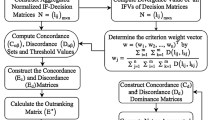
The conventional GRA approach introduced by Deng (1989) is a multifactor assessment procedure to determine the similarity to evaluate the uncertain relations between the options over the criteria (Lin et al. 2009; Liou et al. 2011). It is a fundamental procedure of grey doctrine, which can tackle the imprecise and ambiguous information in GSD on variable parameters and varying atmosphere (Deng 1988; Hsu and Wang 2009). It simply needs a sensible quantity of illustration data, straightforward and effortless evaluation. This method has extensively been used for handling various types of problems which arise in MCDM, data sciences and systems assessment (Kung and Wen 2007; Liou et al. 2011, Kumari and Mishra 2020). The developed algorithm for intuitionistic fuzzy GRA (IF-GRA) framework is presented below (graphically depicted in Fig. 1):

Fig. 1
figure 1

Execution flowchart of IF-GRA approach

Full size image

  • Step 1 Discuss the alternative and criterion sets.

    In the MCDM model, the aim is to select the best option from a set \( S = \left\{ {S_{1} ,S_{2} , \ldots ,S_{m} } \right\} \) of m alternatives under the criterion set \( G = \left\{ {G_{1} ,G_{2} , \ldots ,G_{n} } \right\}. \) Consider a group of \( t \) decision experts \( E = \left\{ {E_{1} ,E_{2} , \ldots ,E_{t} } \right\} \) to establish the most desirable option(s).

  • Step 2 Define the aggregated IF-decision matrix (AIF-DM).

    To merge all the individuals and construct one decision matrix, we have to produce AIF-D matrix \( {\mathbb{N}} = \left( {p_{ij} } \right) = \left\langle {\mu_{ij} ,\nu_{ij} } \right\rangle ,i = 1(1)m,j = 1(1)n. \)

  • Step 3 Assess the ideal (IS) and anti-ideal (AIS) solution based on IFNs.

    The ideal solution for various criteria is diverse and specified as

    $$ \varepsilon_{j}^{ + } = \left\{ {\begin{array}{*{20}l} {\mathop {\hbox{max} }\limits_{i = 1(1)m} \varepsilon_{ij} } \hfill & {{\text{for}}\,{\text{benefit - type}}\,G_{j} } \hfill \\ {\mathop {\hbox{min} }\limits_{i = 1(1)m} \varepsilon_{ij} } \hfill & {\,{\text{for}}\,{\text{cost - type}}\,G_{j} ,} \hfill \\ \end{array} } \right. $$
    (8)

    Similarly, anti-ideal solution for various criteria is depicted as

    $$ \varepsilon_{j}^{ - } = \left\{ {\begin{array}{*{20}l} {\mathop {\hbox{min} }\limits_{i = 1(1)m} \varepsilon_{ij} } \hfill & {{\text{for}}\,{\text{benefit - type}}\,G_{j} } \hfill \\ {\mathop {\hbox{max} }\limits_{i = 1(1)m} \varepsilon_{ij} } \hfill & {{\text{for}}\,{\text{cost - type}}\,G_{j} } \hfill \\ \end{array} } \right.,\,j = 1\left( 1 \right)n. $$
    (9)

  • Step 4 Evaluation of grey relational coefficient (GRC) from IS and AIS.

    The GRC of each option from IS is defined as

    $$ \hbar_{ij}^{ + } = \frac{{\mathop {\hbox{min} \hbox{min} J}\limits_{1 \le i \le m \le 1 \le j \le n} \left( {p_{ij} ,\varepsilon_{j}^{ + } } \right) + \rho \mathop {\hbox{max} \hbox{max} }\limits_{1 \le i \le m \le 1 \le j \le n} J\left( {p_{ij,} \varepsilon_{j}^{ + } } \right)}}{{J\left( {p_{ij} ,\varepsilon_{j}^{ + } } \right) + \rho \mathop {\hbox{max} \hbox{max} }\limits_{1 \le i \le m \le 1 \le j \le n} J\left( {p_{ij,} \varepsilon_{j}^{ + } } \right)}}. $$
    (10)

    Similarly, the GRC of each option from AIS is discussed by

    $$ \mathchar'26\mkern-10mu\lambda_{ij}^{ - } = \frac{{\mathop {\hbox{min} \hbox{min} J}\limits_{1 \le i \le m \le 1 \le j \le n} \left( {p_{ij} ,\varepsilon_{j}^{ - } } \right) + \rho \mathop {\hbox{max} \hbox{max} }\limits_{1 \le i \le m \le 1 \le j \le n} J\left( {p_{ij,} \varepsilon_{j}^{ - } } \right)}}{{J\left( {p_{ij} ,\varepsilon_{j}^{ - } } \right) + \rho \mathop {\hbox{max} \hbox{max} }\limits_{1 \le i \le m \le 1 \le j \le n} J\left( {p_{ij,} \varepsilon_{j}^{ - } } \right)}}. $$
    (11)

    For each \( i = 1\left( 1 \right)m,\,j \in 1\left( 1 \right)n, \) where the coefficient of identification value is \( \rho = 0.5. \) Here, \( J\left( {p_{ij,} \varepsilon_{j}^{ + } } \right) \) and \( J\left( {p_{ij,} \varepsilon_{j}^{ - } } \right) \) denote the divergence measures, given by (7).

  • Step 5 Calculate the degree of GRC of each alternative.

    The GRC degrees of alternative from ideal and anti-ideal solutions are computed as follows:

    $$ \hbar_{i}^{ + } = \sum\limits_{j = 1}^{n} {w_{j} \hbar_{ij}^{ + } ,\mathchar'26\mkern-10mu\lambda_{i}^{ - } = \sum\limits_{j = 1}^{n} {w_{j} \mathchar'26\mkern-10mu\lambda_{ij}^{ - } ,\forall i.} } $$
    (12)

    The doctrine of the GRA framework is that the desirable option must have “largest degree of grey relation” from IS and “smallest degree of grey relation” from AIS. Evidently, for given weight values, the smaller \( \mathchar'26\mkern-10mu\lambda_{i}^{ - } \) and the greater \( \hbar_{i}^{ + } , \) the better option \( S_{i} . \). However, the criteria weights’ information is partially unknown. Thus, to obtain \( \mathchar'26\mkern-10mu\lambda_{i}^{ - } \) and \( \hbar_{i}^{ + } , \) here, we first evaluate the weight information by constructing the objective optimization model as follows:

    $$ \left( {M_{1} } \right):\left\{ {\begin{array}{*{20}l} {\hbox{max} \hbar_{i}^{ + } = \sum\limits_{j = 1}^{n} {w_{j} \hbar_{ij}^{ + } } ,\hbox{min} \mathchar'26\mkern-10mu\lambda_{i}^{ - } = \sum\limits_{j = 1}^{n} {w_{j} \mathchar'26\mkern-10mu\lambda_{ij}^{ - } ;\forall i} } \hfill \\ {{\text{subject}}\,{\text{to}}\,w_{j} \in \Delta } \hfill \\ \end{array} } \right. $$
    (13)

    Each option is non-inferior; consequently, there is no preference relation that exists amongst all options. Thus, the multi-objective optimization procedure (13) is aggregated into the single objective optimization model and is given by

    $$ \left( {M_{2} } \right):\left\{ {\begin{array}{*{20}l} {\hbox{max} \xi = \sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {\left( {\hbar_{ij}^{ + } - \mathchar'26\mkern-10mu\lambda_{ij}^{ - } } \right)w_{j} } } } \hfill \\ {{\text{subject}}\,{\text{to}}\,w_{j} \in \Delta } \hfill \\ \end{array} } \right. $$
    (14)

    Simplifying model \( \left( {M_{2} } \right), \), we obtain the optimal value \( w = \left( {w_{1} ,w_{2} , \cdots ,w_{n} } \right)^{T} , \) and is applied as the criteria weights. Then, we obtain \( \hbar_{i}^{ + } \) and \( \mathchar'26\mkern-10mu\lambda_{i}^{ - } \) by Eq. (14).

  • Step 6 Evaluating the relative relational degree (RRD).

    The RRD of each option from IS is computed by

    $$ \xi_{i} = \frac{{\hbar_{i}^{ + } }}{{\left( {\mathchar'26\mkern-10mu\lambda_{i}^{ - } + \hbar_{i}^{ + } } \right)}},\forall i. $$
    (15)

  • Step 7 Rank the alternative \( S_{i} \left( {i = 1\left( 1 \right)m} \right) \) and choose the optimal alternative according to the highest value of \( \xi_{i} . \)

  • Step 8 End.

5 A case study of telephone service providers selection

In the current section, a case study of Madhya Pradesh (India) is presented for selecting the best telephone service providers (TSPs) amongst a set of alternative TSPs, which illustrate the feasibility of the developed IF-GRA framework. In the Madhya Pradesh circle, BSNL \( \left( {S_{1} } \right) \), Bharti Airtel \( \left( {S_{2} } \right) \), Vodafone \( \left( {S_{3} } \right) \), Reliance Jio \( \left( {S_{4} } \right) \), Idea \( \left( {S_{5} } \right) \) and Tata DOCOMO \( \left( {S_{6} } \right) \) are the most important cellular mobile TSPs. These TSPs are considered under the various operational performances (TRAI report 2017a). Performance guidelines and their details of the parameters are depicted in Table 1. The computation of the IF-GRA framework is given as follows:

Table 1 Performance guidelines and their details
Full size table

Each expert gives his/her valuations for grading of reliability TSPs under considered criteria. Table 2 shows the linguistic terms into IFNs to weigh up the relative importance of the favored evaluation scale. Then, the AIF-DM \( {\mathbb{N}} = \left( {p_{ij} } \right) = \left\langle {\mu_{ij} ,\,\nu_{ij} } \right\rangle , \) for TSPs is constructed in Table 3.

Table 2 Rating of the performance parameters, experts and TSPs in linguistic variables form
Full size table
Table 3 AIF-D matrix of TSPs
Full size table

From Eqs. (8) and (9), the IF-IS and IF-AIS are as follows:

$$ \varepsilon_{j}^{ + } = \left\{ {\left( {0. 5 30,0. 2 6 5} \right),\left( {0. 7 2 5,0. 2 5 6} \right),\left( {0. 6 50,0. 2 7 4} \right),\left( {0. 7 60,0. 1 7 2} \right),\left( {0. 7 7 4,0. 1 6 8} \right),\left( {0. 5 1 2,0. 2 7 4} \right),\left( {0. 7 40,0. 1 8 9} \right)} \right\} $$
$$ \varepsilon_{j}^{ - } = \left\{ {\left( {0. 7 7 4,0. 1 7 7} \right),\left( {0. 4 8 2,0. 30 4} \right),\left( {0. 7 5 6,0. 1 7 9} \right),\left( {0. 5 6 9,0. 3 2 9} \right),\left( {0. 5 50,0. 2 5 2} \right),\left( {0. 6 6 6,0. 1 3 6} \right),\left( {0. 5 4 2,0. 2 5 2} \right)} \right\} $$

Now, with the use of Eqs. (10)–(11), the GRC of every substitute from IF-IS to IF-AIS is estimated and presented in Tables 4, 5.

Table 4 Grey relational coefficient for TSPs with ideal solution
Full size table
Table 5 Grey relational coefficient for TSPs with anti-ideal solution
Full size table

Next, we operate the model to setup the following individual objective model:

$$ \hbox{max} \xi = \hbox{max} \left\{ {1.0565w_{1} + 0.2212w_{2} - 0.2801w_{3} - 0.4377w_{4} - 1.5808w_{5} - 0.6204w_{6} - 0.7578w_{7} } \right. $$
$$ {\text{Subject}}\;{\text{to}}\;\Delta = \left\{ {\begin{array}{*{20}l} {0.2 \le w_{1} \le 0.3,0.05 \le w_{2} \le 0.15,0.01 \le w_{3} \le 0.09,0.12 \le w_{4} \le 0.2,} \hfill \\ {0.065 \le w_{5} \le 0.144,2w_{5} \le w_{4} ,} \hfill \\ {w_{3} - w_{5} \le w_{2} ,0.03 \le w_{6} \le 0.14,0.1 \le w_{7} \le 0.2,} \hfill \\ {\sum\limits_{j = 1}^{7} {w_{j} = 1} ,w_{j} \ge 0.} \hfill \\ \end{array} } \right. $$

Simplifying the model, the criteria weights are computed as \( w_{1} \, = 0. 3 , { }w_{2} \,{ = }\, 0. 1 5 , \) \( w_{3} \, = \, 0. 0 9 , { }w_{4} \, = \, 0. 2 , \)\( w_{5} \,{ = 0} . 0 6 5 , { }w_{6} { = }\, 0. 0 9 5 , { }w_{7} \,{ = 0} . 1. \)Then, we evaluate the degree of GRC of each option from IS and AIS using Eqs. (13)–(14).

$$ \hbar_{1}^{ + } = 0.6991,\,\,\hbar_{2}^{ + } = 0.7485,\,\,\hbar_{3}^{ + } = 0.6886,\,\,\hbar_{4}^{ + } = 0.7802,\,\,\hbar_{5}^{ + } = 0.7292,\,\,\hbar_{6}^{ + } = 0.6650 $$
$$ \mathchar'26\mkern-10mu\lambda_{1}^{ - } = 0.7343,\,\,\mathchar'26\mkern-10mu\lambda_{2}^{ - } = 0.7489,\,\,\mathchar'26\mkern-10mu\lambda_{3}^{ - } = 0.7367,\,\mathchar'26\mkern-10mu\lambda_{4}^{ - } = 0.6371,\,\,\mathchar'26\mkern-10mu\lambda_{5}^{ - } = 0.6890,\,\,\mathchar'26\mkern-10mu\lambda_{6}^{ - } = 0.7454. $$

Finally, we determine the RRD of each option from IS using (15), which is as follows: \( \xi_{1} = 0.4877\,,\,\xi_{2} = 04999\,,\,\xi_{3} = 0.4831\,,\,\xi_{4} = 0.5505\,,\,\xi_{5} = 0.5142\,,\,\xi_{6} = 0.4715. \)

Based on (15), the ranking or preference order of the options is \( \xi_{4} \succ \xi_{5} \succ \xi_{2} \succ \xi_{1} \succ \xi_{3} \succ \xi_{6} , \) and thus, the most desirable alternative is \( \xi_{4} \). As per the performance and subscribers’ perspectives, Reliance Jio has the utmost ranking and Idea has the second one. Similarly, Airtel and BSNL have the third and fourth ranks. Vodafone has the fifth performance level, whereas Tata DOCOMO is the lowest rank service provider using the IF-GRA framework.

5.1 Comparative discussion

Here, a comparison is executed between the outcomes attained from the IF-GRA model and the intuitionistic fuzzy VIKOR (IF-VIKOR) approach. To validate the proficiency and display the irreplaceable merits of the IF-GRA framework, the IF-VIKOR approach is employed to tackle the TSPs concern.

5.1.1 Intuitionistic fuzzy VIKOR (IF-VIKOR) method

  • Step 1–3 Same as the previous method

  • Step 4 Obtain the attribute weights.

    To evaluate attribute weights, we use the formula with proposed divergence measure (7) as follows:

    $$ w_{j} = \tfrac{{\sum\limits_{i = 1}^{m} {\left[ {\tfrac{1}{m - 1}\sum\limits_{k = 1}^{m} {J\left( {p_{ij} ,p_{kj} } \right)} } \right]} }}{{\sum\limits_{j = 1}^{n} {\sum\limits_{i = 1}^{m} {\left[ {\tfrac{1}{m - 1}\sum\limits_{k = 1}^{m} {J\left( {p_{ij} ,p_{kj} } \right)} } \right]} } }},j = 1\left( 1 \right)n. $$
    (16)

  • Step 5 Compute of group utility (GU), individual regret (IR) and compromise measure (CM).

    Based on conventional VIKOR, we use the divergence measure to develop the \( L_{p} \)-metric as follows:

    $$ L_{p,i} = \left( {\sum\limits_{j = 1}^{n} {\left( {w_{j} \frac{{J\left( {\varepsilon_{j}^{ + } ,p_{ij} } \right)}}{{J\left( {\varepsilon_{j}^{ + } ,\varepsilon_{j}^{ - } } \right)}}} \right)^{p} } } \right)^{{{1 \mathord{\left/ {\vphantom {1 p}} \right. \kern-0pt} p}}} , $$
    (17)

    where \( w_{j} \) is the weight vector of \( G_{j} (j = 1(1)n). \)

    With divergence measure-based \( L_{p} \)-metric, we demonstrate the divergence measure-based group utility and individual regret as

    $$ {\mathbb{S}}_{i} = L_{1,\,\,i} = \sum\limits_{j = 1}^{n} {w_{j} \frac{{J\left( {\varepsilon_{j}^{ + } ,p_{ij} } \right)}}{{J\left( {\varepsilon_{j}^{ + } ,\varepsilon_{j}^{ - } } \right)}}} ,\Re_{i} = L_{\infty ,i} = \mathop {\hbox{max} }\limits_{1 \le j \le n} \left( {w_{j} \frac{{J\left( {\varepsilon_{j}^{ + } ,p_{ij} } \right)}}{{J\left( {\varepsilon_{j}^{ + } ,\varepsilon_{j}^{ - } } \right)}}} \right), $$
    (18)

    where \( w_{j} \) is the weight of the criterion \( G_{j} . \)

    The idea of VIKOR approach is used to acquire a CM(s), we construct compromise measure \( Q_{i} \) by the relation

    $$ Q_{i} = \vartheta \frac{{{\mathbb{S}}_{i} - {\mathbb{S}}^{ + } }}{{{\mathbb{S}}^{ - } - {\mathbb{S}}^{ + } }} + \left( {1 - \vartheta } \right)\frac{{\Re_{i} - \Re^{ + } }}{{\Re^{ - } - \Re^{ + } }}, $$
    (19)

    where \( {\mathbb{S}}^{ + } = \min_{i} {\mathbb{S}}_{i} , \)\( {\mathbb{S}}^{ - } = \max_{i} {\mathbb{S}}_{i} , \)\( \Re^{ + } = \min_{i} \Re_{i} , \)\( \Re^{ - } = \max_{i} \Re_{i} \) and \( \vartheta \) is the strategy weight of the majority of criteria or coefficient of decision mechanism. In general, we assume \( \vartheta = 0.5. \) The smaller the degree of \( Q_{i} (i = 1(1)m), \) the better the option \( S_{i} \left( {i = 1(1)\,m} \right). \) The compromise solution can be obtained with “voting by majority” \( \left( {\vartheta > 0.5} \right), \) with “consensus” \( \left( {\vartheta = 0.5} \right), \) with “veto” \( \left( {\vartheta < 0.5} \right). \)

  • Step 6 Rank the options by arranging the degrees of \( {\mathbb{S}}_{i} ,\,\Re_{i} \) and \( Q_{i} \) in decreasing order.

  • Step 7 Determine the optimal option or CM(s).

  • Step 8 End.

For the selection of TSPs here, we examine its application. Sometimes it is difficult to state the necessity of the guidelines and the encounter of TSPs on the guidelines. From Eq. (7), the attribute weights are calculated using the IF-DM and are given by

$$ w = \left( {0.2972,\,\,0.0892,\,\,0.0847,\,\,0.1562,\,\,0.0724,\,\,0.0858,\,\,0.2145} \right)^{T} . $$

From Eq. (18), we compute out the average score of \( S_{i} , \) worst group score of \( \Re_{i} . \) Now, we calculate the values of \( \vartheta \) from Eq. (19) given in Table 6. As of Table 7 and Fig. 2, we observe that Q(S4) values become smaller and Q(S2) values become large as the weight \( \vartheta \) increases.

Table 6 Computation of group utility, individual regret and compromise solution for TSPs
Full size table
Table 7 Sensitivity analysis of compromise solution(s) for different values of \( \vartheta \)
Full size table
Fig. 2
figure 2

Degrees of \( S_{i} \), \( \Re_{i} \) and \( Q_{i} \) for various parameter \( \vartheta \) values

Full size image

Here, based on operational performance, Reliance Jio has the maximum rating and Airtel has the second rank, but applying IF-VIKOR the given two TSPs have the same ranking. Whereas, Idea, Tata DOCOMO, BSNL and Vodafone have different orders and they are on the second, third, fourth and fifth levels using the IF-VIKOR procedure.

The objective of the initial sensitivity discussion is to examine the effect of different values of the factor \( \vartheta . \) Table 7 exposes the corresponding outcomes of the compromise index \( Q_{i\,} , \) the set of compromise solution(s) \( S_{4} ,\,\,S_{2} \) and the optimal rankings of the TSPs according to different parameter values \( \vartheta . \) Furthermore, the outcomes of the sensitivity assessment for different \( \vartheta \) values are discussed graphically in Fig. 2. Later, Fig. 2 demonstrates the comparison of the compromise ratings amongst TSPs with respect to the parameter \( \vartheta . \)

6 Conclusion

In the Madhya Pradesh circle, the TSPs are found comparative in the public and private sectors related to QoS guidelines. The wireless ad wire-line connections are in better condition in the private sector. Numerous factors and sub-factors have been considered in mind before the selection of the location. We need to identify every last footprint of the crucial factors in cellular and wire-line connection. In this paper, the IF-GRA framework is introduced to evaluate the relative performance of various TSPs under the intuitionistic fuzzy environment. The introduced framework is according to the conception of IS and AIS. To evaluate the criterion weights, a divergence measure is developed and employed by relative comparisons. To elucidate the practicality of the introduced framework, an empirical case study of TSPs assessment of Madhya Pradesh has been discussed and the results of the performed analysis confirm its effectiveness. The obtained results prove that the developed framework can effectively handle the issue of TSPs selection in uncertain environments. Comparison and sensitivity assessment prove the authority of the developed model. Furthermore, it offers the TSPs to improve the services by benchmarks the top service providers. We will further study and implement various other MCDM approaches, viz., TOPSIS, ARAS, CoCoSo and COPRAS for assessment of the performance of TSPs.