1 Introduction

Green supply chain management (GSCM) is a policy which reinforces and incorporates the environmental concern into entire supply chain process. Due to increasing environmental issues, several researchers and practitioners have paid attention on GSCM. As the green supplier alternatives influenced by many criteria, it is assumed as an MCDM problem. In the supplier selection, it is not always possible to determine an efficient solution due to inaccurate decision information.

The doctrine of fuzzy sets (FSs) pioneered by Zadeh (1965) have widely received attention from decision makers in the procedure of decision making. On the last two decades, various approaches and doctrines for dealing vagueness and uncertainty have been introduced. Later on, a variety of extensions of FSs have been pioneered. In FSs, the membership of an element is defined to be a number from the interval [0, 1] and the non-membership is simply its complement. But, in reality, this hypothesis does not match with human intuition. To evade the shortcomings of FSs, Atanassov (1986) extended the concept of FSs to intuitionistic fuzzy sets (IFSs) by extending a single membership function into three functions: the membership, the non-membership and the hesitation function such that the addition of the membership and non-membership values is less than or equal to one (Mishra 2016; Mishra et al. 2017a). As the IFSs have more potential than FSs to handle the uncertainty, numerous authors have paid their attention on IFSs and their applications.

In the study of uncertainty, information measures such as divergence, entropy, similarity and distance measures have played a vital role. The divergence measures quantify the degree of discrimination between two objects. Divergence measure for FSs has been firstly developed by Bhandari and Pal (1993), which was based on probabilistic divergence measures. Later on, several different studies have been listed for fuzzy divergence measures in the literature (Fan and Xie 1999; Hooda and Mishra 2015; Mishra et al. 2016a, b). Similar to fuzzy sets, Vlachos and Sergiadis (2007) developed the idea of intuitionistic fuzzy divergence measure and applied in pattern recognition, medical diagnosis and image segmentation. Subsequently, various divergence or cross-entropy measures for IFSs have been established by different reputed authors (Mishra et al. 2017a, b, 2018b; Ansari et al. 2018; Mishra and Rani 2019), and the results have been applied in pattern recognition, medical diagnosis, MCDM and image processing.

Inspired by the idea of information theory, the theory of entropy quantifies the degree of uncertain information (Zadeh 1968). Further, Szmidt and Kacprzyk (2001) suggested the axiomatic definition of entropy according to fuzzy entropy and proposed the entropy for IFSs. Consequently, various entropies have been demonstrated for FSs, IFSs, PFSs and IVIFSs in Bustince and Burillo (1996), Mishra et al. (2015, 2016a, b, 2017a, b, 2018a, b, c, d, 2019a, b, c, 2020), Mishra (2016), Rani and Jain (2017, 2019), Mishra and Rani (2018a, b, 2019), Rani et al. (2018, 2019a, b, c, d) and utilized in various disciplines.

In this study, we have presented complex proportional assessment (COPRAS) and grey relational analysis (GRA) methods under intuitionistic fuzzy atmosphere and implemented in a green supplier selection problem. A new compromising approach named as COPRAS, pioneered by Zavadskas et al. (1994), is an efficient and simple technique to handle the MCDM problems. The main benefits of the COPRAS method are: (1) it is very easy and simply comprehendible; (2) it assumes the ratios to the ideal and the anti-ideal solutions simultaneously; and (3) the outcomes can be attained in a small duration of time. According to these benefits, the COPRAS approach has been extended by various authors from different points of view in latest years (Kouchaksaraei et al. 2015; Liou et al. 2016).

GRA, a part of grey system theory, is a suggested tool to handle the problems with intricate relationships among several discrete data sets. Deng (1989) developed the concept of GRA, is an impact assessment approach which is very simple and straightforward in calculation and can used to determine the degrees of similarity or dissimilarity between two sequences based on the relation. Over the last few decades, GRA has been broadly utilized by many authors for managing the uncertain MCDM problems. GRA is a basic approach of grey theory, which can process the inaccurate and vague information in grey systems under variable factors and changing environment (Deng 1989; Hsu and Wang 2009; Wu and Peng 2016). It only requires a reasonable amount of sample data, just a simple and easy calculation, and GRA has been widespread applied in addressing kinds of real-world application problems in control, decision making, data processing as well as systems analysis (Kung and Wen 2007; Liu et al. 2011, Liang et al. 2018, 2019). Also, Table 1 demonstrates the list of abbreviations applied in the paper. The overview of the earlier literature on COPRAS and GRA approaches is discussed in Table 2.

Table 1 Abbreviations used in the paper
Full size table
Table 2 Outline of several relevant researches on COPRAS and GRA approaches
Full size table

Nowadays, uncertainty has widely risen in decision-making problems and it is obvious that the IFSs are suitable tool to managing the uncertain information, so that this work is presented under intuitionistic fuzzy environment. This work firstly proposes new Jensen–Shannon (JS) divergence measures for IFSs as the divergence measures are an interesting and vital research topic in the study of IFSs. Proposed parametric measure is used for measuring the degree of fuzziness. To do this, divergence measures of order \(\gamma\) are demonstrated which make the decision experts more dependable and flexible for the diverse parameter values. The proposed divergence measures hold several elegant properties which are exposed to enhance their applicability. Further, an MCDM approach named as COPRAS is extended for intuitionistic fuzzy information with partially or completely unknown criteria weights and applied to evaluate the GSS problem, which demonstrate the applicability of the developed method.

The main outcomes of the manuscript are as follows:

  • An integrated intuitionistic fuzzy COPRAS (IF-COPRAS) method, an extension of classical COPRAS method, is introduced for MCDM problems.

  • New information measures are proposed to obtain the criterion weights and established the association between IF-entropy and IF-divergence measures.

  • The developed method is implemented for a GSS problem.

  • Comparison is made of proposed method with intuitionistic fuzzy GRA (IF-GRA) method and other existing methods.

2 Proposed Divergence and Entropy Measures for IFSs

In this section, we have proposed Jensen–Shannon divergence measure for IFSs based on Jensen’s inequality and the Shannon entropy concepts. One of the salient features of the Jensen–Shannon divergence is that we can assign a different weight to each probability distribution. This makes it particularly suitable for the study of decision problems where the weights could be the prior probabilities. Most measures of divergence measure are designed for two probability distributions. For certain applications such as in the study of taxonomy in biology and genetics, one is required to measure the overall difference of more than two distributions. The Jensen–Shannon divergence can be generalized to provide such a measure for any finite number of distributions. This is also useful in multiclass decision making.

Let \(R,\,\,S \in IFSs\left( U \right),\) then corresponding to Ansari et al. (2018), JS-divergence measure for IFSs is proposed as follows:

$$\begin{aligned} & J_{1} \left( {R,S} \right) = \frac{1}{{n\left( {e^{{\left( {1 - 0.5^{\,\gamma } } \right)}} - 1} \right)}}\sum\limits_{i = 1}^{n} {\left[ \begin{aligned} \left( {\frac{\begin{aligned} \mu_{R} \left( {x_{i} } \right) + \mu_{S} \left( {x_{i} } \right) \hfill \\ + 2 - \nu_{R} \left( {x_{i} } \right) - \nu_{S} \left( {x_{i} } \right) \hfill \\ \end{aligned} }{4}} \right)\exp \left( {1 - \left( {\frac{\begin{aligned} \mu_{R} \left( {x_{i} } \right) + \mu_{S} \left( {x_{i} } \right) + 2 \hfill \\ \,\,\,\,\, - \nu_{R} \left( {x_{i} } \right) - \nu_{S} \left( {x_{i} } \right) \hfill \\ \end{aligned} }{4}} \right)^{\gamma } } \right) \hfill \\ \,\, + \left( {\frac{\begin{aligned} \nu_{R} \left( {x_{i} } \right) + \nu_{S} \left( {x_{i} } \right) \hfill \\ + 2 - \mu_{R} \left( {x_{i} } \right) - \mu_{S} \left( {x_{i} } \right) \hfill \\ \end{aligned} }{4}} \right)\exp \left( {1 - \left( {\frac{\begin{aligned} \nu_{R} \left( {x_{i} } \right) + \nu_{S} \left( {x_{i} } \right) \hfill \\ + 2 - \mu_{R} \left( {x_{i} } \right) - \mu_{S} \left( {x_{i} } \right) \hfill \\ \end{aligned} }{4}} \right)^{\gamma } } \right) \hfill \\ \end{aligned} \right.} \\ & \left. {\quad \quad - \frac{1}{2}\left( \begin{aligned} \left( {\frac{{\mu_{R} \left( {x_{i} } \right) + 1 - \nu_{R} \left( {x_{i} } \right)}}{2}} \right)\exp \left( {1 - \left( {\frac{{\mu_{R} \left( {x_{i} } \right) + 1 - \nu_{R} \left( {x_{i} } \right)}}{2}} \right)^{\gamma } } \right) \hfill \\ + \;\left( {\frac{{\nu_{R} \left( {x_{i} } \right) + 1 - \mu_{R} \left( {x_{i} } \right)}}{2}} \right)\exp \left( {1 - \left( {\frac{{\nu_{R} \left( {x_{i} } \right) + 1 - \mu_{R} \left( {x_{i} } \right)}}{2}} \right)^{\gamma } } \right) \hfill \\ + \;\left( {\frac{{\mu_{S} \left( {x_{i} } \right) + 1 - \nu_{S} \left( {x_{i} } \right)}}{2}} \right)\exp \left( {1 - \left( {\frac{{\mu_{S} \left( {x_{i} } \right) + 1 - \nu_{S} \left( {x_{i} } \right)}}{2}} \right)^{\gamma } } \right) \hfill \\ + \;\left( {\frac{{\nu_{S} \left( {x_{i} } \right) + 1 - \mu_{S} \left( {x_{i} } \right)}}{2}} \right)\exp \left( {1 - \left( {\frac{{\nu_{S} \left( {x_{i} } \right) + 1 - \mu_{S} \left( {x_{i} } \right)}}{2}} \right)^{\gamma } } \right) \hfill \\ \end{aligned} \right)} \right]. \\ \end{aligned}$$
(1)

Theorem 1

(Properties of Proposed Divergence Measures for IFSs) Let \(R,\,S,\,T \in {\text{IFSs}}(U)\)and \(\gamma > 0\,(\gamma \ne 1),\)then divergence measure \(J_{1} \left( {R,S} \right)\)given by (1) satisfies the following postulates:

Proof

The Proof of Theorem 1 is provided in “Appendix 2”.□

Theorem 2

(Relation between Entropy and Divergence Measures for IFSs) If \(R \in {\text{IFS}}\left( U \right),\)then the relation between \(H_{\text{AM}} \left( R \right)\)and \(J_{1} \left( {R,\,S} \right)\)is given by \(H_{\text{AM}} \left( R \right) = 1 - J_{1} \left( {R,\,R^{c} } \right),\)where \(R^{c}\)is a complement of \(R\)and \(H_{\text{AM}} \left( R \right)\)is entropy for IFS proposed by Ansari et al. (2018).

Proof

The proof of Theorem 2 is the same as Theorem 3.3 in Mishra and Rani (2019).□

Next, let \(R \in {\text{IFS}}\left( U \right),\) then based on Mishra et al. (2016a) entropy, we develop the entropy based on trigonometric function for IFS as follows:

$$\begin{aligned} & H^{\gamma } (R) = \frac{ - 1}{n\,\sin (\gamma \ln 2)}\sum\limits_{i = 1}^{n} {\left[ {\left( {\frac{{\mu_{R} \left( {x_{i} } \right) + 1 - \nu_{R} \left( {x_{i} } \right)}}{2}} \right)\sin \left\{ {\gamma \ln \left( {\frac{{\mu_{R} \left( {x_{i} } \right) + \quad\quad 1 - \nu_{R} \left( {x_{i} } \right)}}{2}} \right)} \right\}} \right.} \\ & \left. {\quad \quad + \;\left( {\frac{{\nu_{R} \left( {x_{i} } \right) + 1 - \mu_{R} \left( {x_{i} } \right)}}{2}} \right)\sin \left\{ {\gamma \ln \left( {\frac{{\nu_{R} \left( {x_{i} } \right) + 1 - \mu_{R} \left( {x_{i} } \right)}}{2}} \right)} \right\}} \right]. \\ \end{aligned}$$
(2)

Theorem 3

Mapping \(H^{\gamma } \left( R \right)\), given by (2), is an entropy for \({\text{IFS}}\left( U \right).\)

Proof

The Proof of Theorem 1 is provided in “Appendix 3”.□

Inspired by \(H^{\gamma } \left( R \right),\) we define the following Jensen–Shannon divergence measure as follows:

$$\begin{aligned} & J_{2} \left( {R,S} \right) = \frac{ - 1}{{n\,\,\sin \left( {\gamma \ln 2} \right)}}\sum\limits_{i = 1}^{n} {\left[ \begin{aligned} \left( {\frac{\begin{aligned} \mu_{R} \left( {x_{i} } \right) + \mu_{S} \left( {x_{i} } \right) \hfill \\ + 2 - \nu_{R} \left( {x_{i} } \right) - \nu_{S} \left( {x_{i} } \right) \hfill \\ \end{aligned} }{4}} \right)\sin \left( {\gamma \ln \left( {\frac{\begin{aligned} \mu_{R} \left( {x_{i} } \right) + \mu_{S} \left( {x_{i} } \right) + 2 \hfill \\ \,\,\,\,\, - \nu_{R} \left( {x_{i} } \right) - \nu_{S} \left( {x_{i} } \right) \hfill \\ \end{aligned} }{4}} \right)} \right) \hfill \\ \,\, + \left( {\frac{\begin{aligned} \nu_{R} \left( {x_{i} } \right) + \nu_{S} \left( {x_{i} } \right) \hfill \\ + 2 - \mu_{R} \left( {x_{i} } \right) - \mu_{S} \left( {x_{i} } \right) \hfill \\ \end{aligned} }{4}} \right)\sin \left( {\gamma \ln \left( {\frac{\begin{aligned} \nu_{R} \left( {x_{i} } \right) + \nu_{S} \left( {x_{i} } \right) \hfill \\ + 2 - \mu_{R} \left( {x_{i} } \right) - \mu_{S} \left( {x_{i} } \right) \hfill \\ \end{aligned} }{4}} \right)} \right) \hfill \\ \end{aligned} \right.} \\ & \left. {\quad \quad - \frac{1}{2}\left( \begin{aligned} \left( {\frac{{\mu_{R} \left( {x_{i} } \right) + 1 - \nu_{R} \left( {x_{i} } \right)}}{2}} \right)\sin \left( {\gamma \ln \left( {\frac{{\mu_{R} \left( {x_{i} } \right) + 1 - \nu_{R} \left( {x_{i} } \right)}}{2}} \right)} \right) \hfill \\ + \left( {\frac{{\nu_{R} \left( {x_{i} } \right) + 1 - \mu_{R} \left( {x_{i} } \right)}}{2}} \right)\sin \left( {\gamma \ln \left( {\frac{{\nu_{R} \left( {x_{i} } \right) + 1 - \mu_{R} \left( {x_{i} } \right)}}{2}} \right)} \right) \hfill \\ \,\, + \left( {\frac{{\mu_{S} \left( {x_{i} } \right) + 1 - \nu_{S} \left( {x_{i} } \right)}}{2}} \right)\sin \left( {\gamma \ln \left( {\frac{{\mu_{S} \left( {x_{i} } \right) + 1 - \nu_{S} \left( {x_{i} } \right)}}{2}} \right)} \right) \hfill \\ \,\,\,\, + \left( {\frac{{\nu_{S} \left( {x_{i} } \right) + 1 - \mu_{S} \left( {x_{i} } \right)}}{2}} \right)\sin \left( {\gamma \ln \left( {\frac{{\nu_{S} \left( {x_{i} } \right) + 1 - \mu_{S} \left( {x_{i} } \right)}}{2}} \right)} \right) \hfill \\ \end{aligned} \right)} \right] \\ \end{aligned}$$
(3)

Proposition 1

Let \(R,\,S,\,T \in {\text{IFSs}}(U)\)and \(\gamma > 0\,\left( {\gamma \ne 1} \right),\)then divergence measure \(J_{2} \left( {R,S} \right)\)given by (3) satisfies the postulates (P1)–(P10) given in Theorem 1.

2.1 Comparison Results

At first, a survey is conducted at the drawbacks in the existing intuitionistic fuzzy entropy measures.

Wei et al. (2012):

$$H_{W} \left( R \right) = \frac{1}{n}\sum\limits_{i = 1}^{n} {\cos \left( {\frac{{\left| {\mu_{R} \left( {x_{i} } \right) - \nu_{R} \left( {x_{i} } \right)} \right|}}{{2\left( {1 + \pi_{R} \left( {x_{i} } \right)} \right)}}\pi } \right)}$$

Guo and Song (2014):

$$H_{G} \left( R \right) = \frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {\frac{{1 - \left| {\mu_{R} \left( {x_{i} } \right) - \nu_{R} \left( {x_{i} } \right)} \right|^{2} + \pi_{R}^{2} \left( {x_{i} } \right)}}{2}} \right)}$$

Example 1

Consider the following IFSs as follows:

$$R_{1} = \left\{ {\left( {x,0.2,0.6} \right)} \right\},\,R_{2} = \left\{ {\left( {x,0.13,0.565} \right)} \right\},\,R_{3} = \left\{ {\left( {x,0.5,0.3} \right)} \right\}\; {\text{and}}\;R_{4} = \left\{ {\left( {x,0.5,0.5} \right)} \right\}.$$

It is apparent that the fuzziness of \(R_{1}\) and \(R_{2}\) is different, and so are \(R_{3}\) and \(R_{4} .\) However, the obtained values of \(H_{W} \left( R \right)\) and \(H_{G} \left( R \right)\) are \(H_{W} \left( {R_{1} } \right) = H_{W} \left( {R_{2} } \right) = 0.8660\) and \(H_{G} \left( {R_{3} } \right) = H_{G} \left( {R_{4} } \right) = 0.5.\) It is not conformed to the intuitionistic fact.

The proposed entropy measures for IFSs not only consider the influence of the difference between the membership degree and the non-membership degree: \(\mu_{R} \left( {x_{i} } \right) - \nu_{R} \left( {x_{i} } \right),\) but also introduces the hesitation degree which is equally handled through the membership degree and the non-membership degree (Li et al. 2003). Thus, the fuzziness and unknown of uncertainty conveyed by IFSs are well expressed. Consider the examples above where the IFEs \(H_{W} \left( R \right)\) and \(H_{G} \left( R \right)\) cannot distinguish; the results are as follows when applying the proposed entropy measure:

$$\begin{array}{*{20}l} {H^{\gamma } \left( {R_{1} } \right) = 0.8713,\,H^{\gamma } \left( {R_{2} } \right) = 0.8470,\,H^{\gamma } \left( {R_{3} } \right) = 0.9685\;{\text{and}}\;H^{\gamma } \left( {R_{4} } \right) = 1.000,\quad {\text{for}}\;\gamma = 0.4.} \hfill \\ {H^{\gamma } \left( {R_{1} } \right) = 0.8657,\;H^{\gamma } \left( {R_{2} } \right) = 0.8404,\;H^{\gamma } \left( {R_{3} } \right) = 0.9671\;{\text{and}}\;H^{\gamma } \left( {R_{4} } \right) = 1.000,\quad {\text{for}}\;\gamma = 0.7.} \hfill \\ \end{array}$$

Therefore, the proposed IFE has better distinguish ability for IFNs.

3 IF-COPRAS Method for Green Supplier Selection Problem

Initially, the COPRAS method is pioneered for MCDM under deterministic circumstances. Because uncertainty is an unavoidable characteristic of MCDM, an extension of the COPRAS method is demonstrated that can be utilized for MCDM problems in uncertain circumstances.

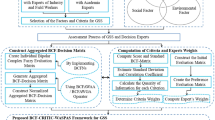
In the MCDM process, our main goal is to select the most appropriate alternative among set of \(m\) alternatives \(A = \left\{ {A_{1} ,\,A_{2} , \ldots ,A_{m} } \right\}\) with respect to the criterion set \(C = \left\{ {C_{1} ,\,C_{2} , \ldots ,\,C_{n} } \right\}.\) Assume that a committee (group) of \(t\) decision experts \(D = \left\{ {D_{1} ,\,D_{2} , \ldots ,\,D_{t} } \right\}\) has been constituted to decide the optimal alternative(s). Now, the outline of intuitionistic fuzzy COPRAS (IF-COPRAS) method has been depicted in following steps (see Fig. 1):

Fig. 1
figure 1

Flowchart of IF-COPRAS with IF-grey relational analysis (IF-GRA) method

Full size image

Step 1 Calculate decision expert’s weights.

Consider that \(t\) decision experts with importance weight \(\lambda = \left( {\lambda_{1} ,\lambda_{2} , \ldots ,\lambda_{t} } \right)^{T} .\) These importance weights are designed as linguistic terms and articulated in IFNs. Let \(R_{k} = \left( {\mu_{k} ,\,\nu_{k} ,\pi_{k} } \right)\) be an IFN for rating of the kth decision expert. Corresponding to Boran et al. (2009), the kth decision experts’ weight is computed by

$$\lambda_{k} = \frac{{\left( {\mu_{k} + \pi_{k} \left( {\frac{{\mu_{k} }}{{\mu_{k} + \nu_{k} }}} \right)} \right)}}{{\sum\nolimits_{k = 1}^{t} {\left( {\mu_{k} + \pi_{k} \left( {\frac{{\mu_{k} }}{{\mu_{k} + \nu_{k} }}} \right)} \right)} }},\quad k = 1\left( 1 \right)t.$$
(4)

Step 2 Compute aggregate decision matrix by rating matrix and decision expert’s weights.

Let \({\mathbb{Z}} = \left( {\xi_{ij}^{k} } \right)_{m\, \times \,n}\) be the decision expert’s evaluation matrices and \(\lambda = \left( {\lambda_{1} ,\lambda_{2} , \ldots ,\lambda_{l} } \right)^{T}\) be the weight of each decision expert such that \(\sum\nolimits_{k = 1}^{t} {\lambda_{k} = 1} ,\;\lambda_{k} \in \left[ {0,\,\,1} \right].\) In the MCDM process, all the individual decision evaluations require to be combined into a group evaluation to create aggregated IF-decision matrix \({\mathbb{N}} = \left( {\ell_{i\,j} } \right)_{m\, \times \,n} .\) To facilitate that, IFWA operator (Xu 2007) is implemented, which is given in “Appendix 2, 3”.

Step 3 Calculate criterion weights based proposed measures.

In the MCDM process, all criteria may not be supposed to be equal importance. Let \(w = \left( {w_{1} ,w_{2} , \ldots ,w_{n} } \right)^{T}\) such that \(\sum\nolimits_{j = 1}^{n} {w_{j} = 1} ,\)\(\,w_{j} \in \left[ {0,\,\,1} \right]\) be an importance vector for criterion set. Consecutively to achieve \(w,\) all the individual decision expert estimations for the importance of each criterion need to be fused.

$$w_{j} = \frac{{\frac{1}{m - 1}\sum\nolimits_{i = 1}^{m} {\sum\nolimits_{k = 1}^{m} {J_{\tau } \left( {\ell_{ij} ,\,\ell_{kj} } \right)} } }}{{\sum\nolimits_{j = 1}^{n} {\left( {\frac{1}{m - 1}\sum\limits_{i = 1}^{m} {\sum\limits_{k = 1}^{m} {J_{\tau } \left( {\ell_{ij} ,\,\ell_{kj} } \right)} } } \right)} }},\quad j = 1\left( 1 \right)n,\quad \tau = 1,2.$$
(5)

Step 4 Sum the criterion values for benefit and cost.

In proposed approach, each alternative is illustrated with its sum of maximizing \(\alpha_{i}\) (benefit type) and minimizing \(\beta_{i}\) (cost type), i.e. optimization results are maximization and minimization, respectively.

To estimate the values of \(\alpha_{i}\) and \(\beta_{i}\) in the IF-decision matrix, firstly criteria are located benefit type and then cost type. On these circumstances, \(\alpha_{i}\) and \(\beta_{i}\) are computed as

Let \(\Delta = \left\{ {1,2, \ldots ,\,l} \right\}\) be a set of benefit criteria, i.e. the maximum values show superior option. Then, compute the index value for each alternative as follows:

$$\alpha_{i} = \mathop \oplus \limits_{j = 1}^{\ell } w_{j} \,\eta_{ij} ,\quad i = 1\left( 1 \right)m,$$
(6)

Let \(\nabla = \left\{ {l + 1,l + 2, \ldots ,\,n} \right\}\) be a set of cost criteria, i.e. the minimum values show superior choice. Then, compute index value for each alternative as follows:

$$\beta_{i} = \mathop \oplus \limits_{j = \ell + 1}^{n} w_{j} \,\,\eta_{ij} ,\,\,i = 1\left( 1 \right)m.$$
(7)

In formulas (6) and (7), \(l\) and \(n\) are numbers of benefit and total number of criteria, respectively.

Step 5 Computation of degree of relative weight.

Degree of relative weight \(\gamma_{i}\) of the alternative is illustrated by

$$\gamma_{i} = {\mathbb{S}}^{*} \left( {\alpha_{i} } \right) + \frac{{\mathop {\hbox{min} }\nolimits_{i} {\mathbb{S}}^{*} \left( {\beta_{i} } \right)\sum\nolimits_{i = 1}^{p} {{\mathbb{S}}^{*} \left( {\beta_{i} } \right)} }}{{{\mathbb{S}}^{*} \left( {\beta_{i} } \right)\sum\nolimits_{i = 1}^{p} {\frac{{\mathop {\hbox{min} }\nolimits_{i} {\mathbb{S}}^{*} \left( {\beta_{i} } \right)}}{{{\mathbb{S}}^{*} \left( {\beta_{i} } \right)}}} }},\quad i = 1\left( 1 \right)m.$$
(8)

Here, \({\mathbb{S}}^{*} \left( {\alpha_{i} } \right)\) is the score value of \(\alpha_{i}\) and \({\mathbb{S}}^{*} \left( {\beta_{i} } \right)\) is the score value of \(\beta_{i} .\)

Equation (8) can be also demonstrated as follows:

$$\gamma_{i} = {\mathbb{S}}^{*} \left( {\alpha_{i} } \right) + \frac{{\sum\nolimits_{i = 1}^{p} {{\mathbb{S}}^{*} \left( {\beta_{i} } \right)} }}{{{\mathbb{S}}^{*} \left( {\beta_{i} } \right)\sum\nolimits_{i = 1}^{p} {\frac{1}{{{\mathbb{S}}^{*} \left( {\beta_{i} } \right)}}} }},\quad i = 1\left( 1 \right)m.$$
(9)

Step 6 Evaluate the priority order.

According to degree of relative weight, the preference relation of alternatives is illustrated. The alternative with maximum degree of relative weight has high preference order (rank) and is the optimal (desirable) one.

$$A^{*} = \,\,\mathop {\hbox{max} }\limits_{i} \gamma_{i} ,\,i = 1\left( 1 \right)m.$$
(10)

Step 7 Determination of the utility degree.

The utility degree is evaluated by comparing the illustrated alternative with the prominent one. The value of utility degree lies between 0 and 100%. The utility degree \(\lambda_{i}\) is computed by

$$\lambda_{i} = \frac{{\gamma_{i} }}{{\gamma_{\hbox{max} } }} \times 100\% ,\quad i = 1\left( 1 \right)m.$$
(11)

where \(\gamma_{i}\) and \(\gamma_{\hbox{max} }\) are the importance of alternatives given in (9).

Here, proposed decision-making method permits for estimating the direct and proportional dependence of the degree of significance and the degree of utility of alternative in a criteria set and weights.

Step 8 End.

4 Application of Green Supplier Selection Problem

Recently, several governmental and non-governmental companies have focused their attention in the promotion of eco-friendly resources. As the increasing environmental issues, various companies have take initiatives to produce green products or to select green suppliers which maximize the business performance and minimize the environmental pollution, emission, hazardous squander, energy consumption. In the process of selecting the best green supplier, the decision makers have many alternative suppliers affected by several criteria. In this section, a case study of green supplier selection problem is evaluated by proposed IF-COPRAS method.

In this problem, a manufacturer company wants to select the best supplier from a set of seven alternatives \(\left( {A_{1} ,\,A_{2} ,\,A_{3} ,\,A_{4} ,\,A_{5} ,\,A_{6} ,\,\,A_{7} } \right).\) For this, a senior executive person of this company has formed a set of four experts \(\left( {D_{1} ,D_{2} ,D_{3} \,\,{\text{and}}\,\,D_{4} } \right)\) to handle the selection problem of most suitable green supplier. These alternatives are evaluated under the eight chosen criteria, which are (1) pollution (\(C_{1}\)), (2) supply consumption (\(C_{2}\)), (3) ecological design (\(C_{3}\)), (4) management system (\(C_{4}\)), (5) commitment of managers to GSCM (\(C_{5}\)), (6) use of green technology (\(C_{6}\)), (7) use of green materials (\(C_{7}\)) and (8) quality management (\(C_{8}\)). Here, \(C_{1}\) and \(C_{2}\) are cost criteria and \(C_{3} ,\,C_{4} ,\,C_{5} ,\,C_{6} ,\,C_{7} ,\,C_{8}\) are benefit criteria (see Fig. 2).

Fig. 2
figure 2

Representation of green supply chain management (GSCM)

Full size image

Table 3 depicts the performance rating of the criteria in terms of linguistic variables and their corresponding IFNs. The weights of experts are calculated from (4) and presented in Table 4. Table 5 presents the performance ratings of green supplier alternatives provided by the experts, and Table 6 shows the importance of each alternative concerning each chosen criteria. Based on experts’ judgments, the aggregated IF-decision matrix is given in Table 7.

Table 3 Rating of the performance of criteria in terms of linguistic variables
Full size table
Table 4 Decision expert weights for rating the energy source selection
Full size table
Table 5 Linguistic variables for performance rating of alternatives
Full size table
Table 6 Performance rating of green supplier selection in linguistic variables
Full size table
Table 7 Aggregated intuitionistic fuzzy decision matrix
Full size table

Based on Step 5 and Table 7, the criterion weights are computed by using Eq. (5) in terms of proposed divergence measure. By using MATLAB software, the criteria’s weights are calculated as follows:

$$w_{j} = \left( {0.1348,0.1274,0.1243,0.1315,0.1124,0.1173,0.1313,0.1210} \right)^{T} .$$

After that, the relative degree or preference value \(\left( {\gamma_{i} } \right)\) and the utility degree \(\left( {\lambda_{i} } \right)\) for each alternative are computed through Eqs. (10) and (11) and as shown in Table 8. The value of index (\(\alpha_{i}\) and \(\beta_{i}\)) for each alternative in Table 8 is obtained by using Eqs. (6) and (7). Hence, \(A_{5}\) is the best green supplier alternative.

Table 8 Overall computational results of IF-COPRAS method for GSSs
Full size table

5 Comparative Study and Sensitivity Analysis

To illustrate the outcomes of the proposed method, we have made comparative study and sensitivity analysis. Recently, numerous approaches have been developed to cope with the GSS problem under different uncertain environment. As the every method has their own characteristics and algorithms which distinguish them from the other methods, in this section, to demonstrate the superiority of the proposed method, firstly a comparative study with some existing approaches has been presented. Based on the available literature, the approaches of [Kuo et al. (2015), Ghorabaee et al. (2016), Chatterjee and Kar (2018)] and proposed extended intuitionistic fuzzy GRA (IF-GRA) methods are preferred for the comparative analysis.

5.1 Comparative Study

Grey method is widely practiced in disciplines, viz. systems analysis, data processing, modelling and decision making. Now, the process of intuitionistic fuzzy GRA (IF-GRA) method has been given in following steps (see Fig. 1):

Steps 1–2 As previous method.

Step 3 Evaluate ideal and anti-ideal solutions on IFNs.

A solution which has optimal criterion value for each criterion is called ideal solution. The ideal values (IS) for various criteria are different and given by

$$\varepsilon_{j}^{ + } = \left\{ {\begin{array}{*{20}l} {\mathop {\hbox{max} }\limits_{i = 1(1)m} \,\,\ell_{ij} \,\,\,\,{\text{for}}\,\,{\text{benefit}}\,\,{\text{criterion}}\,\,C_{j} } \hfill \\ {\mathop {\hbox{min} }\limits_{i = 1(1)m} \,\,\ell_{ij} \,\,\,\,{\text{for}}\,\,{\text{cost}}\,\,{\text{criterion}}\,\,C_{j} } \hfill \\ \end{array} } \right.\quad {\text{for}}\;j = 1\left( 1 \right)n.$$
(12)

On the similar line, the anti-ideal values (AIS) for different criteria are given by

$$\varepsilon_{j}^{ - } = \left\{ {\begin{array}{*{20}l} {\mathop {\hbox{min} }\limits_{i = 1(1)m} \,\,\ell_{ij} \,\,\,\,{\text{for}}\,\,{\text{benefit}}\,\,{\text{criterion}}\,\,C_{j} } \hfill \\ {\mathop {\hbox{max} }\limits_{i = 1(1)m} \,\,\ell_{ij} \,\,\,\,{\text{for}}\,\,{\text{cost}}\,\,{\text{criterion}}\,\,C_{j} } \hfill \\ \end{array} } \right.\quad {\text{for}}\;j = 1\left( 1 \right)n.$$
(13)

Step 4 Determine the coefficient of grey relational (GRC).

The GRC of each alternative from IS is evaluated by

$$\hbar_{ij}^{ + } = \frac{{\mathop {\hbox{min} \hbox{min}\, J}\limits_{1 \le i \le m \le 1 \le j \le n} \left( {\ell_{ij} , \,\varepsilon_{j}^{ + } } \right) + \rho \mathop {\hbox{max} \hbox{max} }\limits_{1 \le i \le m \le 1 \le j \le n} J\left( {\ell_{ij,} \varepsilon_{j}^{ + } } \right)}}{{J\left( {\ell_{ij} ,\,\varepsilon_{j}^{ + } } \right) + \rho \mathop {\hbox{max}\hbox{ max}}\limits_{1 \le i \le m \le 1 \le j \le n} J\left( {\ell_{ij}, \, \varepsilon_{j}^{ + } } \right)}}, \forall \, i,\,\,j.$$
(14)

Similarly, GRC of each alternative from AIS is estimated as follows:

$$\lambda_{ij}^{ - } = \frac{{\mathop {\hbox{min} \hbox{min}\,\, J}\limits_{1 \le i \le m \le 1 \le j \le n} \left( {\ell_{ij} ,\,\varepsilon_{j}^{ - } } \right) + \rho \mathop {\hbox{max} \hbox{max} }\limits_{1 \le i \le m \le 1 \le j \le n} J\left( {\ell_{ij} ,\,\varepsilon_{j}^{ - } } \right)}}{{J\left( {\ell_{ij} ,\varepsilon_{j}^{ - } } \right) + \rho \mathop {\hbox{max}\hbox{ max}}\limits_{1 \le i \le m \le 1 \le j \le n} J\left( {\ell_{ij} ,\,\varepsilon_{j}^{ - } } \right)}},\,\, \forall \,\,i,\,\,j,$$
(15)

where \(\rho = 0.5\) is coefficient of identification.

Step 5 Estimate the GRC degree.

The degree of GRC of each alternative from IS and AIS is computed by

$$\hbar_{i}^{ + } = \sum\limits_{j = 1}^{n} {w_{j} \,\hbar_{ij}^{ + } ,\,\,\lambda_{i}^{ - } = \sum\limits_{j = 1}^{n} {w_{j} \,\lambda_{ij}^{ - } ,\quad i = 1\left( 1 \right)m.} }$$
(16)

The fundamental principal of GRA approach is that preferred alternatives should have “largest degree of grey relation” from the IS and the “smallest degree of grey relation” from the AIS. For the known criteria’s weights, the smaller \(\lambda_{i}^{ - }\) and the larger \(\hbar_{i}^{ + }\) determine the improved alternative \(A_{i}\). To obtain the \(\lambda_{i}^{ - }\) and \(\hbar_{i}^{ + }\) in case of completely unknown weight vector, our task is to determine the criteria’s weight vector. For this, the multi-objective optimization model (MOOM) is presented to evaluate the information of weights:

$$(M_{1} ):\left\{ {\begin{array}{*{20}l} {\hbox{max}\,\hbar_{i}^{ + } = \sum\limits_{j = 1}^{n} {w_{j} \,\hbar_{ij}^{ + } ;} \,\,i = 1\left( 1 \right)m} \hfill \\ {\hbox{min} \lambda_{i}^{ - } = \sum\limits_{j = 1}^{n} {w_{j} \,\lambda_{ij}^{ - } ;\,\,\,} \,i = 1\left( 1 \right)m} \hfill \\ {{\text{subject}}\,\,{\text{to }}\,w_{j} \in \Delta .} \hfill \\ \end{array} } \right.$$
(17)

As each alternative is non-inferior, no priority relation exists between them. Then, we may aggregate the MOOM (17) with equivalent weights into the single-objective optimization model:

$$(M_{2} ):\left\{ {\begin{array}{*{20}l} {\hbox{max}\, \,\xi = \sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {\left( {\hbar_{ij}^{ + } - \lambda_{ij}^{ - } } \right)w_{j} } } } \hfill \\ {{\text{subject}}\,{\text{to}}\,\,w_{j} \in \Delta } \hfill \\ \end{array} } \right.$$
(18)

Solving the model \(\left( {M_{2} } \right),\) the optimal solution \(w = \left( {w_{1} ,w_{2} , \ldots ,w_{n} } \right)^{T} ,\) which is known as criterion weight vector is obtained. Then, we evaluate \(\hbar_{i}^{ + }\)\(\left( {i = 1\left( 1 \right)m} \right)\) and \(\lambda_{i}^{ - }\)\(\left( {i = 1\left( 1 \right)m} \right)\) by Eq. (16).

Step 6 Compute the relative relational degree.

The degree of relative relational of each alternative from IS based on the following expression is computed as

$$\xi_{i} = \hbar_{i}^{ + } /\left( {\lambda_{i}^{ - } + \hbar_{i}^{ + } } \right);\quad i = 1\left( 1 \right)m.$$
(19)

Step 7 Rank the alternative \(A_{i} \left( {i = 1\left( 1 \right)m} \right)\) and choose the optimal one(s) corresponding to the values of \(\xi_{i}\)\(\left( {i = 1\left( 1 \right)m} \right)\). The highest value of \(\xi_{i}\) determines the most suitable alternative.

Step 8 End.

On applying IF-GRA method on the above-mentioned application of green supplier selection, the results are given as below:

Steps 1–2 As previous method.

Step 3 The IS and AIS determined for different criteria by using Eqs. (12) and (13) are given as follows:

$$\begin{aligned} \xi_{j}^{ + } = \left\{ {(0.46,0.477),\,(0.569,0.355),\,(0.95,0.05),} \right.\,(0.913,0.071),\, \hfill \\ \quad \quad \left. {(0.95,0.05),\,(0.831,0.122),\,(0.747,0.210),\,(0.928,0.063)} \right\}, \hfill \\ \end{aligned}$$
$$\begin{aligned} \xi_{j}^{ - } = \left\{ {(0.95,0.05),\,(0.931,0.061)} \right.,\,(0.613,0.3),\,(0.532,0.402), \hfill \\ \quad \quad \left. {(0.578,0.344),\,(0.733,0.344),\,(0.591,0.350),\,(0.644,0.262)} \right\}\, \hfill \\ \end{aligned}$$

Step 4 (a) Calculate the GR coefficient of each alternative from IS by using Eq. (14) and depicted in Table 9.

Table 9 GRC from ideal solution
Full size table

(b) Calculate the GR coefficient of each alternative from AIS by using Eq. (15) and depicted in Table 10.

Table 10 GRC from anti-ideal solution
Full size table

Step 5 Implement the model (M − 2) to construct the single-objective optimization model by using Eq. (18):

$$\begin{aligned} & \hbox{max} \,\xi (w) = \left\{ { - 0.7497w_{1} - 0.7351w_{2} + 0.7621w_{3} + 0.6798w_{4} + 0.6707w_{5} + 0.23w_{6} + 0.2413w_{7} + 0.6763w_{8} } \right\} \\ & {\text{s}} . {\text{t}} .\;\varOmega = \left\{ {0.128 \le w_{1} \le 0.145,\,0.112 \le w_{2} \le 0.135,\,\,0.110 \le w_{3} \le 0.131,\,\,0.130 \le w_{4} \le 0.14,} \right. \\ & \quad \quad \quad \quad 0.099 \le w_{5} \le 0.12,\,\,0.105 \le w_{6} \le 0.125,\,\,0.127 \le w_{7} \le 0.141,\,\,0.118 \le w_{8} \le 0.127, \\ & \quad \quad \quad \quad \left. {w_{2} - w_{3} \le w_{1} - w_{6} ,\,w_{7} \le 2w_{5} ,\,w_{2} + w_{8} \le w_{1} + w_{7} ,\,w_{j} \ge 0,\,\,j = 1(1)8,\,\,\sum\limits_{j = 1}^{8} {w_{j} = 1} } \right\}. \\ \end{aligned}$$
(20)

Solve model (20), the criterion weight vector is computed as

$$w = \left\{ {0.128,\,0.112,\,0.131,\,0.14,\,0.12,\,0.115,\,0.127,\,0.127} \right\}^{T} .$$

Now, the GRC degree of each alternative from IS and AIS is computed by Eq. (16) as follows:

$$\begin{aligned} & \hbar _{1}^{ + } = 0.7629\,,\,\,\,\hbar_{2}^{ + } = 0.7680,\,\,\,\,\hbar_{3}^{ + } = 0.7743,\,\,\,\,\hbar_{4}^{ + } = 0.7907,\,\,\,\hbar_{5}^{ + } = 0.8064,\,\,\,\hbar_{6}^{ + } = 0.7862,\,\,\,\hbar_{7}^{ + } = 0.8757,\, \\ & \lambda_{1}^{ - } = 0.7535\,,\,\,\,\lambda_{2}^{ - } = 0.7343,\,\,\,\,\lambda_{3}^{ - } = 0.7523,\,\,\,\,\lambda_{4}^{ - } = 0.7604,\,\,\,\lambda_{5}^{ - } = 0.7590,\,\,\,\lambda_{6}^{ - } = 0.7456,\,\,\,\,\lambda_{7}^{ - } = 0.8188\,. \\ \end{aligned}$$

Step 6 The degree of relative relational of each alternative is computed by Eq. (19) as follows:

$$\xi_{1} = 0.7535\,,\,\,\,\xi_{2} = 0.7343,\,\,\,\,\xi_{3} = 0.7523,\,\,\,\,\xi_{4} = 0.7604,\,\,\,\xi_{5} = 0.7590,\,\,\,\xi_{6} = 0.7456,\,\,\,\xi_{7} = 0.8188\,.$$

Step 7 The preference relation of the seven GSSs corresponding to the relative relational degree is \(A_{7} \succ A_{5} \succ A_{6} \succ A_{2} \succ A_{4} \succ A_{3} \succ A_{1} .\) Hence, the optimal GSS is \(A_{7}\).

In the comparative discussion, the coefficient Spearman’s rank correlation \(\left( {r_{A} } \right)\) has utilized to compare the outcomes of the proposed method with previous methods. The classification of different values of \(r_{A}\) is presented in Table 11 (Walters 2009). As said by Table 11, if the values of \(r_{A}\) are larger than 0.6, i.e. high degree statistical dependency between outcomes. Table 12 presents the comparison results of proposed and the other methods. According to Table 12, we can see that the correlation coefficient for every pair is greater than 0.6, for that reason, the ranking outcomes have strong and/or very strong relationships. As per the study, we observe that the outcome of the proposed method is consistent with the existing approaches.

Table 11 Classification of Spearman coefficient of correlation (Walters 2009)
Full size table
Table 12 Comparison of the attributes with representative models
Full size table

To provide a better view of the outcomes, the outcomes of the preference order of alternatives computed by the IF-COPRAS and the IF-GRA methods are depicted in Fig. 3. From Fig. 3, we clearly know that the preference orders of alternatives are remarkably different evaluated by proposed methods. By IF-COPRAS method, the best suitable recommended alternative in the above decision-making problem is \(A_{5} ,\) while IF-GRA method gives the optimal option is \(A_{7} .\)

Fig. 3
figure 3

Ranking comparison of IF-COPRAS and IF-GRA methods

Full size image

5.2 Sensitivity Analysis

Here, a sensitivity analysis is performed to validate the obtained results from proposed approach (see Table 13) and determined on the basis of varying values of weights. From Table 13, we can observe that, in every set, there is one criterion that has higher weight and others have lower ones. As a result, the pattern can facilitate us to think about an extensive area for investigating the sensitivity of proposed approach by varying criteria’s weights. Table 14 shows the ranking results and the correlation between the outcomes with various criterion weights sets and graphically shown in Fig. 4. Corresponding to these tables, we can see that the values of \(r_{A}\) are greater than 0.9, so that the developed method has superior stability with diverse weights. On the basis of sensitivity analysis, it can be illustrated that the stability of the developed method can be increased with the use of subjective and objective criteria’s weights combination.

Table 13 Simulated weights of risk criteria in different sets
Full size table
Table 14 Ranking outcomes with different sets of criteria weights and the parameters
Full size table
Fig. 4
figure 4

Sensitivity analysis of sets of green supplier alternatives

Full size image

6 Conclusions

The proper supplier selection plays a predominant role for efficient operation of green supplier selection sectors. Due to increasing complexity and uncertain information, the selection of green suppliers is not an easy task for decision experts. As the IFSs are more flexible to handle with uncertainty, so that, in this paper, the conventional COPRAS method is extended to solve the decision-making problems with IFSs. In this method, a new formula is developed based on divergence measure method, to find the criteria’s weights within the perspective of IFSs. In addition, some new parametric entropy and divergence measures are introduced and established the relationship between them. The parameter of the measures provides the flexibility to the decision experts so a sensitivity analysis is also addressed for describing the influence of the parameter on the performance of the decision making. Hence, we observe that the parametric divergence measure can suitably explain the real-life problem and can be established as an alternative place than of the existing operators or measures.

Further, an application of green supplier selection is evaluated from the proposed intuitionistic fuzzy COPRAS approach, which illustrates the applicability and effectiveness of the developed method. A comparison of the proposed method with existing approaches is presented to validate the obtained result. Also, a sensitivity analysis is executed to demonstrate the stability and efficiency of the developed method with different criterion weights. The main benefits of the developed method are the ease of computation under intuitionistic fuzzy doctrines, new formula for more realistic criteria’s weights and superior stability with different criteria’s weights. In the future, the developed method can be extended with some objective criteria and applied in many other MCDM problems.