A new compound wind speed forecasting structure combining multi-kernel LSSVM with two-stage decomposition technique

Abstract

The aims of this study are to develop a novel compound structure that consists of two-stage decomposition (TSD), hybrid particle swarm optimization gravitational search algorithm (HPSOGSA) and multi-kernel least square support vector machine (MLSSVM) for improving forecasting accuracy. In the most previous wind speed forecasting studies, only one wind speed signal decomposition method is considered, which is insufficient. To better deal with the wind speed time series, TSD method combining complementary ensemble empirical mode decomposition with adaptive noise with wavelet transform is firstly employed in the proposed model to preprocess the wind speed samples; then, binary-valued particle swarm optimization gravitational search algorithm is exploited as feature selection to identify and eliminate the abnormal noise signal within the input candidate matrix that is determined by partial autocorrelation function. The kernel function and the kernel parameters have great influence on the regression performance of LSSVM. To solve these problems, integrations of radial basis function, polynomial (poly) and linear kernel functions by optimal weighted coefficients are constructed as multi-kernel function for LSSVM, namely MKLSSVM, and the parameter combination is tuned by conventional PSOGSA. The feature selection and parameter optimization are realized by hybrid PSOGSA (HPSOGSA) simultaneously. Finally, comprehensive comparison and analysis are carried out using the historical wind speed data from one wind farm of China to illustrate the excellent forecasting performance of TSD–HPSOGSA–MKLSSVM.

1 Introduction

To reduce the greenhouse gas emission, many renewable resources have been exploited and utilized. Among the renewable resources, the utilization of wind energy has experienced a rapid growth in the last few years (Liu et al. 2017). Reported by World Wind Energy Association (WWEA), the global cumulative capacity of wind power has increased from 283 GW in 2012 to 597 GW in 2018. As wind speed time series always present nonlinear and stochastic, the integration of the large scale of wind power is a serious unstable factor for power system, which brings about large power grid voltage fluctuations, flicker and other power quality, and also reduces the stability and reliability of power system. It is known that short-term wind power forecasting (ranging from 1 to 48 h) are critical to reduce the power reserves, lower the operation cost of wind farm, decease the probability of wind power curtailment and increase the safety of the power grid (Sun et al. 2018c; Dong et al. 2017). However, influenced by temperature, humidity, height and other environmental and meteorological factors, it is hard to capture the internal tendency within wind speed times and there exist lots of difficulties in wind power prediction with high accuracy.

In the last decades, various wind speed forecasting models have been developed and these models are mainly classified into four categories, namely physical approaches, statistical models, artificial intelligence and machine learning engines, and hybrid forecasting model. Physical approaches predict the wind power output using local terrain, humidity, temperature and other environmental and meteorological information through complex computation. Statistical models, mainly including Persistence, ARMA, ARIMA and Kalman filter, make wind speed forecasting by capturing the internal relationship among the historical wind speed time series. Artificial intelligence and machine learning engines, mainly including multilayer perceptron (MLP) (Aghajani et al. 2016; Bouzgou and Benoudjit 2011), least squares support vector machine (LSSVM) (Yan et al. 2018; Hu et al. 2015; Kumar et al. 2018), extreme learning machine (ELM) (Zhang et al. 2014, 2017; Sun et al. 2018a), back-propagation neural network (BPNN) (Wang et al. 2016), wavelet neural networks (WNN) (Sun et al. 2019), Elman neutral network (ELMNN) (Du et al. 2017) and support vector regression (SVR) (Santamaria-Bonfil et al. 2016), have good capacity in processing nonlinear components within wind speed time series and are widely employed in wind speed forecasting; however, these approaches make forecasting in implicit ways.

In order to enhance the forecasting results, technicians and researchers always apply hybrid model which integrates and takes advantages of various individual approaches. For example, studies (Dong et al. 2017; Wang et al. 2016, 2017; Santamaria-Bonfil et al. 2016; Osorio et al. 2015) combine artificial intelligent models with signal decomposition and parameter optimization for wind speed forecasting. The case studies in the above literature illustrate that the hybrid models are successfully applied in the wind speed forecasting with satisfactory accuracy.

Among the aforementioned artificial intelligent models and machine learning engines, LSSVM is a powerful tool in dealing with small nonlinearity samples, and it has been widely used in system modeling (Stephen et al. 2014), time series prediction (Yan et al. 2018; Hu et al. 2015; Kumar et al. 2018; Sun et al. 2018b) and fault diagnosis (Zheng et al. 2011). The characteristics of LSSVM are to solve a quadratic programming problem by translating into linear equation, which can improve computational convergence. Thus, LSSVM is also adopted as the core forecasting engine in this study for wind speed forecasting.

LSSVM has better regression performance over the other ANN-based models and SVM (Hu et al. 2015); however, the regression performance of LSSVM is influenced by its configuration which includes the input training samples, the kind of kernel function and the kernel parameter. Therefore, researchers try to enhance the performance of LSSVM in short-term wind speed forecasting from these three aspects. Yuan et al. (2015) selected a suitable kernel function through comparisons and applied GSA to optimize the kernel parameters. In Zhou et al. (2011), LSSVM with linear, polynomial (Poly) or Gaussian kernel function was separately constructed to make wind speed forecasting for finding which kernel function performs best. In Wang et al. (2015a), C–C method is firstly used to process the wind speed time series for phase space reconstruction, which automatically determine the input form for subsequent forecasting; then, the parameters in LSSVM are tuned by PSOGSA and the outputs of LSSVM are corrected by Markov method.

However, there are still some shortages in LSSVM-based wind speed forecasting models.

• i: The existing studies on the application of LSSVM in wind speed forecasting are very limited because only one single particular kernel function (Yuan et al. 2015; Zhou et al. 2011; Wang et al. 2015a) or double kernel functions (Sun et al. 2018b) are considered. As for each kernel function has its characteristics in data process, these methods are not comprehensive.

• ii: Wavelet transform (WT) (Yan et al. 2018; Liu et al. 2014), wavelet packet decomposition (WPD) (Sun et al. 2018a), ensemble empirical mode decomposition (EEMD) (Wang et al. 2016; Sun et al. 2018b), empirical mode decomposition (EMD) (Zhang et al. 2016a), complementary ensemble empirical mode decomposition with adaptive noise (CEEMDAN) (Peng et al. 2017) and variational mode decomposition (VMD) (Zhang et al. 2017; Naik et al. 2018) are commonly wind speed data preprocessing methods. In the previous most wind speed forecasting models, only single individual data preprocessing method is applied to decompose wind speed data, which cannot thoroughly deal with wind speed in that wind speed time series always present intermittence and instability (Sun et al. 2019; Yin et al. 2017).

• iii: Abnormal data or noise within wind speed time series is caused by malfunctioning sensors, measurement error or other factors, which is considered as an obstacle to obtain high forecasting accuracy (Liu et al. 2018).

To address the above problems, the concept of combined model is utilized to develop a new hybrid short-term wind speed forecasting method that is inspired by the forecasting mechanisms in the aforementioned studies.

• i: LSSVM model with a combination of linear, Poly and radial basis function (RBF) kernel functions by optimal weighted coefficients is developed as core forecasting engine, namely multiple kernel functions LSSVM (MKLSSVM), in the wind speed forecasting model. RBF has good local exploitation and Poly has good global exploration capacities in dealing with nonlinear data, and linear kernel function can do well in linear signal processing, which can enhance forecasting performance.

• ii: A novel two-stage wind speed decomposition combining CEEMDAN with WT is utilized for data preprocessing. CEEMDAN is firstly utilized to decompose the original wind speed data into a few IMFs and one residual component with different frequencies; then, WT method is applied to break the highest frequency IMF1 into different subseries, which further lower the regression difficulties of LSSVM.

• iii: To eliminate the abnormal data, coral reefs optimization (CRO) was developed in Salcedo-Sanz et al. (2014) as feature selection to identify the effective input candidates for the forecasting engine ELM. A deep feature selection framework was developed to identify the most suitable candidates from the testing sample for machine learning models in the first layer (Feng et al. 2017). Apart from applying feature selection and parameter optimization on input candidates and artificial intelligent models, respectively, hybrid optimization algorithms have been exploited to realize these functions synchronously. In Luo et al. (2016), hybrid gravitational search algorithm (HGSA) integrating conventional GSA and binary-valued GSA (BGSA) were developed to realize the fault diagnosis of rolling element bearing and optimize the weights and bias parameters in ELM. In Zhang et al. (2017), ELM combined with hybrid backtracking search algorithm (HBSA) was developed for short-term wind speed forecasting, and the HBSA algorithm composes of real-valued BSA (RBSA) and binary-valued BSA (BBSA), which was also exploited to realize the function of feature selection and optimization. Hybrid PSOGSA (HPSOGSA) integrating conventional PSOGSA and binary-valued PSOGSA (BPSOGSA) is introduce to enhance the forecasting performance of MKLSSVM. HPSOGSA extracts the effective candidates from the testing samples and optimizes the parameter combination in MKLSSVM, simultaneously.

Apart from the above introduction, the other parts of this paper are arranged as follows. Section 2 provides the methodology that used in the proposed model. The working mechanism of the proposed forecasting strategy is presented in Sect. 3. Case studies that verify the effectiveness of the proposed forecasting model are carried out in Sect. 4. Conclusions are drawn in Sect. 5.

2 Methodology

2.1 Wind power preprocessing method

2.1.1 Complementary ensemble empirical mode decomposition with adaptive noise

The working mechanism of EMD is to decompose the nonlinear and nonstationary complicated signal into a few relatively stable intrinsic mode functions (IMFs) and one residual (Res) with different frequencies using Hilbert–Huang transform (HHT) approach (Zhang et al. 2016b). EMD method may not correctly extract effective characteristic information of signal in that it suffers from the drawback of the mode mixing.

To solve this problem, Wu and Huang proposed a noise-assisted EMD method (Wu and Huang 2009), namely EEMD. In EEMD, white Gaussian noise is added in the original signal at each shifting procedure for alleviation of the mode mixing in EMD and these white noise signals are eliminated by averaging in the end. However, there exists some white noise that may not be discarded after a finite shifting process, which affects signal reconstruction errors. To overcome this shortage, Torres et al. (2011) proposed a new complete EEMD with adaptive noise (CEEMDAN), which has been successfully applied in complicated time series signal processing (Peng et al. 2017) and fault feature extraction (Han et al. 2019). The decomposition process of any signal x(t) by CEEMDAN can be presented as follows.

• Step 1: Add a number of white Gaussian noise z(t) with N(0, 1) into the original signal, which is expressed as Eq. (1).

  $$\begin{aligned} y (t) = x(t) + \eta _0 z (t) \end{aligned}$$

  (1)

  where $\eta _0$ denotes a noise coefficient;

• Step 2: Decompose the y(t) by EMD method to obtain the corresponding $\hbox {IMF}_1^ i$.

• Step 3: Calculate the first subseries of CEEMDAN by meaning the IMFs obtained by EMD approach, expressed as Eq. (2).

  $$\begin{aligned} \hbox {IMF}'^i_1(t) = \frac{1}{L}\sum \limits _{i = 1}^L {\hbox {IMF}_1^i } \end{aligned}$$

  (2)

• Step 4: Calculate the residual value $r_1(t) =x(t)- \hbox {IMF}'^i_1(t)$

• Step 5: Calculate the first subseries of CEEMDAN by meaning the IMFs obtained by EMD approach again, expressed as Eq. (3).

  $$\begin{aligned} \hbox {IMF}'^i_2 (t) = \frac{1}{L}\sum \limits _{i = 1}^L {E_1 (r_1 (t) + \eta _1 E_1 (z^i (t)))} \end{aligned}$$

  (3)

  where $E_1( \cdot )$ represents the empirical mode decomposition EMD method.

• Step 6: Repeat the above steps to yield the other IMFs until the residual component has no more than two extreme values.

2.1.2 Wavelet transform (WT)

WT, a mathematical method, has been widely used in the time series signal processing (Aghajani et al. 2016; Osorio et al. 2015). WT can extract the effective information in the sample signal without losing information, and it has the ability to capture both frequency and location information in a simultaneous manner. Low-resolution wavelets can approximately capture frequency components of the sample signal, while high-resolution wavelets can catch the high-frequency components. WT can be mainly divided into continuous WT (CWT) and discrete WT (DWT). For overlapping feature and duplicity of neighbor information, CWT is very slow; thus, DWT is adopted in this study to deal with the wind speed data. As shown in Eq. (4), DWT utilizes scale and position parameters by powers of two, which are named as dyadic dilation and translations.

$$\begin{aligned} \hbox {DWT}(m,n) = 2^{\frac{{ - m}}{2}} \sum \limits _{t = 0}^{L - 1} x(t)\psi \left( \frac{{t - n \cdot 2^m }}{{2^m }}\right) \end{aligned}$$

(4)

where L denotes the total length of the sample signal x(t), m and n are two integrate number, $2^m$ and $n\cdot 2^m$ are factor and shifted values, respectively. Three-level decomposition of sample signal by WT is illustrated in Fig. 1.

Fig. 1

Three-level decomposition of signal by WT

As shown in Fig. 1, the sample signal is broken into two components, namely approximation component $A_i$ and detail component $D_i$, using low-pass filter (LPF) and high-pass filter (HPF), respectively. In the decomposition procedure, the sample signal is decomposed into high-frequency component $D_i$ and low-frequency component $A_i$; then, the low-frequency component $A_i$ is continuously decomposed, while the high-frequency component $D_i$ is maintained.

The kind of the mother wavelet function plays great influence on the performance of WT (Haque et al. 2013). Among the common mother wavelet functions, including Morlet, Haar, Mexican Hat and Meyer wavelet functions, Daubechies of order 4 (DB4) can usually provide better results; thus, DB4 is adopted as the wavelet function in this study.

2.2 Particle swarm optimization gravitational search algorithm (PSOGSA)

2.2.1 Particle swarm optimization (PSO)

PSO is an optimization algorithm that determines the optimal solution by simulating the social behavior of birds swarm. A number of particles in PSO, standing for birds in the real world, look for the optimal solution in the region by adjusting their speed and location. PSO can be expressed as Eq. (5).

$$\begin{aligned} \left\{ \begin{array}{l} v_i^{t + 1} = \omega v_i^t + c_1 \times r_1 \times (p_\mathrm{besti} - x_i^t ) + c_2 \times r_2 \times (g_\mathrm{best} - x_i^t ) \\ x_i^{t + 1} = x_i^t + v_i^{t + 1} \\ \end{array} \right. \end{aligned}$$

(5)

where $v_i^t$ and $v_i^{t+1}$ are the velocity of the ith particle at tth and $(t+1)$th iteration, respectively. $\omega$ denotes an inertial weight. $c_1$ and $c_2$ are learning factors; $r_1$ and $r_2$ stand for random number within (0,1); and $x_i^t$ and $x_i^{t+1}$ are the position of the ith particle at tth and $(t+1)$th iteration, respectively.

$$\begin{aligned} p_{besti}^t&= \left\{ \begin{array}{l} \begin{array}{*{20}l} {p_{_\mathrm{besti} }^{t - 1} } &{}\quad \hbox {if}\; {\left( f(x_i^t ) \ge f(p_\mathrm{besti}^{t - 1} )\right) } \\ \end{array} \\ \begin{array}{*{20}c} {x_i^t (t)} &{}\quad \hbox {if}\; {\left( f(x_i^t ) < f(p_\mathrm{besti}^{t - 1} )\right) } \\ \end{array} \\ \end{array} \right. \end{aligned}$$

(6)

$$\begin{aligned} g_\mathrm{best}&= \arg \mathop {\min }\limits _{p_\mathrm{besti}^t } f(p_\mathrm{besti} ) \end{aligned}$$

(7)

The $\omega v_i^t$ in Eq. (5) can offer good exploration capacity for PSO, while $c_1 * r_1 \times (p_\mathrm{besti} - x_i^t ) + c_2 \times r_2 \times (g_\mathrm{best} - x_i^t )$ provides historical memory.

2.2.2 Gravitational search algorithm (GSA)

Inspired by Newton theory, a new heuristic optimization algorithm GSA was firstly proposed by Rashedi et al. (2009). Each agent in GSA stands for candidate solution to the objective function and is considered as an object with masses proportional to the values of the fitness function . In the iteration procedure, all agents obey laws of gravity and motion to attract each other and move.

It is assumed that a system with N agents and n dimensions is shown in Eq.  (8) which scatter randomly in the search space.

$$\begin{aligned} \begin{array}{*{20}c} X_i =\left( x_i^1 ,x_i^2 , \ldots x_i^d , \ldots x_i^n \right) &{} {i = 1,2, \ldots ,N} \\ \end{array} \end{aligned}$$

(8)

At tth iteration, the gravitational force $F_{ij}^d (t)$ of the ith agent acting on the jth agent is expressed as Eq. (9).

$$\begin{aligned} F_{ij}^d (t) = G (t)\frac{{M_{pi} (t) \times M_{aj} (t)}}{{R_{ij} + \varepsilon }}\left( x_j^d (t) - x_i^d (t)\right) \end{aligned}$$

(9)

where $M_{aj} (t)$ and $M_{pi} (t)$ are active mass and passive mass, respectively. $\varepsilon$ denotes a small constant. G(t) and $R_{ij}$ are expressed as Eqs. (10) and (11), respectively.

$$\begin{aligned}&G(t) = G_0 \times \exp ( -\, \alpha \times iter/iter_{\max } ) \end{aligned}$$

(10)

$$\begin{aligned}&R_{ij} = \left\| {X_i (t),X_i (t)} \right\| _2 \end{aligned}$$

(11)

where $G_0$ and $\alpha$ are the initial gravitational constant and the descending coefficient, respectively. iter and $iter_\mathrm{max}$ are the current iteration and the maximum iteration, respectively.

At tth iteration, the accelerated speed of ith agent with d dimension can be expressed Eq. (12).

$$\begin{aligned} a_i^d (t) = \frac{{\sum \nolimits _{j = 1,j \ne i}^N {r_j \times F_{ij}^d (t)} }}{{M_i (t)}} \end{aligned}$$

(12)

where $r_j$ is a random value within (0,1), and $M_i (t)$ is expressed as Eq. (13).

$$\begin{aligned} \left\{ \begin{array}{l} m_i (t) = \frac{{fit_i (t) - worst(t)}}{{best(t) - worst(t)}} \\ M_i (t) = \frac{{m_i (t)}}{{\sum \nolimits _{j = 1}^N {m_j (t)} }} \\ \end{array} \right. \end{aligned}$$

(13)

where fit(t), best(t) and worst(t) stand for the value, minimum value and maximum value of the tth agent fitness function, respectively.

In the end, the speed and location of the ith agent are mathematically expressed as Eq. (14).

$$\begin{aligned} \left\{ \begin{array}{l} v_i^d (t + 1) = rand \times v_i^d (t) + a_i^d (t) \\ x_i^d (t + 1) = x_i^d (t) + v_i^d (t + 1) \\ \end{array} \right. \end{aligned}$$

(14)

where rand stands for a random number within (0,1).

2.2.3 Work principle of PSOGSA

To combine the exploitation ability of GSA with the exploration capacity of PSO, the $p_{besti}-x_i(t)$ in Eq. (5) is replaced by the acceleration $a_i(t)$ in Eq. (12) to construct a new PSOGSA hybrid algorithm; thus, PSOGSA is expressed as Eq. (15) (Zheng et al. 2017; Wang et al. 2015b). Like PSO algorithm, PSOGSA updates its velocity and position by considering not only current state but also previous values.

$$\begin{aligned} v_i (t + 1)&= \omega \times v_i (t) + c_1 \times r_1 \times a_i (t) + c_2 \times r_2 \times (g_{best} - x_i (t)) \end{aligned}$$

(15)

$$\begin{aligned} x_i (t + 1)&= x_i (t) + v_i (t+1) \end{aligned}$$

(16)

2.2.4 Binary PSOGSA

The traditional PSOGSA is a powerful organization algorithm in solving the real continuous problems; however, there exist binary problems that cannot be solved by the traditional PSOGSA. To solve these binary problems, Mirjalili and Hashimx (2012) proposed a binary-valued PSOGSA, namely BPSOGSA. In BPSOGSA algorithm, the velocity of each agent in PSOGSA is transformed into a probability function within (0,1) using the Hyperbolic tangent function, which is expressed as Eq. (17).

$$\begin{aligned} S(v_i^d (t)) = \left| \tanh (v_i^d (t))\right| \end{aligned}$$

(17)

where $\tanh (\cdot )$ represents hyperbolic tangent function. Then, the position of each agent is updated as Eq. (18).

$$\begin{aligned} \left\{ \begin{array}{l} \begin{array}{*{20}l} {x_{i,j}^d (t + 1) = complement(x_{i,j}^d (t))} &{} rand < S\left( x_{i,j}^d (t + 1)\right) \\ \end{array} \\ \begin{array}{*{20}l} {x_{i,j}^d (t + 1) = x_{i,j}^d (t)} &{} {else} \\ \end{array} \\ \end{array} \right. \end{aligned}$$

(18)

where $complement(\cdot )$ stands for the logical negation function.

2.3 Multi-kernel function least squares support vector machine (MKLSSVM)

2.3.1 Working principle of LSSVM

LSSVM is developed on the basis of SVM by using square errors in the cost function and equality constraints instead of nonnegative errors and inequality constraints. As a result, LSSVM regresses by dealing with a linear system rather than quadratic programming problems (Kumar et al. 2018). In recent years, LSSVM has been successfully applied in time series prediction (Yan et al. 2018), fault diagnosis (Kumar et al. 2018) and system modeling (Hemmati-Sarapardeha et al. 2018).

It is assumed training samples $\{(x_i,y_i)| x_i \in R^d, y_i \in R \}$, where $i=1,2, \ldots , N$, N and d are the number of the total samples and the dimension of input variables, respectively. $x_i$ and $y_i$ are the input and output vectors, respectively. Using a nonlinear function $\varphi (x)$, the input vectors are mapped into a high-dimensional feature space Z where the regression procession is carried out. The regression processions can be mathematically expressed as Eq. (19).

$$\begin{aligned} y = \omega ^T \varphi (x) + b \end{aligned}$$

(19)

where $\omega$ and b stand for the weight vector and bias term, respectively, which are estimated in the subsequent calculations in Eqs. (20) and (21).

$$\begin{aligned} C = 0.5\omega ^T \omega + 0.5\gamma \sum \limits _{i = 1}^N {e_i^2 } \end{aligned}$$

(20)

s.t.

$$\begin{aligned} y_i = \omega ^T \varphi (x_i ) + b + e_i \end{aligned}$$

(21)

where $\gamma >0$ is the penalty factor, $e_i$ denotes an error.

To simply the calculation, Lagrange function is constructed as Eq. (22).

$$\begin{aligned} L(\omega ,b,e,\alpha ) = \frac{1}{2}\left( \left\| \omega \right\| ^2 + \sum \limits _{i = 1}^N {e_i^2} \right) - \sum \limits _{i = 1}^N {\alpha _i \left( \omega ^T \varphi (x_i ) + b + e_i - y_i \right) } \end{aligned}$$

(22)

where $\alpha _i$ is the Lagrange multipliers.

Through partially differentiating $\omega$, e, b and $\alpha$, and eliminating $\omega$ and e, the regression results are expressed as Eq. (23).

$$\begin{aligned} y(x) = \omega ^T \varphi (x) + b = \sum \limits _{i = 1}^N {\alpha _i k(x,x_i )} + b \end{aligned}$$

(23)

where $k(x,x_i)$ stands for a positive definite kernel function.

2.3.2 Selection of kernel function

It has been proved that the regression performance and generalization capacity of LSSVM highly depend on the kind of kernel function and its parameters (Sun et al. 2018b). Among the common kernel functions, radial basis function (RBF) has good local exploitation capacity, while polynomial function (Poly) possesses excellent global exploitation ability, which has good capacity in processing nonlinear signal. To enhance the forecasting performance, a weighted multi-kernel function based on RBF, Poly and linear kernel functions is constructed for LSSVM, namely MKLSSVM, which takes advantages of individual approaches. The form of multi-kernel function can be expressed as Eq. (24).

$$\begin{aligned} k (x_i ,x_j ) = \mu _1 k_1 (x_i ,x_j ) + \mu _2 k_2 (x_i ,x_j ) + \mu _3 k_3 (x_i ,x_j ) \end{aligned}$$

(24)

where $k_1$, $k_2$ and $k_3$ stand for RBF, Poly and linear kernel function, respectively. $\mu _i$ denotes weight coefficient within (0, 1) and $\sum {\mu _i = 1}$. RBF, Poly and linear kernel functions are mathematically expressed as Eqs. (25), (26) and (27), respectively.

$$\begin{aligned}&k_\mathrm{RBF} (x_i ,x_j ) = \exp \left( -\, \frac{{||x_i - x_j ||^2 }}{{2\delta ^2 }}\right) \end{aligned}$$

(25)

$$\begin{aligned}&k_\mathrm{Poly} (x_i ,x_j ) = [(x_i \cdot x_j ) + 1]^d \end{aligned}$$

(26)

$$\begin{aligned}&k_\mathrm{line} (x_i ,x_j ) = x_i \cdot x_j \end{aligned}$$

(27)

Thus, the outputs of MKLSSVM can be modified as Eq. (28).

$$\begin{aligned} y = \sum \limits _{i = 1}^N {\alpha _i }\left[ \sum \limits _{j = 1}^3 {\mu _j } k_j (x_i ,x) \right] + b \end{aligned}$$

(28)

By tuning $\mu _j$ value, multi-kernel function exhibits optimal characteristics for different input variables. Although wind speed time series exhibits high nonlinearity, sometimes there exist some certain linear components (Li et al. 2018). The weighted combination of RBF, Poly and linear kernel functions not only processes the nonlinear components, but also solves the linear problems within wind speed data.

3 The working mechanism of the proposed forecasting strategy

3.1 Evaluation index for WSF

To illustrate the forecasting model with the best prediction performance, the definitions of four statistical indices, including RMSE, MAE, MAPE and MASE, are shown in Table 1 and utilized to evaluate and compare different forecasting approaches. Smaller MAE, RMSE, MAPE or MASE values mean that the prediction values are closer to the actual measured wind speed.

Table 1 Forecasting indices and their definitions

3.2 The proposed HPSOGSA-MKLSSVM

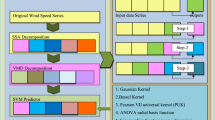
In the proposed HPSOGSA-MKLSSVM model, PSOGSA is employed to optimize the kernel parameters and weighted coefficients, which can make MKLSSVM avoid trapping in over-fitting or local optima. For measurement errors and malfunctioning sensors, there exists abnormal noise in the wind speed time series (Liu et al. 2018). To eliminate these ineffective components, BPSOGSA approach is exploited as feature selection to identify the abnormal data by encoding binary value $``0''$ or $``1''$ ($``0''$ and $``1''$ represent $``discarded''$ and $``selected''$, respectively). The feature selection for selecting effective input candidates and parameter optimization for optimizing the parameter combination in MKLSSVM are carried out by HPSOGSA simultaneously. In this paper, RMSE is applied as the fitness function to evaluate the forecasting results. The specific working steps of HPSOGSA-MKLSSVM model for WSF are illustrated in Fig. 2, and descriptions are shown Algorithm 1.

$$\begin{aligned} \dim = [B_1 ,B_2 , \ldots ,B_l ,\gamma ,\delta ,d,\mu _1 ,\mu _2 ,\mu _3 ]. \end{aligned}$$

(29)

Fig. 2

Feature selection and parameter optimization for MKLSSVM by HPSOGSA

Fig. 3

Framework of the TSD-HPSOGSA-MKLSSVM model

3.3 The working mechanism of the proposed hybrid forecasting model

The forecasting flowchart of the proposed TSD-HPSOGSA-MKLSSVM model is illustrated in Fig. 3, which can be divided into four stages.

• (i) Stage I Wind speed preprocessing. Employ CEEMDAN method to break the original empirical wind speed series into several IMFs and one residual (Res), which can relieve the degree of nonlinearity and fluctuation of wind speed time series. Employ WT approach to further decompose the highest frequency component IMF1 into a few subseries.

• (ii) Stage II Input matrix reconstruction. If the PACF of the ith subseries at lags bigger than parameter p are approximately independent N(0, 1/n) random variables, the correlation coefficients among input values are obtained as p; thus, the dimensions of the input variables are determined as p. For the ith subseries $X_i(t)$, the input variables of MKLSSVM can be represented as $X_i$ = {$x_i(t-1), x_i(t-2), \ldots x_i(t-p)$}, which are utilized to predict the corresponding output of MKLSSVM. To lower the forecasting difficulties, all the subseries are linearly translated into the range [0,1].

• (iii) Stage III HPSOGSA-MKLSSVM training. The confirmed input variables are divided into two parts, the first 1st to 1296th are utilized to train the HPSOGSA-MKLSSVM model and subsequent 1297th to 1440th are applied to test the model. To enhance the forecasting performance, artificial intelligent hybrid algorithm PSOGSA is employed to tune the parameter combination in MKLSSVM, and BPSOGSA is used to identify the effective candidates and discard the abnormal data within the input candidate matrix determined by PACF.

• (iv) Stage IV Wind speed forecasting. The well-trained HPSOGSA-MKLSSVM model is employed to forecast short-term wind speed in different predicting steps. The outputs of MKLSSVM for each decomposed subseries are aggregated after denormalization, and the final forecasting results are obtained. In the end, comparisons between the proposed hybrid model with other forecasting models are carried out using statistical indices.

Fig. 4

Original wind speed time series

Table 2 Statistical description of the empirical wind speed data (m/s)

Fig. 5

Decomposition results of the empirical wind speed time series by TSD

4 Case studies

4.1 Description of the empirical wind speed data

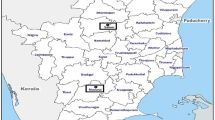
This study develops a hybrid model using the historical wind speed data to forecast the subsequent future short-term wind speed. The wind turbines are installed on the top of the mountain with around 120 m. Two sets of empirical historical wind speed data are collected from the Xuzhou wind farm in Jiangsu of China, illustrated in Fig. 4, to evaluate the proposed hybrid forecasting model. These wind speed data are measured every 10 min. The first 1st to 1296th continuous wind speed data are used to train the proposed model, and the subsequent 1297th to the 1440th wind speed data are utilized to test the proposed model. The statistical descriptions of the empirical wind speed data are listed in Table 2. As shown in Fig. 4 and Table 2, there exist highly nonlinearity and instability in wind speed time series.

Fig. 6

PACF values with 95% confidence

4.2 Wind speed data preprocessing

In this study, TSD method is employed to preprocess the original wind speed to eliminate the uncertainty. Firstly, the wind speed is disassembled by CEEMDAN technique into different IMFs and one Res, which are displayed in Fig. 5a, c. Suggested by Torres, etc. Torres et al. (2011), noise standard deviation $\varepsilon$ and ensemble size I are set as 0.02 and 500, respectively. As seen from the figures, the IMF1–IMF3 with higher frequency reveal the nonlinear information of the empirical wind speed. IMF4–IMF7 reflect the periodic information of the original wind speed, while the Res components illustrate the general tendency. WT is applied to further decompose the highest frequency component IMF1 into four sets of relatively subseries at three levels, which is named as A3, D1, D2 and D3. The decomposed subseries are shown in Fig. 5b, d. After decomposition by TSD technique, the decomposed subseries are converted to [0,1], which can reduce the regression difficulties of MKLSSVM (Hu et al. 2015).

Fig. 7

Inputing and outputing data format for original samples A

Table 3 Feature selection results by BPSOGSA

4.3 Input matrix reconstruction and parameter selection for HPSOGSA-MKLSSVM

4.3.1 Determination of the input dimension

Prior to submit the decomposed subseries to MKLSSVM for wind speed forecasting, the appropriate dimension of the input variables should be determined in advance. In this study, partial autocorrelation function (PACF) is applied to calculate the correlation coefficients among each decomposed subseries, and the correlation coefficients can be considered as the dimension of the input variables for MKLSSVM (Hu et al. 2015; Zhang et al. 2017). The PACF values of the empirical time series for two sets are computed from lags 0 to 25 and the calculated results with 95% confidence interval line are illustrated in Fig. 6. As shown in Fig. 6, the PACF values of original wind speed data A at lags bigger than 8 are within the red horizontal lines, which means that 8 antecedent wind speed time series severely influence the corresponding subsequent multi-step ahead forecasting (Hu et al. 2015; Peng et al. 2017). Thus, the input dimension of the original wind speed for MKLSSVM can be determined as 8, and the input and output data formats are shown in Fig. 7. AS shown in Fig. 7, a rolling forecasting process is adopted in this study. In the 1-step horizontal forecasting, the previous consecutive 8 time series are utilized to predict the 9th point data; then, the forecasting value is used as the historical time series to forecast the next value. The same forecasting strategies are executed for the multi-step forecasting, and the dimensions of the other time series are determined in the similar way.

4.3.2 Construction of the HPSOGSA-MKLSSVM

As described in Sect. 2.3, the regression performance of MKLSSVM is influenced greatly by the kernel parameters and penalty value. These real parameters are optimized by conventional PSOGSA, while BPSOGSA technique is exploited to identify the effective candidates and discard the abnormal components; these parameter optimization and feature selection are executed simultaneously by HPSOGSA. The effective input candidates identified by BPSOGSA method are shown in Table 3.

The parameters in the HPSOGSA-MKLSSVM model are set in Table 4, which are tuned by calculating the RMSE values. The inertial weight $\omega$ in PSO decreases linearly within (0.1, 0.9), which is expressed as Eq. (30).

Table 4 Parameter selection

$$\begin{aligned} \omega (t) = \omega _{\max } - \frac{{\omega _{\max } - \omega _{\min } }}{{it_{\max } }}\times t \end{aligned}$$

(30)

where $\omega _{max }$ and $\omega _\mathrm{min }$ denote constant values 0.9 and 0.1, respectively, and $it_\mathrm{max}$ and t stand for maximum iteration number and iteration time, respectively.

4.4 Comparisons and analysis

All the algorithms are carried out in MATLAB 2014a under Windows 8 Operating System environment. The statistical indices including RMSE, MAE, MAPE and MASE are utilized to measure the forecasting error. All the tests are carried out 20 times and the averages are considered as the final forecasting results to eliminate the statistical errors. A systematic investigation is carried out to illustrate how the LSSVM configuration influences its prediction performance in short-term wind speed forecasting. The regression plots of actual wind speed and forecasting values are shown in Fig. 8.

Fig. 8

Forecasting results by the proposed model

4.4.1 Verification of the effectiveness of TSD

This section mainly investigates the forecasting results of HPSOGSA-MKLSSVM model combining with the further decomposition methods of IMF1-, IMF1–2- and IMF1–3-based TSD method to determine the appropriate quantity of IMFs that should be disassembled, which are given in Table 5. Like IMF1, the subseries IMF2 and IMF3 are also decomposed by WT at three levels. As given in Table 5, the forecasting results of the TSD(IMF1)-HPSOGSA-MKLSSVM model are better than those of TSD(IMF1–2)-HPSOGSA-MKLSSVM and TSD(IMF1–3)-HPSOGSA-MKLSSVM regardless of 1-step or multi-step forecasting.

Compared with HPSOGSA-MKLSSVM with TSD (IMF1–2), the RMSE errors of the HPSOGSA-MKLSSVM with TSD (IMF1) in 1-step, 2-step and 3-step are reduced by 0.0546  m/s, 0.0409 m/s and 0.0387 m/s for wind speed data A, respectively, 0.0560 m/s, 0.0769 m/s and 0.0811 m/s for data B, respectively. Compared with HPSOGSA-MKLSSVM with TSD (IMF1–3), the RMSE errors of the HPSOGSA-MKLSSVM with TSD (IMF1) in 1-step, 2-step and 3-step are reduced by 0.0619 m/s, 0.0519 m/s and 0.0492 m/s for wind speed data A, respectively; and 0.0708 m/s, 0.0856 m/s and 0.0930 m/s for data B, respectively.

Remark

This forecasting results illustrate that the highest frequency components within IMF1 are the main distributing factors for the forecasting accuracy, and further decomposition of IMF2 and IMF3 also influences the forecasting accuracy.

Compared with HPSOGSA-MKLSSVM with CEEMDAN, the RMSE errors of the proposed model in 1-step, 2-step and 3-step are reduced by 0.0488 m/s, 0.0443 m/s and 0.0468 m/s for wind speed data A, respectively; and 0.05 m/s, 0.0496 m/s and 0.0472 m/s for wind speed data B, respectively.

Remark

These forecasting results can be explained that the irregularity of IMF1 with highest frequency is the main factor that influences the forecasting accuracy and the further decomposition by WT can effectively address the irregularity issue of IMF1. Thus, the further decomposition of IMF1 in the proposed TSD-HPSOGSA-MKLSSVM model is appropriate.

Table 5 Forecasting errors of the HPSOGSA-MKLSSVM with CEEMDAN and further decomposition

Table 6 Forecasting errors of the HPSOGSA-MKLSSVM with other different decomposition methods

Table 7 Forecasting errors of the TSD-HPSOGSA-LSSVM based on different kernel functions

Table 8 Forecasting results of the other single forecasting models (I)

Table 9 Forecasting results of the other single forecasting models (II)

Fig. 9

Forecasting results of the other forecasting models for data set A (ori, Per, PMLM and HPMLM stand for original, Persistence, PSOGSA-MKLSSVM and HPSOGSA-MKLSSVM, respectively. The same definitions are in Fig. 10 )

Fig. 10

Forecasting results of the other forecasting models for data set B

4.4.2 Comparisons with other different decomposition methods

To further illustrate the effectiveness of the proposed TSD, the popular wind speed preprocessing methods, including EEMD, EMD, WD and VMD, are employed to combine the HPSOGSA-MKLSSVM model to make multi-step wind speed forecasting. The parameters in EEMD and VMD are set according to Refs. Sun et al. (2018b) and Sun et al. (2019), respectively. The statistical forecasting errors of the decomposition-based model are given in Table 6. As given in Tables 5 and 6, CEEMDAN-based forecasting model outperforms EEMD- and EMD-based forecasting models. For example, compared with the EEMD-based forecasting model, the RMSE values of the proposed CEEMDAN-HPSOGSA-MKLSSVM model in 1-step, 2-step and 3-step are cut by 0.0380 m/s, 0.0235 m/s and 0.0143 m/s for data set A, respectively; and 0.0359 m/s, 0.0274 m/s and 0.0226 m/s for data set B, respectively. Compared with the HPSOGSA-MKLSSVM with EEMD, the RMSE errors of the proposed model for wind speed data A in 1-step, 2-step and 3-step are reduced by 0.0869 m/s, 0.0678 m/s and 0.0610 m/s, respectively; and 0.0869 m/s, 0.0678 m/s and 0.061 m/s for wind speed data B, respectively.

Remark

The underlying reasons are that CEEMDAN method effectively resolves the mode mixing problems existing in decomposition method EMD and completely neutralizes the added white Gaussians noise composing of paired positive and negative signals that added to the original samples. HPSOGSA-MKLSSVM with CEEMDAN also has better forecasting results than HPSOGSA-MKLSSVM with WD and VMD in terms of the statistical indices. In terms of the statistical indices listed in the tables, HPSOGSA-MKLSSVM with TSD also outperforms that with VMD, EMD or WT. Thus, TSD is more effective wind speed preprocessing method.

Table 10 Forecasting results of the other hybrid forecasting models

Fig. 11

Forecasting results of the recently developed forecasting models (EDKLM, WHELM, EGBP and WGSVM stand for EEMD-HGSA-DKLSSVM, WPD-HPSOGSA-ELM, EEMD-GA-BP and WD-GA-SVM, respectively)

4.4.3 Verification of the effectiveness of multi-kernel function

The main aims of this section are to illustrate the forecasting performance of TSD-HPSOGSA-LSSVM based on multi-kernel function over that based on RBF, Poly, linear or RBF&Poly kernel function. The forecasting results of TSD-HPSOGSA-LSSVM based on different kernel functions are shown in Table 7. As given in Table 7, the LSSVM with weighted RBF&Poly kernel functions performs best in terms of the fitness values RMSE among that with linear, RBF and Poly kernel functions, because RBF&Poly kernel function takes advantages of the local exploitation capacity of RBF function and the global exploration ability of Poly function by optimal weighted coefficients. Overall, the LSSVM with the linear kernel function performs the worst in that there are a lot of nonlinear information hiding in the wind speed data that the linear kernel function cannot catch. As given by the statistical error indices in Tables 5 and 7, MKLSSVM integrating Poly, RBF and line kernel functions by optimal weighted coefficients has better forecasting accuracy than LSSVM based on the combination of RBF and Poly kernel functions by optimal weighted coefficients, the reasons of which are that there exist some linear information within the wind speed data.

4.4.4 Comparisons of TSD-HPSOGSA-MKLSSVM with Persistence and the other LSSVM-based forecasting models

In this section, Persistence, LSSVM, PSOGSA-MKLSSVM, HPSOGSA-MKLSSVM are constructed to assess the forecasting performance of TSD-HPSOGSA-MKLSSVM using the four statistical indexes and the forecasting results are listed in Tables 8 and 9. The RBF function is adopted as kernel function in LSSVM and its parameters $\sigma$ and $\gamma$ are set according to Ref. Yuan et al. (2015) and the parameters in couple simulated annealing (CSA)-LSSVM are set according to Ref. Rostami et al. (2019).

The well-known Persistence, a simple approach for time series prediction, is generally utilized as a benchmark to compare with a new proposed forecasting models (Hu et al. 2015; Wang et al. 2017; Zheng et al. 2017). Persistence employs the current values at time t as the forecasting values at the future time $t + k$, namely $\hat{u}_{t+k}= u _t$ where k denotes the forecasting interval. In this study, the forecasting quality of the proposed hybrid model is also compared with the Persistence method. Based on the forecasting error indices listed in Tables 5 and 8, it can be obtained that the RMSE errors differences between the proposed hybrid model and Persistence are 0.3686 m/s, 0.3593 m/s and 0.3514 m/s in 1-step, 2-step and 3-step for data set A, respectively; and 0.3819 m/s, 0.3753 m/s and 0.4206 m/s for data set B, respectively. From the above error indices in the tables, the proposed TSD-HPSOGSA-MKLSSVM model obtains the largest improvement over Persistence.

As given in Tables 5 and 8, the single individual model LSSVM without input data preprocessing and parameter optimization performs much worse than that with parameter optimization and feature selection. Compared with LSSVM, the RMSE errors of PSOGSA-MKLSSVM for data set A in 1-step, 2-step and 3-step predictions are cut by 0.0254 m/s, 0.0143 m/s and 0.039 m/s, respectively. Compared with PSOGSA-MKLSSVM model, the RMSE errors of HPSOGSA-MKLSSVM for data set A in 1-step, 2-step and 3-step predictions are cut by 0.0115 m/s, 0.0239 m/s and 0.0072 m/s, respectively; and 0.0322 m/s, 0.0263 m/s and 0.0298 m/s for wind speed data B, respectively (Fig. 9).

Remark

The reasons of these results are (1) TSD decomposes the nonstationary and nonlinear wind speed time series into a few relatively stable components that can lower the regression difficulty of LSSVMs. (2) BPSOGSA algorithm identifies and discards the noise components that can relieve the negative effect of input candidates on the forecasting results. (3) LSSVM has good capacity in addressing small sample and nonlinear problems (Hu et al. 2015); in addition, the kernel function in LSSVM takes advantages of RBF, Poly and linear functions and the parameter combination is optimized by PSOGSA algorithm. These combination of different kernel functions by optimal parameters can enhance the forecasting results. Tables 5, 6 and 8 show that HPSOGSA-MKLSSVM without signal decomposition method performs much worse than that with signal decomposition method regardless of WT, EMD, EEMD, VMD or TSD when applied in wind speed forecasting. These signal decomposition methods break the wind speed data into the relatively stable subseries that contribute to higher forecasting accuracy; thus, the proposed compound structure taking advantages of various approaches is an effective wind speed forecasting model.

4.4.5 Comparing TSD-HPSOGSA-MKLSSVM with the other recently developed forecasting models

In order to further assess the forecasting performance of the proposed TSD-HPSOGSA-MKLSSVM, the recently developed forecasting models, including EEMD-HGSA-DKLSSVM (Sun et al. 2018b), WPD-HPSOGSA-ELM (Sun et al. 2018a), EEMD-GA-BP (Wang et al. 2016) and WD-GA-SVM (Liu et al. 2014), are constructed as comparative reference and these referenced forecasting models are simply described as follows.

• (i) EEMD-HGSA-DKLSSVM: The original empirical wind speed data are decomposed by EEMD, HGSA make feature selection and parameter optimization, and all the decomposed subseries are used to forecast by well-trained DKLSSVM.

• (ii) WPD-HPSOGSA-ELM: The original empirical wind speed data are decomposed by WPD, HPSOGSA make feature selection and parameter optimization, and all the decomposed subseries are used to forecast by well-trained ELM.

• (iii) EEMD-GA-BP: The original empirical wind speed data are decomposed by EEMD, and all the decomposed subseries are used to forecast by BPNN optimized by GA.

• (iv) WT-GA-SVM: The original empirical wind speed data are decomposed by WT, and all the decomposed subseries are used to forecast by SVM optimized by GA.

All the parameters of each referenced forecasting model are set according to the corresponding paper. These four referenced forecasting models make multi-step wind speed forecasting using the same wind speed data displayed in Fig. 4 and the forecasting results are shown in Table 10.

As given in Tables 5 and 10, it is obviously obtained that: Compared with EEMD-HGSA-DKLSSVM, WPD-HPSOGSA-ELM, EEMD-GA-BP and WD-GA-SVM for data set A in 1-step, the RMSE values of the proposed model are cut by 0.0844 m/s, 0.0875 m/s, 0.103 m/s and 0.13 m/s, respectively; in the 2-step forecasting, the RMSE values of the proposed model are cut by 0.0967 m/s, 0.1005 m/s, 0.1175 m/s and 0.1463 m/s, respectively; in the 3-step forecasting, the RMSE values of the proposed model are cut by 0.0911 m/s, 0.1026 m/s, 0.1185 m/s and 0.1337 m/s, respectively. For data set B, it can be also found that the proposed model outperforms EEMD-HGSA-DKLSSVM, WPD-HPSOGSA-ELM, EEMD-GA-BP and WD-GA-SVM. These forecasting results further illustrate the effectiveness of TSD-HPSOGSA-MKLSSVM in short-term wind speed forecasting (Fig. 11).

5 Conclusion

In this study, a new compound HPSOGSA-MKLSSVM wind speed forecasting model combined with decomposition method TSD is proposed. To illustrate the effectiveness of TSD-HPSOGSA-MKLSSVM, two sets of 10-min wind speed time series selected randomly from one wind farm in China are employed to test the proposed model and other forecasting approaches. Based on the aforementioned comparisons and analysis with other single and hybrid forecasting models, some conclusions can be obtained as follows.

• i: Considering that TSD signal processing method can decompose thoroughly wind speed into more stable components, we adopt TSD method combining CEEMDAN with WT to break the wind speed sample into different components. The testing results illustrate that the decomposed performance of TSD outperforms that of both CEEMDAN and WT. HPSOGSA-MKLSVM with TSD method also has better forecasting results than that with EEMD, EMD, VMD or WT. Thus, TSD is very suitable to be used in the hybrid proposed model.

• ii: Because wind speed time series always present large irregularity, not only single individual LSSVM without signal processing technique but also MKLSSVM with parameter optimization and feature selection cannot make wind speed forecasting with high accuracy. Feature selection and parameter optimization contribute to enhance the forecasting performance of the proposal.

• iii: MKLSSVM takes advantages of RBF kernel function with good capacity in local exploitation, Poly kernel function with excellent ability in global exploration and linear kernel functions by optimal coefficient. Thus, TSD-HPSOGSA-LSSVM based on multiple kernel function has obtained higher forecasting accuracy than that based on RBF, Poly, linear or double kernel function.

• iv: Compared with the recently developed EEMD-HGSA-DKLSSVM, WPD-HPSOGSA-ELM, EEMD-GA-BP and WD-GA-SVM forecasting models, the proposed hybrid model has better forecasting performance.

What is more, the proposed model makes great improvement compared with the base model Persistence. Thus, the proposed TSD-HPSOGSA-MKLSSVM is an effective method for wind speed forecasting. For further studies, it can be applied in energy demand prediction and other similar domain.

Table 11 Abbreviations

Appendix

All abbreviations are collected, and a brief explanation is given in Table 11.