1 Introduction

The essential function of an electric power system (EPS) is to deliver electrical energy to its consumers economically and efficiently. Herein, the economical aspect of electricity delivery covers the problem of optimal power flow (OPF), which is one of the most crucial issues in EPS operation and modern energy management system and it has been among the widely studied subjects by researchers (Naderi et al. 2019; Mandal and Roy 2014). What it is meant by “efficiently” dictates the quality of electric power energy which requires to balance generated, transmitted and distributed active powers. Any undesirable mismatch between generation and load demand resulting from unpredictable internal/external disturbances and/or load changes causes deviation of system operational frequency and interchange tie-line power flow from their scheduled limits. This brings out an aspiration for designing an accurate, efficient and fast control mechanism in PS modeling called load frequency control (LFC) to keep system performance measures, i.e. area frequency and interchange tie-line power, at their scheduled values. Indeed, LFC is one of the most profitable ancillary services to be well handled for the smooth and secure operation of EPS (Singh et al. 2017). It is aiming to diminish quickly transient deviations of area frequency and interchange tie-line power flow between the nearby control areas and to maintain their steady state errors at zero. Such mission in our today’s world where several types of electricity generating units contribute to total electricity generation is becoming much more crucial for offering eligible and reliable electrical power with high quality to the use by the consumer. A summarize of the main tasks of LFC is given as stepdown (Singh et al. 2017; Guha et al. 2016, 2017).

  1. 1.

    The system in the wake of abrupt load disruption and any of disturbances must be kept under control.

  2. 2.

    Undershoot, overshoot and settling time of frequency and tie-line power deviations should be reduced so as to raise the system stability margin.

  3. 3.

    Following a step load perturbation (SLP), area control error (ACE) must be eliminated as much as possible.

  4. 4.

    Each area should accommodate its own load at steady state.

  5. 5.

    Areas in need of power can collaborate with each other at transient state.

In view of the above, researchers worldwide are notably endeavoring to introduce betterment in LFC of EPSs. Since the performance of LFC system is shown to greatly link with the controller structure and the tuning algorithm exploited to optimize the controller gains, this betterment may appear in three ways. A critical literature review on this topic points out that in some works, new high-performance optimization algorithms are employed to optimize the gains of classical techniques (i.e. PI/PID) in order to enhance their capabilities. The second portion of literature survey includes studies where a new controller scheme is proposed and its parameters are tuned by a base search algorithm to avoid misleading control performance owing to improper parameter adjustment. In the last scenario, researchers take benefits of the first two solutions in that a new controller structure is presented and its parameters are adjusted through using a powerful optimizer newly proposed which favorably bestows superior search performance comparing to its predecessors. Among the three approaches, the last one based on an original control scheme and new search algorithm is always appreciated to find a LFC mechanism better than the existing ones in the literature.

Our literature inspection points out that a great number of control approaches in conjunction with proper optimization techniques are available to handle LFC problem of interconnected EPS. It is shown that researches on LFC that concentrate on the design of classical integer controllers are extensive. Some of them are quasi-oppositional grey wolf optimization algorithm (QOGWO)-based PID (Guha et al. 2016), quasi-oppositional symbiotic organisms search (QOSOS) algorithm-based PI/PID (Guha et al. 2017), bacterial foraging optimization algorithm (BFOA)-based PI controller (Ali and Abd-Elazim 2011), artificial bee colony (ABC) technique-based PI/PID (Gozde et al. 2012), hybrid BFOA and particle swarm optimization (PSO) (hBFOA-PSO) algorithm-based PI (Panda et al. 2013), differential evolution (DE) algorithm-based I/PI/PID (Mohanty et al. 2014), backtracking search algorithm (BSA)-based PI/PID (Guha et al. 2018), quasi-oppositional harmony search algorithm (QOHS)-based PID (Shiva et al. 2015), differential search algorithm (DSA)-based PID (Guha et al. 2017), hybrid firefly algorithm-pattern search (hFA-PS) technique-based PI/PID (Sahu et al. 2015), grey wolf optimization (GWO)-based PI/PID (Guha et al. 2016), and DE-based PID (Hota and Mohanty 2016). Also, modified versions of PID control schemes such as bat algorithm-based dual mode PI (Sathya and Ansari 2015), hybrid stochastic fractal search and local unimodal sampling (hSFS-LUS)-based multistage PID (Sivalingam et al. 2017), GWO technique-based cascade PI–PD controller (Padhy et al. 2017), flower pollination algorithm (FPA)-based PI–PD cascade controller (Dash et al. 2016), and different optimization techniques-based two-degree-of-freedom (2DOF) controllers (Sahu et al. 2013, 2016; Dash et al. 2014; Patel et al. 2019) have been proposed. To deal with the nonlinear behavior of LFC problem and guarantee, the system stability under stochastic load pattern and disrupting inputs, alternative control approaches based on sliding modes (Vrdoljak et al. 2010), artificial neural network approach (Saikia et al. 2011), fuzzy logic theory (Sahu et al. 2015, 2016; Nayak et al. 2018; Arya and Kumar 2017), adaptive neuro fuzzy inference system (ANFIS) (Khuntia and Panda 2012) and fractional order calculus (Sondhi and Hote 2014; Arya 2019a, b; c) have been also focused. Clearly, these controllers are computationally more expensive and difficult to design than classical techniques, but they eliminate the restrictions caused by their traditional counterparts and performance increases achieved by them are affirmed significant.

What makes a control strategy essential is that it should have good capability of tackling parameter uncertainties with good disturbance rejection while yielding the desirable dynamic performance as much as possible. Also, the design task of controller applied should not be so complicated for having a practical solution for engineering commissioning. These metrics have always remained major issues and continuous efforts are paid to generate new control schemes which are able to deal with the above-stated concerns. A recent development in this way is the formulation of non-integer or fractional order controllers which does not necessarily suggest the use of integer (i.e. 1.0), but any real numbers for orders of integrator and differentiator. It is unveiled from the literature that the fractional order (FO) controller is known to exhibit better dynamic response with an excellent robustness to parameter uncertainty and external disturbances. It also yields better stability in presence of nonlinear systems (Sondhi and Hote 2014). All these properties make the FO control popular and desirable strategy in several areas such as power electronics, robotics and process control (Jezierski and Ostalczyk 2009; Saha 2010; Jesus et al. 2010). Moreover, researches taking the advantages of FO theory in the field have been emerged densely in the literature such as fractional order PID (FOPID) (Sondhi and Hote 2014), gases Brownian motion optimizer (GBMO) (Zamani et al. 2016), hybridized gravitational search algorithm (DOGSA) (Dahiya et al. 2015) and big bang-big crunch (BBBC) (Kumar et al. 2016)-based FOPID, BFOA-based FO fuzzy PID (FOFPID) (Arya and Kumar 2017; Arya 2019d), imperialist competitive algorithm (ICA)-based fuzzy FO integral derivative (FFOID) (Arya 2019a) and cascaded fuzzy FOPI-FOPID (CFFOPI-FOPID) (Arya 2019b) controllers. Nonetheless, collective functioning of FOPI and FOPD in a cascaded connection, i.e. FOPI–FOPD, has not been yet evaluated as supplementary controller in LFC of EPSs. As such, encouraged by such a research gap, this paper offers a new FOPI–FOPD cascade controller and investigates its application to the problem of LFC. To procure the best set of FOPI–FOPD cascade controller parameters for avoiding improper gain adjustment, dragonfly search algorithm (DSA) is utilized as the powerful optimizer whose application to the studied problem is very rare, and thus needs further investigation. This constitutes the secondary contribution of this work.

DSA is a new nature-inspired algorithm, recently proposed by (Seyedali 2016), which mitigates the identified characteristics of the individual and social intelligence of fancy insects called dragonflies (Odonata). Two essential milestones exist in a dragonfly’s lifecycle namely nymph and adult. The greater portion of dragonflies’ lifespan is spent in nymph and they experience metamorphism thereafter to become adult. Swarming behavior of dragonflies are found interesting and rare in that they swarm for only two aims: hunting and migration. Hunting is called static (feeding) swarm and migration is called dynamic (migratory) swarm which can be considered as the foundation blocks of DSA. In static swarm, dragonflies are divided into small groups and fly within a small area to hunt other flying preys. The salient properties of this sort of swarm are local movements and sudden changes in the flying path. For dynamic swarms, a great number of dragonflies are assumed and they let the swarm migrate in one direction over long distances. The efficacy and competence of DSA is judged for several optimization problems like function optimization and designing a real propeller for submarines (Seyedali 2016), optimal load frequency regulation of micro-grid (Venkatesh and Sudheer 2017), designing a combined fuzzy PID controller for solving LFC problem (Nour et al. 2018), etc., by comparing the results obtained to the prior results in the relevant literature. Though there have been numerous LFC studies with various optimization techniques, few of them tackle the LFC problem employing the DSA approach (Venkatesh and Sudheer 2017; Nour et al. 2018). As a result, the participation of DSA in the concerned problem is a research avenue and worthy to be studied.

In view of the above, a new fractional order proportional integral-fractional order proportional derivative (FOPI–FOPD) cascade controller is constructed to ameliorate LFC performance of interconnected multi-area power units. To get the performance of this controller as nearer to optimality as possible, DSA is employed to tune the controller parameters like proportional gains (\(K_{p} , K_{p1}\)), integral gains (\(K_{i} , K_{i1}\)), order of integrator (\(\lambda\)) and order of differentiator (\(\mu\)) by minimizing the value of integral time absolute error (ITAE) criterion. Widely employed two-area thermal EPS with/without governor dead band (GDB) nonlinearity, three-area hydrothermal EPS with suitable generation rate constraints (GRCs) and also single-/multi-area multi-source EPSs are considered to establish the expected performance of advocated approach. Several results obtained by simulating the networks are presented in comparison with DSA tuned FOPID controller and the available results reported earlier to betoken the reputation of the method. It is divulged that DSA is a powerful means to search for the controller parameters in the studied control application and DSA tuned FOPI–FOPD cascade controller is able to provide valuable contributions to the relevant field.

The rest of the paper is arranged as follows. Section 2 presents the transfer function models of various EPSs tested. A brief overview of fractional calculus is given in Sect. 3. This section also details the structure of proposed FOPI–FOPD cascade controller and its formulation from the optimization point of view. DSA is studied in Sect. 4. To show and verify the contribution of the advocated approach, a comprehensive comparative study on the respective test cases is conducted with several reported methodologies in Sect. 5. Finally, some concluding notes and useful suggestions for future search directions are provided in Sect. 6.

2 Systems investigated

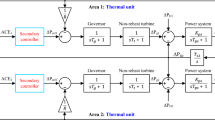
2.1 Classical two-area interconnected thermal power system

Investigations have been performed first on two-area interconnected thermal EPS with and without governor dead band (GDB) nonlinearity. The transfer function models of these systems that are widely employed in the literature for benchmarking LFC solution (Ali and Abd-Elazim 2011; Gozde et al. 2012; Panda et al. 2013; Guha et al. 2017, 2018; Shiva et al. 2015) are sketched in Fig. 1. These systems will be referred to as test system-1 and test system-2, respectively, in this paper. Each area of the EPS is outfitted with one non-reheat turbine and one speed governor-based thermal generating unit.

Fig. 1
figure 1

Transfer function model of two-area interconnected non-reheat thermal EPS a without GDB nonlinearity b with GDB nonlinearity

Full size image

Each control area has three inputs and two outputs. The inputs are the controller output \(\Delta P_{\text{ref}}\), load disturbance \(\Delta P_{\text{D}}\) and tie-line power error \(\Delta P_{\text{tie}}\). The outputs are the generator frequency error \(\Delta f\) and area control error (ACE) represented by Eq. 1.

$${\text{ACE}} = - B\Delta f \pm \Delta P_{\text{tie}}$$
(1)

where \(B\) is the frequency bias parameter.

Non-reheat turbine is modeled by the following transfer function with \(T_{t}\) being the time constant of steam turbine.

$$G_{t} \left( s \right) = \frac{{\Delta P_{t} }}{{\Delta P_{\text{g}} }} = \frac{1}{{sT_{t} + 1}}$$
(2)

The model of a speed governor is first considered linear and represented by Eq. 3 where \(T_{\text{g}}\) is the time constant of speed governor.

$$G_{\text{g}} \left( s \right) = \frac{{\Delta P_{\text{g}} }}{{\Delta P_{v} }} = \frac{1}{{sT_{\text{g}} + 1}}$$
(3)

To get a more realistic insight into the LFC issue, it is required some nonlinearities emerging in a real system be included in EPS modeling. In this direction, a nonlinearity source called governor dead band (GDB) is considered in this paper to investigate its influence on the EPS dynamics. GDB makes the system behave oscillatory and described as the total amount of a maintained speed variation within which valve position does not change. A describing function-based technique is utilized to integrate GDB nonlinearity and the transfer function of governor with dead band is given by

$$G_{\text{g}} \left( s \right) = \frac{{\Delta P_{\text{g}} }}{{\Delta P_{v} }} = \frac{{ - \left( {0.2/\pi } \right)s + 0.8}}{{sT_{\text{g}} + 1}}$$
(4)

The input of speed governor is \(\Delta P_{v}\) which is calculated by subtracting \(\frac{1}{R}\Delta f\) from \(\Delta P_{\text{ref}}\) as in Eq. 5 where \(R\) is a parameter for speed regulation of speed governor and \(\Delta P_{\text{ref}}\) is reference power command to be generated.

$$\Delta P_{v} = \Delta P_{\text{ref}} - \frac{1}{R}\Delta f$$
(5)

The pair of generator (rotating mass) and load is represented by a gain \(K_{\text{ps}}\) and time constant \(T_{\text{ps}}\) given by

$$G_{p} \left( s \right) = \frac{{K_{\text{ps}} }}{{sT_{\text{ps}} + 1}}$$
(6)

Eventually, frequency error or frequency deviation is obtained from the output of the system as

$$\Delta f\left( s \right) = G_{p} \left( s \right)\left[ {\Delta P_{t} \left( s \right) - \Delta P_{\text{D}} \left( s \right) - \Delta P_{\text{tie}} } \right]$$
(7)

\(\Delta P_{\text{tie}}\) is the deviation of tie-line power flowing in-between neighboring control areas at transient states and computed by

$$\Delta P_{\text{tie}} = \frac{{T_{12} }}{s}\left[ {\Delta f_{1} - \Delta f_{2} } \right]$$
(8)

where \(T_{12}\) is the synchronizing time constant of tie-line.

In Fig. 1, the two areas are considered identical and so are the controllers in both areas such that FOPI-FOPD-1 ≡ FOPI-FOPD-2.

2.2 Three-area hydrothermal power system

A three-area hydrothermal EPS is designed and employed to see the ability of the proposed approach in dealing with interconnected multi-area EPS. This system, named as test system-3, has three generating units where areas 1 and 2 are thermal based on single-stage reheat turbines, whereas area 3 is a hydro one driven by an electric governor as depicted in Fig. 2. In such a system, because all the areas are fully connected with each other, tie-line power transfer between two neighboring areas does not necessarily flow directly through the tie lines connecting the associated areas, but may occur over parallel lines via other areas. Since the thermal areas are of the same type, both controllers in these areas are decided identical and different from that in the hydro area. This way, we have reduced the number of controllers in need of being tuned concurrently from three to two for simplification.

Fig. 2
figure 2

Transfer function model of three-area interconnected hydrothermal EPS

Full size image

It is known that the power generation in an EPS cannot change at an infinite rate, but at a certain rate depending on the physical limits of system mechanics and dynamics. To limit the rate of generation, a significant constraint called generation rate constraint (GRC) is considered for all the areas in Fig. 2. The related works in the literature suggest that the standard value of GRC for a thermal area is 3%/min. So, GRC for the ith thermal system is

$$\left| {\Delta P_{Gi} \left( s \right)} \right| \le 0.0005\quad {\text{p}} . {\text{u}}\;{\text{MW}}/{\text{s}}$$

Two saturation blocks restricted by ± 0.0005 are added into the thermal units to evade from excessive generation. Likewise, for the hydro area, different generation amounts, 360%/min for lowering generation and 270%/min for raising generation, are considered. Thus,

$$\begin{aligned} \left| {\Delta P_{G} \left( s \right)} \right| & \le 0.06\quad {\text{p}} . {\text{u}}\;{\text{MW}}/{\text{s}} \Rightarrow \;{\text{for}}\;{\text{lowering}} \\ \left| {\Delta P_{G} \left( s \right)} \right| & \le 0.045\quad {\text{p}} . {\text{u}}\;{\text{MW}}/{\text{s}} \Rightarrow \;{\text{for}}\;{\text{raising}} \\ \end{aligned}$$

This has been taken into account in the system model by including a saturation block limited by − 0.06 and 0.045 in the hydro turbine.

2.3 Extension to multi-source power system

After the initial investigations on linear/nonlinear two-area non-reheat thermal and three-area hydrothermal EPSs, the study is extended to more practical multi-source EPS to further qualify the performance of DSA tuned FOPI–FOPD cascade controller. A single-area and two-area EPS having three generating units in each area are considered in this section. In such systems, collective performance of all generators of different types is interested.

  1. a.

    Multi-source single-area power system

Transfer function model of a multi-source single-area power plant is illustrated in Fig. 3. The plant, designated as test system-4, has three individually controlled generating units of thermal with reheat turbine, hydro and gas units. Each generating unit has its own regulation parameter and participation factor, which decide the contribution of the respective unit to the total generation. The summation of participation factors of all participating generators should be equal to unity in a control area. In Fig. 3, \(R\) is the regulation parameter, \(U_{\text{T}}\), \(U_{\text{H}}\) and \(U_{\text{G}}\) are controller outputs of thermal, hydro and gas units, respectively, \(K_{\text{T}}\), \(K_{\text{H}}\) and \(K_{\text{G}}\) are participating factors of thermal, hydro and gas units, respectively, \(T_{\text{sg}}\) is speed governor time constant of thermal unit, \(K_{\text{r}}\) and \(T_{\text{r}}\) are reheat gain and reheat time constant, respectively, \(T_{\text{t}}\) is steam turbine time constant, \(T_{\text{gh}}\) is main servo time constant of hydro turbine speed governor, \(T_{\text{rs}}\) and \(T_{\text{rh}}\) are reset time and transient droop time constant of hydro turbine speed governor, respectively, and \(T_{\text{w}}\) is given as nominal starting time of water in penstock. As for gas turbine power unit, \(c_{\text{g}}\) is gas turbine valve positioner, \(b_{\text{g}}\) is gas turbine constant of valve positioner, \(X_{\text{c}}\) and \(Y_{\text{c}}\) are lead and lag time constant of gas turbine speed governor, respectively, \(T_{\text{cr}}\), \(T_{\text{f}}\) and \(T_{\text{cd}}\) are combustion reaction time delay, fuel time constant and compressor discharge volume-time constant of gas turbine, respectively. \(K_{\text{ps}}\) and \(T_{\text{ps}}\) are gain and time constant of EPS, respectively, \(\Delta f\) is frequency deviation and \(\Delta P_{\text{D}}\) is incremental change in load.

Fig. 3
figure 3

Transfer function model of multi-source single-area EPS

Full size image
  1. b.

    Two-area multi-source power system

The efficacy of the proposed control scheme is finally examined on test system-5 that considers a two-area six-unit multi-source EPS as shown in Fig. 4. In fact, each area of this plant is familiar with multi-source single-area system in Fig. 3 and the only difference between two power plants is the AC tie line that interconnects two control areas for load sharing purpose during transient state. Since the two areas are assumed identical, we consider the three controllers in both areas to be identical also. This eliminates the necessity for effective tuning of each of six controllers for each generating unit, which is both costly from the optimization viewpoint and impractical in real-time implementation.

Fig. 4
figure 4

Transfer function model of two-area multi-source EPS

Full size image

3 Controller synthesis

3.1 A mini overview of fractional calculus

Control system engineering has witnessed noticeable increase in exploiting fractional order (FO) controllers owing to their properties of short response time, good stability under varying circumstances and excellent robustness to external disturbances. The idea underlying the use of FO dates back the study of Oustaloup et al. (2000). Later on, Podlubny introduced a general scheme of standard PID controller designated as FOPID or PIλDμ controller (Podlubny 1999). Then, many research papers taking benefits of FOPID controller have appeared in several application areas such as automatic voltage regulator (Zeng et al. 2015), twin rotor helicopter (Azarmi et al. 2015), trajectory control (Mousavi and Alfi 2015), solid-core magnetic bearing system (Zhong and Li 2015) as well as load frequency control of diverse EPSs (Khuntia and Panda 2012; Kumar et al. 2016; Arya and Kumar 2017; Arya 2019d; Ismayil et al. 2014; Nithilasaravanan et al. 2019; Pan and Das 2015). The concept of FO controller corresponds to differential equations through fractional calculus (FC), which is the generalization of the ordinary calculus making use of the richness provided by the non-integer order of Laplace variable \(s\). That said, it is an extension of \({\text{d}}^{n} y\left( t \right)/{\text{d}}t^{n}\) concept with \(n\) being an integer number to the concept \({\text{d}}^{\alpha } y\left( t \right)/{\text{d}}t^{\alpha }\) with \(\alpha\) being a non-integer number. As the result of this generalization, another basic operator, named fractional integro-differential operator \(_{a} D_{t}^{\alpha }\), has been evolved as

$$_{a} D_{t}^{\alpha } = \left\{ {\begin{array}{*{20}l} {\frac{{{\text{d}}^{\alpha } }}{{{\text{d}}t^{\alpha } }}} \hfill & {R\left( \alpha \right) > 0} \hfill \\ 1 \hfill & {R\left( \alpha \right) = 0} \hfill \\ {\mathop \int \limits_{a}^{t} \left( {{\text{d}}\tau } \right)^{ - \alpha } } \hfill & {R\left( \alpha \right) < 0} \hfill \\ \end{array} } \right.$$
(9)

where \(a\) and \(t\) are constants associated with initial and final operational bounds, and \(\alpha \in R\) (\(R\) is the set of real numbers) is the fractional order of the integro-differential operator.

There are many applicable definitions available in the literature describing the fractional derivative function, but the mostly applied one pertains to the Riemann–Liouville (RL) definition. In this definition, fractional derivative of order \(\alpha\) of a function \(f\left( t \right)\) is given by

$$_{a} D_{t}^{\alpha } f\left( t \right) = \frac{1}{{\varGamma \left( {n - \alpha } \right)}}\frac{{{\text{d}}^{n} }}{{{\text{d}}t^{n} }}\mathop \int \limits_{a}^{t} \frac{f\left( \tau \right)}{{\left( {t - \tau } \right)^{\alpha - n + 1} }}{\text{d}}\tau$$
(10)

where \(n - 1 < \alpha < n\), n is the integer part of \(\alpha\), \(n \in N\) and \(\varGamma \left( \cdot \right)\) is the Euler’s gamma function given by

$$\varGamma \left( s \right) = \mathop \int \limits_{0}^{\infty } t^{s - 1} e^{ - s} {\text{d}}t,\quad s > 0$$
(11)

\(\varGamma \left( {s + 1} \right)\) is equal to \(s!\), when \(s\) is an integer.

For convenience, the Laplace domain transformation is used to portray the fractional integro-differential process. The Laplace transformation of Eq. 10 under zero initial condition for the fractional derivative can be written as

$$\begin{aligned} & {\mathcal{L}}\left\{ {_{a} D_{t}^{\alpha } f\left( t \right)} \right\} = \mathop \int \limits_{0}^{\infty } e^{ - st}_{a} D_{t}^{\alpha } f\left( t \right){\text{d}}t \\ & \quad = s^{\alpha } F\left( s \right) - \mathop \sum \limits_{k = 0}^{n - 1} s^{k}_{a} D_{t}^{\alpha - k - 1} \left. {f\left( t \right)} \right|_{t = 0} \\ \end{aligned}$$
(12)

for \(n - 1 < \alpha < n\) while \(F\left( s \right) = {\mathcal{L}}\left\{ {f\left( t \right)} \right\}\) signifies the normal Laplace transformation.

FOPID is often referred to as PIλDμ controller, where \(\lambda\) and \(\mu\) are the non-integer orders of integral and derivative parts and can be any real numbers. Owing to the addition of tunable \(\lambda\) and \(\mu\) parameters, controllers composing of different combinations of proportional, integral and/or derivative control action become more flexible and robust while at the same time the system performance could be also boosted, but their design is more complex than their integer order counterpart. Fractional order differential equation of a control system can be given by

$$\begin{aligned} & b_{m} D^{{\beta_{m} }} y\left( t \right) + \cdots + b_{1} D^{{\beta_{1} }} y\left( t \right) + b_{0} D^{{\beta_{0} }} y\left( t \right) \\ & \quad = a_{n} D^{{\alpha_{n} }} u\left( t \right) + \cdots + a_{1} D^{{\alpha_{1} }} u\left( t \right) + a_{0} D^{{\alpha_{0} }} u\left( t \right) \\ \end{aligned}$$
(13)

where \(u\left( t \right)\) and \(y\left( t \right)\) are input and output (state) signals, respectively. \(D^{{\alpha_{n} }} \equiv {}_{0}D_{t}^{{\alpha_{n} }}\) and \(D^{{\beta_{n} }} \equiv {}_{0}D_{t}^{{\beta_{n} }}\) symbolize a fractional order operator under zero initial condition, \(a_{i}\) (i = 0, 1, 2,…, n) and \(b_{j}\) (j = 0, 1, 2,…, m) are arbitrary constants, \(\alpha_{i}\) (i = 0, 1, 2,…, n) and \(\beta_{j}\) (j = 0, 1, 2,…, m) are random real numbers. Assuming the inequalities are \(\alpha_{n} > \alpha_{n - 1} > \cdots > \alpha_{0} \ge 0\) and \(\beta_{n} > \beta_{n - 1} > \cdots > \beta_{0} \ge 0\), the transfer function of Eq. 13 in s-domain can be derived by Eq. 14 with initial conditions of \(\left[ {{}_{0}D_{t}^{{\alpha_{i} - i - 1}} y\left( t \right)} \right]_{t = 0}\) (i = 0, 1, 2,.., n − 1) and \(\left[ {{}_{0}D_{t}^{{\beta_{j} - j - 1}} y\left( t \right)} \right]_{t = 0}\) (j = 0, 1, 2,…, m − 1).

$$G\left( s \right) = \frac{Y\left( s \right)}{U\left( s \right)} = = \frac{{a_{n} s^{{\alpha_{n} }} + a_{n - 1} s^{{\alpha_{n - 1} }} \cdots + a_{1} D^{{\alpha_{1} }} + a_{0} D^{{\alpha_{0} }} }}{{b_{m} s^{{\beta_{m} }} + b_{m - 1} s^{{\beta_{m - 1} }} \cdots + b_{1} s^{{\beta_{1} }} + b_{0} D^{{\beta_{0} }} }}$$
(14)

And one arrives at the following transfer function form of FOPID controller:

$$G_{\text{FOPID}} \left( s \right) = K_{p} + \frac{{K_{i} }}{{s^{\lambda } }} + K_{d} s^{\mu } ,\;\left( {\lambda ,\mu > 0} \right)$$
(15)

In Eq. 15, \(K_{p}\), \(K_{i}\) and \(K_{d}\) are proportional, integral and derivative gains, respectively, and \(\lambda\) and \(\mu\) are liable for order of integration and differentiation. As such, there are five independent parameters to be tuned prior to operation with a FOPID controller. In guidance of Eq. 15, Table 1 is provided to observe the resulting controller structure depending upon the settings of \(\lambda\) and \(\mu\). It is clear from this table that all the classical versions of the PID controller are associated with the unique cases of the fractional PIλDμ controller. For example, if \(\lambda\) and \(\mu\) are both set to 1, the resulting controller structure is a conventional integer order PID controller. Similarly, if \(\mu = 0\), it becomes PIλ, and if \(\lambda = 0\), it becomes PDμ.

Table 1 Controller structure with varying \(\lambda\) and \(\mu\)
Full size table

In computer simulations and real-time implementations of transfer functions including fractional powers of \(s\), it is needed to approximate them with usual integer order transfer functions. To do this properly, a usual transfer function would normally include an infinite number of poles and zeroes. But, approximating with a finite number of poles and zeroes is also possible using the CRONE approximation concept suggested by Oustaloup who uses recursive distribution of N real poles and N real zeroes (Oustaloup et al. 2000). The Oustaloup filter given by Eq. 16 is known to provide a very good approximation/matching with the fractional order elements \(s^{\alpha }\) within a chosen frequency band \(\left[ {\omega_{L} ,\omega_{H} } \right]\) and order N (Pan and Das 2015).

$$G_{f} \left( s \right) = s^{\alpha } = K\mathop \prod \limits_{k = - N}^{N} \frac{{s + \omega_{k}^{z} }}{{s + \omega_{k}^{p} }}$$
(16)

where \(K\) is the filter gain, \(\omega_{k}^{z}\) and \(\omega_{k}^{p}\) are the zeroes and poles of \(G_{f} \left( s \right)\) calculated by

$$K = \omega_{H}^{\alpha }$$
(17)
$$\omega_{k}^{z} = \omega_{L} \left( {\frac{{\omega_{H} }}{{\omega_{L} }}} \right)^{{\frac{{k + N + 0.5\left( {1 - \alpha } \right)}}{2N + 1}}}$$
(18)
$$\omega_{k}^{p} = \omega_{L} \left( {\frac{{\omega_{H} }}{{\omega_{L} }}} \right)^{{\frac{{k + N + 0.5\left( {1 + \alpha } \right)}}{2N + 1}}}$$
(19)

There are two crucial parameters, filter gain \(K\) and approximation order N, having notable influence on the performance of this approximation. \(K\) is tuned so that the gain of the approximation should be unity at 1 rad/s frequency. Low value of N gives rise to simpler approximation and ease from the practical point of view but the approximation performance decays owing to ripple formation in magnitude and phase response. Such problem can be resolved by increasing N, but it will make the approximation complicated and computationally painful in real-time experimentation. Thus, considering the trade-off between the precision and complexity, CRONE approximation is realized in this paper with N = 3 and fitting frequency range equal to [10−2, 102] rad/s.

3.2 Proposed FOPI–FOPD cascade controller

To advance LFC performance in a wide range of EPSs, FOPI–FOPD cascade controller is proposed in this paper. To the author’s knowledge, the designed controller is unique, and has not been employed in LFC studies previously. Thus, its application in the field is a research avenue and improving the system performance by using FOPI–FOPD cascade controller will also be the valuable contributions of the present paper. The block diagram of this controller structure is illustrated in Fig. 5.

Fig. 5
figure 5

Block diagram of FOPI–FOPD cascade controller structure

Full size image

As perceived in Fig. 5, the proposed controller involves two controllers namely FOPI and FOPD connected in cascade. By receiving the ACE signal, the FOPI controller generates a signal, which also acts as input of the FOPD controller. The output of the FOPI–FOPD cascade controller is the reference power setting or control input i.e. \(\Delta P_{\text{ref}}\) for the EPSs to be controlled as mathematically given by Eq. 20.

$$\Delta P_{\text{ref}} = {\text{ACE}} \cdot \overbrace {{\left( {K_{p1} + K_{i} s^{ - \lambda } } \right)}}^{\text{FOPI}} \cdot \overbrace {{\left( {K_{p2} + K_{d} s^{\mu } } \right)}}^{\text{FOPD}}$$
(20)

For \(\lambda = 1\) and \(\mu = 1\), the FOPI–FOPD cascade controller turns into a simpler form of classical PI–PD cascade controller. The red faced variables highlighted in Fig. 5, i.e. \(K_{p1}\), \(K_{p2}\), \(K_{i}\), \(K_{d}\), \(\lambda\) and \(\mu\), are six unknown design parameters to be optimized. Due to the extra two degrees of freedom resulting from the orders of integrator and differentiator, newly structured FOPI–FOPD cascade controller is expected to better cope with the dynamical properties of LFC problem compared to conventional PI–PD cascade controller.

Prior to the FOPI–FOPD cascade controller’s design, we had three goals. Firstly, it should be cost-effective, simple and easy from the perspectives of design and implementation. Thus, the controller has the PID-like control action. Secondly, PI and PD controllers are cascaded, i.e. PI–PD to blend the advantages of distinct features and strengths of the two controllers. On the other hand, in a cascade controller, there are more tuning knobs than a non-cascade controller and it is known that if there are more tuning knobs, improved system performance may be obtained from that controller. Moreover, the cascade control is popular for its quick disturbance rejection ability before it effuses to the other parts of the system. To add more flexibility to controller design and cultivate PI–PD cascade controller performance, it is considered with fractional integrator/derivative order, i.e. FOPI–FOPD in order to fulfill our third aim.

3.3 Optimization of FOPI–FOPD cascade controller

To gain success from the FOPI–FOPD cascade controller to the maximum extent possible, its parameters such as \(K_{p1}\), \(K_{p2}\), \(K_{i}\), \(K_{d}\), \(\lambda\) and \(\mu\) are required to be optimized concurrently. The role of an optimization progress is to find the most promising solution in a feasible region by minimizing a cost function. The choice of this function is specific to the problem at hand and it has a strong impact over the system dynamic behavior. In the present work, ITAE criterion is assumed as cost function \(\left( {J_{\text{ITAE}} } \right)\) to be utilized in the controller optimization task. \(J_{\text{ITAE}}\) declared via Eqs. 21–23 for single-area, two-area and three-area EPSs is the classical one and widely employed in other published works. Compared with other error integrating alternatives, ITAE is recognized to bestow superior results in LFC field (Sivalingam et al. 2017; Sahu et al. 2015).

$$J_{\text{ITAE}} = \mathop \int \limits_{0}^{{t_{\text{sim}} }} t\left| {\Delta f} \right|{\text{d}}t\quad {\text{for}}\;{\text{single}}\;{\text{area}}\;{\text{EPS}}$$
(21)
$$J_{\text{ITAE}} = \mathop \int \limits_{0}^{{t_{\text{sim}} }} t\left( {\left| {\Delta f_{1} } \right| + \left| {\Delta f_{2} } \right| + \left| {\Delta P_{\text{tie}} } \right|} \right){\text{d}}t\quad {\text{for}}\;{\text{two - area}}\;{\text{EPS}}$$
(22)
$$J_{\text{ITAE}} = \mathop \int \limits_{0}^{{t_{\text{sim}} }} t\left( {\left| {\Delta f_{1} } \right| + \left| {\Delta f_{2} } \right| + \left| {\Delta f_{3} } \right| + \left| {\Delta P_{{{\text{tie}}1}} } \right| + \left| {\Delta P_{{{\text{tie}}2}} } \right| + \left| {\Delta P_{{{\text{tie}}3}} } \right|} \right){\text{d}}t\quad {\text{for}}\;{\text{three - area}}\;{\text{EPS}}$$
(23)

where \(t_{\text{sim}}\) is the time horizon of simulation. Consequently, the FOPI–FOPD cascade controller design problem can be formulated as the subsequent optimization problem subject to linear inequalities of the controller parameters bounds:

$$\begin{aligned} K_{p1}^{\hbox{min} } & \le K_{p1} \le K_{p1}^{\hbox{max} } \\ K_{p2}^{\hbox{min} } & \le K_{p2} \le K_{p2}^{\hbox{max} } \\ K_{i}^{\hbox{min} } & \le K_{i} \le K_{i}^{\hbox{max} } \\ K_{d}^{\hbox{min} } & \le K_{d} \le K_{d}^{\hbox{max} } \\ \lambda^{\hbox{min} } & \le \lambda \le \lambda^{\hbox{max} } \\ \mu^{\hbox{min} } & \le \mu \le \mu^{\hbox{max} } \\ \end{aligned}$$
(24)

where the superscripts \(\hbox{min}\) and \(\hbox{max}\) are the minimum and maximum values of FOPI–FOPD cascade controller gains, respectively. There is no certain way to decide these values at design stage of a controller. The task becomes more problematic when introducing a new controller. To ensure both EPS stability and fruitful optimization process, we decide the ranges in this work as follows: the minimum and maximum values for \(K_{p1, p2, i, d}\) are selected as 0.0 and 3.0 for test systems 1, 2 and 3, whereas the respective range is set between −2 and 2 for test systems 4 and 5. However, \(\lambda\) and \(\mu\) values are chosen between 0.0 and 1.5 for all test systems. To enrich EPS dynamic performance, DSA is allowed to search for optimal gain values of FOPI–FOPD cascade controller within this specified range to minimize \(J_{\text{ITAE}}\).

4 Dragonfly search algorithm

Inspecting the literature reveals that the employment of DSA in optimization of controller parameters for LFC of EPS is very limited (Venkatesh and Sudheer 2017; Nour et al. 2018). So, this study is devoted to investigate the capabilities of DSA more thoroughly for proper gain adjustment of the designed controller in presence of different kinds of EPSs. DSA has been recently proposed by Seyedali as an alternative and powerful optimizer to solve some optimization problems that could not be solved by other available algorithms (Seyedali 2016). It is a bioinspired metaheuristic search technique based on the computer programming of identified individual and swarm intelligence of a fancy insect called dragonfly. As shown in Fig. 6, dragonflies have a long thin body with two pairs of large transparent wings that sprawl sideways at rest. This way, they can fly fast and hunt most of other small insects living in nature.

Fig. 6
figure 6

Photography of a dragonfly

Full size image

There are two essential milestones in the lifecycle of a dragonfly: nymph and adult. The significant portion of their lifespan is spent in nymph and then they undergo a metamorphosis with a series of nymphal phases from which the adult appears. Interestingly, the swarming behavior of dragonflies is genuine and rare in nature. They swarm for two objectives only: hunting and migration, which are named as static (feeding) swarm and dynamic (migratory) swarm, respectively (Seyedali 2016). In a static swarm, small sub-swarms are created and dragonflies in these swarms are flied over different areas. Localized movements and sudden changes are the salient properties of this swarm. In a dynamic swarm, however, a greater number of dragonflies form the swarm so as to migrate alongside one direction over long distances. As such, so-called static and dynamic swarming behaviors are the fundamentals of DSA operation and they are very familiar with two important characteristics of metaheuristic search algorithms: exploration (diversification) and exploitation (intensification). Static swarm tries to emphasize on exploration while dynamic swarm provides the algorithm with exploitation. Mathematical modeling of these two phases is described as stepdown.

To maintain surviving, individuals in any swarm should move toward food sources and distract the enemy’s attention from giving harms to themselves. Taking these two behaviors into account, position updating of individuals in swarms is done by five factors such as (1) separation, (2) alignment, (3) cohesion, (4) attraction to food, and (5) distraction from enemy. The following describes each of these behaviors mathematically.

  1. 1.

    Separation

The separation is computed by Eq. 25.

$$S_{i} = - \mathop \sum \limits_{j = 1}^{N} X - X_{j}$$
(25)

where \(X\) is the position of the current individual, \(X_{j}\) speaks for the jth individual in the neighborhood and \(N\) is the count of neighboring individuals.

  1. 2.

    Alignment

Alignment can be computed by the following expression.

$$A_{i} = \frac{{\mathop \sum \nolimits_{j = 1}^{N} V_{j} }}{N}$$
(26)

where \(V_{j}\) shows the velocity of jth neighboring individual.

  1. 3.

    Cohesion

Cohesion is represented as follows.

$$C_{i} = \frac{{\mathop \sum \nolimits_{j = 1}^{N} X_{j} }}{N} - X$$
(27)
  1. 4.

    Attraction toward food source

This behavior is mathematically given by Eq. 28 with \(X^{ + }\) being the position of a food source.

$$F_{i} = X^{ + } - X$$
(28)
  1. 5.

    Distraction from enemy

Mathematical concept for such a distraction outwards from an enemy is presented in Eq. 29 with \(X^{ - }\) being the position of the enemy.

$$E_{i} = X^{ - } + X$$
(29)

In DSA, the behavior of dragonflies is considered dependent on the weighted combination of these five types of attitudes. To update the position of dragonflies and mimic their movements in a search space, two vectors, namely step (\(\Delta X\)) and position (\(X\)), are generated. The former is developed analogous to the velocity vector in PSO. The step vector is liable for the movement direction of dragonflies and represented by

$$\Delta X_{t + 1} = \left( {sS_{i} + aA_{i} + cC_{i} + fF_{i} + eE_{i} } \right) + w\Delta X_{t}$$
(30)

where \(s\), \(a\), \(c\), \(f\) and \(e\) are the weights of the corresponding behaviors, \(i\) is for the ith individual, \(w\) is the inertia weight, and \(t\) is the current iteration.

After calculating the step vector, the position vector is calculated in the same way PSO uses as depicted in Eq. 31.

$$X_{t + 1} = X_{t} + \Delta X_{t + 1}$$
(31)

Using different separation, alignment, cohesion, food and enemy factors (\(s\), \(a\), \(c\), \(f\), and \(e\)), it is possible in DSA to achieve different explorative and exploitative behaviors during the course of optimization. Dragonflies’ neighbors are also very significant, so a neighborhood with a particular radius is considered around every dragonfly in DSA. Given this, by increasing the radii of neighboring solutions proportional to the number of iterations, transitions between exploration and exploitation can be made in the algorithm. Another way to have a good balance between exploration and exploitation is to tune the swarming factors (\(s\), \(a\), \(c\), \(f\) and \(e\)) besides the inertia weight (\(w\)) adaptively during optimization.

To enhance the randomness, stochasticity and explorative behavior of the artificial dragonflies once no neighboring solutions exist, a random walk (Lévy flight) is employed in DSA using the following expression.

$$X_{t + 1} = X_{t} + {\text{L\'e vy}}\left( d \right)\Delta X_{t}$$
(32)

where \(t\) is the current iteration, \(d\) is the dimension of the position vector, and Lévy flight is:

$${\text{L\'evy}}\left( x \right) = 0.01 \cdot \frac{{r_{1} \cdot \sigma }}{{\left| {r_{2} } \right|^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \beta }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\beta $}}}} }}$$
(33)

In Eq. 33, \(r_{1}\) and \(r_{2}\) are random numbers in the range [0, 1], \(\beta\) is a constant, and \(\sigma\) is derived using the following formula.

$$\sigma = \left( {\frac{{\varGamma \left( {1 + \beta } \right) \cdot \sin \left( {\frac{\pi \beta }{2}} \right)}}{{\varGamma \left( {\frac{1 + \beta }{2}} \right) \cdot \beta \cdot 2^{{\left( {\frac{\beta - 1}{2}} \right)}} }}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \beta }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\beta $}}}}$$
(34)

where \(\varGamma \left( x \right) = \left( {x - 1} \right)!\).

For convenience, the pseudocode representation of DSA is depicted in Algorithm 1.

Algorithm 1: Pseudocode representation of DSA

figure a

The results reported in (Seyedali 2016) proved that DSA is able to offer high exploration and high exploitation thanks to its efficient search model based on the identified static and dynamic swarming behaviors of dragonflies. Implementation of such behaviors is easy with only simple mathematical operations to code. Yet it is important to emphasize that DSA and/or its modified version is not the main focus of this paper, but our main contribution is to instead design a unique control scheme for supplementary controller that has not been considered so far in LFC studies. For proper gain adjustment, we prefer the DSA technique as a means to other existing metaheuristics owing to its promising features depicted above and its rare application to address LFC problem. For further details and descriptive figures of DSA, the readers are kindly advised to refer the DSA’s original paper (Seyedali 2016).

5 Simulated results and discussion

To recognize the ability and efficacy of DSA tuned FOPI–FOPD cascade controller, MATLAB/Simulink software version 9.3.0 (2017b) is used to simulate the EPS models under study and obtain the dynamic responses of the systems for a variety of operating scenarios. The simulation sampling-interval is tuned to \(T_{\text{s}} = 1\) ms. The magnitude and location of SLP are selected basing on the works benchmarked for a fair comparison. The tolerance band for calculating settling time \(T_{\text{s}}\) of the responses is defined as 2% of the given SLP for all EPS models in the current study, i.e. if SLP is assumed as 1%, then \(T_{\text{s}}\) is calculated in tolerance band of \(\pm 0.02 \times 0.01 = \pm 0.0002\). The time range considered for the computation of \(J_{\text{ITAE}}\) is the simulation time shown on the plots. The optimizer, DSA, is run in an.m.file script and this file is connected to the Simulink environment for cost function evaluation. According to the results obtained from experiments made on five simulated EPSs, the results in this section have been analyzed in four subsections. In each subsection, a number of studies that we believe are able to challenge the designed controller have been chosen for comparison to check how competitive the proposed approach is. In DSA, the population size (number of search agents) is 50 and the number of iterations is tuned to 50. Optimization process with DSA is repeated 30 times for each model and the final best solution over 30 runs is set as the controller parameters used in simulations.

5.1 Two-area non-reheat thermal power system

The model of this system is shown in Fig. 1a and the relevant system parameters can be found in “Appendix A.1” section. Each area, rigged by FOPI–FOPD cascade controller, has one generating unit based on non-reheat thermal plant. The parameters of FOPID and cascade FOPI–FOPD controllers are optimized by DSA and \(J_{\text{ITAE}}\) considering a 10% SLP at t = 0 in area-1. The final controller parameters along with \(T_{\text{s}} /J_{\text{ITAE}}\) results of frequency and tie-line power deviations are displayed in Table 2. For comparison purpose, the respective data offered by other recent studies based on BFOA (Ali and Abd-Elazim 2011), hBFOA-PSO (Panda et al. 2013) and DE (Rout et al. 2013) optimized PI controllers, PID and 2DOF controllers tuned by teaching learning-based optimization (TLBO) algorithm (Sahu et al. 2016), hybrid PSO and pattern search (PS) optimized fuzzy PID controller (Sahu et al. 2015) and improved stochastic fractal search (ISFS) algorithm-based PID controller (Çelik 2020) is also gathered in Table 2. An entry given by “n/a” in any of the following tables means not available. It is notable in Table 2 that DSA tuned FOPI–FOPD cascade controller is superior to all the techniques as minimum \(J_{\text{ITAE}}\) value (\(J_{\text{ITAE}} = 0.0180\)) is achieved compared to BFOA (\(J_{\text{ITAE}} = 1.8270\)), DE (\(J_{\text{ITAE}} = 0.9911\)) tuned PI controller, TLBO tuned PID controller (\(J_{\text{ITAE}} = 0.2452\)), TLBO tuned 2DOF PID controller (\(J_{\text{ITAE}} = 0.0269\)), hPSO-PS tuned fuzzy PID controller (\(J_{\text{ITAE}} = 0.1438\)) and DSA tuned FOPID controller (\(J_{\text{ITAE}} = 0.0778\)). This accordingly bestows that the proposed approach reaches better performance since minimum settling times of frequency and tie-line power deviations are obtained compared to other indicated solutions. Considering the settling times of \(\Delta f_{1}\) and \(\Delta P_{\text{tie}}\) signals, the second best performer in this case is DSA tuned FOPID controller. Here, it is worth mention that hBFOA-PSO algorithm uses a more comprehensive cost function with three goals: minimizing ITAE, maximizing the minimum damping ratio and minimizing the settling times of \(\Delta f_{1}\), \(\Delta f_{2}\), and \(\Delta P_{\text{tie}}\) signals. Similarly, ISFS optimizes the ITAE of frequency and tie-line power deviations, and also the time rates of changes in these deviations, causing a process of computationally expensive cost function calculation.

Table 2 Optimized controller parameters and \(T_{\text{s}} /J_{\text{ITAE}}\) results of test system-1
Full size table

The comparative time-domain system responses after a 10% SLP at t = 0 in area-1 are illustrated in Fig. 7, from which the settling times reported in Table 2 are measured considering a tolerance band of ± 0.002. Notice that the responses with 2DOF PID and fuzzy PID controller are not shown in Fig. 7 because the respective controllers could not be designed due to their complex structures. The simulated results presented here show that the steady state performance is the same for all the controllers since frequency deviation of each area and tie-line power deviation ceases to zero in the steady state. However, there are notably significant differences in their transient responses. As seen, the response with DSA optimized FOPI–FOPD cascade controller is the pioneer of the other approaches since it is driven back to zero hastily after a far smaller peak undershoot. This is followed by the response with DSA tuned FOPID controller.

Fig. 7
figure 7

Comparison of time-domain responses for test system-1 after a 10% SLP in area-1 a \(\Delta f_{1}\) b \(\Delta f_{2}\) c \(\Delta P_{\text{tie}}\)

Full size image

5.2 Two-area non-reheat thermal power system with GDB nonlinearity

To access the effectiveness of DSA tuned FOPI–FOPD cascade controller in a more realistic case, the nonlinear model of two-area non-reheat thermal EPS exploiting the nonlinear source of governor dead band (GDB) nonlinearity is investigated in this section. Transfer function model of this system is shown in Fig. 1b and the nominal system parameters are given in “Appendix A.2” section. The controller parameters are optimized when there is a SLP of 1% applied to area-1 at t = 0. The optimized controller parameters and the corresponding system results are reported in Table 3. To demonstrate the supremacy of our proposal, results of DSA optimized FOPID controller along with other well-regarded studies such as hBFOA-PSO (Panda et al. 2013) and CRAZYPSO algorithm (Gozde and Taplamacioglu 2011) optimized PI controllers, DE (Mohanty et al. 2014) and ISFS (Çelik 2020) optimized PID controllers and hPSO-PS tuned fuzzy PID controller (Sahu et al. 2015) for the identical EPS are also provided in Table 3. Note that CRAZYPSO and DE-based approaches adopt different and more complex cost functions compared to the \(J_{\text{ITAE}}\) itself. It is noticeable from Table 3 that the \(J_{\text{ITAE}}\) value offered by DSA tuned FOPI–FOPD cascade controller is \(J_{\text{ITAE}} = 0.0034\), which is smaller than that by DSA tuned FOPID (\(J_{\text{ITAE}} = 0.0121\)) and hPSO-PS tuned fuzzy PID (\(J_{\text{ITAE}} = 0.3471\)) controllers. It is also clear from Table 3 that settling times of \(\Delta f_{1}\), \(\Delta f_{2}\), and \(\Delta P_{\text{tie}}\) signals with the proposed method are notably improved compared to all other approaches.

Table 3 Optimized controller parameters and \(T_{\text{s}}/J_{\text{ITAE}}\) results of test system-2
Full size table

The comparative time-domain system responses are given in Fig. 8. It can be seen from Fig. 8 that the SLP in area-1 is rejected very fast in presence of the proposed controller. Thus, the oscillations and time-domain characteristics like settling time/undershoot/overshoot, which are observed to be severe in the existing solutions, are reduced effectively. The second best performance for this system belongs to the DSA tuned FOPID controller.

Fig. 8
figure 8

Comparison of time-domain responses for test system-2 after a 1% SLP in area-1 a \(\Delta f_{1}\) b \(\Delta f_{2}\) c \(\Delta P_{\text{tie}}\)

Full size image

5.3 Three-area hydrothermal power system with GRC

The model of this system is depicted in Fig. 2 and the applicable system parameters are provided in “Appendix A.3” section. The controller parameters are optimized using DSA by minimizing \(J_{\text{ITAE}}\) when a 1% SLP has been enforced in all the three areas simultaneously at t = 0. The optimized gains of FOPI–FOPD cascade controller and the corresponding system results are tabulated in Table 4. To highlight the controller talent, the obtained results are contrasted with the results of DSA optimized FOPID controller, integral controller (Nanda et al. 2006), hBFOA-PSO optimized PI (Panda et al. 2013) and ISFS optimized PID (Çelik 2020) controllers for the same EPS. From Table 4, it is obvious that DSA optimized FOPI–FOPD cascade controller achieves smaller value of \(J_{\text{ITAE}}\) (\(J_{\text{ITAE}} = 147.56\)) than DSA optimized FOPID controller (\(J_{\text{ITAE}} = 156.32\)), verifying that FOPI–FOPD cascade controller outperforms FOPID controller in this scenario. Also, taking the settling times of \(\Delta P_{{{\text{tie}}1}}\) and \(\Delta P_{{{\text{tie}}2}}\) responses the same for ISFS optimized PID and DSA optimized cascade FOPI–FOPD controllers, DSA optimized FOPI–FOPD cascade controller is the most promising controller and yields to significant reduction in settling time in comparison with other approaches.

Table 4 Optimized controller parameters and \(T_{\text{s}}/J_{\text{ITAE}}\) results of test system-3
Full size table

The system dynamic responses are comparatively shown in Fig. 9. Employing the proposed controller, the magnitude of sustained oscillations initially observed is suppressed hastily with time, permitting the responses to converge very early to the reference zero steady state value. As a result, DSA tuned FOPI–FOPD cascade controller is found capable of acting skillfully in multi-area EPS with disruptive effect of GRC.

Fig. 9
figure 9

Comparison of time-domain responses for test system-3 after a 1% SLP in all areas a \(\Delta f_{1}\) b \(\Delta f_{2}\) c \(\Delta f_{3}\) d \(\Delta P_{{{\text{tie}}1}}\) e \(\Delta P_{{{\text{tie}}2}}\) f \(\Delta P_{{{\text{tie}}3}}\)

Full size image

5.4 Extension to multi-source power system

  1. a.

    Multi-source single-area power system

At the first instant, performance comparisons are investigated on multi-source single-area EPS depicted in Fig. 3. Participation factors of generating sources of thermal, hydro and gas units are set to 55%, 32% and 12%, respectively, in parallel with the literature works. Other system parameters are given in “Appendix A.4” section. To better illustrate the advanced tuning performance of proposed DSA technique over the other existing algorithms such as optimal output feedback controller (Parmar et al. 2012), DE (Mohanty et al. 2014), TLBO (Barisal 2015) and modified GWO (MGWO) (Padhy et al. 2017), the system is first considered to be driven through distinct integral controllers only. The gains of these controllers are then optimized employing DSA and \(J_{\text{ITAE}}\) by considering a 1% SLP. DSA tuned controller parameters and the respective numerical results of multi-source single-area EPS with integral controllers are delineated in Table 5. The corresponding solutions pertaining to the above cited studies are also provided in Table 5. It is easily noted from Table 5 that DSA outperforms the competitive approaches since less ITAE value is acquired by DSA (\(J_{\text{ITAE}} = 0.4507\)) compared to optimal controller (\(J_{\text{ITAE}} = 0.9934\)), DE (\(J_{\text{ITAE}} = 0.5165\)), TLBO (\(J_{\text{ITAE}} = 0.5135\)) and MGWO (\(J_{\text{ITAE}} = 0.4514\)), putting forward that the tuning performance of DSA is better than the rest. The best algorithm after DSA is MGWO, which found more or less the same result as DSA. As a result, minimum settling time of frequency deviation is got with DSA and MGWO compared to other optimizers.

Table 5 Optimized integral controller parameters and \(T_{\text{s}}/J_{\text{ITAE}}\) results of test system-4
Full size table

The resulting frequency deviation response following a 1% SLP for the same EPS and identical controller is shown in Fig. 10. It is found that the settling time of DSA- and MGWO-based responses is shorter than others as highlighted by the marks “ ”. The zoom views of the deviations in Fig. 10b also show that DSA tuned integral controller is able to provide smaller peak overshoot than its closest competitor, MGWO optimized integral controller. This improvement observed in the response can be attributed to the less value of \(J_{\text{ITAE}}\) achieved by DSA.

Fig. 10
figure 10

Comparison of frequency deviation responses after a 1% SLP for test system-4 using integral controllers tuned by different approaches

Full size image

To improve the dynamic behavior of test system-4, integral controller is replaced by the designed FOPI–FOPD cascade controller. DSA optimized controller parameters and the respective system results with FOPI–FOPD cascade controller are given and compared in Table 6 with that of DSA tuned FOPID controller and other available results based on recently proposed MGWO tuned PI, PID and cascade PIPD controllers (Padhy et al. 2017). The results in Table 6 showcase easily the excellence of DSA tuned FOPI–FOPD cascade controller in minimizing \(J_{\text{ITAE}}\) value to 0.0070 from MGWO tuned PI (\(J_{\text{ITAE}} = 0.0572\)), PID (\(J_{\text{ITAE}} = 0.0375\)), cascade PIPD (\(J_{\text{ITAE}} = 0.0292\)) and DSA tuned FOPID (\(J_{\text{ITAE}} = 0.0187\)) controllers. Hence, improved settling time of \(\Delta f\) response is achieved by our proposal in comparison with other alternatives.

Table 6 Optimized controller parameters and \(T_{\text{s}}/ J_{\text{ITAE}}\) results of test system-4
Full size table

To investigate the time-domain simulation results, a 1% SLP is applied to the system at the instant t = 0 and system frequency deviations with different optimized controllers are depicted in Fig. 11. Recalling from the previous analysis that the search performance of DSA and MGWO is similar, then it may be noted that the designed FOPI–FOPD cascade controller performs amazingly better than other indicated controllers in substantially boosting the system dynamic response.

Fig. 11
figure 11

Comparison of frequency deviation responses after a 1% SLP for test system-4

Full size image
  1. b.

    Two-area multi-source power system

Our last analysis for corroborating the performance of proposed DSA tuned FOPI–FOPD cascade controller is toward a more realistic EPS model where a total of six generating units are cooperating to supply a given load under different circumstances. The transfer function model of this system is shown in Fig. 4 and the nominal system parameters are provided in “Appendix A.5” section. In this case, the controller parameters are optimized for a 2% SLP enforced in area-1. The optimized controller parameters along with some system results using the designed controller are reported in Table 7. Moreover, comparisons with other approaches such as DE (Mohanty et al. 2014), MGWO (Padhy et al. 2017) and hSFS-PS (Padhy and Panda 2017) optimized PID controllers as well as DSA optimized FOPID controller are also presented. Table 7 divulges that less \(J_{\text{ITAE}}\) value is achieved with DSA tuned FOPID controller (\(J_{\text{ITAE}} = 0.1557\)) in comparison with DE (\(J_{\text{ITAE}} = 1.0566\)), MGWO (\(J_{\text{ITAE}} = 0.9197\)) and hSFS-PS (\(J_{\text{ITAE}} = 0.3818\)) tuned PID controllers. However, the value of \(J_{\text{ITAE}}\) offered by the proposed DSA tuned FOPI–FOPD cascade controller is minimum (\(J_{\text{ITAE}} = 0.0461\)), resulting in smaller settling times of \(\Delta f_{1}\), \(\Delta f_{2}\) and \(\Delta P_{\text{tie}}\) responses. As a result, enriched system performance is gained with DSA tuned FOPI–FOPD cascade controller over all other competing approaches.

Table 7 Optimized controller parameters and \(T_{\text{s}}/J_{\text{ITAE}}\) results of test system-5
Full size table

Comparative dynamic responses of the two-area multi-source EPS for a 2% SLP occurring in area-1 at t = 0 are shown in Fig. 12. Following the critical observation of Fig. 12, it is recognized that the system performance offered by the proposed approach is more prolific in every respect of settling time/undershoot/overshoot than that of DSA tuned FOPID controller and the others prevalent in the literature.

Fig. 12
figure 12

Comparison of time-domain responses for test system-5 after a 2% SLP in area-1 a \(\Delta f_{1}\) b \(\Delta f_{2}\) c \(\Delta P_{\text{tie}}\)

Full size image

6 Conclusions

FOPI–FOPD cascade controller is originally introduced in this paper as an effective remedy for LFC problem of diverse single-/multi-area single-/multi-unit EPSs. To avoid improper gain scheduling, DSA, as the recently proposed powerful optimizer, is adopted to tune the designed controller parameters using \(J_{\text{ITAE}}\). In each of the test cases including linear two-area non-reheat thermal EPS, nonlinear two-area non-reheat thermal EPS with GDB nonlinearity, three-area hydrothermal EPS considering GRC effect, multi-source single-area EPS and two-area multi-source EPS, the performance of the proposed approach is checked by contrasting its responses with that of DSA tuned FOPID controller and also well-recognized contributions recently appeared in the field. The results carefully collected have proved the higher credit of DSA tuned FOPI–FOPD cascade controller compared to DSA tuned FOPID and other existing solutions in terms of minimum value of \(J_{\text{ITAE}}\) and improved settling time/undershoot/overshoot of deviation in area frequency and tie-line power responses. On the other hand, DSA is found to be effective and robust in searching for optimal controller parameters and it is authenticated that the designed DSA tuned FOPI-FOPD cascade controller can be thought of as a prolific solution, contributing notably to LFC performances of several EPSs.

For future works, a number of search directions can be advised for possible further improvements. In lieu of DSA, other latest metaheuristics may be tried out to optimize the proposed controller gains. High voltage direct current (HVDC) link and plug in electric vehicles (PEV) could be also included in the studied models as an axillary service in addition and parallel with existing AC tie-line. Moreover, modifying the existent controllers with taking benefits of fractional calculus would be worthy to investigate.