(1 + PD)-PID cascade controller design for performance betterment of load frequency control in diverse electric power systems

Abstract

In our world of today developing incredibly fast, load frequency control (LFC) is an indispensable and vital element in increasing the standard of living of a country by providing a good quality of electric power. To this end, rapid and notable development has been recorded in LFC area. However, researchers worldwide need for the existence of not only effective but also computationally inexpensive control algorithm considering the limitations and difficulties in practice. Hence, this paper deals with the introduction of (1 + PD)-PID cascade controller to the relevant field. The controller is simple to implement and it connects the output of 1 + PD controller with the input of PID controller where the frequency and tie-line power deviation are applied to the latter controller as feedback signals also, which is the first attempt made in the literature. To discover the most optimistic results, controller gains are tuned concurrently by dragonfly search algorithm (DSA). For the certification purpose of the advocated approach, two-area thermal system with/without governor dead band nonlinearity is considered as test systems initially. Then single/multi-area multi-source power systems with/without a HVDC link are employed for the enriched validation purpose. The results of our proposal are analyzed in comparison with those of other prevalent works, which unveil that despite its simplicity, DSA optimized (1 + PD)-PID cascade strategy delivers better performance than others in terms of smaller values of the chosen objective function and settling time/undershoot/overshoot of the frequency and tie-line power deviations following a step load perturbation.

1 Introduction

In the face of increasing power demand of the today’s world, it is required for a huge number of different generating units to interconnect through existing transmission lines called tie-lines. Controlling of large interconnected power systems (PSs) in consideration of increasing size and complexity of PS, and numerous external/internal disturbances occurring unpredictably is undoubtedly one of the most challenging problems experienced in electric PSs. Even the load demand is continually fluctuating on PS and the alteration in load demand of any area(s) results in transient deviation in frequency, generation and tie-line power flow throughout the PS. Thus, the mismatch between the abrupt demanded power and the temporary insufficient generation is the main reason of these deviations. In a stable, reliable and secured PS, frequency and tie-line power flowing between neighboring areas are mandatory to bring back to their predefined or scheduled values quickly. This is accomplished by equalizing the active power output of generating units to the PS power demand plus losses. Such a control mechanism is named as load frequency control (LFC). LFC, in other words, allows the synchronous generators to regulate their generations in response to the load demands, as a result of which area frequency and tie-line power oscillations/errors are ensured to converge to zero. Improper design of LFC may undermine the system performance causing unwanted large oscillations in generation, area frequency and tie-line power flows which may enforce the system toward instability and loss of synchronism. In view of the above discussion, an advanced and effective control strategy is an inevitable requirement for LFC of PSs. Additionally, suitability and practical potential of a LFC controller in a real-time implementation is another sought-after feature for engineering commissioning.

Pointed out from the comprehensive literature review is that there has been appeared enormous volume of highly cited research works in the field of LFC during the last few decades. Each is endeavoring for further development and can be regarded as one successive and more effective strategy than its earlier counterparts. Some of the recently published studies employing PI/PID structured controllers are bacterial foraging optimization algorithm (BFOA) [1], hybrid BFOA and particle swarm optimization (PSO) (hBFOA-PSO) algorithm [2], fire fly algorithm (FA) [3] optimized PI controllers, the lozi map-based chaotic algorithm [4], genetic algorithm (GA)/differential evolution (DE) [5], ant colony optimization (ACO) [6], improved stochastic fractal search (ISFS) algorithm [7], quasi-oppositional grey wolf optimization (QOGWO) algorithm [8], quasi-oppositional harmony search (QOHS) algorithm [9], differential search algorithm (DSA) [10], DE [11], symbiotic organisms search (SOS) algorithm [12, 13] based PID controllers, quasi-oppositional SOS (QOSOS) [14], artificial bee colony (ABC) [15], backtracking search algorithm (BSA) [16], hybrid FA-pattern search (hFA-PS) [17] and grey wolf optimization (GWO) [18] optimized PI/PID controllers, DE algorithm based I/PI/PID configured controllers [19], jaya algorithm tuned PID with first-order low-pass filter [20]. Classical PI/PID structured controllers are simple to code and perform satisfactorily at specific conditions; however, with parameters tuned at a definite working circumstance, they may not provide the desired system performance under continuously changing load demands, which is most often the case. To ameliorate control performance, other advanced control schemes based on sliding modes [21, 22], H-infinity [23], fractional calculus theory [24,25,26,27,28,29,30,31], artificial neural network approach [32], fuzzy logic theory [29, 30, 33,34,35,36,37,38,39], adaptive neuro fuzzy inference system (ANFIS) [40, 41], nonlinear disturbance observer [42], disturbance observer aided optimized fractional‐order three‐degree‐of‐freedom tilt‐integral-derivative (FO3DOF TID) [43] are recorded in the relevant field. This class of controllers although show favorably increased performance by managing the deficiencies of classical controllers, they are relatively hard to code, addicted to expert intervention and many of them lead to complicated and computationally heavy control laws which may not therefore meet the expectations of engineering commissioning from the view point of practice.

The cascade control concept is famous for its fast rejection of disturbance before it is emitted to other parts of the system and as underscored by many researches a definite cascaded control scheme has potential to offer better performance than the classical feedback controller [44]. Thus, cascade connection of different PID control schemes in attempting to satisfy the requirement of effective and practical controller synthesis has attracted the attention of many scholars recently. In this regard, hybrid stochastic fractal search and local unimodal sampling (hSFS-LUS) algorithm and adaptive differential evolution based multistage PDF plus (1 + PI) controller [45, 46], modified GWO technique based cascade PI-PD controller [47], flower pollination algorithm (FPA) optimized PI-PD cascade controller [48], hybrid stochastic fractal search and pattern search technique (hSFS-PS) based cascade PI-PD controller [49], bat algorithm (BA) optimized PD-PID cascade controller [50], sine–cosine algorithm (SCA) tuned PD-PID with double derivate filter [51] are proposed for LFC of different PSs. The simulated system responses owing to these cascaded control schemes are found to produce competing and worth-appreciating control effort in the area of interest. However, to the authors’ knowledge, system responses, displayed in these works, have still some room for further enrichment considering time-domain performance criteria like settling time, peak undershoot and peak overshoot. Hence, tempted by the simplicity of PI and PID structured controllers and impressive performance of cascade controllers suggested in [28,29,30,31,32], the current study revisits LFC problem by introducing a new cascade controller named as (1 + PD)-PID, whose performance assessment has not been yet evaluated so far. Another salient difference of (1 + PD)-PID cascade control scheme over the existing ones is that the input of PID controller is comprised of the output of 1 + PD controller ordinarily and also both the signals of frequency and tie-line power deviations together for the first time in the literature. This way, the controller can produce a control signal by directly knowing the states of those important signals for fast disturbance rejection. Extensive results on simulating various PS models demonstrate that the advocated approach performs very well although relatively simpler to implement than most of high-performance controllers present in the relevant literature.

In view of the literature inspection, numerous nature-inspired optimization techniques have been employed in LFC studies for a proper gain adjustment to receive the most possible benefit from controllers proposed in them. Exploitation (capacity to concentrate the search in the vicinity of known healthy solutions) and exploration (capacity to generate individuals in as-yet unvisited regions of the search space) are two vital characteristics of metaheuristics expected to be balanced for optimal search performance [52]. Of the algorithms able to offer a good trade-off between exploitative and explorative ability, dragonfly search algorithm (DSA) is a favorable approach and has proven superior over many other algorithms in solving optimization problems in various fields and areas such as machine learning [53], neural network [54], feature selection [55, 56], image processing [57,58,59] and engineering [60,61,62,63,64,65,66]. DSA is a swarm intelligence based algorithm, simulating the individual and social behavior of one of the swarming fancy insects called dragonflies [60]. It is explored that dragonflies have unique and rare swarming intelligence compared with other creatures in nature. They swarm just for two aims: hunting and migration. Hunting relates to static (feeding) swarm whereas migration is connected with dynamic (migratory) swarm. Based on such identified and imitated characteristics of dragonflies’ swarms, DSA can succeed in searching for optimum point by speedier convergence rate and effective local minima avoidance. The depicted features of DSA, as well as its few utilization in LFC problem [61,62,63], are the reason of encouragement to further investigate its involvement in performing the optimization task of the new controller proposed in the current study.

As a result of the available circumstances depicted above, growing interest and rapid development have been witnessed in LFC area, contributing numerous powerful and notable control strategies along with different optimization techniques for the task of controller optimization. Nonetheless, most of the existing controllers are either unfavorable against changeable operating condition or suffering from complex control laws in addition to demanding several tunable design parameters. Proposing a controller that avoids the shortcomings of the existing ones while at the same time offering higher or competing system performance is notably a challenger and the main intention of this research paper. Table 1 endeavors to discriminate the proposed approach from the works prevalent in the literature. Inspecting the activities in Table 1 elicits that cascade (1 + PD)-PID structured controller is a new one that has not been yet considered so far in LFC of single/multi-source PSs. Its design is simple and does not demand tuning of many controller parameters. Furthermore, it is the only one that uses three error signals of area control, area frequency and tie-line power.

Table 1 Comparison of the current and published works

In conclusion, contribution, motivation and significance devoted to this paper can be summarized as:

• 1. To design and simulate a newly structured, simple (1 + PD)-PID cascade controller for LFC of diverse electric PSs.

• 2. To benefit from recently introduced DSA approach with an aim to find out optimal controller gains.

• 3. To examine the performance of DSA tuned (1 + PD)-PID cascade controller and reveal its credit and advantages in comparison with different types of controllers previously emerged in the literature.

• 4. To scrutinize the robustness of DSA approach statistically in solving LFC problem

The paper is documented as follows: Sect. 2 describes the studied PS models. The structure of (1 + PD)-PID cascade controller and its design from the optimization point of view are introduced in Sect. 3. An overview of DSA technique is achieved in Sect. 4. Section 5 is dedicated to in-depth simulation results obtained and their evaluation with reference to the available results. In this section, statistical investigation of the obtained results is also made to showcase the robustness of DSA. Finally, some conclusions and possible research directions for future works are shared in Sect. 6.

2 Power systems under investigation

In order to evaluate the performance of our proposal, different PS models are established and studied in this section. Among those are two-area non-reheat thermal PS, two-area non-reheat thermal PS incorporating the effect of governor dead band (GDB) nonlinearity, single area multi-source PS, two-area multi-source PS and two-area multi-source PS assisted by high voltage direct current (HVDC) link. This set of systems has been selected to challenge the proposed controller in many aspects, giving the possibility to elucidate its efficacy and contribution comprehensively. There are also other cooperative PS models in the literature where power sources, power grids and loads are all contributing to LFC task in a distributed way with the hope of boosting the system frequency regulation [67]. In such systems, power sources are traditional generators driven by a secondary controller and loads can be comprised of additional devices such as energy storage units and grid-friendly appliances controlled via a distributed leader-following consensus cooperated with the chosen secondary controller. As our main intention is toward rather designing a new controller structure, accomplishing LFC in a distributed way falls beyond the scope of this paper.

The major role of secondary controllers in LFC is to reinstate balance between each area load and generation. This is achieved when the control effort assures:

• Frequency at the specified value

• Net interchange tie-line power in-between nearby areas at specified values

Matlab/Simulink software version 9.3.0 (2017b) has been utilized to simulate and obtain the time-domain responses for deviations in area frequency ($\Delta f$) and tie-line power flow ($\Delta {p}_{tie}$) following a step load perturbation (SLP). The nominal parameter values of the systems are provided in Appendix and the list of symbols shown on the studied models is depicted in Nomenclature table as stepdown.

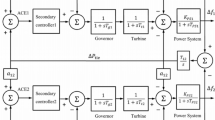
2.1 Two-area non-reheat thermal power system

Transfer function model of an interconnected two-area non-reheat thermal PS, which is exploited many times in the relevant field, is depicted in Fig. 1. For convenience, this system is assigned from now on as test system-1. As shown, each generating unit is composed of a secondary controller, mechanical hydraulic-type governor and non-reheat-type steam turbine. Here, equivalent inertia and damping constant of the whole rotating system are signified as power system. All the components are represented by a first-order transfer function model with a gain and a time constant. The system has generators in both areas with a rated capacity of 2000 MW.

Fig. 1

Transfer function model of an interconnected two-area non-reheat thermal power system

By acting on area control signal (ACE), which is the combination of tie-line power deviation and frequency deviation weighted by $B$, the secondary controller of each area produces a control signal. In other words, it sets reference power of the generating units and accordingly their power generation to maintain the harmony between the generation and demanded power, which allows to preserve frequency and tie-line power flow within recommended edges. Given this, following a SLP, ACE deviates from zero and it should be driven back hastily and ensured at zero in steady state at all times. This is achievable by a well-designed high-performance secondary controller.

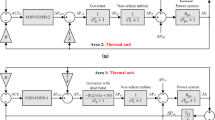
2.2 Two-area non-reheat thermal power system with nonlinearity

In order to make the LFC research more realistic, we need to think all the possible system nonlinearities and include them in the model. It can be concluded that one of the most utilized nonlinear sources in PSs is GDB nonlinearity, which is described by the total amplitude of a maintained speed change within which valve position does not vary [14]. GDB can result in speed pulsation before the valve position changes, thus it causes oscillations in the system with a natural frequency of around ${f}_{0}=\frac{1}{2}$ Hz. To identify the GDB’s influence on system dynamics, a describing function technique that considers the first three terms of Fourier expansion is realized to find the linear transfer function of governor with nonlinearity and it is given by Eq. 1.

$${G}_{\mathrm{g}}\left(s\right)=\frac{-\left(0.2/\pi \right)s+0.8}{{\mathrm{sT}}_{\mathrm{g}}+1}$$

(1)

The transfer function model of this system, which is named as test system-2, is depicted in Fig. 2. This PS works similar to the previous system. Differently, there is only a nonlinear source in the system resulting from GDB mechanism.

Fig. 2

Transfer function model of an interconnected two-area non-reheat thermal power system with GDB nonlinearity

Since the two areas are considered the same in test system-1 and test system-2, the secondary controllers in both areas can be assumed identical also so we engage with only one controller design in these systems.

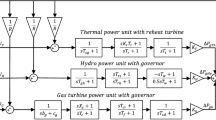
2.3 Single area multi-source power system

Regarding our research on multi-source PS, a single area PS designated as test system-3 is assumed at the first instance. The transfer function model of test system-3 is provided in Fig. 3. As shown, the system has a single area with three different generating units of type reheat thermal, hydro and gas, which are outfitted by speed governor control mechanisms. Each generating unit has its own regulation parameter and participation factor like ${K}_{\mathrm{T}}$, ${K}_{\mathrm{H}}$ and ${K}_{\mathrm{G}}$, which decides the contribution of a unit to the total load on the system and involves economic load dispach. The sum of participation factors of all units should equal to unity. To counteract variations in system frequency expeditiously, reference power settings of the three generating units are carried out by the individual secondary controllers. In LFC analysis of such a system, our attention is devoted to concerted performance of all generators in the system.

Fig. 3

Transfer function model of a single area multi-source power system

2.4 Two-area multi-source power system with AC and AC-DC tie-lines

In this subsection, a two-area multi-source interconnected power plant shown in Fig. 4 is studied to assess the performance of the proposed controller in a more realistic condition. As depicted, each area has generation from reheat thermal, hydro and gas units and the amount of generation of each unit is controlled by the individual secondary controllers. Like the previous PS, the generators participate in the LFC task depending on their participation factors and the summation of participation factors of all generators in a control area is equal to unity. This system is the two-area version of the previous system where two neighboring areas are interconnected together via a tie-line to exchange the power between them, similar to test systems 1 and 2. Thus, the explainations given for the previous systems are valid for this system also.

Fig. 4

Transfer function model of a two-area multi-source power system with AC and AC-DC tie-lines

Here, according to the position of the switch shown in Fig. 4, two cases as test system-4 and test system-5 are investigated. With the switch off, only AC tie-line is used for interconnection of two areas and HVDC link involves in the system in parallel with existing AC link when the switch is turned on. Ignoring any nonlinearities, the representation of a DC link is given by a first-order transfer function model with a gain of ${K}_{dc}$ and time constant of ${T}_{dc}$. HVDC links, in parallel with the present high voltage AC links, start to being used popularly in the LFC area for exchanging power amongst control areas. It is shown that HVDC link operating in parallel with traditional AC link not only provide environmental and economical usefulness but also assures electric power supply in better quality. It also increases the system robustness to small disturbances [33]. The schematic diagram of a two-area power plant interconnected via AC-DC parallel lines is visualized in Fig. 5.

Fig. 5

Schematic diagram of a two-area interconnected power plant with AC-DC parallel lines

3 The proposed approach

Our comprehensive literature inspection points out that the success of a LFC system depends strictly on three elements: structure of secondary controller, intelligent optimization algorithm to tune the controller parameters and performance index that the algorithm uses to evaluate the fitness of solutions. In this regard, many high-performance controllers based on sliding modes [21, 22], cascaded control [45,46,47,48,49,50,51], fractional order calculus [24,25,26,27,28,29,30,31], fuzzy logic controller [29, 30, 33,34,35,36,37,38,39], etc. have been acknowledged in the literature. Moreover, hybridization idea among these control mechanisms is another research avenue that is currently pulling the attention of researchers. Nonetheless, those proposals result in complicated and costly control laws and they are usually prone to many design parameters requiring a proper setting. In view of this, the current paper proposes a new control scheme called as (1 + PD)-PID cascade controller to solve LFC problem alternatively without facing the said problems of the earlier controllers. The details of the structure of (1 + PD)-PID cascade controller are firstly given and then its design from the perspective of optimization is described.

3.1 (1 + PD)-PID cascade controller structure

A unique cascade combination of 1 + PD and PID controllers named (1 + PD)-PID controller is considered and applied for the first time in LFC. As the controller uses 1 + PD and PID in order, it has the merits of classical PID controllers such as good performance, understandable structure, and simple engineering commissioning in real-time implementation, which make it one step ahead for the PS community compared with the complex control schemes found in the literature. Moreover, since the two controllers are incorporated in a cascade connection, it tends to reject disturbance sources fast before they spread out in the system. The structure of (1 + PD)-PID cascade controller is shown in Fig. 6.

Fig. 6

Structure of (1 + PD)-PID cascade controller

Another contribution of this controller over other cascade controller configurations proposed in the relevant field is that it not only uses the respective area control error (ACE) as input signal, but also benefits from two additional signals such as area frequency deviation ($\Delta f$) and tie-line power deviation ($\Delta {P}_{\mathrm{tie}}$) between neighboring areas that is equal to $\Delta {P}_{\mathrm{tie}\_\mathrm{actual}}-\Delta {P}_{\mathrm{tie}\_\mathrm{scheduled}}$. Therefore, to the authors’ best knowledge, the proposed control scheme has not been yet studied so far.

By acting on ACE, $\Delta f$ and $\Delta {P}_{\mathrm{tie}}$ signals, the controller produces the required load reference $\Delta {P}_{\mathrm{ref}}$, which is also the input signal for the PS. The ACE applicable for a single area and two-area PS can be given as

$$\mathrm{ACE}=-\Delta f(\mathrm{single-area-system})$$

(2)

$$\begin{array}{c}{\mathrm{ACE}}_{1}=\\ {\mathrm{ACE}}_{2}=\end{array}\left.\begin{array}{c}-{B}_{1}\Delta {f}_{1}-\Delta {P}_{\mathrm{tie}}\\ -{B}_{2}\Delta {f}_{2}+\Delta {P}_{\mathrm{tie}}\end{array}\right\}(\mathrm{two}-\mathrm{area-system})$$

(3)

where ${B}_{1}={B}_{2}=B$ is frequency response parameter, $\Delta {f}_{i}$ is frequency deviation/error in the ith control area and $\Delta {P}_{\mathrm{tie}}$ is tie-line power deviation/error between two nearby control areas.

The s-domain transfer functions of 1 + PD and PID controllers can be expressed by

$${G}_{1+\mathrm{PD}}\left(s\right)=1+{K}_{p1}+{\mathrm{sK}}_{\mathrm{d}1}$$

(4)

$${G}_{\mathrm{PID}}\left(s\right)={K}_{\mathrm{p}2}+\frac{{K}_{i}}{s}+{\mathrm{sK}}_{\mathrm{d}2}$$

(5)

where ${K}_{\mathrm{p}1}$, ${K}_{\mathrm{d}1}$, ${K}_{\mathrm{p}2}$, ${K}_{i}$ and ${K}_{\mathrm{d}2}$ are proportional, derivative, proportional, integral and derivative parameters, respectively. Thus, we have five degrees of freedom to design a (1 + PD)-PID cascade controller. To achieve optimum performance from this controller, simultaneous optimization of these five parameters is required and DSA is chosen in this paper to accomplish this task. ACE and u is the first controller’s input and output, respectively. Subtracting $\Delta f$ and $\Delta {P}_{\mathrm{tie}}$ from u at the summing point forms the reference signal for the second controller, and finally $\Delta {P}_{\mathrm{ref}}$ is obtained from the output of (1 + PD)-PID cascade controller, which can be mathematically stated by Eq. 6.

$$\Delta {P}_{\mathrm{ref}}=\left(\left\{\mathrm{ACE}\times \left(1+{K}_{\mathrm{p}1}+{\mathrm{sK}}_{\mathrm{d}1}\right)\right\}-\Delta f-\Delta {P}_{\mathrm{tie}}\right)\times \left({K}_{\mathrm{p}2}+\frac{{K}_{i}}{s}+{\mathrm{sK}}_{\mathrm{d}2}\right)$$

(6)

3.2 Design of (1 + PD)-PID cascade controller

3.2.1 Performance measure/objective function

To improve generation-load balance through LFC, the (1 + PD)-PID cascade controller acting as a secondary controller must be designed appropriately. The number of parameters to be tuned for the proposed (1 + PD)-PID cascade controller is 5. Setting these parameters by trial may import control performance far lower than the controller is capable when designed optimally. That is why, we take the design problem as an optimization problem by minimizing an objective function (${J}_{s}$). There are different error integrating objective functions like Integral Squared Error (ISE), Integral Absolute Error (IAE), Integral Time weighted Absolute Error (ITAE), and Integral Time weighted Squared Error (ITSE). Since the ITAE objective function yield controlled response with less settling time and damped oscillation, it is employed in LFC studies more frequently than its other alternatives [2, 16, 32, 33, 47]. Expression of ITAE for single area and two-area PS is given in Eqs. 7 and 8, respectively.

$${J}_{\mathrm{s}}=\mathrm{ITAE}=\underset{0}{\overset{{t}_{\mathrm{sim}}}{\int }}\left|\Delta f\right|.t.\mathrm{d}t$$

(7)

$${J}_{\mathrm{s}}=\mathrm{ITAE}=\underset{0}{\overset{{t}_{\mathrm{sim}}}{\int }}\left|{\Delta f}_{1}+{\Delta f}_{2}+{\Delta P}_{\mathrm{tie}}\right|.t.\mathrm{d}t$$

(8)

where ${t}_{\mathrm{sim}}$ is simulation time that is set to a value long enough for the responses to settle. $\Delta f$ (${\Delta f}_{1}$ and ${\Delta f}_{2}$ in a two-area PS) and ${\Delta P}_{\mathrm{tie}}$ stand for the area frequency and tie-line power deviations, respectively. The main focus of the present work is to minimize ${J}_{\mathrm{s}}$ via DSA because the minimum value of ${J}_{\mathrm{s}}$ corresponds to minimum oscillations and accordingly less settling time with no or small peak undershoot/overshoot in ${\Delta f}_{1}$, ${\Delta f}_{2}$ and ${\Delta P}_{\mathrm{tie}}$ responses against a given SLP.

3.2.2 Problem constraints

Variables so often have limitations or constraints. While endeavoring to solve an optimization problem, it must be guaranteed that the given constraints are not violated. In view of this, the current optimization problem can be formulated as the following constrained optimization problem, where the constraints are in the form of inequalities bounded by the limits of (1 + PD)-PID cascade controller gains.

Minimize ${J}_{s}$, subject to:

$$\left.\begin{array}{c}{{K}_{p1}^{\mathrm{min}}\le K}_{p1}\le {K}_{p1}^{\mathrm{max}}\\ {{K}_{d1}^{\mathrm{min}}\le K}_{d1}\le {K}_{d1}^{\mathrm{max}}\\ \begin{array}{c}{{K}_{p2}^{\mathrm{min}}\le K}_{p2}\le {K}_{p2}^{\mathrm{max}}\\ \begin{array}{c}{{K}_{i}^{\mathrm{min}}\le K}_{i}\le {K}_{i}^{\mathrm{max}}\\ {{K}_{d2}^{\mathrm{min}}\le K}_{d2}\le {K}_{d2}^{\mathrm{max}}\end{array}\end{array}\end{array}\right\}$$

(9)

In Eq. 8, $\mathrm{min}$ and $\mathrm{max}$ refer to minimum and maximum limits of respective ${K}_{p1}$, ${K}_{d1}$, ${K}_{p2}$, ${K}_{i}$ and ${K}_{d2}$ gains for (1 + PD)-PID cascade controller. In order to find out optimistic controller gains on a large scale, the range for all gains is chosen as 0.0 and 3.0 for test systems 1 and 2. Referring to the recent works [45, 68], the range is – 2–10 for test systems 3–5. In conclusion, by exploiting the fruitful search behavior of DSA, optimal or near optimal set of (1 + PD)-PID cascade controller parameters is derived within the recommended edges for the smallest value of ${J}_{\mathrm{s}}$.

4 Overview of DSA technique

Dragonfly algorithm is a stochastic algorithm that has been proposed by Seyedali [60]. Since this algorithm is used as a means for searching, it is given name as dragonfly search algorithm (DSA) in this paper. Like most other metaheuristic algorithms, inspiration of DSA is nature wherein the individual and social intelligence of dragonflies in reaching the food source and evading from enemies are studied. Within this context, DSA can be regarded to be a swarm intelligence based algorithm. Dragonflies (or Odonata) pertain to the class of fancy insects that own mainly two milestones in all of their lives: nymph and adult. They are found in nymph most often throughout their lifespan and then they start their adult lives by metamorphosis. A photograph of a real dragonfly is displayed in Fig. 7 from which it is seen that dragonfly is an amazing and exceptionally good-looking creature.

Fig. 7

A real dragonfly

The identified findings about dragonflies signify that they swarm rarely for only hunting and migration purposes. The first one is referred to as static (feeding) swarm and the second one is referred to as dynamic (migratory) swarm. These two swarming behaviors are analogous to the two important characteristics of metaheuristics: exploration and exploitation. Static swarm is associated with exploration while dynamic swarm emphasizes on exploitation. DSA is therefore an optimizer based on the mathematical models representing the above-described artificial/simulated swarm intelligence adopted by dragonflies. This intelligence is implemented in the algorithm by five factors such as (1) separation, (2) alignment, (3) cohesion, (4) attraction to food, and (5) distraction from enemy.

The separation of the ith individual is represented by Eq. 10.

$${S}_{i}=-\sum_{j=1}^{N}X-{X}_{j}$$

(10)

where $X$ and ${X}_{j}$ are positions of the current individual and jth individual in the neighborhood, and $N$ is the number of individuals in the neighborhood. Using the same variables, cohesion of the ith individual is computed as follows.

$${C}_{i}=\frac{\sum_{j=1}^{N}{X}_{j}}{N}-X$$

(11)

Alignment of the ith individual is given by the following expression.

$${A}_{i}=\frac{\sum_{j=1}^{N}{V}_{j}}{N}$$

(12)

where ${V}_{j}$ stands for the velocity of the jth neighboring individual.

Attracting toward a food source is modeled by Eq. 13, where ${X}^{+}$ is the position of the food source and ${F}_{i}$ is the food source of the ith individual.

$${F}_{i}={X}^{+}-X$$

(13)

And distraction outward from an enemy is computed by Eq. 14, where ${X}^{-}$ is the position of the enemy and ${E}_{i}$ is the position of enemy of the ith individual.

$${E}_{i}={X}^{-}+X$$

(14)

According to the weighted combination of these five factors, dragonflies are assumed to update their position and move toward the promising regions of problem landscape. For this, two vectors are generated: step ($\Delta X$) and position ($X$). Here, notice that the step vector defined in Eq. 14 is similar to the velocity vector in PSO.

$${\Delta X}_{t+1}=\left(s{S}_{i}+a{A}_{i}+c{C}_{i}+f{F}_{i}+e{E}_{i}\right)+w\Delta {X}_{t}$$

(15)

where $s$, $a$, $c$, $f$ and $e$ are swarming factors that form the swarming behavior of dragonflies. Swarming factors can be also named as weights mathematically because they weight and determine the significance of different behaviors such as ${S}_{i}$, ${A}_{i}$, ${C}_{i}$, ${F}_{i}$ and ${E}_{i}$ on ${\Delta X}_{t+1}$, $i$ is for the ith individual, $w$ is inertia weight, and $t$ is current iteration.

After obtaining the step vector, the positions of dragonflies are updated using the following formula.

$${X}_{t+1}={X}_{t}+{\Delta X}_{t+1}$$

(16)

Exploration and exploitation abilities of DSA are highly sensitive to its swarming factors ($s$, $a$, $c$, $f$ and $e$) in addition to the inertia weight $w$. By adjusting these factors during the course of optimization, DSA can undergo transitions from explorative search to exploitative search and vice versa, depending upon the solution quality obtained. To catch a good harmony between exploration and exploitation propensities, we update all the weights adaptively during optimization using the following formulas.

$$w=0.9-\frac{(0.9-0.4)}{L}t$$

(17)

$$k=0.1-\frac{0.2}{L}t$$

(18)

$$\left.\begin{array}{c}s=2\cdot {c}_{1}\cdot k\\ a=2\cdot {c}_{2}\cdot k\\ \begin{array}{c}c=2\cdot {c}_{3}\cdot k\\ \begin{array}{c}f=2\cdot {c}_{4}\cdot k\\ e=k\end{array}\end{array}\end{array}\right\}$$

(19)

where $L$ is the maximum iteration number and ${c}_{1}$ to ${c}_{4}$ are random numbers generated in the range of [0, 1]. One may easily perceive that the values of $w$, $k$ and the swarming factors are adaptively reduced while the algorithm progresses. Decreasing trend of these parameters assists DSA to devote the early iterations of optimization to exploration and then the final iterations to exploitation.

In cases where a dragonfly does not have minimum one neighboring dragonfly, DSA takes also the advantages of Lévy flight as a random and stochastic walk in the search space to deliver more explorative behavior of the artificial dragonflies. In such a case, the position update is carried out using Eq. 20.

$${X}_{t+1}={X}_{t}+\mathrm{L\acute{e} }\mathrm{vy}(d)\cdot {X}_{t}$$

(20)

where $d$ refers to the dimension of position vectors and the function $\mathrm{L\acute{e} }\mathrm{vy}(\cdot )$ is calculated as follows:

$${\text{L}}{\acute{\text{e}}}{\text{vy}}\left( x \right) = 0.01 \cdot \frac{{r_{1} \cdot \sigma }}{{\left| {r_{2} } \right|^{{1/\beta }} }}$$

(21)

where ${r}_{1}$ and ${r}_{2}$ are generated randomly in [0, 1], $\beta$ is a constant equal to 1.5 and $\sigma$ is a variable calculated by

$$\sigma = \left( {\frac{{\Gamma (1 + \beta ) \cdot {\text{sin}}\left( {\frac{{\pi \beta }}{2}} \right)}}{{\Gamma (\frac{{1 + \beta }}{2}) \cdot \beta \cdot 2^{{\left( {\frac{{\beta - 1}}{2}} \right)}} }}} \right)^{{1/\beta }}$$

(22)

$\Gamma \left(x\right)$ is equal to $\left(x-1\right)!$ in Eq. 22.

The DA protocol begins the optimization task by initializing a multiple of random solution for a given problem. Here, the positions of dragonflies and step vectors are randomly generated within the lower and upper bounds of design variables and they are updated using Eqs. 14, 15 and 19 as the algorithm proceeds. Neighboring solution of each dragonfly required for calculating $X$ and $\Delta X$ is determined by computing the Euclidian distance between all dragonflies and keeping $N$ number of them. This position update mechanism is iterated till the given criteria satisfaction. For better clarity, the pseudocode presentation of DSA is provided as stepdown.

The above mathematical equations describing the static and dynamic swarming strategies of artificial dragonflies are utilized to search for optimal controller gains in the given range. The algorithm is programmed in *.m script file in Matlab/M-file platform. Each solution member is called a dragonfly in DSA which defines accordingly a candidate controller to the problem at hand. In our problem, we have five parameters to be tuned for the designed (1 + PD)-PID cascade controller and a dragonfly can be stated by

$$\mathrm{dragonfly}=\left[{K}_{p1},{K}_{d1},{K}_{p2},{K}_{i},{K}_{d2}\right]$$

(23)

The studied five PS models shown in Figs. 1, 2, 3 and 4 are individually designed in Matlab/Simulink environment and each model is linked to the written DSA.m script file. In the beginning of the algorithm, a number of dragonflies are generated and then these dragonflies are moved to the simulink module to simulate and supply the frequency and tie-line power deviations. By operating on this data, DSA calculates the value of ITAE objective function for each dragonfly to evaluate its performance. Next, dragonflies are updated based on their objective function values. This process of moving forward and backward between the simulink module and the optimization module is iterated for the number of maximum iterations. The dragonfly that yields minimum ITAE value in the last iteration is assumed to have optimum values of (1 + PD)-PID cascade controller parameters. This controller setting is used in simulations. The detailed illustration of DSA based optimization procedure for controller gains is depicted in Fig. 8.

Fig. 8

Detailed DSA strategy for optimization of controller gains

We would like to bring the attention of readership to that the main contribution of this article is to propose a new control scheme for frequency regulation in interconnected electric PS. DSA is employed as a secondary means for optimal synthesis of the controller parameters. Another metaheuristics with properly tuned parameters may deliver the same controller parameters as those offered by DSA. However, some reasons behind the selection of DSA for optimization in this paper are:

• 1. As per our literature review justifying the supremacy of DSA on a wide range of optimizing problems, DSA is found to better deal with the balance between exploration and exploitation concepts than its peers. This results in better solution quality and promising convergence trend.

• 2. Operations for implementation are simple and easy to code.

• 3. DSA demands tuning of fewer control parameters than many other algorithms, contributing to enhanced robustness by lowering the probability of undermined performance owing to improper parameter tuning.

• 4. Application of DSA to address LFC issue is limited in the literature with the works [61,62,63]. So, its performance assessment in LFC area is valuable and requires further examination.

5 Results and discussion

Diverse PSs are meticulously investigated to predict the performance of the above-proposed frequency regulation scheme. Several comparisons with other reputable works are also presented for each PS to acknowledge the contribution of our proposal. The main observations of the paper and comparison criteria among the related researches are chosen as peak undershoot (${U}_{\mathrm{s}}$), peak overshoot (${O}_{\mathrm{s}}$), settling time (${T}_{\mathrm{s}}$) and ITAE (${J}_{\mathrm{s}}$) of the responses of frequency and tie-line power oscillations. In DSA, the tunable algorithm parameters have, of course, certain impact on the search performance. The way of adjusting both swarming factors and inertia weight is decribed in Sect. 4. The numbers of dragonflies and maximum iteration are set to 50 and 75 emprically to get the best performance from DSA. Increasing these numbers further does not yield improvement on the obtained results anymore other than lead to excessive computational time. Thus, the experiments utilized the best algorithm parameter settings.

We would like to highlight that the major contribution of this paper is not to compare DSA with other metaheuristic methods based on some algorithmic performance measures like execution time and number of fitness evaluations, as they have been already investigated in previous papers [60, 69]. Reporting already published results would not be only redundant but also repetitive. The scope of the article is to instead solve the LFC problem by recommending (1 + PD)-PID cascade controller and compare its performance with the available controllers in terms of ITAE value and settling time/undershoot/overshoot of the frequency and tie-line power deviations. Even if the algorithm comparisons are to be done, then it demands the presence of execution time and number of fitness evaluations for the compared algorithms, which are, however, not provided in the original works. Besides, reported results on execution time cause wrong conclusions for different computing environments because it is a measure subject to the hardware capacity conducting the experiments.

In line with the literature studies, DSA is independently run 25 times in all the experiments and the best solution of the 25 runs is reported and contemplated as proposed controller gains. The optimum values of ${K}_{p1}$, ${K}_{d1}$, ${K}_{p2}$, ${K}_{i}$ and ${K}_{d2}$ acquired for the minimum value of ${J}_{\mathrm{s}}$ for the five test systems are presented in Table 2.

Table 2 DSA optimized (1 + PD)-PID controller gains for the five test systems

An entry by “n/a” in any of the following tables means not applicable for the respective result and the superior results are highlighted by bold faces. $\left|\bullet \right|$ is absolute value operator.

5.1 Two-area non-reheat thermal power system

Initially, the capability of DSA based (1 + PD)-PID cascade controller is tested in the model of test system-1 shown in Fig. 1. The optimal controller gains are reported in Table 2 when a step load perturbation (SLP) of 200 MW, i.e., 200 MW/2000 MW $=$ 0.1pu (10%), is enforced in area 1 at t = 0 s. The simulated responses of $\Delta {f}_{1}$, $\Delta {f}_{2}$ and ${\Delta P}_{\mathrm{tie}}$ with the proposed approach under such a condition are presented in Fig. 9. For validation of contribution, other well-regarded studies employing such as BFOA [1]/hBFOA-PSO [2]/DE [70] tuned PI, ISFS [7]/TLBO [71] tuned PID, TLBO tuned 2DOF PID [71] and hPSO-PS tuned fuzzy PID [33] controllers for the similar PS are also used. The associated responses except for two with 2DOF PID and fuzzy PID controller are displayed in Fig. 9. It is noticeable from Fig. 9 that the proposed scheme outweighs all other approaches significantly in that $\Delta {f}_{1}$, $\Delta {f}_{2}$ and ${\Delta P}_{\mathrm{tie}}$ signals previously floating at zero are quickly driven back to zero again. In the light of this outcome, the proposed method is able to reject such a disturbance very fast verified by smaller values of ${T}_{\mathrm{s}}$, ${U}_{\mathrm{s}}$ and ${O}_{\mathrm{s}}$.

Fig. 9

Results of test system-1 following a 10% SLP in area 1 a $\Delta {f}_{1}$ b $\Delta {f}_{2}$ c ${\Delta P}_{\mathrm{tie}}$

Time-domain performance indices covering the numerical values of ${T}_{\mathrm{s}}$, ${U}_{\mathrm{s}}$, ${O}_{\mathrm{s}}$ and ${J}_{\mathrm{s}}$ of the system responses are measured from Fig. 9 and presented in Table 3. Critical observation of Table 3 discloses that minimum value of ${J}_{s}$ is achieved with our proposal compared to other indicated approaches. This accordingly yields better values of ${T}_{\mathrm{s}}$ ($\Delta {f}_{1}=0.35$ Hz, $\Delta {f}_{2}=1.17$ Hz, ${\Delta P}_{\mathrm{tie}}=0.74$ s), ${U}_{\mathrm{s}}$ ($\Delta {f}_{1}=0.0361$ Hz, $\Delta {f}_{2}=0.0086$ Hz, ${\Delta P}_{\mathrm{tie}}=0.0032$ puMW) and ${O}_{\mathrm{s}}$ ($\Delta {f}_{1}=8.1\times {10}^{-4}$ Hz, $\Delta {f}_{2}=0$ Hz, ${\Delta P}_{\mathrm{tie}}=0$ puMW). It can be also noticed that SLP causes more undershoot in frequency deviation response for the area to which it is applied than other undisrupted area. Thus, it is inferred that the influence of SLP is mainly local, but it also affects the dynamics of other interconnected control area depending upon the strength of tie line connecting them.

Table 3 Results of ${T}_{s}$ (tolerance band of ± 0.002), ${U}_{s}$/${O}_{s}$ and ${J}_{s}$ for test system-1 at $\Delta {P}_{D1}=$ 0.1 puMW

To provide a better picture of the simulation results, the generated powers in area-1 ($\Delta {P}_{g1}$) and area-2 ($\Delta {P}_{g1}$) are shown in Fig. 10. As per the findings, the thermal power generation in area-1 is $\Delta {P}_{g1}=0.1$ puMW, which is equal to the power demand in this area. However, as no power is demanded in area-2, that is, $\Delta {P}_{D2}=0$ puMW, the area generation is $\Delta {P}_{g2}=0$ puMW. Notice also that there is a cross-coupling in both areas during transient state and then each area produces its own power at steady state.

Fig. 10

Results of power generations in test system-3

5.2 Two-area non-reheat thermal power system with nonlinearity

To credit the performance of DSA optimized (1 + PD)-PID cascade controller in coping with a nonlinear situation, nonlinearity based on the impact of governor dead band is introduced in PS model as depicted in Fig. 2. The optimistic controller gains are searched in the specified range and they are given in Table 2. The system responses of $\Delta {f}_{1}$, $\Delta {f}_{2}$ and ${\Delta P}_{\mathrm{tie}}$ with the proposed approach is contrasted in Fig. 11 with other best-claimed alternatives like hBFOA-PSO [2]/CRAZYPSO [72] tuned PI, DE [73]/ISFS [7] tuned PID and hPSO-PS tuned fuzzy PID [33] controllers in presence of a 1% SLP in area 1 applied at t = 0. It is perceivable from Fig. 11 that the system controlled by our contribution responds to the given disturbance awesomely better than others proposed for the identical system with regard to fast recovery and non-oscillating responses.

Fig. 11

Results of test system-2 following a 1% SLP in area 1 a $\Delta {f}_{1}$ b $\Delta {f}_{2}$ c ${\Delta P}_{\mathrm{tie}}$

Noted in Table 4 are the corresponding numerical values of ${T}_{\mathrm{s}}$, ${U}_{\mathrm{s}}$, ${O}_{\mathrm{s}}$ and ${J}_{\mathrm{s}}$ with the proposed (1 + PD)-PID cascade controller and other published control schemes. Clearly, minimum ${J}_{\mathrm{s}}$ ($0.0015$) and accordingly shorter ${T}_{\mathrm{s}}$ ($\Delta {f}_{1}=1.27$ s, $\Delta {f}_{2}=0.88$ s, ${\Delta P}_{\mathrm{tie}}=0.88$ s), smaller ${U}_{\mathrm{s}}$ ($\Delta {f}_{1}=0.0093$ Hz, $\Delta {f}_{2}=0.0023$ Hz, ${\Delta P}_{\mathrm{tie}}=0.0005$ puMW) and lower ${O}_{\mathrm{s}}$ ($\Delta {f}_{1}=5.3\times {10}^{-4}$ Hz, $\Delta {f}_{2}=0$ Hz, ${\Delta P}_{\mathrm{tie}}=0$ puMW) are attained using the proposed approach in comparison with the earlier works. Overall, DSA tuned (1 + PD)-PID cascade controller has the capability of delivering the most precise (oscillation-free), most stable (minimum ${U}_{\mathrm{s}}$/${O}_{\mathrm{s}}$) and far faster (minimum ${T}_{\mathrm{s}}$) step response for the system under consideration.

Table 4 Results of ${T}_{s}$ (tolerance band of ± 0.0002), ${U}_{\mathrm{s}}$/${O}_{\mathrm{s}}$ and ${J}_{\mathrm{s}}$ for test system-2 at $\Delta {P}_{D1}=$ 0.01 puMW

Figure 12 presents the generation results in test system 2. As shown, the generated powers by the two thermal areas ($\Delta {P}_{g1}$ and $\Delta {P}_{g2}$) are set immediately to the demands, which are $\Delta {P}_{D1}=0.01$ puMW and $\Delta {P}_{D2}=0$ puMW, respectively.

Fig. 12

Results of power generations in test system-2

5.3 Single area multi-source power system

The study is extended to a scenario that considers a standalone PS model shown in Fig. 3 wherein three generating units based on different generation sources contributes to the total generation. Every power plant is tied with a distinct (1 + PD)-PID cascade controller and the controller gains for each unit found after the DSA-guided optimization are provided in Table 2. The frequency deviation response to a 1% SLP obtained by the proposed controller is depicted in Fig. 13. For comparison, the system results with other works recently published such as MGWO optimized PIPD [47], SFS and hSFS-LUS optimized PID [45] and hSFS-LUS optimized multistage PID [45] controllers are also offered in Fig. 13 for the same system. Observe that DSA tuned (1 + PD)-PID cascade controller is capable to deliver almost the ideal transient response where $\Delta f$ signal preserves its desired zero pu steady state position without compromising the settling time, peak undershoot and peak overshoot significantly.

Fig. 13

Results of $\Delta f$ for test system-3 following a 1% SLP

The numerical results of ${T}_{\mathrm{s}}$, ${U}_{\mathrm{s}}$, ${O}_{\mathrm{s}}$ and ${J}_{\mathrm{s}}$ corresponding to $\Delta f$ response based on our contribution and other control schemes are reported in Table 5. As we can notice, minimum ${J}_{s}$ ($6.7216\times {10}^{-4}$), ${T}_{\mathrm{s}}$ ($0.83$ s), ${U}_{\mathrm{s}}$ ($0.0001$ Hz) and ${O}_{\mathrm{s}}$ ($1.3\times {10}^{-4}$ Hz) are attained by the proposed controller in comparison with the existing approaches. As a result, DSA tuned (1 + PD)-PID cascade controller can be graded as the pioneer one for test system-3 also.

Table 5 Results of ${T}_{s}$ (tolerance band of ± 0.0002), ${U}_{s}$/${O}_{s}$ and ${J}_{s}$ for test system-3 at $\Delta {P}_{D}=$ 0.01 puMW

The power generations by three distinct units are obtained and exposed in Fig. 14. The powers generated by thermal, hydro and gas unit are $\Delta {P}_{\mathrm{gTh}}=0.007599$ puMW, $\Delta {P}_{\mathrm{gHy}}=2.895\times {10}^{-4}$ puMW and $\Delta {P}_{\mathrm{gG}}=0.002112$ puMW, respectively. Thus, the total power generation is $\Delta {P}_{g}=\Delta {P}_{gTh}+\Delta {P}_{\mathrm{gHy}}+\Delta {P}_{\mathrm{gG}}=0.01$ puMW, which is equalized to the load demanded $\Delta {P}_{\mathrm{D}}=0.01$ puMW quickly. This outcome reveals that the proposed approach fulfills the LFC requirement effectively.

Fig. 14

Results of power generations in test system-3

5.4 Two-area multi-source power system with AC and AC-DC tie-lines

Additionally, the competing performance of the proposed scheme is confirmed on a more realistic two-area multi-source PS that is interconnected by two ways based on AC tie-line (without HVDC link) and AC-DC tie-lines (with HVDC link) as sketched in Fig. 4. The final controller settings using DSA for the associated PS with AC tie-line only are presented in Table 2. Like in the previous exercise, the recently proposed SFS and hSFS-LUS optimized PID [45] and hSFS-LUS optimized multistage PID [45] controllers are chosen to challenge our proposal for this PS under identical conditions. The respective dynamics responses of the system considering 1% SLP in area 1 at t = 0 are painted in Fig. 15 for $\Delta {f}_{1}$ and $\Delta {f}_{2}$. Notice that comparisons for ${\Delta P}_{\mathrm{tie}}$ are not present in Fig. 15 because it is not available in the work utilized [45]. Time-domain characteristics of $\Delta {f}_{1}$ and $\Delta {f}_{2}$ signals in terms of ${T}_{\mathrm{s}}$, ${U}_{\mathrm{s}}$, ${O}_{\mathrm{s}}$ and ${J}_{\mathrm{s}}$ are also illustrated in Table 6.

Fig. 15

Results of test system-4 following a 1% SLP in area 1 a $\Delta {f}_{1}$ b $\Delta {f}_{2}$

Table 6 Results of ${T}_{s}$ (tolerance band of ± 0.0002), ${U}_{s}$/${O}_{s}$ and ${J}_{s}$ for test system-4 at $\Delta {P}_{D1}=$ 0.01 puMW

As per the findings acquired from Fig. 15 and Table 6, DSA tuned (1 + PD)-PID cascade controller is able to achieve minimum ${J}_{\mathrm{s}}$ ($0.18\times {10}^{-2}$) and accordingly shorter ${T}_{\mathrm{s}}$ ($\Delta {f}_{1}=0.40$ s, $\Delta {f}_{2}=0$ s), smaller ${U}_{\mathrm{s}}$ ($\Delta {f}_{1}=0.0012$ Hz, $\Delta {f}_{2}=0.0002$ Hz) and lower ${O}_{\mathrm{s}}$ ($\Delta {f}_{1}=6.0\times {10}^{-5}$ Hz, $\Delta {f}_{2}=1.1\times {10}^{-5}$ Hz). These are superior results to the results offered by the comparison approaches.

The generation results in area-1 ($\Delta {P}_{\mathrm{gArea}-1}$) and area-2 ($\Delta {P}_{\mathrm{gArea}-2}$) are also provided in Fig. 16. In area-1, the thermal, hydro and gas units contribute to the power generation as $\Delta {P}_{\mathrm{gTh}-1}=0.008$ puMW, $\Delta {P}_{\mathrm{gHy}-1}=1.389\times {10}^{-4}$ puMW and $\Delta {P}_{\mathrm{gG}-1}=0.001858$ puMW, respectively. The total power generation is thus $\Delta {P}_{\mathrm{g}1}=\Delta {P}_{\mathrm{gTh}-1}+\Delta {P}_{\mathrm{gHy}-1}+\Delta {P}_{\mathrm{gG}-1}=0.01$ puMW that is equal to the demanded load in area-1 $\Delta {P}_{D1}=0.01$ puMW. Hoewever, in area-2, as $\Delta {P}_{\mathrm{D}2}=0$ puMW, $\Delta {P}_{\mathrm{gTh}-2}=0$ puMW, $\Delta {P}_{\mathrm{gHy}-2}=0$ puMW, $\Delta {P}_{\mathrm{gG}-2}=0$ puMW, and thus $\Delta {P}_{\mathrm{g}2}=\Delta {P}_{\mathrm{gTh}-2}+\Delta {P}_{\mathrm{gHy}-2}+\Delta {P}_{\mathrm{gG}-2}=0$ pu MW.

Fig. 16

Results of power generations in test system-4 a $\Delta {P}_{\mathrm{gArea}-1}$ b $\Delta {P}_{\mathrm{gArea}-2}$

Lastly, to complement the impressive control ability of our proposal and study the effect of DC link in interconnected PS, HVDC link is included in the model of test system-4 to obtain test system-5 which can, in this way, provide the flow of interchange power between neighboring areas through not only AC line but also DC link. The switch with on state shown in Fig. 4 stands for the model of such a system. By considering a SLP of 1% in area 1 at t = 0, the gains of (1 + PD)-PID cascade controller are optimized with DSA in presence of HVDC link and they are presented in Table 2. To illustrate the controller contribution for test system-5, its results are benchmarked with the prevalent results that are derived from DE [19], TLBO [68] and differential search algorithm (DSA) [10] optimized PID structured controllers. The simulated system responses with HVDC link are comparatively painted in Fig. 17. The associated time-domain performance measures of the responses are also computed from Fig. 17 and reported in Table 7. They show the effectiveness of DSA tuned (1 + PD)-PID cascade controller over other published techniques in terms of least ${J}_{\mathrm{s}}$ ($1.7\times {10}^{-3}$), ${T}_{\mathrm{s}}$ ($\Delta {f}_{1}=0.4$ s, $\Delta {f}_{2}=0$ s, ${\Delta P}_{\mathrm{tie}}=0$ s), ${U}_{\mathrm{s}}$ ($\Delta {f}_{1}=9\times {10}^{-4}$ Hz, $\Delta {f}_{2}=2\times {10}^{-4}$ Hz, ${\Delta P}_{\mathrm{tie}}=5.5\times {10}^{-5}$ puMW) and ${O}_{\mathrm{s}}$ ($\Delta {f}_{1}=5.4\times {10}^{-5}$ Hz, $\Delta {f}_{2}=1.0\times {10}^{-5}$ Hz, ${\Delta P}_{\mathrm{tie}}=4.5\times {10}^{-6}$ puMW). Thus, using (1 + PD)-PID cascade controller, $\Delta {f}_{1}$, $\Delta {f}_{2}$ and ${\Delta P}_{\mathrm{tie}}$ signals, after yielding minimum undershoot, immediately settle to the reference zero steady state value without any undesirable oscillations.

Fig. 17

Results of test system-5 following a 1% SLP in area 1 a $\Delta {f}_{1}$ b $\Delta {f}_{2}$ c ${\Delta P}_{\mathrm{tie}}$

Table 7 Results of ${T}_{\mathrm{s}}$ (tolerance band of ± 0.0002), ${U}_{\mathrm{s}}$/${O}_{\mathrm{s}}$ and ${J}_{\mathrm{s}}$ for test system-5 at $\Delta {P}_{D1}=$ 0.01 puMW

Comparing the results in Table 7 with that in Table 6 also divulges that the values of ${J}_{\mathrm{s}}$, ${U}_{\mathrm{s}}$ and ${O}_{\mathrm{s}}$ for both $\Delta {f}_{1}$ and $\Delta {f}_{2}$ are further improved with (1 + PD)-PID cascade controller, which is contributed by the inclusion of HVDC link as an additional area interconnection in parallel with AC link.

Finally, the generated powers 1 in area-1 ($\Delta {P}_{\mathrm{gArea}-1}$) and area-2 ($\Delta {P}_{\mathrm{gArea}-2}$) of this PS are displayed in Fig. 18. What we see in Fig. 18 is that in area-1 the generated power by the thermal unit is $\Delta {P}_{\mathrm{gTh}-1}=0.008113$ puMW, which is bigger than that by hydro unit ($\Delta {P}_{\mathrm{gHy}-1}=1.21\times {10}^{-6}$ puMW) and gas unit ($\Delta {P}_{\mathrm{gG}-1}=0.001885$ puMW). Therefore, the total power generation in area-1 is $\Delta {P}_{\mathrm{g}1}=0.01$ puMW that matches the power demand. On the other hand, the power demand in area-2 is $\Delta {P}_{\mathrm{D}2}=0$ puMW, and as a result, $\Delta {P}_{\mathrm{g}2}=\Delta {P}_{\mathrm{gTh}-2}=\Delta {P}_{\mathrm{gHy}-2}=\Delta {P}_{\mathrm{gG}-2}=0$ puMW.

Fig. 18

Results of power generations in test system-5 a $\Delta {P}_{\mathrm{gArea}-1}$ b $\Delta {P}_{\mathrm{gArea}-2}$

5.5 Statistical results of DSA

To provide a valuable insight into the DSA based optimization procedure, a statistical analysis is performed in this section. The algorithm parameters are similar to that previously described. The statistical information of best, mean, worst and standard deviation of ITAE values obtained over 25 independent runs is presented in Table 8 for each test system. Furthermore, time consumption of simulating the respective PS model and the overall optimization time are averaged and included in this table. It is obvious from Table 8 that for test system-1 DSA tuned (1 + PD)-PID cascade controller achieves the best ITAE value of 0.011001, which deviates from the worst solution by only 0.48%. As a result, much smaller standard deviation is found with a value of 2.5 × 10^–5, justifying the robustness of DSA method. It is also easy for other test systems to draw similar conclusions.

Table 8 Statistical analysis of DSA for the studied test systems

Operating on a Windows computer with i5-7400 CPU and 8 GB RAM, optimization time consumed during the optimization of controller parameters in test system-1 is found to be around 18 min which includes the time on DSA operations as well as costly ITAE evaluations. Each ITAE value required in DSA is calculated from the system dynamic responses after simulating test system-1, which takes 0.1825s as reported in Table 8. It is also apperant in Table 8 that as the model intricacy increases, both the simulation and optimization time raise up.

6 Conclusions and future plan

A (1 + PD)-PID cascade controller has been introduced in this work for devising an efficient solution to LFC issue in electric PSs. For optimal controller synthesis, DSA is harnessed to jointly optimize the five parameters of (1 + PD)-PID cascade controller using ITAE criterion. The capability of this controller is initially tested on a well-accepted two-area thermal PS with and without the impact of GDB nonlinearity and then on single/multi-area multi-source PSs with and without considering a HVDC link. Several results are presented to validate the performance and merits of the proposed controller. Furthermore, the superiority of the controller is also betokened by comparing its responses with the available ones in literature. Comparisons are conducted under fair conditions considering the same PS models exposed to SLP of same location and magnitude. Significant advantages of the proposed DSA optimized (1 + PD)-PID cascade controller can be summarized as follows:

• 1. In the control scheme designed, the output of 1 + PD controller is connected with the input of PID controller. Meanwhile, in contradistinction to all the controllers appeared in literature which mostly benefits from ACE only, our proposal not only makes use of ACE, but also area frequency deviation and tie-line power deviation. The signals used are controllable and measurable from the system with ease.

• 2. The implementation of (1 + PD)-PID cascade controller is simple and has understandable inherent structure familiar to experts/engineers unlike other existing controllers suffering from complex and heavy control rules often not suitable for real-time implementation.

• 3. In view of minimum ITAE value and reduced settling time/peak undershoot/peak overshoot indices, DSA tuned (1 + PD)-PID cascade controller provides healthier profiles of frequency and tie-line power deviations for the respective PSs than PI/PID/multistage PID/2DOF PID/fuzzy PID/PIPD structured controllers tuned via various recent optimization strategies.

• 4. Therefore, DSA based (1 + PD)-PID cascade controller has the aptness of offering more accurate (minimum oscillation), more stable (minimum peak undershoot/overshoot) and faster (minimum settling time) dynamic responses than other indicated approaches, thus satisfying the LFC requirement in a more effective way.

• 5. Statistical investigation of the DSA approach is carried out, which reveals that DSA is robust against all the test cases.

• 6. We would like to highlight that the problem that we endavour to solve is a problem facing frequently in real life. Depending on the extent that the simulated systems reflect the real ones, we can obtain dynamic responses in real-time experimentation similar to the simulated frequency and tie-line power deviations, which show least deviations from the reference 0 steady state value.

As directions of future plan, the system performance may be further escalated by considering a fuzzy logic controller in front of our proposal and/or amalgamating fractional calculus theory with the controller at the cost of increased complexity. On the other hand, other recent optimizers may be tried out to tune the proposed controller gains. The effects of renewable energy sources (wind farm, photovoltaic grid) and energy storage systems on the dynamic performance of studied models may be surveyed. The performance justification of (1 + PD)-PID cascade controller in other PSs or different control applications is also worthy exploring. Moreover, we recommend the diligent researchers to use the signals of frequency and tie-line power deviations in their cascaded control schemes as suggested in this paper.

Appendices

Appendix

Nominal parameters of test systems in order

Test system-1 [1, 2, 7, 33, 71];

$f=60$ Hz, $B=0.425$ p.u MW/Hz, $R=2.4$ Hz/pu, ${T}_{\mathrm{g}}=0.03$ s, ${T}_{\mathrm{t}}=0.3$ s, ${K}_{\mathrm{ps}}=120$ Hz/pu, ${T}_{\mathrm{ps}}=20$ s, ${T}_{12}=0.545$ p.u MW/rad.

Test system-2 [2, 7, 15, 71];

$f=60$ Hz, $B=0.425$ p.u MW/Hz, $R=2.4$ Hz/pu, ${T}_{\mathrm{g}}=0.2$ s, ${T}_{\mathrm{t}}=0.3$ s, ${K}_{\mathrm{ps}}=120$ Hz/pu, ${T}_{\mathrm{ps}}=20$ s, ${T}_{12}=0.444$ p.u MW/rad.

Test system-3 [19, 45, 47, 68];

$f=60$ Hz, $R=2.4$ Hz/pu, ${T}_{\mathrm{sg}}=0.08$ s, ${K}_{\mathrm{r}}=0.3$, ${T}_{\mathrm{r}}=10$ s, ${T}_{\mathrm{t}}=0.3$ s, ${T}_{\mathrm{gh}}=0.2$ s, ${T}_{\mathrm{rs}}=5$ s, ${T}_{\mathrm{rh}}=28.75$ s ${T}_{\mathrm{w}}=1$ s, ${b}_{\mathrm{g}}=0.05$ s, ${c}_{\mathrm{g}}=1$, ${X}_{\mathrm{c}}=0.6$ s, ${Y}_{\mathrm{c}}=1$ s, ${T}_{\mathrm{cr}}=0.01$ s, ${T}_{\mathrm{f}}=0.23$ s, ${T}_{\mathrm{cd}}=0.2$ s, ${K}_{\mathrm{T}}=0.543478$ pu, ${K}_{\mathrm{H}}=0.326084$ pu, ${K}_{\mathrm{G}}=0.130438$ pu, ${K}_{\mathrm{ps}}=68.9566$ Hz/pu MW, ${T}_{\mathrm{ps}}=11.49$ s.

Test system-4 [19, 45, 47, 49];

$f=60$ Hz, $B=0.4312$ pu, $R=2.4$ Hz/pu, ${T}_{\mathrm{sg}}=0.08$ s, ${K}_{\mathrm{r}}=0.3$, ${T}_{\mathrm{r}}=10$ s, ${T}_{\mathrm{t}}=0.3$ s, ${T}_{\mathrm{gh}}=0.2$ s, ${T}_{\mathrm{rs}}=5$ s, ${T}_{\mathrm{rh}}=28.75$ s ${T}_{\mathrm{w}}=1$ s, ${b}_{\mathrm{g}}=0.05$ s, ${c}_{\mathrm{g}}=1$, ${X}_{\mathrm{c}}=0.6$ s, ${Y}_{\mathrm{c}}=1$ s, ${T}_{\mathrm{cr}}=0.01$ s, ${T}_{\mathrm{f}}=0.23$ s, ${T}_{\mathrm{cd}}=0.2$ s, ${K}_{\mathrm{T}}=0.543478$ pu, ${K}_{\mathrm{H}}=0.326084$ pu, ${K}_{\mathrm{G}}=0.130438$ pu, ${T}_{12}=0.0433$, ${K}_{\mathrm{ps}}=68.9566$ Hz/pu MW, ${T}_{\mathrm{ps}}=11.49$ s.

Test system-5 [10, 19, 68];

$f=60$ Hz, $B=0.4312$ pu, $R=2.4$ Hz/pu, ${T}_{\mathrm{sg}}=0.08$ s, ${K}_{\mathrm{r}}=0.3$, ${T}_{\mathrm{r}}=10$ s, ${T}_{\mathrm{t}}=0.3$ s, ${T}_{\mathrm{gh}}=0.2$ s, ${T}_{\mathrm{rs}}=5$ s, ${T}_{\mathrm{rh}}=28.75$ s ${T}_{\mathrm{w}}=1$ s, ${b}_{\mathrm{g}}=0.05$ s, ${c}_{\mathrm{g}}=1$, ${X}_{\mathrm{c}}=0.6$ s, ${Y}_{\mathrm{c}}=1$ s, ${T}_{cr}=0.01$ s, ${T}_{\mathrm{f}}=0.23$ s, ${T}_{\mathrm{cd}}=0.2$ s, ${K}_{\mathrm{T}}=0.543478$ pu, ${K}_{\mathrm{H}}=0.326084$ pu, ${K}_{\mathrm{G}}=0.130438$ pu, ${T}_{12}=0.0433$, ${K}_{\mathrm{ps}}=68.9566$ Hz/pu MW, ${T}_{\mathrm{ps}}=11.49$ s, ${K}_{dc}=1$, ${T}_{\mathrm{dc}}=0.2$ s.