A binary social spider algorithm for continuous optimization task

Abstract

The social spider algorithm (SSA) is a new heuristic algorithm created on spider behaviors. The original study of this algorithm was proposed to solve continuous problems. In this paper, the binary version of SSA (binary SSA) is introduced to solve binary problems. Currently, there is insufficient focus on the binary version of SSA in the literature. The main part of the binary version is at the transfer function. The transfer function is responsible for mapping continuous search space to discrete search space. In this study, four of the transfer functions divided into two families, S-shaped and V-shaped, are evaluated. Thus, four different variations of binary SSA are formed as binary SSA-Tanh, binary SSA-Sigm, binary SSA-MSigm and binary SSA-Arctan. Two different techniques (SimSSA and LogicSSA) are developed at the candidate solution production schema in binary SSA. SimSSA is used to measure similarities between two binary solutions. With SimSSA, binary SSA’s ability to discover new points in search space has been increased. Thus, binary SSA is able to find global optimum instead of local optimums. LogicSSA which is inspired by the logic gates and a popular method in recent years has been used to avoid local minima traps. By these two techniques, the exploration and exploitation capabilities of binary SSA in the binary search space are improved. Eighteen unimodal and multimodal standard benchmark optimization functions are employed to evaluate variations of binary SSA. To select the best variations of binary SSA, a comparative study is presented. The Wilcoxon signed-rank test has applied to the experimental results of variations of binary SSA. Compared to well-known evolutionary and recently developed methods in the literature, the variations of binary SSA performance is quite good. In particular, binary SSA-Tanh and binary SSA-Arctan variations of binary SSA showed superior performance.

1 Introduction

Evolutionary computation has become an attractively efficient device of optimization for rapidly increasing complex modern optimization problems. Evolutionary computation based on natural facts can be separated into two important groups. These are evolutionary algorithms (EAs) and swarm intelligence-based algorithms. EAs include very successful methods that are mainly created by inspirations from nature. There are a lot of EAs which solve real-world problems and global optimization problems. The main ones of these are the genetic algorithm (GA), genetic programming (GP), evolutionary strategies (ES) and differential evolution (DE). These algorithms have had very successful results, especially in solving convex optimization problems (Talbi 2009; Mallipeddi et al. 2011).

For the last 20 years, swarm intelligence-based algorithms, which are based on a new evolutionary computation method, attract attention. The term of a swarm expresses a community that consists of individuals who are in communication with each other. Swarm intelligence-based algorithms study main social animal and insect behaviors for solving problems. These algorithms imitate the behaviors of ant, fish, bird, bee, bacteria, butterfly, etc. Thus, the problems which seem hard are able to be solved (Parpinelli and Lopes 2011; Yu and Li 2015). Three well-known pioneers of this area are: particle swarm optimization (PSO), ant colony optimization (ACO) (Kennedy and Eberhart 1995; Dorigo 1990) and artificial bee colony (ABC) optimization algorithm (Karaboga 2005). Particle swarm optimization is an optimization method, which is developed by Kennedy and Eberhart (1995) inspired by flocking fish and insects. ACO is an algorithm inspired by ants’ behaviors. The aim is to find the shortest path to food sources for an ant colony. Karaboga has designed an artificial bee colony (ABC) optimization algorithm inspired by bees’ behaviors (Omkar et al. 2011).

1.1 Binary optimization problem (BOP)

The binary optimization problem (BOP) is shown as a binary-based problem space that represents an important class of the combinatorial optimization problems (Rizk-Allah et al. 2018). In continuous optimization, search agents take continuous values in search space, while in binary optimization search agents in the search space take {0, 1} values. “0” represents the absence, and “1” represents the presence. Many problems can be solved in a binary space by using these two values in the search space. Some algorithms are capable of solving problems with continuous search spaces, while some problems have discrete search spaces (Mirjalili and Lewis 2013; Kennedy and Eberhart 1997; Rashedi et al. 2009). BOP has many applications. They need binary algorithms for their solution. These include facility location (including emergency vehicles, health centers and commercial bank branches) and scheduling tasks (including budgeting, flexible manufacturing systems, telecommunications, mass transit services and wind turbine placement) (Prescilla and Immanuel 2013; Korkmaz et al. 2017; Beskirli et al. 2018). Also, the BOP is used in the solution of well-known NP-hard problems [including knapsack problem, resource allocation problem, dimensionality reduction, feature selection, network optimization, unit commitment and cell formation (Rizk-Allah and Hassanien 2018; Rizk-Allah 2014; Fan et al. 2013; Pal and Maiti 2010; Babaoglu et al. 2010; Qiao et al. 2006; Emary et al. 2016)]. In the literature, many traditional methods [including relaxation methods, Lagrangian techniques, branch-and-bound methods, reduction schemes and integer programming (Rizk-Allah et al. 2018)] have been proposed to solve the BOP. Although these methods perform well in small-scale problems, they do not perform well in large-scale problem solutions. Although there are many methods for the solution of BOPs, the solution with meta-heuristic algorithms has given us many advantages. In particular, it has shortened the solution time of large-scale problems. Due to these limitations in the deterministic methods, more and more are becoming interested in the meta-heuristic algorithms inspired by specific phenomena (Shukla and Nanda 2018; Pereira et al. 2014; Rizk-Allah et al. 2018; Mirjalili and Lewis 2013; Kennedy and Eberhart 1997; Rashedi et al. 2009; Prescilla and Immanuel 2013; Korkmaz et al. 2017; Beskirli et al. 2018; Rizk-Allah and Hassanien 2018; Babaoglu et al. 2010; Emary et al. 2016; Ling et al. 2010a, b). There are different methods to develop the binary version of a continuous heuristic algorithm while preserving the concepts of the search process (Mirjalili and Lewis 2013). For instance, Ling et al. developed a probability estimation operator in order to solve binary problems by DE (BDE) (Ling et al. 2010a). The binary magnetic optimization algorithm (BMOA) and binary gravitational search algorithm (BGSA) have been proposed utilizing transfer functions and position updating rules (Mirjalili and Mohd Hashim 2012; Rashedi et al. 2009). Binary harmony search (BHS) algorithm has been employed a set of harmony search considerations and pitch adjustment rules (Ling et al. 2010b). Kennedy and Eberhart (1997) proposed binary versions of PSO. They have used two different components for BPSO (a new transfer function and a different position updating procedure). Rizk-Allah and Hassanien (2018) proposed a binary version of the bat algorithm (BBA). Cuevas et al. (2013) have developed social spider optimization (SSO). Shukla and Nanda (2018) developed a binary social spider optimization algorithm (BSSO) for high-dimensional data sets. Rizk-Allah et al. (2018) proposed binary salp swarm algorithm (BSalpSA) and Rizk-Allah (2018) proposed binary sine cosine algorithm (BSCA).

Yu and Li (2015) have offered social spider algorithm (SSA) which is configured according to social spider behaviors. Some spider species, which generally live solitary, can live as colonies. Spiders live in colonies can communicate with each other by a web structure. The spiders enable this communication with the vibration that they produce on the web. They can make random walks to each other by the vibration information they share (Yu and Li 2015). There are not many studies on SSA in the literature. El-Bages and Elsayed have solved the static transmission expansion planning problem by using SSA. In the proposed method, the DC power flow subproblem is solved by developing an SSA-based web and adding potential solutions to the result (El-Bages and Elsayed 2017). Yu and Li have solved economic load dispatch (ELD) formulation by developing an SSA-based new approach. ELD is one of the essential components in power system control and operation (Yu and Li 2016). Mousa and Bentahar have adapted a QoS-aware web service selection process to the SSA approach (Mousa and Bentahar 2016). Elsayed et al. (2016) have solved the non-convex economic load dispatch problem with an SSA-based approach.

Social spider optimization (SSO) is another heuristic algorithm that is very similar to the SSA algorithm, but totally different from it. Cuevas et al. (2013) have developed SSO algorithm by inspiring from spider behaviors. In SSO, there are two different searching agents (spider) in the search space of SSO. These are male and female spiders. Depending upon the gender, each individual operates a range of different evolutionary operators that imitates various collaboration behaviors that typically exist in colonies. In SSO, the vibration structure is very different. There are three special vibration types in SSO approach. Vibci: They are perceived by the individual i (Si) as a result of the information transmitted by the member c (Sc) who is an individual that has two important characteristics: It is the nearest member to i and possesses a higher weight (wc > wi). Vibbi: They are perceived by the individual i as a result of the information transmitted by the member b (Sb), with b being the individual holding the best weight (best fitness value). Vibfi: They perceived by the individual i (Si) as a result of the information transmitted by the member f (Sf), with f being the nearest female individual to i. There are also various different studies in the literature with SSO. Shukla and Nanda (2018) have developed a parallel social spider clustering algorithm for high-dimensional data sets and a BSSO algorithm for unsupervised band selection in compressed hyperspectral images. Pereira et al. (2014) have developed a SSO-based artificial neural networks training and applied its applications for Parkinson’s disease identification. Sun et al. (2017) have developed the hybrid SSO algorithms and applied it for the estimation of thermophysical properties of phase change material.

1.2 Binary SSA for continuous optimization task

The spider social algorithm is a heuristic algorithm developed to solve continuous optimization problems. The aim of this study is to introduce a binary social spider algorithm (binary SSA) for solving general BOPs. SSA is chosen in this study because it is a new heuristic algorithm and there is not enough focus on binary SSA in the literature. Furthermore, there is no study in the literature on the performance of binary SSA with respect to different transfer functions. The main part of the binary optimization is at transfer function. SSA is modified again according to four different transfer functions for mapping the continuous search space to the binary search space. In this paper, four binary variations of the binary SSA (i.e., binary SSA-Tanh, binary SSA-Sigm, binary SSA-MSigm and binary SSA-Arctan) are proposed based on four transfer functions. In order to ensure the balance between exploration and exploitation, two different techniques (similarity measurement and logic gate techniques) are developed at the candidate solution production schema in the variations of the binary SSA. The similarity measurement technique is named as SimSSA, and the logic gate technique is named as LogicSSA. Thus, the variations of binary SSA based on SimSSA and LogicSSA is developed in this study. The logic gate technique has a newly developed method in recent years and preferred for the developed binary SSA. The logic gate technique provides a strong local search capacity. Logic gates are very suitable for binary optimizations due to their structure. Input and output values of logic gates are 0 or 1 value. In binary optimizations, the search space consists of 0 or 1 value. 0 means the absence of a value, and 1 indicates its existence. So, it is appropriate to use logic gates in the search space. The similarity measurement technique is used to measure the similarity between two different binary structures, and the exploration ability of binary SSA is increased with the similarity measurement technique. This ensures that global optimum is found in the search space instead of local optimums. The convergence speed of binary SSA is also increased by SimSSA and LogicSSA.

The primary contributions of this paper are as follows:

• (a) We propose a binary SSA to solve general BOPs. The SSA has modified again according to different transfer functions for mapping the continuous search space to the binary search space.

• (b) Four different variations of binary SSA (i.e., binary SSA-Tanh, binary SSA-Sigm, binary SSA-MSigm and binary SSA-Arctan) are developed with four different transfer functions.

• (c) In order to ensure the balance between exploration and exploitation, two different techniques (SimSSA and LogicSSA) are developed at the candidate solution production stage in the variations of the binary SSA. There are advantages that both techniques offer different types. For example, LogicSSA has a strong local search capacity around the current spider, and SimSSA is good at discovering the new points on the solution space. So new candidate solutions (new spiders) are produced by using similarity and logic gates and more efficient individuals are obtained by comparing with the current individuals.

• (d) The variations of binary SSA based on SimSSA and LogicSSA have been tested on various unimodal and multimodal benchmark functions. Thus, the performances between variations of binary SSA are compared.

The rest of the paper is organized as follows: SSA is presented in Sect. 2, the variations of binary SSA based on SimSSA and LogicSSA are studied in Sect. 3 and the variations of binary SSA are tested by various unimodal and multimodal benchmark functions in Sect. 4 and the obtained results are compared with each other and well-known heuristic methods and new methods in the literature. The results are evaluated.

2 Social spider algorithm (SSA)

Social spider algorithm (SSA) is a heuristic algorithm that is created by imitating spiders’ behaviors in nature. SSA is created for organizing searching space of optimization problems as a high-dimensional spider web. In SSA, spiders are SSA agents that perform optimization. At the beginning of the algorithm, a predetermined number of spiders are placed on the web. Each spider on the web has a memory. Spider information has stored this memory (the position of spider, the movement of spider, the dimension mask of spider, etc.) (Yu and Li 2015). The locations of spiders are initially set at random. Each spider produces a vibration when it moves from a position to a different location. The severity of the vibration is related to the fitness value. The vibration is the most important feature that distinguishes SSA from other optimization algorithms. Vibration can spread over the web, and other spiders on the web can feel it. Thus, other spiders on the web can obtain the personal information of the spider. Equation 1 is used to calculate the vibration intensity (Yu and Li 2015).

$$ I\left( {P_{g} ,P_{g} ,t} \right) = \log \left( {\frac{1}{{f\left( {p_{g} } \right) - C}}} \right) + 1 $$

(1)

where I(P_g, P_g, t) is the vibration value produced by the spider in the source position at time t. “g” represents a spider. P_g(t) defines the position of spider g at time t and it is shown simply as P_g if the time argument is t. f(P_g) represents the spider of fitness value in its current position. C is a confidently small constant such that all possible fitness values are larger than C value for minimization problems. Logarithms are used for operations with numbers that are too large or too small.

$$ {\text{Dis}}\left( {P_{g} ,P_{b} } \right) = P_{g} - P_{b} $$

(2)

Dis(P_g, P_b) is showing the distance between spider g and spider b. This distance is calculated by Eq. 2 (Yu and Li 2015). Manhattan distance structure is used when calculating this distance. The vibration attenuation over distance is calculated by Eq. 3 (Yu and Li 2015). For vibration attenuation, the vibration value produced by the spider in the source position and distance are two important properties.

$$ I\left( {P_{g} ,P_{b} ,t} \right) = I\left( {P_{g} ,P_{g} ,t} \right) \times \exp \left( { - \frac{{{\text{Dis}}\left( {Pg,Pb} \right)}}{{ \bar{\sigma } \times r_{a} }}} \right) $$

(3)

where I(P_g, P_b, t) is the felt value of the spider’s vibration in “g” point, by the spider in “b” point. P_g(t) or simply P_g represents the position of spider g at time t. P_b(t) or simply P_b represents the position of spider b at time t. I(P_g, P_g, t) is the vibration value produced by the spider in the “g” position at time t. $\bar{\sigma }$ represents the mean of the standard deviation of the positions of all spiders in each dimension. r_a is represented as a user-controlled parameter r_a ∈ (0, ∞). This parameter controls the attenuation rate of the vibration intensity over the distance. The larger the r_a is, the weaker the attenuation imposed on the vibration (Yu and Li 2015). The value of r_a is selected from the set {1/10, 1/5, 1/4, 1/3, 1/2, 1, 2, 3, 4, 5, 10}. Yu and Li (2015) have used for five 10-dimensional benchmark functions to investigate the impact of this parameter on the performance of SSA. According to their results, r_a = 1 is determined.

In the initialization phase, each spider is assigned a fixed size memory for storing spider information. The positions of spiders are randomly generated in the search space. Fitness values of the spiders calculated and stored. All spiders produce vibration using their position (Eq. 1). The algorithm uses vibrations to activate the propagation process (Eq. 3). “V” represents spiders’ vibrations. Each spider receives the vibrations generated by other spiders. A spider selects the strongest of these vibration values. This value shows as V ^best_g , g represents a spider. Spider g stores the target vibration in the memory as V ^tar_g . Each spider g compares V ^best_g and V ^tar_g values. If the intensity of the V ^best_g is greater than V ^tar_g , the V ^tar_g is changed to as V ^best_g . The random walk of each spider is calculated by Eq. 4 (Yu and Li 2015).

$$ P_{g} \left( {t + 1} \right) = P_{g} + \left( {P_{g } - P_{g} \left( {t - 1} \right)} \right) \times r + \left( {P_{g}^{\text{follow}} - P_{g} } \right) \odot R $$

(4)

where R is a vector of random float point numbers generated from zero to one uniformly. $\odot$ denotes element-wise multiplication. Spider g first moves along its previous direction, which is the direction of movement in the previous iteration. The distance along this direction is a random portion of the previous movement. Then spider g approaches P ^follow_g along each dimension with random factors generated in (0, 1). P ^folow_g represents the following position. Each spider decides the following position (P ^follow_g ) by looking at the dimension mask.

The dimension mask is determined so that a random walk can be performed toward the V ^tar_g . The dimension mask is a {0, 1} binary vector of length D, and D is the dimension of the optimization problem. Figure 1 shows the dimension mask for SSA (Population size × Dimension).

Fig. 1

Dimension mask for SSA (Population size x Dimension)

The dimension mask in SSA is a structure different from the mutation operator of the genetic algorithm. In the genetic algorithm, the mutation operator is used to prevent new solutions from copying the previous solution and to reach the result faster (Holland 1975; Kurt and Sematay 2001). For example, in a sequence using a binary encoding, a new sequence is obtained by changing the element value randomly selected by the mutation operator to 1 if it is 0 or 1 if it is 0. In the SSA, the dimension mask guides the random walk phase. Dimension mask is not an individual, candidate solution or gene. Using the dimension mask, spiders move toward the V ^tar_g or a random spider during the random walk. Each spider decides the following position (P ^follow_g ) by looking at the dimension mask (in Eq. 5). With the dimension mask, SSA achieves both global search capability and local search capability. In SSA, a spider obtains local search capability by performing move toward the V ^tar_g and global search capability by performing move toward a random spider.

In SSA, all bits of the dimension mask are zero at first. In each iteration, spiders have a probability of 1 − p ^cs_c to change its dimension mask. p_c ∈ (0, 1) is a user-defined attribute that describes the probability of changing mask. If the dimension mask is decided to be changed, each bit of the vector has a probability of p_m. p_m is also a user-controlled parameter defined in (0, 1). The values of p_c and p_m are selected from the set {0.01, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 0.99}. Yu and Li are used five 10-dimensional benchmark functions to investigate the impact of these parameters on the performance of SSA. According to their results, p_c and p_m values are determined as 0.7 and 0.1, respectively. cs is the number of iterations that the spider has last changed its target vibration. Each bit of the dimension mask is changed independently. The new dimension mask does not have any correlation with the previous dimension mask.

After the dimension mask is determined, a new following position P ^follow_g is generated based on the dimension mask. P ^follow_g value is calculated by Eq. 5 (Yu and Li 2015). If the bit value of the dimension mask is 0, it moves to the position of the target spider in the memory of the spider or to the position of a random spider.

$$ P_{g,i}^{\text{follow}} = \left\{ {\begin{array}{*{20}l} {P_{g,i}^{\text{tar}} , } \hfill & {dimension\_mask_{g,i} = 0} \hfill \\ {P_{g,i}^{r} ,} \hfill & {dimension\_mask_{g,i} = 1} \hfill \\ \end{array} } \right. $$

(5)

where r is a random integer value generated in [1, population size] and dimension_mask_g,i stands for the ith dimension of the dimension mask of spider g.

After each spider performs a random walk, the spiders may move out of the web. They violate the constraint of the optimization problem. Equation 6 is used to prevent population members from moving out of the search space.

$$ P_{g,i} \left( {t + 1} \right) = \left\{ {\begin{array}{*{20}l} {\left( {\overline{{x_{i} }} - P_{g,i} } \right) \times r} \hfill & { {\text{if}}\,P_{g,i} \left( {t + 1} \right) > \overline{{x_{i} }} } \hfill \\ {\left( {P_{g,i} - \underline{{x_{i} }} } \right) \times r} \hfill & {{\text{if}}\,P_{g,i} \left( {t + 1} \right) < \underline{{x_{i} }} ,} \hfill \\ \end{array} } \right. $$

(6)

where $\overline{{x_{i} }}$ shows upper border and $\underline{{x_{i} }}$ shows a lower border. P_g,i(t + 1) defines the position of a spider g for the ith dimension at time t + 1. r is a random integer value generated in [1, population size].

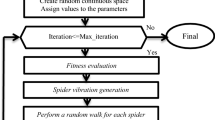
Flowchart for SSA is shown in Fig. 2. The work steps of SSA are shown in Fig. 3.

Fig. 2

Flowchart for SSA

Fig. 3

Work steps of SSA

3 A binary social spider algorithm (binary SSA)

In general, there are many problems interested in binary search spaces, such as feature selection and diminishing dimensionality. In addition, algorithms that have continuous real search spaces can solve binary optimization problems (BOPs) by converting variables into binary variables. Regardless of the type of BOPs, binary search space has its own unique structure with some limitations. A binary search space can be considered as a hypercube. The agents (spiders) of a binary optimization algorithm can only shift to nearer and farther corners of the hypercube by flipping various numbers of bits (Kennedy and Eberhart 1997). Hence, in designing the binary version of SSA, the position updating process must be modified. In SSA, social spiders continually change their positions as a random position in the search space according to the lower and upper limit ranges. In binary optimization, the solution is restricted to the binary {0, 1} values.

It has been noticed that there is not enough focus on the binary version of SSA in the literature. The transfer functions, which are the main part of the binary transformation, are handled individually and their performance is not studied. There is no study on the performance of SSA to solve general BOPs. For these reasons, we have proposed a binary SSA to perform general binary tasks in this paper. We have obtained different binary SSA versions using various transfer functions and compared their performance. In binary SSA, two new different techniques (SimSSA and LogicSSA) are developed in the candidate solution production scheme to provide the balance between exploration and exploitation in search space. These are based on similarity measurement (SimSSA) and logical gate (LogicSSA) techniques. There are advantages offered by different types of both techniques. For example, LogicSSA is very powerful in local search and SimSSA is very good at discovering new solutions in solution space. Since both techniques have advantages offered in different types.

In the binary SSA, social spiders update their positions on the binary search space according to Eq. 4. In the binary SSA, the solution pool is represented by {0, 1} binary string values. The position of a spider is updating through 0–1 flipping operation. This flipping process is performed by a certain threshold value that is related to the transfer function. The transfer function is the most important part of converting to binary form. A transfer function defines the probability of changing a position vector’s elements from 0 to 1 and vice versa (Kennedy and Eberhart 1997). There are many S-shaped and V-shaped transfer functions in the literature. Transfer function families of S-shaped and V-shaped are shown in Table 1. In this paper, two S-shaped (sigmoidal transfer function and modified sigmoidal transfer function) and two V-shaped (tangent hyperbolic transfer function and arctan transfer function) transfer functions are used. Thus, four different binary SSA variations such as binary SSA-Tanh, binary SSA-Sigm, binary SSA-MSigm and binary SSA-Arctan are formed. The transfer function to be selected for binary conversion affects the performance of the algorithm used in the BOPs. A transfer function should offer both a high probability and a small possibility of changing positions.

Table 1 S-shaped and V-shaped transfer functions (Mirjalili and Lewis 2013)

3.1 According to the transfer functions, the variations of binary SSA

3.1.1 Binary SSA-Tanh (tangent hyperbolic transfer function)

In binary SSA-Tanh, a tangent hyperbolic transfer function is used as the transfer function. The positions of the social spiders are converted into binary form according to the tangent hyperbolic transfer function. This function works as a threshold limit and converts positions between 0 and 1 values. The tangent hyperbolic transfer function is calculated by Eq. 7 (Rizk-Allah et al. 2018).

$$ T\left( {x_{i}^{j} \left( {t + 1} \right)} \right) = \text{Tanh} \left( {x_{i}^{j} \left( {t + 1} \right)} \right) = \frac{{e^{{\left( {2x_{i}^{j} \left( {t + 1} \right)} \right)_{ - 1} }} }}{{e^{{\left( {2x_{i}^{j} \left( {t + 1} \right)} \right)_{ + 1} }} }} \quad \Delta_{i}^{j} \left( {t + 1} \right) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {{\text{if}}\,T\left( {x_{i}^{j} \left( {t + 1} \right)} \right) > \lambda_{1} } \hfill \\ 0 \hfill & {\text{Otherwise}} \hfill \\ \end{array} } \right. $$

(7)

where λ₁ is a random number in [0–1]. $x_{i}^{j} \left( {t + 1} \right)$ is the position of spider i at iteration t in jth dimension.

3.1.2 Binary SSA-Sigm (sigmoidal transfer function)

In binary SSA-Sigm, a sigmoidal transfer function is used as the transfer function. The positions of the social spiders are converted into binary form according to the sigmoidal transfer function. This function works as a threshold limit and converts positions between 0 and 1 values. The sigmoidal transfer function is calculated by Eq. 8 (Rizk-Allah et al. 2018).

$$ S\left( {x_{i}^{j} \left( {t + 1} \right)} \right) = {\text{Sig}}\left( {x_{i}^{j} \left( {t + 1} \right)} \right) = \frac{1}{{1 + e^{{ - x_{i}^{j} \left( {t + 1} \right)}} }} \quad \Delta_{i}^{j} \left( {t + 1} \right) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {{\text{if}}\,S\left( {x_{i}^{j} \left( {t + 1} \right)} \right) > \lambda_{2} } \hfill \\ 0 \hfill & {\text{Otherwise}} \hfill \\ \end{array} } \right. $$

(8)

where λ₂ is a random number in [0–1]. $x_{i}^{j} \left( {t + 1} \right)$ is the position of spider i at iteration t in jth dimension.

3.1.3 Binary SSA-MSigm (modified sigmoidal transfer function)

In binary SSA-MSigm, a modified sigmoidal transfer function is used as the transfer function. The positions of the social spiders are converted into binary form according to the modified sigmoidal transfer function. This function works as a threshold limit and converts positions between 0 and 1 values. The modified sigmoidal transfer function is calculated by Eq. 9 (Rizk-Allah et al. 2018).

$$ {\text{MS}}\left( {x_{i}^{j} \left( {t + 1} \right)} \right) = {\text{MSig}}\left( {x_{i}^{j} \left( {t + 1} \right)} \right) = \frac{1}{{1 + e^{{ - 10(x_{i}^{j} \left( {t + 1) - 0.5} \right)}} }}\quad \Delta_{i}^{j} \left( {t + 1} \right) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {{\text{if}}\,{\text{MS}}\left( {x_{i}^{j} \left( {t + 1} \right)} \right) > \lambda_{3} } \hfill \\ 0 \hfill & {\text{Otherwise}} \hfill \\ \end{array} } \right. $$

(9)

where λ₃ is a random number in [0–1]. $x_{i}^{j} \left( {t + 1} \right)$ is the position of spider i at iteration t in jth dimension.

3.1.4 Binary SSA-Arctan (arctan transfer function)

In binary SSA-Arctan, an arctan transfer function is used as the transfer function. The positions of the social spiders are converted into binary form according to the arctan transfer function. This function works as a threshold limit and converts positions between 0 and 1 values. The arctan transfer function is calculated by Eq. 10 (Rizk-Allah et al. 2018).

$$ A\left( {x_{i}^{j} \left( {t + 1} \right)} \right) = A\left( {x_{i}^{j} \left( {t + 1} \right)} \right) = \left| {\frac{2}{\pi }\arctan \left( {\frac{2}{\pi }x_{i}^{j} \left( {t + 1} \right)} \right)} \right| \quad \Delta_{i}^{j} \left( {t + 1} \right) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {{\text{if}}\,A\left( {x_{i}^{j} \left( {t + 1} \right)} \right) > \lambda_{4} } \hfill \\ 0 \hfill & {\text{Otherwise}} \hfill \\ \end{array} } \right. $$

(10)

where λ₄ is a random number in [0–1]. $x_{i}^{j} \left( {t + 1} \right)$ is the position of spider i at iteration t in jth dimension.

3.2 Similarity-based social spider algorithm (SimSSA)

3.2.1 Similarity measurement for binary structures

The similarity measurement technique is developed to measure the similarity between two different binary structures. There are 76 similarity measurement techniques for binary data (Qiao et al. 2006). One of the most commonly used general-purpose similarity measurement techniques is shown in Eq. 11 (Jaccard’s similarity measurement technique) (Çınar and Kiran 2018).

$$ {\text{Similarity}}\left( {X_{i} ,Y_{i} } \right) = \frac{{m_{11} }}{{m_{01} + m_{10} + m_{11} }} $$

(11)

where X_i and Y_i represent two binary structured individuals. “D” is the dimensionality of the problem for X_i and Y_i. X_id ∈ {0, 1}, X_i = [x_i1, x_i2, …, x_id], Y_id ∈ {0, 1}, Y_i = [y_i1, y_i2, …, y_id]. In order to measure the similarity between X_i and Y_i, we compare them by means of their bit values. There are four possible cases, and they are shown in Table 2.

Table 2 Possible cases in similarity

m₁₁ indicates the number of bits when x_id = 1 in X_i and y_id = 1 in Y_i, where i = 1, 2,…, D and D is the dimensionality of the problem, which is obtained as follows (Emary et al. 2016):

$$ m_{11} = \mathop \sum \limits_{d = 1}^{D} I_{d} ,\quad {\text{where}}\quad I_{d} = \left\{ {\begin{array}{*{20}l} {1, } \hfill & {{\text{if}}\,\left( {x_{id } = 1\,{\text{and}}\,y_{id } = 1} \right)} \hfill \\ {0,} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right. $$

(12)

m₁₀ indicates the number of bits when x_id = 1 in X_i and y_id = 0 in Y_i, where i = 1, 2,…, D and D is the dimensionality of the problem, which is obtained as follows (Emary et al. 2016):

$$ m_{10} = \mathop \sum \limits_{d = 1}^{D} I_{d} ,\quad {\text{where}}\quad I_{d} = \left\{ {\begin{array}{*{20}l} {1, } \hfill & {{\text{if}}\,\left( {x_{id } = 1\,{\text{and}}\,y_{id } = 0} \right)} \hfill \\ {0,} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right. $$

(13)

m₀₁ indicates the number of bits when x_id = 0 in X_i and y_id = 1 in Y_i, where i = 1, 2,…, D and D is the dimensionality of the problem, which is obtained as follows (Emary et al. 2016):

$$ m_{01} = \mathop \sum \limits_{d = 1}^{D} I_{d} ,\quad {\text{where}}\quad I_{d} = \left\{ {\begin{array}{*{20}l} {1, } \hfill & {{\text{if}}\,\left( {x_{id } = 0\,{\text{and}}\,y_{id } = 1} \right)} \hfill \\ {0,} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right. $$

(14)

m₀₀ indicates the number of bits when x_id = 0 in X_i and y_id = 0 in Y_i, where i = 1, 2,…, D and D is the dimensionality of the problem, which is obtained as follows (Emary et al. 2016):

$$ m_{00} = \mathop \sum \limits_{d = 1}^{D} I_{d} ,\quad {\text{where}}\quad I_{d} = \left\{ {\begin{array}{*{20}l} {1, } \hfill & {{\text{if}}\,\left( {x_{id } = 0\,{\text{and}}\,y_{id } = 0} \right)} \hfill \\ {0,} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right. $$

(15)

m₀₀ is not used in Jaccard’s similarity measurement technique, because the value of 0 between two binary structures does not make sense in Jaccard’s similarity measurement technique.

By taking into account Jaccard’s coefficient of similarity, an intuitive measure of dissimilarity between X_i and Y_i, which defines how far apart X_i and Y_i are from each other, can be calculated as follows (Çınar and Kiran 2018):

$$ {\text{Dissimilarity}}\left( {X_{i} ,Y_{i} } \right) = 1 - {\text{Similarity}}\left( {X_{i} ,Y_{i} } \right) = 1 - \frac{{m_{11} }}{{m_{01} + m_{10} + m_{11} }} $$

(16)

where dissimilarity (X_i, Y_i) is in the range of [0, 1].

3.2.2 Generating a new solution in SimSSA

Two different spider values are used to generate a new solution in SimSSA (present spider and best spider (spider_best in spider population) or present spider and randomly selected neighbor spider). In order to generate a new solution in the binary search space for binary SSA, Eq. 17 is used.

$$ {\text{Dissimilarity}}\left( {X_{\text{new}} ,X_{i} } \right) \approx \varphi \times \,{\text{Similarity}}\left( {X_{i} ,Y_{i} } \right) $$

(17)

where X_new is the newly generated spider (the candidate solution) for the current spider (X_i), X_i is the current spider, Y_i is a random spider and φ is a positive random scaling factor. And ≈ is the almost equal operator. In other words, to produce the new binary solution X_new, the value of the following three variables (M₁₁, M₁₀ and M₀₁) must be determined.

$$ \hbox{min} \left| {\left( {1 - \frac{{M_{11} }}{{M_{11} + M_{10} + M_{01} }}} \right) - \varphi \times \left( {1 - \frac{{m_{11} }}{{m_{11} + m_{10} + m_{01} }}} \right)} \right| $$

(18)

$$ M_{11} + M_{01} = n1 $$

(19)

$$ M_{10} \le n0 $$

(20)

$$ M_{10} , M_{01} , M_{11} \ge 0\,{\text{and}}\,{\text{integer}} $$

(21)

where n1 is the total number of bits with value 1 in X_i and n0 is the total number of bits with value 0 in X_i. For determining the values of M₀₁, M₁₀ and M₁₁, the integer mathematical model given by Eqs. (18)–(21) must be solved. After solving the mathematical model and getting the optimal values of M₀₁, M₁₀ and M₁₁, the X_new candidate solution can be obtained using the new binary solution generator (NBSG). The workings of the NBSG algorithm are explained with the example for 16-bit individuals below:

Let X_i = [0011010110101110], Y_i = [1000101111000110] and φ = 0.7

m₁₁ = 4, m₀₁ = 4, m₁₀ = 5, m₀₀ = 3 [m₀₀ is not used in Jaccard’s similarity measurement technique (Ling et al. 2010b)].

$$ \begin{aligned} & {\text{Dissimilarity}}\left( {X_{i} ,Y_{i} } \right) = 1 - {\text{Similarity}}\left( {X_{i} ,Y_{i} } \right) = 1 - \frac{{m_{11} }}{{m_{01} + m_{10} + m_{11} }} = 1 - \frac{4}{4 + 4 + 5} = 1 - \frac{4}{13} = 0.69 \\ & A = \varphi \times {\text{Dissimilarity}}\left( {X_{i} ,Y_{i} } \right) = 0.7 \times 0.69 = 0.48 \\ \end{aligned} $$

According to the integer mathematical model given by Eqs. (18)–(21):

$$ \begin{aligned} & \hbox{min} f\left| {\left( {1 - \frac{{M_{11} }}{{M_{11} + M_{10} + M_{01} }}} \right) - A} \right| = \hbox{min} f\left| {\left( {1 - \frac{{M_{11} }}{{M_{11} + M_{10} + M_{01} }}} \right) - 0.48} \right| \\ & M_{11} + M_{01} = 8\left( {n1} \right) \\ & M_{10} \le 8 \left( {n0} \right) \\ & M_{10} , M_{01} , M_{11} \ge 0\,{\text{and}}\,{\text{integer}} \\ \end{aligned} $$

After the model is solved by using an enumeration scheme, the optimal output is obtained as M₀₁ = 0, M₁₀ = 5 and M₁₁ = 8 and f = 0.1. After all, X_new is generated as a 1 × 16 zero-bit array by using the NBSG algorithm given as follows:

Inheritance phase The positions of the bits that are equal to 1 in X_i are found (Ones_Xi = [3, 4, 6, 8, 9, 11, 13, 14, 15]) and M₁₁ = 8 bit positions are selected from the OnesXi (assume that the random selection [3, 4, 6, 8, 9, 11, 13, 15], and the bits of X_new in these positions are changed to 1. The new state of X_new is [0011010110101010].

Disinheritance phase The positions of the bits that are equal to 0 in X_i are found (Zeros_Xi = [1, 2, 5, 7, 10, 12, 16]) and the M₁₀ = 5 bit position is selected from the ZerosX_i (assume that the random selection includes [1, 2, 5, 12, 16]), and the bit of X_new in these positions is changed to 1. After this change, the final state of the candidate solution X_new is [1111110110111011].

Some examples of using the NBSG algorithm can be seen in (Çınar and Kiran 2018; Jaccard 1901; Choi et al. 2010). NBSG algorithm operation steps are shown in Table 3.

Table 3 NBSG algorithm (Jaccard 1901)

3.3 Logic gate-based social spider algorithm (LogicSSA)

Logic gates are very suitable for working on binary structures in binary solution space. The input and output values of these gates are binary values {0, 1}. There are basically three gates. These are “AND,” “OR” and “Exclusive or (XOR)” logic gates. Exclusive or (XOR) logic gate is a combination of “AND” and “OR” logic gates and is widely used in logical situations (Çinar and Kiran 2018; Aslan et al. 2019; Kiran and Gunduz 2013). In LogicSSA, the “XOR” logic gate is used in a new candidate solution (new spider) production stage. Because the changing probability of the bit (bit value = 0 and bit value = 1) in the solution is 50% in this gate. In the “OR” logic gate, the changing probability of the bit (bit value = 1) in the solution is 75% and the changing probability of the bit (bit value = 0) in the solution is 25. In the “AND” logic gate, the changing probability of the bit (bit value = 1) in the solution is 25% and the changing probability of the bit (bit value = 0) in the solution is 75. In the “XOR” logic gate, the probabilities are equal to each other. The truth tables and these situations are given in Table 4. “+” symbol represents “OR” logic gate, “&” symbol represents “AND” logic gate and “⊕” symbol represents “XOR” logic gate. In order to improve the search capability of binary SSA, the XOR gate is used in candidate solution production and the behavior of the ST control parameter is slightly changed. In this paper, the control parameter value of ST is taken as 0.3 (Çınar and Kiran 2018). In LogicSSA, a new candidate solution (spider) has been created with Eq. 22.

$$ S_{kj} = \left\{ {\begin{array}{*{20}l} {X_{ij} \oplus \left( {B_{j} \oplus N_{rj} } \right),} \hfill & {{\text{if}}\,\left( {{\text{rand}}_{ij} < {\text{ST}}} \right)} \hfill \\ {X_{ij} ,} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right. $$

(22)

where S_kj is the jth dimension of kth new spider (candidate solution) produced for the ith spider, X_ij is the jth dimension of ith spider, B_j is the jth dimension of best spider obtained so far and N_rj is the jth dimension of neighbor spider randomly selected from the search space.

Table 4 OR, AND and XOR truth tables

3.4 Binary SSA based on similarity measurement and logic gate

Binary SSA is an algorithm consisting of a combination of LogicSSA and SimSSA techniques. We use both techniques in the production of candidate solutions in binary SSA. One of the SimSSA or LogicSSA techniques is selected according to a randomly generated variable in the [0, 1] range. This selection process is shown in Eq. 23.

$$ {\text{Candidate}}\,{\text{Solution}}\,{\text{Production}}\,{\text{Method}} = \left\{ {\begin{array}{*{20}l} {{\text{SimSSA}},} \hfill & {{\text{if}}\,({\text{rand}} < 0.5)} \hfill \\ {{\text{LogicSSA}},} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right. $$

(23)

In the binary SSA approach, one of the SimSSA or LogicSSA techniques is selected for the production of new candidate solutions. Both techniques (SimSSA and LogicSSA) in search space have some advantages. LogicSSA has a strong local search capacity, and SimSSA is good at discovering the points on the solution space. Therefore, binary SSA based on SimSSA and LogicSSA is also useful to provide a balanced search in the solution space. So new candidate solutions (new spiders) are produced by using similarity measurement and logic gate techniques, and more efficient individuals are obtained by comparing with the current individuals. Since both techniques have advantages in different views, the probability of selecting any of the techniques is determined as 0.5. This fixed selection rate can be changed according to the structure of BOPs. The detailed pseudocode of the binary SSA is shown in Fig. 4.

Fig. 4

Detailed pseudocode of the binary SSA

According to Fig. 4, the proposed binary SSA consists of three main stages. In the first stage, the basic parameters are defined and random binary positions for the social spiders are determined in binary space. In the second stage, the fitness function is run in binary space for the spiders and the best fitness value is calculated. Vibrations are calculated for each spider, random walking is performed. Spider positions in the continuous search space are calculated according to the transfer function, and their equivalents in the binary space are determined. They are converted to binary {0, 1} according to a certain threshold value. In addition, we show the binary SSA as binary SSA-Tanh when k = 1, binary SSA-Sigm when k = 2, binary SSA-MSigm when k = 3 and binary SSA-Arctan when k = 4. In the third stage, the candidate solutions production method (including SimSSA and LogicSSA) is run to produce candidate solutions (new spiders). Produced candidate solutions are compared with the existing spider population. If the fitness values of the candidate solutions are better than the fitness values of the current population individuals, the population of individuals is swapped mutually with the candidate solutions. Otherwise, no changes will be made. The best result is obtained.

In this paper, the continuous test function is handled as a BOP where each dimension is encoded by Q-bit binary string such that first bit for the sign of the number, the subsequent P bits for the integer part and the final Q − P − 1 bits for a fractional part of the number. The values of Q and P were chosen for each test function according to the range values of the number. For example, for f1 benchmark function, we used Q = 13, P = 7, the first bit of Q = the sign of bit and a fractional part = Q − (P + 1(the sign bit)) = 13 − (7 + 1) = 5 where the problem is handled with binary strings until the termination condition is satisfied. Afterward, each of these Q-bit strings is converted into a real number, and the fitness value is computed.

4 Experimental results and analysis

Binary social spider algorithm is tested on MATLAB R2014a that installed over windows 7, 64 bit, the system of 2.30 GHz processor with 4 GB RAM. Each binary SSA variation is tested twenty independent runs with the same maximum number of iterations for each run. To have fair comparisons, all binary SSA variations have been carefully run in the same programming language, similar platform and similar parameter values. In experimental studies, eighteen different unimodal and multimodal benchmark functions, which are shown in Table 5, are solved separately. Wilcoxon signed-rank test is applied for the variations of binary SSA for obtained fitness values of spider populations.

Table 5 Classical benchmark functions used in the experimental study

Benchmark functions divided into two groups according to their type. These functions are obtained from various sources (Yu and Li 2015; Rizk-Allah et al. 2018; Surjanovic and Bingham 2019; Jamil and Yang 2013).

Group I Unimodal benchmark functions f1–f11, which has only one global optimum and can evaluate the exploitation capability of the investigated algorithms.

Group II Functions f12–f18 (multimodal), which include many local optimal whose number increases exponentially with the problem size, become highly useful when the purpose is to evaluate the exploration capability of the investigated algorithms.

For each benchmark function, four measures are used to evaluate the performance of each algorithm to solve that function. These measures include (1) average (mean), (2) standard deviation (sd), (3) minimum value (best) and (4) maximum value (worst) any they defined as in Table 6. n_run represents the total number of runs.

Table 6 Performance measure

4.1 Determination of initial population size on the fitness function

Different combinations of population size are tested on f1, f5, f15 and f17 selected randomly unimodal and multimodal benchmark functions. The results are shown in Table 7. According to the results, the most appropriate values are determined as 30 for the initial population size.

Table 7 Mean of the fitness values according to different combinations of population size (N) on f1, f5, f15 and f17

The same parameters used in the variations of binary SSA comparison, which are population size (N), maximum iteration value and other parameters, are shown in Table 8.

Table 8 Parameter setup for binary SSA variations (i.e., binary SSA-Tanh, binary SSA-Sigm, binary SSA-MSigm and binary SSA-Arctan)

4.2 Comparison between different variations of binary SSA

The variations of binary SSA based on SimSSA and LogicSSA (i.e., binary SSA-Tanh, binary SSA-Sigm, binary SSA-MSigm and binary SSA-Arctan) are tested in eighteen different unimodal and multimodal benchmark functions. Each benchmark function is run 20 times. The best, worst, mean and standard deviation (SD) are done for obtained benchmark function results. The best, worst, mean and standard deviation (SD) comparison results, which are obtained for unimodal benchmark functions (f1–f11) by selecting population size (N) = 30 and maximum iteration = 50 values for binary SSA, are shown in Table 9. The standard deviation results, the mean results and the best results of variations of binary SSA’s superior performance are marked in bold.

Table 9 Comparison of binary SSA-Tanh, binary SSA-Sigm, binary SSA-MSigm and binary SSA-Arctan with population size = 30 in unimodal benchmark functions with the maximum number of iterations = 50

According to the standard deviation results, binary SSA-Arctan has shown better performance than binary SSA-Tanh, binary SSA-Sigm and binary SSA-MSigm in all unimodal benchmark functions. The binary SSA-Arctan variation shows success at roughly 81.81% of unimodal benchmark functions for 9 out of 11 benchmark functions (f1, f2, f3, f4, f5, f6, f7, f9 and f10). According to the mean results, binary SSA-Arctan has shown better performance than binary SSA-Tanh, binary SSA-Sigm and binary SSA-MSigm in all unimodal benchmark functions. The binary SSA-Arctan variation shows success at roughly 63.63% of unimodal benchmark functions for 7 out of 11 benchmark functions (f1, f3, f5, f6, f7, f9 and f10). According to the best results, binary SSA-Arctan has shown high performance in all unimodal benchmark functions. The binary SSA-Arctan variation shows success at roughly 100% of unimodal benchmark functions for 11 out of 11 benchmark functions. The reason for this success is due to a more balanced diversification between the candidate solutions with the similarity measurement and logic gate techniques and type of the transfer function.

The best, worst, mean and standard deviation (SD) comparison results, which are obtained for multimodal benchmark functions (f11–f18) by selecting population size (N) = 30 and maximum iteration = 50 values for binary SSA, are shown in Table 10.

Table 10 Comparison of binary SSA-Tanh, binary SSA-Sigm, binary SSA-MSigm and binary SSA-Arctan with population size = 30 in multimodal benchmark functions with the maximum number of iterations = {50, 50, 50, 50}

For Table 10, according to the standard deviation results, binary SSA-Arctan has shown better performance than binary SSA-MSigm, binary SSA-Sigm and binary SSA-Tanh in all multimodal benchmark functions. The binary SSA-Arctan variation shows success at roughly 71.43% of multimodal benchmark functions for 5 out of 7 benchmark functions (f12, f13, f14, f15 and f18). According to the mean results, binary SSA-Arctan has shown better performance than binary SSA-MSigm, binary SSA-Sigm and binary SSA-Tanh in all multimodal benchmark functions. The binary SSA-Arctan variation shows success at roughly 57.14% of multimodal benchmark functions for 4 out of 7 benchmark functions (f13, f14, f15 and f18). According to the best results, binary SSA-Arctan has shown better performance than binary SSA-Tanh, binary SSA-Sigm and binary SSA-MSigm in all multimodal benchmark functions. The binary SSA-Arctan variation shows success at roughly 57.14% of multimodal benchmark functions for 4 out of 7 benchmark functions (f13, f14, f15 and f16). According to the best results, binary SSA-Arctan and binary SSA-MSigm variations show success at roughly 57.14% of multimodal benchmark functions for 4 out of 7 benchmark functions and binary SSA-Tanh variation shows success at roughly 71.43% of multimodal benchmark functions for 5 out of 7 benchmark functions. According to the results, binary SSA-Tanh and binary SSA-Arctan have shown superior performance compared to other variations of binary SSA according to many measurement criteria (best, worst, mean and SD). Based on the observed results, it can conclude that binary SSA-Tanh and binary SSA-Arctan have good quality and stability than the others. Binary SSA-Tanh and binary SSA-Arctan variations have established a more stable balance between exploration and exploitation.

The comparison results of fitness value, which are obtained for eighteen unimodal and multimodal benchmark functions by selecting population (N) size as 30 and maximum iteration as 50 for variations of binary SSA, are shown in Fig. 5. Based on the convergence graphics of the benchmark functions, three significant conclusions can be drawn: (1) Binary SSA-Tanh and binary SSA-Arctan provide the best convergence speed on almost selected functions, and also, binary SSA-Tanh and binary SSA-Arctan perform better than the other comparative variations of binary SSA. (2) The binary SSA-Tanh and binary SSA-Arctan provide stable solutions on almost selected benchmark functions, which imply the reliability of solutions, especially for large-scale instances. (3) Most results of the binary SSA-Tanh, binary SSA-MSigm and binary SSA-Arctan exhibit a continuous improvement during the optimization process.

Fig. 5

Convergence graphics for variations of binary SSA for benchmark functions (f1–f18)

In particular, the variation of binary SSA-Arctan has quickly reached an optimum solution in almost all benchmark test functions. The convergence speed of this algorithm is increased by the logic gate and similarity measurement techniques added during the candidate solution production stage. With the similarity measurement technique (SimSSA), this algorithm has succeeded in finding new points in binary search space and finding global optimum instead of local optimums. Logic gates, a new and successful technique, have become very popular in recent years. In this paper, the LogicSSA technique is proposed, which is based on logic gates. With the LogicSSA technique, binary SSA has been saved from local traps in the local search space and the ability to discover local optimums has been increased.

4.3 Wilcoxon signed-rank test and evaluation of binary SSA variations

In this paper, variations of binary SSA are operated with 20 times various eighteen unimodal and multimodal benchmark functions with population size = 30 and maximum iteration = 50. Twenty trials are done in each of the unimodal and multimodal benchmark functions, and twenty data sets are obtained. Whether there is a significant difference in this data set is searched by using the Wilcoxon signed-rank test (Derrac et al. 2011). The test results are shown in Table 11 for unimodal benchmark functions, and Table 12 shows multimodal benchmark functions. In Wilcoxon signed-rank test, alpha = 0.05 meaning level and determined value are 52 for n = 10 (n is data set number) (Acılar 2013). Two hypotheses are evaluated in the results. In the H₀ hypothesis, M_data1 = M_data2, and in H₁ hypothesis, M_data1 ≠ M_data2. H₀ hypothesis is rejected in h = 1 values and it is called that there is a semantic difference between the algorithms. The p values of the hypothesis are calculated by using MATLAB R2014a software. By these hypothesizes, the superiority among two optimizers can be determined. In this paper, we investigated whether there is a significant difference between variations of the binary SSA results. All variations of binary SSA are tested with Wilcoxon signed-rank test. If the obtained results in benchmark functions are equal, the Wilcoxon signed-rank test is not applied and the result is “NaN.” According to the obtained results through implementing the Wilcoxon signed-rank test for pair-wise comparisons between variations of the binary SSA, there is not a semantic difference between the results obtained from binary SSA-Arctan and binary SSA-MSigm.

Table 11 Wilcoxon signed-rank test on variations of binary SSA in the maximum number of iterations = 50 and population size = 30 in unimodal benchmark functions (f1–f11)

Table 12 Wilcoxon signed-rank test on variations of binary SSA in the maximum number of iterations = 50 and population size = 30 in multimodal benchmark functions (f12–f18)

Table 13 shows the obtained results through implementing the Wilcoxon signed-rank test for comparisons between binary SSA-Arctan and the other variations of the binary SSA. From these results, we can conclude that the binary SSA-Arctan has a superior performance over the other variations.

Table 13 Wilcoxon signed-rank test for comparison results in Tables 9 and 10

4.4 Comparison of binary SSA with other meta-heuristic algorithms

Case Study 1 Well-known heuristic algorithms of the literature and recently developed binary algorithms are shown in Table 14. In this paper, particle swarm optimization (PSO), genetic algorithm (GA), binary hybrid particle swarm optimization with wavelet mutation (BHPSOWM), BSalpSA, binary particle swarm optimization (BPSO), binary bat algorithm (BBA), BSCO, BSSO and binary SSA are compared in various unimodal and multimodal benchmark functions in equal comparison parameters. The parameters used in all comparison algorithms are shown in Table 15.

Table 14 Keys commonly used for comparative algorithms

Table 15 Parameters of all algorithms

BPSO, BBA, BSCA, BSalpSA, BSSO and variations of binary SSA (i.e., binary SSA-Tanh, binary SSA-Sigm, binary SSA-MSigm and binary SSA-Arctan) algorithms are compared according to four different criteria. There are the mean, the standard deviation (SD), the best and the worst criteria. In the compared algorithms, the population size (N) is determined as 30 and a maximum number of iterations is determined as 50 for variations of binary SSA equally. The comparison results are shown in Table 16.

Table 16 Variations of binary SSA and its comparison with comparative algorithms in BPSO, BBA, BSCA and BSalpSA

In Table 16, the standard deviation, the mean and the best results of variations of binary SSA’s superior performance are marked in bold. The variations of binary SSA have displayed an extremely good performance in selected benchmark functions in various comparison criteria according to comparison results. According to the standard deviation results, binary SSA has shown better performance than BPSO, BBA, BSCA and BSalpSA in all the unimodal and multimodal benchmark functions. According to the standard deviation, mean and best results, the binary SSA shows success at roughly 88.89% of multimodal benchmark functions for 8 out of 9 benchmark functions (f1, f3, f4, f5, f6, f15, f16 and f17). BSalpSA is the second-best performing algorithm after binary SSA. The results show that binary SSA finds superior solutions with satisfactory standard deviation values. Binary SSA has achieved this success thanks to its similarity measurement and logic gate methods. Thus, the exploration and exploitation capability of binary SSA in the binary search space has been improved. Thus, it is more advantages than other comparison algorithms.

Case Study 2 Social spider optimization is another comparative heuristic algorithm that is very similar to the SSA algorithm, but totally different from it. In SSO, there are two different searching agents (spider) in the search space of SSO. These are male and female spiders. Depending upon the gender, each individual operates a range of different evolutionary operators that imitates various collaboration behaviors that typically exist in colonies (Cuevas et al. 2013; Shukla and Nanda 2018). In SSA, there is no gender discrimination between the spiders. There is a single type searching agent (spider) in search space. In this paper, BSSO and binary SSA are also compared in various unimodal and multimodal benchmark functions in equal comparison parameters. Table 17 shows the parameters for both algorithms. The results of the best, mean, worst and standard deviation are shown in Tables 18 and 19 for unimodal and multimodal benchmarks, respectively. According to the mean of fitness results, binary SSA shows a higher success than BSSO. According to the standard deviation of fitness results, the binary SSA shows high success at roughly 94.44% of benchmark functions for 17 benchmarks out of 18 benchmarks (f1, f2, f3, f4, f5, f6, f7, f8, f9, f10, f11, f12, f13, f14, f15, f16 and f18) and the BSSO shows success at roughly 38.89% of benchmark functions for 7 benchmarks out of 18 benchmarks (f1, f3, f5, f7, f10, f13 and f17). According to the mean of fitness results, the BSSO shows success at roughly 22.22% of benchmark functions for 4 benchmarks out of 18 benchmarks (f1, f5, f10 and f17). Thanks to the logic gate and similarity measurement techniques, binary SSA has passed BSSO. It has developed the ability to search locally and search globally in binary space.

Table 17 Parameter settings for BSSO and binary SSA

Table 18 Variations of binary SSA and its comparison with BSSO in all the unimodal benchmark functions

Table 19 Variations of binary SSA and its comparison with BSSO in all the multimodal benchmark functions

Case Study 3: Other meta-heuristic algorithms which are BHPSOWM, PSO, GA and variations of binary SSA are compared according to four different criteria. These are the mean, the standard deviation (SD), the best and the worst criteria. In the compared algorithms, the population size (N) is determined as 30 and the maximum number of iterations is determined as 50 for variations of binary SSA equally. The comparison results are shown in Table 20. The standard deviation, the mean and the best results of variations of binary SSA’s superior performance are marked in bold. According to the standard deviation and mean results, binary SSA has shown better performance than BHPSOWM, PSO and GA in all the unimodal and multimodal benchmark functions. The SimSSA and LogicSSA techniques have a significant impact on the performance of binary SSA. Based on the obtained results, it is concluded that the proposed binary SSA has promising results for BOPs.

Table 20 Variations of binary SSA and its comparison with comparative algorithms in BHPSOWM, PSO and GA

4.5 Discussion about the variations of binary SSA

In this paper, the SSA is modified again according to four different transfer functions for mapping the continuous search space to the binary search space. Four variations of binary SSA are proposed based on four transfer functions. In order to ensure the balance between exploration and exploitation, two different techniques (SimSSA and LogicSSA) are developed at the candidate solution production stage. Performances of the variations of binary SSA are tested with eighteen benchmark functions which are widely used unimodal and multimodal benchmark functions in the literature. The variations of binary SSA are compared according to four different criteria. There are the mean, the standard deviation (SD), the best and the worst criteria. Performances of the variations of binary SSA are also compared with well-known and recently developed binary methods in the literature.

f2, f7, f8, f9, f10, f11, f12, f13 and f14 benchmark functions are also used as a test function for variations of binary SSA, and the obtained results are compared with variations of binary SSA. But, related performance comparisons could not be performed and are not mentioned in this paper as there are not many papers that are studied with the benchmark functions in the literature.

According to the comparisons among the variations of binary SSA, we can state that binary SSA-Tanh and the binary SSA-Arctan variations have high performance among other variations of binary SSA and comparative algorithms. In this context, the advantages behind this high performance are due to one reason: Binary SSA combines the methods of SimSSA and LogicSSA which can make the balance between exploration and exploitation capabilities. The transfer function is supported by these methods. Thus, binary SSA’s binary optimization problem-solving success is increased.

5 Conclusion

Social spider algorithm (SSA) is a heuristic algorithm that is created by imitating spider behaviors in nature. In this paper, SSA has studied details and a binary SSA has been proposed to solve binary optimization problems (BOPs). In order to obtain binary search space in binary SSA, four different transfer functions are used. Four different variations of binary SSA (binary SSA-Tanh, binary SSA-Sigm, binary SSA-MSigm and binary SSA-Arctan) have been developed. Two new techniques (SimSSA and LogicSSA) are developed during the candidate solutions production phase in binary SSA, and the variations of binary SSA based on SimSSA and LogicSSA are developed. The SimSSA technique uses Jaccard’s similarity in a new spider (candidate solution) production phase, and the LogicSSA technique uses consist of XOR logic gate in the new spider (candidate solution) production phase. In the binary SSA, one of the SimSSA or LogicSSA techniques is selected for the production of new candidate solutions at any time. Binary SSA’s local search capability has been improved with logic gates that are frequently used in the BOPs in recent years. With the similarity measurement technique, the power of binary SSA to discover new points in binary search space is increased. With the similarity measurement technique, this algorithm guarantees to find global optimum instead of local optimums. The variations of binary SSA are operated in eighteen different unimodal and multimodal benchmark functions in order to evaluate their performances. The performance of variations of binary SSA is compared in various criteria. Wilcoxon signed-rank test is operated on obtained results. Particle swarm optimization (PSO), genetic algorithm (GA), BSalpSA, BHPSOWM, BPSO, BBA, BSCA and BSSO which are well-known heuristics algorithms in the literature are compared with the variations of binary SSA.

According to the comparisons among the variations of binary SSA, we can state that binary SSA-Arctan and binary SSA-Tanh variations have high performance among other variations of binary SSA. The comparison results affirmed the superiority of the binary SSA-Arctan and binary SSA-Tanh variations in providing a good quality of solutions for most tests.

In future research, we will design new transfer functions. Besides, we will measure the performance of our proposed method in different applications including knapsack problems and feature selection in classification.

5.1 Replication of results

Most of the codes required to replicate the results in this paper are available under open-source licenses and are maintained in version control repositories. The spider social algorithm and the spider social optimization are available from GitHub (https://github.com/James-Yu/SocialSpiderAlgorithm). Benchmark test functions are available from http://www.sfu.ca/ssurjano.