RETRACTED ARTICLE: New SVM kernel soft computing models for wind speed prediction in renewable energy applications

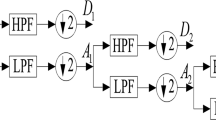
Abstract

This paper proposes a hybrid multi-step wind speed prediction model based on combination of singular spectrum analysis (SSA), variational mode decomposition (VMD) and support vector machine (SVM) and was applied for sustainable renewable energy application. In the proposed SSA–VMD–SVM model, the SSA was applied to eliminate the noise and to approximate the signal with trend information; VMD was applied to decompose and to extract the features of input time series wind speed data into a number of sub-layers; and the SVM model with various kernel functions was adopted to predict the wind speed from each of the sub-layers, and the parameters of SVM were fine-tuned by differential evolutionary algorithm. To investigate the effectiveness of the proposed model, various prediction models are considered for comparative study, and it is demonstrated that the proposed model outperforms with better prediction accuracy.

1 Introduction

The energy crisis is one of the major problems faced by our country, and the availability of fossil fuels will no longer exist in the future due to the growth of population and massive development of industrialization. The pollution-free renewable energy which is available abundantly on earth is wind energy, but the large-scale integration of wind turbines with grid is always a challenging task because of the nonlinear and uncertain nature of wind speed. This non-stationary wind speed imposes many challenges on power system such as fluctuation in frequency, power quality disturbances, uncertainty in the generated power, and load scheduling. These issues can be handled effectively with prior wind speed prediction, which ensures the stability of the power to be synchronized with grids. The wind speed prediction can be made as per the requirements; a-day-ahead prediction helps proper scheduling of wind forms to achieve optimal operating cost and planning for unit commitment, and the generation control can be made easy with 6-h-ahead prediction; load dispatch and load scheduling can be made easy with obtained results of 30-min- to 6-h-ahead prediction; few-seconds to 30-min-ahead prediction can be utilized for control of frequency, voltage regulation and turbine action, respectively. The existing few wind speed prediction methodologies were made under the detailed review as follows (Alencar et al. 2018; Shao et al. 2016; Khodayar et al. 2017; Gendeel et al. 2018; Luo et al. 2018; Haiqiang et al. 2017; Zhang et al. 2018; Jawad et al. 2018; Shi et al. 2018; Karakuş et al. 2017; Kaur et al. 2016; Chang et al. 2016; van der Walt and Botha 2016; Singh et al. 2016; Giannitrapani et al. 2016; Hu et al. 2015; Mao et al. 2016; Ren et al. 2014, 2016).

Alencar et al. (2018) proposed a hybrid forecasting model for multi-step wind forecasting with the combination of seasonal autoregressive integrated moving average (SARIMA) and neural networks. Initially, forecasting carried out for the determined explanatory variables, and then the actual forecasting of entire series has been carried out by the combination of the predicted forecasted series data and past history of data. The proposed model outperforms the other forecasting methods under comparative study. Based on the estimated frequency spectral components, a short term wind speed forecasting model was presented by Shao et al. (2016). The combined model of wavelet transformation (WT) and AdaBoost technique has been proposed to analyze the wind speed distribution for different seasons based on their scalogram percentage of energy distribution. The effectiveness of the proposed model was demonstrated with a case study. For ultra-short-term and short-term wind speed forecasting, a deep neural networks model with stacked autoencoder (SAE) and stacked denoising autoencoder (SDAE) is discussed by Khodayar (2017). The uncertainties in wind speed data are taken care by the SAE and SDAE; the experimental studies demonstrated better accuracy of the predicted results than other conventional neural network forecasting models. Gendeel et al. (2018) discussed about a hybrid prediction model with the combination of VMD and neural networks. The original wind speed data was decomposed into various intrinsic components, and the neural network was employed to present corresponding sub-models for each IMFs. The experimental results were made under the comparative study of other prediction models including NN with wavelet decomposition and empirical mode decomposition and demonstrated that the proposed model outperforms with better accuracy. To handle large data set of wind speed prediction models, Luo et al. (2018) presented a hybrid model of stacked extreme learning machine (SELM) and deep neural networks with generalized correntropy measure. The proposed model achieved a better computing performance and enhanced accuracy than any other models considered under comparison. Haiqiang et al. (2017) proposed a spatial and temporal correlation model for ultra-short-term wind speed prediction. The samples are grouped with similar correlation coefficient, and the representative time series of this group is modeled by autoregressive moving average (ARMA) model. Those which are not grouped under class are modeled by artificial neural networks. With meteorological data, the spatial correlation between the predicted and target farm has been investigated. Wind speed prediction model based on Lorenz disturbance and IPSO-BP neural network was presented by Zhang et al. (2018). The weights of backpropagation neural network are fine-tuned by the IPSO algorithm. The prediction results of the back propagation neural network model were improved by applied Lorenz disturbance.

Jawad et al. (2018) presented a short- and medium-term wind speed prediction based on a genetic algorithm-based nonlinear autoregressive neural network (GA–NARX–NN) model. The effective prediction accuracy of the proposed model has been demonstrated by numerical simulations. A wavelet neural network (WNN)-based multi-objective interval prediction model has been proposed by Shi et al. (2018) for short-term wind speed prediction. The prediction intervals were directly constructed by the generated Pareto optimal solutions. The coevolutionary algorithms were employed to fine-tune the weights of the proposed WNN wind prediction model. Karakus et al. (2017) presented a novel polynomial autoregressive model for 1-day-ahead wind speed and power prediction with improved accuracy. Further the adaptive neuro-fuzzy inference system (ANFIS) has been employed to carry out comparative study with the performance of PAR model, and the proposed model outperforms all other prediction models.

Artificial neural network-based short-term wind speed prediction model proposed by Kaur et al. (2016). Various ANN predictions models were developed, and their prediction accuracy was validated by MSE as performance metric. Chang et al. (2016) discussed about new hybrid wind forecasting model based on autoregressive integrated moving average (ARIMA) and radial basis function neural network (RBFNN). The hybrid model possesses a classic and nonlinear prediction model for linear and nonlinear components of the original wind speed data, respectively. The simulation results demonstrated that the proposed model was found to be a suitable model for wind speed prediction with better accuracy. van der Walt and Botha (2016) made a comparative study on regression algorithms for wind speed prediction. The regression models under the study included support vector regression, ordinary least squares and Bayesian ridge regression models, and the results depicted that the SVM regression showed improved performance over other two regression models. Singh et al. (2016) presented a neural network model for wind speed prediction for both Indian and UK power plant with better prediction accuracy. A-day-ahead wind prediction model was proposed by Giannitrapani et al. (2016), where stochastic optimization models were presented to obtain optimal solution. The least square SVM regression model was developed by Hu et al. (2015) for short-term wind speed forecasting with heteroscedasticity and stochastic gradient descent algorithm to solve the model. Mao et al. (2016) discussed on short-term wind speed wind speed prediction based on SVMs and backpropagation (BP) prediction algorithm. With better error correction method, the proposed methodology demonstrates significant improvement in prediction accuracy. Ren et al. (2016) presented EMD–SVM-based wind forecasting methodology, where the original wind speed series is decomposed in various IMFs. The proposed model outperforms several models in the literature. The comparative study made by Ren et al. (2014) on EMD, EEMD, CEEMD and CEEMD with adaptive noise (CEEMDAN). It was suggested that the performance of SVR significantly improved by EMD and marginally by ANN and further CEEMDAN–SVR among the EMD-based hybrid methods.

Considering the reviews made from the existing literature, it is observed that the following works were implemented—improvement in computational convergence of SVM based on its nature of transforming the quadratic problem into linear equations, improvement in the robustness and accuracy of short-term and very short term wind speed prediction strategies, developed ensemble algorithms and intelligent search algorithms, decomposing data with multi-decomposition models. The proposed wind speed prediction strategy employed SSA–VMD–SVM model where the data are pre-processed by employing SSA and sample entropy such that the trend information is extracted from original wind speed series, VMD is employed for further decomposition of the sub-series as EMD associated with limitations of its recursive nature; finally, the optimized SVM predictor is presented with various effective kernel functions for effective prediction. The proposed wind prediction model outperforms the existing literature, and it is more robust with highly optimized system parameters.

2 The SSA–VMD–SVM model

2.1 The framework of the proposed SSA–VMD–SVM model

The framework of the proposed SSA–VMD–SVM model can be summarized as follows:

• 1. The main idea of SSA is to decompose the original wind speed time series data into various independent components and noise, and the unpredictability of the each sub-series is evaluated by sample entropy concept, detailed in Sect. 2.2.

• 2. The high entropy sub-series are further decomposed into number of sub-layers by the adopted VMD technique, detailed in Sect. 2.3.

• 3. The SVM models are designed with various kernel functions to predict the wind speed data with the provided sub-layer data series, and the forecasted sub-layer data series is reconstructed to present multi-step forecasting sub-series, detailed in Sect. 2.4.

• 4. The differential evolution algorithm is adopted for fine-tuning SVM parameters, detailed in Sect. 2.5.

• 5. The forecasted sub-series are combined with original wind speed sub-series to present a multi-step forecasting sub-series and the wavelet filter adopted to deny the extra frequency components of the combined series, detailed in Sect. 2.6.

• 6. The experimental verification of the proposed model with case studies is detailed in Sect. 3.

• 7. To evaluate the performance of the designed models, various predictions models from the existing literature are considered for comparison, detailed in Sect. 3.3.

2.2 Singular spectrum analysis

Singular spectrum analysis is a nonparametric spectral extraction algorithm widely used in time series analysis. It decomposes the input time series into periodic and quasi-periodic components, and thus the noise can be reduced. The four stages of SSA algorithm include the embedding stage, decomposition stage, grouping and averaging stage. The working steps of the algorithm described as follows (Hassani 2010):

Stage 1: Embedding

In this step, the original wind speed data $X = (x_{1} ,x_{2} , \ldots x_{N} )$ are shifted to multi-dimensional vector space $Y = (y_{1} ,y_{2} \ldots y_{L} )$ with dimension $L$, where $1 < L < N$. The elements of $L$-lagged vector can be defined as:

$$ y_{i} = \left[ {x_{i} ,x_{i + 1} , \ldots x_{i + L - 1} } \right]^{T} $$

where $i = 1,2, \ldots K$ and $K = N - L + 1$ is the number of L-lagged vectors.

$$ Y = \left[ {\begin{array}{*{20}c} {x_{1} } & {x_{2} } & \cdots & {x_{K} } \\ {x_{2} } & {x_{3} } & \cdots & {x_{K + 1} } \\ \cdots & \cdots & \cdots & \cdots \\ {x_{L} } & {x_{L + 1} } & \cdots & {x_{N} } \\ \end{array} } \right] $$

(1)

Stage 2: Singular value decomposition

In this step, the matrix $Y$ is decomposed into $n$ components, where $n = rank(Y)$. Assuming the $L \times Llag$ covariance matrix $S = YY^{T}$, the eigenvalues of $S$ can be determined in descending order represented as, $\lambda_{1} ,\lambda_{2} , \ldots \lambda_{n}$, and their corresponding orthonormal system is represented as $u_{1} ,u_{2} , \ldots ,u_{d}$. Now, the SVD of the matrix $Y$ is represented as follows:

$$ Y = Y_{1} + Y_{2} + \cdots + Y_{n} $$

(2)

where $Y_{i} = \sqrt {\lambda_{i} u_{i} v_{i}^{T} }$, $i = 1,2, \ldots ,n$ and $n = \hbox{min} (L,K)$, $v_{i} = X^{T} u_{i} /\sqrt {\lambda_{i} }$ represents the principal component of the $L$-trajectory matrix $Y$, the set {$\sqrt {\lambda_{i} }$} is the spectrum of matrix $Y$, and $(\lambda_{i} ,u_{i} ,v_{i} )$ is the eigentriples of the matrix $YY^{T}$ in descending order of $\lambda_{i}$.

Stage 2: Reconstruction

Grouping:

The trend components $m$ out of $n$ eigentriplets are selected in this step, denote $I = \{ I_{1} ,I_{2} , \ldots I_{m} \}$ and $Y_{l} = Y_{l1} + Y_{l2} + \cdots + Y_{lr}$, where $Y_{l}$ represents the original component of the wind speed data $Y$ and remaining components $(n - m)$ eigentriples are corresponding to noise.

Averaging:

Based on Hankelization procedure, renovate the matrix group $Y_{l} = Y_{l1} + Y_{l2} + \cdots + Y_{lr}$ into a time series group $\{ X_{l1} ,X_{l2} , \ldots X_{lm} \}$. The reconstructed wind speed time series can be denoted as follows:

$$ X = H(Y_{l1} ) + H(Y_{l2} ) + \cdots + H(Y_{lm} ) + H(\varepsilon ) = X_{l1} + X_{l2} + \cdots + X_{lm} + H(\varepsilon ) $$

(3)

It can be rewritten as $X = X_{\text{trend}} + X_{\text{noise}}$, where $X_{trend} = X_{l1} + X_{l2} + \cdots + X_{lm}$ and $X_{\text{noise}} = H(\varepsilon )$.

2.3 Sample entropy

The thermodynamic concept employed to explain the degree of disorder of thermodynamic system is entropy. It was proposed by Richman and Moorman (2000) and has wide range of application in statistical fields (Tsai et al. 2012) and health monitoring (Widodo et al. 2011). The modified form of entropy is sample entropy with advantages such as data length independence and trouble-free implementation.

For the time series data $x = \{ x(1),x(2) \ldots x(N)\}$ of length $N$, the run length $m$ and tolerance window $r$, the sample entropy is applied as follows:

Step 1: Reconstruct the considered time series data into matrix form,

$$ X = \{ X_{m} (1),X_{m} (2), \ldots X_{m} (N - m + 1)\} , $$

(4)

$$ {\text{Where}},\;\;X_{m} (i) = \{ x(i),x(i + 1), \ldots x(i + m - 1)\} \;\;{\text{for}}\;\;1 \le i \le N - m + 1. $$

(5)

Step 2: The distance of $X_{m} (i)$, $X_{m} (j)$ and $d[X_{m} (i),X_{m} (j)]$ is defined as the absolute difference between their scalar components.

$$ d[X(i),X(j)] = \mathop {\hbox{max} }\limits_{k = 0 \sim m - 1} \left| {x(i + k) - x(j + k)} \right| $$

(6)

Step 3: For the defined $x_{m} (j)$, the number of elements in the collection $\{ j|d[X_{m} (i),X_{m} (j)] < r,j \ne i,\,1 \le j \le N - m\}$ is represented as count number $C_{i}$.

The ratio of $N_{m} (i)$ to total distance is defined as:

$$ C_{i}^{m} (r) = \frac{{C_{i} }}{N - m + 1} $$

(7)

Step 4: Evaluate the average $C_{i}^{m} (r)$ for all $i$, the probability matching of two sequence for m points denoted as:

$$ C^{m} (r) = \frac{1}{N - m}\sum\limits_{i = 1}^{N - m} {B_{i}^{m} (r)} $$

(8)

Step 5: For m = m + 1, repeat the steps (1–4) and calculate $C^{m + 1} (r)$.

Step 6: The sample entropy of $x$ is theoretically defined as:

$$ {\text{Sample}}\;{\text{Entropy}}(m,r) = \mathop {\lim }\limits_{N \to \infty } \left\{ { - \ln \left[ {\frac{{C^{m + 1} (r)}}{{C^{m} (r)}}} \right]} \right\} $$

(9)

For definite time series length, the entropy is estimated as:

$$ {\text{Sample}}\;{\text{Entropy}}\;(N,m,r) = - \ln \left[ {\frac{{C^{m + 1} (r)}}{{C^{m} (r)}}} \right] $$

The parameters of entropy are tuned based on Pincus (2001), in this paper $r = 0.1$ times the standard deviation of the wind speed time series and $m = 1$.

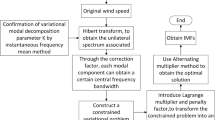
2.4 Variational mode decomposition (VMD)

Dragomiretskiy and Zosso (2014) proposed a new state-of-the-art decomposition algorithm called the variational mode decomposition (VMD). In VMD, the original time series data $x(t)$ are decomposed into discrete number of modes $u_{k} (t)$ with sparsity properties; each mode looks for the central frequency $\omega_{k}$ of limited bandwidth $B(u_{k} (t))$ by applying Hilbert transform of the associated signal such that the reconstruction of all modes reproduces the original time series signal. For the considered time series $x(t)$, it is decomposed into various predefined number of modes $u_{k} (t)$, for $k = 1,2, \ldots K$, where $K$ is number of modes.

$$ u_{k} (t) = A_{k} (t)\cos (\phi_{k} (t)) $$

(10)

where $A_{k} (t)$ is a nonnegative envelope, $\phi_{k} (t)$ is a non-decreasing phase function, and the instantaneous frequency that varies lower than $\phi_{k} (t)$ is $\omega_{k} (t) = \phi_{k}^{'} (t)$. The algorithmic steps followed to decompose the input time series signal into its various modes around a central frequency with limited bandwidth as follows:

Step 1: The analytical signal $u_{k,A} (t)$ for each mode $u_{k} (t)$, which has unilateral spectrum of nonnegative frequencies, is determined through Hilbert transform,

$$ Hu_{k} (t) = \frac{1}{\pi }p.v\int\limits_{R} {\frac{{u_{k} (v)}}{t - v}{\text{d}}v} $$

(11)

$$ u_{k,A} (t) = u_{k} (t) + jHu_{k} (t)A_{k} e^{{j\phi_{k} (t)}} $$

(12)

Step 2: For each mode $u_{k} (t)$, the frequency spectrum is shifted its base band by the following equation:

$$ u_{k,M} (t) = u_{k,A} (t)e^{{ - j\omega_{k} t}} $$

(13)

Step 3: For the above signals,$L^{2}$-norm of the gradient is estimated, and the bandwidth of the demodulated signal is expressed as:

$$ B(u(k)) = \left\| {\partial_{t} \left[ {\left( {\delta (t) + \frac{j}{\pi t}} \right)*u_{k} (t)} \right]e^{{ - j\omega_{k} t}} } \right\|_{2}^{2} $$

(14)

The variational problem is expressed as,

$$ \mathop {\hbox{min} }\limits_{{u_{k} ,\omega_{k} }} \left\{ {\sum\limits_{k = 1}^{K} {\left\| {\partial_{t} \left[ {\left( {\delta (t) + \frac{j}{\pi t}} \right)*u_{k} (t)} \right]e^{{ - j\omega_{k} t}} } \right\|_{2}^{2} } } \right\}\,\,\,\,\,{\text{subject}}\;{\text{to}}\,\,\,\sum\limits_{k = 1}^{K} {u_{k} = x(t)} $$

(15)

where $\delta (t)$ is the Dirac distribution.

The solution for the above variational problem is obtained by introducing Lagrangian multipliers $\lambda (t)$ which convert the problem into dual unconstrained problem and a quadratic penalty term $\alpha$ which retains the reconstruction accuracy.

$$ L(\{ u_{k} \} ,\{ \omega_{k} \} ,\lambda ): = \alpha \sum\limits_{k} {\left\| {\partial_{t} \left[ {\left( {\delta (t) + \frac{j}{\pi t}} \right)*u_{k} (t)} \right]e^{{ - j\omega_{k} t}} } \right\|_{2}^{2} } + \left\| {x(t) - \sum\limits_{k} {u_{k} (t)} } \right\|_{2}^{2} + \left\langle {\lambda (t),x(t) - \sum\limits_{k} {u_{k} (t)} } \right\rangle $$

(16)

Equation (15) is solved by obtaining saddle point of (16) by alternate direction method of multipliers.

2.5 Support vector machine

The statistical learning algorithm is developed to map the input data into high-dimensional future space via kernel functions. The nonlinear mapping eliminates the overfitting issues in the case of small data sets. So it is widely applied in pattern recognition, optimal control, regression and other fields. The basic concept of SVM regression model is explained as follows (Müller et al. 1997; Mukherjee et al. 1997).

For given input data set $\{ (x_{1} ,y_{1} ),(x_{2} ,y_{2} ) \ldots (x_{i} ,y_{i} )\}_{i = 1}^{N}$, where $x_{i} (x_{i} \in \Re^{d} )$ is the input vector of the first $i$ training samples, $x_{i} = \left[ {x_{i}^{1} ,x_{i}^{2} , \ldots ,x_{i}^{d} } \right]^{T}$ and $y_{i} \in \Re$ is the corresponding output data. The linear regression function $f(x) = \sum\nolimits_{i = 1}^{D} {w_{i} \phi_{i} (x) + b}$ is established in high-dimensional future space, where $\left\{ {\phi_{i} (x)} \right\}_{i = 1}^{D}$ are the features; $b$ and $\{ w_{i} \}_{i = 1}^{D}$ are the coefficients estimated by minimizing the function,

$$ R(w) = \frac{1}{N}\sum\limits_{i = 1}^{N} {\left| {f(x_{i} ) - y_{i} } \right|}_{\varepsilon } + \gamma \left\| {\left\| w \right\|} \right\|^{2} $$

(17)

$$ \left| {f(x,\alpha ,\alpha ^{*} )} \right|_{\varepsilon } = \left\{ {\begin{array}{*{20}l} {\left| {f(x) - y} \right| - \varepsilon } \hfill & {{\text{for}}\;\left| {f(x_{i} - y_{i} )} \right| \ge \varepsilon } \hfill \\ 0 \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right. $$

(18)

where $\gamma$ is the regularization constant and $\left| {f(x,\alpha ,\alpha^{*} )} \right|_{\varepsilon }$ is the cost function.

$$ {\text{The}}\;{\text{minimizing}}\;{\text{function is}}\;{\text{expressed}}\;{\text{as}}\;f\left( {x,\alpha ,\alpha^{*} } \right) = \sum\limits_{i = 1}^{N} {(\alpha_{i} - \alpha_{i}^{*} )k(x_{i} ,x_{j} ) + b} , $$

(19)

$\alpha_{i} \alpha_{i}^{*} = 0$, $\alpha_{i} ,\alpha_{i}^{*} \ge 0$ $i = 1,2, \ldots ,N$ and $k(x_{i} ,x_{j} ) = \phi (x_{i} ).\phi (x_{j} )$ represents the kernel function.

The coefficients of $\alpha_{i} \alpha_{i}^{*}$ determined by maximizing the following expression:

$$ \begin{aligned} & R(\alpha^{*} ,\alpha ) = - \varepsilon \sum\limits_{i = 1}^{N} {(\alpha_{i}^{*} + \alpha_{i} ) + \sum {y_{i} (\alpha_{i}^{*} - \alpha_{i} ) - \frac{1}{2}\sum\limits_{i,j = 1}^{N} {(\alpha_{i}^{*} + \alpha_{i} )} \times (\alpha_{i}^{*} - \alpha_{i} )k(x_{i} ,x_{j} )} } \\ & {\text{Subjected}}\;{\text{to}}\;\sum\nolimits_{i = 1}^{N} {(\alpha_{i}^{*} - \alpha_{i} ) = 0,\,\,\,\,\,\,0 \le \alpha_{i} } ,\alpha_{i}^{*} \le C \\ \end{aligned} $$

(20)

The parameters $C$ and $\varepsilon$ is to be optimally decided in following sections.

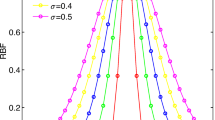
The following kernel functions are adopted in this paper for wind speed prediction:

• 1. Gaussian function:

  $$ k(x_{i} ,x_{j} ) = \exp \left( { - \frac{{\left\| {x_{i} - x_{j} } \right\|^{2} }}{{2\sigma^{2} }}} \right) $$

  (21)

• 2. Bessel function:

  $$ k(x_{i} ,x_{j} ) = - {\text{Bassel}}_{nu + 1}^{n} (\sigma \left| {x_{i} - x_{j} } \right|^{2} ) $$

  (22)

• 3. Pearson VII universal kernel (PUK) function:

  $$ k(x_{i} ,x_{j} ) = 1/\left[ {1 + \left( {2\sqrt {\left\| {x_{i} - x_{j} } \right\|}^{2} \sqrt {2^{(1/\omega )} - 1/\sigma } } \right)^{2} } \right]^{\omega } $$

  (23)

• 4. ANOVA radial basis function

  $$ k(x_{i} ,x_{j} ) = \left( {\sum\limits_{k = 1}^{n} {\exp ( - \sigma (x_{i}^{k} - x_{j}^{k} )^{2} )} } \right)^{d} $$

  (24)

• 5. Linear spline function in one dimension

  $$ k(x_{i} ,x_{j} ) = 1 + x_{i} x_{j} \hbox{min} (x_{i} + x_{j} ) - \frac{{x_{i} + x_{j} }}{2}\left( {\hbox{min} (x,x^{i} )^{2} } \right) + \frac{{x_{i} + x_{j} }}{3}\left( {\hbox{min} (x,x^{i} )^{3} } \right) $$

  (25)

2.6 Differential evolution algorithm

The performance of SVM greatly influenced by its parameters configuration, kernel functions, and kernel parameter settings. Because of these limitations, there are only limited existing studies on wind prediction models using SVM or all the existing studies are limited to particular few general kernel functions. In this paper, differential evolution algorithm is employed to fine-tune the SVM parameters and kernel parameters and their forecasting accuracies are investigated (Fig. 1).

Fig. 1

The framework of the SSA–VMD–SVM model

2.6.1 Initialization

DE is a population-based evolutionary algorithm and works with population of solutions rather than single solution. DE has $G$ generations of $P$ populations and possesses NP solution vectors; each of individual represents the solution for the concern optimization strategy.

$$ P^{(G)} = X_{i}^{G} = x_{j,i} ,\,\,\,\,i = 1,2, \ldots NP;\,\,\,\,j = 1,2, \ldots ,D;\,\,\,\,G = 1,2, \ldots ,G_{\hbox{max} } $$

(26)

The population is initialized with random values within the given boundary limits.

$$ x_{j,i}^{G = 0} = x_{j}^{\hbox{min} } + rand_{j} [0,1].(x_{j}^{\hbox{max} } - x_{j}^{\hbox{min} } )\;\;\forall \;\;i \in [1,NP];\;\;\forall \;\;j \in [1,D], $$

(27)

where $rand_{j} [0,1]$ represents the randomly initialized values from 0 to 1 (Fig. 2).

Fig. 2

Algorithm of VMD

2.6.2 Mutation

The mutant vector $V_{i}^{G + 1} = (V_{i,1}^{G + 1} ,V_{i,2}^{G + 1} , \ldots ,V_{i,D}^{G + 1} )$ is determined for each individual of the population at generation $G$ using the following expression:

$$ v_{i,j}^{(G + 1)} = x_{{i,r_{3} }}^{G} + F*(x_{{i,r_{1} }}^{G} - x_{{i,r_{2} }}^{G} ) $$

(28)

where $i \in [1,NP];$ $j \in [1,D];$ $r_{1} ,r_{2} ,r_{3} \in [1,D];$ are randomly selected but $r_{1} \ne r_{2} \ne r_{3} \ne i$, $k = (\text{int} (rand_{i} [0,1] \times D + 1),$ and $CR( = 0.9) \in [0,1]$, $F( = 0.5) \in [0,1]$. The mutually different vectors $r_{1} ,r_{2} ,r_{3}$ are randomly chosen population vectors, and they differ from running index $i$(for each vector) (Fig. 3)

Fig. 3

Differential evolution

2.6.3 Crossover

Unlike other evolutionary algorithms, DE has special population recombination scheme, and the population of next generation $P^{G + 1}$ is obtained from current population $P$. The trail vector $U_{i}^{G + 1} = (U_{i,1}^{G + 1} ,U_{i,2}^{G + 1} , \ldots ,U_{i,D}^{G + 1} )$ for each mutant vector is generated as follows:

$$ u_{i,j}^{(G + 1)} = \left\{ {\begin{array}{ll} {x_{{i,r_{3} }}^{G} + F*(x_{{i,r_{1} }}^{G} - x_{{i,r_{2} }}^{G} ),} & {{\text{if}}\;rand[0,1] < CR\, \vee \,\,j = k} \\ {x_{i,j}^{(G)} } & {\text{otherwise}} \\ \end{array} } \right. $$

(29)

For each randomly chosen index k for each vector in the interval, $j \in [1,2 \ldots D]$ to make sure that at least one vector parameter of individual trail vector originates from the mutated vector (Fig. 3).

2.6.4 Selection

The decision of the vector $U_{i}^{G + 1}$ to be member of future population is carried out in this step. The vector is compared with its corresponding population vector of generation by the following equation, and decision is made for the member of future population comprising the next generation.

$$ X_{i}^{G + 1} = \left\{ {\begin{array}{ll} {U_{i}^{G + 1} } & {{\text{if}}\;f(U_{i}^{G + 1} < f(X_{i}^{G} ))} \\ {X_{i}^{G} } & {\text{otherwise}} \\ \end{array} } \right. $$

(30)

3 Experimental setup

In this paper, the real-time wind speed data are gathered from Suzlon Energy Limited, Coimbatore, for 1 year. To evaluate the prediction accuracy of the proposed prediction methodology, three sets of 1 h average wind speed data series are used as the experiment data. Each set has 1000 data samples: 1–700 samples are used for training, and remaining 300 samples are used for testing. Three sets of 1-h average wind speed input series are shown in Fig. 4.

Fig. 4

Three sets of 1-h averaged wind speed series

3.1 Data preprocessing

To improve the prediction accuracy, the preprocessing of original wind speed series is important. To approximate the real-time data within the range of 0–1, the min–max normalization technique is employed. The real-time data are transformed into normalized data by the following equation.

$$ {\text{Normalized}}\;{\text{input}},\;\;I_{i}^{'} = \left( {\frac{{I_{i} - I_{\hbox{min} } }}{{I_{\hbox{max} } - I_{\hbox{min} } }}} \right)\left( {I_{\hbox{max} }^{'} - I_{\hbox{min} }^{i} } \right) + I_{\hbox{min} }^{'} $$

(31)

where $I_{i}$ is original input data, $I_{\hbox{min} }$ is the minimum input value, $I_{\hbox{max} }$ is the maximum input value, $I_{\hbox{max} }^{'}$ is the maximum target value, and $I_{\hbox{min} }^{'}$ is the minimum target value.

3.2 Performance evaluation

3.2.1 Error evaluation

The forecasting accuracy of the proposed model is investigated using three performance metrics including AE, MAE, MSE, and MAPE, which are tabulated in Tables 1 and 2 for 30-min-ahead prediction and 60-min-ahead prediction, respectively.

Table 1 Performance metric of 30-min-ahead prediction multi-step for Experiments 1, 2 and 3

Table 2 Performance metric of 60-min-ahead prediction multi-step for Experiment 1, 2 and 3

• 1. AE (absolute error)

  The absolute error reflects the positive and negative errors between original data and the predicted data.

  $$ {\text{AE}} = \frac{1}{N}\sum\limits_{t = 1}^{N} {(Y_{t}^{'} - Y_{t} )} $$

  (32)

• 2. MAE (mean absolute error)

  
  

  The mean absolute error reflects the level of error between the original data and the predicted data.

  $$ {\text{MAE}} = \frac{1}{N}\sum\limits_{t = 1}^{N} {\left| {Y_{t}^{'} - Y_{t} } \right|} $$

  (33)

• 3. MSE (mean square error)

  
  

  The average prediction errors can be predicted by employing MSE, which is the mean of prediction error squares.

  $$ {\text{MSE}} = \frac{1}{N}\sum\limits_{t = 1}^{N} {(Y_{t}^{'} - Y_{t} )}^{2} $$

  (34)

• 4. MAPE (mean absolute percentage error)

  
  

  The measure of prediction accuracy is demonstrated by employing MAPE, the common methodology employed in statistics.

  $$ {\text{MAPE}} = \frac{100}{N}\sum\limits_{t = 1}^{N} {\left| {(Y_{t}^{'} - Y_{t} )/Y_{t}^{'} } \right|} $$

  (35)

• 5. DA (direct accuracy)

  The direct prediction accuracy of the forecasted series is demonstrated by DA and expressed as follows:

  $$ {\text{DA}} = \frac{1}{N}\sum\nolimits_{i = 1}^{N} {w_{i} ,\,\,w_{i} = \left\{ {\begin{array}{ll} {0,} & {\text{otherwise}} \\ {1,} & {{\text{if}}\;(Y_{t + 1} - Y_{t}^{'} )(Y_{t + 1}^{'} - Y_{t}^{'} ) > 0} \\ \end{array} } \right.} $$

  (36)

  where N is the number of data samples, $Y_{t}^{'}$ is actual data, and $Y_{t}$ is the predicted output.

3.2.2 Pearson test

The prediction accuracy of the proposed models further is evaluated by Pearson test. Scientist Karl Pearson presented the Pearson test for statistical analysis. According to the test, if the Pearson correlation coefficient is equal to 1, then there exists a linear relationship between the actual and predicted outputs. And if the correlation coefficient is equal to 0, there exists no relationship between the actual and predicted outputs. For the given model of predictor with the actual data $Y_{t}^{'}$ and predicted data $Y_{t}$, the Pearson correlation coefficient can be expressed as follows:

$$ P = \frac{{\sum\nolimits_{t = 1}^{T} {(Y_{t}^{'} - Y_{m}^{'} )} (Y_{t} - Y_{m} )}}{{\sqrt {\left( {\sum\nolimits_{t = 1}^{T} {(Y_{t}^{'} - Y_{m}^{'} )^{2} \times \sum\nolimits_{t = 1}^{T} {(Y_{t} - Y_{m} )^{2} } } } \right)} }} $$

(37)

where $Y_{m}^{'}$ and $Y_{m}$ are the means of actual and predicted data, respectively.

3.3 Analysis made with the predicted outputs

The real-time wind speed data for 1 year are gathered from Suzlon Energy Limited, Coimbatore, and is averaged into three series: the individual series are utilized for Experiment 1, Experiment 2 and Experiment 3, respectively. The initial step of the proposed prediction model is to decompose the original wind speed input series and to extract the trend information with removal of noise by employing SSA. The unpredictability of each decomposed component is estimated by employing sample entropy. The sub-series of having most unpredictable data are further allowed for decomposition in VMD, and the modes obtained for Experiment 1 are shown in Fig. 5. Differential evolutionary algorithm employed to fine-tune the SVM parameters and kernel function parameters in order to improve the prediction accuracy. The obtained sub-sub-series are reconstructed in VMD and allowed for multi-step sub-series framework, and the extra frequency components are denied by wavelet filter. SVM predictor with various kernel functions process the multi-step sub-series, the resulted predicted output allowed for various performance metrics and reported in Tables 1 and 2 and Figs. 6, 7, 8 and 9.

Fig. 5

SSA and VMD results of Experiment-1

Fig. 6

Step-1 prediction of Experiment 1

Fig. 7

Step-2 prediction of Experiment 1

Fig. 8

Step-2 prediction of Experiment 1

Fig. 9

Performance analysis of proposed wind speed prediction model

The following analysis is made based on Figs. 6, 7, 8, 9 and Tables 1, 2, 3:

Table 3 Comparison made with different prediction models

• 1. The prediction accuracy for the proposed models are in order for all the experiments which indicates that the proposed models can be used for accurate wind speed prediction and the obtained results depend on the employed models of specified kernel function.

• 2. It is observed from Tables 1 and 2 that the values of DA decrease for steps and the values of performance indices increase, respectively.

• 3. Among the proposed individual models, the Gaussian–SVM model exhibits poor performance than the other models under the study. The MAPE of SSA–VMD–Gaussian–SVM is reported to be 15.925%, 17.036%, 15.260% for Experiments 1, 2 and 3, respectively, of 30-min-ahead prediction and 16.35%, 15.472%, 13.096%, respectively, for 60-min-ahead prediction.

• 4. The SSA–VMD–PUK–SVM model outperforms the other models except for Experiment 1 of 30-min-ahead prediction, the reported MAPE for PUK–SVM model is 12.368%, 11.023%, 10.180%, respectively, for Experiments 1, 2 and 3, respectively, of 30-min-ahead prediction and 12.116%, 11.348%, 9.9261% for 60-min-ahead prediction, respectively; in the case of Experiment 1 of 30-min-ahead prediction, ANOVA radial basis function reported better performance with MAPE value of 11.348% whereas 12.368% for PUK function.

• 5. The SSA–VMD–Bessel SVM model outperforms the SSA–VMD–Gaussian–SVM, and the reported MAPE is 14.638%, 15.795%, 12.348% for 30-min-ahead prediction and 13.628%, 12.483% and 11.002% obtained for 60-min-ahead prediction.

• 6. Next to Bessel model, the SVM model with linear spline kernel function exhibits a better performance with MAPE of 12.239%, 13.245%, 11.360% for 30-min-ahead prediction and 15.036%, 14.238% and 12.420% for 60-min prediction, respectively.

• 7. The performance of SSA–VMD–ANOVA radial basis function SVM has better performance to the linear spline–SVM model with reported MAPE of 11.348%, 12.364%, 10.749% for 30-min prediction and 12.981%, 12.001%, 10.136% for 60-min-ahead prediction, respectively.

• 8. The other performance metrics such as AE, MAE, MSE also follows the order of the above-discussed evaluation and which is reported in Tables 1 and 2.

• 9. The experimental results suggested that the Pearson VII universal kernel (PUK) function outperforms other kernels for SVM regression applications, and the performance order of the considered kernels next to PUK function is ANOVA radial basis function, linear spline kernel function, Bessel function and general Gaussian function, respectively.

3.4 Comparison of performance of proposed model with few existing literatures

To validate the effectiveness of the proposed prediction models, the performance of the proposed model was compared with general SVM predictor, neural network predictors, hybrid VMD and neural network predictors, hybrid VMD and SVM predictors. The performance evaluation of the comparative models is reported in Table 3, and the estimated MAPE value for predicted results of the considered models on wind speed data series-1 was demonstrated for both 30-min-ahead and 60-min-ahead prediction. Further, the prediction accuracy of the proposed model was demonstrated by conducting DM test with all considered models as reported in Table 4.

Table 4 The Pearson test results for proposed models

• 1. The prediction accuracy of individual models is worse than the hybrid models, and the MAPE value of SVM predictor of 32.25% is found to be better than that of neural network predictor of 33.83%.

• 2. The MAPE value of hybrid VMD and SVM predictor improved than hybrid VMD–NN predictor of 28.86% and 29.86%, respectively, for 30-min-ahead prediction. For 60-min-ahead prediction, the accuracy of SVM improved than NN predictor, but reported with near values.

• 3. On employing SSA prior to the prediction block further improved the prediction accuracy. The MAPE of SSA–VMD–BPN is 25.95% for 30-min-ahead prediction and 24.37% for 60-min-ahead prediction, whereas 31.53% and 30.57% for VMD–BPN on 30-min-ahead and 60-min-ahead prediction, respectively.

• 4. On comparing all the models under the study, the proposed SSA–VMD–SSA predictors of all kernel function outperformed, which implies that for very short term and short-term wind speed prediction SVM predictors perform better than the neural network predictors.

• 5. If prediction time increases, the performance of neural network predictor gets improved.

The accuracy of the proposed model is expressed in terms of Pearson test results as follows:

• 1. The Pearson test reported with near acceptance value for all proposed prediction models of SSA–VMD–SVM with various kernel functions.

• 2. The SSA–VMD–SVM model with PUK kernel function reported higher accuracy in Pearson test result of 0.9394, which is almost near to 1.

• 3. From Table 5, it is inferred that higher predictability was achieved for hybrid models rather than individual SVM or NN model. On comparing the Pearson test values, the prediction accuracy improved for SVM models than for NN models. From Tables 4 and 5, it is demonstrated that the proposed model outperforms the other comparison models.

  Table 5 The Pearson test results for models under comparison

From the various performance evaluations of the proposed prediction models, it is suggested that SSA–VMD–SVM model exhibits effective prediction for short-term and very short term wind speed forecasting than any other models considered under the study.

4 Conclusion

In this paper, SSA–VMD–SVM wind prediction model of various kernel functions was presented and their performance was analyzed with various performance evaluation criteria. In this study, the original wind speed series real-time data were gathered from Suzlon Energy Limited, Coimbatore, and these data series was averaged into three different input series and utilized for three experiments. Initially, the original wind speed series has been decomposed into its trend component and noise by employing SSA, and the unpredictability of the sub-series was determined by employing sample entropy. The sub-series further decomposed into its various components by VMD, where the each sub-sub-series has been utilized for SVM predictors of various kernel functions. In this research, various kernel functions were analyzed and presented an effective kernel for SVM regression models. To improve the prediction accuracy, the parameters of SVM predictors were optimally tuned by differential evolution algorithm. From the performance analysis made with the proposed prediction models and the models under comparison, the proposed SSA–VMD–SVM prediction models were reported with higher accuracy and suggested as the effective wind speed predictor.