1 Introduction

Cloud computing has emerged as a new paradigm to provide ubiquitous, convenient and flexible services to individual users and enterprises (Sim 2015). Many companies including Amazon, Google and Microsoft are offering public cloud computing services, such as Amazon’s Elastic Compute Cloud (EC2) and Microsoft Windows Azure (Zaman and Grosu 2013b). In public cloud computing environment, various infrastructure resources, applications and platforms are supplied as utility services to users in a pay-as-you-go method.

Infrastructure resources are utilized more efficiently and cost-effectively for both providers and users in cloud computing. Actually, users can gain the benefits of the infrastructures without the need to complement and administer it directly. Cloud providers can maximize their revenue by charging cloud users. Currently, in cloud computing environment, there are three pricing schemes offered by commercial cloud providers, namely spot market, long-term reservation and short-term on-demand plans (Toosi et al. 2015).

The spot market plan allows price-sensitive cloud customers to accomplish short-time tasks. Customers bid for the use of resources with the maximum price which they are willing to pay, and gain access to the acquired resources as long as their bid exceeds current spot price. Spot market plan is less reliable because users’ tasks may be arbitrarily terminated by providers. In the reservation plan, end users pay an upfront reservation fee for a specific period of time (e.g., one year or two), and receive a cheaper price for the hourly resource usage. But this plan may result in resource over-provisioning or under-provisioning problems. On the other hand, price in on-demand plan is charged by hourly usage without upfront fee and a long-term commitment, and providers impose service provisioning to guarantee the quality of service (QoS). Consumers pay a high price to purchase this plan to meet fluctuated and unpredictable requests occasionally. As far as we know, only Amazon’s EC2 offers spot market plan with dynamic pricing. The others adopted by most of commercial cloud providers are static pricing strategies, which usually cannot meet market demand and utilize resource capacity efficiently to maximize provider’s profit. Hence, it is necessary to explore an efficient dynamic resource pricing and allocation strategy in cloud computing.

Some dynamic resource pricing and allocation strategies were proposed by researchers to tackle revenue maximization problems for providers. For instance, auction-based mechanism (Lampe et al. 2012) and combinational auction mechanism (Zaman and Grosu 2013b) were investigated. In these mechanisms, cloud consumers bid for their resource bundles, and their payments are determined based on the market supply and demand, or are calculated based on their valuations. And game-based theoretical approaches were also applied to address this problem (Ardagna et al. 2013; Di Valerio et al. 2013). In these approaches, cloud providers and customers were modeled as players and their strategies for resource pricing and allocation constituted an equilibrium solution in the revenue maximization problem. In practice, users always choose to access inexpensive and high-quality service. When QoS is guaranteed, low resource price will attract more customers. But if cloud users are overcharged by a provider, they probably choose other providers, then that provider’s revenue will decline dramatically. Therefore, the pricing policies of providers have a great impact on users’ willingness to access services and in turn affect their revenues. However, this is ignored by most existing approaches and indeed plays an important role in cloud providers’ revenues.

In this paper, we aim to tackle the revenue maximization problem, for both IaaS and SaaS providers, in resource provisioning to users. In cloud computing model, IaaS providers want to earn the payment not only cover their operation cost but also gain as many extra profits as possible. Therefore, IaaS providers seek the optimal prices per unit time for different types of VM instances in order to maximize their revenues. Each SaaS provider aims to minimize its cost by determining the optimal number of VM instances needed to purchase. At the same time, each SaaS provider needs to comply with SLA contract which affects the revenue on the basis of the achieved performance level. The profit of each SaaS provider equals to the payment from users minus the cost of utilizing infrastructure resources supplied by IaaS providers. We model this revenue maximization problem as a Stackelberg game and propose a dynamic resource pricing and allocation algorithm to seek the Stackelberg equilibrium of the game. Moreover, in the process of seeking the optimal price of VM instances, we consider the influence of VM instance price on the choice of users who request services.

The rest of this paper is organized as follows. Section 2 discusses related works. In Sect. 3, the system model and the Stackelberg game formulation in the cloud computing are presented. Section 4 proves the existence of Stackelberg equilibrium and presents an algorithm for solving the proposed game. Simulation results are discussed in Sect. 5. Finally, conclusions are drawn in Sect. 6.

2 Related works

Resource pricing and allocation in cloud computing have attracted considerable attentions and have been investigated in some research works from different points of view in both industrial and academic research areas. At present, pricing strategies adopted by most commercial cloud providers, for example, Google and Microsoft, ask customers to pay a fixed price to access cloud service. However, this static pricing strategy cannot be able to update dynamically to improve the revenue. Thus, many researchers proposed various alternative schemes.

Some auction-based approaches have been proposed in the literature. In practice, pricing policy of Amazon EC2 spot instance (SI) is auction-based. Wee (2011) showed that spot instance price is 52.3% cheaper than its corresponding standard price. In Javadi et al. 2013, the authors analyzed all types of SIs in terms of spot price and determined the time dynamics for spot price in hour-in-day and day-of-week. Song et al. (2012) proposed a profit-aware dynamic bidding algorithm for SIs to maximize the time average profit. In Agmon Ben-Yehuda et al. 2013, the authors showed that the SI prices are probably determined within a tight price range via a dynamic hidden reserve price. In Zhang et al. (2011), the authors aimed to address problem of best matching customer demand in terms of both supply and price, and of dynamically allocating computing resources in Amazon SIs to maximize revenue. Some research works focused on the design of auction mechanisms for resource allocation in cloud computing. The authors in Lampe et al. (2012) proposed an equilibrium price auction allocation mechanism based on linear programming and heuristic approach, which achieved profits that correspond to about 96.7% of the optimal solution on average. In Prasad et al. (2012), the resource allocation problem was formulated as a procurement auction, and the multiple resource procurement from several cloud vendors participating in bidding was addressed by assigning dynamic pricing for these resources. Similar studies can be found in Bonacquisto et al. (2014, 2015), Di Modica et al. (2013) and Prasad and Rao (2014). The authors of Zaman and Grosu 2013a developed a combinatorial auction-based mechanism to allocate VM instances, which is approximately efficient and generates higher revenue than fixed price mechanism, but requires static provisioning. They further designed an auction-based mechanism for dynamic VM provisioning and allocation, in which the user demand was taken into account and no VM instance was allocated for less than the reserved price (Zaman and Grosu 2013b). A double auction resource allocation model considering the benefits of both users and providers was investigated in Samimi et al. (2016), Sun et al. (2014) and Zheng et al. (2015).

None of the works mentioned above considered the SLA contract between cloud providers and consumers. SLA guarantees specific quality attributes to cloud consumers, which also plays an important role in revenue. The authors in Macías and Guitart (2014) proposed two sets of policies to manage SLAs, in order to achieve business objects of cloud providers: client classification and revenue maximization. Focused on designing resource allocation algorithms for SaaS providers, Wu et al. (2014) proposed customer driven SLA-based resource provisioning algorithms. By minimizing SLA violations, customer satisfaction levels were improved, and cost savings were optimized as well. A two-stage resource provisioning scheme was presented in Abundo et al. (2014), which addressed the problem of allocating the optimal number of VMs for SaaS providers to satisfy their SLAs and maximizing their revenues at the same time. The problems of cost minimization or revenue maximization with SLA constraints were also investigated in Feng et al. (2012) and Goudarzi and Pedram (2011).

Besides, game-based theoretical approaches have been adopted to handle various problems in cloud computing. In Wang et al. (2016), a Stackelberg game was formulated to decide price and amount of execution units that mobile devices are willing to offer in mobile cloud computing environment. Di Valerio et al. (2013) modeled revenue maximization problem as a Stackelberg game to seek equilibrium price and allocation strategy for both SaaS and IaaS providers. Exploiting coalitional game to improve revenue or minimize wastage was explored in Hassan et al. (2014), Mashayekhy et al. (2015) and Pillai and Rao (2016). In Ardagna et al. 2013, SaaS providers want to maximize their revenues from SLAs while minimizing the cost of use of resources supplied by the IaaS provider. On the other hand, the IaaS provider want to maximize revenues obtained. The authors took the perspective of SaaS providers and modeled this service provisioning problem as a generalized Nash game. In similar scenario, to capture the conflict between SaaSs and PaaS, the service provisioning problem of cloud PaaS systems was modeled as a generalized Nash equilibrium problem to seek social optimum of cloud computing (Anselmi et al. 2014).

Inspired by the above works, in this paper, we model profit maximization problem as a Stackelberg game. In the game, the IaaS providers are game leaders and SaaS providers are followers. IaaS providers want to maximize their profits by seeking the optimal prices of VM instances. It is known that service demands are affected by resource price, so simply setting the highest price allowed is not a good choice. SaaS providers comply with SLA contracts with end users and want to minimize the cost of using VM instances. However, different from works mentioned above, we consider the impact of resource price on the willingness of end users requesting services. Moreover, SLA is taken into consideration as a factor in determine market share and price of services for SaaS providers.

3 System model and problem formulation

3.1 System model

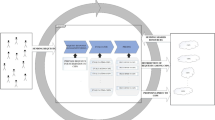
In this subsection, we present an overview of resource pricing and allocation model in cloud computing. As depicted in Fig. 1, the model consists of one IaaS provider, several SaaS providers and a number of cloud users. The IaaS provider has an infrastructure center providing resources to SaaS providers in the form of different VM instance types. Each VM instance type has different resource capacities in terms of CPU capacity, RAM size, disk storage, I/O bandwidth and so on. SaaS providers locate at different places and deploy their applications on the infrastructure center, and are charged by IaaS provider for VM instances usage. On the other hand, SaaS providers can gain revenue by offering software services such as online games and social web activities with SLA contracts to users.

Fig. 1
figure 1

A resource pricing and allocation procedure in cloud computing

Full size image
Table 1 Mathematical notations
Full size table

It is assumed that there are N SaaS providers in the cloud market, and the number of VM instance types is K. \(p^{k}\) with \(k\in [1,\dots ,K]\) is the unit price of VM instance k charged by the IaaS provider. The number of software service types offered by SaaS providers is denoted by L. Each user can request to run one or several services at the same time, and these requests can be submitted to the same or different SaaS providers. The number of service type l that SaaS provider n received is denoted as \(u_{n}^{l}\) with \(l\in [1,\dots ,L]\) and \(n\in [1,\dots ,N]\). And \(d _{n}^{lk}\) denotes the amount of VM instances k needed to perform the service type l offered by SaaS provider n. In order to achieve acceptable QoS, each user has a SLA contract with SaaS provider n, which indicates QoS level \(q_{n}^{l}\) of service type l. The main notations adopted in this paper are presented in Table 1.

Learning curve model (Truong-Huu and Tham 2014) is adopted to capture the operation cost of the IaaS provider. This model assumes that when the number of production units is doubled, the marginal cost of production decreases by a fixed factor, and learning factor is defined as one minus this factor. We denote \(\varphi \in (0,1)\) as the learning factor of the IaaS provider, and it is assumed that learning factor is the same for all VM instance types. Let \(v^{k}\) denote the total number of VM instance type k, which is calculated as \(v^{k} = \mathop \sum \nolimits _{n = 1}^N v_{n}^{k}\), where \(v_{n}^{k}\) is the number of VM instance k purchased by SaaS provider n to run application service. Hence, the total operation cost of the IaaS provider can be defined as

$$\begin{aligned} C_{I}=\sum \limits _{k=1}^{K}{\frac{c^{k}{({v}^{k}})^{1+{{{\mathrm{log}} }_{2}}\varphi }}{1+{{{\mathrm{log}} }_{2}}\varphi }}, \end{aligned}$$
(1)

where \(c^{k}\) is the operation cost of the first instance of VM type k. And the revenue of the IaaS provider charged from all SaaS providers is calculated as

$$\begin{aligned} R_{I}({p}^{k})=\sum \limits _{k=1}^{K}{{{v}^{k}}{{p}^{k}}}. \end{aligned}$$
(2)

In this paper, the price of service type l is not fixed, and the pricing strategy adopted by each SaaS provider is based on the base price, the amount of VM instance purchased and the QoS level. The service price is defined as follows

$$\begin{aligned} p_{n}^{l} = \gamma _{n}^{l}{{\mathrm{log}} _2}\left( 1 + v_{n}^{k}(Q_{n}^{l} + q_{n}^{l})/Q_{n}^{l}\right) , \end{aligned}$$
(3)

where \(\gamma _{n}^{l} > 0\) is the base price of service type l, \(v_{n}^{k} = \sum \nolimits _{l = 1}^{L} {u_{n}^{l}d_{n}^{lk}} \) is the number of VM instance k that SaaS provider n purchased and \(Q_{n}^{l}\) is the maximum QoS level of service type l that SaaS provider n can achieve. Obviously, \(q_{n}^{l} \le Q_{n}^{l}\), \(\forall n\) and \(\forall l\). So the revenue of SaaS provider n can be calculated as

$$\begin{aligned} {R^n}(\gamma _{n}^{l}, v_{n}^{k}) = \mathop \sum \limits _{k = 1}^K \alpha _{n}^{l}{\varOmega _{l}}\gamma _{n}^{l}{{\mathrm{log}} _2}\left( 1 + v_{n}^{l}(Q_{n}^{l} + q_{n}^{l})/Q_{n}^{l}\right) ,\nonumber \\ \end{aligned}$$
(4)

where \(\varOmega _{l}\) denotes the market capacity of service type l, i.e., the total number of users requested service type l, and \(\alpha _{n}^{l}\) represents the market share of service type l of SaaS provider n. Market share \(\alpha _{n}^{l} \in (0,1)\) is determined by the ratio of QoS level \(q_{n}^{l}\) to base price \(\gamma _n^l\), which is computed as

$$\begin{aligned} \alpha _{n}^{l}\mathrm{{ = }}\frac{{q_{n}^{l}/\gamma _{n}^{l}}}{{\sum \nolimits _{n = 1}^N {q_{n}^{l}/\gamma _{n}^{l}}}}. \end{aligned}$$
(5)

3.2 Game formulation

In cloud computing market, the IaaS provider supplies infrastructure resources and wants to maximize its profit of selling resources, while SaaS providers offer software services to end users and intend to reduce the cost of purchasing resources. That means the IaaS provider seeks higher prices of VM instances and needs to sell more VM instances, while SaaS providers want to purchase less VM instances in lower prices and need to comply with QoS requirements, specified in SLA contracts with end users. Therefore, there exists interest competition between the IaaS provider and SaaS providers.

In order to capture the behaviors of the IaaS provider and SaaS providers in this conflicting situation, it is natural to model the IaaS provider and SaaS providers as the opposite players in a Stackelberg game. Stackelberg game is a strategic game that consists of leaders and followers who compete with each other on certain resources. The leaders take their strategies first and the followers then adjust their strategies according to the leaders’ actions.

When taking the Stackelberg game as basic model, the IaaS provider can be taken as the game leader who can determine the prices of VM instances to improve profit. Then SaaS providers, which are taken as the game followers, decide the quantity of VM instances needed to purchase according to the prices of VM instances determined by the IaaS provider. To improve the profit, the IaaS provider will set the price of VM instances again based on the number of VM instances purchased. This process will iterate repeatedly.

From the above description, the price and amount of VM instances are the exchange and reciprocal variables in the Stackelberg game. By optimizing these coupled variables individually and repeatedly, IaaS providers and SaaS providers take the nested interaction continuously and obtain the profit balance.

The profit of each SaaS provider equals to the revenue charged from users minus the costs which has to pay for using infrastructure resources. And the cost can be formulated as \(C_{n}=\mathop \sum \nolimits _{k = 1}^K v_{n}^{k} p^{k}\). So the utility function of each SaaS provider n can be formulated as

$$\begin{aligned} U_{n}(\gamma _{n}^{l}, v_{n}^{k}) = R_{n}(\gamma _{n}^{l}, v_{n}^{k}) - C_{n}. \end{aligned}$$
(6)

If the number of users requesting services remains the same, the less quantity of VM instances is purchased, less expenses each SaaS provider need to pay, and then, profit can be effectively improved. But from Eqs. 3 and 5, it is known that if QoS level is promoted by purchasing more VM instances, the prices of software services and the market share rise; then, revenue of SaaS provider increases subsequently. So given prices of VM instances, each SaaS provider seeks the optimal number of VM instances needed to purchase. Substituting Eq. 4 into Eq. 6, we obtain the profit maximization problem for each SaaS provider

$$\begin{aligned} \mathop {{\mathrm{max}} }\limits _{v_{n}^{k}} U_{n}(\gamma _{n}^{l}, v_{n}^{k})= & {} \mathop \sum \limits _{k = 1}^K \alpha _{n}^{l}{\varOmega _{l}}\gamma _{n}^{l}{{\mathrm{log}} _2}\left( 1 + v_{n}^{k}(Q_{n}^{l} + q_{n}^{l})/Q_{n}^{l}\right) \nonumber \\&-\,\sum \limits _{k = 1}^K v_{n}^{k} p^{k}. \end{aligned}$$
(7)

The IaaS provider’s target is to find an optimal price \(p^{k}\) for every VM instance k to generate more revenue. The utility function of the IaaS provider is defined as

$$\begin{aligned} U_{I}({p}^{k}) = R_{I}({p}^{k}) - C_{I}, \end{aligned}$$
(8)

where the first term in Eq. 8 is the revenue charged from all SaaS providers and the second term is total operation cost. So the profit maximization problem for the IaaS provider is

$$\begin{aligned} \mathop {{\mathrm{max}} }\limits _{p^{k}} U_{I}({p}^{k}) = \mathop \sum \limits _{k=1}^{K}{{{v}^{k}}{{p}^{k}}} - \sum \limits _{k=1}^{K}{\frac{c^{k}{({v}^{k}})^{1+{{{\mathrm{log}} }_{2}}\varphi }}{1+{{{\mathrm{log}} }_{2}}\varphi }}. \end{aligned}$$
(9)

Intuitively, it seems that the higher price \(p^{k}\) is, the more profit the IaaS provider gains. However, in that case, SaaS providers will cost much more for infrastructure resource usage accordingly. In order to make profits, SaaS providers have to increase base price \(\gamma _{n}^{l}\), which may affect willingness of users to access service because of too much fee charged. Therefore, the number of users requesting services declines; then, the quantities of VM instances purchased by SaaS provider decrease accordingly, resulting in diminishment of IaaS providers’ total profits in turn. So there exists a trade-off between the prices of VM instances and the number of users. In this paper, it is assumed that the relationship between quantities of VM instances purchased by all SaaS providers and prices of VM instances can be represented as follows:

$$\begin{aligned} v^{k} = \frac{{(v^{k})_{{\mathrm{max}} }{e^{(a - bp^{k})}}}}{{1 + {e^{(a - bp^{k})}}}}, \end{aligned}$$
(10)

where \((v^{k})_{{\mathrm{max}} }\) is the maximal quantity of VM instances that all SaaS providers could purchase, and a and b are the price sensitivity factors that indicate the impact of VM instance price on quantities of VM instance purchased. And Fig. 2 shows curves of \(v^{k}\) when \(a=7\), \(b=30\) and \(a=2\), \(b=8\).

Fig. 2
figure 2

Resource demand versus VM instance price

Full size image

4 Analysis of the proposed game

4.1 The optimal solutions of the problem

Because SaaS provider n aims at maximizing its utility \(U_{n}(\gamma _{n}^{l}, v_{n}^{k}) \) by seeking an optimal quantity of VM instance \(v_{n}^{k}\) needed to purchase, it is natural to observe how \(U_{n}(\gamma _{n}^{l}, v_{n}^{k}) \) varies with \(v_{n}^{k}\). From the definition in Eq. 6, we know that

$$\begin{aligned} \frac{\partial {U_{n}}(\gamma _{n}^{l}, v_{n}^{k})}{\partial v_{n}^{k}} = \frac{{\partial {R_{n}(\gamma _{n}^{l}, v_{n}^{k})}}}{{\partial v_{n}^{k}}} - {p^{k}}. \end{aligned}$$
(11)

If \(p^{k} < \frac{{\partial {R_{n}(\gamma _{n}^{l}, v_{n}^{k}) }}}{{\partial v_{n}^{k}}}\) satisfies for VM instance \(k \in [1,\ldots , K]\), we can get \(\frac{\partial {U_{n}(\gamma _{n}^{l}, v_{n}^{k}) }}{\partial v_{n}^{k}} > 0\), which means that SaaS provider n can obtain a larger \(U_{n}(\gamma _{n}^{l}, v_{n}^{k}) \) by increasing \(v_{n}^{k}\), Otherwise, SaaS provider n needs to reduce the number of VM instance k purchased.

Taking the derivative of \(U_{n}(\gamma _{n}^{l}, v_{n}^{k}) \) in Eq. 6 with respect to \(v_{n}^{k}\) and letting it equal to zero,

$$\begin{aligned} \frac{{\partial {U_{n}}(\gamma _{n}^{l}, v_{n}^{k}) }}{{\partial v_{n}^{k}}} = \frac{{\partial {R_{n}}(\gamma _{n}^{l}, v_{n}^{k}) }}{{\partial v_{n}^{k}}} - {p^{k}} = 0. \end{aligned}$$
(12)

Substituting Eq. 4 into Eq. 12, we have

$$\begin{aligned} \frac{\partial {U_{n}}(\gamma _{n}^{l}, v_{n}^{k}) }{\partial v_{n}^{k}} = \frac{1}{{1n2}} \frac{\alpha _{n}^{l}{\varOmega _{l}}\gamma _{n}^{l}(Q_{n}^{l} + q_{n}^{l})}{Q_{n}^{l} + v_{n}^{k}(Q_{n}^{l} + q_{n}^{l})} - p^{k}=0. \end{aligned}$$
(13)

Because \(p^{k} > 0\), the optimal number of VM instances \(v_{n}^{k}\) is

$$\begin{aligned} v_{n}^{k*} = \frac{\alpha _{n}^{l}\varOmega _{l}\gamma _{n}^{l}(Q_{n}^{l} + q_{n}^{l}) - \ln 2{p^{k}} Q_{n}^{l}}{{\ln 2{p^{k}}(Q_{n}^{l} + q_{n}^{l})}}. \end{aligned}$$
(14)

In order to obtain the optimal prices of VM instances to maximize profit of the IaaS provider, taking the derivative of \(U_{I}(p^{k}) \) with respect to \( p^{k}\) and letting it to zero, we can get

$$\begin{aligned} \frac{\partial U_{I}(p^{k}) }{\partial p^{k}} = v^{k} + p^{k}\frac{\partial v^{k}}{\partial p^{k}} - \frac{\partial C_{I}}{\partial p^{k}} = 0. \end{aligned}$$
(15)

Substituting Eq. 14 and \(v^{k} = \mathop \sum \nolimits _{n = 1}^N v_{n}^{k}\) into Eq. 15, after some manipulations, the above equation of \(p^{k}\) is solved and the optimal price is denoted as

$$\begin{aligned} p^{k*} = \frac{1}{{\ln 2}}\sum \limits _{n = 1}^N {\frac{\alpha _{n}^{l}{\varOmega _{l}} \gamma _{n}^{l}}{v_{n}^{k*}}}. \end{aligned}$$
(16)

4.2 Analysis of equilibrium existence

In this subsection, we will verify the existence and uniqueness of game equilibrium. It is assumed that \(v_{n}^{k*}\) and \(p^{k*}\) are the Stackelberg equilibrium of the proposed game; then, a definition is given as follows:

Definition 1

The Stackelberg equilibrium of the proposed game is \(v_{n}^{k'}\) and \(p^{k'}\), which satisfy the following conditions

  1. 1.

    For every \(k \in \{ 1,\ldots ,K\} \), \(U_{I} (p^{k'}) \ge U_{I} (p^{k})\);

  2. 2.

    For every \(n \in \{ 1,\ldots ,N\} \), \(U_{n}(\gamma _{n}^{l}, v_{n}^{k'}) \ge U_{n} (\gamma _{n}^{l}, v_{n}^{k})\);

Next, some properties are presented to prove that (\(v_{n}^{k*}\), \(p^{k*}\)) is the Stackelberg equilibrium of the proposed game.

Property 1

Utility function \(U_{n}(\gamma _{n}^{l}, v_{n}^{k})\) of SaaS provider n is concave, if \(v_{n}^{k} \ge 0\), and \(p^{k}\) is fixed, \(\forall n \in \{ 1,\ldots ,N\} \).

Proof

Taking the second-order derivatives of the utility function \(U_{n}(\gamma _{n}^{l}, v_{n}^{k})\) with respect to \(v_{n}^{k}\), we can get

$$\begin{aligned} \frac{{\partial ^2}{U_{n}}(\gamma _{n}^{l}, v_{n}^{k})}{\partial (v_{n}^{l})^2} = \frac{ - \ln 2\alpha _{n}^{l}{\varOmega _{l}} \gamma _{n}^{l}{{(Q_{n}^{l} + q_{n}^{l})}^2}}{{{(\ln 2Q_{n}^{l})}^2} + {{[\ln 2v_{n}^{k}(Q_{n}^{l} + q_{n}^{l})]}^2}} < 0.\nonumber \\ \end{aligned}$$
(17)

Obviously, \(U_{n}(\gamma _{n}^{l}, v_{n}^{k})\) is strictly concave. \(\square \)

According to Property 1, we know that \(v_n^{k*}\) is the global optimal solution of profit maximization of SaaS provider n, \(\forall n \in \{ 1,\ldots ,N\}\). Hence, the second condition in Definition 1 is satisfied and \(v_{n}^{k*}\) is the Stackelberg equilibrium point.

It is mentioned in Sect. 3.2 that there is a trade-off between the prices of VM instances and the number of users, which can be validated by the following property:

Property 2

The utility function \(U_{I}(p^{k})\) of the IaaS provider is concave in VM instance price \(p^{k}\) if the quantity of VM instance k purchased by each SaaS provider n is \(v_{n}^{k*}\) in Eq. 14.

Proof

Because \(p^{k} > 0\), and \(v_n^{k*}\) is a continuous function of \(p^{k}\), substituting Eq. 14 into Eq. 8 and taking the derivatives of \(U_{I}(p^{k})\), we can obtain

$$\begin{aligned} \frac{\partial U_{I}(p^{k}) }{\partial p^{k}}= & {} \sum \limits _{n = 1}^N {\sum \limits _{l = 1}^L v_n^{k*} } - \frac{{\sum \nolimits _{n = 1}^N {\alpha _{n}^{l}\varOmega _{l}\gamma _{n}^{l}} }}{\ln 2p^{k}} \nonumber \\&-\,\frac{c^{k}\sum \nolimits _{n = 1}^N {\alpha _{n}^{l}{\varOmega _{l}}\gamma _{n}^{l}} {{\left( \sum \nolimits _{n = 1}^N {\sum \nolimits _{l = 1}^L v_{n}^{k*} }\right) }^{{{{\mathrm{log}} }_2}\varphi }}}{\ln 2(p^{k})^2}.\nonumber \\ \end{aligned}$$
(18)

And the second derivative of \(U_{I}\) is

$$\begin{aligned} \frac{{{\partial ^2}U_{I}(p^{k}) }}{{\partial (p^{k})^2}} = - \frac{{2c^{k}\varOmega _{l}\sum \nolimits _{n = 1}^N {\alpha _{n}^{l}\gamma _{n}^{l}}{{\left( \sum \nolimits _{n = 1}^N {\sum \nolimits _{k = 1}^K {v_n^{k*}} } \right) }^{{{{\mathrm{log}} }_2}\varphi }} }}{(p^{k})^3}.\nonumber \\ \end{aligned}$$
(19)

Because each term on the right-hand side of Eq. 19 is positive, it is obvious that \(\frac{{{\partial ^2}U_{I}(p^{k}) }}{{\partial (p^{k})^2}} < 0\). Therefore, \(U_{I}(p^{k})\) is concave with respect to \(p^{k}\). \(\square \)

From Properties 1 and 2, we know that both \(U_{n}(\gamma _{n}^{l}, v_{n}^{k})\) and \(U_{I}(p^{k})\) are concave, and thus, for every \(v_{n}^{k}\) and \(p^{k}\), \(U_{I}(p^{k*}) \ge U_{I}(p^{k})\), \(\forall k \in [1,\ldots ,K]\) and \(U_{n}(\gamma _{n}^{l}, v_{n}^{k*}) \ge U_{n} (\gamma _{n}^{l}, v_{n}^{k})\), \(\forall l \in [1,\ldots , L]\), \(\forall n \in [1,\ldots ,N]\). So it is concluded that \(v_{n}^{k*}\) in Eq. 14 and \(p^{k*}\) in Eq. 16 are the Stackelberg equilibrium of the proposed game, and the existence and uniqueness are also verified.

4.3 Price updating strategy for IaaS provider

The utility of the IaaS provider varies when the prices of VM instances fluctuate. To achieve the optimal utility, a strategy adopted by the IaaS provider is presented. First, at the beginning of Stackelberg game, in order to attract customers to purchase more VM instances, it is natural for the IaaS provider to set price \(p^{k}\) equal to \(({p^{k}})_{\mathrm{min}}\), which can keep the balance between income and expenditure at that moment. Then IaaS provider will increase VM instance price by a fixed step size. In detail, at the \(i + 1\) step, the price can be updated as \({p^{k}}(i + 1) = {p^{k}}(i) + \lambda \), and \(\lambda \) is the step size. Because the utility function \(U_{I}\) is concave with respect to \(p^{k}\), if \(U_{I}({p^{k}}(i + 1)) > U_{I} ({p^{k}}(i))\), the IaaS provider will continue to increase \(p^{k}\) until \(U_{I} ({p^{k}}(i + j)) < U_{I} ({p^{k}}(i+j-1))\) at the \(i + j\) step. Then \(\lambda \) is set to \(\lambda = - \mu \lambda \), \(\mu \in (0,1)\) is the coefficient of the step size, and \({p^{k}}(i + j + 1) = {p^{k}}(i + j) + \lambda \). \(U_{I} ({p^{k}}(i + j + 1))\) and \(U_{I} ({p^{k}}(i + j ))\) are compared again: If \(U_{I} ({p^{k}}(i + j + 1))\) is bigger, then in the next step \(\lambda \) will not be changed; otherwise, \(\lambda \) is set to \(\lambda = - \mu \lambda \), and \({p^{k}}\) is set to \({p^{k}} + \lambda \) once again. The IaaS provider will execute the above iteration repeatedly until \(U_{I}\) does not change, and finally, \(p^{k*}\) is found.

Meanwhile, once the IaaS provider updates its price \(p^{k}\), each SaaS provider calculates the optimal quantity of VM instances needed to purchase at the current price. By letting \(\frac{{\partial {U_{n}}(\gamma _{n}^{l}, v_{n}^{k})}}{{\partial v_{n}^{k}}} = 0\), and from Eq. 14, it is known that once \(p^{k}\) converges to the optimal price \(p^{k*}\), \(v_{n}^{k}\) converges to \(v_{n}^{k*}\), which means that both \(p^{k}\) and \(v_{n}^{k}\) converge to Stackelberg equilibrium of the game. The algorithm is given in Algorithm 1.

figure a

5 Numerical simulations

In this section, numerical simulations is conducted to evaluate performance of the proposed resource pricing and allocation strategy in cloud computing. At the beginning, the parameter settings are given, and the sensitivity analysis of critical parameters on the performance is performed. Then the convergence of the proposed game is shown. Finally, the proposed strategy is compared with fixed pricing scheme and an auction-based mechanism (Zaman and Grosu 2013b) in revenue and resource utilization.

5.1 Setting of simulation parameters

In the simulation, for simplicity, it is assumed there are three SaaS cloud providers, i.e., \(N = 3\), and all the three SaaS providers supply only one service type, and the IaaS provider supplies one type of VM instance as well, i.e., \(L = 1\) and \(K = 1\). The maximum market capacity supplied by SaaS providers equals to \(3\times {10^5}\). Moreover, QoS level \(q_{n}^{l}\) is set to 5, 7 and 8, base price \({\gamma _{n}^{l}}\) is set to 0.045, 0.05 and 0.046, and \(Q_{n}^{l}\) is set to 10, \(n={1, 2, 3}\) and \(l=1\). Besides, learning factor \(\varphi = 0.65\) and first VM instance cost \({c^{k}} = \$1.8\).

Fig. 3
figure 3

Quantitative analysis of operation cost \(c^{k}\) in influencing the IaaS provider’s profit

Full size image

5.2 Sensitivity analysis

In this subsection, in order to investigate which factors have the most influence on the profits of IaaS provider and SaaS providers, a quantitative analysis of every system parameter is carried out.

Firstly, for the IaaS provider, we know that the operation cost of first VM instance \(c^{k}\) and learning factor \(\varphi \) have impact on the profit from Eq. 9. Let \(\varphi \) equal to 0.65, and \(c^{k}\) is set to $1, $10, $20 and $30. As shown in Fig. 3, the equilibrium profit of the IaaS provider is $\(4.93\times {10^4}\), $\(4.67\times {10^4}\), $\(4.39\times {10^4}\) and $\(4.11\times {10^4}\), respectively. From the definition of \(U_{I}(p^{k})\), it is known that the equilibrium profit of the IaaS provider linearly decreases, while \(c^{k}\) is increasing. Actually, \(c^{k}\) varies in a small range change and usually is less than $4 per instance per hour in practice. For example, price of most Amazon EC2 VM instance is less than $4 per hour, and price of Microsoft Azure VM instance is much cheaper (Amazon 2016; Microsoft 2016). If \(c^{k}\) is set to $4, \(U_{I}(p^{k})\) equals to $\(4.84\times {10^4}\). Obviously, \(U_{I}(p^{k})\) is slightly affected by \(c^{k}\).

In Fig. 4, set \(c^{k} = \$1.8\), and let learning factor \(\varphi \) equal to 0.4, 0.65, 0.75 and 0.8. When game equilibrium is achieved, the IaaS provider gains $\(4.96\times {10^4}\), $\(4.9\times {10^4}\), $\(4.54\times {10^4}\) and $\(3.82\times {10^4}\), respectively. We can find that when \(\varphi \) increases from 0.4 to 0.65, \(U_{I}(p^{k*})\) decreases by $\(0.06\times {10^4}\). But when \(\varphi \) increases from 0.75 to 0.8, \(U_{I}(p^{k*})\) decreases suddenly by $\(0.72\times {10^4}\). The reason is that total cost \(C_{I}\) increases exponentially with the increase in learning factor \(\varphi \). It is observed that if \(\varphi \) is bigger than 0.7, \(C_{I}\) increases dramatically, which influences the profit of the IaaS provider a lot.

Fig. 4
figure 4

Quantitative analysis of learning factor \(\varphi \) in influencing the IaaS provider’s profit

Full size image

For SaaS providers, parameters that may influence profits are QoS level \(q_{n}^{l}\), base price of software service \(\gamma _{n}^{l}\) and price sensitivity factors a and b.

Let \(\gamma _{n}^{l} \), a and b remain the same, and QoS level \(q_{n}^{l}\) increases linearly from 3 to 9. As shown in Fig. 5, at equilibrium point of the game, the maximum profit of SaaS provider n increases nearly linearly from $\(0.94\times {10^4}\) to $\(2.84\times {10^4}\). From Eq. 4, we know that the influence of QoS level \(q_{n}^{l}\) on the revenue of SaaS provider includes two aspects: One is market share of SaaS provider, which is concave function of \(q_{n}^{l}\), and the other is service price \(p_{n}^{l}\), which increases logarithmically with \(q_{n}^{l}\). However, in cloud computing model, \(q_{n}^{l}\) is less than 10 and has a small variation range. Hence, QoS level \(q_{n}^{l}\) influences profit of SaaS providers slightly. We know that base price of software service \(\gamma _{n}^{l}\) is proportional to the price of VM instance, when \(\gamma _{n}^{l}/p_{I}^{k}\) increases linearly from 0.2 to 0.8. At the game equilibrium, the maximum profit of SaaS provider n increases nonlinearly, which is shown in Fig. 6.

Fig. 5
figure 5

Quantitative analysis of QoS level \(q_{n}^{l}\) in influencing SaaS providers’ profits

Full size image
Fig. 6
figure 6

Quantitative analysis of base price coefficient \(\alpha _{n}^{l} \) in influencing SaaS providers’ profits

Full size image

As shown in Fig. 7, when \(b = 20\) and a is set to 3, 5.5, 8 and 10.5, the maximum profit of SaaS provider equals to $\(1.06\times {10^4}\), $\(2.48\times {10^4}\), $\(4.14\times {10^4}\) and $\(5.93\times {10^4}\), respectively. The results show that with the increase of a, the profit of SaaS provider increases dramatically. When a increases from 3 up to 10.5, the profit rises 450%. However, if \(a = 5.5\), letting b equal to 20, 45, 70 and 95, the maximum profit of SaaS provider n is $\(2.48\times {10^4}\), $\(1.1\times {10^4}\), $\(0.7\times {10^4}\) and $\(0.52\times {10^4}\), respectively. Obviously, when parameter b rises, the maximum profit of SaaS provider n decreases significantly, and the profit falls by 79% when b increases from 20 up to 95, as shown in Fig. 8. According to the analysis above, we know that a and b play important roles in profits of SaaS providers.

Fig. 7
figure 7

Quantitative analysis of price sensitivity factor a in influencing SaaS providers’ profits

Full size image
Fig. 8
figure 8

Quantitative analysis of price sensitivity factor b in influencing SaaS providers’ profits

Full size image

5.3 Convergence of the proposed algorithm

With the given parameters, after executing Algorithm 1 described in Sect. 4.3, the optimal price of VM instance and the optimal quantity of VM instances purchased by SaaS providers were obtained. Based on that, we computed the maximum profit of both the IaaS provider and SaaS providers. The convergence of the pricing policy of the IaaS provider and the number of VM instances purchased by all SaaS providers are presented in Fig. 9. The convergence of the profits of all providers is shown in Fig. 10.

Fig. 9
figure 9

Convergence of unit price of VM instance and total number of VM instances purchased by all SaaS providers

Full size image
Fig. 10
figure 10

Convergence speed of profit of the IaaS provider and all the three SaaS providers

Full size image

As shown in Fig. 9, the price of VM instance equals to \(\$0.06\) in the beginning, but the total quantity of VM instances purchased by all SaaS providers is \(2.93\times {10^5}\). The reason is that at first the price is set quite low by the IaaS provider, in order to keep existing users and attract newcomers. At this moment, the number of users is large. SaaS providers purchase a large number of VM instances to meet the market demand and guarantee the QoS level.

After that, the price linearly increases, and the number of VM instances purchased gradually decreases. During this process, the cost of SaaS providers grows up when price of VM instance rises. Therefore, SaaS providers increase the price of software service in order to improve profit, which results in a decrease in quantity of the purchased VM instances. However, the profit of the IaaS provider increases all the time. Within 30 iterations, the game converges to the equilibrium state, where \(p^k = \$1.44\), \(v^k =2.3\times {10^5}\). In fact, as shown in Fig. 9, an approximately optimal price can be attained after about 10 iterations.

As shown in Fig. 10, in general, the profit of the IaaS provider increases. But profits of the three SaaS providers decline, until the game converges to the equilibrium state. According to Algorithm 1, the IaaS provider increases the price of VM instance to improve the revenue until it attains the maximal profit. With the increase in the price, cost of infrastructure resource usage of SaaS providers rises, and the number of users decreases due to higher price charged. Therefore, profits of SaaS providers decrease consequently.

At the beginning, the profits of the IaaS provider, SaaS providers 1, 2 and 3 are $\(1.7\times {10^4}\), $\(1.05\times {10^4}\), $\(2.03\times {10^4}\) and $\(2.35\times {10^4}\), respectively. When the game converges to the equilibrium state, the profits of the IaaS provider, SaaS providers 1, 2 and 3 are $\(3.25\times {10^4}\), $\(2.58\times {10^3}\), $\(7.86\times {10^3}\) and $\(9.28\times {10^3}\), respectively. Among the three SaaS providers, SaaS provider 3 attains the most profit. The reason is that SaaS provider 3 offers service with the highest QoS level but relatively low base price, and owns the largest market share. Although SaaS provider 1 offers the lowest base price, the QoS level provided is poor and cannot meet cloud users’ requirement, which results in the lowest profit gained.

5.4 Comparison with other schemes

In order to evaluate the performance in profit maximization and resource utilization, the proposed mechanism is compared with other two resource pricing and allocation strategies:

  • Fixed pricing mechanism In this mechanism, IaaS provider sets a fixed price for each type of VM instance, and all SaaS providers also choose a constant price for each software service. Even though the cloud computing market varies greatly, the price usually would not be changed accordingly.

  • Auction-based pricing mechanism Unlike the proposed strategy and fixed pricing mechanism, in this approach, prices of VM instances are determined by SaaS provider. Each SaaS provider submits a bid to the IaaS provider, which includes the requested VM bundles and the price it is willing to pay to use the requested bundle of VM instances. But IaaS provider still needs to set a reserve price to determine the winning bidders.

In fixed pricing mechanism, the price is set to $0.18, and in auction-based pricing model, the reserve price set by the IaaS provider is $0.1. In the auction period, the bid prices of the three SaaS providers are $0.14, $0.15 and $0.16, respectively.

As shown in Fig. 11, the total quantities of VM instances sold and profit gained by the IaaS provider with the three mechanism are compared. It is shown that the total quantities of VM instances sold are about \(2.3\times 10^5\) with the proposed approach. And the number of VM instances sold by the IaaS provider is relatively small with the fixed pricing and auction-based pricing mechanism, which are about \(1.13\times 10^5\) and \(1.86\times 10^5 \), respectively. But the corresponding profits of the IaaS provider with the three mechanisms are \(\$4.95\times 10^4\), \(\$3.39\times 10^4\) and \(\$4.42\times 10^4\), respectively.

Fig. 11
figure 11

Comparison of IaaS provider’s profit and number of VM instance between our proposed methods and fixed pricing, auction-based mechanism

Full size image

Obviously, compared with the other two approaches, the proposed mechanism makes a higher profit for the IaaS provider and fully utilizes infrastructure resources as well. This is attributed to the fact that the proposed mechanism adjusts the price of VM instance dynamically according to the market demands. Although profit per VM instance is highest with the fixed mechanism, the least profit is obtained. Thus, high price of VM instance makes the service less attractive to users, which has a significantly negative effect on customer’s intention to access services, resulting in that few VM instances are sold. For auction-based pricing strategy, under the premise of profitability, the IaaS provider set the price of VM instance equal to $0.1 to let as many as possible bidders to outbid the specific price, with the purpose of gaining more profit, but this relatively low price also deceases the profit.

The comparison of profits attained by all SaaS providers with the three strategies is depicted in Fig. 12. In our strategy, the profits of SaaS provider 1, 2 and 3 are \(\$3.03\times {10^4}\), \(\$4.9\times {10^4}\) and \(\$5.91\times {10^4}\), respectively, which is the highest profit that each SaaS provider gains among the three strategies. And in auction-based mechanism, accordingly, the profits are \(\$1.81\times {10^4}\), \(\$3.33\times {10^4}\) and \(\$4.26\times {10^4}\). In fixed pricing mechanism, every SaaS provider gains the least profit. From analysis mentioned above, we find that both the IaaS provider and SaaS providers gain the most profits with the proposed mechanism, and a higher utilization of infrastructure resource is achieved as well compared with the other two strategies.

Fig. 12
figure 12

Comparison of SaaS providers’ profit between our proposed methods and fixed pricing, auction-based mechanism

Full size image

6 Conclusion and future work

In this paper, we model the pricing and resource allocation problem between the IaaS cloud provider and SaaS cloud providers as a Stackelberg game, with the purpose of addressing revenue maximization problem of both SaaS providers and the IaaS provider. Specifically, considering the QoS requirements from SaaS providers, we take SLA as the influence factor for the market share and the pricing strategies of SaaS providers. Moreover, the functional relationship between the service demands and the prices of VM instances is given. Simulation results show that the proposed approach can obtain better profits for both IaaS provider and SaaS providers, compared to fixed pricing and auction-based pricing methods, which means the social welfare is efficiently improved in cloud computing environments. In the future, we will consider competition and cooperation among multiple IaaS providers, which will give customers a chance to choose more suitable providers.