1 Introduction

The emergence of computer-aided diagnosis systems has demonstrated the reliability of artificial intelligence in real-world problems. For example, in Liao et al. (2018) the authors show the efficiency of deep convolutional neural networks for the diagnosis of multiple types of cancer, in Erkaymaz and Ozer (2016) the authors introduce an approach based on feedforward neural networks for the diagnosis of diabetes with interesting results, in Babapour Mofrad et al. (2019) the authors propose to use a decision tree for the interpretation of CSF biomarkers in the diagnosis of Alzheimer’s disease, and more cases can be found in the literature, for example Saritas (2012), Subasi (2013), Elyan and Gaber (2016), Davari Dolatabadi et al. (2017), Asl and Zarandi (2017), Rakhmetulayeva et al. (2018), Vogado et al. (2018), Wang et al. (2018), Acharya et al. (2018), Qi et al. (2019), Afifi et al. (2019).

The present paper aims at designing a computer-aided diagnosis system based on General Type-2 Fuzzy Logic and called General Type-2 Fuzzy Classifier (GT2 FC). The methodology for obtaining the parameters of the system and a new approach to estimate the uncertainty of the system is presented.

The main contribution of the present paper is applying the concept of embedded Type-1 Fuzzy memberships for the parameterization of the Footprint of Uncertainty (FOU) of GT2 membership functions in a GT2 Fuzzy Classifier. Remembering that the FOU is modeling the uncertainty in the Type-2 Fuzzy Systems, it is proposed that is possible to find the parameters for modeling the uncertainty based on n subsets resulting from applying a uniform sampling with replacement, and based on multiple Type-1 Fuzzy membership functions (one per each subset) it is possible to generate a single GT2 Fuzzy Classifier. The proposed approach is in focused on Diagnosis problems; however, the methodology for uncertainty modeling can be extended to other kind of problems for example time series. The concept of embedded Type-1 fuzzy membership functions is not new, it was presented for example in Hagras (2008), but the methodology to be applied in classification problems and especially in diagnosis problems is interesting and obtains interesting results.

2 Materials and methods

In this section, a brief introduction of the necessary concepts and definitions for understanding the proposed approach is presented. On the other hand, the methodology for the design of the proposed GT2 Fuzzy Classifier is explained.

2.1 Uniform sampling with replacement

The uniform sampling with replacement is a technique for sampling, where the data has the same probability to be selected even for multiple samplings. This technique considers that every sampling is independent of the others and with the same population. One of the main applications of this technique is the bagging meta-algorithm for example in Hothorn and Lausen (2005), Baraldi et al. (2011), Fernández-Carrobles et al. (2016).

The method consists on generating N new training sets with size M from the D standard training set uniformly and with replacement. Based on these new training subsets, a clustering algorithm can be performed obtaining N sets of equivalent clusters.

Figure 1 illustrates the Uniform sampling with replacement.

Fig. 1
figure 1

Uniform sampling with replacement

Full size image

2.2 Type-2 fuzzy logic

Type-1 fuzzy logic was originally introduced by Liang and Mendel (2000) as an approach to represent vagueness. On the other hand with the emergence of the Interval Type-2 Fuzzy Logic (Liang and Mendel 2000), this approach provides a method to handle uncertainty, and this uncertainty is modeled by an area between two type-1 fuzzy sets and is called Footprint of Uncertainty (FOU) (Mendel et al. 2006).

However, the present paper introduces an approach to generate the FOU for General Type-2 Fuzzy Inference Systems (GT2 FIS). The main difference with respect to an Interval Type-2 Fuzzy Inference System (IT2 FIS) is in handling uncertainty, this is because in IT2 FIS the uncertainty is considered to be uniform, on the other hand, in GT2 FSs the uncertainty is defined by a secondary membership function on the secondary axis, and Eqs. 1 and 2 describe the IT2 FIS and GT2 FIS, respectively (Mendel et al. 2016).

$$ J_{x} = \left\{ {\left( {\left( {x,u} \right)} \right)|u \in \left[ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\mu }_{{\tilde{A}}} \left( x \right),\bar{\mu }_{{\tilde{A}}} \left( x \right)} \right]} \right\} $$
(1)
$$ J_{x} = \left\{ {\left( {\left( {x,u} \right)} \right)\left| {u \in \left[ {0,1} \right],\mu_{{\tilde{A}}} \left( x \right)} \right\rangle 0} \right\} $$
(2)

where X is the primary axis of the corresponding input and the secondary axis J is related to the uncertainty.

The Footprint of Uncertainty (FOU) (Mendel and John 2002; Ontiveros et al. 2018a) is represented as the area between the boundaries of the Type-2 Fuzzy Sets. For example, in Interval Type-2 Fuzzy Sets the FOU is the area between the lower and the upper membership functions (Fig. 2).

Fig. 2
figure 2

IT2 MF

Full size image

On the other hand, the rules of the Type-2 Fuzzy Systems are very similar to the Type-1 Fuzzy Systems. In this case, there is an antecedent and a consequent, the inference is realized by the introduction of the extension of the T-Norm and S-Norm now called meet and join, respectively. The structure of the Type-2 Fuzzy rules is expressed in Eq. (3).

$$ \begin{aligned} & R^{l} :{\text{IF}}\, x_{1} \,{\text{is}}\, \tilde{F}_{1}^{l}\, {\text{and}} \ldots {\text{and}}\, x_{p} \, {\text{is}}\,\tilde{F}_{p}^{l} , {\text{THEN}}\, y\, {\text{is}}\, {\tilde{G}}^{l} , \\ & \quad \quad {\text{where}}\, l = 1, \ldots , M \\ \end{aligned} $$
(3)

2.2.1 \( \alpha \)-plane representation

The \( \alpha \)-plane representation is an approach for modeling the GT2 FIS in order to achieve a good approximation of this system (Mendel et al. 2009; Ontiveros et al. 2018b). This representation consists on approximating the GT2 FIS by horizontal slices called \( \alpha \)-planes and finally aggregating the results. These slices can be computed as IT2 FIS and have a high computational cost, but are computable for applications that not require real-time execution. Equation (4) represents the expression of the \( \alpha \)-planes and Eq. (5) represents the aggregation of the \( \alpha \)-planes.

$$ \tilde{J}_{\alpha } = \left\{ {\left( {\left( {x,u} \right)} \right)|u \in \left[ {0,1} \right],\mu_{{\tilde{A}}} \left( x \right) = \alpha } \right\} $$
(4)
$$ \tilde{\tilde{J}} = {\cup}\,\tilde{J}_{\alpha } $$
(5)

A method for approximating a GT2 FIS by the \( \alpha \)-planes representation is presented in Fig. 3.

Fig. 3
figure 3

GT2 FIS based on α-planes

Full size image

The aggregation of the results of the \( \alpha \)-planes is performed by (6).

$$ \tilde{\tilde{A}} = \frac{{\sum \alpha \tilde{A}_{\alpha } }}{\sum \alpha } $$
(6)

The number of \( \alpha \)-planes impact the performance of the GT2 FIS; however, it was found that 10 \( \alpha \)-planes can be enough for obtaining a good performance in many applications (Melin et al. 2014).

2.2.2 Double Gaussian general type-2 membership function

In order to define the Double Gaussian GT2 Membership Function, it is necessary to model the FOU of the MF, remembering that the FOU is basically the first α-plane of the representation and is equivalent to an IT2 MF. Based on this, the Double Gaussian IT2 Membership Function (DGaussIT2MF) is proposed inspired in the GT2 membership functions presented in Mendel (2017). Figure 4 illustrates this function, and Eq. (7) describes the mathematical expression.

Fig. 4
figure 4

Double Gaussian IT2 MF

Full size image
$$ \mu_{{\bar{A}}} \left( x \right) = \left\{ {\begin{array}{*{20}l} {\bar{\mu }_{t} \left( x \right) = \left\{ {\begin{array}{*{20}l} {\exp \left( {\left( { - 1/2} \right)\left( {x - m_{1} } \right)^{2} /\sigma_{1}^{2} } \right) x <; m_{1} } \\ {{1} \quad m_{1} < x < m_{2} } \\ {\exp \left( {\left( { - 1/2} \right)\left( {x - m_{2} } \right)^{2} /\sigma_{1}^{2} } \right) x > m_{2} } \\ \end{array} } \right.} \hfill \\ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\mu }_{t} \left( x \right)\left\{ {\begin{array}{*{20}c} {\exp \left( {\left( { - 1/2} \right)\left( {x - m_{1} } \right)^{2} /\sigma_{2}^{2} } \right) x < \frac{{\left( {m_{1} + m_{2} } \right)}}{2}} \\ {\exp \left( {\left( { - 1/2} \right)\left( {x - m_{2} } \right)^{2} /\sigma_{2}^{2} } \right) x > \frac{{\left( {m_{1} + m_{2} } \right)}}{2}} \\ \end{array} } \right.} \hfill \\ \end{array} } \right. $$
(7)

where \( \bar{\mu }_{t} \left( x \right) \) and \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\mu }_{t} \left( x \right) \) are the upper and lower membership functions and are obtained by the evaluation of the \( {\text{DGaussIT2MF}}\left( {x,\left[ {\sigma_{1} ,\sigma_{2} ,m_{1} m_{2} } \right]} \right) \) function, and based on these membership functions as boundaries, Eq. (8) express the Double Gaussian General Type-2 Membership Function (DGaussGT2MF).

$$ \begin{aligned} & {\text{DGaussGT2MF}}\left( {x,\left[ {\sigma_{1} ,\sigma_{2} ,m_{1} m_{2} } \right]} \right) \\ & \quad \quad = \left\{ {\left. {\left( {\left( {x,u} \right),{\text{trimf}}\left( {u,\left[ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\mu }_{t} \left( x \right),\frac{{\bar{\mu }_{t} \left( x \right) + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\mu }_{t} \left( x \right)}}{2},\bar{\mu }_{t} \left( x \right)} \right]} \right)} \right)} \right|\forall u \in \left[ {\bar{\mu }_{t} \left( x \right), \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\mu }_{t} \left( x \right)} \right]} \right\} \\ \end{aligned} $$
(8)

This General Type-2 Membership Function has a triangular function as secondary membership function. However, this function can be substituted in the future for different kinds of membership functions. The triangular function (trimf) is defined as follows by Eq. (9)

$$ {\text{trimf}}\left( {x,\left[ {a,b,c} \right]} \right) = \left\{ {\begin{array}{*{20}l} {\frac{x - a}{b - a}} \hfill & {a < x < b} \hfill \\ {\frac{c - x}{c - b}} \hfill & {b < x < c} \hfill \\ 0 \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right. $$
(9)

For a GT2 MF represented with \( \alpha \)-planes, the number of \( \alpha \)-planes depend on the discretization of u, and the approximation is better with the increase in the discretization level of u. On the other hand, the computational cost is proportional to u.

A graphical illustration of the GT2 Double Gaussian Membership Functions can be observed in Fig. 5.

Fig. 5
figure 5

a FOU of GaussG GT2MF b GaussG GT2MF

Full size image

2.3 Proposed approach to generate the FOU

Based on the concepts above presented, we propose the use of uniform sampling with replacement to generate subtraining sets and with this model the FOU of the General Type-2 Fuzzy Sets based on multiple embedded Type-1 Fuzzy Sets.

The T1 Membership Functions are generated based on the subtraining sets, the number of clusters is proportional to the number of membership functions of the system and is proportional to the number of inputs and the number of granules, and the steps to generate the FDS are presented in Fig. 6.

Fig. 6
figure 6

Steps for FDS generation

Full size image

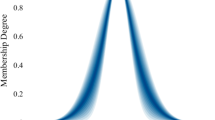
The first step consists on obtaining the centers of the Type-1 Gaussian Membership Functions, and these centers are obtained by the implementation of a clustering algorithm, in this case, the Fuzzy C-Means (FCM) algorithm. For example, consider the variable “years old” of the Mammographic dataset. The output data provided for the FCM algorithm are the centers of the clusters and the membership degree for every cluster, and Fig. 7 illustrates an example of this membership degrees, the data is the years old parameter of the mammographic dataset. The centers of the Gaussian membership functions in this paper are proposed to be the centers of the clusters provided by the FCM algorithm.

Fig. 7
figure 7

FCM clusters membership functions for years old feature in mammographic dataset

Full size image

The second step consists on obtaining the Standard deviations; based on the membership degrees obtained with the FCM algorithm, and this is expressed in Eq. (10), and this equation is the result of a least square regression.

$$ \sigma^{n} = \sqrt {\frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {x_{i} - m^{n} } \right)^{4} }}{{ - 2\left( {\ln \left| {\mu_{i}^{n} } \right|} \right)\mathop \sum \nolimits_{i = 1}^{d} \left( {x_{i} - m^{n} } \right)^{2} }}} $$
(10)

where \( \sigma^{n} \) is the standard deviation of the nth membership function, \( m^{n} \) is the center of the nth membership function, \( x_{i} \) is the input data and \( \mu_{i}^{n} \) is the membership degree of the ith data to the nth cluster. As we can observe, the \( \sigma^{n} \) depends on the \( m^{n} \), for the proposed approach, the \( m^{n} \) is considered the center of the nth cluster obtained with the FCM algorithm.

Based on the multiple Type-1 Gaussian MFs generated for every training subset, Eq. (11) describes the General Type-2 Double Gaussian MFs obtained for every cluster.

$$ \bar{\bar{\mu }}_{i} \left( {x,u} \right) = {\text{DGaussGT2MF}}\left( {x,\left[ {m_{\hbox{max} }^{i} , m_{\hbox{min} }^{i} ,\sigma_{\hbox{max} }^{i} ,\sigma_{\hbox{min} }^{i} } \right]} \right) $$
(11)

where \( m_{\hbox{max} }^{i} \) and \( m_{\hbox{min} }^{i} \) are the maximum and minimum m parameters of the ith cluster and \( \sigma_{\hbox{max} }^{i} \,{\text{and}}\, \sigma_{\hbox{min} }^{i} \) are the maximum and minimum standard deviations of the ith cluster.

2.4 Type-2 fuzzy inference systems for diagnosis

The architecture of the General Type-2 Fuzzy Classifier (GT2 FC) proposed in the present paper is illustrated in Fig. 8. This architecture is inspired by ANFIS the architecture proposed in Jang (1993) and widely used for complex problems.

Fig. 8
figure 8

Proposed architecture of GT2 FC

Full size image

The parameters of the input membership functions are estimated as was explained in the previous section. However, in this section, is defined how the output parameters of this architecture are obtained. The output of the architecture is defined in Eq. (12)

$$ \tilde{\tilde{Z}} = \frac{{\sum \alpha Z_{\alpha } }}{\sum \alpha } $$
(12)

where Z represents the different outputs of every α-plane and the output is the α-planes aggregation. However, in order to reduce the computational cost, and considering that the secondary membership function is a triangular membership function, we decide to use only three α-planes and implement the equation proposed in Ontiveros et al. (2018b) that consists on a high-order α-planes integration based on Newton–Cotes integrators. Then, the output with this consideration is expressed in Eq. (13).

$$ \tilde{\tilde{Z}} = \frac{{{\mathbf{Z}}_{1} + 2\varvec{Z}_{2} + \varvec{Z}_{3} }}{3} $$
(13)

where Z1 has an \( \alpha = 0^{ + } \), in Z2\( \alpha = 0.5 \) and for Z3\( \alpha = 1^{ - } \).

On the other hand, the solution of the individual α-planes is realized based in the Wu–Mendel type reduction (Wu and Tan 2005), that is one of the fastest methods for this process. Equation (14) expresses the output of the IT2 FIS corresponding to the lth α-plane.

$$ \begin{aligned} \left[ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{Z}_{l} ,\bar{Z}_{l} } \right] = \left[ {\sum\limits_{i = 1}^{N} {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varPhi }_{i}^{l} } \,\overrightarrow {f}_{i} ,\sum\limits_{i = 1}^{N} \overline{{\varPhi^{l} }}_{i} \overrightarrow {f}_{i} } \right] \\ Z_{l} = \frac{{(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{Z}_{l} + \bar{Z}_{l} )}}{2} \\ \end{aligned} $$
(14)

where \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{Z}_{l} \) and \( \bar{Z}_{l} \) are the left and right output of the lth α-plane and \( Z^{l} \) is the output of the lth α-plane, \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varPhi }^{l}_{i} \) and \( \overline{{\varPhi^{l} }}_{i} \) represents the normalized firing force of the ith rule of the lth α-plane, and finally \( \vec{f}_{i} \) is the Sugeno polynomial of the ith rule. It is interesting to observe that this polynomial does not change for the different α-planes and is the same for the left and right outputs, and this is because in this paper we consider that the uncertainty is handled in the input membership functions and not in the consequent. Equation (15) expresses the Sugeno polynomial.

$$ \vec{f}_{i} = a_{0}^{i} + a_{1}^{i} x_{1} + \cdots + a_{m}^{i} x_{m} $$
(15)

where \( a_{n}^{i} \) represents the Sugeno coefficient of the ith rule and the mth input.

These Sugeno coefficients in the present paper are proposed to be obtained by minimizing Eq. (16).

$$ e = \sum \left( {T - \mathop \sum \limits_{i = 1}^{N} \left( {\frac{{\overline{{\varPhi^{3} }}_{i} + \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varPhi }^{3}_{i} }}{2}} \right)\vec{f}_{i} } \right)^{2} $$
(16)

where T is the target \( \overline{{\varPhi^{3} }}_{i} \) and \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\varPhi }^{3}_{i} \) are the normalized firing force of the ith rule of the third α-plane that have an \( \alpha = 1^{ - } \), the process consists in a Least Square Error optimization.

3 Experimental results

This section introduces the results obtained by the experimentation with a set of benchmark medical diagnosis datasets, and the structure of this section is described as follows. First, the results by Hold-Out data separation with 60% for training and 40% for testing are presented, and the documented results are the average of thirty experiments for each dataset. On the other hand, it is presented a statistical comparison with respect another approach of GT2 Fuzzy Systems applied in diagnosis that is based on the principle of justifiable granularity presented by Sanchez et al. (2017).

3.1 Benchmark problems

The datasets selected for experimentation have been widely used for evaluating the performance of different kinds of diagnosis systems or classifiers, and a brief description is provided below in Table 1.

Table 1 Diagnosis datasets
Full size table

Before presenting the results obtained for the presented datasets, the membership functions obtained by uniform sampling with replacement for Type-1 Fuzzy Sets and the proposed approach of General Type-2 Fuzzy Sets are presented. Figures 9 and 10 illustrate the membership functions of the first three inputs (Features) of two of the first datasets presented, and for the Type-1 membership functions used for the estimation of the FOU.

Fig. 9
figure 9

Breast Cancer Wisconsin (original) dataset

Full size image
Fig. 10
figure 10

Haberman’s survival dataset

Full size image

3.2 Hold-out validation

In order to evaluate the performance of the proposed approach, we realize a Hold-Out validation. However, before doing the comparison with other fuzzy approaches we evaluate the performance of the proposed approach by increasing the number of clusters of the systems. The performance results have been reported with accuracy, sensitivity, and specificity. These metrics are illustrated in Fig. 11.

Fig. 11
figure 11

Performance metrics

Full size image

Tables 2, 3 and 4 summarize the results of the different performance measures, accuracy, sensitivity and specificity, respectively.

Table 2 Accuracy results with different number of clusters
Full size table
Table 3 Sensitivity results with different number of clusters
Full size table
Table 4 Specificity results with different number of clusters
Full size table

As can be noted, the accuracy decreases with the increasing of the number of clusters; this can be related to the architecture proposed where the number of rules is defined by the number of clusters and are very simple.

For the case of sensitivity, the behavior is a little chaotic, this performance measure can be affected for the data sampling, because can be obtained different measures for unbalanced samples.

By similar way, the specificity results are very chaotic and also can be related to the sample data, this is the reason to have standard deviation very large in comparison with the accuracy measure.

Figures 12, 13, 14, 15, 16, 17, 18, 19, 20, 21 and 22 illustrate the accuracy of every dataset with the different number of clusters. This kind of graphic illustrates better the point observed in Table 3, the objective is to observe the accuracy of the T2 Fuzzy Classifiers with different number of clustering and conclude over how many clusters are recommendable for this approach.

Fig. 12
figure 12

Breast Cancer Wisconsin (original) dataset

Full size image
Fig. 13
figure 13

Haberman’s survival dataset

Full size image
Fig. 14
figure 14

Fertility dataset

Full size image
Fig. 15
figure 15

Indian liver dataset

Full size image
Fig. 16
figure 16

Breast Cancer Wisconsin (Diagnostic) dataset

Full size image
Fig. 17
figure 17

Pima Indians diabetes dataset

Full size image
Fig. 18
figure 18

Statlog (heart) dataset

Full size image
Fig. 19
figure 19

Breast Cancer Coimbra dataset

Full size image
Fig. 20
figure 20

Mammographic mass dataset

Full size image
Fig. 21
figure 21

Immunotherapy dataset

Full size image
Fig. 22
figure 22

Cryotherapy dataset

Full size image

In Fig. 12, we can recommend two clusters, for example, the performance decrease with the increasing of clusters number.

In Fig. 13, we also can recommend to use two clusters, for the Haberman’s survival dataset.

For Fertility dataset, the best performance is obtained also for two clusters.

Also for Indian Liver dataset, the best performance is obtained for two clusters.

In Breast Cancer Wisconsin (Diagnostic) dataset, the best performance is obtained for four clusters.

For Pima dataset, the best performance is obtained for three clusters.

For Statlog dataset, the best performance is obtained for three clusters.

For Breast Cancer Coimbra, the best accuracy is obtained with two clusters.

Also for Mammographic Mass dataset, the best performance is obtained with two clusters.

For Immunotherapy dataset, we obtain a perfect performance with two clusters.

Finally, and similar than other cases, for Cryotherapy dataset, the best performance is obtained with two clusters.

As can be observed in the experimental results, the best results are obtained for only two clusters, and this can be related to the rules of the systems that are predefined as the first approach of ANFIS.

3.3 Statistical comparison with another approach of FOU generation

The statistical comparison was made between the proposed method and another approach for selecting the FOU of GT2 FC, which was presented by Sanchez et al. (2017) and is based on granular computing. Below is presented an statistical comparison based in Z-Test, this is because the results provided for the authors (Sanchez et al. 2017) are the mean of 30 experiments. Table 5 introduces the parameters of the statistical test.

Table 5 Z-test parameters
Full size table

Table 6 summarizes the results of the statistical test that was realized by a Z-test.

Table 6 Statistical comparison versus Sanchez et al. (2017)
Full size table

As can be observed, the proposed approach has sufficient evidence to be considered better than (Sanchez et al. 2017) in two of the four datasets that were compared. However, for the other two datasets we do not have sufficient evidence to demonstrate a superiority of one of the compared approaches. An explanation for the cases where we do not have enough evidence to show an improvement is because for these cases the architecture proposed for the reference provides a better uncertainty handling, and the fuzzy rules probably describe by a better way the information.

3.4 Cross-validation performances

In this section, the obtained performances for different values of cross-validation are presented and compared with respect to other fuzzy approaches introduced in the literature to solve diagnosis problems. Tables 7, 8 and 9 report the performances obtained for the proposed approach and other approaches of the literature for three, five and tenfolds cross-validation.

Table 7 Comparison using threefolds CV
Full size table
Table 8 Comparison using fivefolds CV
Full size table
Table 9 Comparison using tenfolds CV
Full size table

The not available results for the cited reference are expressed with a “−,” and the reason of these missing values is because the cited papers are not focused in diagnosis problems, as they report results of fuzzy classifiers but we are interested only in the diagnosis datasets for the present paper.

4 Conclusions and future work

The generation of a single GT2 FC based on a set of embedded T1 fuzzy membership functions is interesting because we can consider every T1 membership function as a fuzzy observation and the GT2 FC as the model that aggregates the observations handling the uncertainty.

Regarding the comparison with respect to different fuzzy logic approaches applied in diagnosis problems we conclude that the proposed approach offers competitive performances considering that the proposed approach can be improved in the future with optimization methods, such as metaheuristic algorithms or another kind of algorithms, for example the optimization algorithms presented in Caraveo et al. (2016), Castillo et al. (2016), Olivas et al. (2017), Peraza et al. (2017).

In comparison with respect to the approach proposed in Sanchez et al. (2017), we have enough evidence to demonstrate that the proposed approach is better in two of the four datasets compared and is worst in one of the four, on the other hand, for the other dataset no one shows to be better than the other.

As future work, we have to test the proposed methodology with other kinds of applications, for example, fault diagnosis or time series. On the other hand, is interesting to test different architectures of the system, for example with some methods for selecting the rules of the system or different kinds of membership functions. Maybe some hybridization with other classification methods could be made, for example statistical methods or methods such as Support Vector Machines.