Integrated fuzzy AHP and fuzzy TOPSIS methods for multi-objective optimization of electro discharge machining process

Abstract

In the present work, the working of an electro discharge machining process was studied in which four factors, namely pulse on time, duty cycle, discharge current, and gap voltage, were considered to be the controllable parameters, each at three levels, for monitoring three responses, namely material removal rate, tool wear ratio, and tool overcut. Statistical design of experiments using Taguchi’s orthogonal array (OA) technique has been utilized to determine the optimum level of process parameters so that they are least affected by noise factors for obtaining a robust design of the parameters. Acknowledging the limitation that Taguchi’s OA technique can determine optimal setting of controllable parameters for one output or response at a time, integrated fuzzy AHP and fuzzy TOPSIS methods were used in the scheme of multi-response experiment so that Taguchi’s OA technique may be applied successfully for parametric optimization. The results show that none of the factors were highly significant although discharge current had the highest contribution (31.63%) among all.

1 Introduction

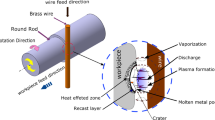
Electro discharge machining (EDM) is a popular material removal technique based upon the concept of material removal from a metallic part by electric discharges. The emergence of electrical discharge machining (EDM) from an innovation to a highly practical and profitable process is clearly reflected in its numerous applications and the challenges being faced by the modern manufacturing industries from the development of new materials that are hard and difficult to machine such as carbides, composites, ceramics, super alloys, stainless steels, heat resistant steel. This noncontact machining technique has been continuously evolving from a mere tool and die making process to a micro-/nanoscale manufacturing applications (Kunieda et al. 2005). Parametric optimization has been carried out by several researchers to find out the machine settings that yield single responses, viz. optimum material removal rate (MRR), surface roughness (SR), tool overcut (TOC), tool wear ratio (TWR), etc., based on Taguchi’s robust design technique (Spedding and Wang 1997; Puri and Bhattacharyya 2003; Ramakrishnan et al. 2003). However, multiple responses need to be optimized in order to have a better control over the process and increase production rate, which are not possible with conventional Taguchi’s orthogonal array technique. ANN model was developed, and multi-objective optimization of process parameters of wire EDM was performed based on multi-response signal-to-noise ratio (MRS/N) (Ramakrishnan and Karunamoorthy 2008). Different weights were assigned to responses, and subsequently MRS/N ratio was obtained for optimization. Technique for order preference by similarity to ideal solution (TOPSIS) was applied to optimize multiple responses, viz. MRR, TWR, SR in EDM (Senthil et al. 2014). The optimal parameters obtained using TOPSIS were agreed upon by practitioners. Taguchi-based grey relational analysis (GRA) was used to optimize SR and kerf width in WEDM (Khan et al. 2014). Pulse on time was found to be the most significant of all process parameters used. A multi-response optimization approach was presented (Nayak and Mahapatra 2013) to determine the optimal process parameters in wire electrical discharge machining process. They combined the multiple responses into a single response using analytic hierarchy process (AHP) and TOPSIS. Optimal cutting parameters were determined using Taguchi’s robust design technique. Multiple responses were optimized, viz. white layer thickness (WLT), surface crack density (SCD), and surface roughness (SR), based on different input parameters in EDM with the help of grey relational analysis combined with fuzzy logic (Dewangan et al. 2015). Analysis of variance (ANOVA) showed pulse on time to be the most significant factor responsible for multiple performance characteristics of surface integrity based. A fuzzy TOPSIS method was used (Pattnaik et al. 2015) to optimize multiple responses, viz. surface roughness, material removal rate, and tool wear rate in EDM based on various process parameters. Recast layer thickness and SR were optimized (Rupajati et al. 2014) using Taguchi-based fuzzy logic technique. This technique significantly improved multiple responses in WEDM. A combination of Taguchi and fuzzy TOPSIS methods was developed that deals with multi-response optimization problems in green manufacturing (Sivapirakasam et al. 2011). They have considered the case of EDM and tried to minimize the hazardous effects of EDM. Based on previous studies, it has been seen that coupling fuzzy logic with optimization technique could provide better results since fuzzy logic is suitable in uncertain environments like in EDM where responses calculated or measured always have some error due to characterization technique, resolution of measuring instruments, random errors, etc. An attempt has been made in this paper to utilize Taguchi’s orthogonal array (OA) technique for parametric optimization of multiple responses by integrating fuzzy AHP and fuzzy TOPSIS methods. Fuzziness was introduced to account for the uncertainty in the responses due to various controllable and uncontrollable factors.

2 Evaluation framework

Multi-criteria decision making (MCDM) is a powerful tool used widely for solving decision and planning problems involving multiple criteria (Majumder 2015). A clear and systematic structuring of the decision-making problem is carried out by MCDM techniques. It therefore becomes easy for decision makers to examine the problem and scale it as per their requirements (Isiklar and Buyukozkan 2006). The main objective of this paper as mentioned above is to select the optimal parameters of machining in EDM based on multiple responses. To achieve this, fuzzy AHP was used to determine the priorities of different responses followed by fuzzy TOPSIS to convert the multiple responses to single response and finally optimize the response using Taguchi’s OA technique. The scheme for evaluation is shown in Fig. 1 and described in the following steps below.

Fig. 1

Flowchart for multi-response optimization

• (a) Identification of responses that are considered to be the most important from manufacturing point of view.

• (b) Construction of hierarchical structure for responses and process parameters.

• (c) Calculation of weights of responses with the help of fuzzy AHP method.

• (d) Conversion of multiple responses into signal response using fuzzy TOPSIS.

• (e) Performing signal-to-noise ratio to determine optimal parameters

• (f) Analysis of variance (ANOVA) to determine significance of process parameters on the response.

3 Fuzzy AHP and fuzzy TOPSIS methods

3.1 Fuzzy AHP

AHP was proposed (Saaty 1977, 1980) to model subjective decision-making processes based on multiple attributes in a hierarchical system (Tzeng and Huang 2011). The AHP model has some limitations. The AHP method is suitable in cases having crisp information decision application. The scale of converting subjective responses into numerical form in AHP has a very unbalanced scale of judgment. The ranking is basically done with the opinion of humans but does not take into consideration the uncertainty in judgment due to natural language. The judgment of decision maker has a great effect on their preferences. This indirectly affects the results of AHP. To avoid these, several researchers have integrated fuzzy theory with AHP to improve the uncertainty. The process of fuzzy AHP is as follows (Sun 2010):

Fig. 2

Hierarchical structure of AHP/fuzzy AHP

Table 1 Membership function of linguistic scale

• (a) Construct the hierarchical structure of goal, criteria (responses), and alternatives of the multi-response optimization problem (Fig. 2).

• (b) Construct pairwise comparison matrices among all the criteria/alternatives of the hierarchy system. Assign appropriate linguistic terms to the pairwise comparisons with the help of questionnaires or decision maker regarding which criteria/alternative is more important for each of two dimensions. The linguistic terms will be converted to fuzzy numbers shown in Table 1. The matrices formed will be of the form as shown by Eq. (1):

  $$\begin{aligned} \tilde{\varvec{A}}= & {} \left[ {{\begin{array}{cccccc} \mathbf{1}&{}\quad {\tilde{\varvec{a}} _{\varvec{12}} }&{}\quad .&{}\quad .&{}\quad .&{}\quad {\tilde{\varvec{a}} _{\varvec{1n}} } \\ {\tilde{\varvec{a}} _{\varvec{21}} }&{}\quad \mathbf{1}&{}\quad .&{}\quad .&{}\quad .&{}\quad {\tilde{\varvec{a}} _{\varvec{2n}} } \\ .&{}\quad .&{}\quad .&{}\quad .&{}\quad .&{}\quad . \\ .&{}\quad .&{}\quad .&{}\quad .&{}\quad .&{}\quad . \\ {\tilde{\varvec{a}} _{\varvec{n1}} }&{}\quad {\tilde{\varvec{a}} _{\varvec{n2}} }&{}\quad .&{}\quad .&{}\quad .&{}\quad 1 \\ \end{array} }} \right] \nonumber \\= & {} \left[ {{\begin{array}{cccccc} \mathbf{1}&{}\quad {\tilde{\varvec{a}} _{\varvec{12}} }&{}\quad .&{}\quad .&{}\quad .&{}\quad {\tilde{\varvec{a}} _{\varvec{1n}} } \\ {\varvec{1}/\tilde{\varvec{a}} _{\varvec{12}} }&{}\quad \mathbf{1}&{}\quad .&{}\quad .&{}\quad .&{}\quad {\tilde{\varvec{a}} _{\varvec{2n}} } \\ .&{}\quad .&{}\quad .&{}\quad .&{}\quad .&{}\quad . \\ .&{}\quad .&{}\quad .&{}\quad .&{}\quad .&{}\quad . \\ {\varvec{1}/\tilde{\varvec{a}} _{\varvec{1n}} }&{}\quad {\varvec{1}/\tilde{\varvec{a}} _{\varvec{2n}} }&{}\quad .&{}\quad .&{}\quad .&{}\quad \mathbf{1} \\ \end{array} }} \right] \nonumber \\ \tilde{a} _{ij}= & {} 9^{-1},8^{-1},7^{-1},6^{-1},5^{-1},4^{-1},3^{-1},2^{-1},\nonumber \\&2,3,4,5,6,7,8,9;i\ne j\nonumber \\ \tilde{a} _{ij}= & {} 1;\qquad i=j \end{aligned}$$

  (1)

• (c) To determine fuzzy weights of each criterion, geometric mean method is used. Fuzzy addition and fuzzy multiplication are used to determine the fuzzy weights (Hsieh et al. 2004).

Let two fuzzy numbers $\tilde{A} =\left( {l,m,n} \right)$ and $\tilde{B} =\left( {p,q,r} \right)$, where l, m, n denote the lower, middle, and upper bounds of fuzzy number $\tilde{A}$ and p, q, r denote the lower, middle, and upper bounds of fuzzy number $\tilde{B}$, respectively. Therefore,

Fuzzy addition:

$$\begin{aligned}&\tilde{{{\varvec{A}}}} \oplus \tilde{{{\varvec{B}}}} =\left( {{{\varvec{l,m,n}}}} \right) \oplus \left( {{{\varvec{p,q,r}}}} \right) =\left( {{{\varvec{l}}+{{\varvec{p}}},{{\varvec{m}}}+{{\varvec{q}}},{{\varvec{n}}}+{{\varvec{r}}}}} \right) \end{aligned}$$

Fuzzy multiplication:

$$\begin{aligned}&\tilde{A} \otimes \tilde{B} =\left( {l,m,n} \right) \otimes \left( {p,q,r} \right) =\left( {lp,mq,nr} \right) \\&{{\varvec{l}}},{{\varvec{m}}},{{\varvec{n}}},{{\varvec{p}}},{{\varvec{q}}},{{\varvec{r}}}>{{\varvec{0}}} \end{aligned}$$

The fuzzy weights can then be determined by Eqs. (2–3):

$$\begin{aligned} \tilde{r} _j= & {} \left( {\tilde{a} _{j1} \otimes \tilde{a} _{j2} \otimes \ldots \tilde{a} _{jn} } \right) ^{\frac{1}{n}} \end{aligned}$$

(2)

$$\begin{aligned} \tilde{w} _j= & {} \tilde{r} _j \otimes \left( {\tilde{r} _1 \oplus \tilde{r} _2 \oplus \ldots \tilde{r} _n } \right) ^{-1} \end{aligned}$$

(3)

$\tilde{\varvec{a}} _{\varvec{ij}}$ :

Comparative fuzzy value of criterion ${{\varvec{i}}}$ to criterion ${{\varvec{j}}}$

$\tilde{\varvec{r}} _{\varvec{j}}$ :

Geometric mean of fuzzy comparison value of criterion j to each of the other criteria

$\tilde{\varvec{w}} _{\varvec{j}}$ :

Fuzzy weight of the $j{\mathrm{th}}$ criterion. It is indicated by a triangular fuzzy number

$\tilde{w} _j =\left( {lw_j ,mw_j ,nw_j } \right)$, where $lw_j ,mw_j ,nw_j$ represent the lower, middle, and upper values of the fuzzy weight of the $j{\mathrm{th}}$ criterion.

Table 2 Transformation for fuzzy membership functions

3.2 Fuzzy TOPSIS

In order to use fuzzy logic in EDM, we deliberately transform the existing precise values to five levels after normalizing the ratings. Fuzzy linguistic variables selected are: Very Low (VL), Low (L), Medium (M), High (H), and Very High (VH). A triangular fuzzy number has been used to represent the five-level fuzzy linguistic variables. Each rank was assigned an evenly spread membership function with interval of 0.30 or 0.25 (Table 2) (Torfi et al. 2010). For example, the fuzzy variable, L, has its associated triangular fuzzy number with the minimum of 0.15, mode of 0.30, and maximum of 0.45. The same definition is then applied to all other fuzzy variables (Fig. 3) [19]. Decision makers find it difficult to assign performance based on crisp values; hence, the use of fuzzy numbers allows them to assign relative importance of criteria.

Fig. 3

Fuzzy triangular membership functions

The process of fuzzy TOPSIS is described in the following steps (Torfi et al. 2010):

Let us consider a set of alternatives, $A=\{A_i |i=1,2\ldots n\}$, and a set of criteria, $C=\{C_j |j=1,2\ldots m\}$

• (a) A matrix is constructed with performance rating of each alternative with respect to each criterion. Rows should be criteria, and columns should be the alternatives. In case of quantitative analysis, these ratings can be the experimental data, which correspond to each alternative or some quantity provided by the company/organization. In case of qualitative analysis, the ratings can be given with the help of questionnaires or can be based upon the experience of the decision maker. The fuzzy MCDM can be conveniently expressed in the following matrix format as Eqs. (4–5).

$$\begin{aligned} A= & {} \left[ {{\begin{array}{cccccc} {\tilde{x} _{11} }&{}\quad {\tilde{x} _{12} }&{}\quad .&{}\quad .&{}\quad .&{}\quad {\tilde{x} _{1n} } \\ {\tilde{x} _{21} }&{}\quad {\tilde{x} _{22} }&{}\quad .&{}\quad .&{}\quad .&{}\quad {\tilde{x} _{2n} } \\ .&{}\quad .&{}\quad .&{}\quad .&{}\quad .&{}\quad . \\ .&{}\quad .&{}\quad .&{}\quad .&{}\quad .&{}\quad . \\ {\tilde{x} _{m1} }&{}\quad {\tilde{x} _{m1} }&{}\quad .&{}\quad .&{}\quad .&{}\quad {\tilde{x} _{mn} } \\ \end{array} }} \right] \end{aligned}$$

(4)

$$\begin{aligned} W= & {} \left[ {\tilde{w} _1 \tilde{w} _2 \ldots \tilde{w} _j } \right] \end{aligned}$$

(5)

$\tilde{x} _{ij}$ :

$i=1,2,\ldots m; j=1,2,\ldots n;$ represents performance rating of the $i{\mathrm{th}}$ alternative $A_i$ with respect to $j{\mathrm{th}}$ criterion, $C_j$

$\tilde{w} _j$ :

Represents weight of $j{\mathrm{th}}$ criterion,$C_j$. The weights are calculated using fuzzy AHP.

$\tilde{x} _{ij}$ and $\tilde{w} _j$ are linguistic triangular fuzzy numbers, $\tilde{x} _{ij} =\left( {a_{ij} ,b_{ij} ,c_{ij} } \right)$ and $\tilde{w} _j =\left( {a_{j1} ,b_{j2} ,c_{j3} } \right)$; a, b, c represent lower, modal, and upper bounds of the fuzzy numbers. Since the range of normalized triangular fuzzy numbers lies in the interval [0, 1], it eliminates the process of normalization. However, for experimental results, data obtained have to be normalized and then appropriate linguistic variables are plotted against each rating, which corresponds to a particular interval of the fuzzy number $\tilde{x} _{ij}$ .

Fig. 4

Die-sinking EDM

• (b) Normalize the fuzzy decision matrix and prepare normalized fuzzy decision matrix shown in Eqs. (6–7).

  $$\begin{aligned} \tilde{R}= & {} \left[ {\tilde{r} _{ij} } \right] _{m\times n} \end{aligned}$$

  (6)
  $$\begin{aligned} \tilde{r} _{ij}= & {} \left( {\frac{a_{ij} }{c_j^+ },\frac{b_{ij} }{c_j^+ },\frac{c_{ij} }{c_j^+ }} \right) \end{aligned}$$

  (7)

  $\tilde{{{\varvec{r}}}} _{{{\varvec{ij}}}}$ normalized value of fuzzy number $\tilde{{{\varvec{x}}}} _{{{\varvec{ij}}}}$

  $$\begin{aligned} c_j^+ =\mathrm{max}_i \left\{ {c_{ij} |i=1,2,\ldots n} \right\} \end{aligned}$$

• (c) Construct the weighted normalized fuzzy decision matrix as shown in Eq. (8). To construct this, the values of Eq. (6) and weights $\tilde{w} _j$ obtained from fuzzy AHP are required.

  $$\begin{aligned} V= & {} \left[ {{\begin{array}{cccccc} {\tilde{v} _{11} }&{}\quad {\tilde{v} _{12} }&{}\quad .&{}\quad .&{}\quad .&{}\quad {\tilde{v} _{1n} } \\ {\tilde{v} _{21} }&{}\quad {\tilde{v} _{22} }&{}\quad .&{}\quad .&{}\quad .&{}\quad {\tilde{v} _{2n} } \\ .&{}\quad .&{}\quad .&{}\quad .&{}\quad .&{}\quad . \\ .&{}\quad .&{}\quad .&{}\quad .&{}\quad .&{}\quad . \\ {\tilde{v} _{m1} }&{}\quad {\tilde{v} _{m2} }&{}\quad .&{}\quad .&{}\quad .&{}\quad {\tilde{v} _{mn} } \\ \end{array} }} \right] =\tilde{w} _j \otimes \tilde{r} _{ij}\nonumber \\= & {} \left[ {{\begin{array}{ccccccccccccc} {\tilde{w} _1 \,\times \tilde{r} _{11} }&{}\quad {\tilde{w} _2 \,\times \tilde{r} _{12} }&{}\quad .&{}\quad .&{}\quad .&{}\quad {\tilde{w} _n \,\times \tilde{r} _{1n} } \\ {\tilde{w} _1 \,\times \tilde{r} _{21} }&{}\quad {\tilde{w} _2 \,\times \tilde{r} _{22} }&{}\quad .&{}\quad .&{}\quad .&{}\quad {\tilde{w} _n \,\times \tilde{r} _{2n} } \\ .&{}\quad .&{}\quad .&{}\quad .&{}\quad .&{}\quad . \\ .&{}\quad .&{}\quad .&{}\quad .&{}\quad .&{}v . \\ {\tilde{w} _1 \,\times \tilde{r} _{m1} }&{}\quad {\tilde{w} _2 \,\times \tilde{r} _{m2} }&{}\quad .&{}\quad .&{}\quad .&{}\quad {\tilde{w} _n \,\times \tilde{r} _{mn} } \\ \end{array} }} \right] \nonumber \\ \end{aligned}$$

  (8)

• (d) Identify positive ideal $\left( {V^{+}} \right)$ and negative ideal $\left( {V^{-}} \right)$ solutions from the weighted normalized matrix. The fuzzy positive ideal solution $\left( {FPIS,V^{+}} \right)$ and the fuzzy negative ideal solution $\left( {FNIS,V^{-}} \right)$ are shown in Eqs. (9–10).

  $$\begin{aligned} V^{+}= & {} \left\{ {\tilde{v} _1^+ ,\tilde{v} _2^+ ,\ldots \tilde{v} _m^+ } \right\} \nonumber \\= & {} \left\{ {\left( {\max \tilde{v} _{ij} \left( x \right) |j\in J_1 } \right) \left| {\left( {\min \tilde{v} _{ij} \left( x \right) |j\in J_2 } \right) } \right| }\right. \nonumber \\&\left. {i=1,2,\ldots n} \right\} \end{aligned}$$

  (9)
  $$\begin{aligned} V^{-}= & {} \left\{ {\tilde{v} _1^- ,\tilde{v} _2^- ,\ldots \tilde{v} _m^- } \right\} \nonumber \\= & {} \left\{ {\left( {\min \tilde{v} _{ij} \left( x \right) |j\in J_1 } \right) \left| {\left( {\max \tilde{v} _{ij} \left( x \right) |j\in J_2 } \right) } \right| }\right. \nonumber \\&\left. {i=1,2,\ldots n} \right\} \end{aligned}$$

  (10)

  J$_{1}$ and J$_{2}$ are benefit and cost attributes, respectively.

  Max and min operations do not give triangular fuzzy numbers. However, ideal solutions can be obtained as fuzzy numbers. The elements $\tilde{v} _{ij} \,\forall \hbox {i},\hbox {j}$ are normalized positive triangular fuzzy numbers whose ranges lie in the interval [0, 1]. Thus, we can define the FPIS $\tilde{v} _j^{+}$ as $\left( {1,1,1} \right)$ for benefit criteria or $\left( {0,0,0} \right)$ for cost criteria. Likewise, the FNIS $\tilde{v} _j^{-}$ is $\left( {0,0,0} \right)$ for benefit criteria or $\left( {1,1,1} \right)$ for cost criteria.

• (e) The distance between two fuzzy numbers $\tilde{a}$and $\tilde{b}$ can be found out by the following formula:

  $$\begin{aligned} d\left( {\tilde{a} ,\,\tilde{b} } \right) =\sqrt{\frac{1}{3}\left[ {\left( {a_1 -b_1 } \right) ^{2}+\left( {a_2 -b_2 } \right) ^{2}+\left( {a_3 -b_3 } \right) ^{2}} \right] }, \end{aligned}$$

  where $\tilde{a} =\left( {a_1 ,\,a_2 ,\,a_3 } \right)$ and $\tilde{b} =\left( {b_1 ,\,b_2 ,\,b_3 } \right)$

The separation measures are calculated based on the above formula. The distance of each alternative from $V^{+}$ and $V^{-}$ can be calculated using Eqs. (11–12), respectively (Torfi et al. 2010).

$$\begin{aligned} d_i^+= & {} \mathop \sum \limits _{j=1}^n d\left( {\tilde{v} _{ij} \,,\tilde{v} _j^+ } \right) ;i=1,2,\ldots m \end{aligned}$$

(11)

$$\begin{aligned} d_i^-= & {} \mathop \sum \limits _{j=1}^n d\left( {\tilde{v} _{ij} \,,\tilde{v} _j^- } \right) ;i=1,2,\ldots m \end{aligned}$$

(12)

• (f) The similarities to ideal solution (closeness coefficients) are calculated. This step solves the similarities to an ideal solution using Eq. (13). With the help of closeness coefficient, the multiple responses obtained from experiments have been converted to single response with priorities as obtained from fuzzy AHP.

$$\begin{aligned} CC_i= & {} \frac{d_i^- }{d_i^+ +d_i^- }\nonumber \\ {{\varvec{CC}}}_{{\varvec{i}}}\in & {} \left[ {{{\mathbf{0,1}}}} \right] \forall {{\varvec{i}}} ={{\mathbf{1,2}}},\ldots {{\varvec{n}}} \end{aligned}$$

(13)

Table 3 Machine specification of the EDM process

4 Experimental details

4.1 Details of experiment

The experiments were conducted on a die-sinking EDM setup at CNC Laboratory of Tool Room Training Centre (Fig. 4). The specifications of the machine are given in Table 3.

Table 4 Dimensions of tool and workpiece

The workpiece material (anode) used was stainless steel (AISI304). The tool (cathode) material was copper. The dimensions of tool and workpiece are shown in Table 4. Straight polarity was used for all the experiments.

Fig. 5

Process parameters and responses in EDM process (used in our study)

During experiments, there were some parameters which were kept constant throughout. Figure 5 shows the process parameters, viz. input parameters, constant parameters (with their fixed values during experiment), and the responses obtained after experimentation. The input parameters (four in number at three levels each) used to determine the responses are given in Table 5. The dielectric fluid used was SERVO oil (Grade 52).

The input parameters considered during experiments were pulse on time ($\mathbf{T}_{\mathbf{ON}}$), duty cycle (DC), discharge current (I), and gap voltage (V). Since four factors were chosen with three levels each, $\hbox {L}_{9}$ orthogonal array was selected for conducting the experiments. It is worthwhile to mention that no significant interaction effect was found among the factors as observed during initial set of experiments. The $\hbox {L}_{9}$ orthogonal array is shown in Table 6. The table contains the input parameters in coded form.

4.2 Determination of output parameters

4.2.1 Material removal rate (MRR)

MRR is defined as the ratio of the difference in weight of the workpiece before and after machining to the density of the material and the machining time (mm$^{3}$/min). This is shown in Eq. (14)

$$\begin{aligned} \mathrm{MRR}=\frac{W_{W_i } -W_{W_f } }{\rho _W \times t} \end{aligned}$$

(14)

• $W_{W_i } =$ Initial weight of the workpiece before machining (g)

• $W_{W_f } =$ Final weight of the workpiece after machining (g)

• $t=$ Machining time (s)

• $\rho _W =$ Density of stainless steel (SS304) = 8000 kg/m$^{3}$

Table 5 Input parameters

Table 6 $\hbox {L}_{9}$ orthogonal array (refer to Table 3 for data)

4.2.2 Tool wear ratio (TWR)

Tool wear ratio (TWR) is defined as the ratio of the volume of material removed from the tool to the volume of material removed from the workpiece. It is generally expressed in percentage. It is given by Eq. (15)

$$\begin{aligned} \mathrm{TWR}=\frac{W_{T_i } -W_{T_f } }{W_{W_i } -W_{W_f } }\times \frac{\rho _W }{\rho _T } \end{aligned}$$

(15)

• $W_{T_i } =$ Initial weight of the tool before machining (g)

• $W_{T_f } =$ Final weight of the tool after machining (g)

• $\rho _T =$ Density of copper = 8940 kg/m$^{3}$

4.2.3 Tool overcut

Tool overcut (TOC) is calculated as half the difference of the diameter of the hole produced on the workpiece to the tool diameter as shown in Eq. (16)

$$\begin{aligned} \mathrm{TOC}=\frac{D_0 -D_i }{2} \end{aligned}$$

(16)

• $D_0 =$ Diameter of the hole on the workpiece (mm)

• $D_i =$ Tool diameter (mm)

Table 7 Normalized responses of EDM process

The experimental data obtained were normalized and are shown in Table 7. Normalization of responses were carried out to convert them into fuzzy numbers. Normalization of MRR is done by using Eq. 17, where high amount of material removal is desired, whereas normalization of TWR and TOC is done based on Eq. 18, where minimal amount of tool wear and overcut is required.

• For benefit criteria (larger is better),

  $$\begin{aligned} r_{kj} \left( x \right) =\frac{x_{kj} -x_{\mathrm{min}} }{x_{\mathrm{max}} -x_{\mathrm{min}} } \end{aligned}$$

  (17)

  $x_{\mathrm{max}} =$ Desired/aspired level

  $x_{\mathrm{min}} =$ Worst level

• For cost criteria (smaller is better),

  $$\begin{aligned} r_{kj} \left( x \right) =\frac{x_{\mathrm{min}} -x_{kj} }{x_{\mathrm{min}} -x_{\mathrm{max}} } \end{aligned}$$

  (18)

5 Optimization by integrated Taguchi’s OA, fuzzy AHP, and fuzzy TOPSIS

5.1 Fuzzy AHP

The weights of responses were assigned linguistic variables as shown in Table 1. Each linguistic variable was described using a triangular fuzzy number, and the scale of fuzzy number was also shown. Four experts in the field of EDM rated weight of each attribute with respect to a linguistic term. The pairwise comparison of responses is shown in Table 8. The fuzzy weights of the criteria are calculated (Eqs. 2–3) as shown in Table 9. These weights indicate the lower, modal, and upper values of the fuzzy number, respectively.

Table 8 Pairwise comparison of criteria

Table 9 Fuzzy weights of the responses

Table 10 Normalized fuzzy decision matrix

Table 11 Weighted normalized matrix

5.2 Fuzzy TOPSIS for determination of closeness coefficients

In fuzzy TOPSIS, the alternatives were chosen as the nine experiments in L$_{9}$ array. Table 10 shows the normalized fuzzy decision matrix. It is expressed by first normalizing the experimental data. The normalized data are shown in Table 7. They are then converted into fuzzy numbers using Table 2. Table 11 shows the weighted normalized ratings by taking into account the fuzzy weights obtained in Table 9. The weighted normalized ratings basically combine the fuzzy weights of the criteria and the performance ratings of the alternatives with respect to criteria. It is calculated using Eq. 8. Considering FPIS $\left( {\tilde{v} _j^+ } \right)$ as $\left( {1,1,1} \right)$ for MRR and $\left( {0,0,0} \right)$ for TWR & TOC and the FNIS $\left( {\tilde{v} _j^- } \right)$ as $\left( {0,0,0} \right)$ for MRR and $\left( {1,1,1} \right)$ for TWR & TOC, the respective separation measure for each alternative is found out using Eqs. (11–12). The values are shown in Table 12. Next, using Eq. 13, the closeness coefficient of each alternative has been found out (Table 13). It indicates which alternative is nearest to PIS and farthest from NIS. Higher value of closeness coefficients indicate higher rank.

Table 12 Separation measures from ideal solutions

Table 13 Signal-to-noise ratio (S/N ratio)

Fig. 6

Mean of S/N ratio versus process parameters

A short interpretation of Table 12 is as follows: ${{\varvec{d}}}_{{\varvec{i}}}^+$ for alternative 1 is higher compared to alternative 9. This indicates that alternative 1 is at a greater distance from PIS than alternative 9. Same principle can be used for separation measures with respect to NIS.

5.3 Signal-to-noise ratio (S/NR)

After determination of closeness coefficient $\left( {CC_i } \right)$ values using fuzzy TOPSIS, the preferred parameter settings in EDM are then determined through analysis of the “signal-to-noise” (S/N) (measured in dB) ratio using the $CC_i$ values, where factor levels that maximize the appropriate S/NR are optimal. There are three standard types of S/N ratios depending on the desired performance response. The S/N ratio can be obtained using Eq. 19 (larger the better) as higher closeness coefficients are preferred. This is shown in Table 13 along with the closeness coefficients.

$$\begin{aligned} \textit{S}/\textit{N} ratio=-10\log \left( {\frac{1}{n}\mathop \sum \limits _{i=1}^n \frac{1}{y_i^2 }} \right) \end{aligned}$$

(19)

• n Number of trials/experiments

• $y_i$ Response of $i{\mathrm{th}}$ experiment

• $\bar{y}$ Mean of the responses $=\frac{1}{n}\sum \nolimits _{i=1}^{n} y_i$

Now, plotting S/N ratio against each factor, we get the main effects plot. These graphs are shown in Fig. 6. It indicates the effect of parameters at each level on the S/N ratio. The optimum level is selected based on this graph. It is done by considering the levels of factors which have the highest S/N ratio following the concept of larger-the-better design of parameters. From Fig. 6, the optimum cutting parameters of the die-sinking EDM obtained are shown in Table 14. At the optimum condition, the S/N ratio is found out to be 7.38.

Table 14 Optimum cutting parameters

5.4 Analysis of variance (ANOVA)

Analysis of variance (ANOVA) was done which shows the percentage contribution of each factor on the responses and the significant factors. This is shown in Table 15.

Table 15 ANOVA table

The degree of freedom for the error is zero. Hence, an approximate estimate of the error sum of squares is obtained by pooling the sum of squares corresponding to the factors having the lowest mean square. As a rule of thumb, the sum of squares corresponding to the bottom half of the factors (as defined by lower mean square) is used to estimate the error sum of squares (NPTEL IITB). It indicates the percentage contribution of factors with respect to the responses, and the F ratio suggests which factor is significantly affecting the response. From Table 15, no significance was observed at conventionally used value of 95%. It is seen that discharge current

(I) has the highest contribution on the response (31.63%) while gap voltage has the least (18.37%). A summary of the results is shown in Table 16.

Confirmation experiments were conducted for validating conclusions drawn from Table 16, and the S/N ratio at optimal setting along with that obtained from fuzzy AHP–fuzzy TOPSIS–Taguchi’s OA technique is also presented in Table 17. Experimental results correlated well with the optimal settings predicted based on fuzzy AHP–fuzzy TOPSIS–Taguchi’s OA technique.

Table 16 Summary of Results

Table 17 Results of the confirmation experiment

6 Conclusion

The present work combines Taguchi’s orthogonal array (OA) technique with integrated fuzzy AHP and fuzzy TOPSIS methods to convert multiple responses to a single response so that Taguchi’s OA technique may be applied successfully. Moreover, this was done in order to avoid the tedious process of using each response and finding their signal-to-noise ratio separately in numerous tabular forms for optimizing the machining parameters. The following conclusions can be derived from this study:

• Priorities of the responses can be incorporated by using fuzzy AHP as required by the decision maker or the expert.

• Closeness coefficients obtained from fuzzy TOPSIS enable to convert multiple responses to a single output, which helps in finding optimal solution using signal-to-noise ratio.

• The proposed method of integration of Taguchi’s OA, fuzzy AHP, and fuzzy TOPSIS is quite suitable for determining optimum level of parameters of any machining process which may involve uncertainties in the maximization or minimization of responses.