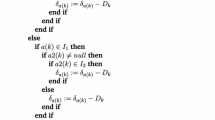1 Introduction

One of the most popular facility location problems is the covering location problem (Hamacher and Drezner 2002). The objective of a simple version of this problem is to determine the optimal location and number of facilities in order to cover all customers. A customer is said to be covered or served by a facility if it falls within the service distance of that facility. The covering location problem has several applications in emergency and military services as well as in public services such as locating police stations, schools, plants, bus stops, fire stations to name a few (Chung 1986; Schilling et al. 1993). An important and related problem in this context is the maximum covering location problem (MCLP) (Adenso-Diaz and Rodriguez 1997; Church and ReVelle 1974; Galvão et al. 2000; Hamacher and Drezner 2002; Lorena and Pereira 2002; Resende 1998; ReVelle and Eiselt 2005; Rodriguez et al. 2012). MCLP is considered when it is not feasible to cover all customers due to many problems like budgetary constraints or insufficient resources. For a simple model of MCLP, the objective is to locate a given number of facilities such that the number of customers covered by these facilities is maximized.

figure a

Since MCLP is NP-hard in general (Berg et al. 2009; Gary and Johnson 1979; Megiddo et al. 1983), genetic algorithms (GAs) (Goldberg 1989) could be a better choice for solving MCLP. GAs are popular search and optimization strategies guided by the principle of Darwinian evolution. Here, the parameters of the search space are encoded in the forms of strings (chromosomes). The population consisting of a set of chromosomes is initialized randomly. The goodness of a chromosome is measured using a fitness function which is usually related to the objective function to be optimized. Some biologically inspired operators such as selection, crossover and mutation are applied to create the child population. Subsequently, elitism is performed to evolve the next generation population using the most-fit chromosomes of the parent and child populations. The algorithm terminates if some specific criterion is met or the maximum generation limit is reached. The best-fit chromosome of the final generation provides the solution. Algorithm 1 shows the pseudocode of a typical GA.

Suitably designed GAs are known to perform well to produce near-global optimal results for NP-hard problems. However, these techniques are often criticized for their relatively high computation time. GAs were used by Jaramillo et al. (2002) for solving different types of location problems including MCLP. Fazel Zarandi et al. (2011) also developed a customized GA to solve MCLP and they applied this to large instances of MCLP with up to 2500 nodes. However, some studies have indicated that although classical GA is very good in quickly locating high performance regions in a large and complex search place, it is not good enough in fine-tuning the solutions that are very near to some optimal solution. GA spends most of the time in refining the initially obtained good solutions to convert them into best ones. The performance of GA can be improved substantially by incorporating some local improvement strategies applied on the solutions encoded in chromosomes (García-Martínez and Lozano 2007). Motivated by this, in this article, an improved GA-based approach is proposed to solve MCLP. In this approach, the chromosomes of GA encode possible locations of facilities. Fitness of each chromosome is computed by the percentage of coverage by the solution encoded by it. A local refinement strategy is adopted to improve the chromosomes locally for faster convergence of GA by quickly fine-tuning the solutions. The results obtained using the proposed GA-based technique with local refinement are compared with the results given by Lagrangian/surrogate heuristic-based approach in Lorena and Pereira (2002) as well as the customized GA-based approach in Fazel Zarandi et al. (2011). It is found to outperform both the approaches in terms of percentage of coverage and computational time in most of the cases. Moreover to emphasize the effectiveness of the local refinement strategy, the results obtained using the proposed GA without this strategy are also mentioned in this article.

The rest of the article is organized as follows. Related works are discussed in Sect. 2. Section 3 formally defines MCLP. In Sect. 4, the proposed GA-based technique is described in detail. In Sect. 5, the experimental results are reported and discussed. Finally, Sect. 6 concludes the article.

2 Literature review

Since the introduction of MCLP by Church and ReVelle on a network (Church and ReVelle 1974), many of its alternative versions have been considered in facility location literature (Assis Corrêa et al. 2009; Atta and Mahapatra 2013; Berman et al. 2010; Davari et al. 2011; Drezner and Hamacher 2001; Farahani et al. 2012; Karasakal and Karasakal 2004; Karmakar 2011; Lee and Lee 2010; Mahapatra 2012; Moore and ReVelle 1982; Pereira et al. 2015; ReVelle and Eiselt 2005; Spieker et al. 2016). In the present work, we consider the model of MCLP proposed by Galvão and ReVelle (1996). In this model, each customer is considered as a point in a plane and each of them has an associated demand. These demands can also be considered as the weights of the points. The potential location of each facility is restricted to be the locations of customers. Each facility has its own service distance, within which only, it can provide its service. The service area of each facility is considered to be circular with the service distance as the radius of the circle. The service distance, a parameter of MCLP, is taken to be same for all the facilities. Therefore, the objective of MCLP under this model is to locate a given number of facilities such that the maximal possible demands of customers is served within a given service distance. Moreover, the geometric version of MCLP in this model can be stated as follows. Given a set of n weighted points on a plane, a number of facilities k, and a service distance r, find a placement of k circles, each of having radius r, so that the sum of the weights of the input points covered by k such circles is maximized.

Many researchers focus on different heuristic approaches for solving this problem. Galvão and ReVelle developed a Lagrangian heuristic for MCLP in Galvão and ReVelle (1996) where they tested their heuristic in a network of up to 150 vertices. They improved both the lower and upper bounds of the problem and hence provided a better approximate solution for MCLP compared to Weaver and Church (1984). Galvão et al. compared the solutions of MCLP obtained by the two heuristics based on Lagrangian and surrogate relaxation in Galvão et al. (2000). Comparison was done using 331 test problems available in the literature with number of vertices ranging from 55 to 900. Later on, Lorena and Pereira (2002) developed another Lagrangian heuristic using Unified Linear Model given by Hillsman (1984) to obtain better solution for MCLP in reduced computational time. They got better percentage of coverage than that obtained by Galvão and ReVelle (1996) and Galvão et al. (2000). Other approaches used for MCLP are dubbed greedy adding (Church and ReVelle 1974), greedy adding with substitution (Church and ReVelle 1974), greedy randomized adaptive search (Resende 1998), genetic algorithms (GAs) (Fazel Zarandi et al. 2011; Jaramillo et al. 2002). Although MCLP is NP-hard in general, recently deterministic algorithms were proposed to solve the problem using the tools of computational geometry (De Berg et al. 2000; Preparata and Shamos 1993) when the number of given facilities is small and service area of each facility is either circular (Berg et al. 2009) or square (Mahapatra 2007; Mahapatra et al. 2015) or rectangular (Mahapatra 2012) in shape.

3 Problem definition

Let us assume that the customers are represented by a set P of m points in a plane. Each point \(p_j \in P\), \(j=1, 2, \ldots , m\), has a nonnegative demand which is considered as the weight of the corresponding point. The service area (or coverage area) of each facility is circular in shape, each having the radius r, which is a constant. This distance r is known as the service distance. The center of the circle with radius r is the location of the facility to be installed. Let the given number of facilities to be installed be k, \(1 \le k \le m\) and the set of centers of these k facilities be \(\{c_1, c_2, \ldots , c_k\}\). Here, the potential location of each of the k facilities is restricted to the locations of the customers itself. This implies that \(c_i \in P\), \(1 \le i \le k\).

A point \(p_j \in P\) is said to be covered (enclosed) by a circle with center at \(c_i,~1 \le i \le k\), if and only if the Euclidean distance between \(p_j\) and \(c_i\), denoted as \(d(p_j, c_i)\), is at most r; otherwise the point \(p_j\) is not covered by the corresponding circle. If a point is covered by more than one circle then the corresponding customer can avail the service from any one of the facilities which are installed at the centers of such circles. However, we assume that a customer cannot avail the service from more than one facility. Note that the objective of MCLP is to find the locations of k facilities such that the sum of the demands of the customers covered by k facilities is maximized.

Let r be the service distance for MCLP, \(P = \{p_1, p_2, \ldots , p_m\}\) be the set of customers, \(I = \{c_1, c_2, \ldots , c_m\}\) be the set of potential facility sites, and \(f_j\) be the demand of customer \(p_j\). Suppose \(a_{ij} = 1\) if customer \(p_j \in P\) can be covered by a facility located at \(c_i \in I\), and \(a_{ij} = 0\) otherwise. Let k be the number of facilities to be established. Also \(x_j = 1\) if customer \(p_j\) is covered, and \(x_j = 0\) otherwise; \(y_i = 1\) means that a facility must be located at site \(c_i \in I\), and \(y_i = 0\) otherwise. The mathematical formulation of the objective function of MCLP, v(MCLP), given by Galvão et al. (2000) is as follows:

$$\begin{aligned} v(MCLP) = \max \sum \limits _{p_j \in P} f_jx_j \end{aligned}$$
(1)

subject to the constraints

$$\begin{aligned}&\sum \limits _{c_i \in I} a_{ij}y_i - x_j \ge 0,\quad p_j \in P, \end{aligned}$$
(2)
$$\begin{aligned}&\sum \limits _{c_i \in I} y_i = k, \end{aligned}$$
(3)
$$\begin{aligned}&x_j \in \{0, 1\},\quad p_j \in P, \end{aligned}$$
(4)
$$\begin{aligned}&y_i \in \{0, 1\},\quad c_i \in I. \end{aligned}$$
(5)

In this formulation, the objective function denotes the total demands covered and the goal is to maximize the value of the objective function. Constraint (2) denotes that a customer \(p_j \in P\) is covered if and only if there is at least one facility \(c_i \in I\) such that \(d(p_j, c_i) \le r\). Constraint (3) restricts the number of facilities to be exactly k. Constraints (4) and (5) guarantee the \(0-1\) nature of the decision variables of the problem. In this work, we consider the locations of the customers as the potential locations of the facilities to be placed. Hence, the set I and the set P are analogous for the problem considered in this article.

4 Proposed GA for MCLP

In this section, the proposed GA-based solution for the aforementioned MCLP is described. The overall procedure of the proposed GA-based solution of MCLP is demonstrated in Fig. 1. In the following subsections, we describe each step of the proposed method in detail.

Fig. 1
figure 1

Flowchart of the proposed GA-based method for solving MCLP

Full size image

4.1 Chromosome encoding

In GAs, possible solutions for the optimization problem in hand are encoded in the form of strings called chromosomes. A possible solution of MCLP is a set of potential locations of k facilities to be chosen from the set of m customers \(P=\{p_1,p_2,\ldots ,p_m\}\). Thus a chromosome here encodes an integer string \(\{t_1,t_2,\ldots ,t_k\}\) of length k representing the indices of the k customers chosen as the facilities. Each element \(p_{t_i}\in P\), \(i=1, 2, \ldots ,k\), since the potential locations of k facilities are restricted to the locations of the customers itself. For example, if \(m=100\) and \(k=5\), then a chromosome \(\{2,34,75,87,92\}\) implies that the customers \(p_2, p_{34}, p_{75}, p_{87}\) and \(p_{92}\) are chosen as the potential locations of facilities as per the solution encoded in the chromosome.

4.2 Population initialization

The initial population consists of \(\mathcal{P}\) chromosomes where \(\mathcal{P}\) is a user defined parameter called population size. Each chromosome of the initial population is generated by selecting k random indices from the set \(\{1,2,\ldots ,m\}\). In this work, we set \(\mathcal{P}=20\) which is chosen experimentally.

4.3 Fitness computation

Fitness of a chromosome represents the goodness of the solution encoded in it with respect to MCLP. The objective of MCLP is to maximize the coverage (i.e., the percentage ratio of total demands of the customers covered by some facilities to the total demands of all customers). Hence, the coverage of the solution encoded in a chromosome is considered as the fitness of the chromosome, as shown in Eq. 1. The fitness is to be maximized.

4.4 Genetic operators

Three genetic operators, namely selection, crossover and mutation are used to create the next generation population from the current one.

4.4.1 Selection

Selection is the process of making a mating pool from the population. The chromosomes selected in the mating pool are capable of taking part in crossover. Here well-known binary tournament selection (Goldberg 1989) is used. In binary tournament selection, two chromosomes are randomly picked up from the population and the better one (with respect to the fitness value) is put in the mating pool. The process is repeated \(\mathcal{P}\) times (\(\mathcal{P}\) being the population size) to create a mating pool consisting of \(\mathcal{P}\) parents.

Table 1 Test problems
Full size table

4.4.2 Crossover

Crossover operation is done for information exchange between two parents to create two offspring solutions. Single-point crossover operation is used here. In each crossover operation, two chromosomes are randomly chosen from the mating pool and their elements are swapped beyond a randomly chosen crossover point within length of the chromosomes. The crossover operation is controlled by crossover probability \(\mu _c\) and repeated \(\frac{\mathcal{P}}{2}\) times to fill up the child population with \(\mathcal{P}\) offspring solutions. The crossover probability \(\mu _c\) is kept constant as 0.9 throughout all the generations.

4.4.3 Mutation

Unlike crossover, mutation refers to perturbation of a single parent. The following mutation procedure is adopted here. For each chromosome, each element is tested for a possible mutation with a mutation probability \(\mu _m\). If an element (a potential facility location) is to be mutated, it is replaced by a random point (customer) from the set of its first \(\mathcal{N}\%\) nearest neighbors. Here, \(\mathcal{N}\) is chosen as 5 as it is found to provide good result. Note that the list of first \(\mathcal{N}\%\) nearest neighbors of each point is precomputed to avoid run-time computation. The mutation probability is initialized to a small value of 0.01 and not changed for all the generations where the chromosomes undergo local refinement procedure (see Sect. 4.5). This ensures that mutation does not disrupt the chromosomes much when they proceed towards initial convergence through local refinements. Once the local refinement procedure is not done any more, i.e., when the chromosomes have already converged well towards optimal solutions, mutation probability is increased to 0.8 to explore the search space around the near-optimal solutions with the expectation of obtaining some better solutions.

4.5 Local refinement

After mutation, each chromosome (solution) is locally updated. Local improvement is done as follows. First, the customers are clustered with respect to the facilities, i.e., each customer \(p_i\) is assigned to its nearest facility \(c_j\). A cluster \(clst_j\) is formed around each facility at \(c_j\) with the customers assigned to it (Jain et al. 1999; Mukhopadhyay et al. 2015). Thereafter, each facility at \(c_j\) encoded in a chromosome is updated with \(c_t\) such that

$$\begin{aligned} t = \underset{p_i \in clst_j}{\text{ argmin }}\sum _{p_l\in clst_j}f_l d(p_i,p_l). \end{aligned}$$
(6)

Hence, each facility location is updated by the point which has minimum weighted sum of distances to the other points within the cluster corresponding to that facility. This ensures that the facility locations are shifted towards more centrally located points with higher demand values, which increases the overall coverage quickly. Hence, use of this refinement in the early stages helps faster convergence. Moreover, it may be noted that in most of the cases, the quality of the service deteriorates as the distance between customer and facility increases. Therefore, this refinement strategy also tries to provide better service to the customers near to the facility compared to the customers which are far away from the facility. However, once the best fitness function does not change for 50 consecutive generations, the local refinement procedure is not applied any more to allow the chromosomes evolve freely.

4.6 Elitism

Elitism is employed to avoid losing good solutions due to randomness of the genetic operators. For this, the parent and child population for a particular generation are merged and then the top \(\mathcal{P}\) solutions according to the fitness values are propagated to the next generation. This ensures that the best chromosome obtained so far is not lost.

Table 2 Computational results for G&R100
Full size table
Table 3 Computational results for G&R150
Full size table

4.7 Termination criterion

The loop of fitness computation, selection, crossover, mutation, local refinement and elitism is iterated through generations. As mentioned earlier, the local improvements of the chromosomes are done until the best fitness value is saturated for 50 generations. Thereafter no local refinement is performed and the chromosomes are left to evolve freely. The loop continues until the best fitness value is saturated for the last 100 generations. The best solution (corresponding to the highest coverage value) is considered as the output of GA.

Table 4 Computational results for B700
Full size table
Table 5 Computational results for B900
Full size table
Table 6 Computational results for SJC324
Full size table
Table 7 Computational results for SJC402
Full size table
Table 8 Computational results for SJC500
Full size table
Table 9 Computational results for SJC708
Full size table
Table 10 Computational results for SJC818
Full size table
Table 11 Computational results for ZDS1800
Full size table
Table 12 Computational results for ZDS2500
Full size table

5 Experimental results

In this section, first the test problems on which the experiments are performed are discussed. Then, the results of the experiments are reported and discussed in detail.

5.1 Test problems

The performance of the proposed algorithm is tested with both real-world data and random data sets. The test problems considered in this article are summarized in Table 1 where p and S denote the number of facilities and the service distance respectively.

The random data sets G&R100 and G&R150 were used by Galvão and ReVelle (1996) and by Galvão et al. (2000). These two data sets correspond to two random networks of 100 and 150 vertices respectively. Here, the number of vertices indicates the number of customers. The number of arcs in these networks are determined by a pre-established density \(\delta \) which is defined as the ratio of the number of arcs in the network to the number of arcs in the corresponding complete network (Galvão and ReVelle 1996). Galvão et al. considered \(\delta \) as 0.10 and 0.05 for G&R100 and G&R150 respectively. They set the length of each arc for both the networks as an integer value taken randomly from a uniform distribution in the range [40, 60]. Then, Floyd’s algorithm is used to obtain the corresponding distance matrices. The demand of each customer for G&R100 is sampled from a uniform distribution in the range [20, 30]. For G&R150, the demands are obtained from a normal distribution with mean and standard deviation equal to 80 and 15 respectively.

Fig. 2
figure 2

Performance comparison for G&R100. GA: maximum percentage coverage using proposed GA with local refinement mentioned in column 15 of Table 2, other1: reference coverage percentage mentioned in column 4 of Table 2, other2: maximum coverage percentage mentioned in column 6 of Table 2

Full size image
Fig. 3
figure 3

Performance comparison for G&R150. GA: maximum percentage coverage using proposed GA with refinement mentioned in column 15 of Table 3, other1: reference coverage percentage mentioned in column 4 of Table 3, other2: maximum coverage percentage mentioned in column 6 of Table 3

Full size image
Fig. 4
figure 4

Performance comparison for B700. GA: maximum percentage coverage using proposed GA with refinement mentioned in column 15 of Table 4, other1: reference coverage percentage mentioned in column 4 of Table 4, other2: maximum coverage percentage mentioned in column 6 of Table 4

Full size image
Fig. 5
figure 5

Performance comparison for B900. GA: maximum percentage coverage using proposed GA with refinement mentioned in column 15 of Table 5, other1: reference coverage percentage mentioned in column 4 of Table 5, other2: maximum coverage percentage mentioned in column 6 of Table 5

Full size image
Fig. 6
figure 6

Performance comparison for SJC402. GA: maximum percentage coverage using proposed GA with refinement mentioned in column 8 of Table 7, other: coverage percentage mentioned in column 4 of Table 7

Full size image
Fig. 7
figure 7

Performance comparison for SJC708. GA: maximum percentage coverage using proposed GA with local refinement mentioned in column 8 of Table 9, other: coverage percentage mentioned in column 4 of Table 9

Full size image
Fig. 8
figure 8

Performance comparison for SJC818. GA: maximum percentage coverage using proposed GA with refinement mentioned in column 8 of Table 10, other: reference coverage percentage mentioned in column 4 of Table 10

Full size image
Fig. 9
figure 9

Performance comparison for ZDS1800. GA: maximum percentage coverage using proposed GA with refinement mentioned in column 13 of Table 11, other: coverage percentage mentioned in column 5 of Table 11, other2: maximum coverage percentage mentioned in column 7 of Table 11

Full size image
Fig. 10
figure 10

Performance comparison for ZDS2500. GA: maximum percentage coverage using proposed GA with refinement mentioned in column 13 of Table 12, other1: coverage percentage mentioned in column 5 of Table 12, other2: maximum coverage percentage mentioned in column 7 of Table 12

Full size image

In addition, from Beasley’s OR Library (Beasley 1990), the data sets pmed32 and pmed39 with 700 and 900 vertices respectively are obtained to form the distance matrices of B700 and B900 respectively. These data sets are for p-median problem (Hamacher and Drezner 2002; Mladenović et al. 2007). That is why these data sets do not include the demand of each customer. So the demand of each customer is sampled from a normal distribution with mean 80 and standard deviation 15 (Galvão et al. 2000).

Besides these, some real-world data are also considered to test the performance of the proposed GA. These data sets are taken from the geo-referenced database of São José dos Campos city, Brazil. The data sets SJC324, SJC402, SJC500, SJC708, and SJC818 consist of 324, 402, 500, 708, and 818 vertices, respectively. Lorena and Pereira (2002) used these data available in the following website: http://www.lac.inpe.br/~lorena/instancias.html.

The data sets ZDS1800 and ZDS2500 are used to check the performance of the proposed algorithm for large instances of MCLP. Fazel Zarandi et al. (2011) used these random data sets having the following specifications. ZDS1800 and ZDS2500 correspond to networks of 1800 and 2500 nodes respectively. The locations of the nodes are generated randomly from a uniform distribution in the range [0, 30], and the demand of each node is sampled from a uniform distribution in the range [0, 100].

5.2 Results and discussion

The proposed GA is programmed using MATLAB and run on Intel Core 2 duo with 2.2 GHz processor and 3 GB RAM having Windows XP operating system. The computational results are compared with the data given by Lorena and Pereira (2002) and Fazel Zarandi et al. (2011). The percentage of coverage values and computational times obtained using the proposed GA without local refinement and with local refinement are reported in Tables 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12 for all the data sets. The better or same values obtained by the proposed GA with local refinement as compared to the other existing algorithms are marked in bold. For some instances, the proposed GA with local refinement takes more time than that reported by  Lorena and Pereira (2002) and Fazel Zarandi et al. (2011). However, these extra computational times can be afforded if percentage of coverage is improved. It may be noted that the improvement in percentage of coverage is crucial when high budgets are involved for setting up the facilities. Moreover, the facilities are installed only once and thus the locations of the facilities corresponding to the maximum coverage are always taken. Hence, higher improvement in percentage of coverage is more important than the computational cost. In this article, the results corresponding to the maximum coverage are taken for comparison. The three parameters of the problem, viz., number of customers, number of facilities and service distance are indicated by the columns n, p and S, respectively in Tables 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12.

The computational results for the networks with 100, 150, 700 and 900 vertices (customers) are shown in Tables 2, 3, 4 and 5, respectively. In these four tables, the best values of coverage reported by Galvão and ReVelle (1996) and Galvão et al. (2000) and the respective computational times are indicated in the columns Ref. Cov. (\(\%\)) and Ref. Time (\(\%\)) respectively. It is evident that in terms of maximum coverage the proposed GA with local refinement gives better results for all the instances of the data set G&R100 in comparison with the maximum coverage reported by Lorena and Pereira (2002) as shown in Table 2. The proposed GA with local refinement performs better in 19 instances out of total 23 instances for the data set G&R150 as shown in Table 3. The proposed GA with refinement strategy gives better or same results in 7 instances out of total 9 instances and 6 instances out of total 9 instances for data sets B700 and B900 respectively as shown in Tables 4 and 5, respectively. For better understanding of the results obtained using the proposed GA with refinement strategy, the difference between the obtained maximum percentage coverage using the proposed GA with local refinement with the reference coverage percentage and the maximum coverage percentage given in the columns 4 and 6 of Tables 2, 3, 4 and 5 are been plotted in Figs. 2, 3, 4 and 5, respectively. In Figs. 2, 3, 4 and 5, other1 and other2 refer to the reference coverage percentage and the maximum coverage percentage corresponding to the columns 4 and 6 of Tables 2, 3, 4 and 5, respectively.

The computational results for the data sets SJC324, SJC402, SJC500, SJC708 and SJC818 are shown in Tables 6, 7, 8, 9 and 10, respectively. In terms of maximum coverage compared to Lorena and Pereira (2002), the proposed GA with refinement strategy yields better or same results in all the instances of the data sets SJC324 and SJC500 as shown in Tables 6 and 8, respectively. Moreover, the proposed GA with local refinement provides better or same maximum coverage compared to Lorena and Pereira (2002) in 10, 18 and 24 instances out of 11, 21 and 26 instances of the data sets SJC402, SJC708 and SJC818 respectively as depicted in Tables 7, 9, and 10, respectively. For visual illustration, the difference between the obtained maximum percentage coverage (given in column 8) using the proposed GA with the coverage percentage given in the column 4 of Tables 7, 9 and 10 are plotted in Figs. 6, 9 and 10, respectively. In Figs. 6, 7 and 8, other refers to the coverage percentage corresponding to the column 4 of Tables 7, 9 and 10 given by Lorena and Pereira (2002).

The computational results for the data sets ZDS1800 and ZDS2500 are reported in Tables 11 and 12, respectively. It appears from the tables that the proposed GA with local refinement performs better for all the instances of the data sets ZDS1800 and ZDS2500 in terms of maximum coverage given by Fazel Zarandi et al. (2011). The better performance of the proposed GA with refinement is also demonstrated in Figs. 9 and 10. In these figures, other1 and other2 refer to the coverage percentage obtained using CPLEX and maximum coverage percentage corresponding to the columns 5 and 7 of Tables 11 and 12.

It is evident from the results reported in all the tables that the proposed GA with local refinement performs better than the proposed GA without local refinement in terms of percentage of coverage. For few instances, the proposed GA without refinement strategy gives same percentage of coverage as obtained using the GA with refinement using more computation time. This signifies the effectiveness of the local refinement strategy to the proposed GA in terms of solution quality and convergence. It is also evident from the results reported in all the tables and the figures that whenever the proposed GA with local refinement outperforms the results given by Lorena and Pereira (2002) and Fazel Zarandi et al. (2011), the improvement in terms of maximum coverage is significant. However, for the few cases, where the proposed GA with refinement strategy fails to improve the results given by Lorena and Pereira (2002), the failure is marginal. As a whole, the proposed GA with local refinement is found to provide better results in reasonable time in most of the cases for both random and real-world data sets. It has also performed equally well for both small and large instances of the problem.

6 Conclusion

In this article, we have proposed a GA-based approach for solving the maximal covering location problem. The proposed GA-based approach utilizes a local refinement strategy during initial generations to guide the search for potential facility locations. Use of this local refinement strategy improves its overall rate of convergence. The performance of the proposed technique has been demonstrated on several benchmark data sets. Moreover, its performance has been compared with that of existing heuristic approaches and other GA-based approaches and illustrated both numerically and visually. The proposed approach has been found to outperform the existing approaches in most of the cases.