Optimal design of wideband digital integrators and differentiators using hybrid flower pollination algorithm

Abstract

In this paper, a recently proposed metaheuristic optimization technique called hybrid flower pollination algorithm (HFPA) is applied to design wideband infinite impulse response digital differentiators (DDs) and digital integrators (DIs). In recent years, benchmark nature-inspired optimization algorithms such as particle swarm optimization (PSO), simulated annealing, and genetic algorithm have been employed for the design of wideband DDs and DIs. However, individually, these algorithms show major drawbacks such as premature convergence, thus leading to a sub-optimal solution. HFPA, however, is a hybrid approach which combines the efficient exploitation and exploration capabilities of two different metaheuristics, namely PSO and flower pollination algorithm (FPA), respectively. The HFPA-based designs have been compared with real-coded genetic algorithm, PSO, differential evolution, success-history-based adaptive differential evolution with linear population size reduction (L-SHADE), self-adaptive differential evolution (jDE), and FPA-based designs with respect to the solution quality, robustness, convergence, and optimization time. Simulation results demonstrate that among all the algorithms, the HFPA-based designs consistently achieve superior performances in the least number of function evaluations. Exhaustive experimentations are conducted to determine the best values of the control parameters of HFPA for the optimal design of DDs and DIs. The proposed designs also outperform the recently reported designs based on non-optimal, classical, and nature-inspired optimization approaches in terms of magnitude response. The lower orders of the proposed designs render them suitable for real-time applications.

1 Introduction

The frequency response of an ideal differentiator and an ideal integrator are given by (1) and (2), respectively.

$$\begin{aligned}&D(\omega )=j\omega \end{aligned}$$

(1)

$$\begin{aligned}&I(\omega )=1/(j\omega ) \end{aligned}$$

(2)

where $j=\sqrt{-1}$ and $\omega$ is the angular frequency. The DDs and the DIs are the digital counterparts of the ideal differentiator and integrator, respectively, and find applications in edge detection of images (Al-Alaoui 2010), designing the controllers and compensators in digital control systems (Franklin et al. 1990), obtaining information about velocity and acceleration from position in radars and sonars (Skolnik 1980), and biomedical instrumentation (Shiro and Imidror 1982; Laguna et al. 1990). Hence, a considerable interest lies in designing DDs and DIs which can efficiently and accurately approximate their ideal characteristics with a wideband magnitude response and a smaller group delay. The design and implementation of DDs and DIs can be divided into two broad categories, namely the IIR filter-based approach and the finite impulse response (FIR) filter-based method. The IIR filters are preferred over the FIR filters for implementation of DDs and DIs because IIR filters provide higher computational efficiency, need much lower order than that of a FIR filter to meet the same magnitude response specifications, and linear phase response is not essential for many practical applications. This paper focuses on the implementation of DDs and DIs based on IIR filters.

Different approaches have been proposed in the literature to design DDs and DIs. Recursive-type DD of second order based on Simpson integration rule was proposed by Al-Alaoui (1994). DDs and DIs employing linear interpolation technique and magnitude stabilization rules were also reported by Al-Alaoui (1993, 1995). Optimization based on linear programming was used to determine the optimal set of coefficients of DIs by Papamarkos and Chamzas (1996). Tseng employed iterative quadratic programming approach to design IIR-type DD in Tseng (2000). Numerical integration rules to design wideband DI and DD of third order were reported by Ngo (2006). Design of rational approximations to the integrator based on numerical integration and the concept of delay filter were proposed by Tseng (2006, 2007). Designs of DDs in the low frequency range were proposed by Al-Alaoui (2007a). Al-Alaoui (2007b) and Tseng and Lee (2008a, b) employed fractional sample delay to control the magnitude and phase responses of IIR-type DIs and DDs. Tseng et al. employed discrete Hartley transform interpolation approach to design IIR DIs in Tseng and Lee (2009). Gupta et al. used linear interpolation rules to design wideband DIs and DDs of different orders in Gupta et al. (2010, 2011). Recursive wideband DDs and DIs were reported by Upadhyay (2010, 2012), Upadhyay and Singh (2011), Jain et al. (2012). Peano kernel- based DDs were designed by Pei et al. (2010). Candan reported wideband DDs exhibiting highly accurate phase response in Candan (2011). In recent years, wideband IIR DIs and DDs with much improved magnitude responses have been reported using classical optimization techniques such as pole, zero, and constant combined with minimax algorithm (Jain et al. 2013), constrained optimization approach (Nongpiur et al. 2014), and Fletcher–Powell algorithm (Al-Alaoui and Baydoun 2013), and nature-inspired optimization algorithms such as simulated annealing (SA) (Al-Alaoui and Baydoun 2013; Al-Alaoui 2011), genetic algorithm (GA) (Al-Alaoui and Baydoun 2013), and PSO (Gupta et al. 2014; Jalloul and Al-Alaoui 2015).

The gradient-based search techniques cannot efficiently explore the infeasible regions in the nonlinear, non-uniform, multimodal, and multidimensional design problem search space (Yang 2014). Also, benchmark nature-inspired optimization algorithms such as PSO and GA show drawbacks of stagnation and early convergence. Hence, applying such individual metaheuristic-based approaches also results in a degraded performance in dealing with the problems involving nonlinearities and large dimensions since these algorithms can get trapped in local optima. Thus, these algorithms can also lead to sub-optimal solution (Karaboga 2009). However, a hybrid algorithm such as HFPA (Abdel-Raouf et al. 2014) combines the efficient search exploration capabilities of FPA (Yang 2012) and the search exploitation capabilities of PSO algorithm (Kennedy and Eberhart 1995) and hence achieves a better balance between the diversification and the intensification phases as compared with the capability of the individual algorithm. In HFPA, the solution obtained after exploration and exploitation stages of the PSO phase is considered as the initial solution for FPA, and the global best solution of PSO phase is regarded as the best initial solution for FPA phase. FPA further ensures larger coverage of the problem search space by mimicking the behaviour of pollen-carrying insects/birds which travel over large distances. Mimicking this phenomenon by employing Lévy flight guarantees an efficient exploration of the global search space. The global pollination and the local pollination processes occur based on the judiciously chosen value of switch probability which ensures the proper balance between the diversification and the intensification phases. This paper employs HFPA to design IIR wideband DDs and DIs with accurate magnitude responses. The noteworthy contributions of this paper are:

• (i) This paper shows the applicability of HFPA for the optimal design of stable, accurate, and wideband IIR-type DDs and DIs of second and third order.

• (ii) The simulation results justify the superiority in the performance of the HFPA-based DDs and DIs over those of the designs based on different nature-inspired optimization algorithms such as RGA, PSO, DE, L-SHADE, jDE, and FPA. The performances of the algorithms are compared in terms of the solution quality, consistency, convergence rate, and computational time.

• (iii) Exhaustive experimentations are carried out to determine the best values of the control parameters of HFPA for the optimal design of DDs and DIs. The effects due to the variation in the values of the parameters of HFPA on the performances of the designed DDs and DIs are also extensively analysed.

• (iv) This paper also demonstrates the superiority of the proposed designs over all recently reported designs with respect to magnitude response.

The rest of the paper is structured as follows. Section 2 describes the mathematical formulation of the DD and DI design. Section 3 discusses the optimization algorithms employed in this research work. Simulation results are presented in Sect. 4. Finally, conclusions are drawn in Sect. 5.

2 Optimization problem

The transfer function of the IIR-type DD and DI of order N is given by (3) and (4), respectively.

$$\begin{aligned} H_{{\mathrm{DD}}} \left( z \right) =\frac{\sum _{i=0}^N {a_i z^{-i}} }{\sum _{i=0}^N {b_i z^{-i}} } \end{aligned}$$

(3)

where $a_{i}$ and $b_{i}$, $i=0, 1, \ldots , N$, are the numerator and denominator coefficients of $H_{{\mathrm{DD}}}(z)$, respectively.

$$\begin{aligned} H_{{\mathrm{DI}}} \left( z \right) =\frac{\sum _{i=0}^N {c_i z^{-i}} }{\sum _{i=0}^N {d_i z^{-i}} } \end{aligned}$$

(4)

where $c_{i}$ and $d_{i}$, $i=0, 1, \ldots , N$, are the numerator and denominator coefficients of $H_{{\mathrm{DI}}}(z)$, respectively.

Thus, the frequency responses of the DD and the DI are given by (5) and (6), respectively.

$$\begin{aligned} H_{{\mathrm{DD}}} \left( \omega \right)= & {} \frac{a_0 +a_1 \mathrm{e}^{-j\omega }+a_2 \mathrm{e}^{-2j\omega }+\cdots +a_N \mathrm{e}^{-Nj\omega }}{b_0 +b_1 \mathrm{e}^{-j\omega }+b_2 \mathrm{e}^{-2j\omega }+\cdots +b_N \mathrm{e}^{-Nj\omega }} \end{aligned}$$

(5)

$$\begin{aligned} H_{{\mathrm{DI}}} \left( \omega \right)= & {} \frac{c_0 +c_1 \mathrm{e}^{-j\omega }+c_2 \mathrm{e}^{-2j\omega }+\cdots +c_N \mathrm{e}^{-Nj\omega }}{d_0 +d_1 \mathrm{e}^{-j\omega }+d_2 \mathrm{e}^{-2j\omega }+\cdots +d_N \mathrm{e}^{-Nj\omega }} \end{aligned}$$

(6)

In the DD and DI design configuration, HFPA is employed to search the optimal values of coefficients of the IIR digital filters $H_{{\mathrm{DD}}}$($\omega$) and $H_{{\mathrm{DI}}}$($\omega$) such that their input–output characteristics accurately match the response of the ideal differentiator and integrator, respectively.

The input–output relations of the ideal differentiator and the proposed DD are given by (7) and (8), respectively.

$$\begin{aligned}&y_D (k)=D(\omega )\times x(k) \end{aligned}$$

(7)

$$\begin{aligned}&y_{{\mathrm{DD}}} (k)=H_{{\mathrm{DD}}} (\omega )\times x(k) \end{aligned}$$

(8)

where x(k) is the input signal, $y_D (k)$ represents the output of the ideal differentiator, and $y_{{\mathrm{DD}}} (k)$ is the output of the proposed DD.

The input–output relations of the ideal integrator and the proposed DI are given by (9) and (10), respectively.

$$\begin{aligned}&y_I (k)=I(\omega )\times x(k) \end{aligned}$$

(9)

$$\begin{aligned}&y_{{\mathrm{DI}}} (k)=H_{{\mathrm{DI}}} (\omega )\times x(k) \end{aligned}$$

(10)

where $y_I (k)$ is the output of the ideal integrator and $y_{{\mathrm{DI}}} (k)$ represents the output of the proposed DI.

In this paper, HFPA is employed to determine the optimal values of the coefficients of $H_{{\mathrm{DD}}} (\omega )$ and $H_{{\mathrm{DI}}} (\omega )$ to minimize the root-mean-square error (RMSE) for DD and DI as defined by (11) and (12), respectively.

$$\begin{aligned} J_D= & {} \sqrt{\frac{1}{L}\sum _{k=1}^L {[y_D (k)-y_{{\mathrm{DD}}} (k)]^{2}} } \end{aligned}$$

(11)

$$\begin{aligned} J_I= & {} \sqrt{\frac{1}{L}\sum _{k=1}^L {[y_I (k)-y_{{\mathrm{DI}}} (k)]^{2}} } \end{aligned}$$

(12)

where L is the total number of input samples. At the end of the stopping criteria of the specified number of function evaluations, the search agent of HFPA which achieves the least value of RMSE is declared as the global optimal solution vector containing the optimal set of coefficients of $H_{{\mathrm{DD}}} (\omega )$ and $H_{{\mathrm{DI}}} (\omega )$, respectively.

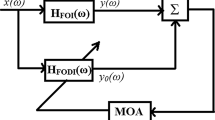
The block diagram of the HFPA-based IIR-type DD and DI design configurations is shown in Figs. 1 and 2, respectively.

Fig. 1

Block diagram of HFPA-based IIR DD design configuration

Fig. 2

Block diagram of HFPA-based IIR DI design configuration

The optimal values of coefficients for DDs and DIs to minimize the objective function given in (11) and (12), respectively, are also determined using RGA, PSO, DE, L-SHADE, jDE, and FPA.

Fig. 3

Pseudocode of RGA

The comparison of performances of the designed DDs and DIs is evaluated in terms of the maximum absolute magnitude error (MAME) metric. The MAMEs expressed in decibel (dB) unit for DDs and DIs are defined by (13) and (14), respectively.

$$\begin{aligned} {\textit{MAME}}_D= & {} \max \{20\log _{10} \left| {\left| {D(\omega )} \right| -\left| {H_{{\mathrm{DD}}} (\omega )} \right| } \right| \}\hbox {dB} \end{aligned}$$

(13)

$$\begin{aligned} {\textit{MAME}}_I= & {} \max \{20\log _{10} \left| {\left| {I(\omega )} \right| -\left| {H_{{\mathrm{DI}}} (\omega )} \right| } \right| \}\hbox {dB} \end{aligned}$$

(14)

For the real-time signal processing applications, a smaller group delay response of the designed system is desirable. Group delay for DDs and DIs is defined by (15) and (16), respectively.

$$\begin{aligned} \tau _D (\omega )= & {} -\frac{\mathrm{d}\theta _D (\omega )}{\mathrm{d}\omega } \end{aligned}$$

(15)

$$\begin{aligned} \tau _I (\omega )= & {} -\frac{\mathrm{d}\theta _I (\omega )}{\mathrm{d}\omega } \end{aligned}$$

(16)

where $\theta _D (\omega )=\angle H_{{\mathrm{DD}}} (\omega )$ and $\theta _I (\omega )=\angle H_{{\mathrm{DI}}} (\omega )$ are the phase responses of the $H_{{\mathrm{DD}}} (\omega )$ and $H_{{\mathrm{DI}}} (\omega )$, respectively.

Performance analysis of the phase response of the DDs and DIs is investigated in terms of the average group delay as given by (17) and (18), respectively.

$$\begin{aligned} \tau _{{\textit{aD}}}= & {} \frac{1}{\pi }\int \limits _0^\pi {\tau _D (\omega )} \mathrm{d}\omega \end{aligned}$$

(17)

$$\begin{aligned} \tau _{{\textit{aI}}}= & {} \frac{1}{0.997\pi }\int \limits _{0.003\pi }^\pi {\tau _I (\omega )} \mathrm{d}\omega \end{aligned}$$

(18)

3 Hybrid flower pollination algorithm (HFPA)

In recent years, nature-inspired algorithms have been employed to design optimal digital filters (Saha et al. 2012, 2013a, b, c; Mahata et al. 2016, 2017). In this section, the metaheuristic algorithms used for the optimal design of wideband DDs and DIs are described.

Fig. 4

Pseudocode of PSO

3.1 Real-coded genetic algorithm (RGA)

RGA (Goldberg 1989) is a nature-inspired, probabilistic search optimization approach based on the operations of crossover, mutation, and selection from a population. The crossover and mutation operations can either take place at a single point or at multiple points in the chromosomes. Multi-point crossover increases the search efficiency of RGA. Appropriate tuning of parameters, namely type of crossover, rate of crossover, type of mutation, rate of mutation, and type of selection of candidate solutions, plays a crucial role in the quality of solution generated by RGA. The pseudo code of RGA is shown in Fig. 3.

3.2 Particle swarm optimization (PSO)

PSO (Kennedy and Eberhart 1995; Eberhart and Shi 2001) is swarm intelligence-based metaheuristic optimization algorithm that is inspired by the intelligent social behaviour of a flock/swarm of birds or fish. In PSO, the equations that model the velocity and the position of a particle/agent are given by (19) and (20), respectively.

$$\begin{aligned} v_i ^{t+1}=w\times v_i ^{t}+\beta _1 \times z_1 \times (pbest_i ^{t}-s_i ^{t})+\beta _2 \times z_2 \times (gbest_i ^{t}-s_i ^{t}) \end{aligned}$$

(19)

where $v_i ^{t+1}$ and $v_i ^{t}$ are the velocities of the ith search agent at the ($t+1$)th and tth iteration, respectively; w is the inertia weight; $\beta _1$ and $\beta _2$ are two acceleration constants or learning parameters which control the cognitive and social learning ability, respectively, of an agent; $z_{1 }$and $z_{2}$ are two random numbers drawn from a uniform distribution, $z_1 ,z_2 \in [0,1]$; $pbest_i ^{t}$ and $gbest_i ^{t}$ are the personal best solution of a particle and the best solution achieved by the swarm, respectively, till the tth iteration.

$$\begin{aligned} s_i ^{t+1}=s_i ^{t}+v_i ^{t+1} \end{aligned}$$

(20)

where $s_i ^{t}$ and $s_i ^{t+1}$ is the position of the ith agent at tth and ($t+1$)th iteration, respectively.

The pseudocode of PSO is shown in Fig. 4.

3.3 Differential evolution (DE)

DE (Storn and Price 1997) is a bio-inspired, vector-based, and derivative-free search optimization algorithm based on mutation, crossover, and selection. Although DE is similar to RGA in many respects, however, unlike RGA, DE uses explicit updating equations. The donor vector v at the (t+1)th iteration is modelled by (21).

$$\begin{aligned} v_i ^{t+1}=x^{t}_p +F(x^{t}_q -x^{t}_r ) \end{aligned}$$

(21)

where ${{\varvec{x}}}_{p}$, ${{\varvec{x}}}_{q}$, and ${{\varvec{x}}}_{r}$ are three different vectors at the tth iteration and F is a control parameter called differential weight.

The selection and the updating of the candidate solutions are modelled by (22).

$$\begin{aligned} x_i ^{t+1}= & {} u_i ^{t+1}\quad \hbox {if}\quad f(u_i ^{t+1})\le f(x^{t}_i )\nonumber \\= & {} x^{t}_{i},\quad \hbox {otherwise} \end{aligned}$$

(22)

The pseudocode of DE algorithm is presented in Fig. 5.

Fig. 5

Pseudocode of DE

3.4 Flower pollination algorithm (FPA)

FPA (Yang 2012) is a metaheuristic optimization algorithm which draws inspiration from the process of pollination in flowering plants. Since FPA is inspired by the biological processes in nature, it falls under the category of bio-inspired optimization algorithms as defined by the classification list reported in Fister et al. (2013). FPA employs four different rules to mimic the pollination process.

• Rule 1: Global pollination occurs in biotic and cross-pollination processes with the flight of pollen-carrying pollinators (e.g. insects, birds) obeying Lévy distribution.

• Rule 2: The process of abiotic and self-pollination does not require any pollinators and hence is considered as local pollination.

• Rule 3: Flower constancy is considered as the reproduction probability that is proportional to the similarity of two flowers involved in pollination.

• Rule 4: The choice of performing local pollination or global pollination is controlled by a parameter called switch probability $p \in [0 1]$.

With an appropriate tuning of control parameters of FPA, these four rules can efficiently model the diversification and the intensification search processes of a metaheuristic optimization algorithm. FPA has been applied to solve real-world engineering problems (Bekdas et al. 2015). A survey on the qualitative and the quantitative analyses of FPA has been reported in Draa (2015).

Table 1 Values of control parameters of algorithms for the design of DDs and DIs

The steps of FPA for the optimal design of DDs/DIs are described below.

• Step 1. Each search agent/flower consists of all the coefficients for the DD/DI to be designed. The control parameters of FPA are initialized as shown in Table 1.

• Step 2. Randomly generate n number of flowers in the search space.

• Step 3. Compute the initial fitness for all the flowers. Find the best solution B in the initial population.

• Step 4. Generate a random number ${ rand }\in [0, 1]$ for each flower. If ${ rand} < p$, perform the global pollination according to (23). Else, perform the local pollination as per (25).

  $$\begin{aligned} x_i ^{t+1}=x_i ^{t}+\gamma \times L(\lambda )\times (B-x_i ^{t}) \end{aligned}$$

  (23)

  where $x_i ^{t+1}$ and $x_i ^{t}$ are the ith flower at the ($t+1$)th and tth iteration, respectively, $\gamma$ is a scaling factor which controls the step size, and $L(\lambda )$ is a Lévy flight parameter which determines the strength of the pollination and is defined by (24). Since the pollen-carrying pollinators travel over large distances, FPA mimics this phenomenon in the form of the Lévy parameter. Thus, global pollination allows for the problem search space to be effectively explored.

  $$\begin{aligned} L(\lambda )\sim \frac{\lambda \times \Gamma (\lambda )\times \sin (\pi \lambda /2)}{\pi }\times \frac{1}{s^{1+\lambda }} \end{aligned}$$

  (24)

  where $\Gamma (.)$ is the standard gamma function and s is the step size.

  $$\begin{aligned} x_i ^{t+1}=x_i ^{t}+\varepsilon \times (x_j ^{t}-x_k ^{t}) \end{aligned}$$

  (25)

  where $x_j ^{t}$ and $x_k ^{t}$ are the jth and kth flowers, respectively, at the tth iteration, and $\varepsilon \in [0,1]$ is a random number drawn from a uniform distribution.

• Step 5. Evaluate the fitness of all the new flowers. Update gbest if a new solution is better.

• Step 6. Go to step 4 and repeat until the stopping criterion is met.

• Step 7. Declare B as the optimal solution vector.

The pseudocode of FPA is shown in Fig. 6.

Fig. 6

Pseudocode of FPA

3.5 Hybrid flower pollination algorithm (HFPA)

HFPA (Abdel-Raouf et al. 2014) is a hybrid metaheuristic, nature-inspired optimization algorithm that combines the efficient search exploration capabilities of FPA and the proficient search exploitation capabilities of PSO to attain the global optimal solution. In HFPA, the optimization process goes through two phases, namely the PSO phase followed by the FPA phase. Each search agent in HFPA consists of all the coefficients of the DD/DI to be designed. The total number of decision variables is $D=(N+1)\times 2$. Thus, the ith search agents in HFPA for the design of DDs and DIs are represented as: $\mathbf{x}_{{\mathbf{DD}}i}=[a_{0i}a_{1i }\ldots a_{\mathrm{N}i} b_{0i} b_{1i} \ldots b_{\mathrm{N}i}]$ and $\mathbf{x}_{\mathbf{DI}i}=[c_{0i} c_{1i }\ldots c_{\mathrm{N}i} d_{0i} d_{1i} \ldots d_{\mathrm{N}i}$], respectively. In the PSO phase, the velocity and the position of the agents are updated as per (19) and (20), respectively. After determining the fitness of all the agents, the pbest and the gbest vectors are updated at the end of the PSO phase of HFPA. The optimal solution achieved by the PSO phase (gbest) is considered as the best starting solution B for the FPA phase, i.e. $B={ gbest}$. All the agents pass through the PSO phase at any iteration t and go through the local pollination as per (25) or the global pollination as per (23) in the FPA phase based on the chosen value of switch probability. At the end of the FPA phase, the pbest and the gbest vectors are updated if the new fitness value achieved is better than the previous one. Finally, at the end of the terminating criterion of the maximum number of function evaluations, the solution vector B is declared as the near-global optimal solution.

In this work, the steps used for the design of HFPA-based DDs and DIs are described below.

• Step 1. Randomly initialize the search agents/particles in the search space.

• Step 2. Initialize the other parameters of HFPA as per Table 1.

• Step 3. Determine the initial fitness for each particle.

  PSO Phase

• Step 4. Determine the initial pbest for every particle and the gbest solution.

• Step 5. Modify the velocity and position of each particle according to (19) and (20), respectively.

• Step 6. Compute the fitness of all the particles. Based on the fitness value, update gbest andpbest vectors.

  FPA Phase

• Step 7. Consider B = gbest.

• Step 8. Generate a random number, ${ rand} \in [0,1]$, for each flower. If rand $< p$, execute global pollination according to (23). Otherwise, execute local pollination as per (25).

• Step 9. Evaluate the fitness of all the new solution vectors (pollens). Update pbest and gbest if the new solutions are better.

• Step 10. Repeat from Step 5 until the stopping criterion is met.

• Step 11. Declare B as the global optimal solution vector.

The pseudocode of the HFPA for the design of DDs and DIs is shown in Fig. 7.

Fig. 7

Pseudocode of HFPA

The flow chart of HFPA for the design of DDs and DIs is shown in Fig. 8.

Fig. 8

Flow chart of HFPA for the optimal design of DD/DI

4 Simulation results and discussions

The experiments are carried out in the following environment—CPU: i3 processor (1.70 GHz), RAM: 2 GB, operating system: Windows 7, programming language: MATLAB, software version: MATLAB 7.5.

4.1 Choice of the values for the control parameters

The termination criteria for all the competing algorithms, namely RGA, PSO, DE, L-SHADE, jDE, and FPA, and the proposed HFPA for the design of DDs and DIs are considered as the total number of objective function evaluations $(\hbox {FEs}) = 10000\times D$ in order to ensure a fair comparison among all the algorithms (Liang et al. 2012), and the initial population size is set to 50. After extensive simulation runs, the values of the control parameters for each algorithm which yielded the best performances for the designed DDs and DIs are shown in Table 1. For a detailed analysis of the L-SHADE and the jDE algorithms, readers can refer to the original papers in Tanabe and Fukunaga (2014) and Brest et al. (2009), respectively.

The following observations are made while selecting the values of the control parameters for the algorithms.

• (i) With respect to RGA, selecting the value of the crossover rate parameter above 0.80 results in stagnation of chromosomes and premature convergence in the search space, hence producing sub-optimal solutions. On the other hand, choosing crossover rate below 0.80 causes wide oscillations and revisiting of the same solution in the problem search space. Thus, crossover rate of 0.80 provides the best balance in the evolutionary efficiency of RGA with the two-point type of crossover. With the Gaussian type of mutation, it is revealed that selection of the mutation rate with a value lower than 0.01 creates solutions which lack diversity. Thus, these chromosomes are unable to properly explore the multimodal and multidimensional DD/DI design problem landscape. On the other hand, mutation rate set at a value higher than 0.01 results in solutions which deviates away from the near-global optima. Proper selection which results in DDs and DIs yielding the least value of absolute magnitude error is observed with Roulette-wheel selection type.

• (ii) With respect to PSO, the memory action of the algorithm is emphasized by the inertia weight (w) parameter. It is observed that starting with a high value of w results in good diversification in the initial stages of PSO. As the algorithm proceeds, w is linearly decreased while the particles gain in cognitive and social learning experience. This leads to improved convergence behaviour. Through exhaustive experimentations, it is found that the gradual decrease of w from 0.9 to 0.4 provides the best solution. Different values of acceleration constants/learning rates $(\beta _1 ,\beta _2 )$ are chosen to determine the best possible combination to provide the balance between the cognitive and the social learning rates of the particles. It is found that choosing a value of $\beta _1 ,\beta _2 >2.0$ results in the particles moving away from the optimal solution due to a reduced emphasis on the memory component. On the other hand, selecting values of the acceleration constants lower than 2.0 decreases the learning ability of the particle. Hence, $\beta _1 =\beta _2 =2.0$ provides the near-global optimal DDs and DIs for PSO.

• (iii) With respect to DE, choosing a value of differential weight $F=0.50$ provides an optimum balance between the diversification and the intensification phases. Selecting $F>0.50$ generates diversified solutions which result in wide oscillations in the convergence of DE, whereas a smaller value of F does not create enough variety of solutions, thereby leading to sub-optimal exploration of the DD/DI design problem landscape. A crossover probability $(C_{r})$ less than 0.30 generates poor quality of solution due to the incapability of the agents to explore the infeasible regions.

• (iv) In FPA, the switch probability (p) controls the balance between the intensification and the diversification phases. After exhaustive trial runs, it is found that choosing a value of p lower than 0.75 results in lack of diversity. Hence, the flowers are unable to efficiently explore the infeasible regions in this multimodal design problem search space. On the other hand, $p>$0.75 results in a restricted local search, thereby deteriorating the solution quality. The Lévy parameter $L(\lambda )$ and the scaling factor ($\gamma$) control the exploration of the landscape. A small value of the Lévy distribution factor ($\lambda$) and $\gamma$ lead to an inefficient global search. On the other hand, choosing a larger value for $\lambda$ and $\gamma$ produces a higher diversity in solutions. This results in divergence from the global optima. Thus, the best choice of values for $\lambda$ and $\gamma$ are 1.50 and 0.12, respectively.

A detailed study of control parameter sensitivity of HFPA for the design of DDs and DIs is presented in Sect. 4.4.

Table 2 Optimal coefficients and performance metrics for the designed DDs

4.2 Digital differentiator

Table 2 presents the optimal coefficients of the DDs with $N=2$ and 3, achieved by the competing algorithms and the HFPA.

4.2.1 Comparison of frequency responses among the designed DDs

Table 2 shows that the HFPA-based DDs achieve the least values of ${ MAME}_{D}$ metric and also demonstrate a competitive performance in terms of $\tau _{{\textit{aD}}}$. The magnitude, absolute magnitude error (AME), phase, and group delay response comparison plots of the designed DDs are shown in Fig. 9a–h which confirms the effectiveness of HFPA in accurately yielding the rational digital approximations to the ideal differentiator.

Fig. 9

a Comparison of magnitude responses for DDs of order 2. b. Comparison of AME responses for DDs of order 2. c Comparison of phase responses for DDs of order 2. d Comparison of group delay responses for DDs of order 2. e Comparison of magnitude responses for DDs of order 3. f Comparison of AME responses for DDs of order 3. g Comparison of phase responses for DDs of order 3. h Comparison of group delay responses for DDs of order 3

4.2.2 Average case performance analysis

Based on fifty independent runs, the evaluation of the performance in terms of the best, worst, mean, and standard deviation (std. dev.) indices with respect to the ${ MAME}_{D}$ metric among the competing algorithms and the HFPA-based designed DDs is shown in Table 3. The HFPA-based designs achieve the best performances in terms of all the statistical indices. Also, the least values of std. dev. achieved by the HFPA-based DDs demonstrate the robustness of HFPA. Figure 10a, b shows the variation of the ${ MAME}_{D}$ metric of the designed DDs of orders 2 and 3, respectively, with respect to the total number of independent runs.

Table 3 Statistical results of ${ MAME}_{D}$ (dB) metric for the designed DDs

Fig. 10

a. Variation of MAME $_{D}$ (dB) with respect to the number of independent trial runs for DDs of order 2. b Variation of ${ MAME}_{D}$ (dB) with respect to the number of independent trial runs for DDs of order 3

4.2.3 Consistency analysis

In this section, the validation of the consistency in the performance of the competing algorithms and HFPA using the t test (Montgomery and Runger 2003) and the Mann–Whitney U test (Montgomery and Runger 2003), Derrac et al. (2011) is presented. The null hypothesis statement for both these tests is considered as: “No significant difference in terms of the ${ MAME}_{D}$ metric is achieved”. The confidence level (CL) for both the tests is set at 99%. The number of samples considered for the competing algorithms and HFPA is fifty each for conducting the two- sample t test. For performing the Mann–Whitney U test, sample sizes of ($n_{1}, n_{2})$ are considered, where $n_{1}$ and n$_{2}$ represent the size of the sample obtained for the competing algorithm and the HFPA, respectively. The decision regarding the hypothesis is represented by the index H ($H=0$: accept; $H=1$: reject). The tests results in terms of the H index, the p value (p val), and the confidence interval (ci) are shown in Table 4. Results confirm that HFPA rejects the null hypothesis for nearly all cases, except when compared with FPA.

Table 4 Hypothesis tests results for the designed DDs

4.2.4 Convergence analysis

The convergence of the algorithms for the design of DDs of orders 2 and 3 is shown in Fig. 11a, b, respectively, which justify the effectiveness of HFPA in converging to the near-global optima in the least number of FEs.

Fig. 11

a Convergence profiles of algorithms for the design of DDs of order 2. b Convergence profiles of algorithms for the design of DDs of order 3

Table 5 Execution time needed for the design of DDs

4.2.5 Execution time analysis

Fifty independent runs are carried out to determine the best, worst, mean, and std. dev. indices with respect to the optimization time (in seconds) required to reach the termination criteria by the algorithms for the optimal design of DDs. Based on the results presented in Table 5, it is confirmed that HFPA being a hybrid algorithm of FPA and PSO is outperformed by both PSO and FPA individually. However, as compared with RGA, DE, L-SHADE, and jDE, HFPA reaches the termination criteria in the least time. Since computational cost is one of the performance indices to determine an algorithms’ efficiency, it can be concluded that a hybridization of FPA with RGA or DE will result in an increased computational time as compared with the fusion of FPA with PSO. Hence, a hybrid of FPA and PSO provides a better balance between the quality of solution and the optimization time.

Table 6 Comparison summary of the HFPA-based DDs with the literature

4.2.6 Comparison of the proposed HFPA-based DDs with the literature

The comparison summary of the magnitude responses in terms of ${ MAME}_{D}$ metric and the phase responses in terms of $\tau _{{\textit{aD}}}$ metric for the proposed HFPA-based DDs with those of the designs based on various state-of-the-art approaches is shown in Table 6. The HFPA-based designs outperform all the reported designs by yielding the least value of ${ MAME}_{D}$. Figure 12a–h shows the magnitude, phase, AME, and group delay comparison plots of the HFPA-based designs with the reported DDs.

4.3 Digital integrator

Table 7 presents the optimal coefficients of the DIs of orders 2 and 3 achieved by the various algorithms used in this paper.

4.3.1 Comparison of frequency responses among the designed DIs

Comparison of frequency response performances for the DIs designed by the various algorithms is shown in Table 7. The HFPA-based designs yield the least value of ${ MAME}_{I}$ metric and also demonstrate a competitive performance in terms of $\tau _{{\textit{aI}}}$. Figure 13a–h show the magnitude, phase, AME, and group delay response comparison plots of the designed DIs which clearly demonstrate the superiority of the HFPA- based designs in accurately approximating the frequency response of the ideal integrator.

Fig. 12

a Comparison of magnitude responses of the HFPA- based DD of order 2 with the literature. b Comparison of phase responses of the HFPA-based DD of order 2 with the literature. c Comparison of absolute magnitude error responses of the HFPA-based DD of order 2 with the literature. d Comparison of group delay responses of the HFPA-based DD of order 2 with the literature. e Comparison of magnitude responses of the HFPA-based DD of order 3 with the literature. f Comparison of phase responses of the HFPA- based DD of order 3 with the literature. g Comparison of absolute magnitude error responses of the HFPA-based DD of order 3 with the literature. h Comparison of group delay responses of the HFPA- based DD of order 3 with the literature

Table 7 Optimal coefficients and performance metrics for the designed DIs

4.3.2 Average case performance analysis

The evaluation of the performances in terms of different statistical performance indices with respect to the ${ MAME}_{I}$ metric among the algorithms for the design of DIs is carried out based on fifty independent runs, and the results are shown in Table 8. The HFPA-based DIs outperform all the designs based on the competing optimization algorithms. The least value of std. dev. for ${ MAME}_{I}$ metric yielded by HFPA-based designs justifies the robustness of the algorithm. Figure 14a, b shows the variation of ${ MAME}_{I}$ of the designed DIs of orders 2 and 3, respectively, with respect to the total number of independent runs.

Fig. 13

a Comparison of magnitude responses for DIs of order 2. b Comparison of AME responses for DIs of order 2. c Comparison of phase responses for DIs of order 2. d Comparison of group delay responses for DIs of order 2. e Comparison of magnitude responses for DIs of order 3. f Comparison of AME responses for DIs of order 3. g Comparison of phase responses for DIs of order 3. h Comparison of group delay responses for DIs of order 3

Table 8 Statistical results of ${ MAME}_{I}$ (dB) metric for the designed DIs

Fig. 14

a Variation of ${ MAME}_{I}$ (dB) with respect to number of independent trial runs for DIs of order 2. b Variation of ${ MAME}_{I}$ (dB) with respect to number of independent trial runs for DIs of order 3

4.3.3 Consistency analysis

The consistency in the performance of the HFPA for the design of DIs is conducted by employing the hypothesis tests, and the results are presented in Table 9. The null hypothesis statement for both of these tests is defined as: “No significant difference in terms of the ${ MAME}_{I}$ metric is achieved”. The significance level and the total number of samples considered for the algorithms for performing the tests are the same as followed in Sect. 4.2.3. Results confirm that HFPA rejects the null hypothesis in all cases with respect to the t test. However, the Mann–Whitney U test results show similarity between the performances of FPA- and HFPA- based DIs of order 2.

Table 9 Hypothesis tests results for the designed DIs

4.3.4 Convergence analysis

Comparison of the fitness convergence of the algorithms for the design of DIs of orders 2 and 3 is shown in Fig. 15a, b, respectively. HFPA achieves the fastest convergence to the global optima with respect to the number of FEs.

4.3.5 Execution time analysis

Based on fifty independent runs, the best, worst, mean, and std. dev. indices of computational time required to complete $10000\times D$ FEs by the algorithms for the design of DIs are shown in Table 10. HFPA being an association of PSO and FPA achieves the third fastest execution time.

4.3.6 Comparison of the proposed HFPA-based DIs with the literature

Table 11 shows the comparison summary of frequency responses for the proposed HFPA-based DIs with those of the designs based on both classical and nature-inspired optimization approaches published in the literature. The HFPA-based designs attain the smallest value of ${ MAME}_{I}$. Competitive performances in terms of $\tau _{{\textit{aI}}}$ are also achieved by the proposed designs. Figure 16a–h shows the magnitude, phase, AME, and group delay comparison plots with the published literature.

4.4 Sensitivity analysis

The effects due to the variation in the control parameters of HFPA, namely inertia weight (w), acceleration constants $(\beta _1 ,\beta _2 )$, switch probability (p), Lévy distribution factor ($\lambda$), scaling factor ($\gamma$), and population size (n) on the performance of the designed DDs and DIs with respect to the ${ MAME}_{D}$ and the ${ MAME}_{I}$ metrics, are presented in this section. The number of trial runs considered for each case is fifty. While varying a specific parameter of HFPA, the values of the other control parameters are selected as per Table 1.

4.4.1 Effect due to the variation in the inertia weight (w)

The results with respect to the different statistical indices in terms of the ${ MAME}_{D}$ and the ${ MAME}_{I}$ metrics due to the variation in the value of w for the HFPA-based DDs and DIs are shown in Tables 12 and 13, respectively. The value of w is linearly decreased in three different ranges, viz. from 0.7 to 0.4, 0.8 to 0.4, and 0.9 to 0.4. Results demonstrate the superior performance of the proposed DDs and DIs when w is varied from 0.9 to 0.4. Hence, it can be concluded that starting with a large value of w followed by its gradual decrease results in a better diversification in the initial stages and an intense local search during the final stages of the PSO phase of HFPA.

Fig. 15

a Convergence profiles of algorithms for the design of DIs of order 2. b Convergence profiles of algorithms for the design of DIs of order 3

Table 10 Execution time needed for the design of DIs

Table 11 Comparison summary of the HFPA-based DIs with the literature

Fig. 16

a Comparison of magnitude responses of the HFPA-based DI of order 2 with the literature. b Comparison of phase responses of the HFPA-based DI of order 2 with the literature. c Comparison of absolute magnitude error responses of the HFPA-based DI of order 2 with the literature. d Comparison of group delay responses of the HFPA-based DI of order 2 with the literature. e Comparison of magnitude responses of the HFPA-based DI of order 3 with the literature. f Comparison of phase responses of the HFPA-based DI of order 3 with the literature. g Comparison of absolute magnitude error responses of the HFPA-based DI of order 3 with the literature. h Comparison of group delay responses of the HFPA- based DI of order 3 with the literature

Table 12 Performance of HFPA-based DDs based on different values of inertial weight (w)

Table 13 Performance of HFPA-based DIs based on different values of inertia weight (w)

4.4.2 Effect due to the variation in the acceleration constants ($\beta _1$ and $\beta _2 )$

Three different combinations of the acceleration constants $(\beta _1 ,\beta _2 )$ are considered in order to analyse the performance of the HFPA-based DDs and DIs in terms of the magnitude response error metrics, and the results are presented in Tables 14 and 15, respectively. Results demonstrate that choosing $\beta _1 =\beta _2 =2$ provides the best performance with respect to all the different statistical indices for the ${ MAME}_{D}$ and the ${ MAME}_{I}$ metrics. Since $\beta _1$ and $\beta _2$ emphasize the cognitive and the social learning ability, respectively, of a particle, hence, choosing a high value for both these learning parameters provides a better performance in the PSO phase of HFPA.

Table 14 Performance of HFPA-based DDs based on different values of acceleration constants $(\beta _1 ,\beta _2 )$

Table 15 Performance of HFPA-based DIs based on different values of acceleration constants $(\beta _1 ,\beta _2 )$

4.4.3 Effect due to the variation in the switch probability (p)

Tables 16 and 17 present the optimal coefficients and the comparison summary in terms of various statistical indicators for ${ MAME}_{D}$ and the ${ MAME}_{I}$ metrics achieved by HFPA-based DDs and DIs, respectively, for different values of p. Results confirm that $p=0.75$ achieves an optimal balance between the exploitation and the exploration phases in the multimodal DD and DI design problem search space.

Table 16 Performance of HFPA-based DDs based on different values of switch probability (p)

Table 17 Performance of HFPA-based DIs based on different values of switch probability (p)

4.4.4 Effect due to the variation in the Lévy distribution factor ($\lambda$)

The optimal coefficients and the values of the performance indices with respect to the error metrics for the DDs and DIs designed using HFPA with the values of $\lambda$ chosen as 1.20, 1.50, and 1.75 are presented in Tables 18 and 19, respectively. Results demonstrate that the best performance for HFPA is obtained with $\lambda$ of 1.50. Hence, $\lambda =1.50$ provides an improved global search and helps to overcome the infeasible regions in the search space during the FPA phase of HFPA.

Table 18 Performance of HFPA-based DDs based on different values of Lévy distribution factor ($\lambda$)

Table 19 Performance of HFPA-based DIs based on different values of Lévy distribution factor ($\lambda$)

Table 20 Performance of HFPA-based DDs based on different values of scaling factor ($\gamma$)

Table 21 Performance of HFPA-based DIs based on different values of scaling factor ($\gamma$)

Table 22 Performance of FPA- and HFPA-based DDs based on different values of population size (n)

Table 23 Performance of FPA- and HFPA-based DIs based on different values of population size (n)

4.4.5 Effect due to the variation in the scaling factor ($\gamma$)

Tables 20 and 21 show the optimal coefficients and the values of different statistical performance indices yielded by HFPA-based DDs and DIs, respectively, with different values of scaling factor. Since the HFPA-based designs achieve the best performance with $\gamma$ of 0.12, hence, the best control of step size during the global search process of FPA phase in HFPA is achieved with ${\gamma } = 0.12$.

4.4.6 Effect due to the variation in the population size (n)

The optimal values of coefficients and the statistical performance indicators for the ${ MAME}_{D}$ and the ${ MAME}_{I}$ metrics for the DDs and DIs designed using FPA and HFPA with n of 20, 50, and 100 particles are presented in Tables 22 and 23, respectively. It is found that choosing $n=20$ yields the designs with lower accuracy, while the designs obtained for $n=100$ yield only a slightly better performance at the cost of increased execution time as compared with those achieved with $n=50$. Hence, considering the trade-off between accuracy and computational time, the best performance for both the algorithms is obtained with $n=50$.

5 Conclusions

In this paper, a nature-inspired metaheuristic optimization technique obtained by hybridizing PSO and FPA, called hybrid flower pollination algorithm, has been efficiently used to design wideband IIR digital differentiators and digital integrators. The lower orders of the proposed designs are suitable for real-time signal processing applications due to their lower computational complexity and smaller memory requirements. The efficiency of the proposed designs has been extensively investigated with respect to the designs based on six other metaheuristics in terms of solution quality, reliability, convergence rate, and computational time. Hypothesis tests confirm the consistently superior performance of the proposed designs as compared with RGA, PSO, DE, L-SHADE, and jDE. HFPA achieves the fastest convergence to the global optimal solution in terms of the function evaluations. With respect to the computational time, it is observed that HFPA is faster than RGA, DE, L-SHADE, and jDE, but is outperformed by PSO and FPA. Exhaustive simulation studies are also conducted to determine the best parameter values of HFPA for this optimization problem. The proposed designs outperform all the reported designs based on both classical and nature-inspired optimization approaches with respect to magnitude response. This paper confirms that HFPA can be considered as a potential tool for the design of stable, and wideband IIR-type DDs and DIs. In future, it will be interesting to employ HFPA to design one-dimensional and two-dimensional DDs and DIs using a constrained pole–zero optimization approach.