1 Introduction

With the continuous development of science and technology, many global optimization problems (GOPs) constantly exist in all most of engineering and science fields, such as portfolio investment (Shalan and Ykhlef 2015), queueing system (Wei et al. 2013) and structural design (Aydogdu et al. 2016). Since these GOPs are more and more complex, and they are characterized as multimodality, discontinuity, highly non-linearity, non-differentiability and non-convexity, these kinds of GOPs are difficult or even impracticable to be solved by traditional optimization methods, especially for the gradient-based methods (Hu et al. 2015, 2016). Thus, many swarm-based intelligence evolution algorithms (EAs), such as Particle Swarm Optimization (PSO) (Kennedy and Eberhart 1995; Kuo et al. 2011), Ant Colony Optimization (ACO) (Dorigo et al. 1996; Mavrovouniotis and Yang 2011), Genetic Algorithm (GA) (Tang et al. 1996; Hunter and Chiu 2000), and Differential Evolution (DE) (Storm and Price 1997; Teo 2006), Artificial Bee Colony (ABC) algorithm, have been proposed to address this challenge task (Cui and Gao 2012) and they also have shown great potential.

In this paper, we focus on the study of artificial bee colony algorithm firstly proposed by Karaboga (2005), which inspired by the intelligent foraging behavior of real bee colony. The performance of ABC is firstly demonstrated by the comparison with other EAs, such as GA, PSO and DE, on many benchmark functions. The results of the simulation experiments show that the performance of ABC is better than or at least comparable to PSO, GA and DE (Karaboga and Basturk 2007, 2008; Karaboga and Akay 2009). Due to its simply structure, ease to implementation and outstanding performance, ABC has attracted great attention and has been successfully applied to solve multi-objective optimization problems (Reza et al. 2012), constrained optimization problems (Karaboga and Akay 2011), binary optimization problems (Ozturk et al. 2015), clustering problems (Banharnsakun et al. 2013) and many practical optimization problems (Ma et al. 2011; Sun et al. 2011; Krink and Paterlini 2011). However, like other EAs, ABC often shows slow convergence speed since its solution search does well in exploration, but badly in exploitation (Karaboga 2005). It is well known that both exploration and exploitation are necessary for a population-based optimization algorithm, and the performance of the EAs depends on whether a suitable balance between exploration and exploitation can be found or not (Kiran et al. 2015; Gao et al. 2014, 2015c). Therefore, the performance of ABC can be improved by enhancing the exploitation ability and finding better balance between exploration and exploitation. A large number of improved ABC variants have been presented by exploiting the valuable information from the current best solution or other good solutions, such as literatures (Zhang et al. 2015; Gao and Liu 2011). The experimental results demonstrate that the population moderately guided by the current best solution or other good solutions can effectively improve the exploitation ability and enhance the performance of ABC. Based on this outcome, in this paper, we firstly propose a novel search strategy to make use of the current best solution, in which the original solution search equation and a new solution search equation exploiting the current best solution are corporately used according to a probability parameter P for generating a candidate food source. Secondly, in order to utilize other good solutions, we introduce a novel probability model on onlooker bee phase, in which the good food sources could attract more onlooker bees to search. The new search strategy and novel probability model are embedded into original ABC to form a new variant of ABC, named MPGABC.

To evaluate the performance of MPGABC, some extensive experiments are conducted on 22 common benchmark functions (Gao et al. 2013a), 22 real-world problems (Das and Suganthan 2010) and 28 real-parameter optimization problems (Liang et al. 2013). The comparison results with other variants of ABC (i.e., GABC Zhu and Kwong 2010, qABC Karaboga and Gorkemli 2014, best-so-far ABC Banharsakunm et al. 2011, dABC Kiran and Findik 2015 and MABC Gao and Liu 2012) validate the effectiveness and efficiency of MPGABC in terms of solution quality, robustness and convergence speed.

The remainder of this paper is organized as follows. Section 2 introduces the original ABC algorithm briefly. A review on the improved ABC variants is given in Sect. 3. The details of MPGABC, which mainly includes the novel search strategy and the novel probability model, are described in Sect. 4. The experimental results and corresponding analysis are given in Sect. 5. Finally, Sect. 6 concludes this paper.

2 The original ABC

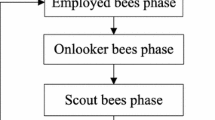
The ABC algorithm is a process of searching the optimal solution by simulating the collective foraging behavior of honey bees. In ABC, a food source position denotes a possible solution of the optimal problem, and the nectar amount of each food source represents the quality of the corresponding solution. In order to find better food sources, three types of bees, namely employed bee, onlooker bee and scout bee, search collectively. Firstly, employed bees are composed of the first half of the colony, which are mainly responsible for randomly searching better food sources in the neighborhood of the corresponding parent food source. Moreover, employed bees will share the quality information of their food sources with onlooker bees after all employed bees find out a new food resource. Secondly, onlooker bees are consisted of the second half of the colony, which are mainly responsible for searching better food sources in the neighborhood of the good solutions according to the information provided by employed bees. Thirdly, if a better food source cannot be found by a preset number of times (limit) in the neighborhood of a certain food source, it will be abandoned by its employed bee, and this employed bee will become a scout bee to search a new food source randomly in all search space. The original ABC includes four phase, i.e., initialization phase, employed bee phase, onlooker bee phase and scout bee phase. After the initialization phase, ABC enters a loop of employed bee phase, onlooker bee phase and scout bee phase until the termination condition is met. The detailed descriptions of each phase are described as follows.

Initialization phase The initial population is generated according to Eq. (1), which contains SN food sources (solutions),

$$\begin{aligned} x_{i,j}=x_{j}^{\mathrm{min}}+{ {rand}}(0,1) \cdot (x_{j}^{\mathrm{max}}- x_{j}^{\mathrm{min}}) \end{aligned}$$
(1)

where \(i=1,\;2,\;\ldots SN\), \(j=1,\;2,\;\ldots D\). SN is the number of employed bees or onlooker bees; D is the dimensionality of the search space; \(x_{j}^{\mathrm{max}}\) and \(x_{j}^{\mathrm{min}}\) represent the upper bound and lower bound of the jth dimension, respectively. Moreover, the fitness value of each food source will be calculated by Eq. (2),

$$\begin{aligned} {{fit}}(x_i )=\left\{ {\begin{array}{l@{\quad }l} \frac{1}{1+f(x_i )}&{}\quad \hbox { if (}f(x_i )\ge 0\hbox {)} \\ 1+{\text{ abs }}(f(x_i ))&{}\quad \hbox { otherwise} \\ \end{array}} \right. \end{aligned}$$
(2)

where \({{fit}}( {x_i })\) represents the fitness value of the ith food source \(x_{i}\) and \(f( {x_i })\) is the objective function value of food source \(x_{i}\) for the optimization problem.

Employed bee phase Each employed bee selects a distinct food source to search and generate a candidate food source in the neighborhood of this selected food source according to Eq. (3),

$$\begin{aligned} v_{i,j}=x_{i,j}+\phi _{i,j}\cdot (x_{i,j}-x_{k,j}) \end{aligned}$$
(3)

where \(v_{i}\) is the ith candidate food source and \(x_{i}\) is the ith food source. \(x_{k}\) is randomly selected from the population, which is different from \(x_{i}\). \(\phi _{i,j}\) is the uniformly distributed random number in the range of [\(-1\), 1] and j is randomly selected from \(\left\{ {1,\;2,\ldots ,D} \right\} \). If the fitness value of \(v_{i}\) is better than its parent \(x_{i}\), \(x_{i}\) will be replaced by \(v_{i}\), and the counter which records the number of the consecutive unsuccessful updates of the food source \(x_{i}\) is reset to 0. Otherwise, \(x_{i}\) is kept to enter into the next generation and counter is increased by 1.

Fig. 1
figure 1

The pseudo-code of original ABC

Full size image

Onlooker bee phase After each employed bee finishes its search task, it will show the quality information of its food source with onlooker bees. Each onlooker bee will select a food source to search based on the probability of each food source, which is calculated as Eq. (4). Obviously, the better the fitness value is, the bigger the selection probability is. And then it will further search better food source in the neighborhood of the selected food source by using Eq. (3). If a candidate food source obtained by the onlooker bee is better than its parent food source, the parent food source will be replaced by the new one, and its counter is reset to 0. Otherwise, the old one is kept and counter is increased by 1.

$$\begin{aligned} p(x_i )=\frac{{{fit}}(x_i )}{\sum _{j=1}^{{\textit{SN}}} {{{fit}}(x_j )} } \end{aligned}$$
(4)

Scout bee phase The food source with the highest counter value is selected. If its counter value is bigger than the limit value, the selected food source will be abandoned by its employed bee, and then, this employed bee will become a scout bee to seek a new food source randomly according to Eq. (1). After the new food source is generated, the corresponding counter value is reset to 0, and the scout bee returns to be an employed bee.

Note that if the jth variable \(v_{i,j} \) of the ith candidate food source violates the boundary constraints in employed bee phase and onlooker bee phase, it will be reset according to Eq. (1). The detailed procedure of ABC is shown in Fig. 1.

3 The improved ABC variants

Over the past decade, a lot of in-depth research works on ABC have been conducted to achieve a better performance on solving GOPs. A brief survey of the improved ABC approaches can be generally classified into three categories, i.e., modified solution search equation, combination with other technologies and hybridization of ABC with other EAs. They are, respectively, introduced as follows.

  1. (1)

    Modified solution search equation Inspired by PSO, Zhu and Kwong (2010) propose an improved ABC algorithm, called as GABC, which incorporates the valuable information of the global best solution into their solution search equation to improve the exploitation ability of ABC. The experimental results show that GABC is better than the original ABC on most of cases. Banharnsakun et al. (2011) propose a new ABC variant, named best-so-far ABC, which introduces the best-so-far selection method and an adjustable search radius into the solution search equation. In best-so-far ABC, the current best solution is shared globally among the entire population. Inspired by the DE mutation operator DE/best/1 and DE/rand/1, Gao and Liu (2011; 2012) propose two novel search equations ABC/best/1 and ABC/rand/1. Besides, in order to appropriately take advantage of them, a selective probability P is used to control the frequency of employing ABC/rand/1 and ABC/best/1. Moreover, a new algorithm, named ABCgbest (Gao et al. 2012), is proposed by them, in which bees only search around the current best food source. Recently, Karaboga and Gorkemli (2014) present a new version of search equation for onlooker bee (qABC), which uses the valuable information of the best solution among the neighbors to improve the search efficiency of ABC. Gao et al. (2015a) propose a Gaussian search equation (BABC), which exploits the current best solution and Gaussian distribution to produce candidate solutions in the onlooker bee phase. Luo et al. (2013) present a new solution search equation for the onlooker bee, which exploits the best solution of the previous iteration to guide the search of new candidate solutions (called COABC). Gao et al. (2014, 2015c) propose two modified search equations. The one of them utilizes the beneficial information of best solutions in a cluster, which is employed in employed bee phase. And the other one learns from the current best solution, which is used in onlooker bee phase. Since different search equations have distinct advantages and perform differently on different problems or at different stages on the same problem, some methods with multiple search equations are proposed to enhance the comprehensive performance of ABC, such as MEABC (Wang et al. 2014), ABCVSS (Kiran et al. 2015) and MuABC (Gao et al. 2015b). In addition, Kiran and Findik (2015) add the directional information into ABC and design a new search mechanism, which selects search equation to produce candidate solution according to the previous directional information (named dABC).

  2. (2)

    Combination with other technologies Inspired by the concept of Grenade Explosion Method (GEM), two modified versions of ABC (namely GABC1 and GABC2) are proposed by Zhang et al. (2015), which show high robustness and fast convergence speed. Gao and Liu (2012; 2013a) employ the chaotic map (Feng et al. 2011) and opposition-based learning method in the initial phase and the orthogonal learning method to enhance the performance of ABC. Moreover, Gao et al. (2013b) also use the Powell’s method as a local search tool to improve the exploitation ability of ABC. In addition, Kang et al. (2011a; b) proposed two new ABC variants (called RABC and HJABC), in which the original ABC is used to realize the exploration ability and the exploitation phase is completed by the rotational direction method and Hooke Jeeves pattern search technology, respectively. Moreover, Akay and Karaboga (2012) propose two control parameters, i.e., modification rate (MR) and scaling factor (SF), to control frequency and magnitude of perturbation, respectively. Loubiere et al. (2016) apply a sensitivity analysis method, i.e., Morris’ OAT method (One-At-Time), to select dimensions with high influence on the objective result for preferential evolvement. Xiang and An (2013) employ the chaotic search technique on initialization phase and scout bee phase to, respectively, enhance the global convergence and prevent falling into local optimum (called ERABC). In addition, the memory-save technology has attracted much attention. Kiran and Babalik (2014) add a memory board to save the solutions whose qualities are better than the average fitness value. On the contrary, Bayraktar (2014) uses the short-term tabu list (STTL) of tabu search to memorize the abandoned solution. Moreover, Li and Yang (2016) introduce a new ABC variant named ABC with memory algorithm (ABCM), which memorizes the previous successful experiences of foraging behavior to guide the current foraging behavior.

  3. (3)

    Hybridization of ABC with other EAs Kang et al. (2009) take the advantages of Nelder–Mead simplex method and ABC to develop a hybrid ABC, named HSABCA. Xiang et al. (2014) propose a well-known hybrid algorithm named hABCDE, which incorporates a modified ABC with a modified DE. In addition, Shi et al. (2010) present a hybrid intelligent algorithm (named IABAP) based on the information exchange process, in which all population share beneficial information between particle swarm and bee colony. Marinakis et al. (2009) propose a hybrid algorithm for clustering by combining ABC optimization with the greedy randomized adaptive search procedure (GRASP method). Xiao and Chen (2011) propose a novel hybrid algorithm, which consists of ABC algorithm and artificial immune network algorithm to address multi-mode resource constrained multi-project scheduling problem. Sharma and Pant (2011) embed the DE mutation operators into the framework of ABC algorithm and develop a hybrid ABC (called DE-ABC). Hsieh et al. (2012) introduce PSO into ABC and propose a new hybrid algorithm, named EABC-PGSVM. Abraham et al. (2012) invent a novel hybrid differential artificial bee colony algorithm (called HDABCA), which combines DE strategy with standard ABC algorithm. Besides, Tuba and Bacanin (2014) combine ABC with firefly algorithm, Fister et al. (2012) mix ABC with memetic search, and Chen et al. (2012) integrate ABC with annealing algorithm, and so on.

4 The proposed algorithm

In this section, the proposed algorithm is described in detail. Firstly, we give the motivations of our proposed algorithm. Secondly, the novel search strategy and the novel probability model are presented, respectively. Finally, the complete proposed algorithm is shown.

4.1 Motivations

Generally, the performance evaluation of Evolutionary Algorithms (EAs) depends on that a suitable trade-off between exploration and exploitation can be maintained. Usually, exploiting the information of the current best solution and other good solutions could enhance the exploitation ability, while excessively exploiting could degrade the exploration ability. Therefore, the key issue is how to exploit the current best solution and other good solutions. On the one hand, in the search Eq. (3) of the original ABC, only the target solution and a randomly selected solution are used to generate new solution, which does well in exploration but badly in exploitation. On the other hand, in the search equations of other ABC variants (Zhang et al. 2015; Wang et al. 2014), the current best solution is always used, which performs well in exploitation but relatively underperforms in exploration. Therefore, the incorporation of the original solution search equation and a new search equation utilizing the best solution could get a better balance between exploration and exploitation. Moreover, in the onlooker bee phase of original ABC, the onlooker bee selects a food source to search according to the information provided by employed bees. In theory, the food source with higher quality could attract more onlooker bees to search. However, if the qualities (fitness values) of all food sources have no significant difference, all food sources will obtain nearly the same probability according to Eq. (4), which makes that the good solutions are not fully exploited. Therefore, a new probability model should make sure that the good solutions are more likely to be chosen by onlooker bee for searching, which could enhance the performance of ABC.

Fig. 2
figure 2

The pseudo-code of the novel search strategy

Full size image

4.2 The novel search strategy

In order to enhance the exploitation ability and accelerate the convergence speed of ABC, Zhu and Kwong (2010) propose a new solution search equation in GABC as Eq. (5),

$$\begin{aligned} v_{i,j}=x_{i,j}+\phi _{i,j} \cdot (x_{i,j}-x_{k,j})+\varphi _{i,j} \cdot (x_{\mathrm{{best}},j}-x_{i,j}) \end{aligned}$$
(5)

where \(x_{\mathrm{{best}}}\) is the current best solution of the population, and \(x_{i}\) is the ith food source. \(x_{k}\) is a randomly selected food source from the population, which is different from \(x_{k}\). \(\phi _{i,j}\) is the uniformly distributed random number in the range of [\(-1\), 1] and \(\varphi _{i,j}\) is a uniform random number in the range of [0, 1.5]; j is randomly selected from \(\left\{ {1,\;2,\ldots ,D} \right\} \).

Although Eq. (5) exploits the current best solution, there are two drawbacks. Firstly, as claimed in Gao et al. (2013a), Eq. (5) may cause the oscillation phenomenon when the guidance of the last two terms \((\phi _{i,j} \cdot (x_{i,j} -x_{k,j} )\) and \(\varphi _{i,j} \cdot (x_{\mathrm{{best}},j} -x_{i,j} ))\) is in opposite direction, which could degrade convergence. Secondly, Eq. (5) may easily make the new solution \(v_{i,j}\) violate the boundary constraints when the last two terms are in identical direction, which also could hinder convergence. In order to address these issues, we propose a novel search strategy shown in Algorithm 2 (Fig. 2).

In Algorithm 2, P is a parameter defined by the user. \(x_{\mathrm{{best}}}\) is the current best solution of the population, and \(x_{i}\) is the ith food source. \(x_{k}\) is a randomly selected food source from the population, which is different from \(x_{i}\). \(\phi _{i,j}\) is the uniformly distributed random number in the range of [\(-1\), 1] and \(\varphi _{i,j}\) is a uniform random number in the range of [0, 1.5]. j is randomly selected from \(\left\{ {1,\;2,\;\ldots ,\;D} \right\} \). Obviously, with the guidance from only one term, the novel search strategy can easily avoid the oscillation phenomenon and violating the boundary constraints. Moreover, parameter P could be used to control how to appropriately exploit the valuable information of the current best solution. The effectiveness of the novel search strategy is validated through extensive experiments in Sect. 5.2, and the sensitiveness of parameter P is analyzed experimentally in Sect. 5.4.

4.3 The novel probability model

In the onlooker bee phase of the original ABC, onlooker bees mainly select good solutions to search according to the information shared by the employed bees. From our above analysis, the original probability model Eq. (4) for onlooker bee phase is unable to make sure that the good solutions could attract more onlooker bees than the bad solutions to search. In order to address this issue, we propose a novel probability model as Eq. (6),

$$\begin{aligned} p(x_i )=\frac{0.8}{({\text{ e }}^{r(x_i )/SN})^{\sqrt{r(x_i )}}} \end{aligned}$$
(6)

where \(p\left( {x_i } \right) \) is the selected probability of the ith food source and SN is the number of employed bees or onlooker bees. \(r\left( {x_i } \right) \) is the ranking of the ith food source in ascending order among all food sources according to the objective function value. For example, the ranking of the current best food source and worst food source is 1 and SN, respectively. To explain clearly, when SN \(\,=\,\)50, the selection probability of each food source is illustrated in Fig. 3, where X axis denotes the ranking of the food source, and Y axis denotes the corresponding probability. Obviously, the selected probability of a good solution is significantly larger than a bad solution. The effectiveness of the novel probability model is validated in Sect. 5.2.

Fig. 3
figure 3

An illustrated example of the novel probability model

Full size image

4.4 The complete proposed algorithm (MPGABC)

In this subsection, we put forward a novel ABC variant (named MPGABC) by combining the novel search strategy and the novel probability model with the basic framework of ABC. The pseudo-code of the complete MPGABC is demonstrated in Fig. 4. Obviously, the differences of Algorithm 1 (ABC) and Algorithm 3 (MPGABC) are shown in lines 4, 13 and16.

Table 1 Benchmark functions in experiments
Full size table

5 Experimental results

5.1 Benchmark test functions and experimental settings

In this paper, 22 well-known benchmark functions (Gao et al. 2013a; Kiran et al. 2015; Zhang et al. 2015) with low dimension \((D\,{=}\,30)\), middle dimension \((D\,{=}\,50)\) and high dimension \((D\,{=}\,100)\) are employed to validate the performance of MPGABC. These functions have different characteristics, such as continuous unimodality function \((f_{1}-f_{6}\) and \(f_{8})\), multimodality functions \((f_{11}-f_{22})\), discontinuous step function \((f_{7})\) and noisy-quartic function \((f_{9})\). Particularly, \(f_{10}\) is the Rosenbrock function, which is unimodal for \(D\,{=}\,2\) and \(D\,{=}\,3\), but it may have many optimal solutions when \(D\,{>}\,3\). Generally speaking, the unimodal functions can be used to test the exploitation ability and the multimodal functions can be employed to demonstrate the exploration ability. The mathematical expression, search range, the global optimal value and the “acceptable value” of each function are listed in columns 2, 3, 4 and 5 of Table 1, respectively. When the objective function value of the best solution obtained by an algorithm in a run is less than the acceptable value, this run is regarded as a successful run.

To evaluate the performance of MPGABC, three evaluation metrics are used in our experiments. The detailed descriptions are given as follows:

  1. (1)

    The mean and standard deviation (mean/std): They are utilized to evaluate the accuracy of the best objective function value for different algorithms. For minimum optimization problem, the smaller the value of mean and standard deviation is, the higher quality/accuracy of the solution has.

  2. (2)

    The average number of function evaluation (AVEN): It is required to reach the acceptable value, which is adopted to evaluate the convergence speed. The smaller AVEN is, the faster the convergence speeds is. Note that AVEN will be only calculated for the successful runs. If an algorithm cannot find any solution whose objective function value is smaller than the acceptant value in all runs, AVEN will be denoted by “NAN.”

  3. (3)

    The successful rate (SR): The successful rate (SR %) of the 25 independent runs is utilized to evaluate the robustness or reliability of different algorithms. The greater the value of this metric is, the better the robustness/reliability is.

There are five parts in our experiments. Experiment 1 validates the effectiveness of our proposed algorithmic components (i.e., the novel search strategy and the novel probability model). Experiment 2 evaluates the performance of MPGABC by the comparison with other outstanding ABC variants on some common benchmark functions. Experiment 3 analyzes the sensitiveness of parameter P on the performance of MPGABC. Experiment 4 demonstrates the performance of MPGABC by the comparison of MPGABC and other ABC variants on real-world problems of CEC 2011. Experiment 5 investigates the effectiveness of MPGABC by the comparison with ABC variants on the real-parameter optimization problems of CEC 2013.

Table 2 Comparisons of MPGABC variants and corresponding ABC on 22 functions with 30D
Full size table
Fig. 4
figure 4

The pseudo-code of MPGABC

Full size image
Fig. 5
figure 5

Average FES are needed to reach the accept value (a), 30D (b), 50D (c) and 100D (d)

Full size image
Fig. 6
figure 6

The evolutionary frequency of each individual

Full size image

5.2 Experiment 1: the effectiveness of the proposed algorithmic components

In order to demonstrate the effectiveness and efficiency of the two proposed algorithmic components (i.e., the novel search strategy and the novel probability model), the original ABC, GABC and the following three ABC variants (MGABC, PABC and MPGABC) are used to study in this experiment on 22 benchmark functions with 30D.

  1. (1)

    ABC only combines with the novel search strategy, denoted by MGABC (the modified GABC).

  2. (2)

    ABC only combines with the novel probability model, denoted by PABC.

  3. (3)

    ABC combines with the novel search strategy and the novel probability model, denoted by MPGABC.

Each algorithm will be conducted 25 times (Shan et al. 2015; Omidvar et al. 2014) independent run for all test functions. For a fair comparison, we use the maximum number of function evaluation (maxFES) as the termination condition, which is set to 150000 (Wang et al. 2014). Moreover, the same parameter settings \((SN\,{=}\,50,{{limit}}\,{=}\,SN\cdot D)\) are used in all compared algorithms. P is set to 0.3 in the novel search strategy. The experimental results are shown in Table 2.

It can be seen from Table 2 that MGABC and PABC are better than or at least comparable to GABC and the original ABC, respectively, in terms of solution accuracy and convergence rate on most cases. To be specific, MGABC is significant better than GABC on all functions except \(f_{6}\), \(f_{9}\), \(f_{10}\) and \(f_{13}\). Moreover, PABC outperforms the original ABC on all functions excluding \(f_{4}\), \(f_{5}\), \(f_{14}\), \(f_{15}\) and \(f_{19}\). In addition, MPGABC outperforms MGABC and PABC on all cases excluding \(f_{6}\) and \(f_{10}\). This phenomenon effectively validates that each of our proposed components can make contribution to ABC and improve the performance of ABC. Besides, through the combination of two proposed algorithmic components, the performance of ABC can be further significantly improved.

To clearly show the convergence rate, the AVEN of GABC, MGABC, the original ABC, PABC and MPGABC are plotted in Fig. 5a, which clearly indicates that MGABC and PABC are better than GABC and ABC, respectively, regarding to convergence speed on most test functions. This result demonstrates that the novel search strategy and the novel probability model can independently enhance the exploitation of ABC and accelerate the convergence speed. Moreover, MPGABC is better than GABC and MGABC on most cases, which means that the combination of the novel search strategy and the novel probability model can further enhance the exploitation ability of ABC. Note that some points are vacant in Fig. 5a, such as \(f_{6}\) and \(f_{8}\). The reason is that some algorithms cannot find an acceptable solution in 25 independent runs.

Overall, it can be concluded that either the novel search strategy or the novel probability model can make a contribution to ABC. Moreover, the performance of ABC can be further enhanced by integrating these two proposed algorithmic components.

As shown in Table 2, PABC is better than ABC on most test functions especially in terms of convergence speed. The distinction between PABC and ABC is mainly caused by the novel probability model. In order to clearly show the difference between the novel probability model and the original probability model, the evolutionary frequency (the number of evolution/maxFES) of each individual in population on some selected representative functions with 30D (unimodal functions \(f_{3}\), \(f_{6}\), and multimodal functions \(f_{13}\), \(f_{18})\) is illustrated in Fig.  6, where X axis denotes the index of the individual, and Y axis denotes the evolutionary frequency (Fre). Note that the same initial population is employed by PABC and ABC on each function. Obviously, there is no significant difference between individuals’ evolutionary frequencies in ABC, which means that the original probability model is unable to ensure the good food sources attract more onlooker bees to search. However, some frequencies are always significantly larger than others in PABC, which demonstrates that the novel probability model can make sure the good food sources can be selected to search by more onlooker bees. Therefore, the novel probability model can fully exploit the valuable information hidden in the good food sources and enhance the exploitation ability of ABC.

Table 3 Parameters setting of all compared algorithms
Full size table

5.3 Experkipment 2: comparison on benchmark functions

In this experiment, in order to verify the performance of our proposed MGPABC, five state-of-the-art ABC variants (i.e., GABC, qABC, best-so-far ABC, dABC and MABC) are used to compare with MPGABC on 22 test functions with 30D, 50D and 100D. To make a fair comparison, for all compared algorithms, SN is set to 50, and maxFES is set to 150,000, 250,000 and 500,000 (Wang et al. 2014; Zhang et al. 2015) corresponding to 30D, 50D and 100D, respectively. The detailed parameter settings of all algorithms are given in Table 3, which are set as the same as the original papers. Each algorithm will be conducted 25 (Shan et al. 2015; Omidvar et al. 2014) independent runs for all test functions. In addition, the Wilcoxon’s rank-sum test (Shi et al. 2010), which is a nonparametric statistic test for independent samples, is also used in experiment results at 5% significance level to show the significant differences between MPGABC and other algorithms. The detailed experimental results are given in Tables 4, 5 and 6, and the best results are marked with boldface. It is noted that the symbols “−”, “+”, “=” denote that the performance of the corresponding algorithm is worse than, better than and similar to that of MPGABC, respectively, according to Wilcoxon’s rank-sum test at a 0.05 significance level.

Table 4 Comparisons of MPGABC with ABC variants on 22 test functions with 30D
Full size table
Table 5 Comparisons of MPGABC with ABC variants on 22 test functions with 50D
Full size table
Table 6 Comparisons of MPGABC with ABC variants on 22 test functions with 100D
Full size table
Fig. 7
figure 7

Convergence curve of different ABCs on 22 test functions with \(D=30\)

Full size image

Table 4 gives the experimental result on 30D functions. It can be clearly observed that MPGABC is significantly better than all compared algorithms in terms of solution accuracy and convnce rate on most test functions. To be specific, MPGABC outperforms all other algorithms on all unimodal functions \((f_{1}-f_{6}\) and \(f_{8})\) except \(f_{6}\). Since the global optimal solution of Step function (\(f_{7})\) is a region rather than a point, all algorithms can obtain the global optimal solution and show similar performance in terms of solution quality. But the convergence speed of MPGABC is better than all competitors except GABC and qABC. Moreover, MPGABC also outperforms or at least is competitive to all compared algorithms on Quartic function \((f_{9})\) and Rosenbrock function \((f_{10})\). Concerning multimodal functions \(f_{11}-f_{22}\), MPGABC is better than or at least comparable to competitors on all functions excluding \(f_{13}-f_{15}\), \(f_{18}\) and \(f_{20}\). With respect to Griewank function \(f_{13}\), MPGABC is beaten by qABC and best-so-far ABC, but it has better convergence rate than all compared algorithms. For Schwefel2.26 function \(f_{14}\), MPGABC is superior to all competitors except GABC. On \(f_{15}\), \(f_{18}\) and \(f_{20}\), MPGABC is only beaten by MABC. Regarding to the remainder functions, MPGABC is better than or at least comparable to all compared algorithms. Overall, MPGABC outperforms GABC, qABC, best-so-far ABC (BsfABC), dABC and MABC on 9, 15, 18, 18 and 7 out of 22 functions. On the contrary, MPGABC is only beaten by GABC, qABC, best-so-far ABC (BsfABC) and MABC on 2, 2, 1, 1 and 4 functions, respectively. Furthermore, MPGABC is faster than all other competitors on a larger proportion of test functions (i.e., \(f_{1}-f_{5}\), \(f_{8}\), \(f_{13}\), \(f_{15}-f_{17}\) and \(f_{19})\). For the convenience and clearness of illustration, the convergence curves of mean objective function value for all functions are presented in Fig. 7, which clearly indicates that MPGABC has better solution accuracy and convergence rate than all other competitors on most test functions.

The results on functions with 50D and 100D are given in Tables 5 and 6, respectively, which also clearly show that MPGABC has better solution accuracy and convergence rate than all the competitors on most test functions. To be specific, regarding to 50D functions, MPGABC is better than GABC, qABC, best-so-far ABC(BsfABC), dABC and MABC on 14, 15, 18, 17 and 7 out of 22 functions, and MPGABC is only beaten by GABC, qABC, dABC and MABC on 1, 3, 1 and 4 functions, respectively. Concerning 100D functions, MPGABC is better than GABC, qABC, best-so-far ABC, dABC and MEABC on 13, 15, 19, 17 and 8 out of 22 functions, respectively, and MPGABC is only beaten by GABC, qABC, dABC and MEABC on 1, 4, 1 and 4 functions, respectively. Therefore, the superiority of MPGABC is not affected by the growth of the search space dimension. In order to clearly show the convergence rate of all compared algorithms, the AVEN of all compared algorithms on 30D, 50D and 100D functions is, respectively, presented in Fig. 5b–d, which clearly illustrates that MGABC can obtain the best AVEN value on most functions.

In addition, according to the Friedman test, the final ranking of all ABC variants for each benchmark function with 30D, 50D and 100D is shown in Table 7. The best results are marked in boldface. Evidently, the average ranking of MPGABC on all functions is better than that of all other ABC variants on 30D and 100D. But MABC performs slightly better than MPGABC on 50D. Therefore, it clearly shows that MPGABC is better than or at least competitive to all competitors on all the test functions.

Table 7 The rankings of competitors for each problem based on the Friedman test
Full size table
Table 8 Average runtime (in seconds) used by ABC and MPGABC on 22 functions with D=30
Full size table

Furthermore, we compare the average runtime between MPGABC and original ABC on 22 commonly benchmark functions with 30D. MPGABC and ABC are conducted 25 independent runs on each function. The average runtime and Ratio are given in Table 8, where Ratio denotes the value that the average runtime of MPGABC is divided by that of original ABC. As shown in Table 8, the Ratio values are prominently less than 1 for all functions. This phenomenon indicates the average runtime of MPGABC is significantly less than that of original ABC on all cases. The reason is that in original ABC, the selection probabilities of all food source positions are similar and small, which means it is a time-consuming procedure that the onlooker bee selects a food source position to search by roulette wheel method. While in MPGABC, the selection probabilities of some good food source positions are significantly enlarged by the novel probability model, and therefore, the time of the onlooker bee choosing a food source position to search by roulette wheel method is significantly less than that of ABC. Overall, the average runtime of MPGABC is better than that of ABC.

Fig. 8
figure 8

Mean best values and AVEN with different values of parameter P

Full size image

5.4 Experiment 3: sensitiveness analysis of parameter P

In MGABC, an additional parameter P is used to control the operating frequency of the original solution search equation (the operating frequency of the new solution search equation learning the beneficial information from the current best solution is 1\(-P)\), which could adjust the exploration ability and exploitation ability of MPGABC. In order to analyze the influence of the parameter P on the performance of MPGABC, five different values of P (i.e., 0.1, 0.3, 0.5, 0.7 and 0.9) are utilized to study on some selected representative functions (unimodal functions \(f_{1}\) and \(f_{3}\), multimodal functions \(f_{11}\), \(f_{14}\), \(f_{15}\) and \(f_{21})\) with 30D. In this experiment, SN is set to 50, and maxFES is set to 150000. Each value on each test function is run independently by 25 times. The mean of the best objective function values and AVEN obtained by each value are used to evaluate their performance. The experimental results are illustrated in Fig. 8, which clearly shows that for unimodal functions, the smaller values of P (e.g., \(P\,{=}\,0.1\) or \(P\,{=}\,0.3\)) can make MPGABC achieve stronger exploitation ability and better optimization performance according to mean best value and AVEN. Moreover, the smaller the value of P is, the better the performance is. The reason of this phenomenon is that since unimodal function has only one global optimal solution, the current best solution could always guide the correct evolution direction, and thus, the current best solution could be fully utilized to improve the performance. Regarding to multimodal functions, MGABC could obtain better performance when \(P\,{=}\,0.3\). This is because multimodal function has multiple local optimal solutions and thus the current best solution cannot always point to the correct direction. It means both the overuse and nonuse of the current best solution cannot obtain a better trade-off between exploration and exploitation. Therefore, based on the comprehensive consideration of unimodal and multimodal function, a proper value of P should be close to 0.3.

5.5 Experiment 4: comparison on CEC2011 real-world problems

In this subsection, MPGABC is tested on 13 kinds of real-world optimization problems (22 problems in total), which are all derived from CEC2011 (Das and Suganthan 2010), to further compare the performance of MPGABC with GABC, best-so-far ABC (BsfABC), dABC and MABC. To make a fair comparison, the parameter settings of all competitors are set the same as the settings used in their original papers. And according to the requirements of CEC2011 (Das and Suganthan 2010), maxFES is employed as the termination condition, which is set to 50,000, and all compared algorithms are independently conducted 25 runs on each real-world optimization problem. The mean and standard deviation of the objective functions value are used to evaluate the performance. The experimental results are given in Table 9, and the best result is highlighted in boldface.

5.6 Experiment 5: comparison on CEC2013 real-parameter problems

In this subsection, to further demonstrate the effectiveness of MPGABC in solving more complex problems, we compare MPGABC with three ABC variants (i.e., GABC, qABC and dABC) on 28 test functions with \(D\,{=}\,50\) and \(D\,{=}\,100\), which are derived from the CEC 2013 special session on real-parameter optimization (Liang et al. 2013). In this experimental study, the parameter settings of all competitors are set the same as the settings used in their original papers. According to the requirements of CEC2013 (Liang et al. 2013), the maxFES of all functions is set to \(10000\cdot D\), and each compared algorithm is independently conducted 51 runs on each function. The average and standard deviation of the function error value \(f(X_{\mathrm{{best}}} )\)-\(f(X^{*})\) are employed to evaluate the optimization performance, where \(X_{\mathrm{{best}}} \) is the best solution found by the algorithm in each run and \(X^{*}\) is the true global optimal solution of the test function. Moreover, the Wilcoxon’s rank-sum test with the 5% significant level is conducted on the experimental results to obtain the reliable statistic conclusion. The experimental results are given in Tables 10 and 11 for \(D\,{=}\,50\) and \(D\,{=}\,100\), respectively. For the sake of clarity, the best results are highlighted in boldface.

Table 9 Comparisons of MPGABC with four state-of-the-art ABC variants on 22 real-world problems
Full size table
Table 10 Comparisons of MPGABC with ABC variants on CEC2013 functions with 50D
Full size table
Table 11 Comparisons of MPGABC with ABC variants on CEC2013 functions with 100D
Full size table

The experimental results on all functions with \(D\,{=}\,50\) are presented in Table 10. It can be seen that MPGABC is better than or at least comparable to all compared algorithms on these test functions. To be specific, with regard to unimodal functions (F1–F5), MPGABC outperforms all compared algorithms on F3 and F5, and MPGABC is only beaten by qABC on F2, F4, and dABC on F1. For basic multimodal functions (F6–F20), MPGABC is better than or at least comparable to all compared algorithms on F7, F11, F15, F17 and F19, respectively. Moreover, MPGABC can obtain the second best results, respectively, on F10, F12, F13, F18 and F20. In addition, MPGABC is only beaten by GABC on F9, qABC on F6 and F16, qABC and dABC on F14, respectively. Furthermore, all compared algorithms can obtain the similar performance on F8. Concerning composition functions (F21–F28), MPGABC is better than or at least comparable to all compared algorithms on F21–F23, F26 and F28. On the contrary, MPGABC is only beaten by GABC on F24, F25 and F27. Overall, MPGABC outperforms GABC, qABC and dABC on 14, 10 and 16 functions, respectively. On the contrary, MPGABC is only beaten by GABC, qABC and dABC on 8, 6 and 2 functions. According to the above analysis, it can be concluded that MPGABC is better than or at least comparable to all compared algorithms when considering all the test functions with \(D\,{=}\,50\).

In order to investigate the performance of MPGABC on the CEC2013 test functions with high dimensionality, we further compare MPGABC with GABC, qABC and dABC on these test functions with \(D\,{=}\,100\). The experimental results are given in Table 11. Clearly, as shown in Table 11, MPGABC is better than all other algorithms in terms of solution accuracy on unimodal functions F3 and F5, and MPGABC also can obtain the second best results, respectively, on F1 and F2. Moreover, MPGABC is only beaten by qABC on F4. With regard to basic multimodal functions (F6–F20), MPGABC is better than or at least comparable to all compared algorithms on F6, F11, F15, F16, F17, F19 and F20, respectively. Moreover, MPGABC is only beaten by GABC on F7, F12, F13 and F18, and qABC on F10, respectively. In addition, all compared algorithms show similar performance on F8 and F9. However, MPGABC performs worst on F14, which may be caused by the property that the number of local optimal solution of F14 is huge and the second better local optimal solution is far from the global optimum. For composition functions (F21–F28), MPGABC is better than or at least comparable to all compared algorithms on F26, and MPGABC also exhibits the second best performance on F21, F23–F25 and F28, respectively. But MPGABC is, respectively, beaten by qABC and dABC on F22, GABC and dABC on F27. In summary, MPGABC outperforms GABC, qABC and dABC on 16, 13 and 15 functions, respectively. On the contrary, MPGABC is only beaten by GABC, qABC and dABC on 9, 7 and 4 functions. Therefore, MPGABC can also perform better than the recent ABC variants on these complex test functions with \(D\,{=}\,100\). According to the above analysis, it can be concluded that the superiority of MPGABC is not affected by the growth of the dimensions in search space.

Furthermore, an insightful phenomenon should be point out that all ABC methods are able to obtain the near optimal solution on F1, F5 and F11, but fail to get the near optimal solution on others functions. The reason for this phenomenon may be that F1, F5, F11 and F22 are separable, while all other functions are non-separable. Therefore, the property of changing one variable at one time in ABCs may determine that ABCs are suitable for solving separable problems.

6 Conclusion and future work

In this paper, to improve the exploitation ability and further enhance the performance of ABC, we propose two new algorithmic components by suitably exploiting the current best solution and other good solutions. The one component is the novel search strategy, which exploits the useful information of the current best solution according to a probability parameter P. The other one is the novel probability model, which can make sure that the good solutions can always attract more onlooker bees to search. Through combining these two new algorithmic components with the basic framework of ABC, a new ABC variant is produced, named MPGABC. The performance of MPGABC has been validated by the comparison with other outstanding ABC variants (i.e., GABC, qABC, best-so-far ABC, dABC and MABC) on 22 benchmark test functions with 30D, 50D and 100D, 22 real-world problems and 28 CEC2013 real-parameter optimization problems with 50D and 100D in terms of solution accuracy, robustness and convergence speed.

Since the current best solution and other good solutions have valuable information, how to effectively employ them to further improve the performance of ABC is still worth studying in the future. Moreover, MPGABC could be extended to solve constraint optimization problems, multi-objective optimization problems (Lin et al. 2015) and real-world practice optimization problems.