1 Introduction

Soft computing plays an important role in data and text mining, and in recent times, soft computing has also been applied in temporal data mining (see Schultz et al. 2009; Chen et al. 2016; Radhakrishna et al. 2015d, e). Although several similarity measures exist in hard computing, there are no measures defined in the soft computing context which can be directly applied to temporal context and identify patterns whose prevalence variation is similar to those of the chosen reference. We also observe that while fuzzy logic has played a significant role in soft computing (see Radhakrishna et al. 2016, 2015a, b, c; Borgelt 2013; McClean et al. 2013; Hong et al. 2002; Wan et al. 2016; Radhakrishna et al. 2015d, e), there is no known fuzzy dissimilarity measure which can be used to discover and retrieve identical patterns from a temporal database. In addition, there has been no attempt toward mapping the Euclidean space on fuzzy space. In this paper, we introduce a novel fuzzy similarity measure, which holds the monotonicity property and can be used to efficiently discover temporal similar patterns.

Finding frequent itemsets (patterns) in non-temporal (static) databases has been extensively studied in the literature. Specifically, a number of algorithms designed to find frequent itemsets, while achieving space and time efficiency, have been proposed. Finding temporal frequent itemsets has also been studied. However, existing studies generally do not consider finding similar temporal patterns whose prevalence (support) values are similar or satisfy subset specifications, with the exceptions of Yoo and Shekhar (2009), Yoo and Shekhar (2008), Yoo (2012), Radhakrishna et al. (2016, 2015a, b, c). The subset specification involves specifying the distance measure, reference support vector, and user interest threshold value.

An approach for finding temporal frequent patterns is discussed in Jin et al. (2006), which uses TFP-tree. The authors in Hirano and Tsumoto (2002) discuss the importance of temporal frequent patterns in the context of medical and time series applications. In Yoo and Shekhar (2009), temporal patterns are extracted from the input database using bounds of supports. In the research reported in Yoo and Shekhar (2008) and Yoo (2012), temporally similar natured patterns are retrieved for a set of pre-defined subset specifications. The subset constraints involve specifying reference support vector, user interest threshold value and an appropriate distance metric. The drawback of such an approach is in the use of Euclidean distance. In Chen et al. (2015), patterns are mined from the underlying time interval based data using Gaussian function.

In this work, we introduce a fuzzy dissimilarity measure to compute distance in fuzzy space. We also introduce expressions to estimate the support bounds. This allows us to discover temporal patterns whose prevalence value variations are similar to those of the reference sequence. Our approach also reduces the computational overhead in finding the support values of itemsets. There is no known distance measure that holds the monotonicity property w.r.t temporal context, and this is the gap we seek to fill. Specifically, we present a measure that holds the monotonicity property. We regard the following as the contributions of this paper:

  1. 1.

    Designing of a novel fuzzy Gaussian-based membership function which retains the monotonicity property.

  2. 2.

    Designing of novel expressions to estimate the maximum possible prevalence and minimum possible prevalence value of temporal patterns.

  3. 3.

    Designing of expression for mapping threshold value to fuzzy space and using a suitable standard deviation value in the fuzzy function.

The rest of the paper is organized as follows. Section 2 reviews related literature, and Sect. 3 describes our proposed method. The case study and results are presented in Sect. 4. Section 5 presents our discussion, and the last section concludes this paper.

2 Related work

In practice, sequence databases generally consist of items with different frequencies. When all these items are set to minimum support, we may encounter the “rare item problem”. This problem is addressed in Hu et al. (2015), which presented the “rep-Prefix scan” algorithm designed to support multiple minimum retention support value for items.

Terrain landscapes are likely to experience temporal phenomena over time and have been the subject of active research. In Schultz et al. (2009), the authors present a spatio-temporal prediction method to predict terrain, forestry landscapes state for a specific time period and forestry evolution using soft computing-based approach. Specifically, they use the sequence of preprocessed binary images obtained from remote sensing images, which are generated from a specific set of regions.

Hydro climate variables are probabilistic in nature; thus, estimating global warming accurately based on these variables is challenging when studying the impacts of climate changes. Atmospheric predictors are also high dimensional. In Sarhadi et al. (2016), a multivariate approach, MRNBC (Multivariate Recursive Nesting Bias Correction), is designed to correct spatial and temporal bias values that exist in climate model simulations. The authors address the high-dimensional feature space problem using a nonlinear supervised dimensional reduction algorithm and two nonlinear soft computing machine learning algorithms, SVR (support vector regression) and RVM (Relevance vector machine).

In real-time applications, transactions often contain quantitative values which can be associated with a life span from a temporal database. The latter includes geographical, health records maintained over some time period. In Chen et al. (2016), the authors present an approach to discover fuzzy temporal association rules. The algorithm first transforms all such quantitative values to their equivalent fuzzy set by the use of fuzzy membership functions. The transformation process is used to generate a temporal information table to record the lifetime of items.

In Borgelt (2013), the authors discuss how soft computing-based pattern mining methods can be employed to address challenges of selective participation and temporal imprecision related to a high level mechanism of neural information processing. They also discuss the importance of adopting a soft computing approach to testing the spatio-temporal coding and temporal coincidence coding hypothesis.

Providing personalized web services is increasingly popular, which is not surprising due to advances in data and web mining technologies and potential financial benefits (e.g., generating higher sales). This requires prediction and discovery of hidden user behavioral patterns which can be discovered from web user logs. Although there are a number of studies in the prediction of user trends and behavioral patterns, this area is understudied in the context of discovering temporal web usage patterns (see Xu (2016); Xu et al. (2016)). In Tseng et al. (2008), the authors consider the temporal property in web usage evolution and then present temporal n-gram algorithm to mine temporal navigation patterns. Similarly n-gram analysis has been used in other related studies (see Peng et al. 2016a, b, inpress).

Retrieving historical information requires formulating queries by specifying temporal constraints. This is the drawback of information retrieval systems as they do not store and record structured temporal information, and they do not have well-defined temporal boundaries for historical events. A framework to address these issues in presented in Schockaert et al. (2010). In McClean et al. (2013), the authors present an approach to discover sequences consisting of heterogeneous symbolic data that have an underlying temporal similar pattern. An approach based on propositional logic to discover high coherent utility fuzzy patterns is presented in Chen et al. (2014). In Hong et al. (2002), the authors use linguistic data to study temporal user behavioral patterns. Segmentation is a preprocessing step in time series pattern matching, which transforms high-dimensional input data sequence to its low-dimensional equivalent representation.

In Wan et al. (2016), the authors evaluate the accuracy and effectiveness of a time series pattern matching using four approaches, namely decision tree based, rule based, hybrid and symbolic aggregate approximation. In Mahmoud et al. (2013), soft computing techniques are used to predict the behavior of occupant suffering from dementia in an inhabited intelligent environment. The movement patterns are recorded using sensors, and occupancy data are transformed to a temporal sequence of activities, which are later used to predict the behavior of the occupant.

The author in Kudłacik et al. (2016) proposes a user command-based intrusion detection based on fuzzy logic. The approach consists of creating two user profiles called the local profile and the fuzzy user profile. The purpose of the fuzzy user profile is to maintain user information in a generalized form. The proposed approach is also motivated from the work detailed in Lin et al. (2014). Other recent soft computing approaches based on similarity computations include those reported in Wang and Ma (2016) and Wang and Feng (2016). A genetic learning and the neuro-fuzzy approach for “team level service climate is proposed in Sangaiah et al. (2015), Sangaiah and Thangavelu (2014).

3 Proposed method to obtain similar temporal patterns

Similar temporal patterns are those whose pattern prevalence variations are similar to those of a reference sequence, which are of primary interest to the user and satisfy certain set of specifications Yoo and Shekhar (2008). This is an understudied area. For example, in Yoo and Shekhar (2009), Yoo and Shekhar (2008) and Yoo (2012), the authors propose an approach to find similar temporal itemsets. They compute true supports of all itemsets in the previous stage when estimating supports of superset patterns. They adopt the basic Euclidean measure, which is widely used in the literature. The authors use the Euclidean distance measure and introduce the concept of bounds. They then show that the maximum possible minimum distance computed using the Euclidean distance w.r.t the maximum possible support sequence holds the monotonicity property. The notations used in this paper are introduced in the Table 1.

Table 1 Notations
Full size table

Let us consider the brute force approach, to retrieve similar temporal association patterns for a specified reference sequence, R, for a given threshold value, \(\Delta \). For itemset with ‘N’ items, this approach requires generating \((2^{\mathrm{N}}-1)\) itemset combinations and then computing true support values for all these \(2^{\mathrm{N}}\)-1 itemset combinations. The complexity is, thus, O \((2^{\mathrm{N}})\). This means that the complexity is exponential, which indicates that the complexity class of this approach is NP-class. The present research is motivated from this fact. The objective of this research is, thus, to reduce the computational overhead in computing true supports by estimating support bounds of itemsets. The true support for itemset is computed if, and only if, it is really needed and required. In Sects. 3.1 and 3.2, we present the design expressions used to estimate the pattern support bounds and fuzzy Gaussian dissimilarity measure which is used to find similarity degree between two temporal patterns. This is then followed by outlining the proposed approach in Sect. 3.3, and the expressions used to compute the upper and lower distance bounds and discussion of monotonicity property in Sects. 3.4 and 3.5, respectively.

3.1 Design expressions to estimate support bounds

Let N be the number of items in the finite set of items, denoted by F with pattern size denoted by L. We design the expressions to estimate bounds of supports of temporal patterns by considering two cases, including all pattern combinations with length (also called size) classified as (i) \({\vert }\hbox {L}{\vert }=2\) and (ii) \({\vert }\hbox {L}{\vert }>2\).

Case-1: Temporal pattern length, |L| =2

Let, \(T_{\mathrm{m}}\) and \(T_{\mathrm{n} }\) be two temporal singleton patterns at Level-1, such that \(T_m =\left( {T_{m_1 } ;T_{m_{2} } ;T_{m_{3} }, \ldots , T_{m_p } } \right) \) and \(T_n =\left( {T_{n_1 } ;T_{n_{2} } ;T_{n_{3}},\ldots , T_{n_p } } \right) \) where each \(T_{m_i } \) and \(T_{n_i } \) is the respective support value at ith timeslot. Then, the maximum prevalence and minimum prevalence bounds of temporal patterns, \({\vert }\hbox {L}{\vert }=2\), are, respectively, obtained using Eqs. 1 and 2.

$$\begin{aligned}{}[T_m, T_n ]_{\max }= & {} \langle {\min }\left( {T_{m_1 } ,T_{n_1 } } \right) , \quad {\min }\left( {T_{m_2 } ,T_{n_2 } } \right) ,\ldots ,\nonumber \\&\times \, {\min }\left( {T_{m_p } ,T_{n_p } } \right) \rangle \end{aligned}$$
(1)
$$\begin{aligned}{}[T_m T_n ]_{ \min }= & {} \langle \max \left\{ (1-\overline{T_{m_1}}-\quad \overline{T_{n_1 } }), 0\right\} ,\nonumber \\&\times \, \max \{(1-\overline{T_{m_2 } }-\overline{T_{n_2 } },0\},\ldots ,\nonumber \\&\times \,\max \left\{ (1-\overline{T_{m_p } }-\overline{T_{n_p } }), 0\right\} \rangle \end{aligned}$$
(2)

In Eqs. (1) and (2), notations, \(T_m\) and \(\bar{T}_n\), are the positive and negative prevalence sequence, respectively.

Case-2: Temporal pattern length, \(|\mathbf{L}| \mathbf{2}\)

Let, \(T_m, T_n\) be the temporal pattern of size, \({\vert }\hbox {L}{\vert }\) greater than two, for which we must estimate support bounds. We divide all such patterns into two subpatterns. The first subpattern \((T_m)\) is assumed to be of length, \({\vert }\hbox {L}{\vert }-1\), and second subpattern \((T_n )\) is equal to length, \({\vert }\hbox {L}{\vert }=1\). To estimate support bounds of temporal pattern of the form \(T_m, T_n \) whose size is \({\vert }\hbox {L}{\vert }>2\), we assume that, \(T_m \) is the temporal association pattern of length (n − 1) i.e., \({\vert }\hbox {L}{\vert }=(\hbox {n}-1)\) and \(T_n\) is singleton temporal pattern.

Let, \(T_m \) and \(T_n \) be two temporal patterns, such that \(T_m =\left( {T_{m_1 } ;T_{m_{2} } ;T_{m_{3} }; \ldots ; T_{m_{p} } } \right) \) and \(T_n =\left( {T_{n_1 } ;T_{n_{2} } ;T_{n_{3} }; \ldots ;T_{n_{p} } } \right) \) where each \(T_{m_i } \) and \(T_{n_i } \) is support value at ith timeslot. The maximum prevalence and minimum prevalence bounds of temporal patterns, \({\vert }\hbox {L}{\vert }>2\), are obtained using Eqs. 3 and 4

$$\begin{aligned}{}[T_m T_n ]_{\max }= & {} \langle \left( T_{m_1 } -\max \left\{ {\left( {1-\overline{T_{m_1} } -T_{n_1 } } \right) ,0} \right\} \right) ,\nonumber \\&\times \left( T_{m_2 } -\max \left\{ {\left( {1-\overline{T_{m_2 } } -T_{n_2 } } \right) ,0} \right\} \right) ,\nonumber \\&\times \left( T_{m_3 } -\max \left\{ {\left( {1-\overline{T_{m_3 } } -T_{n_3 } } \right) ,0} \right\} \right) ,\ldots \nonumber \\&\times \left( T_{m_p } -\max \left\{ {\left( {1-\overline{T_{m_p } } -T_{n_p } } \right) ,0} \right\} \right) \rangle \end{aligned}$$
(3)
$$\begin{aligned}{}[T_m T_n ]_{\min }= & {} \langle \max \left\{ (1-\overline{T_{m_1 } } - \overline{T_{n_1 } } ), 0\right\} , \max \{(1-\overline{T_{m_2 } } \nonumber \\&-\overline{T_{n_2 } } ,0\},\ldots .\max \left\{ (1-\overline{T_{m_p } } -\overline{T_{n_p } } ), 0\right\} \rangle \nonumber \\ \end{aligned}$$
(4)

In the Eqs. (3) and (4), \(T_m\) and \(T_n \) are positive temporal pattern, \(\overline{T}_m\) and \(\overline{T}_n \) is the negative singleton temporal pattern.

The support bound values of the superset temporal pattern (whose size is say, ‘S’) are estimated considering each of its proper subset temporal association pattern (whose size is ‘S − 1’). The maximum support sequence denoted as \([T_m, T_n ]_{\max } \) is the minimum support sequence possible w.r.t each time slot, and the minimum support sequence denoted as \([T_m, T_n ]_{\min } \) is the maximum support sequence possible w.r.t each time slot obtained by using Eqs. (3) and (4).

3.2 Proposed fuzzy gaussian dissimilarity measure

Let \(T_m\) and \(R_s \) be the pattern and reference prevalence (support) sequence denoted as \(T_m =\left( {T_{m_1 } ;T_{m_{2} } ;T_{m_{3} }; \ldots ; T_{m_n } } \right) \) and \(R_s =\left( {R_{s_1 } ;R_{s_{2} } ;R_{s_{3} }; \ldots ;R_{s_n } } \right) \). Then, the average fuzzy similarity value between these two temporal patterns is computed using the expression given in Eq. (5)

$$\begin{aligned} \mu _\mathrm{reference}^\mathrm{pattern} =\frac{\sum \nolimits _{p=1}^{p=n} 0.5*\left[ {1+exp^{-\left( {\frac{T_{m_p } -R_{s_p } }{\sigma }} \right) ^{2}}} \right] }{\left| p \right| } \end{aligned}$$
(5)

The fuzzy dissimilarity between two temporal patterns is, hence, given by Eq. (6) as defined below,

$$\begin{aligned} D^\mathrm{gaussian}=\frac{1-\mu _\mathrm{reference}^\mathrm{pattern} }{2} \end{aligned}$$
(6)

The standard deviation denoted as \(\sigma \) in Eq. (5) is defined as a function of threshold given by Eq. (7)

$$\begin{aligned} \sigma =\frac{\Delta }{\sqrt{\log _e \frac{1}{1-\Delta ^{2}}}} \end{aligned}$$
(7)

where, \(\Delta \) is the threshold value specified in the Euclidean space and \(\sigma \) is the deviation used when estimating fuzzy similarity value between pattern and reference.

The threshold in Euclidean space mapped to its equivalent Gaussian space is given by Eq. (8)

$$\begin{aligned} \Delta ^{\mathrm{gaussian}}=1-0.5*\left( {1+e^{-0.5*\left( \frac{\mathrm{threshold}}{\mathrm{deviation}}\right) ^{2}}} \right) \end{aligned}$$
(8)

Equation (8) gives the equivalent threshold which we must consider to test, if the distance is holds good for user defined threshold in fuzzy space.

3.3 Proposed similar temporal association pattern mining algorithm

Now, we present the algorithm outlining proposed method in this section.

Algorithm : Mining similar temporal patterns

Input: Temporal Database with time-stamped transactions; Reference sequence; User specified dissimilarity threshold and proposed distance function.

Output: Similar temporal patterns

Step-1: Determine true prevalence value of singleton patterns

Obtain Positive Prevalence and Negative Prevalence for each singleton temporal item (temporal pattern) from the finite set of items defined by F. This is the first time; we compute true support values of all temporal items initially.

Step-2: Determine true prevalence sequence of singleton patterns

Obtain Positive Prevalence Sequence and Negative Prevalence Sequence for each singleton temporal item (temporal pattern) using prevalence values computed in step-1.

Step-3: Pruning stratergy-1 for singleton patterns of size, L = 1

Compute true distance between reference and each temporal pattern of size = 1. If the true distance satisfies dissimilarity constraint, then the pattern is treated as similar and retained. If the true distance exceeds dissimilarity constraint, the pattern is treated dissimilar. To decide to prune or not, we compute distance \((D^{\mathrm{U}})\) which is the maximum possible deviation above reference sequence defined in Section 1.1. If this distance exceeds threshold value, then prune the temporal pattern. In this case, we say the temporal pattern is not retained. Otherwise (dissimilarity condition is satisfied), then we retain the candidate temporal pattern to compute prevalence values (support values) of higher size temporal patterns.

Step-4: Pruning stratergy-2 for temporal patterns of size, L > 1

Case-1: Obtain the Maximum Pattern Bound Support Sequence and Minimum Possible Support Bound for all patterns of size>1. Now, if the Minimum Possible Support Bound \((D^{\mathrm{\min }})\) exceeds threshold, then the pattern is dissimilar. To decide whether this temporal pattern be pruned or not, we compute distance \((D^{\mathrm{U}})\) which is the maximum possible minimum deviation above temporal pattern. If \(D^{\mathrm{U}}>\) threshold, \(\Delta \), then prune the temporal pattern. In this case, we say the temporal pattern is not retained. However, if dissimilarity condition is satisfied, then we retain the candidate temporal pattern to compute prevalence values (support values) of higher size temporal patterns.

Case-2: Obtain Minimum Possible Support Bound \((D^{\mathrm{\min }})\) for all patterns of size >1. Now, if the Minimum Possible Support Bound \((D^{\mathrm{\min }})\) satisfies threshold, then the pattern may be similar, but this may not always be the case as it is dependent on itemset distribution. This is because we are estimating maximum and minimum possible bounds and comparing these with reference. So, to decide whether this temporal pattern is temporally similar, we scan the database to find patterns true support sequence and from this support sequence, we find its true distance with reference, R by using proposed measure. If the true distance \(\le \) threshold, then temporal pattern is similar and is also retained. If the true distance is violating dissimilarity condition then we find if \(D^{\mathrm{U}}>\) threshold, \(\Delta \), if so, we prune the temporal pattern. In this case, we say the temporal pattern is not retained. However, if \(D^{U} \le \Delta \), then we retain the candidate temporal pattern to compute prevalence values (support values) of higher size temporal patterns.

Step-5: Prune all infeasible candidate temporal patterns

In the process of verifying temporal patterns for similarity w.r.t reference, discard and prune all temporal superset patterns, if there is at least one subset pattern of this superset pattern which is not retained. In other words, for temporal pattern T to be considered similar, all its subpatterns must satisfy the retaining condition. If there is at least one subset such that it does not satisfy dissimilarity condition, then the superset pattern, T, is not similar.

Step-6: Output all candidate temporal patterns which are similar and retained.

The similar patterns are all those patterns which are considered similar and retained in previous steps.

3.4 Computing distance bounds

To estimate distance bounds, we use Eqs. (9)–(11) presented in Sects. 3.4.1 and 3.4.2. Equations (9)–(11) are inspired from Yoo and Shekhar (2009), Yoo and Shekhar (2008) and Yoo (2012) where the distance measure chosen is Euclidean. In this work, we use the proposed measure to estimate distance bounds \((D^{\mathrm{U}}\) and \(D^{\mathrm{L}})\).

3.4.1 Maximum possible minimum dissimilarity, \((D^{\mathrm{U}})\)

Let \(T_m =\left( {T_{m_1 } ;T_{m_{2} } ;T_{m_{3} };\ldots ; T_{m_{n} } } \right) \) and \(R_s =\left( {R_{s_1 } ;R_{s_{2} } ;R_{s_{3} };\ldots ;R_{s_{n} } } \right) \) be the Maximum Pattern Bound Support Sequence and reference sequence, respectively. Now, \(D^{\mathrm{U}}\) is defined by Eq. 9.

$$\begin{aligned} D^{u}=\left( {\frac{1-\frac{\sum \nolimits _{p=1}^{p=n} 0.5*\left( {1+e^{-\left( {\frac{T_{m_p } -R_{s_p } }{\sigma }} \right) ^{2}}} \right) }{\left| P \right| }}{2}} \right) \end{aligned}$$
(9)

\(\forall \) i, where \(R_{s_i } >T_{m_i }\)

For all cases, when the above condition fails in which the support values of temporal association pattern do not exceed the support values of the reference, \(D^{\mathrm{U} }= 0\).

3.4.2 Minimum possible minimum dissimilarity, \((D^{\mathrm{L}})\)

Let \(T_m =\left( {T_{m_1 } ;T_{m_{2} } ;T_{m_{3} };\ldots ;T_{m_{n} } } \right) \) and \(R_s =\left( {R_{s_1 } ;R_{s_{2} } ;R_{s_{3} };\ldots ; R_{s_{n} } } \right) \). be the Minimum Pattern Bound Support Sequence and reference sequence, respectively. Now, \(D^{\mathrm{L}}\) is defined by Eq. 10.

$$\begin{aligned} D^{L}=\left( {\frac{1-\frac{\sum \nolimits _{p=1}^{p=n} 0.5*\left( {1+e^{-\left( {\frac{T_{m_p } -R_{s_p } }{\sigma }} \right) ^{2}}} \right) }{\left| P \right| }}{2}} \right) \end{aligned}$$
(10)

\(\forall \) i, where \(R_{s_i } < T_{m_i }\).

For all time slots, in which the support values of temporal association pattern exceed the support values of the reference, the value of \(D^{\mathrm{L} }= 0\).

3.4.3 Minimum possible support bound, \((D^{{\min }}\))

This is the distance used to decide whether the pattern is similar or not and is given by Eq. (11)

$$\begin{aligned} D^{{\min }}\hbox {}=D^{\hbox {U}}\hbox {}+D^{\hbox {L}} \end{aligned}$$
(11)

3.5 Monotonicity property of maximum possible minimum bound distance \((D^{u})\)

To find the dissimilarity degree between two patterns, we propose a novel fuzzy-based Gaussian distance measure as represented by Eqs. 5–7. We found that the distance computed using the proposed dissimilarity fuzzy Gaussian measure did not satisfy monotonicity property directly.

We deduced that the maximum possible minimum distance computed using proposed measure satisfies monotonicity property. This property is used to prune the superset patterns. This is because the distance of any superset pattern shall be greater than or at most equal to its subset patterns. Therefore, if a subset pattern is not similar at the previous level, then all the superset patterns at the next level are implicitly not similar and we need not compute their true supports to decide whether they are similar or not.

3.5.1 When to estimate and discard estimating supports and computation of true supports of temporal patterns

Fig. 1 depicts the generalized flow of the proposed approach.

Fig. 1
figure 1

Flowchart of proposed approach to discover similar temporal patterns

Full size image

Case-1 When considering a temporal pattern, P at level-(k+1) to determine whether it is similar or not, with respect to a user specified reference support sequence, R, we check if all subset patterns of this temporal pattern, P at level-k satisfies either of two conditions

  1. (i)

    Similar and Retained

  2. (ii)

    Not Similar and Retained

If so, we consider the temporal pattern for possibility of it being a similar pattern and proceed by estimating support bounds of P. If the minimum bound distance computed using estimated support bounds exceeds threshold, then we directly prune the temporal pattern and do not retain it and consider the pattern as dissimilar. Since the pattern is not retained, we terminate all its superset patterns and declare them dissimilar, without computing their true supports. We eliminate true support computations in this case.

Case-2 Alternately, if maximum possible minimum distance is less than or equal to threshold in fuzzy space, then we compute the true support of temporal pattern and find its distance using proposed fuzzy Gaussian function. If true distance computed w.r.t reference is less than the threshold, then the pattern is similar. In this case, pattern is retained.

Case-3 When the true distance of temporal pattern P exceeds threshold, then the pattern is dissimilar. Now, to determine whether the temporal pattern P is to be retained or not, we compute the maximum possible minimum bound distance w.r.t reference. If it does not exceed threshold, then we retain it for next stage computations; otherwise, we do not retain the pattern.

Case-4 When we have a situation where at least one subset temporal pattern is not similar and also not retained, we prune the superset temporal pattern P without the need to estimate support bounds.

3.5.2 Correctness of \(\mathbf{D}^{\mathbf{U}}\)

To output all the similar patterns, we compute the distance, \(D^{\mathrm{U}}\) and true distance (denoted as \(D^{\mathrm{gaussian}})\) using the proposed fuzzy function. By the correctness of \(D^{\mathrm{U}}\), we mean that the computed dissimilarity between the reference pattern and a temporal pattern never exceeds the threshold for all temporal patterns whose outputs are similar. Since, pruning is also based on \(D^{\mathrm{U}}\), this distance to the true distance can be computed using the proposed measure. Based on the maximum possible minimum distance given by Eq. 9, we have the following:

$$\begin{aligned} D^{U}=\left\{ {{\begin{array}{ll} {0.5*\left( {1-\frac{\mathop \sum \nolimits _{p=1}^{p=n} 0.5*\left( {1+e^{-\left( {\frac{T_{m_p } -R_{s_p } }{\sigma }} \right) ^{2}}} \right) }{\left| P \right| }} \right) } &{};\quad \forall \hbox { i where }R_{s_i } >T_{m_i } \\ 0&{} ;\quad else \\ \end{array} }} \right. \end{aligned}$$
(12)

From Eq. (12), we obtain three situations, as discussed below.

Case-1: Worst case In the worst case, all ‘p’ time slots have support values satisfying the constraint, \(R_{s_i } >T_{m_i } .\) In this case, the computed distance shall be same as the true distance of temporal pattern to reference in fuzzy space, i.e., \(D^{U}=D^\mathrm{gaussian}\). This implicitly implies distance, \(D^{L}=0\) in the fuzzy space.

Case-2: Best case In the best case, all ‘p’ time slots have supports such that, \(R_{s_i } \le T_{m_i } .\) In this case, the distance computed i.e., \(D^{U}=0\).

Case-3: Average case The average distance value is observed, when for some time slots, support values of temporal pattern being considered are less than the reference value and for all other remaining time slots, support values of temporal pattern are either equal to or higher than reference support. For the case, where the temporal pattern support value at a given time slot is greater than or equal to reference, distance is zero; otherwise, this value is nonzero.

Deduction: It is seen that in the worst case, \({\varvec{D}}^{\varvec{U}}\) is equal to the true distance obtained using the proposed fuzzy membership distance function. In other words, true distance and \({\varvec{D}}^{\varvec{U}}\) hold the relation represented by:

$$\begin{aligned} D^{U}\le D^{\mathrm{gaussian}} \end{aligned}$$
(13)

Hence, if \(D^{\mathrm{U}}\) computed for a temporal pattern considering its true support does not satisfy the threshold condition, then the true distance (\(D^\mathrm{gaussian})\)computed shall also not satisfy the dissimilarity condition.

4 Case study

We used the well-known IBM Quest data generation system (http://www.almaden.ibm.com/software/quest/resources/) to generate synthetic datasets. A detailed discussion about synthetic data generator is addressed in Sect. 5. We use the following input parameters to generate the time-stamped temporal database. These include the number of time slots, number of items, average number of items per transaction and number of transactions per time slot. Based on the input parameters, the system generates the dataset consisting of customer transaction information.

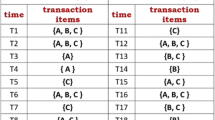
Table 2 is the temporal database generated using the IBM synthetic generator by considering number of time slots, \(T = 3\), number of items, \(I=4\), average number of items per transaction, \(L=2\) and number of transactions per time slot, TD = 10. In other words, the temporal database is defined over three timeslots \(t_{1}, t_{2}, t_{3}\) with each timeslot consisting of 10 time-stamped transactions, and the itemset consists of only 4-items A, B, C and D. Thus, there are a total of 30 transactions and any transaction must be performed only from these four items.

Table 2 Temporal database of time-stamped transactions defined over three time slots
Full size table

The computations in Table 3 show the true supports of all temporal patterns and their corresponding true distances computed using Euclidean distance measure. In this example, the Euclidean distance considered is the normalized Euclidean distance. The reason for considering normalized distance is from the fact that Euclidean distance does not have the upper limit. To make it lie between 0 and 1, we normalize the distance obtained based on number of time slots. Table 3 shows the positive, negative prevalence values of singleton temporal patterns respectively. We choose the threshold, \(\varDelta =0.2\) and \(R=(0.4, 0.6, 0.6)\) as reference sequence. The threshold value chosen is 0.2 in Euclidean space which is then mapped to its equivalent value \(\varDelta =0.0101\) in the Gaussian space using the transformation equation presented in Sect. 3. The distance measure used to find similar (or dissimilar patterns) is the novel fuzzy Gaussian-based distribution function, which is one of the contributions in this research inspired from Lin et al. (2014).

Table 3 also represents, the similar (denoted using symbol, \(\checkmark \)) and dissimilar temporal patterns (denoted using symbol, ✘) obtained using the brute force approach. The number of possible patterns using 4 items is 15, i.e (\(2^{4}-1\)). Hence, for applying the brute force approach, we require 15 true support computations to decide whether the corresponding patterns are similar or not. In general, we require \(2^{\mathrm{n}}-1\) support computations for ‘n’ items. We considered the worst case scenario input for our case study. In such a case, the proposed approach requires only ten true support computations as compared to 15 support computations required using brute force approach. For a huge number of pattern combinations, the true supports to be found are naturally reduced.

In the best case scenario, we require only four true support computations. This is because all patterns at level-2 have their estimated lower bound distance bounds exceeding dissimilarity threshold limit. Hence, we need not compute true supports for those patterns (Table 4). One disadvantage that we have with use of Euclidean distance is that the Euclidean distance measure does not hold true for finding similar or dissimilar patterns in temporal context when considered directly Yoo and Shekhar (2009). The reason is that it does not hold monotonicity property. For example, using the Euclidean distance, the distance of patterns A, B, C, D w.r.t reference computed using the Table 2, denoted as d(A), d(B), d(C) and d(D) are 0.1732, 0.0577, 0.0577 and 0.0577, respectively. The reference support sequence is denoted in Table 5. The dissimilarity value of patterns AB, AC and AD denoted by d(AB), d(AC), d(AD) is 0.1414, 0.2160 and 0.2645, respectively. Also, the dissimilarity of d(ABC) is 0.3366. According to the monotonicity property, the distance of superset pattern must be greater than or equal to distance of all its subset patterns w.r.t reference chosen. If we consider the distance of pattern AB, and its subsets A and B w.r.t reference support sequence, we have d(AB) > d(B) but d(AB) < d(A).

Table 3 True support computations
Full size table

This clearly shows that the monotonicity property does not hold when using Euclidean distance for pruning the patterns of next stage. The true distance and upper bound value of each singleton temporal pattern is recorded in Table 5. It is seen from Table 5 that the temporal patterns [A], [B], [C], [D] are similar and are also retained. If a pattern is similar, then it is retained. In the event that the true distance of temporal pattern exceeds the threshold, we find the corresponding highest possible minimum distance from reference. If it does not exceed threshold, then we retain the pattern and consider it for the next stage support computations; otherwise, the temporal pattern is discarded (Table 6).

Table 4 Positive and negative supports
Full size table
Table 5 Level-1 patterns
Full size table
Table 6 Threshold transformation
Full size table
Table 7 Estimation of support bounds of temporal pattern [AB]
Full size table
Table 8 Testing similarity and retaining conditions for pattern [A B]
Full size table
Table 9 Estimation of support bounds of temporal patterns, size 2
Full size table

Table 7 outlines the estimated value of highest possible support sequence bound (HPSSB) and lowest possible support sequence bound (LPSSB) of pattern [A B], its corresponding highest possible minimum and lowest possible minimum distances from the reference and the lower bound distance \((D^{{\min }} = D^{\mathrm{U}} + D^{\mathrm{L})}\) computed using proposed dissimilarity function. Since \(D^{{\min }}< 0.0101\), the pattern [AB] has chances of being similar w.r.t reference. In such a case, we need to compute the true support. The true support computation shall be eliminated whenever the distance denoted by \(D^{{\min }}\) exceeds the value of threshold.

Table 8 shows the true support value of temporal pattern [A B]; true distance w.r.t reference computed using novel fuzzy Gaussian distribution function, and the highest possible minimum bound value. The true distance computed is 0.005026 < 0.01010 and hence; the temporal pattern [A B] is similar. It is also retained to verify, if a superset pattern of [A B] may be considered for similarity or not in future.

Table 10 Testing similarity and retaining conditions for size two patterns
Full size table

Table 9, outlines the highest possible support sequence bound (HPSSB) and lowest possible support sequence bound (LPSSB) of all size two temporal patterns, corresponding highest possible minimum and lowest possible minimum distances from the reference and the lower bound distance \((D^{{\min }} = D^{\mathrm{U}} + D^{\mathrm{L})}\) computed using proposed distance function. Since \(D^{{\min }}<\) 0.0101, for all patterns, each pattern may be similar w.r.t reference. In such a case, we need to compute the true support of all these patterns. The true support computation shall be eliminated, whenever the distance denoted by \(D^{{\min }}\) exceeds the value of threshold.

Table 10, shows the true support value of all size two temporal patterns; their true distance w.r.t reference computed using proposed function, highest possible minimum bound value. The minimum bound distances for patterns [AC], [AD], [BC], [BD] and [CD] exceed threshold value, 0.010102. So, these patterns are not similar temporally and are called dissimilar patterns. The corresponding highest possible minimum bound distance of these temporal patterns is computed to determine whether they can be retained. Since this value also exceeds the threshold value, all these temporal patterns are not retained. Since we consider the worst case situation, we had true distance and highest possible minimum bound distance to be same, which is not the typical case.

Table 11 Estimation of support bounds of temporal patterns, size 3 for verification
Full size table
Table 12 Testing similarity and retaining conditions for size three patterns w.r.t true supports
Full size table

Figure 2 shows the lattice structure for 15 itemsets or patterns formed from 4 items. Level-1 consists of four patterns, level-2 consists of six (6) temporal patterns, and level-3 and level-4 has four and one temporal pattern, respectively. Each temporal pattern is annotated with the highest possible minimum bound distance value (also called upper lower bound). The proposed Gaussian-based fuzzy distribution function satisfies the monotonicity property w.r.t highest possible minimum bound distances, which may be verified from distances annotated in Fig. 1.

The temporal patterns at level-3 include, [ABC], [ABD], [ACD], [BCD]. Since the subset temporal patterns for these four temporal patterns are not retained in the level-2, we directly say these patterns are not similar, without computing true supports of these patterns. We also need not estimate the highest and lowest possible support values in this case. Thus, the patterns denoted by [ABC], [ABD], [ACD], [BCD] are dissimilar temporal patterns. Now if we consider level-4, we have [ABCD] as the only temporal pattern. As all its subset patterns denoted by [ABC], [ABD], [ACD], [BCD] are not retained and also are not similar, so this superset pattern [ABCD] is not temporally similar. We eliminate true support computations in this case also.

Fig. 2
figure 2

Lattice diagram representing monotonicity property of proposed measure w.r.t true supports upper lower bound distance to reference sequence

Full size image

However, for verification and validation, we give the support bounds and distance bounds for level-3 and level-4 patterns to prove our argument hold true. The computations in Tables 11 and 12 give the estimated support and distance bounds and corresponding true support and distance values. The patterns are denoted as not similar using the symbol, ✘.

Fig. 3
figure 3

Comparison of execution time

Full size image
Fig. 4
figure 4

Threshold versus execution time

Full size image

5 Findings

Fig. 5
figure 5

True support computations

Full size image

The data generator system mainly consists of two generators. The first generator was used to generate the transaction data which may be used to retrieve the sequential patterns or association patterns. Since the data generator system did not generate temporal database of time-stamped transactions, we modified it to suit our requirements. To generate the temporal database consisting of time-stamped transactions for the experiments, we considered the following parameters which include the number of time slots, number of items, average number of items per transaction, number of transactions per timeslot. Based on these input parameters, the system generates dataset consisting customer transaction information.It also generates transactions randomly for different specifications given by user.

Fig. 6
figure 6

Candidate items retained for different user threshold values

Full size image
Fig. 7
figure 7

Candidate patterns retained at each level for \(\varDelta \) = 0.45

Full size image
Fig. 8
figure 8

True support comparisons at \(\varDelta \) = 0.4

Full size image
Fig. 9
figure 9

Execution for different thresholds on TD1000-L10-I20-T100

Full size image

Finding similar temporal association patterns whose support value varies w.r.t reference is initiated in Yoo and Shekhar (2009), Yoo and Shekhar (2008) and Yoo (2012). The authors present sequential approach for mining patterns and compare their approach with the sequential approach as there is no other work prior to this in the literature except for the brute force approach. In this research, we compare the brute force, sequential approaches for retrieving similar temporal patterns with our proposed measure and bound estimation approach. We also compared the proposed approach with algorithms in Yoo and Shekhar (2009) and Yoo and Shekhar (2008).

We generated the temporal database, TD1000-L10-I20-T100. The results are the average readings obtained for all experiments. Here, TD denotes 1000 (X100) transactions and L, is the average size of transaction, I indicates items; T is number of time slots considered.

Figure 3 shows a comparative summary of the execution time for the brute force approach and the proposed approach using fuzzy dissimilarity measure. In the brute force approach, after Level-7, the execution time is exponential, while the proposed approach is polynomial and terminates in finite time. Figure 4 presents the comparative summary of the proposed and the brute force approaches for variable threshold values of values 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45 w.r.t execution time and true support computations. Figures 5 and 6 denote the number of true support computations performed and candidate temporal pattern retained by proposed approach, respectively. Figures 7 and 8 depict the candidate patterns retained and true support computations at different levels for \(\varDelta =0.45\) and \(\varDelta =0.40\) using the brute force and proposed approaches considering TD1000-L10-I20-T100 dataset generated using the IBM synthetic data generator, respectively. The parameters are chosen such that number of time slots \(=\) 100, number of items \(=\) 20, number of transactions \(=\) 1,00,000, number of transactions per time slot \(=\) 1000.

From Figs. 7 and 8, it is seen that the number of true support computations and candidate temporal patterns retained is linear using the proposed approach and exponential with the brute force approach. This clearly demonstrates that our approach outperforms the brute force approach.

In Fig. 9, we vary the threshold values and compare the execution times of proposed and sequential approaches in Yoo and Shekhar (2009), Yoo and Shekhar (2008) for different threshold values. The graph is plotted by considering threshold w.r.t x-axis, and execution time in seconds w.r.t y-axis.

Fig. 10
figure 10

Execution times for both algorithms for different timeslots

Full size image

In Fig. 10, we vary the time slots and record execution times of both proposed and sequential approaches Yoo and Shekhar (2009), Yoo and Shekhar (2008) for different time slots such as 100, 150, 200, 250 and 300. The graph is plotted by considering timeslots w.r.t x-axis, and execution time in seconds w.r.t y-axis.

Fig. 11 illustrates the threshold on x-axis and execution time on y-axis for 40 items, 10,000 transaction/timeslot and 500 timeslots. From Fig. 11, we observe that an increase in the threshold will also result in an increase in the execution time.The increase is linear and the time taken to output similar temporal patterns is finite. However, the time taken using the sequential and brute force approaches is not finite.

Fig. 11
figure 11

Threshold versus execution time for large dataset

Full size image
Fig. 12
figure 12

Execution times of our approach and SPAMINE

Full size image
Fig. 13
figure 13

Sample screen shot

Full size image

Figure 12, illustrates the results obtained on TD1000-L10-I20-T100 using the proposed and spamine approaches in Yoo and Shekhar (2009), Yoo and Shekhar (2008) and Yoo (2012). From Fig. 12, we observe that as the threshold increases, so does the time taken for the execution. However, the time taken using the proposed approach is comparitively less w.r.t spamine approach. The threshold values are varies from 0.15 to 0.45 insteps of 0.05.

Figure 13, is a screen capture of our temporal pattern mining proof-of-concept used to generate the temporal database, enter input parameter values. Figure 14 depicts the trends of similar temporal patterns obtained w.r.t reference (shown in red color).

Fig. 14
figure 14

Graph showing pattern trends

Full size image

6 Conclusion

The problem of finding temporal association patterns whose prevalence variations are similar to reference sequence is understudied in the literature, which is first coined in Yoo and Shekhar (2009). Discovering temporal patterns which are similar for a chosen reference is a challenging problem as it requires reducing both the number of database scans and number of true support computations at the same time retrieving all possible similar patterns efficiently in a finite time.

In this research, we presented novel expressions to gauge the maximum and minimum possible prevalance values of temporal patterns and retrieving similar temporal patterns using fuzzy-based gaussian distribution function. The dissimilarity measure designed also holds the monotonicity property, which is used to eliminate unnecessary true pattern prevalence computations so as to prune dissimilar patterns. We then presented the expression for equivalent threshold in fuzzy space for its corresponding threshold value specified in the euclidean space. Our findings demonstrated that the proposed approach outperforms the brute force approach, sequential approaches and SPAMINE Yoo (2012). Also, the gaussian function used to find dissimilarity value has finite maximum and minimum bounds which fail w.r.t Euclidean measure. The pruning is dominated by the factors such as choice of reference, data distribution and distance allowable for considering similarity.

In this paper, we focus on the design of fuzzy measure and its suitability to retrieve all valid temporal patterns but with varying scale w.r.t base pattern. To achieve this, we considered the whole pattern to compute the similarity degree. Often, it may also be required to find subsequence of a sequence in which the patterns are similar. This is one direction in which the present work may be extended.The choice of reference, data distribution and the value of permissible distance limit to evaluate similarity between patterns are the dominating parameters which affect the pruning process. We are also examining the possibility of designing similarity measures which can hold monotonicity and efficiently retrieve the valid similar temporal patterns. Future work also includes using the normal distribution concept to estimate pattern support bounds.