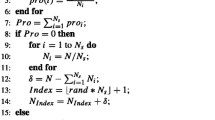APDDE: self-adaptive parameter dynamics differential evolution algorithm

Abstract

In real-time high-dimensional optimization problem, how to quickly find the optimal solution and give a timely response or decisive adjustment is very important. This paper suggests a self-adaptive differential evolution algorithm (abbreviation for APDDE), which introduces the corresponding detecting values (the values near the current parameter) for individual iteration during the differential evolution. Then, integrating the detecting values into two mutation strategies to produce offspring population and the corresponding parameter values of champion are retained. In addition, the whole populations are divided into a predefined number of groups. The individuals of each group are attracted by the best vector of their own group and implemented a new mutation strategy DE/Current-to-lbest/1 to keep balance of exploitation and exploration capabilities during the differential evolution. The proposed variant, APDDE, is examined on several widely used benchmark functions in the CEC 2015 Competition on Learning-based Real-Parameter Single Objective Optimization (13 global numerical optimization problems) and 7 well-known basic benchmark functions, and the experimental results show that the proposed APDDE algorithm improves the existing performance of other algorithms when dealing with the high-dimensional and multimodal problems.

1 Introduction

Fig. 1

Main stages of the DE algorithm

DE (differential evolution) was presented at the Second International Contest on Evolutionary Optimization in 1997, and it turned out as one of the best among the competing algorithms (Storn and Price 1997; Price 1997). Since late 1990s, DE started to find several significant applications to the optimization problems. There are many reasons why the researchers have been looking at DE as an attractive optimization tool. For instance, it is simple and straight forward to implement, and the number of control parameters in DE is very few, and the space complexity of DE is low (Das and Suganthan 2011). Its performance, however, is still quite having some limitations; if DE cannot produce offspring better than the parent, the algorithm will be to a standstill. The reason is that: In every stage of the optimization process, the mobile is limited. Obviously, the differential evolution algorithm to successfully solve a specific optimization problem depends on the results of the mutation strategy and the three control parameters: the population size (NP), crossover rate (CR) and the scale factor (F). The best settings for the control parameters can be different according to those practical optimization problems and the same functions with different requirements for consumption time and accuracy. Otherwise, the mobile restrictions will be to a standstill. Therefore, researchers have developed some DE variants with adaptive control parameters and trial vector generation strategies to suit various requirements during the evolution process. In the DE family of Storn and Price, DE/rand/1/bin is the most frequently used mutation strategies and many algorithms are developed based on it for its robustness and efficiency in terms of convergence rate. And DE/rand/2/dir (Feoktistov and Janaqi 2004) implements greedy DE strategies to generate offspring. However, a greedy DE variant such as DE/current-to-best/1/bin which employs the information of the best solution in the current population is less useful or difficultly to be developed. The reason seems to be very intuitive: less reliable and may lead to premature convergence. But Das and Suganthan (2011) noted that for non-separable and unimodal functions, DE/current-to-best/1/bin consistently showed the best phenomenon and it was also successful in optimizing some multimodal and separable benchmarks. Hence, these greedy DE variant strategies have great development of space; Zhang and Sanderson (2009) proposed a new algorithm which implements a new mutation strategy DE/current-to-pbest with optional external archive and achieved considerably good results.

The remaining part of this paper is organized in the following manner. In Sect. 2, we introduce the standard DE algorithm. Sect. 3 gives a detailed description about some recent variants that are commonly considered as the state of the art, such as JADE (Zhang and Sanderson 2009), MDE (Ali et al. 2013), CODE (Wang et al. 2011), MDESELF (Li and Yin 2014) and EPSDE (Mallipeddi et al. 2011). Section 4 presents the proposed APDDE algorithm. Section 5 makes comparative experiments on the CEC 2015 test suite and analyzes the related experimental results. Conclusions are drawn in Sect. 6.

2 Basic operations of DE

DE is a simple real-coded evolutionary algorithm. It works through a simple cycle of stages. The basic idea of the algorithm is: DE perturbs current generation vectors with the scaled difference in two randomly selected population vectors. The result is to generate a donor vector; it corresponds to each population vector (also known as target vector). Then, the donor vector exchanges its components with the target vector under crossover operation to produce a trial vector. In selection stage, the trial (or offspring) vector competes against the population vector; the better one will be used as the parent vector in the next generation. Hence, the population either gets better or remains current status, but never deteriorates, guiding the population to tend to the optimal solution.

Stages of DE presented in Fig. 1 includes: (1) initial parameter population, (2) mutation with difference vectors to produce the donor vector, (3) setting the violating components within the predefined boundary constraints, (4) crossover operation between the target vector and its corresponding donor vector, (5) selecting operation through the objective function value of each trial vector compared with that of its corresponding target vector, and so on.

2.1 Initialization of the parameter vectors

DE searches for a global optimum parallelly in D-dimensional real-parameter space. It begins with an initiated population of NP with D-dimensional real-valued parameter vectors, which should cover the entire search space as much as possible by uniformly randomizing the initial individuals within the prescribed search space. For example, according to a uniform distribution:

$$\begin{aligned} x_{j,i}^{\mathrm{Low}} \le x_{j,i} \left( 0 \right) \le x_{j,i}^{up} ,i=1,2,\ldots ,\hbox {NP};j=1,2,\ldots ,D, \end{aligned}$$

The initial value of the jth parameter of the ith individual at generation $g= 0$ is generated by:

$$\begin{aligned} x_{j,i} \left( 0 \right) =x_{j,i}^{\mathrm{Low}} +\mathrm{rand}\left( {0,1} \right) \cdot \left( {x_{j,i}^{Up} -x_{j,i}^{\mathrm{Low}} } \right) , \end{aligned}$$

(1)

where $x_{j,i}^{Low}, x_{j,i}^{Up}$ is the prescribed minimum and maximum bounds, D is the dimension of the problem, NP is the population size, and $\hbox {rand}(0,1)$ is a uniformly distributed random number between 0 and 1 and is instantiated independently for each component of the ith vector.

Fig. 2

Crossover operation process

2.2 Mutation with difference vectors

During DE-mutation of DE/rand/1, in order to produce the donor vector for each ith target vector from the current population, three other distinct parameter vectors, $x_{r1} (g),x_{r2} (g),x_{r3} (g)$ are sampled randomly from the current population. The indices $r_{1}, r_{2}$ and $r_{3}$ are distinct integers uniformly chosen from the set $\{1, 2\ldots \hbox {NP}\}\backslash \{i\}$. These indices are randomly generated once for each mutant vector. The difference in any two of these three vectors is scaled by a scalar number F and added to the third one. So, the donor vector $v_i (g)$ can be expressed as formula (2).

$$\begin{aligned} v_i (g)=x_{r1} (g)+F\cdot \left( {x_{r2} \left( g \right) -x_{r3} (g)} \right) . \end{aligned}$$

(2)

The following are other different mutation strategies frequently used in the literature:

• 1. DE/rand/2

  $$\begin{aligned} v_i \left( g \right)= & {} x_{r1} \left( g \right) +F\left( {x_{r2} \left( g \right) -x_{r3} \left( g \right) } \right) \nonumber \\&+F\left( {x_{r4} \left( g \right) -x_{r5} \left( g \right) } \right) \end{aligned}$$

  (3)

• 2. DE/current-to-best/1

  $$\begin{aligned} v_i \left( g \right)= & {} x_i \left( g \right) +F\left( {x_\mathrm{best} \left( g \right) -x_i \left( g \right) } \right) \nonumber \\&+F\left( {x_{r1} \left( g \right) -x_{r2} \left( g \right) } \right) \end{aligned}$$

  (4)

• 3. DE/best/1

  $$\begin{aligned} v_i \left( g \right) =x_\mathrm{best} \left( g \right) +F\left( {x_{r2} \left( g \right) -x_{r3} \left( g \right) } \right) \end{aligned}$$

  (5)

2.3 Correction operation

After mutation, some components of the trial vector may go to the predefined boundary constraints. There are many solutions to tackle this problem, such as penalty schemes, resetting schemes. Here, a simple but the most frequent correction strategy (Wang et al. 2011) is used.

$$\begin{aligned} v_i \left( g \right) \!=\!\left\{ {{\begin{array}{l} {\min \left\{ {x_{j,i}^{Up} ,\left. {2x_{j,i}^{Low} -v_i \left( g \right) } \right\} ,\hbox {if}\,v_i \left( g \right) <x_{j,i}^{Low} } \right. } \\ {\max \left\{ {x_{j,i}^{Low} ,\left. {2x_{j,i}^{Up} -v_i \left( g \right) } \right\} ,\hbox {if}\,v_i \left( g \right) >x_{j,i}^{Up} } \right. } \\ \end{array} }} \right. .\nonumber \\ \end{aligned}$$

(6)

2.4 Crossover

In order to enhance the potential diversity of the population, the crossover operation happens after generating the donor vector through mutation. Crossover operators from DE exchange donor vector $v_{j,i} (g)$’s components with the target vector $x_{j,i} (g)$, which is different from the other EA that exchanges several target vectors each other from parent generation. The scheme may be described as formula (7).

$$\begin{aligned} u_{j,i} \left( g \right) =\left\{ {{\begin{array}{ll} {v_{j,i} \left( g \right) ,}&{}\quad {\hbox {if}\;rand\left( {0,1} \right) \le \hbox {CR}\, \hbox {or}j=j_\mathrm{rand} } \\ {x_{j,i} \left( g \right) ,}&{}\quad \mathrm{otherwise} \\ \end{array} }} \right. ,\nonumber \\ \end{aligned}$$

(7)

where CR is the crossover rate, ${\hbox {CR}\in }[0, 1]$. A large CR speeds up convergence. $j_\mathrm{rand}$ is a randomly chosen integrand $j_\mathrm{rand} \in [1, D]$, which ensures $u_{j,i} (g)$ gets at least one component from $v_{j,i}(g)$.

The binomial crossover operator copies the jth parameter of the donor vector $v_{j,i} \left( g \right)$ to the corresponding element in the trial vector $u_{j,i} \left( g \right)$ if $\hbox {rand}\left( {0,1} \right) \le \hbox {CR}\,\,\hbox {or}j=j_\mathrm{rand}$. Otherwise, it is copied from the corresponding target vector $x_{j,i} (g)$. The possible trial vectors due to binomial crossover are illustrated in Fig. 2. It is clear that there are 6 genes on the chromosome and $j_\mathrm{rand} =3$.

2.5 Selection operation

After above operation, a selection operation is performed to determine whether the objective function value of each target vector $f\left( {x_i (g)} \right)$ or the corresponding trial vector $f\left( {u_i (g)} \right)$ survives to the next generation, i.e., at $g=g+1$. The selection operation is described as formula (8).

$$\begin{aligned} x_i \left( {g+1} \right) =\left\{ {{\begin{array}{ll} {u_i \left( g \right) ,}&{}\quad {\hbox {if}\;f\left( {u_i (g)} \right) \le f\left( {x_i (g)} \right) } \\ {x_i (g),}&{}\quad {\hbox {otherwise}} \\ \end{array} }} \right. . \end{aligned}$$

(8)

2.6 Pseudocode for the standard DE algorithm

The detailed pseudocode of this variant is presented as follows in Table 1.

Table 1 Pseudocode for the standard DE algorithm

3 The related research

DE, nevertheless, also has the shortcomings of all other intelligent techniques. The performance of DE deteriorates with the growth of the dimensionality of the search space. DE suffers from the problem of premature convergence, where the search process may be trapped in local optima in multimodal objective function and lose its diversity. It also suffers from the stagnation problem, where the search process may occasionally stop proceeding toward the global optimum even though the population has not converged to a local optimum or any other point. Sporadically, even new individuals may enter the population, but the algorithm does not progress by finding any better solutions. While the global exploration ability of DE is considered adequate, its local exploitation ability is regarded weak and its convergence velocity is too low. DE is sensitive to the choice of the control parameters, and it is difficult to adjust them for different problems.

For the above drawbacks, many researchers have done many attempts to significantly enhance the overall performance of the standard DE algorithm. Yang et al. (2013) proposed a method of population adaptation which is incorporated into the jDE algorithm (Brest et al. 2009). The proposed method measured the Euclidean distances between individuals of a population which can identify the moment when the population diversity is poor or the population stagnates. Once the moment is identified, the population will be regenerated to increase diversity or to remove the stagnation issue. An improved DE named HEDE was applied to solve waveform inversion problem in Gao et al. (2014). In HEDE, a new population evolution strategy (PES) to decrease the population size based on the differences among individuals during an evolution process is embedded into the cooperative coevolutionary DE (CCDE) and obtained a new highly efficient DE. A new control parameter called cognitive learning factor (CLF) is introduced in Sharma et al. (2015). In this algorithm, a weight factor (CLF) is associated with the individual’s experience in the mutation operation. In addition, the range of scale factor F is also dynamically varied in the prescribed range. By varying CLF and F, exploration and exploitation capabilities of DE may be balanced, thus improving the performance of DE. Qinqin Fan and Xuefeng Yana proposed self-adaptive DE algorithm with discrete mutation control parameters (DMPSADE) in Fan and Yan (2015). In DMPSADE, each variable of each individual has its own mutation control parameter, and each individual has its own crossover control parameter and mutation strategy. Poikolainen et al. (2015) proposed a procedure to perform an intelligent initialization for population-based algorithms. Iipo Poikolainen and Ferrante Neri introduced a component for preprocessing the initial solutions to generate an initial population for DE algorithms. The proposed component is not dependent on any assumption on the optimization problem (except it being continuous). YuChen and WeichengXie (Ali et al. 2013) proposed a binary learning differential evolution (BLDE) algorithm which can perform well on continuous optimization problems (COOPS). The algorithm can efficiently locate the global optimal solutions by learning the information of individuals, the best explored solution and the difference between individuals in the last population. Yi et al. (2015) proposed a new DE algorithm with a hybrid mutation operator to categorize the population into two parts to process different types of mutation operators and self-adapting control parameters which are used in jDE (Brest et al. 2009) and applied in the proposed HSDE (Liu et al. 2015b) to initialize the new population when a change is detected, and proposed a modified prediction model which uses the historical optimal sets obtained in the last two times. Guo et al. (2015) adopted a distributed topology to construct a trial vector generation pool and proposed the membership cloud model in the selection process. Multiobjective optimization algorithms have a wide range of applications, and the experts and scholars of various countries have given a wide range of attention (Giagkiozis et al. 2015; Yuan et al. 2014). At present, differential evolution algorithm has also been applied to many fields. The CPDE (differential evolutionary algorithm based on cloud population) proposed concepts of cloud group, and distribution chain concept increased the population diversity. In the algorithm, the intrusion operator will implant winners’ distribution to other individuals in the process of evolution, which improves individual diversity. The cooperation mechanism and differential operation are introduced by the cooperative operator. The results prove that CPDE is an effective high-dimensional evolutionary algorithm, which has a certain advantage in optimizing the network security situation prediction model (Hu and Qiao 2016). In addition to coefficient of variation scale and cross probability strategy to improve algorithm convergence speed and solution precision, various mutation strategies are employed to increase multiplicity of the population and avoid falling to local optimal. And the results in the three-tank system show that it is effective and available, with a good feature for application in industry (Liu et al. 2015c).

A new differential evolution algorithm, APDDE, has been presented to improve optimization performance by implementing a new mutation strategy and automatically updating control parameters, which demonstrates a significant performance improvement over the JADE (Zhang and Sanderson 2009), MDE (Ali et al. 2013), CODE (Wang et al. 2011), MDESELF (Li and Yin 2014) and EPSDE (Mallipeddi et al. 2011). In order to better understand these advancements, the main contribution of JADE (Zhang and Sanderson 2009), MDE (Ali et al. 2013), CODE (Wang et al. 2011), MDESELF (Li and Yin 2014) and EPSDE (Mallipeddi et al. 2011) should be briefly summarized.

3.1 Adaptive DE with optional external archive (JADE)

There are three different improvements in JADE variant of adaptive differential evolution (Zhang and Sanderson 2009) extending the standardized DE concept: current-to-pbest mutation, archive and a new adaptive control of parameters F and CR.

• 1. Current-to-pbest mutation

In JADE, the following manner will generate the mutant vector $u_{i}$

$$\begin{aligned} u_i =x_i +F(x_\mathrm{pbest} -x_i )+F(x_{r1} -x_{r2}) \end{aligned}$$

(9)

where $x_\mathrm{pbest}$ is randomly chosen as one of the top 100 p% individuals in the current population with $p \in (0,1]$, here the input parameter p is initialized to be 0.5 recommended in Zhang and Sanderson (2009). The vector $x_{r1}$ is randomly selected from $P (r1 \ne i), and x_{r2}$ is randomly selected from the union $P\cup A (r2 \ne i \ne r1)$ of the current population P and the archive A.

• 2. Archive

The archive provides information about the progress direction and is also capable of increasing the diversity of the population. In every generation, parent individuals replaced by better offspring individuals are put into the archive; the archive is initiated to be empty, and size is controlled within NP individuals by randomly dropping surplus individuals.

• 3. A new adaptive control of parameters F and CR

F and CR are the mutation factor and the crossover probability that are associated with $x_{i}$ and are independently regenerated at each generation by the adaptation process; CR is generated from the normal distribution of mean $u_\mathrm{CR}$ and standard deviation 0.1, truncated to [0, 1]. F is generated from a Cauchy distribution with location parameter $u_{F}$ and scale parameter 0.1 and then truncated to be 1 if $F \ge 1$ or regenerated if $F \le 0$.

3.2 Improving DE algorithm by synergizing different improvement mechanisms (MDE)

Ali et al. (2013) proposed a simple and modified DE framework, called MDE, which is a fusion of three modifications in DE: opposition-based learning (OBL), tournament method for mutation and single population structure.

1. Opposition-based learning (OBL) for generating initial population

OBL helps in giving a good initial start to DE; if ${X=(x_{1}, x_{2}, {\ldots }, x_{n})}$ is a point in n-dimensional space and $x_{i}\in [l_{i}, u_{i}]\; \forall \; {{}_{i}\in }\{1, 2, {\ldots }, n\}$, then the opposite point ${X'=(x_{1}', x_{2}'}, {\ldots }, x'_{n})$ is completely defined by its components

$$\begin{aligned} x_i^{\prime } =l_i +u_i -x_i \end{aligned}$$

(10)

Here $l_{i}$ and $u_{i}$ indicate the lower and upper bounds of the variables. Then, evaluate the fitness of both points f(X) and $f({{X'}})$. If $f ({{X}'}) \le f(X)$, then replace X with ${{X}'}$; otherwise, continue with X.

2. Tournament method for mutation

A modified mutation equation is reformulated and expressed as:

$$\begin{aligned} v_i \left( g \right) =x_{tb} \left( g \right) +F\cdot \left( {x_{r2} \left( g \right) -x_{r3} \left( g \right) } \right) . \end{aligned}$$

(11)

where $x_{tb}(g)$ is the point with the best fitness function value among the three distinct points $x_{r1}, x_{r2}$, and $x_{r3}$ which are selected randomly from the population corresponding to target point $x_{i}$. Here assume that $x_{tb} (g) = x_{r1}$.

3. Single population structure

In the single structure of DE, only one population is maintained and the individuals are updated as the newly found better solutions can take part in the mutation and crossover operation in the current generation itself as opposed to basic DE (where two populations are maintained and the better solutions take part in mutation and crossover operations in the next generation).

3.3 DE with composite trial vector generation strategies and control parameters (CODE)

CODE is a simple but efficient algorithm (Wang et al. 2011). Yong Wang only used two candidate pools: the strategy candidate pool and the parameter candidate pool. The strategy candidate pool contains three trial vector generation strategies (rand/1/bin, rand/2/bin, current-to-rand/1), and three control parameters ($[F=1.0,\hbox {CR}=0.1], [F=1.0,\hbox {CR}=0.9], [F=0.8,\hbox {CR}=0.2]$) constitute the parameter candidate pool. Then, at each generation, each target vector uses the three trial vector generation strategies; each combines with a control parameter setting randomly chosen from the parameter candidate pool, to generate three trial vectors, and the chosen best one enters the next generation if it is better than its target vector.

3.4 Modified DE with self-adaptive parameters method (MDESELF)

The modified algorithm in Li and Yin (2014) named MDE is the same as in Ali et al. (2013); so in order to be distinguished, we shall refer to it as MDESELF in the present study. Overall, there are also three modifications are proposed in Li and Yin (2014): modified mutation strategy, randomized scale factor and self-adaptive crossover rate.

1. Modified mutation strategy

The new mutation strategy is similar to the formula (9); the difference is that it does not use the external archive, and the random vectors are used instead of the current individual; in other words, the vectors $x_{r2}$ in (9) are no longer randomly selected from the union $P\cup A$, but only from P, the current individual $x_i$ becomes the random vectors. In addition, the new mutation strategy is combined with the basic mutation strategy ‘rand/2/bin’(3) through some probability rules. It can be expressed as follows:

$$\begin{aligned} \text {If rand }&\le \upomega \text { then }v_i \left( g \right) =x_{r1} \left( g \right) +F\left( {x_\mathrm{best}^P \left( g \right) -x_{r1} \left( g \right) } \right) \nonumber \\&\quad +F\left( {x_{r2} \left( g \right) -x_{r3} \left( g \right) } \right) \nonumber \\&\qquad \text {Else }v_i \left( g \right) =x_{r1} \left( g \right) +rand\left( {x_{r2} \left( g \right) -x_{r3} \left( g \right) } \right) \nonumber \\&\quad +F\left( {x_{r4} \left( g \right) -x_{r5} \left( g \right) } \right) \nonumber \\&\text {End if } \end{aligned}$$

(12)

Here the input parameter ${\omega }={ g/gmax}$ is the probability value and recommended in Li and Yin (2014), and gmax is the maximum generation number.

2. Randomized scale factor

The value of F is generated as two Gaussian distributions: $F1= \hbox {Gaussian}(0.3,0.3), F2=\hbox {Gaussian}(0.7,0.3)$. If $\hbox {rand}() \le \hbox {rand}()$, then $F=F1$; otherwise, $F=F2$.

3. Self-adaptive crossover rate

The author proposed a relative success ratio selecting one of two new parameters in the previous periods; according to it, the algorithm selects the evolution method for each individual. (Details of CR adaptation are shown in Li and Yin (2014)).

3.5 DE algorithm with ensemble of parameters and mutation strategies (EPSDE)

EPSDE (Mallipeddi et al. 2011) also have two candidate pools (a pool of mutation strategies and a pool of control parameters), which is similar to CODE, but the strategy candidate pool includes DE/best/2/bin, DE/rand/1/bin, DE/current-to-rand/1/bin and parameter candidate pool in which CR values range from 0.1–0.9 in steps of 0.1; the F values range from 0.4 to 0.9 in steps of 0.1, which are different from CODE. Each member (target vector) is randomly assigned a mutation strategy and united parameter values taken from the respective pools to generate offspring (trial vector). If $f(x_{i}(g))$ (function values of target vectors) $\le f(u_{i}(g))$ (function values of target vectors), then the combination of the mutation strategy and the parameter values is stored in the successful combinations pool; otherwise, reinitialize the mutation formula from the respective pools or from the successful combinations pool with equal probability. In Fig. 3, we will see the process which generates the successful combination pool.

Fig. 3

Process of generating the successful combination pool

4 The APDDE

This section proposes APDDE (a self-adaptive differential evolution algorithm).

The APDDE imitates the sniffing behavior of canine animals like, especially, dogs in the biological world. We know dogs have a unique way of sniffing around when they walk or hunt for food; inspired by this, we apply this behavior to differential evolution algorithm, so the whole algorithm optimization process has certain direction. In addition, we propose a new mutation strategy DE/local-to-best/1 and control F and CR in an adaptive manner for each individual to balance between the exploration and the exploitation. In general, three modifications are proposed in this paper and they are elucidated as follows.

4.1 DE/Current-to-lbest/1

The DE/Current-to-lbest/1 strategy is a variant of the DE/Current-to-pbest strategy. In the DE/Current-to-pbest strategy, in order to enrich the individuals of the population, the individuals are mutated under the guidance of one individual which is randomly chosen from the top 100p% individuals in the current population with $p\in (0,1]$. However, in DE/Current-to-lbest/1, the population is attracted by the multiple locally best individuals instead of one of the top 100p% best individuals.

In the proposed strategy, combining the idea of SFLA, we make improvements on aspects of the population reconstruction. The whole population is divided into a predefined number of groups simply based on the vector indices. Each group contains the same number of vectors, and the members of each group are kept unchanged during the algorithm’s iteration. The members of each equal-size groups, in fact, are assigned randomly from the population, since the vector indices are sorted randomly during initialization. The population is divided into several subgroups; in iterative process, each subgroup can obtain a local optimal value, and then, the local information obtained by subgroups is shared among the population in order to increase diversity as much as possible to make the population to avoid falling into local optimum and also, at the same time, to obtain the global optimal.

Fig. 4

Grouping and procedures of each subgroup. a Random initial. b Dividing the population into several subgroup. c Exploration in each subgroup

All individuals within the population are marked with random numbers, each group with 10 individuals, and each individual is assigned to different groups according to their random numbers. For example, the individuals with 1–10 numbers are assigned to the first group, 10–20 are assigned to the second group, and so on. The characteristics of each group are random, and no better or worse, because the groups are not divided by the sorting fitness value. The reason for this randomization is that it increases not only the diversity of the entire population, but also diversity of each packet. And the DE/Current-to-lbest/1 strategy can be expressed as follows:

$$\begin{aligned} u_i =x_i +F_i (x_\mathrm{lbest} -x_i)+F_i (x_{r1} -x_{r2}), \end{aligned}$$

(13)

where the subscript lbest denotes the best vector in the group with respect to target vector $i, x_{r1}$ is selected from the current population, while $x_{r2}$ is randomly chosen from the union, the current population and archive (initialed to be empty, the parent solutions that fail in the selection process are added to the archive, and the archive size are kept at NP). The vivid description of grouping and procedures of each subgroup is shown in Fig. 4. Among the serial numbers, 1, 2, 3 and 4 is the order of exploration of each group. In this paper, this new mutation strategy is integrated into the basic mutation strategy DE/rand/1/bin to form a strategy pool.

Fig. 5

Generating the CR_de and CR_ad when $p=0.1$

Fig. 6

Process of detecting in algorithm

4.2 Parameter adaptation

Storn and Price suggested that F should be 0.6 or 0.5 as a good initial choice and the value of F smaller than 0.4 or larger than 1.0 will lead to decrease in convergence speed (Storn and Price 1997), In contrast, Ronkkonen et al. (2005) said that $F=0.9$ would be a good initial choice and F should be chosen from the range [0.4, 0.95]. Storn and Price argued that the value of CR should be set to 0.1 or 0.9 and thought 1.0 can be tried to increase the convergence speed, while in Ronkkonen et al. (2005), the value of CR choice from the range (0.3, 0.9) will be best. CR should be between 0.0 and 0.2 for separable functions, while for multimodal and non-separable, the best choice is from the range (0.9, 1.0).

In general, in our APDDE algorithm, the parameter F will be chosen in the range [0.5, 1] in the steps of p (in this paper, the value of p is 0.1), and the pool of CR values taken in the range [0.4, 0.9] in steps of p is similar to EPSDE (Mallipeddi et al. 2011). In the algorithm, each vector in the population is extended with parameter F, CR(i.g. $x_{1,i}(g), x_{2,i}(g), {\ldots }. x_{D,i}(g), F_{i,g}, \mathrm{CR}_{i,g})$ and the value is randomly selected from the respective pool in the initialization. During evolution, the self-adaptive process of F and CR is as follows:

• 1. $F\_de = F_{i,g} - p$,

  $\begin{array}{l} F\_ad = F_{i,g} + p;\\ \hbox {If}\; F_{i,g} = 0.5\\ \;\mathrm{then}\; F\_de = 0.5.\\ \hbox {If}\; F_{i} =1\\ \;\mathrm{then}\; F\_ad = 1.\\ \end{array}$

• 2. $\mathrm{CR}\_de = \mathrm{CR}_{i,g} -p$,

  $\begin{array}{l} \mathrm{CR}\_ad = \mathrm{CR}_{i,g} + p;\\ \hbox {If}\; \mathrm{CR}_{i,g} = 0.1\\ \;\hbox {then}\; \mathrm{CR}\_de=0.1.\\ \hbox {If}\; \mathrm{CR}_{i,g} = 0.9\\ \;\hbox {then}\; \mathrm{CR}\_de=0.9.\\ \end{array}$

In Fig 5, the process of generating the CR_de and CR_ad is shown. The red indicator hand is the current parameter $\mathrm{CR}_{i,g}$.

In each iteration, the current parameters $F_{i,g}$ and $\hbox {CR}_{i,g}$ will generate, respectively, the corresponding detection values: F_de and F_ad, CR_de and CR_ad. The vivid description of the process is show in Figs. 6 and 7, respectively.

Fig. 7

Illustration of the DE/current-to-lbest/1 mutation strategy adopted in APDDE

The dashed curves display the contours of the optimization problem. $V_{i,1}$ and $V_{i,2}$ are the mutation vector generated for individual $X_{i}$ by the associated mutation factor F_de and F_ad.

4.3 Procedure of APDDE

According to 4.2, each individual in the initial population will generate four groups of control parameters: [F_de, CR_de], [F_de, CR_ad], [F_ad, CR_de] and [F_ad, CR_ad]. Each group is integrated into the mutation strategy in the strategy pool and generates eight groups:

• ${[}DE/Current-to-lbest/1, F\_de, CR\_de], [DE/Current-to-lbest/1, F\_de, CR\_ad]$.

• ${[}DE/Current-to-lbest/1, F\_ad, CR\_de], [DE/Current-to-lbest/1, F\_ad, CR\_ad]$.

• ${[}DE/rand/1, F\_de, CR\_de], [DE/rand/1, F\_de, CR\_ad]$.

• ${[}DE/rand/1, F\_ad, CR\_de], [DE/rand/1, F\_ad, CR\_ad]$.

Table 2 Pseudocode for the APDDE algorithm

The population individuals (target vectors) produce offspring (trial vectors) using these eight assigned combinations. If the best of these eight generated trial vectors produced is better than the target vector, the corresponding parameter values are retained with trial vector which becomes the parent (target vector) in the next generation. In APDDE, new mutation strategies DE/Current-to-lbest/1 and basic mutation strategy DE/rand/1/bin are applied, and mutation operator F, crossover CR, produce their different detection values F_de, F_ad, CR_de and CR_ad; 8 kinds of strategies pool are produced through Cartesian operation. According to above chart of the APDDE, the pseudocode of the APDDE is shown in Table 2. In the iterative process, each variation vector carries out crossover operation to form eight intermediate vector individuals, and the fitness value of each new produced intermediate vector individuals is obtained with a variable detection. Choose the best fitness of intermediate individual from eight variables. The more different mutation strategies with different intermediate vectors (within certain limits), the greater possibility of reaching the optimal direction. At the same time, different variations can also maintain the diversity of population.

5 Experimentation

In this section, the proposed APDDE is compared with the EPSDE, JADE, MDE, CODE, MDESELF.

Table 3 Dimensions, search ranges, and brief descriptions of test functions

5.1 Description of benchmark functions

Those 13 test instances were proposed in the CEC 2015 Competition on Learning-based Real-Parameter Single Objective Optimization, and 7 well-known basic benchmarks have been selected to verify the performance of the APDDE.

• 1. $f_{1}(x) ={\sum }_{i=1}^N x_i^2$ is continuous, convex and symmetric function.

• 2. $f_{2}(x) ={\sum }_{i=1}^N \left( {x_i^2 -10\, cos \left( {2\pi x_i } \right) +10} \right)$, Rastrigin function has several local minima. It is highly multimodal, but locations of the minima are regularly distributed.

• 3. $f_{3}(x) = -{\sum }_{i=1}^N\; sin (x_i )\left[ {sin \left( {ix_i^2 /\pi } \right) } \right] ^{2m}$, Michalewicz function has dimensional (here is 50) local minima. The parameter m defines the steepness of the valleys and ridges; a larger m leads to a more difficult search. The m is set to 10 in this paper.

• 4. $f_{4}(x) ={\sum }_{i=1}^N \left| {x_i } \right| +{\prod }_{i=1}^n \left| {x_i } \right|$, Schwefel’s problem 2.22 function is a unimodal problem whose global minimum is 0.

• 5. $f_{5}(x)=\left( {{\sum }_{i=1}^5 i\,cos \left( {\left( {i+1} \right) x_1 +i} \right) } \right) \left( {\sum }_{i=1}^5 i\,cos\right. \left. \left( {\left( {i+1} \right) x_2 +i} \right) \right)$, it is a low-dimensional multimodal function with a few local optima.

• 6. $f_{6}(x) =-20exp\left( {-0.2\sqrt{\frac{1}{n}{\sum }_{i=0}^N x_i^2 }} \right) -exp\left( \frac{1}{n}\right. \left. cos\left( {2\pi x_i } \right) \right) +20+e$, Ackley function has one narrow global optimum basin and many minor local optima.

• 7. $f_{7}(x) = {\sum }_{i=1}^N {\sum }_{j=1}^i x_j^2$ is continuous, convex and unimodal. It is an extension of the axis parallel hyper-ellipsoid function, also referred as the sum squares function.

• 8. $f_{8}(x) = {\sum }_{i=1}^N \left( {10^{6}} \right) ^{i-1/n-1}z_i^2 +100, z=M_1 \left( {x-o_1 } \right) , o_1 =[o_{11} ,o_{12} ,\ldots o_{1n} ]$: the shifted global optimum. Its property is non-separable, quadratic ill-conditioned.

• 9. $f_{9}(x) = z_1^2 +10^{6}{\sum }_{i=2}^N z_i^2 +200, z=M_2 \left( {x-o_2 } \right) , o_2 =[o_{21} ,o_{22} ,\ldots o_{2n} ]$: the shifted global optimum. Its property is non-separable, smooth but narrow ridge.

• 10. $f_{10}(x)=-20\exp \left( {-0.2\sqrt{\frac{1}{n}{\sum }_{i=0}^{N} z_{i}^2 }} \right) -\exp \left( {\frac{1}{n}\cos \left( {2{\uppi z}_{i} } \right) } \right) +20+e+300, z=M_3 \left( {x-o_3 } \right) , o_3 =[o_{31} ,o_{32} ,\ldots o_{3{n}}$]: Its property is shifted global optimum and non-separable.

• 11. $f_{11}(x) = {\sum }_{i=1}^{N} \left( {z_{i}^2 -10\cos \left( {2{\uppi z}_{i} } \right) +10} \right) +400, z=M_4 \left( {5.12\left( {x-o_4 } \right) /100} \right)$, $o_4 =[o_{41} ,o_{42} ,\ldots o_{4n}$]: the shifted global optimum. Its property is non-separable, and local optima’s number is huge.

• 12. $f_{12}(x) = 418.9829\times n-{\sum }_{i=1}^{N} g\left( {y_{i} } \right) +500, y_{i} =z_{i} +4.209687462275036e+002$,

  

  $z=M_5 \left( {1000\left( {x-o_5 } \right) /100} \right) , \quad o_3 =[o_{31} ,o_{32} ,\ldots o_{3n} ]:$ the shifted global optimum. Its property is non-separable, local optima’s number is huge, and second better local optimum is far from the global optimum.

• 13. $f_{13}(x)$ is hybrid function; three basic functions used to construct it are modified Schwefel’s function, Rastrigin’s function and high conditioned elliptic function.

• 14. $f_{14}(x)$ is hybrid function; 4 basic functions used to construct it are Griewank’s function, Weierstrass function, Rosenbrock’s function and Scaffer’s F6 function.

• 15. $f_{15}(x)$ is hybrid function; 5 basic functions used to construct it are Scaffer’s F6 function, HGBat function, Rosen rock’s function, modified Schwefel’s function and high conditioned elliptic function.

• 16. $f_{16}(x), f_{17}(x), f_{18}(x), f_{19}(x), f_{20}(x)$ is composition function and has different properties for different variables subcomponents; the details of constructing such functions are presented in Liang et al. (2015).

All the definitions of the benchmark functions are given according to the number in Table 3.

Table 4 Mean and std difference in test functions about seven algorithms

5.2 Experimental setting and parameterization

In order to ensure fairness, the initial conditions of each algorithm are consistent, such as initial velocity. The population size is set to 100. The size of the subgroup in APDDE is set to 10, and the size of archive in APDDE and JADE is set to 100. The 50-dimensional test function of 25 independent experiments demonstrate their general performances.

Experimental environment configuration: operation system is Windows 7; minimum memory is 4G; processor type is Intel-Core-i5; development tool and version is MATLAB-R2012a.

If it is not easy to distinguish the effect of different functions in figure, the value of ordinate should be set into the $\log (f(x)-Y)$, in which Y is a constant. We also can set $Y=f(x^{*})$; then, Y or $f(x^{*})$ represents the theoretical optimal value. Of course, if the result in the figure is easy to distinguish, the value of ordinate is function value or fitness.

5.3 Computational results and discussion

For each test function, Table 4 shows the comparison results of APDDE, EPSDE, JADE, MDE, CODE and MDESELF, in which mean indicates the average optimum function value of the 25 runs and std means the standard deviation of the optimum function value.

Figure 8 illustrates the detailed convergence curves of APDDE, EPSDE, JADE, MDE, CODE and MDESELF for the 20 benchmark functions, which were drawn by using the average value of the 25 runs.

From Fig. 8 and Table 4, we can observe that the convergence speed and accuracy of APDDE are much better than other differential evolution algorithms with the same dimension in solving great majority benchmark functions.

It has d! local optima for the dth-dimensional Michalewicz function. The parameter d actually measures the ‘steepness’ of the valleys or edges. For large d, the function behaves like a needle in the haystack; the function values for points outside the narrow peaks give very little information on the location of the global optimum. Table 4 shows that EPSDE, JADE, MDE, CODE and MDESELF have trouble with finding the needle. On the contrary, the hybrid scheme MFSLA-EO is very attractive in that it is able to reach the global optimum quickly with a higher success ratio. For Schwefel’s problem 2.22, APDDE’s accuracy and stability are the highest, but the convergence rate in early stage is lower than EPSDE’s. When iteration reaches to 400 times, APDDE, JADE and MDE began to converge fast. APDDE is the best, and JADE is the second best. At last, APDDE reached the best accuracy, and on the whole, APDDE outperforms others. Another multimodal function, Shubert function, in the initial stage of algorithm, APDDE ‘s convergence speed is the fastest, but in 100–600 times, six algorithms also fall into the local optimum, and from 600 times, APDDE algorithm is able to find the hidden optimal value, jump out of local optimum and continue to optimize. Of course, stability is far from CODE; this is because the CODE falls into the same local optimal value each time, but not jump out of it. For Schwefel’s problem, APDDE and MDESELF have the same best value in $f_9$. In $f_{10}$, APDDE is the best from the accuracy to the convergence rate; CODE is better in handling the multipeak function. While in $f_{13}$, APDDE’s performance is not good, EPSDE has the best performance, followed by MDE; before the iteration reaches 700 times, MDE is better than EPSDE, but in the later stage of the algorithm, EPSDE has outstanding performance. The experimental results of $f_{15}$ are similar to $f_6$, in which their mixed function is almost the same; MDESELF shows a good advantage, followed by MDE. And APDDE performance is poor, that is to say, APDDE is weak to deal with the relatively strong mixture test functions. For $f_{17}$, we can see that the exact value of MDESELF is relatively good, but before reaching 800 times, the convergence rate is weaker than MDE. But the stability of APDDE outperforms others. APDDE, EPSDE, CODE and MDESELF get the same best value on $f_{18}$. F20 contains 10 functions, which has a very high comprehensive performance. On the one hand, the algorithm on the test functions generally showed poor performance; this results can also reflect that various algorithms are trapped in the local optimum; on the other hand, it can also test the algorithm’s limit ability.

In multi -modal functions, APDDE provides equal or better results except $f_8, f_{13}, f_{15}, f_{17}$. In unimodal functions, the results indicate that APDDE is better than the other algorithms for 50 dimensions. These results indicate that in 50 dimensions, the overall performance of APDDE is better than other algorithms.

APDDE exhibits similar performance on $f_{18}(x)$ and $f_{20}(x)$ test functions. In other words, APDDE has stronger global search ability and faster convergence speed compared with EPSDE, JADE, MDE, CODE and MDESELF. But its performance is not perfect at $f_8(x), f_{13}(x), f_{15}(x), f_{17}(x)$. Clearly, MDESELF is the best among others algorithms on these functions; MDE is the second best. This may be because MDESELF uses complex self-adaptive crossover rate, while the adaptive method of APDDE mainly pursues saving time. MDE use OBL for generating initial population at each iteration, but APDDE generates initial population only once and does not change during evolution.

Fig. 8

Convergence curve of the 20 test functions in different algorithms

In order to show advantages of the APDDE, we do some T test and F test by using the data from the experiment and compare mean optimum values by T test matched-pairs mean analysis, F test matched-pairs standard difference analysis and Wilcoxon signed ranks test. Wilcoxon matched-pairs signed ranks test is a nonparametric test employed in hypothetical testing situation involving two samples (Kiranyaz et al. 2011), and it is a pair-wise test that can be used to detect significant differences between the behavior of APDDE and EPSDE, JADE, MDE, CODE and MDESELF with fixed study parameters. The data column of mean optimization value obtained by APDDE was noted as the first sample, while the results column obtained by EPSDE, JADE, MDE, CODE, MDESELF with fixed study parameter was noted as the second sample, respectively.

Let $\theta _D$ be the median of the difference in the underlying population represented by the two samples. Let $H_{0}$ be the null hypothesis, $H_{0}:\theta _D =0$; which means that there is no difference between the means of two samples. The alternative hypothesis is $H_{1}:\theta _D <0$, which is a directional hypothesis.

We use the SPSS11.0 (Statistic Package for Social Science) software, which calculates the T test and F test, as shown in Tables 5 and 6.

Table 5 T test: matched-pairs mean test of $f_{1}(x)$ function for APDDE and EPSDE

Table 6 F test: matched-pairs standard variance test of $f_{1}(x)$ function for APDDE and EPSDE

We reject the null hypothesis with a level of significance ${\upalpha }=0.05$ and conclude that APDDE does obtain better optimum values than EPSDE, JADE, MDE, CODE and MDESELF. The smallest level of significance that results in the rejection of the null hypothesis, p value $P(T_{t})$ singular tail, is 0.023789017364247. So is the same with SD of the optimum values.

Under Wilcoxon matched-pairs signed ranks test, the SD of optimum values of APDDE is significantly smaller than that of EPSDE with p value 0.023789017364247, too. If p value is less than 0.05, then the APDDE method has remarkable difference which is indicated by plus ‘+’ in column, otherwise minus ‘−’is used, as shown in Table 7.

As far as others (2–20 functions), T test matched-pairs standard deviation analysis (as shown in Table 8) and Wilcoxon matched-pairs signed ranks test (as shown in Table 9) is summarized, respectively.

Table 7 Wilcoxon matched-pairs signed ranks test of $f_{1}(x)$ function for variants

Table 8 T test and F test of Func.# 2–20 test functions

In Table 9, the percentage of the ‘+’ during all the results is the effectiveness of the APDDE in handling the test problems; for example, as to the test function nos. 2, 3, 6, 7, 8, 9, 13, 14, 17, 19, there are no values (numbers of minus ‘−’) greater than 0.05, and ten (numbers of plus ‘+’) are less than 0.05, which shows that the effectiveness of the APDDE method in handling those relative problems is equivalent to about 100 %. The result of T test, F test and Wilcoxon matched-pairs signed ranks test on APDDE is shown in Table 9. All the percentages are over (176+/190) 92.63 %, which means that the experimental data are reliable and universal; the APDDE really has good performance in reducing the computational complexity and calculating cost. It is clear from Fig. 8 that, for most test problems, convergence speed of APDDE is faster among the considered algorithm.

Table 9 Wilcoxon matched-pairs signed ranks test of 19 test functions

The results of APDDE have also been compared with the results of the standard PSO, SFLA and MSFLA presented in Li et al. (2012), the basic ABC, ABCMR, dABC algorithms in Kıran and Fındık (2015), ETLBO (elite teaching–learning-based optimization), CoBiDE (differential evolution based on covariance matrix learning and bimodal distribution parameter setting), GABC (Gbest-guided artificial bee colony algorithm), EDS (elite differential search algorithm) in Liu et al. (2015a).

Table 10 Comparison results of function optimization

Table 10 shows that the effect of APDDE is better than that of other algorithms; especially for F2 function, APDDE can achieve the best value by 100 % probability, and convergence of F1 function is far higher than that of other intelligent algorithms.

5.4 Convergence analysis of the APDDE

APDDE contains not only inner iterative operation, but also information exchange among subpopulations; in order to analyze the convergence, we first analyze one subgroup.

Definition 1

Assume X(t) is the tth iteration state of the population and $F^{{*}}$ is the global optimal fitness; if the formula (14) is established, then the APDDE is global convergence.

$$\begin{aligned} \mathop {\lim }\limits _{t\rightarrow \infty } P\left\{ {f\left( {P{X}\left( t \right) } \right) =F^{{*}}} \right\} =1 \end{aligned}$$

(14)

Definition 2

For $\forall x_{i} \in X, \forall x_{j} \in X$, in APDDE’s iteration process, individual state changes from $x_{i}$ to $x_{j}$ by one step which is denoted as $T_{x} \left( {x_{i} } \right) =x_{j\circ }$

Theorem 1

For population state sequence $\{X(t): t\ge 0\}, M$ is a closed set in population state space of X, which is optimal individual vector state set.

Assume $\forall x_{j} \notin M,\forall x_{i} \in M$, for any iteration times $l,l\ge 1$, according to Chapman–Kolmogorov:

$$\begin{aligned} P_{x_i ,x_j }^l= & {} {\sum }_{x_{r_1 } \in X} \ldots {\sum }_{x_{r_2 } \in X} P(T_x \left( {x_i } \right) =x_{r_1 } )\nonumber \\&\quad P\left( {T_x \left( {x_{r_1 } } \right) =x_{r_2 } } \right) \ldots P\left( {T_x \left( {x_{r_{l-1} } } \right) =x_{j} } \right) \end{aligned}$$

(15)

$P_{x_{i} ,x_{j} }^{l}$ is the probability of population state from $x_i$ to $x_{j}$ by l iteration. Since each expansion probability is 0 in formula (15), $P_{x_{i} ,x_{j}}^{l} = 0$. We can conclude that M is a closed set of X.

Theorem 2

Population state space X of the differential evolution does not have non-empty closed set G, so $M\cap G\ne \emptyset _{\circ }$

Theorem 3

Assume Markov chain has a non-empty closed set C and another non-empty closed set D, which makes $C\cap D\ne \emptyset$, does not exist. Then, when $j\in C:\mathop {\lim }\nolimits _{n\rightarrow \infty } P\left( {Y_{n} =j} \right) ={\uppi }_{j}$, and $j\notin C, \mathop {\lim }\nolimits _{n\rightarrow \infty } P\left( {Y_{n} =j} \right) =0$.

Theorem 4

when the iteration in subgroup tends to infinity, the population state sequence will enter the optimal state sequence set M.

The conclusion is proved by the above Theorems 1, 2 and 3.

6 Conclusion

In nature, there are many things worthy of human beings to learn from the social life of ants to the foraging behavior of bees. Many natural phenomena inspire people to think. This paper generates the corresponding detection values for individual per iteration; the whole APDDE algorithm optimization process can have certain direction. In addition, in order to enrich the diversity of the population, the whole population can be divided into a predefined number of groups. The individuals of each group are attracted by the best vector of their own group. After integrating the values of sniffer into two mutation strategy to produce offspring population, the experimental studies in this paper show that the proposed APDDE algorithm improves the existing performance of other algorithms compared to some same benchmark.