Two new meta-heuristics for no-wait flexible flow shop scheduling problem with capacitated machines, mixed make-to-order and make-to-stock policy

Abstract

This paper focuses on solving no-wait flexible flow shop scheduling problem with capacitated machines and mixed make-to-order and make-to-stock production management policy restrictions. The considered objective function is minimization of the sum of tardiness cost, weighted earliness cost, weighted rejection cost and weighted incomplete cost. Considering the literature, this problem is known as NP-hard. Hence, the cloudy-based simulated annealing (CSA) and artificial immune system are developed to solve the considered problem. Due to the fact that the parameters may influence the meta-heuristic algorithms, the parameters tuning is performed by Taguchi method. Finally, the performances of algorithms are evaluated by solving the randomly generated problems. Computational experiments show that the CSA algorithm obtains higher-quality solutions than another one.

1 Introduction

Scheduling is an integral part of advanced manufacturing systems (Davendra et al. 2013). In the most manufacturing systems, it is required that for completion of a job, a set of processes needs to be performed serially (Javadi et al. 2008). In scheduling, this system is called flow shop. Emergence of advanced manufacturing systems such as computer-aided design/computer-aided manufacturing (CAD/CAM), flexible manufacturing system (FMS) and computer-integrated manufacturing (CIM) has increased the importance of flow shop scheduling (Solimanpur et al. 2004).

The goal of flow shop scheduling problems is determination of a job sequence that optimizes one or more performance measures such as maximum completion time (makespan), total tardiness and work in process. In the flow shop environments, where the processing route is the same for all jobs, the problem is called permutation flow shop. On the other hand, where the jobs sequence may be different on each machine, the problem is known as non-permutation flow shop.

The general assumption in flow shop applications is that the sequencing of jobs relies on buffers, which are assigned in consecutive machines. However, in many scheduling environments, some or all jobs need to be proceeded continuously through all machines. This situation is commonly known as “no-wait” (Seido Nagano and Almeida da Silva 2012). A typical example of no-wait condition is steel-making production where the molten steel must be carried out between production stages continuously to reduce its energy loss. Since, in the no-wait flow shop environments, the jobs are not allowed to be idle between machines, the jobs sequence on the machines cannot be changed. So this problem is necessarily a permutation flow shop (Ruiz and Allahverdi 2007). These types of problems are reviewed in detail in Hall and Sriskandarajah (1996), Framinan and Nagano (2008) and Framinan et al. (2010).

From the viewpoint of production management policy, products can be produced according to make-to-stock (MTS), make-to-order (MTO) or mixed MTS/ MTO strategy in industrial environments. Under make-to-order policy, a production order is released to the manufacturing facility only after a firm demand has been received (Hadj Yousssef et al. 2004). Unlike, under make-to-stock policy, products are manufactured based on anticipation of future market demand and stored in warehouses.

In this study, a manufacturing system that can produce a number of specific products is considered. The jobs, which must be proceed in this system, can be divided into two categories: a set of MTS jobs and a number of MTO job sets (orders), which are released to system in a deterministic times and have certain due dates. Since the available time of each machine is limited, some of the MTO job sets may be rejected. Due to this situation, the goal is to find a sequence of jobs, which are either belong to accepted MTO sets or MTS jobs.

As an example, in a steel factory, production rate of each product is determined by studying on market behavior in past periods. In addition, some customers may release their orders to this factory. In this situation, to optimize the goals of system, decision makers determine which order should be accepted and which one will be rejected.

Due to the time restriction of machines and possibility of rejection one or more MTO job sets, in this study, objective function is included of three parts: costs of rejected orders, costs of earliness and tardiness of each order and the costs of incomplete orders. This objective function can adapt to the philosophy of just-in-time production, which emphasizes producing goods only when they are needed since jobs are scheduled to complete as close as possible to their due dates (Valente Jorge and Alves Rui 2005).

The no-wait flow shop is usually used to some of the important industries such as plastic industries, steel factories and chemical processes. On the other hand, the mixed MTO/MTS strategy can be used to every manufacturing environment which its goal is achieving to a balance between keeping market portion and on-time delivery to customer.

According to the literature, there is no research for combining mixed MTO/MTS policy and no-wait flow shop scheduling. To reduce the gap between scheduling theories and practical applications in industrial environments, two new meta-heuristic algorithms, cloud theory-based simulated annealing (CSA) and artificial immune system (AIS), are proposed for solving the considered problems.

Cloud theory is a model of the fuzzy theory, which relates to quality concepts and quantity data (Deyi et al. 1995). Cloud theory can help to generate a group of continuous temperatures close to a fixed temperature in simulated annealing. Generating random temperature based on cloud theory can preserve diversity and prevents algorithm from being trapped in a local optimum acceptability (Torabzadeh and Zandieh 2010).

Artificial immune system algorithm is a new population based on meta-heuristic approach, which is inspired of biological immune system (BIS). In comparison with other meta-heuristics, the AIS has the lower complexity, so it is simple to code.

The rest of the paper is organized as follows: In Sect. 2, a literature review of no-wait flow shop scheduling problem, MTO and MTS policies, cloud theory and artificial immune algorithm is presented. Section 3 describes the problem and presents mathematical model. In Sect. 4, the principles of meta-heuristic approaches are described. The computational results and evaluation of proposed algorithm performances are presented in Sect. 5. Finally, conclusions are provided in Sect. 6.

2 Literature review

A highly prominent class of job scheduling problems is identified by a no-wait production environment, in which there is no storage between the machines. Thus, jobs must be processed from start to finish, without any interruptions in the machines or between them (Jolai et al. 2013).

The no-wait flow shop scheduling problem with single objective was proved strongly NP-hard by Rock (Hadj Yousssef et al. 2004) when the number of machines is more than two. Therefore, the efforts have been devoted to finding high-quality solutions in reasonable time by using the heuristic and meta-heuristic approaches.

Some heuristic approaches were proposed to solve the no-wait flow shop scheduling problem. For instance, Reddi and Rama-moorthy (1972), King and Spachis (1980) proposed their methods. In addition, in the 1990s, Gangadharan and Rajendran (1993) and Rajendran (1994) proposed two heuristic methods GAN-RAJ and RAJ, which were shown by experiments that these methods outperformed the previous heuristic approaches reported in the literature. In recent years, Seido Nagano et al. (2015) proposed a constructive heuristic methods named QUARTS that breaks the problem to quartets in order to minimize the total flow time. Liu et al. (2013) proposed six heuristics approaches for no-wait flow shops with total tardiness criterion and proved that the modified NEH algorithm (MNEH) is the best.

Several meta-heuristic algorithms were proposed for solving this problem. Qian et al. (2009) proposed an effective hybrid differential evolution (HDE) for the no-wait flow shop scheduling problem with the makespan restriction. Tavakkoli-Moghaddam et al. (2008) presented the immune algorithm approach for solving multi-objective no-wait flow shop. Pan et al. (2009) applied a novel differential evolution algorithm for bi-criteria no-wait flow shop scheduling problem. Wang et al. (2010) proposed a new accelerated tabu search algorithm for no-wait flow shop problem with maximum lateness criterion. Tseng and Lin (2011) presented a hybrid genetic algorithm for no-wait flow shop with makespan as objective function. More recently, Seido Nagano and Almeida da Silva (2012) applied a new clustering search for this problem with total flowtime criterion. Ch et al. (2012) studied on no-wait flow shop manufacturing cell with sequence-dependent family setup times and presented a number of meta-heuristics for this problem. Davendra et al. (2013) also solved no-wait makespan flow shop by using discrete self-organizing migrating algorithm. Arabameri and Salmasi (2013) used several meta-heuristic approaches for solving $F_m \left| {nwt, S_{ijk} } \right| \sum W_j' E_j +W_j'' T_j$. As newest studies, Shabtay et al. (2014) defined a combined robot selection and scheduling problem (RSSP) for a set of Q nonidentical robots characterized by different costs and job transfer and empty movement times. Laha and Sapkal (2014) presented a constructive heuristic based on the assumption that the priority of a job in the initial sequence is given by the sum of its processing times on the bottleneck machines to minimize total flowtime criterion for no-wait flow shop scheduling problem.

It is more realistic to assume that at least one stage has more than one machine in flow shop environments. So in recent years, the flexible flow shop has attracted wide attention in both of academic and industrial societies. As an example of the no-wait flexible flow shop, Jolai et al. (2009) proposed a genetic algorithm for no-wait flexible flow shop with due window and job rejection. Jolai et al. (2013) also applied bi-objective simulated annealing approaches for no-wait two-stage flow shop problems. Wang and Liu (2013) studied on this problem and proposed the genetic algorithm for solving it. Ramezani et al. (2013) considered the no-wait flow shop with uniform parallel machines in each stage with sequence-dependent setup time constraint. In addition, Pang (2013) presented a genetic algorithm (GA)-based heuristic approach to solve the problem of two-machine no-wait flow shop scheduling problems that the setup times of machines are class dependent, and the objective is to minimize the maximum lateness. Liu and Feng (2014) studied on two-machine no-wait flow shop scheduling problems in which the processing times of jobs are functions of their positions in the sequence and solved it by using the classic KM (Kuhn–Munkres) algorithm.

According to the above MTO and MTS definitions, an important problem in MTS systems is the high inventory holding costs. On the other hand, an important drawback in MTO policies is the challenge of products on-time delivery, so in recent years the combination strategies attracted wide attention in both academic and industrial fields. For example, Adan and Wall (1998), Federgruen and Katalan (1999) and Soman et al. (2004).

Corresponding to the characteristics of producible products, the MTO and MTS strategy are implemented by different methods. As examples, Eivazy et al. (2009) used hybrid MTO/MTS policy for semiconductor manufacturing systems. Hadj Yousssef et al. (2004) studied on efficient scheduling rules in combined MTO/MTS strategy in manufacturing systems. Zaerpour et al. (2009) combined analytical hierarchy process (AHP) and technique for order performance by similarity to ideal solution (TOPSIS) methodologies.

Cloud theory is an expansion of membership function of fuzzy theory (Deyi and Yi 2005) so many scientists use its applications like intelligence control (Deyi et al. 1998; Feizhou et al. 1999), knowledge representation (Cheng et al. 2005; Deyi et al. 2000), data mining (Di et al. 1999; Kaichang et al. 1998; Shuliang et al. 2003; Yingjun and Zhongying 2004), spatial analysis (Cheng et al. 2006; Haijun and Yu 2007), target recognition (Fang et al. 2007), intelligent algorithm improvement (Yunfang et al. 2005) and so on (Torabzadeh and Zandieh 2010). As an example, Torabzadeh and Zandieh (2010) used cloudy simulated annealing approach for solving two-stage assembly flow shop and the could theory obtained good solutions, so in this study cloudy simulated annealing with various sizes of solutions is proposed to solve the considered problem.

The field of immunological computation (IC) or artificial immune system (AIS) has been evolving steadily (Nunes de castro and Von Zuben 1999) since 1985. In recent years, several researchers have developed computational models of the immune system that attempt to capture some of its most remarkable features such as its self-organizing capability (Coello Coello and Cruz Cort’es 2005).

Recently, the AIS algorithm has been applied with success for different variants of scheduling problems, for examples Lin and Ying (2013) proposed revised version of the AIS algorithm for flow shop with limited buffer scheduling problem. Zandieh et al. (2006) applied clonal selection principle to solve flow shop with sequence-dependent setup times.

3 Problem description and mathematical model

In this section, at first the problem statement is described. Then, assumptions and mathematical model are presented.

The flexible no-wait flow shop with mixed MTO/MTS production management policy and time limitation of machines is defined as follows:

Let n be the number of product types (J $=$ 1, 2... n) which each of them has a deterministic processing time in each stage $(p_{js} )$. This system must be produced a set of jobs, which is called MTS jobs ($i=1)$. In addition, a given number of order sets (i = 2, ..., N) are released to system as MTO sets. Both MTS and MTO sets are presented by $O_i =\left\{ {h_{1i} , \ldots , h_{ni} } \right\}$ where $h_{ni}$ is the request number of product type n in order set i.

Due to the time limitation of machines, some of the MTO sets may be rejected and even some of the accepted orders may be incomplete.

From the above definition if $N=5$ and $n=3$ and the accepted order sets are $\left\{ {O_1 , O_3 , O_4 } \right\}$, the jobs must follow though the systems are $\{\left( {h_{11} , h_{13} ,h_{14} } \right) ,\left( {h_{21} , h_{23} ,h_{24} } \right) , \left( {h_{31} , h_{33} ,h_{34} } \right) \}$ and $Z=\left( {h_{11} +h_{13} +h_{14} } \right) +( h_{21} + h_{23} +h_{24} )+\left( {h_{31} + h_{33} +h_{34} } \right)$.

All accepted jobs must be produced in flexible no-wait flow shop system, which has $m_s$ identical parallel machines at stages. Each machine is available at time zero to $ca_{sk}$ and after that gets unavailable (for example maintenance).

In no-wait flow shop, each job may be delayed to satisfy the no-wait condition. So, some of available time of machines will be idled and some of accepted jobs may be incomplete.

After determination of accepted orders, all of them and MTS jobs are sequenced ($q=1, \ldots , Z$, where Z is the total of jobs will be scheduled) to flow through the manufacturing system. To follow the no-wait restriction, all of consecutive operations of each job must be done continuously.

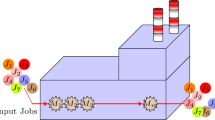
The schematic definition of the considered problem is depicted in Fig. 1.

Fig. 1

Presentation of a flexible no-wait flow shop problem with capacity restriction and mixed MTO/MTS policy

It is remarkable that the proposed nonlinear mathematical model in this study is a developed version of the presented mathematical model by Jolai et al. (2013).

Following assumptions are taken into account for the considered problem:

• All machines are available at time zero.

• In each stage, there is one machine at least, and one stage must have more than one machines at least.

• Each machine can process at most one job, and each job must be processed only by one machine at each stage.

• Machines of all stages are identical.

• A deterministic release date and due date are defined for each order. The release dates and due dates of make-to-stock jobs are equal to zero and a large number, respectively.

• If two consecutive jobs are from different types on a machine, the setup time must be considered.

• Travel times between stages are negligible.

The parameters, decision variables and the mathematical model are as follows:

Parameters:
k: Index of machines at stage s	$s = 1,\ldots ,S, k = 1,\ldots ,ms$
j: Index of product types that can be processed in manufacturing system	$j=1, \ldots ,n$
i: Index of order set	$i=1, \ldots , N$
t: Index of job in each order set	$t=1, \ldots , \hbox {sum}_i , i=1, \ldots , N$
($\hbox {sum}_i$: The summation of the number of jobs in each order set)
q: Index of location of each job in sequence	$q=1, \ldots , Z$
$R_i :$ Release date of order i	$i=2, \ldots , N$
(The MTS jobs are available at time zero)
$D_i :$ Due date of order i	$i =2, \ldots , N$
(The MTS jobs are delivered at the end of time horizon)
$Wt_i :$ The tardiness penalty of order i for each time unit of tardiness	$i=2, \ldots , N$
$We_i :$ The earliness penalty of order i for each time unit of earliness	$i=2, \ldots , N$
$Wr_i :$ The rejection cost of order i	$i=2, \ldots , N$
$Wg_i :$ The incompleteness cost of order i for each job of it	$i=1, \ldots , N$
$ca_{sk} :$ Time constraint of machine k on stage s	$s=1, \ldots , S, k=1, \ldots , m_s$
$p_{js} :$ Processing times of job type j on stage s	$j=1, \ldots , n, s=1, \ldots ,S$
$h_{ji} :$ The number of job type j in order i	$i=1, \ldots , N, j=1, \ldots , n$
$s_{j{j}'sk} :$ Setup time of job type ${j}'$ when ${j}'$ is processed immediately after job type j on stage s on machine k	$j,{j}'=1,\ldots ,n, j\ne {j}' s=1, \ldots ,S, k=1, \ldots ,m_s$
Decision variables:
$x_{tiq} :1$ if tth job from order i is located in position q of job sequence. 0 otherwise	$t=1, \ldots , \hbox {sum}_i , i=1, \ldots , N, q=1, \ldots , Z$
$y_{qsk} :1$ if the job where is located in position q is processed on machine k at stage s. 0 otherwise	$q=1, \ldots , Z,, s=1, \ldots ,S, k=1, \ldots ,m_s$
$v_{qj} :1$ if the job where is located in position q is type of j. 0 otherwise	$q=1, \ldots , Z, j=1, \ldots ,n$
$O_i :1$ if order i is accepted. 0 otherwise.	$i=1, \ldots , N$
$st_{qs} :$ Start time of the job where is located in position q at stage s	$q=1, \ldots , Z, s=1, \ldots ,S$
$c_{qs} :$ Completion time of the job where is located in position q at stage s	$q=1, \ldots , Z, s=1, \ldots ,S$
$de_q :$ Delay value of the job where is located in position q	$q=1, \ldots , Z$
$av_{qs} :$ Available time of the job where is located in position q at stage s	$q=1, \ldots , Z, s=1, \ldots ,S$
$at_{qsk} :$ Available time of the job where is located in position q at stage s on machine k	$q=1, \ldots , Z, s=1, \ldots ,S, k=1, \ldots , m_s$
$g_q :1$ if the job where is located in position q is completed. 0 otherwise	$q=1, \ldots , Z$
$\hbox {nond}_i :$ The number of incomplete jobs in order i	$i=1\ldots , N$

The nonlinear mathematical model:

$$\begin{aligned} \hbox {min} Z= & {} \left( {\mathop \sum \limits _{i=2}^N tardi_i \times O_i \times Wt_i } \right) \nonumber \\&+\left( {\mathop \sum \limits _{i=2}^N earli_i \times O_i \times We_i } \right) \nonumber \\&+\left( {\mathop \sum \limits _{i=2}^N Wr_i \times \left( {1-O_i } \right) } \right) \nonumber \\&+\left( {\mathop \sum \limits _{i=1}^N \left( {\hbox {sum}_i -\hbox {nond}_i } \right) \times O_i \times Wg_i } \right) \end{aligned}$$

(1)

Subject to:

$$\begin{aligned}&at_{qsk} y_{qsk} +\mathop \sum \limits _{j=1}^n v_{qj} p_{js} \le ca_{sk},\quad q=1, \ldots , Z, \nonumber \\&\quad s=1, \ldots , S, k=1, \ldots , m_s\end{aligned}$$

(2)

$$\begin{aligned}&O_1 \ge 1\end{aligned}$$

(3)

$$\begin{aligned}&\hbox {sum}_i =\mathop \sum \limits _{j=1}^n h_{ji},\quad i=1,\ldots , N\end{aligned}$$

(4)

$$\begin{aligned}&Z=\mathop \sum \limits _{i=1}^N \hbox {sum}_i O_i,\quad i=1,\ldots ,N\end{aligned}$$

(5)

$$\begin{aligned}&\mathop \sum \limits _{t=1}^{\hbox {sum}_i } x_{tiq} =1,\quad q=1,\ldots ,Z\, and\, i=1,\ldots ,N\end{aligned}$$

(6)

$$\begin{aligned}&\mathop \sum \limits _{q=1}^Z x_{tiq} =1,\quad t=1,\ldots ,\hbox {sum}_i \,and\, i=1,\ldots ,N\end{aligned}$$

(7)

$$\begin{aligned}&\mathop \sum \limits _{k=1}^{m_s } y_{qsk} \times at_{qsk} \le av_{qs} , \quad q=1,\ldots ,Z \,and\, s=1, \ldots ,S\end{aligned}$$

(8)

$$\begin{aligned}&\mathop \sum \limits _{k=1}^{m_s } y_{qsk} \le 1, \quad q=1,\ldots ,Z\, and\, s=1, \ldots ,S\end{aligned}$$

(9)

$$\begin{aligned}&de_q =\max \left( \mathop \sum \limits _{i=1}^N \mathop \sum \limits _{t=1}^{\hbox {sum}_i } r_i O_i x_{tiq},\right. \nonumber \\&\quad \quad \left. \left( {av_{qs} -av_{qs-1} } \right) ,\ldots , \left( {av_{q2} -av_{q1} } \right) \right) ,\nonumber \\&\quad q=1,\ldots ,Z\end{aligned}$$

(10)

$$\begin{aligned}&st_{q1} =\hbox {max}(de_q +av_{q1} ), \quad q=2,\ldots ,Z\end{aligned}$$

(11)

$$\begin{aligned}&st_{qs} =c_{qs-1},\quad s=2,\ldots , S \,and\, q=2,\ldots ,Z\end{aligned}$$

(12)

$$\begin{aligned}&c_{qs} =st_{qs} +\mathop \sum \limits _{j=1}^n v_{qj} p_{js} ,\quad s=1,\ldots ,S\end{aligned}$$

(13)

$$\begin{aligned}&a{t_{qks}} = ma{x_{1 \le q' \le q - 1}}\left( {{C_{q's}}{y_{q'sk}}} \right) , \quad s = 1, \ldots ,S,\nonumber \\&\quad q = 2, \ldots ,Z, k = 1, \ldots ,{m_s}\end{aligned}$$

(14)

$$\begin{aligned}&av_{qs} =min_{1\le k\le m_s } \left( {at_{qsk} } \right) , s=1,\ldots ,S\, and\nonumber \\&\quad q=2,\ldots ,Z\end{aligned}$$

(15)

$$\begin{aligned}&tardi_i =\max \left( {0,\left( {\mathop {\max }\limits _{1\le q\le z} \left( {\mathop \sum \limits _{t=1}^{\hbox {sum}_i } x_{tiq} c_{qs} } \right) -d_i } \right) } \right) ,\nonumber \\&\quad i=2,\ldots ,N\, and\, s=S\end{aligned}$$

(16)

$$\begin{aligned}&earli_i =\max \left( {0,\left( {d_i -\mathop {\max }\limits _{1\le q\le z} \left( {\mathop \sum \limits _{t=1}^{\hbox {sum}_i } x_{tiq} c_{qs} } \right) } \right) } \right) , \nonumber \\&\quad i=2,\ldots ,N \,and \,s=S\end{aligned}$$

(17)

$$\begin{aligned}&S-\mathop \sum \limits _{s=1}^S \mathop \sum \limits _{k=1}^{m_s } y_{qsk} \ge \left( {1-g_q } \right) ,\quad q=1, \ldots , Z\, and\nonumber \\&\quad s=1, \ldots , S\end{aligned}$$

(18)

$$\begin{aligned}&\hbox {nond}_i =\hbox {sum}_i -\mathop \sum \limits _{t=1}^{\hbox {sum}_i } \mathop \sum \limits _{q=1}^Z g_q x_{tiq}\qquad i=1, \ldots , N \end{aligned}$$

(19)

The objective function, as presented in Eq. (1), is minimization of the total weighted earliness, tardiness, missed orders and incomplete orders. Constraint (2) ensures that a machine cannot be assigned to a given job unless its time limitation is satisfied by that job. Constraint (3) ensures that the MTS jobs are processed. Constraint (4) calculates the number of jobs which are requested by each order set. Constraint (5) determines the summation of jobs which are requested by accepted order sets. Constraints (6) and (7) determine the job sequence. Constraint (8) ensures that each job is allocated to a machine which will be available sooner than the other ones at each stage. Constraint (9) completes the process of assigning machines to jobs and ensures each job at each stage is allocated to one machine at most. Constraint (10) calculates the minimum delay on the first machine before the job processes are started in order to satisfy the no-wait condition. Constraints (11) and (12) compute the start time of jobs at each stage. Constraint (13) calculates the completion times of jobs at each stage. For each job, constraint (14) computes the available time of each machine. In addition, available time of each stage for each job is determined by constraint set (15). Since the goal of this problem is on-time delivery of orders, constraints (16) and (17) compute the earliness and tardiness of each order set. Constraint (18) counts the number of completed jobs in each order set. For a job, if a machine is assigned at each stage, so the job is called completed job. Constraint (19) computes the incomplete jobs of each accepted order set. If the nound value for each order set is greater than zero, the order set is known as incomplete order set.

We use the following example to illustrate how the above model works. Suppose there are 3 types of products $(n=3)$, two stage $(m_1 =3, m_2 =2)$ and 4 order sets are released to system $(N=4)$. According to the previous agreement, the first-order set contains the MTS jobs and the other ones are MTO job sets. If we suppose that the third-order set is accepted $(O_3 =1)$ and the others are rejected, one possible sequence of accepted jobs is shown below (Q).

$$\begin{aligned}&r_3 =5\\&d_3 =50\\&Wt_i =We_i =Wr_i =Wg_i =5, i=1, \ldots , N\\&p=\left[ {{\begin{array}{l} {2 4} \\ {5 3} \\ {4 5} \\ \end{array} }} \right] \\&O_1 =\left\{ {1, 2, 1} \right\} \rightarrow \hbox {sum}_1 =4\rightarrow \left\{ {{\begin{array}{l} {number: \left\{ {1, 2, 3, 4} \right\} } \\ {type:\qquad \left\{ {1, 2, 2, 3} \right\} } \\ {order:\quad \, \left\{ {1, 1, 1, 1} \right\} } \\ \end{array} }} \right. \\&O_3 =\left\{ {1, 1, 1} \right\} \rightarrow \hbox {sum}_3 =3\rightarrow \left\{ {{\begin{array}{l} {number: \left\{ {1, 2, 3} \right\} } \\ {type:\qquad \left\{ {1, 2, 3} \right\} } \\ {order:\quad \, \left\{ {3, 3, 3} \right\} } \\ \end{array} }} \right. \\&Z=\hbox {sum}_1 +\hbox {sum}_2 =7\\&Q=\left\{ {{\begin{array}{l} {q:\quad \left\{ {1, 2, 3, 4, 5, 6, 7} \right\} } \\ {t:\quad \left\{ {1, 3, 3, 1, 4, 2, 2} \right\} } \\ {type:\quad \left\{ {1, 2, 3, 1, 3, 2, 2} \right\} } \\ {i:\quad \left\{ {3, 1, 3, 1, 1, 3, 1} \right\} } \\ \end{array} }} \right\} \rightarrow x_{131} =1, v_{11} =1 \end{aligned}$$

Based on sequence Q, the equations of the model are calculated in Table 1.

Table 1 A numerical example data

Based on the results of Table 1, it is clear that $earli_3 =25, tardi_3 =0$ and the objective function is 135. The Gantt chart of this example is shown in Fig. 2.

Fig. 2

The Gant chart of numerical example

4 Solution approaches

In this section, the solution approaches are proposed. As well known, the meta-heuristic algorithms have significant role in tackling all category of combinatorial problems. Scheduling problems are kind of optimization problems, which was solved by meta-heuristic algorithms in recent years (Li et al. 2012).

As far as we know, the considered problem in this paper is not solved before this, and this study presents two newest meta-heuristic algorithms for solving it.

The cloudy simulated annealing (CSA) represents the single-point methods and the artificial immune system (AIS) as a population-based algorithm is applied to solve the considered problem.

In this part of paper, each algorithm is briefly described and then is implemented for the considered problem.

4.1 Cloud theory-based simulated annealing algorithm

4.1.1 Simulated annealing algorithm in general

Simulated annealing algorithm (SA) is a random optimization method that is based on Monte Carlo iterative strategy (Laarhoven and Aarts 1987). SA is inspired of the physical annealing process, which minimizes potential energy in a solid object. This algorithm starts with a primary solution $(S_0 )$ and primary temperature $(T_0 )$, and this improving mechanism consists of the following steps: $T_0$ is decreased according to specific cooling schedule function, and a new solution $(S_1)$ is found in the neighborhood of the current solution $(S_0)$. If the value of objective function $(f\left( {S_1 } \right) )$ is less than the value of objective function $(f\left( {S_0 } \right) )$ in minimization problems, the new solution will be accepted, otherwise it will be accepted with probability $p=e^{\frac{-\Delta }{T}}$ (Boltzmann distribution function), where $\Delta =\frac{f\left( {S_1 } \right) -f\left( {S_0 } \right) }{f\left( {S_1 } \right) }$ and T is the current temperature. This process is continued until the termination criterion is met.

4.1.2 Basic concept of cloud theory

The cloud theory is a model that contains the transferring procedure of uncertainty between quality concept and quantity data representation by using natural language (Valente Jorge and Alves Rui 2005). Cloud theory is innovation and development of membership function of fuzzy theory (Di et al. 1999).

Let D be the language value of domain u and mapping $C_D \left( x \right) :u\rightarrow \left[ {0,1} \right] , \forall x\in u, x\rightarrow C_D \left( x \right)$, if the distribution of $C_D \left( x \right)$ is normal, it is named a normal cloud model (Deyi et al. 1995).

Cloud theory generates a group of random numbers which have a same distribution, usually normal distribution. These numbers are determined by expectation$E_x$, entropy $E_n$ and super entropy He. They reflect the quantitative characteristics of the generated cloud (Fig. 3).

A generator Y, condition cloud generator can generate a drop of cloud $(drop\left( {x_i ,u_0 } \right) )$ with three characters $E_x , E_n , He$ and a certain $u_0$ as follows (Deyi and Yi 2005):

• 1. Input: $\left\{ {E_x , E_n , He} \right\} , n, u_0$

• 2. Output: $\left\{ {\left( {x_1 ,u_0 } \right) , \left( {x_2 ,u_0 } \right) , \ldots , \left( {x_n ,u_0 } \right) } \right\}$

• 3. For $i=1$ to n

• 4. $E_n^{\prime } =randn\left( {E_n , He} \right)$

• 5. $x_i =Ex\pm E_n^{\prime } \sqrt{-2\hbox {ln}\left( {u_0 } \right) }$

• 6. drop$\left( {x_i ,u_0 } \right)$

• 7. End

Where $randn\left( {E_n , He} \right)$ will produce a random number with normal distribution which expectation is $E_n$ and standard deviation is He (Deyi et al. 1995) (Fig. 3).

Fig. 3

Three digital characteristics of a normal cloud (Adan and Wall 1998)

Fig. 4

The numerical example of how consider all of combinations of orders

4.1.3 Cloud theory-based simulated annealing algorithm

Based on the SA concept, since the algorithm accepts deteriorate solutions easily, it has not good convergence rate with high temperature; on the other hand, SA accepts good solutions hardly with low temperature, so it may drop to local minimum trap. Therefore, it is necessary to find other cooling mechanism that improves searching ability and obtains better solutions.

In the cloud theory-based simulated annealing algorithm, random numbers by same normal distribution which are generated by Y generator normal cloud are used for continuous annealing process. The cloud theory has the characteristics of randomness and stable tendency, so the annealing temperature changes randomly, and it can preserve the diversity of searching and therefore avoid being trapped in local minimum (Valente Jorge and Alves Rui 2005).

At first, the initial temperature $(T_0 )$ has to be unified. Then, all possibility combination of orders as accepted orders are determined $(2^{N-1})$. It is noticeable that the make-to-stock jobs are always considered as the accepted orders. Therefore, CSA algorithm is applied for all of combination of accepted orders by the following manner:

$T_0$ is decreased according to specific cooling schedule. For each temperature which is generated according to the cloud theory function, a random permutation of accepted orders is determined as an initial solution $(S_0)$. A new solution $(S_1)$ is generated by the mutation methods, and then, the new solution will be accepted if the objective function value of new solution is better than the objective value of the current solution, otherwise the new solution will be accepted with certain probability. These steps are repeated until the termination conditions are satisfied.

In order to explain how the all combination of orders is considered, the following example is provided.

According to the previous example (Table 1), by considering a 4-order $(N=4)$ and 3-producible job $(n=3)$ problem, all combination of orders are shown in Fig. 4.

As shown in Fig. 4, $O_1$ represent the MTS jobs and other sets are referred to the MTO order sets. Since the MTS order is always accepted, the number of all combination of orders as accepted orders is $2^{3}=8$.

According to Fig. 4, if only order 3 is accepted, order 3 and order 1 (MTS jobs) must be processed. So, the number of jobs is equal to $\left( {1+1+1} \right) +\left( {1+2+1} \right) =7$.

Solution representation

In order to represent the solution of the problem, a matrix with three rows is generated. The first row represents the number of each job in each accepted order. In the second row, the type of each job is determined and the third row includes the order numbers of jobs.

As an example of solution representation, the job sequence of previous example (Q in Table 1) is shown in Fig. 5.

Fig. 5

The numerical example of solution representation

Fig. 6

The pseudo-code of the proposed cloud theory-based simulated annealing algorithm

In both of CSA and AIS algorithms, the solutions are represented similarly.

Neighborhood solution generation

The purpose of generating neighborhood solutions is to find the better solutions from the neighborhood space of a solution. The neighborhood of $S_0$ is defined as the set of all solutions that can be generated by applying a specific operator to $S_0$. In this study, two common insertion and swap operators are designed for generating the neighborhood solutions.

Insertion operator will be selected and eliminated a job randomly, and then, the solution is reproduced by reinserting the eliminated job in a new randomly selected location.

For swap operator, at first, two jobs of the $S_0$ are randomly selected. Then, they are swapped in their positions.

The advantage of CSA algorithm is neighborhood search (local search) ability. In each iteration (temperature) of algorithm, a set of temperature is produced by the cloud model. These temperatures will create an inner loop that its task is local search.

Annealing process

In general SA, the annealing temperature is a fixed value at each step and the searching process is completed between neighbors (Framinan et al. 2010).

In proposed CSA algorithm, the temperature is updated by using an exponential function, which is shown in Eq. 20.

$$\begin{aligned} T=T_0 \lambda ^{k} \qquad k=1, 2, \ldots ,0< \lambda <1 \end{aligned}$$

(20)

where $\lambda$ is the annealing index and k is the step counter.

In addition by using Y generator and current temperature, a set of new temperatures which are distributed around the current temperature is generated. This set is called “cloud.”

Termination criterion

In this study, the proposed CSA algorithm is terminated if T is lower than the pre-specified final temperature $T_f$.

The pseudo-code of the proposed CSA algorithm is shown in Fig. 6.

It is necessary to notice that the value of iteration is depended on the number of jobs in the current sequence; in other words, where the size of sequence is increased, the number of temperatures which are generated by Y generator is increased too. The iteration for each combination of accepted orders is calculated by Eq. 21.

$$\begin{aligned} \textit{iteration}=\textit{size}\,\textit{of}\,\textit{considered}\,\textit{combination}\times 10 \end{aligned}$$

(21)

4.2 Artificial immune system

The biological immune system (BIS) is a robust and adaptive system that its duty is defending the body from foreign elements that called pathogens. BIS is able to recognize both body cells and non-body cells. The immune defense mechanisms include either nonspecific (innate) or specific (acquired) (Khoo and Situmdrang 2003).

The algorithms that are inspired of BIS are called artificial immune systems (AISs). AIS includes three branches: clonal selection, negative selection and immune network. The clonal selection principles explain how the BIS recognizes the pathogens and can generate the best antibodies for eliminating them. For applying clonal selection method of AIS algorithm for the considered problem, all possibility combination of orders as accepted orders are determined. Then, AIS algorithm is applied for all combination of accepted orders by the following steps:

• 1. Generate a fixed number (pop size) of antibodies as a primarily antibody population.

• 2. Calculate affinity function values (based on objective function) for each antibody.

• 3. Select the best fixed number $(n_c )$ of antibodies.

• 4. Clone each selected antibody according to its affinity value.

• 5. All antibodies in the clone population are mutated (based on their affinity values).

• 6. The worst $n_c$ antibodies in the current population are replaced by the best $n_c$ mutated antibodies.

These steps are repeated until the termination criterion is satisfied.

4.2.1 Initial population

The initial population consists of popsize randomly generated solutions. The antibody representation of AIS algorithm is similar to the solution representation (4.1.3.1) of CSA algorithm (Fig. 5).

4.2.2 Affinity calculation

Each antibody has an affinity value, which is referred to its objective function value. The affinity value for each antibody is calculated by the $\left( {- objective\, function} \right)$. From this value, it is clear that a solution with a higher affinity value is better than a solution with lower one.

4.2.3 Cloning phase

During the AIS algorithm, $n_c$ antibodies with highest affinity values are selected for cloning step. Based on the idea of Wang and Liu (2013), the clone number of each $n_c$ selected antibody is calculated by $(n_c -k+1)$, where k denotes the antibody with the kth highest affinity function value in the antibody population (Lin and Ying 2013). So the antibodies with higher affinity values have a higher number of clones.

4.2.4 Mutation phase

In proposed AIS algorithm, two mutation operators (swap and insertion) are considered. Based on the AIS algorithm concepts, for each antibody the replication number of mutation step (iteration) is increased where the k value of its antibody is increased.

4.2.5 Stopping criterion

In this study, the maximum number of generations (maxgen) is considered as the termination condition. Since in each combination of accepted orders the number of jobs is changed, the maxgen for each combination is calculated by Eq. 22.

$$\begin{aligned} \textit{maxgen}=\textit{size}\, \textit{of}\, \textit{considered}\, \textit{combination}\times 10 \end{aligned}$$

(22)

The pseudo-code of AIS algorithm is shown in Fig. 7.

Fig. 7

The pseudo-code of the proposed artificial immune system algorithm

Table 2 Problem parameters and their values

5 Computational experiments

In this section, to examine the effectiveness of the proposed algorithms, after tuning parameters, their performances are evaluated by solving the randomly generated test problems and the results of this evaluation are described.

In addition, apart from what algorithm is better, some tests are performed to show the effects of management decisions to the performance measurements.

5.1 Test instance generation

Due to the unavailability of the standard test problems for the considered problem, to evaluate the effectiveness of the proposed algorithms, test problems are generated randomly.

The data that are required to generate the random problems are: the number of orders, the number of producible jobs, the maximum number of jobs which can be ordered by each order family, the number of stages, the number of machines in each stage, processing time of each job at each stage, time limitation of machines, release date and due date of each order family and weights of earliness, tardiness, rejection and incompletion of each order family. Table 2 shows the generated problem. It is remarkable that in order to generate the parameter values, we used Ramezani et al. (2013) benchmark problems. These values are adopted for a flexible no-wait flow shop system such as a steel factory.

It is necessary to notice that the defined formula for generating due dates in Table 2 is an adopted version of the presented formula by Jolai et al. (2013) for the same goal.

Table 3 CSA algorithm factors and their levels

Table 4 The orthogonal array L9

To conduct the experiments, one problem which is randomly generated is selected and is run five times to reduce the error (Table 5).

Fig. 8

The mean S/N ratio plot for each level of CSA factors

5.2 Algorithm calibration

Parameters may influence on the algorithm performance. Considering the effect of parameters, in recent years the algorithm configuration is attracted wide attention. There are many ways to design experiments (Wang and Liu 2013), but the most frequency used approach is Taguchi method. In this study, the factors of CSA algorithm are $\gamma ,T_0 , T_f$, respectively, which their levels are given in Table 3. The considered orthogonal array with three factors and three levels of Taguchi method (L9) is presented in Table 4.

As shown in Fig. 8 and Table 5, the optimal levels of the factors are 1, 3 and 2, respectively.

Table 5 Average S / Nratio table

Table 6 Small-scale test problems

Table 7 Large-scale test problems

Table 8 The ARPD results of the small-scale problems

5.3 The results

In this section, two evaluations are presented. At first, to examine the effectiveness of the proposed solution approaches (AIS and CSA), 32 benchmark problems are run by each algorithm. Then, to analysis the influences of each parameter, one of the test problems is selected and the sensitive of percentage of MTS/MTO and order $family\left( N \right) /SUM$ (number of orders/number of jobs in each order) on performance measurements are evaluated.

Table 9 The ARPD results of the large-scale problems

It is remarkable that in this study the algorithms are coded in MATLAB 2012 and the mathematical model is coded by Lingo 9. All of them are run on a PC with an Intel Core 4 Duo 2.5GHz CPU with 4GB of RAM under a Windows 8 environment. Based on suggested approach by Ramezani et al. (2013), algorithms are run under their termination condition and their average of computational time is saved. Since the average computational time of AIS is bigger than the average computational time of CSA, to compare the performances, AIS algorithm is run for each test problem 5 times and then the CSA algorithm is run at the average of these times. The relative percentage deviation (RPD) is used as the performance measurement. For each test problem, these algorithms are run 5 times for each instance. The best solution is denoted by $Best_{sol}$. So RPD is calculated by following formula:

$$\begin{aligned} \hbox {RPD}=\frac{Alg_{sol} -Best_{sol} }{Best_{sol} }\times 100 \end{aligned}$$

(23)

Where $Alg_{sol}$ is the objective function value obtained for a given algorithm and test problem. The average relative percentage error is defined according to Eq. 24.

$$\begin{aligned} \hbox {ARPD}=\frac{\mathop \sum \nolimits _{i=1}^{Number\, of\, runs} \hbox {RPD}_i }{Number\, of\, runs} \end{aligned}$$

(24)

The effectiveness of the algorithms is evaluated by solving 32 different problems. These problems are given in Tables 6 and 7. In addition, the solutions obtained for these problems by the proposed algorithms are summarized in Tables 8 and 9 and Figs. 9 and 10.

Table 8 and Fig. 9 show that for small-scale problems, CSA algorithm has been yielded the better results $(\frac{15}{16}\times 100=93.75\,\% )$ than another algorithm.

Fig. 9

The comparison between the ARPD of CSA and AIS algorithms in small-scale problems

Fig. 10

The comparison between the ARPD of CSA and AIS algorithms in large-scale problems

Table 9 and Fig. 10 illustrate the results of experiments for the large-scale problems. As can be seen, CSA algorithm has been yielded the better results in $\frac{11}{16}\times 100=68.75\,\%$ of the problems. Also, AIS algorithm is obtained the better solutions in $\frac{5}{16}\times 100=31.25\,\%$ of the problems.

It is clear from Tables 8 and 9 the performance of CSA algorithm for small-scale problems is better than its performance for large-scale problems. Unlikely, by increasing the size of the problems, the performance of AIS algorithm will be improved.

Fig. 11

The interaction between stage and performance of algorithms

Fig. 12

The interaction between maximum number of jobs and performance of algorithms

Tables 8 and 9 show that for $93.75\,\%$ of small-scale problems the obtained $Best_{sol}$ is equal to the $Best_{CSA}$. For $81.25\,\%$ of the large-scale problems, the $Best_{sol}$ of algorithms is equal to the $Best_{AIS}$. It means that for small-scale problems CSA performs better than AIS and for large-scale problems AIS performs better than CSA. In addition, Figs. 11 and 12 show that the proposed meta-heuristic algorithms are sensitive to the number of stages and the maximum number of jobs. Moreover, Fig. 13 demonstrates the convergence speed of algorithms in the same iteration. As shown in Fig. 13, AIS has higher convergence speed and is obtained the better solutions than the CSA algorithm in the same iteration number.

One of the important factors that affect decisions is the ratio of MTS/MTO. Generally, in order-based industries, the demand of orders from MTS policy is considered less than MTO policy. Here, for analyzing the impact of MTS/MTO ration, a test problem is selected and the results are shown in Figs. 14 and 15.

According to Fig. 14, by increasing the ratio of MTS/MTO, because of limitation of machines capacity some of MTO jobs will be accepted and most of them should be rejected, and the value of objective function will be dropped.

Another factor that could be effect on performance measurements is the percentage of order family(N)/SUM. It will be asked that accepting more orders with less jobs is appropriate or accepting less orders with more jobs. This is one of the most important problems to achieve the balance between keeping market portion and on-time delivery of orders. Figure 16 illustrates the selection of the second approach.

Fig. 13

The convergence speed of algorithms for problem 1 of large-scale problems

Fig. 14

The influence of MTS/MTO ratio on the objective function

Fig. 15

The influence of MTS/MTO ration on the number of accepted order

Fig. 16

The influence of order family(N)/SUM ratio on the objective function

Figure 16 shows clearly that in the same number of orders when the number of jobs is increased, the objective function will be increased. On the other hand, in the same number of jobs, increasing the number of orders can be improved the objective function value. These results are predictable. Because, as mentioned above, the available time of machines is constant. So, when the number of orders is increased while the number of ordered jobs becomes constant or less, the number of accepted orders becomes increased and the objective function gets better. Unlikely, increasing the number of jobs when the number of orders becomes constant, the number of accepted orders becomes less, and in result, the objective function value gets worse.

Due to the above results, for every manufacturing system accepting more orders with less number of jobs may be better than accepting fewer orders with more number of jobs. It is obviously because increasing the accepted orders not only has more financial profit but also improves the company’s image. It is remarkable note that this approach can be useful in the specified situation which the rejection costs of all orders are nearly equal to it.

It is important note that in Figs. 14, 15 and 16 the AVERAGE curve illustrates the average of obtained results by both algorithms.

6 Conclusion

This paper considered the no-wait hybrid flow shop with time limitation of machines and mixed MTO/MTS production management strategy. Due to the wide application of different variants of no-wait flow shop system in the various industries such as steel factories, plastic industries and chemical processes, studying on this system is very important. This study can be useful and valid for all above-considered industries. A new mathematical model is proposed, and as the solution approaches, two new meta-heuristics are proposed for this problem: the artificial immune system (AIS) as a population-based method and the cloudy-based simulated annealing (CSA) as a single-point approaches.

The results of experiments revealed that, however, CSA is obtained the better results but AIS has higher convergence speed.

In this study, all jobs are divided into MTO or MTS groups. The results show that increasing the MTO jobs decreases the MTS jobs production rate and this matter may reduce the market portion of company. In addition, increasing the production rate of MTS jobs causes the more orders are rejected, and in result their financial profits are lost and the worth of brand becomes less. So, to achieve balance between keeping market portion and increasing the financial and spiritual worth of company accepting the orders which have less jobs may be good approach.

This study can be useful for every industries which use flexible no-wait flow shop production line and produce MTO and MTS jobs separately or in a same time.

Several ideas deserve further investigation. First, the combined MTO/MTS policy is rarely studied, but it has great potential to develop this idea in other manufacturing systems. Second, in this study the MTO and MTS products have the same characteristics. But, in many modern industries the custom products may have different characteristics.