A novel evolutionary technique based on electrolocation principle of elephant nose fish and shark: fish electrolocation optimization

Abstract

Elephant nose fish searches its food such as larvae by active electrolocation. It discharges electric pulse through its electric organ in tail and detects the object by analyzing the geometrical property of projected electrical image on it. The capacitance value found out from that electric image helps the fish to reach near the food source. Shark also uses passive electrolocation for the same purpose. It can target its prey by sensing the electrical wave generated due to the muscle twitching of small living beings in water. Both the above physiological phenomena, concerning the active and passive electrolocation of fish, has been mathematically developed as nature-inspired meta-heuristic technique named fish electrolocation optimization (FEO). A comparative study based on benchmark functions has been done amongst real coded genetic algorithm, accelerated particle swarm optimization, particle swarm optimization, harmony search and the proposed algorithm. Furthermore, comparative study has been done with simulated annealing and differential evolution on eggcrate function. The proposed technique has also been implemented on real-world optimization problem related to cost-based reliability enhancement in radial distribution system. It can be said by comparing percentage of success, mean number of function evaluation and standard deviation that FEO algorithm works better than other mentioned meta-heuristic techniques.

1 Introduction

Many natural procedures were mimicked as soft computing-based optimization tool. In the early 1970s Holland (1975) adopted the idea of Charles Darwin’s theory of natural selection to formulate genetic algorithm. Later Goldberg (1989) studied that elaborately for making it fit for optimization and machine learning. Kirkpatrick et al. (1983) developed simulated annealing considering the metal’s annealing process. That process behind the algorithm includes the metal’s cooling and freezing phenomena into crystalline state with larger crystal size and minimum energy. Moscato (1989) had established mimetic algorithm derived from genetic algorithm and martial art. Deb (1991) applied genetic algorithm for engineering optimization problem. He also developed an efficient constraint handling method for genetic algorithm (Deb 2000). Reynolds (1994) proposed cultural algorithm considering belief space and population space as the two main ingredients. Kennedy and Eberhat (1995) established particle swarm optimization (PSO) on the basis of swarm behavior of birds. Later that algorithm had been improved. That improved PSO was applied for optimal power flow (Vo and Schegner 2013). Storn (1996) proposed differential evolution (DE) as a useful tool for function optimization. Later Storn and Price (1997) applied that technique for global optimization over continuous spaces. Foraging behavior of ants especially built on chemical messenger pheromone was studied (Dorigo 1992). Dorigo and Caro (1999) presented that meta-heuristic technique as ant colony optimization.

On the other hand, meta-heuristic techniques had been generated from swarm intelligence and bee colony behavior. Honey bee mating optimization was developed by Afshar et al. (2007) for doing optimal reservoir operation. Artificial bee colony algorithm was proposed by Karaboga and Basturk (2007). Bee colony optimization was also developed in this regard (Teodorovic’ and DelĺOrco 2005). Nakrani and Tovey (2004) proposed honey bee algorithm. Later Yang (2005) proposed virtual bee algorithm for implementation in engineering optimization. Pham et al. (2005) studied the concept of honey bee’s behavior and developed bee algorithm. Later bee algorithm was also studied and applied to find optimal solution (Yuce et al. 2015). Geem et al. (2001) proposed harmony search algorithm inspired by harmony of music. Later that technique was applied for continuous engineering optimization problem (Lee and Geem 2005). Biogeography-based optimization technique was developed by Simon (2006). Firefly algorithm was formulated on the basis of flashing characteristics of fireflies (Yang 2009). Bat’s echolocation (Muhaureq et al. 2010; Yang 2010a, b) had also been considered to develop meta-heuristic technique conceptualizing prey catching phenomena of it. Later firefly algorithm and bat algorithm had been implemented for optimal placement and sizing of static VAR compensator for enhancement of voltage stability (Rao and Kumar 2015). On the other hand, cuckoo’s breeding procedure had also got the attention of researcher to build a meta-heuristic technique (Yang and Deb 2009). Foraging behavior of few animals was also mathematically studied as optimization method. Passino (2002) developed bacterial foraging algorithm conceptualizing survival mechanism of Escherecia coli in changing environment. Monkey search algorithm was formulated imitating the behavior of monkey climbing trees in its search for food (Seref and Akcali 2002). Bioluminescence (Krishnanand and Ghose 2005; Olivera et al. 2011) had also been selected for developing higher level searching tool. Not only the animal’s behavior was imitated, but also the plant’s growth (Tong et al. 2004) and its photosynthesis process (Yang 2010a, b) was also considered for this kind of technique development. Cai et al. (2008) developed plant growth optimization on the basis of leaf growth, branching, phototropism and spatial occupancy. Most of the above algorithms were modified and also hybridized to have better soft computing tool (Hedar and Fukushima 2006; Das et al. 2008; Haldar and Chakraborty 2011a, b).

However, prey searching technique had also become an encouraging research context for developing meta-heuristic technique. Group hunting of animals such as lions, wolves, and dolphins was studied as a soft computing technique named hunting search algorithm (Oftadeh et al. 2010). On the other hand, collective animal (Cuevas et al. 2012) and animal searching behavior (He et al. 2009) were also chosen to formulate optimization algorithm. Fish’s electrolocation is an interesting prey searching procedure. This is identified in this research work for developing an optimization method.

Elephant nose fish Gnathonemus petersii has electric discharge organ (Baffet et al. 2008; Emde 1998, 1999, 2004a, b). Generated electric wave from that organ strikes surrounding objects inside water. The difference in sensing, the electrical field with and without objects, creates an electrical image on the surface of that fish’s body. It then analyzes that image minutely. Depending on image parameters it calculates electrical capacitance value of that object. The capacitance value of food particles is already known to fish. If it feels that the targeted object is within the range of known capacitance then proceeds towards it calculating the distance from the targeted object. Otherwise it generates electric wave of new amplitude. On finding the desired object, it stops its electric organ discharge.

On the other hand, like active electrolocation, passive electrolocation is used by shark fish Scyliorhinus canicula for food catching purpose (Kalmijn 1971; Passive electrolocation in fish). Shark does not generate electric wave like elephant nose fish. It can sense feeble electric pulse generated from the muscle contraction of other living beings in the water. If the shark finds out that kind of electric pulse, then it quickly targets the direction from which the electrical wave is coming. This food searching technique of the above said electric fishes can be useful as an optimization technique.

However, active electrolocation of elephant nose fish was studied on robotic sensor technology (Startchev et al. 2011). Algorithm inspired from the electrolocation behavior of electric fish has been implemented in autonomous robot. Artificial sensor array was developed by mimicking that biological process (Maciver and Nelson 2001). That could provide electro-sensory capabilities to a submarine robotic explorer. Robotic sensing system was designed to locate objects underwater (Solberg et al. 2008, 2013). This was done through active movement of an electric field emitter and sensor apparatus. Echolocation and electrolocation were both biologically studied as sensory acquisition in active sensing system (Nelson and Maciver 2006). Recently Ammari et al. (2013) proposed a complex conductivity model problem for the quantitative analysis of that electrolocation phenomenon. However, concept of electrlocation as an optimization method has been hardly found in the literature. Passive electrolocation of shark has also not been conceptualized as searching tool hitherto. Here a soft computing-based meta-heuristic method called fish electrolocation optimization (FEO) is developed by mixing both active and passive electrolocation procedure of two fish, viz. elephant nose fish and shark, respectively. This has been implemented on some test bed functions. However, the proposed algorithm’s theoretical background has been briefly described in the next section.

2 Theoretical background of fish electrolocation optimization (FEO)

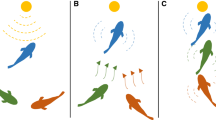
Fish electrolocation optimization has been thought on the context of electro-sensory perception of electric fish. Nocturnal animals generally rely on other senses instead of vision for object localization and prey catching. Weakly electric fish strongly depends on its electro-sensory organs which are more or less situated throughout its whole body (Emde and Schwarz 2002). Electrolocation is an adopted navigational approach for finding food item. Elephant nose fish G. petersii adopts this navigational procedure in dark and fulfills basic need. Its electric organ discharges in water. It generates electrical wave of a certain voltage amplitude and waveform from its tail electric organ. This is shown in Fig. 1.

Fig. 1

Active electrolocation of elephant nose fish (G. petersii) (electric fish identifies the food objects or prey by judging the electric image projected on their body surface. The big circular lines in the water signify the electric field developed due the tail organ discharge. The black circular spot on the fish’s body is denoted as the projected electric image)

Figure 1 depicts electric field lines as circular lines fencing the electric fish. After the electrical discharge in water, electric image is projected on the skin of that fish. The black circular spots shown in Fig. 1, on the fish’s body, are denoted as the projected electric image of food and other non-food particles inside water. The electric image is formed on the basis of change in electrical voltage amplitude and waveform distortion with and without the object in the surrounding water. The fish searches its food depending on that image slope, image width; distance from the object, resistance and capacitance value (active electrolocation). Food objects, which are water plant or larvae, have specific impedance in respect of electrical characteristics. Additionally, food objects have a certain range of electrical capacitance value. The fish’s electro-sensory organs are sensitive within that certain interval of electrical capacitance value. Beyond that limit whether it is in the lower or upper boundary area concerning electrical capacitance value, the fish is insensitive. That means it cannot sense any more. Depending on this judged electrical capacitance value and distance from the targeted object, it approaches towards the prey. Interestingly, the resistance value depends on the voltage or electrical wave amplitude, but capacitance value depends on the wave form distortion. On the other hand, image slope is considered as transition from rim to center area of image and its necessary to obtain the distance from the prey. The ratio of image slope and voltage peak amplitude has been considered as distance from the targeted object. Depending on both targeted object distance from fish’s body and quantity and quality of that object, the fish develops electric pulse and proceeds towards it. Finally, it fetches the food object without using any vision but using active electrolocation intelligently (Hopkins 2005).

Unlike elephant nose fish, shark utilizes its sense of passive electrolocation for detecting small fishes inside water (Shieh et al. 1996; Electric fish)). A glimpse of passive electrolocation by shark is shown in Fig. 2. Dotted circular lines surrounding small fishes in Fig. 2 show the low-voltage signals. The shark has such strong electro-sensory organ that it can sense muscular twitch of a fish dug in sand. It also uses passive electrolocation for navigation purpose analyzing ocean currents and earth’s magnetic field.

Fig. 2

Passive electrolocation of shark (S. canicula) (shark can judge meagre electric pulse coming out due to the muscular organism of small fishes. The dotted circular lines fencing the small fishes define that weak electric wave. Shark in the picture fetches its prey by sensing those electric signals)

In this work, a conceptual electro-fish has been considered to develop FEO. The fish has both the sense of active and passive electrolocation like the previously discussed elephant nose fish and shark, respectively. Not only it can create electrical wave and judge the electric image on the basis of electrical characteristics, but also can sense meagre electric pulse from other fishes. How it detects and localizes an object that has been mathematically developed as an algorithm in the next section.

3 Mathematical development of FEO as optimization tool

Fish electrolocation optimization has been mathematically developed through logical expression related to the conceptual electro-fish. The fish searches its food item by sensing feeble electric wave and also analyzing projected electric image. It simultaneously emanates electric pulse and senses feeble electrical wave. Feeble electrical wave is sensed in narrow range, whereas projected electric image gives the vision of surrounding environment. Sometimes it acts like elephant nose fish and sometimes it acts like shark. It toggles between active and passive electrolocation. This role reversal is linked with the capacitance and distance value owing to toggle switch judgment. Resistance value, discussed in the previous section as a judgmental issue of elephant nose fish, has not been taken into consideration. This is done to restrict the list of parameters of this developed technique. However, FEO algorithm works through range discrimination/development, electric pulse calculation from slope analysis, distance calculation from the prey object; capacitance detection from waveform distortion value, toggle switch judgment through capacitance evaluation and finally electric organ discharge with tuned voltage amplitude. How these have been mathematically developed is described below sequentially.

3.1 Range development/discrimination

The developed electro-fish uses electrolocation dividing their search domain in a few zones. These zones have certain solution values with a definite difference between two consecutive values inside two limiting margins. Three kinds of range have been formulated based on difference between variable’s maximum and minimum value, i.e., diff and different multiplication factors. The diff value is shown in (1). The longrange is defined as the constant long search domain in (2). Constant terms $p1_l$ $p2_l$ and $p3_l$ are multiplied with the diff value for defining the lower margin, gap value and higher margin, respectively. The domain consists of solution points between higher range, i.e., ${diff}\times p1_l$ and lower range, i.e., ${diff}\times p3_l$ with interval of ${diff}\times p2_l$ between any two consecutive values. Similarly, shortrange is also restricted between ${diff}\times p1_s$ and ${diff}\times p3_s$ with a gap of ${diff}\times p2_s$ between two consecutive values in (3). The last solution domain which is used by the conceptual electro-fish is the vshortrange mimicking the feeble electric pulse sensation of shark. This range is constricted within $\frac{x^{\min }}{{diff}}$ and $\frac{x^{\max }}{{diff}}$ with an interval gap of vs between two consecutive values in (4).

$$\begin{aligned}&{diff}=x^{\max }-x^{\min }\end{aligned}$$

(1)

$$\begin{aligned}&{longrange}=\left\{ {{diff}\times p1_l :{diff}\times p2_l :{diff}\times p3_l } \right\} \nonumber \\ \end{aligned}$$

(2)

$$\begin{aligned}&{shortrange}=\left\{ {{diff}\times p1_s :{diff}\times p2_s :{diff}\times p3_s } \right\} \end{aligned}$$

(3)

$$\begin{aligned}&{vshortrange}=\left\{ {\frac{x^{\min }}{{diff}}:{\mathrm{vs}}:\frac{x^{\max }}{{diff}}} \right\} \end{aligned}$$

(4)

3.2 Electric pulse calculation from longrange and slope analysis

The electric pulse, i.e., ${elec}^{{pulse}}$ is calculated depending on projected image slope and developed longrange. The slope of the projected image is considered as the absolute difference between the best and worst found individual value amongst population at iteration t in (5). The value of ${elec}^{{pulse}}$ is important for formation of electric organ discharge by the conceptual electro-fish discussed later. However, the ${elec}^{{pulse}}$ is mathematically developed as a product of two terms in (6). The first term is chosen by taking a random value from longrange. The other term is considered as the ratio of slope and addition of two terms.

$$\begin{aligned} {slope}= & {} \left| {x_{{best}}^t -x_{{worst}}^t } \right| \nonumber \\ S= & {} {randperm}\left\{ {{length}( {{longrange}})} \right\} \nonumber \\ n\in & {} S \end{aligned}$$

(5)

$$\begin{aligned} {elec}^{{pulse}}={longrange}(n)\times \frac{{slope}}{[ {( {{slope}^{{const}}\times {rand}})+x_{{best}}^t } ]} \end{aligned}$$

(6)

However, the distance from the targeted object by the conceptual electro-fish need to be found just like calculation of ${\varvec{elec}^{{pulse}}}$. This has been detected below.

3.3 Distance calculation from the prey object

The obtained minimum and maximum objective function value for all the individuals amongst population is considered as ch1 and ch2 at first iteration in (7). The nearness value towards targeted prey or food object is conditionally evaluated in (8).

$$\begin{aligned} \begin{array}{l} {ch1}=\min \left\{ {f( {x_i })} \right\} \quad i=1,\ldots \ldots ,n \\ {ch2}=\max \left\{ {f( {x_i })} \right\} \quad i=1,\ldots \ldots ,n \\ \end{array} \end{aligned}$$

(7)

$$\begin{aligned} {Distance}=\left\{ \begin{array}{ll} \frac{g1}{1+g2\left| {{ch1}-{ch2}} \right| }&{}\quad {\mathrm{if}}\,\,x_{{best}}^t ={ch1} \\ \frac{g1}{1+g2\left| {x_{{best}}^t -{ch1}} \right| }&{}\quad {\mathrm{otherwise}} \\ \end{array} \right\} \end{aligned}$$

(8)

After calculation of distance value, the conceptual electro-fish tries to find out the capacitance value of the targeted object.

3.4 Capacitance detection from waveform distortion value

Running capacitor value, i.e., ${cap}^{{run}}$ is found by taking the standard deviation value amongst all the objective function values generated from every individual of population. The waveform distortion value is considered as the standard deviation value shown in (9). Capacitor upper limit, for judging whether the object is a food particle or not, is selected as capint and caphover for first and next iterations, respectively. This is shown in (10).

$$\begin{aligned} {cap}^{{run}}=\sigma \left\{ {f( {x_1 }),f( {x_2 }),\ldots ,f( {x_n })} \right\} \end{aligned}$$

(9)

$$\begin{aligned} capu=\left\{ {{\begin{array}{ll} capint&{}\quad \mathrm{if}\,\,iter=1 \\ caphover&{}\quad \mathrm{otherwise} \\ \end{array} }} \right\} \end{aligned}$$

(10)

Conceptual electro-fish reaches the decision formation part when it gets the capacitance value.

3.5 Toggle switch judgment through capacitance evaluation

Toggle switch acts like changeover switch for the conceptual electro-fish’s action. It is made ‘1’ when running capacitor value is within the upper and lower limit and Distance value is less than setdist. It is made ‘0’ if the above condition is not satisfied. This is shown in (11). The setdist value works like a variable throughout the iterations guiding the distance, i.e., nearness from the targeted object. This is manipulated as represented in (12).

$$\begin{aligned} {toggle}=\left\{ {{\begin{array}{ll} 1&{}\quad {\mathrm{if}}\,\,\,{capl}<{cap}^{{run}}<{capu}\,\,\,{{and}}\,\,\,{Distance}<{setdist} \\ 0&{}\quad {\mathrm{otherwise}} \\ \end{array} }} \right\} \end{aligned}$$

(11)

$$\begin{aligned}&{setdist}={Distance}\,\,\,{{if}}\,\,\,{capl}<{cap}^{{run}}<{capu}\nonumber \\&\quad {{and}}\,\,\,{Distance}<{setdist} \end{aligned}$$

(12)

After the decision formation, conceptual electro-fish gears up its electric organ for emanation of next electrical wave.

3.6 Electric organ discharge with tuned voltage amplitude

The conceptual electro-fish generates new electric wave as xnew considering toggle switch operation in (13). If toggle switch shows ‘1’ then xnew is generated incorporating ${elec}^{{pulse}}$ obtained earlier by doing slope analysis.

$$\begin{aligned} {xnew}=x_{{best}}^t +{elec}^{{pulse}}\times {randn}\quad {if}\,\,\,{toggle}=1 \end{aligned}$$

(13)

When the $\varvec{toggle}$ switch shows ‘0’ then electrical wave is generated analyzing three kinds of probabilities. The three probabilities are ${\varvec{prob}^{{sel}}}, {\varvec{prob}^{{div}}}$ and ${\varvec{prob}^{{rng}}}$, respectively. Probability of selection, i.e., ${\varvec{prob}^{{sel}}}$ selects either randomization/diversification operation or localization operation. Randomization operation has taken place when the random variable ${\varvec{rand}}$ is greater than ${\varvec{prob}^{{sel}}}$. Apart from the above condition the conceptual electro-fish does localization. This is shown in (14).

$$\begin{aligned}&if\,\,\,rand>prob^{sel}\nonumber \\&do:randomization/diversification\nonumber \\&else\nonumber \\&do:localization\nonumber \\&end \end{aligned}$$

(14)

3.6.1 Divergence operation

Divergence operation helps to create new electrical wave governed by the $\varvec{prob^{div}}$. The new electrical wave is generated randomly by the conceptual electro-fish in the whole search region. This is nothing but the randomization concept described in (15).

$$\begin{aligned} xnew=\left\{ {{\begin{array}{ll} x^{\min }+diff\times rand_i&{}\quad \mathrm{if}\,\,\,rand>prob^{div} \\ x^{\min }+diff\times rand_i^j &{}\quad \mathrm{otherwise}\\ \end{array} }} \right\} \end{aligned}$$

(15)

3.6.2 Localization operation

Under the localization operation the imagined electro-fish emanates electric wave around the best found individual, i.e., $x_{best}^t$ at iteration t. It does that with the influence of ${prob}^{{rng}}$. The two terms c2 and c3 are taken randomly from the set of shortrange and vshortrange, respectively. How those terms have been chosen is shown in (16) and (17), respectively. When the random variable rand is greater than ${prob}^{{rng}}$, the new electrical wave xnew is formulated in vicinity of c2 and c3 shown in (18). It is also shown in (18) that if the random variable rand is not greater than ${prob}^{{rng}}$, new electrical wave is generated around the $x_{best}^t$ taking ${elec}^{{pulse}}$ and c3 into consideration.

$$\begin{aligned}&m1=randperm( {length( {shortrange})})\nonumber \\&h1\in m1\nonumber \\&c2=shortrange(h1) \end{aligned}$$

(16)

$$\begin{aligned}&m2=randperm( {length( {vshortrange})})\nonumber \\&h2\in m2\nonumber \\&c3=shortrange(h2) \end{aligned}$$

(17)

$$\begin{aligned} xnew=\left[ {{\begin{array}{ll} \left\{ {{\begin{array}{ll} x_{best}^t -c2+2\times c2\times rand&{}\quad \mathrm{for}\,\,\,j=2,\ldots ,pop-1 \\ x_{best}^t+c3&{}\quad \mathrm{for}\,\,\,j=1\\ \end{array} }} \right\} &{}\quad \mathrm{if}\,\,\,rand>prob^{rng}\\ \left\{ {{\begin{array}{ll} x_{best}^t +elec^{pulse}\times randn&{}\quad \mathrm{for}\,\,\,j=2,\ldots ,pop-1 \\ x_{best}^t +c3&{}\quad \mathrm{for}\,\,\,j=1\\ \end{array} }} \right\} &{}\quad \mathrm{otherwise} \\ \end{array} }} \right] \end{aligned}$$

(18)

How this newly developed FEO works as a meta-heuristic algorithm is written in the next section.

3.7 Algorithmic steps of fish electrolocation optimization (FEO)

Fish electrolocation optimization works through a few steps. These have been described below.

Step 1. :

Initialize $\varvec{longrange}$, $\varvec{shortrange}$ and $\varvec{vshortrange}$

Step 2. :

Set $\varvec{capint}$, $\varvec{caphover}$, $\varvec{capl}$ and $\varvec{setdist}$

Step 3. :

Set maximum iteration number

Step 4. :

Select three probabilities $\varvec{prob^{div}}$, $\varvec{prob^{rng}}$ and $\varvec{prob^{sel}}$

Step 5. :

Generate electrical wave randomly in the total search domain

Step 6. :

Analyze the objective function values tocalculate $\varvec{slope}$, $\varvec{cap^{run}}$ and $\varvec{x_{best}^t}$ and $\varvec{x_{worst}^t}$.

Step 7. :

Determine the $\varvec{elec^{pulse}}$ value and $\varvec{Distance}$ or nearness value from the targeted object.

Step 8. :

Do $\varvec{toggle}$ switch judgement and evaluate $\varvec{setdist}$ value

Step 9. :

If $\varvec{toggle}$ switch shows ‘1’ then do $\varvec{longrange}$ operation otherwise consider $\varvec{shortrange}$ and $\varvec{vshortrange}$ for doing diversification and localization operation based on three mentioned probabilities to generate electrical wave.

Step 10. :

Repeat steps 6 to 9 until the convergence criterion is met or maximum iteration number is reached otherwise stop iteration process.

4 Fish electrolocation optimization (FEO) implementation and evaluation

Fish electrolocation optimization could not have been an optimization algorithm without proper testing. In this section, this testing has been shown with different kinds of benchmark functions. The developed meta-heuristic technique is simulated in the technical software MATLAB$^{\textregistered }$ 7.0. The code is written in Intel Core i3 2.4 GHz personal computer. While doing simulation it has been observed that FEO has two types of parameters. One is generalized parameters which remain more or less same irrespective of nature of the problem. The other one is objective function-dependent parameters. Thirteen different kinds of objective functions have been chosen considering the dimension of the problem for examining the effectiveness of FEO. The best values are achieved by fixing the generalized parameters and problem-dependent parameters to certain values. These are shown in Tables 1 and 2, respectively, for the chosen benchmark functions.

Table 1 Generalized parameter of FEO

Table 2 Objective function or problem-dependent parameters of FEO

The performance of the developed FEO has been compared with other well-known algorithms, viz. Real coded genetic algorithm (RCGA), accelerated particle swarm optimization (ACPSO), particle swarm optimization (PSO) and harmony search (HS). The study has been done for 100 time single independent run for every soft computing technique. These selected techniques apart from FEO have been implemented with population 50 and maximum number of iteration as 5000. The proposed algorithm FEO has also been implemented with the same maximum iteration number. Population, i.e., the number of electro-fish, has been considered here as eight. It would be a reasonable question as to why the population has not been fixed at 50 like others. The answer is that the performance of FEO is good at a certain range of population, but deteriorates with increment of population from that range. This has been demonstrated through extensive study done on Schwefel function in later section. However, Camel Back (CB), Martin & Gaddy (MG), two-dimensional ($d = 2$) Rosenbrock (Rk), Branin (Br), Goldstein & Price (GP), four-dimensional ($d = 4$) Shekel (Shk), six-dimensional ($d = 6$) Sphere (Sp), B2, Shubert (Su), Rastrigin (Ra), two- and five-dimensional ($d = 2, 5$) Schwefel (Sch) and two-dimensional ($d = 2$) Michaelwicz (Mi) functions have been considered for implementation purpose (Hedar 2005). The range and expression of these chosen functions are shown in Table 3.

Table 3 The selected test bed functions with chosen range for doing minimization

Real coded genetic algorithm (RCGA) has been applied in two variant forms. Two variations have been considered on the basis of mutation phenomena, whereas crossover operation is taken as in literature (Wright 1991). One variant, i.e., RCGA$^{1}$ is considered by doing mutation according to (19). Another one, i.e., RCGA$^{2}$ is considered as (20).

$$\begin{aligned}&if\,\,\,rand>P^{mut}\nonumber \\&if\,\,\,fix( {2\times rand})>0\nonumber \\&k=floor( {pop\times rand})+1\nonumber \\&x_i^k =x_i^{\min } +diff\times rand\nonumber \\&end\nonumber \\&end \end{aligned}$$

(19)

$$\begin{aligned}&if\,\,\,rand>P^{mut}\nonumber \\&k=floor( {pop\times rand})+1\nonumber \\&if\,\,\,rand>0.5\nonumber \\&x_{i}^{k} =x_{i}^{k} +\left| {x_{i}^{\max } -x_{i}^{k}} \right| \times rand\nonumber \\&else\nonumber \\&x_{i}^{k} =x_{i}^{k} -\left| {x_{i}^{k} -x_{i}^{\min }} \right| \times rand\nonumber \\&end\nonumber \\&end \end{aligned}$$

(20)

The probability of mutation and crossover, i.e., $P^{mut}$ and $P^{cross}$ for RCGA$^{1}$ and RCGA$^{2}$ are taken to be considered as 0.01 and 0.98 and 0.05 and 0.88, respectively. APSO and PSO have been implemented according to (21) and (22) where $x_i^{new}$, $x_i^{best}$ and $g^{best}$define the newly calculated variable value, current and global best value, respectively (Wright 1991). The parameters alpha, $\gamma$ and beta values are chosen as 0.7, 8 and 2, respectively, for ACPSO. On the other hand, parameters alpha and beta for PSO have been selected as 1.8 and 1.7, respectively.

$$\begin{aligned} x_i^{new}= & {} x_i +alpha^\gamma \times ( {rand-0.5})+beta\times rand\nonumber \\&\times ( {g^{best}-x_i }) \end{aligned}$$

(21)

$$\begin{aligned} x_i^{new}= & {} x_i +alpha\times rand\times ( {x_i^{best} -x_i })+beta\times rand\nonumber \\&\times ( {g^{best}-x_i }) \end{aligned}$$

(22)

Harmony search (HS) has also been applied with harmony memory accept rate, pitch adjusting rate, harmony size and pitch range as 0.85, 0.7, 20 and $[100,\ldots ,100]$, respectively (Yang 2010a, b). All the above-mentioned parameters for different kinds of algorithms have been chosen after several trials. This is done for doing comparative study with the proposed FEO. The parameters of FEO have also been selected by doing several trials shown earlier in Tables 1 and 2. The chosen evolutionary algorithms are implemented on above-mentioned objective functions with convergence criterion shown in (23). That has been implemented for 100 times single independent run said earlier. Mean number of function evaluation (NF), standard deviation (dev) and percentage of success (% S) are considered as the evaluation criteria. The defined maximum iteration number is considered as 5000.

$$\begin{aligned} \left| {f-f^*} \right| <\varepsilon _1 f+\varepsilon _2 \end{aligned}$$

(23)

The constants $\varepsilon _1$ and $\varepsilon _2$ in (23) are selected as 10$^{-4}$. The term f and $f^*$ define the optimal value achieved and global optimal value, respectively, as shown in (23). The comparative study amongst the algorithms is shown in Tables 4, 5, 6 and 7, respectively.

Table 4 Comparative study amongst soft computing techniques

Table 5 Comparative study amongst soft computing techniques contd

Table 6 Comparative study amongst soft computing techniques contd

It has been observed from Tables 4, 5, 6 and 7 that proposed FEO outperforms other algorithms in 9 amongst the chosen 13 minimization problems in respect of mean number of function evaluation and percentage of success. It is shown in Table 4 that proposed FEO outperforms RCGA$^{1}$ and RCGA$^{2}$ in large difference but remains slightly ahead to ACPSO, PSO and HS for Camel Back function. Fish electrolocation optimization takes 184 mean number of function evaluation with standard deviation of 100 for Martin & Gaddy function. RCGA$^{1}$, RCGA$^{2}$, ACPSO, PSO and HS take 65,095, 8456, 420, 420 and 1909 mean number of function evaluation with standard deviation of 19,964, 3562, 58, 85 and 970, respectively. It has also been shown that for Rosenbrock function FEO outperforms other chosen algorithms with mean number of function evaluation and standard deviation as 337 and 227, respectively. It is shown in Table 5 that in case of Branin function ACPSO and PSO perform better than FEO. RCGA$^{1}$, RCGA$^{2}$ and HS takes more number of function evaluation than FEO to reach the desired convergence for Branin function. In the case of Goldstein & Price function, PSO outperforms all the other evolutionary algorithms including FEO. It has also been observed from Table 5 that FEO reaches desired convergence for Shekel function with mean number of function evaluation and standard deviation as 838 and 396, respectively. It fulfills the convergence criteria with 100 % success. RCGA$^{1}$, RCGA$^{2}$, ACPSO, PSO and HS achieve that desired convergence with 80, 18, 29, 36 and 45 % success, respectively. The other chosen soft computing techniques viz. RCGA$^{1}$, RCGA$^{2}$, ACPSO, PSO and HS take mean number of function evaluation and standard deviation as 71,269 and 25,519; 237,808 and 112,495; 15,753 and 11,964; 7373 and 22,056 and 10,380 and 4068, respectively. On the other hand, it is shown in Table 6 that FEO outperforms other chosen algorithms in respect of mean number of function evaluation and percentage of success for Sphere, B2 and Shubert function, respectively. It is shown in Table 7 that FEO takes less number of function evaluations in Rastrigin and five-dimensional Schwefel function. On the other hand, FEO takes more number of function evaluations for two-dimensional Michalewicz and Schwefel function. Interestingly it has been observed that RCGA$^{1}$ does not achieve the said convergence for two- and five-dimensional Schwefel function. RCGA$^{2}$ remains unsuccessful for doing minimization in five-dimensional Schwefel and two-dimensional Michalewicz function. Harmony search (HS) fails to achieve set convergence criteria similar like RCGA$^{1}$. It has been observed that proposed FEO has achieved 100 % success in both two- and five-dimensional Schwefel function. APSO and PSO have achieved 49 and 85 and 3 and 13 % success for two- and five-dimensional Schwefel function, respectively. It can be stated that FEO outperforms in 10 amongst 13 minimization problems if two-dimensional Schwefel function is considered. This new win is on the basis of percentage of success as an addition to nine win in comparison to other algorithms stated earlier. From this comparative study it has been typically observed that chosen soft computing techniques apart from FEO severely stumble to get desired convergence for minimization of Schwefel function. On the other hand, only generalized parameters of FEO have been fixed for doing all the comparative study. Problem-dependent parameters have been suitably changed for getting the above shown results in Tables 4, 5, 6 and 7, respectively. A special study has been done on Schwefel function for that chosen solution range described in Table 3. This is done to make the fuzziness of generalized and problem-dependent parameter clear. This has been briefly discussed in the next segment.

5 More implementation of FEO on Schwefel function

Fish electrolocation optimization has been extensively applied on Schwefel function. The optimization tool FEO has been implemented on this said function for various dimensions. It has been applied by varying number of electro-fish or population for 100 time single independent run, maximum iteration number as 5000 and convergence criteria shown in (22). This is shown in Tables 8 and 9, respectively, starting with lower dimension 10 and ending with higher dimension 200. It has been noticed that FEO achieves 100 % success for all the test conditions. That is why it is not shown in Tables 8 and 9, respectively.

Table 7 Comparative study amongst soft computing techniques contd

Table 8 FEO implementation on Schwefel function for different dimension

Table 9 FEO implementation on Schwefel function for different dimension contd

It has been observed from Tables 8 and 9 that computation time increases with the increase in dimension number. Computation time varies with population, but not like the just said variation with dimension number. It can be observed from Table 8 that for dimension 60, the computation time in second for 5, 10, 20, 40, 60, 80, 100, 150, 200 and 300 number of electro-fish are 11.971, 10.491, 7.867, 7.411, 6.913, 8.676, 8.938, 9.838, 10.329 and 11.929, respectively. This can be comprehended that when the number of electro-fish is 60 the run time is least. On the contrary, when it comes the case of mean number of function evaluation then FEO reaches 100 % success by taking mean number of function evaluation and standard deviation as 722 and 543; 1081 and 651; 1280 and 861; 1695 and 1151; 1839 and 1208; 2518 and 1531; 2722 and 1909; 3180 and 2175; 2175 and 2383 and 4074 and 2500 for 5, 10, 20, 40, 60, 80, 100, 150, 200 and 300 number of conceptual electro-fish, respectively. It can be comprehended that FEO takes lesser number of function evaluations as the population or number of fish decreases and vice versa. There is only one defaulter at population 150. This trend of taking less number of function evaluations at lesser number of population remains more or less constant for the entire tested dimension shown in Tables 8 and 9, respectively. There is one defaulter at population number 150 for 60- and 80-dimensional Schwefel function. This outcome of mismatch or default value is due to stochastic nature of FEO. One thing is common in entire tests shown in Tables 8 and 9, i.e., FEO achieves 100 % success to get the desired convergence. The convergence criterion has been made more stringent by considering number of objective function evaluation as a limit. This is done to have variation in percentage of success. This study is shown in Tables 10 and 11, respectively.

Table 10 Study of implementation of FEO on Schwefel function ($d = 200$) by varying maximum number of function evaluation as an extra convergence criterion

It can be observed from Tables 10 and 11 that maximum number of function evaluation has been varied from 4000 to 500 as an extra convergence criteria to that of (22). It has been observed from Table 10 that FEO reaches 100 % success for all its chosen population when the maximum number of function evaluation is 4000. The set limit of function evaluation is 3000. Fish electrolocation optimization gets 90, 94, 94, 83, 82, 70, 65, 62, 56, 54 and 42 percentage of success for chosen population number of 5, 10, 20, 40, 60, 80, 100, 150, 180, 200 and 300, respectively. This trend of decreasing percentage of success with the increase in population number continues up to 500 maximum number of function evaluation. Percentage of success (%S) increases with the increase of population number. There are some defaulters also in that said pattern for maximum limit of 2000, 1000 and 500, respectively. Maximum number of function evaluation is set at 1000. The percentage of success increases from 21 to 27, from 11 to 19 and from 9 to 12 with the increase of population number from 40 to 60, from 80 to 100 and from 180 to 200, respectively. It is also shown in Table 11 that FEO becomes unsuccessful to achieve the convergence coupled with maximum number of function evaluation as 500 for population number of 180, 200 and 300, respectively. It has also been noticed that computation time is highest at population number 5. That gradually decreases up to population number 60, 60, 100, 60 and 60, respectively. Then it increases up to 300 for maximum number of function evaluation of 4000, 3000, 2000, 1000 and 500, respectively. However, from the total above analysis it can be concluded that percentage of success is higher with the lower number of electro-fish. Mean number of function evaluation is lower with the lower number of electro-fish. Run time is lower with the moderate number of electro-fish. This analysis more or less justifies the cause of fixing population number at lower value, i.e., 8 for doing comparative study. Though study of variation in population number and also set convergence condition gives clarification of inner strength of FEO but can’t accommodate the entire parameters of this technique. There are problem-dependent parameters too apart from generalized parameters. That is number of electro-fish or population. These parameters include different range discrimination constants and probabilities. The study of variation of shortrange and longrange constants are described in the next section.

Table 11 Study of implementation of FEO on Schwefel function ($d = 200$) by varying maximum number of function evaluation as an extra convergence criterion contd

Table 12 Study of application of FEO on Schwefel function ($d = 200$) by varying the shortrange constants $( {p1_s ,p2_s ,p3_s })$ fixing longrange constants $( {p1_l ,p2_l ,p3_l })$ at (10$^{-2}$, 5 $\times$ 10$^{-3}$, 5 $\times$ 10$^{-2})$

Table 13 Study of application of FEO on Schwefel function ($d = 200$) by varying the shortrange constants $( {p1_s ,p2_s ,p3_s })$ fixing longrange constants $( {p1_l ,p2_l ,p3_l })$ at (10$^{-2}$, 5 $\times$ 10$^{-3}$, 5 $\times$ 10$^{-2})$ contd

5.1 Variation in shortrange constants

shortrange constants $p1_s$, $p2_s$ and $p3_s$ are varied by fixing the longrange constants at 10$^{-2}$, 5 $\times$ 10$^{-3}$ and 5 $\times$ 10$^{-2}$, respectively. The mean number of function evaluation (NF) and standard deviation (dev) and computation time are calculated for population number 5, 20, 60, 100, 150, 200 and 300, respectively, in Tables 12 and 13. This is done for 200-dimensional Schwefel function with selected Table 3. This study is done without disturbing the other parameters of FEO shown in Table solution domain as depicted in 1 and Table 2, respectively.

It has been observed from Table 12 that the run time in seconds, for a particular population number 5, gradually increases from 23.876 to 43.848. That has been observed with the decrease of shortrange constants value from 10$^{-2}$, 10$^{-3 }$ and 10$^{-1}$–10$^{-3}$, 10$^{-4 }$and 10$^{-2}$. Then it decreases to 40.584 when shortrange constants values are 10$^{-4}$, 10$^{-5}$ and 10$^{-3}$, respectively. It can be noticed from Table 13 that run time in seconds again decreases to 25.553 from the just said run time in Table 12. It remains more or less constant within 24.738 and 25.553 with the decrease in shortrange constants value. Not only the runtime is restricted to a small span, but also the mean number of function evaluation is observed to be restricted between 529 and 541. Fish electrolocation optimization achieves better results when the shortrange constant values exceed a certain boundary in comparison to sticking with a certain value. That can be observed from Tables 12 and 13, respectively. However, this study is done considering the longrange constants at a fixed value. The variation of the constant values regarding longrange is considered for study purpose in the very next segment.

5.2 Variation in longrange constants

The longrange constants, i.e., $p1_l$, $p2_l$ and $p3_l$ has been varied while the shortrange constants are kept fixed at 10$^{-4}$, 10$^{-5}$ and 10$^{-3}$, respectively. It is done for implementation of FEO on 200-dimensional Schwefel function. The computed results are shown in Tables 14 and 15, respectively. The longrange. constants are varied for population number 5, 20, 60, 100, 150, 200 and 300, respectively.

Table 14 Study of application of FEO on Schwefel function ($d = 200$) by varying the longrange constants $( {p1_l ,p2_l ,p3_l })$ fixing shortrange constants $( {p1_s ,p2_s ,p3_s })$ at (10$^{-4}$, 10$^{-5}$, 10$^{-3})$

Table 15 Study of application of FEO on Schwefel function ($d = 200$) by varying the longrange constants $( {p1_l ,p2_l ,p3_l })$ fixing shortrange constants $( {p1_s ,p2_s ,p3_s })$ at (10$^{-4}$, 10$^{-5}$, 10$^{-3})$ contd

It has been observed from Tables 14 and 15 that mean number of function evaluation (NF) and computation time changes with the decrement of longrange constant values. That said change is more in comparison to previously discussed changes observed in Tables 12 and 13, respectively. It can be observed from Tables 14 and 15 that for population number 100, run time in seconds and mean number of function evaluation are 18.914 and 2345; 23.493 and 2685; 88.108 and 11,022 and 422.243 and 49,812 for longrange constant values of 10$^{-1}$, 5 $\times$ 10$^{-2}$ and 5 $\times$ 10$^{-1}$; 10$^{-3}$, 5 $\times$ 10$^{-4}$ and 5 $\times$ 10$^{-3}$; 10$^{-4}$, 5 $\times$ 10$^{-5}$ and 5 $\times$ 10$^{-4}$and 10$^{-5}$, 5 $\times$ 10$^{-6}$ and 5 $\times$ 10$^{-5}$, respectively. It is also shown earlier in Table 9 that the run time in seconds and mean number of function evaluation are 21.985 and 2823 for longrange constant value of 10$^{-2}$, 5 $\times$ 10$^{-3}$ and 5 $\times$ 10$^{-2}$ at population number 100. The other selected population number more or less obeys this kind of drastic change. That is shown in Tables 14 and 15, respectively, with the changes of longrange constant. This said pattern of function evaluation and computation time describes that the change in longrange constant value in this way can be very sensitive to computation. Even the percentage of success value drops down to 68, 94 and 99 for population number 20, 60 and 100, respectively. That has been observed for the longrange constant are 10$^{-5}$, 5 $\times$ 10$^{-6}$ and 5 $\times$ 10$^{-5}$, respectively. It can be stated from the study done on Schwefel function that longrange constants should be strictly restricted within a definite zone. That is to avoid bad results. On the other hand, shortrange constants analyzed in the previous section can be fine-tuned to have better results.

However, FEO has not been compared with well established technique differential evolution and simulated annealing. This has been done on eggcrate function in the next section.

6 Comparative study of fish electrolocation optimization with differential evolution and simulated annealing on eggcrate function

Fish electrolocation optimization has been compared with differential evolution (DE) and simulated annealing (SA) in this section. This extra comparative study has been done to show the effectiveness of FEO with other well established meta-heuristic techniques such as DE and SA. These stated algorithms have been implemented on two-dimensional eggcrate function shown in expression (24).

$$\begin{aligned} f( {x,y})=x^2+y^2+25( {( {\sin x})^2+( {\sin y})^2}) \end{aligned}$$

(24)

The range of eggcrate function has been considered here as [$-$5, 5]. The global minimum value of this function is at (0, 0) for each variable and the global minimum value is 0. The convergence criterion for this comparative study has been considered same as earlier denoted expression (23). The number of population individual has been chosen as 30 for all the considered soft computing techniques. In this case, the number of population individuals has not been considered as eight as described earlier. The population number has been considered here as stated thirty for the proposed technique to have similarity with other algorithms’ implementation. The maximum iteration number of this comparative study has been chosen as the stopping criteria if the desired convergence has not been achieved. This has been chosen as 5000 for every soft computing technique. The study has been done for hundred time single independent run by changing the random number seed every time. Differential evolution has been implemented for two schemes on eggcrate function. The scheme I and scheme II regarding differential evolution varies on the principle of generation of mutation matrix. The genesis of mutation vector $\overrightarrow{V_m }$ for scheme I and scheme II have been shown in expressions (25) and (26), respectively.

$$\begin{aligned} \overrightarrow{V_m } =\overrightarrow{X_{r1,G} } +F_m .( {\overrightarrow{X_{r2,G} } -\overrightarrow{X_{r3,G} } }) \end{aligned}$$

(25)

$$\begin{aligned} \overrightarrow{V_m } =\overrightarrow{X_{i,G} } +\lambda .( {\overrightarrow{X_{best,G} } -\overrightarrow{X_{i,G} } })+F_m .( {\overrightarrow{X_{r2,G} } -\overrightarrow{X_{r3,G} } }) \end{aligned}$$

(26)

The notations $\overrightarrow{X_{r1,G} }$, $\overrightarrow{X_{r2,G} }$ and $\overrightarrow{X_{r3,G} }$ define the different population individual values inside population at G${\mathrm{th}}$ iteration. The terms $\overrightarrow{X_{i,G} }$ and $\overrightarrow{X_{best,G} }$ in (26) denote the ith individual and current best individual at the Gth iteration, respectively. The $F_m$ value has been considered as 0.8 for both the schemes after several trial runs. The value of $\lambda$ is chosen as 0.3 for the scheme II related to differential evolution in (26). On the other hand, the initial temperature for the simulation of simulated annealing (SA) has been considered as 1. The minimum temperature for SA has been chosen as 10$^{-10}$. The Boltzmann constant for SA has been selected as 1. The cooling factor value for SA has been chosen as 0.9. The energy norm value for SA has been selected as 10$^{-5}$. The above said parameters for implementation of simulated annealing have been chosen after several trial runs. In the case of FEO, the generalized parameter values except the number of electro-fish have been chosen for optimization of eggcrate function. This is already shown in Table 1 in the earlier section. The number of electro-fish, i.e., the population size has been considered as 30 as said earlier. The three probabilities values have been considered same as Martin and Gaddy function optimization in Table 2. The longrange multiplying factors have been chosen same as for Michaelwicz function optimization in Table 2. The shortrange multiplying factors have been selected same as for Sphere function optimization in Table 2. The problem-dependent and generalized parameters of FEO have been chosen after several trial runs.

The comparative study is shown in Table 16. It has been observed from Table 16 simulated annealing takes mean number of function evaluation and standard deviation as 5854 and 3289, respectively. The percentage of success of simulated annealing has been found as 84 in Table 16 for 100 time single independent runs. The total running time taken by simulated annealing is 167.08 s. It has been noticed from Table 16 that mean number of function evaluation and standard deviation taken by differential evolution (Scheme I) are 3138 and 378 for achieving the desired convergence. The percentage of success is 100 in this case in Table 16. The total running time taken by this differential evolution (scheme I) is 83.71 s for 100 time single independent run in Table 16. Finally, mean number of function evaluation and standard deviation have been observed as 2813 and 480, respectively, for differential evolution (scheme II) in Table 16. Again the percentage of success in this case is 100. The total running time taken by this algorithm is 75.08 s for 100 time single independent run in Table 16. Lastly, it has been noticed from Table 16 that FEO takes mean number of function evaluation and standard deviation as 1076 and 591 for eggcrate function optimization with the desired convergence. The percentage of success for 100 time single independent runs is 100. Significantly the total running time for FEO is 11.87 s. It can be said from the above description that FEO works quite better than differential evolution and simulated annealing for this kind of continuous function optimization.

Table 16 Comparative study with differential evolution and simulated annealing for 100 independent runs

The newly developed soft computing technique FEO has been successfully implemented on eggcrate function to find the global minimum point. The simulation study regarding FEO has been done for continuous variable related optimization problem hitherto. The proposed technique has not been tested for real-world discrete combinatorial optimization problem. This study has been done in the next section for reliability worth enhancement by optimal capacitor and distributed generator placement.

7 Implementation of FEO on real-world optimization problem

Fish electrolocation optimization has been applied to real-world optimization problem. The real-world problem is cost-based reliability enhancement in radial distribution system. Cost-based reliability has been improved by suitably placing capacitors and distributed generators at the sensitive buses. Capacitor allocation and distributed generation penetration have been considered to minimize the reliability worth as well as real power loss. The objective function has been described in (27) as:

$$\begin{aligned} Minimize\,\,\,S. \end{aligned}$$

(27)

The term S is reliability worth. That is depicted in (28) as Relworth.

$$\begin{aligned} S=Relworth \end{aligned}$$

(28)

The reliability worth value has been illustrated in (29) as:

$$\begin{aligned} {Relworth}\, = \sum \limits _{{j = 1}}^{{nbr}} {La(j).} C(j).\lambda (j). \end{aligned}$$

(29)

In that expression, La( j) is the connected load at branch j and C( j) is the interruption cost at branch j. Furthermore, $\lambda ( j)$ in expression (29) is the failure rate of branch j. The value of $\alpha _i$ is depicted in (30) as:

$$\begin{aligned} \alpha _i =\frac{Inew^i}{Iold^i}. \end{aligned}$$

(30)

It is a ratio between absolute or modal value of new current to old current. The new current value is generated after DG penetration and capacitor placement. The old current value is the current amplitude of original configuration, i.e., without capacitor placement and DG penetration. The expression of new failure rate is illustrated in (31) as:

$$\begin{aligned} \lambda ^{new}=\alpha _i ( {\lambda ^{uncomp}-\lambda ^{comp}})+\lambda ^{comp}. \end{aligned}$$

(31)

In that Eq. (31), $\lambda ^{uncomp}$ is the failure rate of AC cable without any DG penetration and capacitor allocation. The another term in Eq. (31) is $\lambda ^{comp}$. This term is considered as the minimum failure rate owing to capacitor placement and DG penetration. The Eq. (31) is valid when the value of $\alpha _i$ is greater than 0.5. Otherwise the minimum failure rate is considered as the new failure rate. The expression of cost-based reliability index called CBRI is illustrated in (32) as:

$$\begin{aligned} \mathrm{CBRI}=\frac{( {Relworth^{ini}-Relworth^{it}})\times loss^{ini}}{loss^{it}\times cost^{it}}. \end{aligned}$$

(32)

It can be observed from the RHS of expression (32) that CBRI is a ratio of two terms. The numerator of that ratio is the multiplication of two terms. One term is the difference of two reliability worth. The first reliability worth is without any capacitor placement and DG penetration. The second reliability worth is after capacitor placement and DG penetration. The multiplication factor with that said difference of two reliability worth is the initial real power loss without any capacitor placement and DG penetration. The denominator term of the discussed ratio related to CBRI is the multiplication of two terms. One term is the real power loss at certain iteration. The second term is the cost term connected to the real power loss in (33) as:

$$\begin{aligned} cost^{it}=K_P \cdot loss^{it}. \end{aligned}$$

(33)

The discussed ratio CBRI is actually one type of difference of two reliability worth connected with real power lost and concerning cost. As discussed earlier the objective is to minimize reliability worth. So the reliability worth after capacitor allocation and DG penetration is necessarily lower than the reliability worth of original configuration, i.e., without any capacitor and DG placement. That is why the ratio value is positive if the objective of the optimization problem is fulfilled. And more to it, the CBRI value will be proportionately higher with the decrement of reliability worth value after capacitor and DG placement.

Table 17 Comparative study of results after DG and capacitor placement

Fish electrolocation optimization has been implemented for cost-based reliability enhancement. It has been intelligently done by suitable choosing DG and capacitor values at particular bus positions. The DG penetration has been considered as the 10 % of the total active power load. The DG values have been chosen as 100 and 200 kW, respectively, for implementation of the soft computing techniques. The dollar conversion constant term $K_{P}$ has been chosen as US$ 168/kW. The simulation work is done on technical software MATLAB. A standard 34 bus radial distribution system has been considered for implementation of this said soft computing technique (Mekhamer et al. 2003). The scheme chosen for capacitor allocation and DG penetration in this radial distribution system is applying disconnects between buses and fuse gear protection at lateral junction point. The failure rate for maximum impedance and minimum impedance of line data has been considered as 0.5 and 0.1, respectively. The other failure rate has been enumerated between the two mentioned limits linearly with the rest impedance value. The value of failure rate after full compensation related to capacitor allocation and DG penetration has been chosen as 85 % of the uncompensated failure rate as denoted earlier. The interruption cost value has been chosen as US$ 15.4752, US$ 7.6317 and US$ 1.86 for 4, 2 and 0.5 h of outage time, respectively. A comparative study with real coded genetic algorithm (RCGA$^{2})$ and PSO is shown in Table 17. It can be observed from the Table 17 that without placing any capacitor and DG into the radial distribution system, the real power loss has been found out at 221.5 kW. The reliability worth for that mentioned situation is found out at US$ 163,478.43 in Table 17. It has been observed from Table 17 that the cost-based reliability index named CBRI has been found at zero for that said condition. It is shown in Table 17 that utilizing RCGA$^{2}$, the real power loss has been reduced from 221.5 to 152.12 kW. It has been observed from Table 17 that with the implementation of PSO, the real power loss has been decreased from 221.5 to 150 kW. On the other hand, the real power loss has been observed to be reduced from 221.5 to 145.59 kW with the implementation of the proposed algorithm FEO in Table 17. This said reduction of real power loss has been occurred due to the reactive power compensation by capacitor placement and reduction of line loading by DG penetration. It has been observed from Table 17 that reliability worth has been reduced from US$ 163,478.43 to US$ 159,690 with the application of RCGA$^{2}$. Reliability worth has been observed to be reduced from US$ 163,478.43 to US$ 160,150 with the implementation of PSO. On the other hand, with the implementation of proposed algorithm FEO reliability worth has been reduced from US$ 163,478.43 to US$ 156,100. The reliability worth value in (29) is linked with the failure rate of the cable. After doing capacitor allocation and DG penetration the failure rate decreases. That is why the reliability worth reduces after suitable choosing capacitor and DG’s location and value, respectively, by those mentioned techniques. It has been noticed from Table 17 that the reliability index CBRI has been increased from zero to 0.2162 with the implementation of RCGA$^{2}$. The reliability index CBRI has been observed to be increased from zero to 0.1949 with the utilization of PSO in Table 17. On the other hand, it is shown in Table 17 that the reliability index CBRI has been increased from zero to 0.4591 with the implementation of the said algorithm FEO. The proposed algorithm FEO has got higher and better CBRI value amongst all the chosen soft computing techniques. It has been observed from Table 17 that RCGA has chosen DG values as 200 and 200 kW for bus positions 26 and 29, respectively. It is shown in Table 17 that PSO has selected 200 kW DG value for the bus number 18. On the other hand, three DG values are chosen by proposed algorithm FEO for bus locations 15, 31 and 32, respectively. The selected DG values for those said locations are 100, 100 and 200 kW in Table 17. As said earlier reactive power compensation by capacitor allocation has been done by all the mentioned techniques. It is shown in Table 17 that capacitor value of 900, 150, 300 and 150 kVAR have been chosen by RCGA$^{2}$ for bus position 5, 15, 21 and 22, respectively. It has been noticed from Table 17 that six capacitor values have been selected by PSO for bus position 1, 18, 21, 22, 29 and 33, respectively. The six capacitor values for those mentioned locations are 300, 900, 450, 600, 150 and 450 kVAR in Table 17. On the other hand, it has been observed from Table 17 that capacitor values of 1200, 1200, 150, 150 and 600 kVAR have been chosen by FEO for 5, 6, 14, 21 and 23, respectively. It can be concluded from the discussion that proposed algorithm FEO has beaten other chosen soft computing techniques viz. RCGA$^{2}$ and PSO. The said algorithm FEO has reduced the real power loss at a higher degree in comparison to RCGA$^{2}$ and PSO. It has also been discussed that the reliability worth related to customer interruption cost has been decreased by FEO at a higher degree in comparison to RCGA$^{2}$ and PSO. Furthermore, the cost-based reliability index CBRI has been increased at a higher degree by FEO in comparison to RCGA$^{2}$ and PSO as discussed in this section. Finally, it can be said that the proposed algorithm FEO works better in finding the suitable DG and capacitor value for certain locations. It does the above engineering work to enhance the reliability economically and also technically.

However, the FEO has been successfully applied on real-world optimization problem. The critical issues regarding the proposed algorithm should be discussed. This has been stated in the next section.

Table 18 Experiment on eggcrate function applying FEO for 10 times run

8 Analysis of critical issues of fish electrolocation optimization

There are many critical issues of an algorithm. They are robustness, flexibility, benefits, feasibility, divergence and convergence capability, stopping criteria, stability and reliability, efficiency and effectiveness, productivity, computational complexity and advantages and disadvantages of the proposed method, etc. The important issues amongst the above-mentioned criteria have been discussed here for FEO.

• Robustness In computer science, robustness of an algorithm is defined as the capability to pursue computation despite abnormalities in input, enumeration, etc. Though random number generation is the governing factor for creation of population individual in FEO, there are three kinds of probabilities and three kinds of ranges in the proposed technique. If there are any abnormalities in input, the three kinds of ranges, i.e., longrange, shortrange and vshortrange make it feasible to have some nearness to the global optimal point. Furthermore, electrical capacitance value by the toggle switch judgment helps it to continue enumeration in the converging path. An experiment has been done to show the robustness of FEO. This is shown in Table 18. It has been observed from Table 18 that with the tuning of probabilities the minimum and maximum objective function value for the minimization problem change very little. Whereas it has been observed that with less population number FEO performs best. This simulation study tells about the robustness of FEO.

• Flexibility FEO is flexible in nature. It can be applied to one-dimensional problem as well as multidimensional objective function. The discussion in the earlier sections is the evidence of that. It has been applied to continuous optimization problem. It can also be applied to discrete optimization problem if the three kinds of ranges have been chosen judiciously. It can be said from the description stated in the previous sections that proposed FEO is more flexible than simulated annealing and differential evolution and it performs well for combinatorial optimization problem. This has been shown in Sect. 7.

• Benefits Benefits of FEO are primarily the advantages of utilizing the proposed method. The simulation studies done in the entire research work tell that FEO algorithm is robust, flexible, efficient and effective in finding not only theoretically correct optimal solution but also it can find real-world feasible optimal solution. This also states about the stability of the proposed method.

• Feasibility FEO has been tested for continuous optimization problem as well as combinatorial optimization problem. The simulation results show that the solutions are feasible especially for real-world optimization problem studied in Sect. 7.

• Divergence and convergence capability Divergence and convergence capability of an evolutionary algorithm are considered as the randomization and localization capability towards the global optimal point. The randomization of the FEO is expressed through Eq. (15). The localization phenomenon of the proposed technique has been illustrated by the expressions (16), (17) and (18), respectively. The proposed algorithm divergence and convergence criteria are governed by the ${prob}^{{div}}$ and ${prob}^{{rng}}$, respectively. It has been observed in earlier sections that FEO has better divergence and convergence capability than PSO and real coded genetic algorithm. In Sect. 6, it has been found that the randomization and localization quality of FEO is better than simulated annealing and differential evolution.

• Stopping criteria stopping criteria of the FEO have been considered as the desired convergence criterion as expressed in Eq. (23) and maximum iteration number.

• Stability and reliability Stability of an algorithm is defined as how changes to the training data influence the result of the algorithm. It can be said that from earlier discussion that proposed FEO is more stable than genetic algorithm and PSO. The proposed method as discussed earlier is also able to find out the real-world feasible solution in Sect. 7. On the other hand, reliable product in computer science means that it would be totally free of technical errors. So, it depends on the carefulness and diligence of the person coding FEO in a certain computer language. Furthermore, it can be said from the discussion written in the earlier section that proposed FEO is more stable and reliable than simulated annealing and differential evolution.

• Efficiency and effectiveness Previous simulation studies tell about the efficiency of FEO. The various parameters of FEO have been set on the basis of several run and best efficiency. The effectiveness of FEO has been tested with Gaussian elimination method on system of linear equations (Ikotun et al. 2011). It has been observed from Table 19 that FEO has obtained all the three sets of solutions for the system of linear equations, whereas the Gaussian elimination method has found out only one set of results. This simulation study shows the effectiveness of FEO.

• Productivity Productivity has been considered here as the ratio of number of source code line and computation time in i3, 2.4 GHz machine. The source code line in MATLAB is 206 for implementing FEO on the system of linear equations in Table 19. The computation time is 0.62 s. The productivity for this case is 332.25.

• Computational complexity Computational complexity is a subject of computer science. It is of two types. One is time complexity and the other one is space complexity. Time complexity of an algorithm is defined as the amount of time taken by that algorithm to run. It is quantified as a function of the length of string representing the input. Generally, time complexity is calculated by counting the number of elementary operations performed by the algorithm. Significantly the elementary operation takes a fixed amount of time. Time complexity is a property of deterministic algorithm. But FEO is a stochastic or non-deterministic algorithm. Time complexity of this kind of algorithm would be number of generation multiplied by the population size. But the number of generation varies with random number generation as the genesis of population individual is governed by it. Furthermore, the number of generation of this kind of evolutionary algorithm is problem specific.

Space complexity of an algorithm is defined by the total space taken by that algorithm with respect to input size. The space complexity of the proposed FEO is O(m.NL). Here m is the number of rows in one column vector or population individual. It can be said that m is the dimensionality of the objective function. The other term NL is the population size or number of population individuals.

Table 19 Experiment on system of linear equations

• Advantages and disadvantages There are a few advantages and disadvantages of FEO. The advantages are as follows:

  • 1. The convergence time or computation time is quicker than the other well established algorithms.

  • 2. The algorithm is flexible and robust.

  • 3. It has good divergence and convergence capability.

The disadvantages are as follows:

• 1. There are three kinds of ranges in the algorithm. One has to carefully design the three ranges for continuous as well as discrete or combinatorial optimization problem.

• 2. There are a few parameters in the algorithm. Those are more or less problem specific.

9 Conclusion

Optimization algorithm based on the behavior of electrolocation technique of elephant nose fish and shark has been successfully developed and tested. It has been observed that FEO algorithm works better on test bed function than established evolutionary algorithm such as genetic algorithm, particle swarm optimization, differential evolution, simulated annealing, etc. Comparative study shows that the method has got potential to be applied like other well established techniques. The proposed method has also outperformed chosen soft computing techniques for real-world optimization problem related to reliability worth enhancement in radial distribution system. Finally, hybridization of this proposed method with other well established techniques can also be done to reap the benefit of the participating techniques.