Soft computing-based new interval-valued hesitant fuzzy multi-criteria group assessment method with last aggregation to industrial decision problems

Abstract

Recent studies have identified that multi-criteria group analysis methods should take the concepts of risk and uncertainty into account. In some real-life situations, determining the exact values for the potential alternatives’ performances and criteria weights is so difficult. To overcome with these situations, their values should be regarded as fuzzy and fuzzy intervals. In this respect, interval-valued hesitant fuzzy sets (IVHFSs) as a suitable modern fuzzy sets theory can be considered because this theory allows decision makers (DMs) to assign some interval-values membership degrees for an alternative in terms of selected criteria under a set to margin of errors. Hence, this paper proposes a novel soft computing approach, namely IVHF-MCGA, based on new interval-valued hesitant fuzzy complex proportional assessment (IVHF-COPRAS) method that can be applied in solving the multi-criteria group decision-making (MCGDM) problems under uncertainty. In this approach, preference values of potential alternatives versus the selected criteria and weights of each criterion are expressed by linguistic variables and then are transformed to interval-valued hesitant fuzzy elements (IVHFEs). In addition, an interval-valued hesitant fuzzy entropy (IVHF-entropy) method is extended to determine the criteria weights by considering the DMs’ opinions about the relative importance. Also, a new interval-valued hesitant fuzzy compromise solution (IVHF-CS) method is introduced to estimate the weight of each DM in the group decision-making process along with the last aggregation for the DMs’ judgments to avoid the data loss. Then, three practical applications about the robot selection, industrial site selection and rapid prototyping process selection problems are considered to explain steps of the proposed IVHF-MCGA approach and to indicate its validity and applicability. Finally, a comparative analysis between the proposed approach and fuzzy group TOPSIS method is presented based on four comparison parameters, including adequacy to changes of alternatives and criteria, agility in decision process, influence of DMs’ weights and impact of first and last aggregations, to show its suitability.

1 Introduction

In the last decade, industrial selection problems received extensive attention by numerous researchers in the manufacturing industry. The industrial selection problem is an important issue for manufacturing companies to enhance their performance and productivity (Mousavi et al. 2013b). Hence, an effective evaluation and decision method for selecting the best industrial alternative among several potential candidates is very consequential when a company makes a decision to choose a candidate for performing a special task among various types and models according to different specifications and factors, such as related cost, risk, complexity, demand, service level and flexibility.

In the related literature, many studies have presented methods and tools to solve the selection problems under uncertainty. In this regard, Ölçer and Odabaşi (2005) designed a fuzzy multi-attribute group decision-making model for solving the propulsion system selection problem. Li et al. (2007) proposed a grey method for solving the supplier selection problem under uncertainty. In addition, for solving the robot selection problem; for instance, Agrawal et al. (1991) considered the technique for order preference by similarity to an ideal solution (TOPSIS method); Goh (1997) considered the analytic hierarchy process (AHP) method; Malek et al. (2000) focused on a decision support system (DSS) with respect to analytical algorithms; Chu and Lin (2003) proposed a fuzzy TOPSIS method, in which the rating of an alternative among the selected criteria and the criteria weights are expressed basing on the linguistic terms; Bhangale et al. (2004) used the graphical and TOPSIS methods; Karsak (2005) presented a multi-criteria decision-making (MCDM) method based on Choquet integral; Chatterjee et al. (2010) used two Vlse Kriterijumska Optimizacija I Kompromisno Resenje (VIKOR) and elimination and choice translating reality (ELECTRE) methods; Rao et al. (2011) proposed a decision-making method using fuzzy logic to convert the qualitative attributes into the quantitative attributes regarding objective and subjective preferences; and İç et al. (2013) introduced a DSS based on fuzzy AHP method.

For selection problems in reality for overcoming the uncertainty in classical fuzzy sets theory, it is difficult for decision makers (DMs) or experts to exactly specify their opinions as a number under an interval [0,1] (e.g., Mousavi et al. 2013b, 2015; Vahdani et al. 2014). Thus, it is more appropriate to demonstrate their opinions by an interval (Mousavi et al. 2013b, a; Zhao et al. 2014). Gorzałczany (1987) and Turksen (1986) have been firstly introduced the interval-valued fuzzy sets. This theory is widely used in real-world selection problems such as approximate reasoning (Bustince 1994; Gorzałczany 1987) and preference modeling (Türkşen and Bilgiç 1996). Yao and Yu (2004) illustrated the unknown potential alternatives effectiveness scores using the statistical data under an interval-valued fuzzy environment. Vahdani et al. (2010) and Vahdani and Hadipour (2011) developed VIKOR and ELECTRE methods based on interval-valued fuzzy sets for solving the MCDM problems, respectively.

In addition, Devi (2011) focused on the VIKOR method in intuitionistic fuzzy setting for solving the MCDM problems, in which rating of the candidate alternatives and the criteria weights were judged by triangular intuitionistic fuzzy sets. Vahdani et al. (2013) proposed a modified TOPSIS method based on the interval-valued fuzzy situations and the weight of criteria and rating of alternatives were expressed by linguistic terms which converted to triangular interval-valued fuzzy numbers. Liu et al. (2014) hybridized an MCDM method based on the TOPSIS with the interval 2-tuple linguistic for selection and evaluation of the robot selection problem. Wang (2015) extended an MCDM model based on the simple additive weighting method and relative preference index in which DMs assigned their judgments by triangular fuzzy numbers.

Modern fuzzy sets theory has been introduced that could help to solve the multi-criteria group decision-making (MCGDM) problems. In this regard, one of the powerful and effective fuzzy sets theories that could cope with uncertainty is interval-valued hesitant fuzzy sets (IVHFSs). This concept has been first introduced by Chen et al. (2013) by generalizing the concept of hesitant fuzzy set (HFS) and interval value form. The IVHFSs have expressed that experts or DMs could assign some membership degrees for an element under a set by interval values. Recently, some researchers have focused on this concept and solved MCGDM problems with the HFS and IVHFS. Chen et al. (2013) developed an approach to group decision making by considering the interval-valued hesitant preference relations. In their study, the opinions of each DM are considered unequal. Farhadinia (2013) focused on relationship between entropy, distance measure, and similarity measure for the HFS and IVHFS. Then, two clustering algorithms are extended under the hesitant fuzzy environment. Xu and Zhang (2013) based on the maximizing deviation method established an optimization model to determine the criteria weights. Then, they extend the TOPSIS method based on the hesitant fuzzy and interval-valued hesitant fuzzy situations. Zhang and Xu (2014) presented an interval-based programming model for MCGDM problems under hesitant fuzzy environment with incomplete preference over candidate alternatives. Li and Peng (2014) proposed some Hamacher operations under IVHFS and then extended a practical approach for selection the shale gas areas. Consequently, the gap of recent literature is shown in Table 1. This table shows that determining the DMs’ weights and aggregating the DMs’ judgments in the last steps are not considered in the literature as two important features for decreasing the errors and loss of data.

Table 1 Fuzzy decision-making methods and their characteristics

The review thus suggests that there is a need for a new group decision-making method for solving the selection problems and for decreasing the errors by overcoming the risk and uncertainty issues and by fulfilling the DMs’ requirements. This study proposes a soft computing approach based on two new interval-valued hesitant fuzzy complex proportional assessments (IVHF-COPRAS) and interval-valued hesitant fuzzy compromise solution (IVHF-CS) methods with last aggregation, and aims to fill the gap in the selection problems and decrease the loss for the industrial selection problems. In this presented interval-valued hesitant fuzzy multi-criteria group assessment (IVHF-MCGA) approach under uncertain environment, some operators are needed to be extended, such as summation, multiplication, subtraction, and division that are introduced for making decisions under uncertainty. Moreover, in the group decision analysis, determining the weight of each criterion and the weight of each DM or expert is very significant issues that have been considered in the recent literature (Ayağ 2010; Yue 2011).

In this paper, a soft computing approach, IVHF-MCGA, is presented, in which a new IVHF-CS method is developed for estimating the relative importance of each DM under uncertainty. In addition, the classical entropy method is extended under an interval-valued hesitant fuzzy environment for specifying the weight of each criterion. In sum, the main contributions of this study are:

• Proposing a new version of the classical entropy method for the weight of each criterion under interval-valued hesitant fuzzy environment;

• Presenting a new interval-valued hesitant fuzzy weighting method based on the compromise solution for each DM or expert;

• Extending a new version of the classical COPRAS method under interval-valued hesitant fuzzy environment for the evaluation process;

• Developing a novel soft computing approach based on aggregating the DMs’ judgments at end of the group decision-making process for the prevention of the data loss; and

• Introducing some IVHF operators that are used in the proposed soft computing approach.

The paper is arranged as follows: in Sect. 2, we review some basic concepts and operations for IVHFSs. Also, some operators that are considered in the proposed soft computing approach are developed. In Sect. 3, we develop two new COPRAS and compromise solution methods under the interval-valued hesitant fuzzy environment to solve the MCGDM problems. In Sect. 4, three illustrative examples are provided to show the application of the proposed IVHF-MCGA approach in selecting the most suitable candidates. In addition, the comparative analysis for proposed IVHF-MCGA approach and the fuzzy group TOPSIS method from the literature is presented in Sect. 5. Finally, some conclusions and suggestions are demonstrated in Sect. 6.

2 Preliminaries

In this section, some basic assumptions and relations for the IVHFSs are defined. In the following, the subtraction and division operations are extended for the IVHFS.

Definition 1

(Torra 2010; Torra and Narukawa 2009) Let X be a universe set, then HFS on X in terms of a function E as which applied to X returns to subset of [0, 1].

$$\begin{aligned} E=\{<x,h_E (x)>\vert x\in X\} \end{aligned}$$

(1)

where $h_E (x)$ is defined as set of membership degrees for an element in subset of [0,1].

Definition 2

(Atanassov 1986, 1989, 2000) Let X be a reference set, then E on X is intuitionistic fuzzy set (IFS). In this respect, the membership degree and non-membership degree have been denoted by $\mu _E (\text{ x }_i )$ and $\nu _E (\text{ x }_i )$, respectively, such that $0\le \mu _E (x_i )+\nu _E (x_i )\le 1$ for $x_i \in X$.

$$\begin{aligned} E=\left\langle {x_i ,\mu _E (x_i ),\nu _E (x_i )} \right\rangle \quad \text{ for } \quad x_i \in X \end{aligned}$$

(2)

Definition 3

(Chen et al. 2013) Let X be a universe set, then the IVHFS on X is demonstrated as follows:

$$\begin{aligned} \tilde{E}=\left\{ {\left\langle {x_i ,\tilde{h}_{\tilde{E}} ( {x_i })} \right\rangle \vert x_i \in X,\,i=1,2,\ldots ,n} \right\} \end{aligned}$$

(3)

where $\widetilde{h}_{\widetilde{E}} ( {x_i })$ is represented by interval membership degrees for an element $x_i \in X$ under set E. Interval-valued hesitant fuzzy element (IVHFE) is shown by $\widetilde{h}_{\widetilde{E}} ( {x_i })$that satisfies the relation as below:

$$\begin{aligned} \widetilde{h}_{\widetilde{E}} ( {x_i })=\left\{ {\widetilde{\gamma }\vert \widetilde{\gamma }\in \widetilde{h}_{\widetilde{E}} ( {x_i })} \right\} \end{aligned}$$

(4)

where $\widetilde{\gamma }=\left[ {\widetilde{\gamma }^L,\widetilde{\gamma }^U} \right]$ is an interval number where $\widetilde{\gamma }^L$ and $\widetilde{\gamma }^U$ express the lower and upper bound of $\widetilde{\gamma }$, respectively.

Definition 4

(Chen et al. 2013). Let $\widetilde{h},\widetilde{h}_1$and $\widetilde{h}_2$ be three IVHFEs, then the following relations are defined:

$$\begin{aligned}&\widetilde{h}^c=\left\{ {\left[ {1-\widetilde{\gamma }^U,1-\widetilde{\gamma }^L} \right] \vert \widetilde{\gamma }\in \widetilde{h}} \right\} ;\end{aligned}$$

(5)

$$\begin{aligned}&\widetilde{h}_1 \cup \widetilde{h}_2 =\left\{ \left[ {\max ( {\widetilde{\gamma }_1^L ,\widetilde{\gamma }_2^L }),\max ( {\widetilde{\gamma }_1^U ,\widetilde{\gamma }_2^U })} \right] \right. \nonumber \\&\qquad \qquad \quad \left. \vert \widetilde{\gamma }_1 \in \widetilde{h}_1 ,\widetilde{\gamma }_2 \in \widetilde{h}_2 \right\} ;\end{aligned}$$

(6)

$$\begin{aligned}&\widetilde{h}_1 \cap \widetilde{h}_2 =\left\{ \left[ {\min ( {\widetilde{\gamma }_1^L ,\widetilde{\gamma }_2^L }),\min ( {\widetilde{\gamma }_1^U ,\widetilde{\gamma }_2^U })} \right] \right. \nonumber \\&\qquad \qquad \quad \left. \vert \widetilde{\gamma }_1 \in \widetilde{\gamma }_1 ,\widetilde{\gamma }_2 \in \widetilde{h}_2 \right\} ;\end{aligned}$$

(7)

$$\begin{aligned}&\widetilde{h}^\lambda =\left\{ {\left[ {( {\widetilde{\gamma }^L})^\lambda ,( {\widetilde{\gamma }^U})^\lambda } \right] \vert \widetilde{\gamma }\in \widetilde{h}} \right\} ,\quad \lambda >0;\end{aligned}$$

(8)

$$\begin{aligned}&\lambda \widetilde{h}=\left\{ {\left[ {1-( {1-\widetilde{\gamma }^L})^\lambda ,1-( {1-\widetilde{\gamma }^U})^\lambda } \right] \vert \widetilde{\gamma }\in \widetilde{h}} \right\} ,\quad \lambda >0;\end{aligned}$$

(9)

$$\begin{aligned}&\widetilde{h}_1 \oplus \widetilde{h}_2 =\left\{ \left[ {\widetilde{\gamma }_1^L +\widetilde{\gamma }_2^L -\widetilde{\gamma }_1^L \widetilde{\gamma }_2^L ,\widetilde{\gamma }_1^U +\widetilde{\gamma }_2^U -\widetilde{\gamma }_1^U \widetilde{\gamma }_2^U } \right] \right. \nonumber \\&\qquad \qquad \quad \left. \vert \widetilde{\gamma }_1 \in \widetilde{h}_1 ,\widetilde{\gamma }_2 \in \widetilde{h}_2 \right\} \end{aligned}$$

(10)

$$\begin{aligned}&\widetilde{h}_1 \otimes \widetilde{h}_2 =\left\{ {\left[ {\widetilde{\gamma }_1^L \widetilde{\gamma }_2^L ,\widetilde{\gamma }_1^U \widetilde{\gamma }_2^U } \right] \vert \widetilde{\gamma }_1 \in \widetilde{h}_1 ,\widetilde{\gamma }_2 \in \widetilde{h}_2 } \right\} \end{aligned}$$

(11)

Definition 5

Let $E=\left\{ {\widetilde{h}_1 ,\widetilde{h}_2 ,\ldots ,\widetilde{h}_n } \right\}$ be a collection of IVHFEs, then we propose the following extended operations based on Definition 4:

$$\begin{aligned}&\mathop \oplus \limits _{i=1}^n \widetilde{h}_i =\cup _{\widetilde{\gamma }_1 \in \widetilde{h}_1 ,\widetilde{\gamma }_2 \in \widetilde{h}_2 ,\ldots ,\widetilde{\gamma }_n \in \widetilde{h}_n }\nonumber \\&\quad \left\{ {\left[ {1-\prod \limits _{i=1}^n {(1-\widetilde{\gamma }_i^L ),1-\prod \limits _{i=1}^n {(1-\widetilde{\gamma }_i^U )} } } \right] } \right\} \end{aligned}$$

(12)

$$\begin{aligned}&\widetilde{h}_1 \otimes \widetilde{h}_2 \otimes \cdots \otimes \widetilde{h}_n=\cup _{\widetilde{\gamma }_1 \in \widetilde{h}_1 ,\widetilde{\gamma }_2 \in \widetilde{h}_2 ,\ldots ,\widetilde{\gamma }_n \in \widetilde{h}_n } \nonumber \\&\quad \left\{ {\left[ {\prod \limits _{i=1}^n {\widetilde{\gamma }_i^L } ,\prod \limits _{i=1}^n {\widetilde{\gamma }_i^U } } \right] } \right\} \end{aligned}$$

(13)

Theorem 1

Let $\widetilde{h}_1 =\left[ {\widetilde{\gamma }_1^L ,\widetilde{\gamma }_1^U } \right] ,\widetilde{h}_2 =\left[ {\widetilde{\gamma }_2^L ,\widetilde{\gamma }_2^U } \right] ,\widetilde{h}_3 =\left[ {\widetilde{\gamma }_3^L ,\widetilde{\gamma }_3^U } \right]$ be three IVHFEs; then, we have

$$\begin{aligned}&\tilde{h}_1^c \oplus \tilde{h}_2^c \oplus \tilde{h}_3^c =( {\tilde{h}_1^ \otimes \tilde{h}_2^ \otimes \tilde{h}_3 })^c\end{aligned}$$

(14)

$$\begin{aligned}&\tilde{h}_1^c \otimes \tilde{h}_2^c \otimes \tilde{h}_3^c =( {\tilde{h}_1 \oplus \tilde{h}_2 \oplus \tilde{h}_3 })^c \end{aligned}$$

(15)

Proof

For three IVHFEs $\tilde{h}_1 , \tilde{h}_2$ and $\tilde{h}_3$, we have

$$\begin{aligned}&\tilde{h}_1^ \oplus \tilde{h}_2^ \oplus \tilde{h}_3^ =\cup _{\tilde{\gamma }_1 \in \tilde{h}_1 ,\tilde{\gamma }_2 \in \tilde{h}_2 ,\tilde{\gamma }_3 \in \tilde{h}_3 } \nonumber \\&\quad \left\{ \left[ \tilde{\gamma }_1^L +\tilde{\gamma }_2^L +\tilde{\gamma }_3^L -\tilde{\gamma }_1^L \tilde{\gamma }_2^L -\tilde{\gamma }_1^L \tilde{\gamma }_3^L -\tilde{\gamma }_2^L \tilde{\gamma }_3^L +\tilde{\gamma }_1^L \right. \right. \nonumber \\&\quad \times \tilde{\gamma }_2^L \tilde{\gamma }_3^L ,\tilde{\gamma }_1^U +\tilde{\gamma }_2^U +\tilde{\gamma }_3^U -\tilde{\gamma }_1^U \tilde{\gamma }_2^U -\tilde{\gamma }_1^U \tilde{\gamma }_3^U -\tilde{\gamma }_2^U \tilde{\gamma }_3^U \nonumber \\&\quad \left. \left. +\tilde{\gamma }_1^U \tilde{\gamma }_2^U \tilde{\gamma }_3^U \right] \right\} \end{aligned}$$

(16)

$$\begin{aligned}&\tilde{h}_1^c \oplus \tilde{h}_2^c \oplus \tilde{h}_3^c =\cup _{\tilde{\gamma }_1 \in \tilde{h}_1 ,\tilde{\gamma }_2 \in \tilde{h}_2 ,\tilde{\gamma }_3 \in \tilde{h}_3 } \nonumber \\&\quad \left\{ {\left[ {1-\tilde{\gamma }_1^L .\tilde{\gamma }_2^L .\tilde{\gamma }_3^L ,1-\tilde{\gamma }_1^U .\tilde{\gamma }_2^U .\tilde{\gamma }_3^U } \right] } \right\} =( {\tilde{h}_1^ \otimes \tilde{h}_2^ \otimes \tilde{h}_3 })^c \end{aligned}$$

$$\begin{aligned}&\tilde{h}_1^ \otimes \tilde{h}_2^ \otimes \tilde{h}_3^ =\cup _{\tilde{\gamma }_1 \in \tilde{h}_1 ,\tilde{\gamma }_2 \in \tilde{h}_2 ,\tilde{\gamma }_3 \in \tilde{h}_3 } \left\{ {\left[ {\tilde{\gamma }_1^L \tilde{\gamma }_2^L \tilde{\gamma }_3^L ,\tilde{\gamma }_1^U \tilde{\gamma }_2^U \tilde{\gamma }_3^U } \right] } \right\} \nonumber \\&\qquad \times \tilde{h}_1^c \otimes \tilde{h}_2^c \otimes \tilde{h}_3^c =\cup _{\tilde{\gamma }_1 \in \tilde{h}_1 ,\tilde{\gamma }_2 \in \tilde{h}_2 ,\tilde{\gamma }_3 \in \tilde{h}_3 }\nonumber \\&\qquad \left\{ {\left[ {( {1-\tilde{\gamma }_1^L })( {1-\tilde{\gamma }_2^L })( {1-\tilde{\gamma }_3^L }),( {1-\tilde{\gamma }_1^U })( {1-\tilde{\gamma }_2^U })( {1-\tilde{\gamma }_3^U })} \right] } \right\} \nonumber \\&\quad =\left[ 1-\tilde{\gamma }_1^L -\tilde{\gamma }_2^L -\tilde{\gamma }_3^L +\tilde{\gamma }_1^L \tilde{\gamma }_2^L +\tilde{\gamma }_1^L \tilde{\gamma }_3^L +\tilde{\gamma }_2^L \tilde{\gamma }_3^L -\tilde{\gamma }_1^L \tilde{\gamma }_2^L \tilde{\gamma }_3^L ,\right. \nonumber \\&\left. 1-\tilde{\gamma }_1^U -\tilde{\gamma }_2^U -\tilde{\gamma }_3^U +\tilde{\gamma }_1^U \tilde{\gamma }_2^U +\tilde{\gamma }_1^U \tilde{\gamma }_3^U +\tilde{\gamma }_2^U \tilde{\gamma }_3^U -\tilde{\gamma }_1^U \tilde{\gamma }_2^U \tilde{\gamma }_3^U \right] \nonumber \\&\quad =( {\tilde{h}_1 \oplus \tilde{h}_2 \oplus \tilde{h}_3 })^c \end{aligned}$$

(17)

The generalized of relation (16) is represented, equivalent to Eq. (12), as follows:

$$\begin{aligned}&\tilde{h}_1 \oplus \tilde{h}_2 \oplus \cdots \oplus \tilde{h}_n^ =\cup _{\tilde{\gamma }_1 \in \tilde{h}_1 ,\tilde{\gamma }_2 \in \tilde{h}_2 ,\ldots ,\tilde{\gamma }_n \in \tilde{h}_n } \nonumber \\&\quad \left\{ \left( \sum \limits _{i=1}^n {\tilde{\gamma }_i^L } -\mathop {\sum \limits _{i=1}^{n-1} {\tilde{\gamma }_i^L .\tilde{\gamma }_j^L } }\limits _{\forall j=i+1,\ldots ,n} +\mathop {\mathop {\sum \limits _{i=1}^{n-2} {\tilde{\gamma }_i^L .\tilde{\gamma }_j^L .\tilde{\gamma }_k^L } }\limits _{\forall j=i+1,\ldots ,n-1} }\limits _{\forall k=j+1,\ldots ,n} -\cdots \right. \right. \nonumber \\&\quad \left. \left. +\prod \limits _{i=1}^n {\tilde{\gamma }_i^L } ,\sum \limits _{i=1}^n {\tilde{\gamma }_i^U } -\mathop {\sum \limits _{i=1}^{n-1} {\tilde{\gamma }_i^U .\tilde{\gamma }_j^U } }\limits _{\forall j=i+1,\ldots ,n} +\mathop {\mathop {\sum \limits _{i=1}^{n-2} {\tilde{\gamma }_i^U .\tilde{\gamma }_j^U .\tilde{\gamma }_k^U } }\limits _{\forall j=i+1,\ldots ,n-1} }\limits _{\forall k=j+1,\ldots ,n} -\cdots +\prod \limits _{i=1}^n {\tilde{\gamma }_i^U } \right) \right\} \nonumber \\&\quad \quad \forall i\ne j\ne k \end{aligned}$$

(18)

Thus, the proof of theorem 1 is complete $\square$

Definition 6

(Liao and Xu 2014) The subtraction and division operations for the HFS are defined by considering the operations of the IFS and regarding the correlation between IFS and HFS as follows:

(19)

(20)

Definition 7

We extend the subtraction and division operators based on definition 5 under IVHFSs as follows:

$$\begin{aligned}&\tilde{h}_1 -\tilde{h}_2 =\cup _{\tilde{\gamma }_1^l \in \tilde{h}_1 ,\tilde{\gamma }_2^l \in \tilde{h}_2 ,\tilde{\gamma }_1^u \in \tilde{h}_1 ,\tilde{\gamma }_2^u \in \tilde{h}_2 }\nonumber \\&\quad \left\{ {{\begin{array}{ll} {\left[ {\frac{\tilde{\gamma }_1^l -\tilde{\gamma }_2^l }{1-\tilde{\gamma }_2^l },\frac{\tilde{\gamma }_1^u -\tilde{\gamma }_2^u }{1-\tilde{\gamma }_2^u }} \right] } &{}\quad {\mathrm{if}\,\tilde{\gamma }_1^l \ge \tilde{\gamma }_2^l ,\tilde{\gamma }_1^u \ge \tilde{\gamma }_2^u \,\,\text{ and }\,\,\tilde{\gamma }_2^l ,\tilde{\gamma }_2^u \ne 1;} \\ 0 &{}\quad {\text{ otherwise }} \\ \end{array} }} \right\} \end{aligned}$$

(21)

$$\begin{aligned}&\frac{\tilde{h}_1 }{\tilde{h}_2 }=\cup _{\tilde{\gamma }_1^l \in \tilde{h}_1 ,\tilde{\gamma }_2^l \in \tilde{h}_2 ,\tilde{\gamma }_1^u \in \tilde{h}_1 ,\tilde{\gamma }_2^u \in \tilde{h}_2 }\nonumber \\&\quad \left\{ {{\begin{array}{ll} {\left[ {\frac{\tilde{\gamma }_1^l }{\tilde{\gamma }_2^l },\frac{\tilde{\gamma }_1^u }{\tilde{\gamma }_2^u }} \right] } &{}\quad {\text{ if }\,\tilde{\gamma }_1^l \le \tilde{\gamma }_2^l ,\tilde{\gamma }_1^u \le \tilde{\gamma }_2^u ,\,\,\tilde{\gamma }_1^l .\tilde{\gamma }_2^u \le \tilde{\gamma }_2^l .\tilde{\gamma }_1^u \,\text{ and }\,\,\tilde{\gamma }_2^l ,\tilde{\gamma }_2^u \ne 0;} \\ 1 &{}\quad {\text{ otherwise }} \\ \end{array} }} \right\} \end{aligned}$$

(22)

Theorem 2

Let $h_{1}$ and $h_{2}$ be two IVHFEs, then

$$\begin{aligned}&(\tilde{h}_1 -\tilde{h}_2 )\oplus \tilde{h}_2 =\tilde{h}_1\end{aligned}$$

(23)

$$\begin{aligned}&\left( {\frac{\tilde{h}_1 }{\tilde{h}_2 }}\right) \otimes \tilde{h}_2 =\tilde{h}_1 \end{aligned}$$

(24)

Proof

For two IVHFEs $\tilde{h}_1$ and $\tilde{h}_2$, we have

$$\begin{aligned}&(\tilde{h}_1 -\tilde{h}_2 ) \oplus \tilde{h}_2 =\tilde{h}_1 \nonumber \\&\quad =\cup _{\tilde{\gamma }_1^l \in \tilde{h}_1 ,\tilde{\gamma }_2^l \in \tilde{h}_2 ,\tilde{\gamma }_1^l \ge \tilde{\gamma }_2^l ,\tilde{\gamma }_2^l \ne 1,{\tilde{\gamma }_1^u \in \tilde{h}_1 ,\tilde{\gamma }_2^u \in \tilde{h}_2 ,\tilde{\gamma }_1^u \ge \tilde{\gamma }_2^u ,\tilde{\gamma }_2^u \ne 1}}\nonumber \\&\quad \quad \left\{ {\frac{\tilde{\gamma }_1^l -\tilde{\gamma }_2^l }{1-\tilde{\gamma }_2^l },\frac{\tilde{\gamma }_1^u -\tilde{\gamma }_2^u }{1-\tilde{\gamma }_2^u }} \right\} \oplus \tilde{h}_2 \nonumber \\&\quad =\cup _{{\tilde{\gamma }_1^l \in \tilde{h}_1 ,\tilde{\gamma }_2^l \in \tilde{h}_2 ,\tilde{\gamma }_1^l \ge \tilde{\gamma }_2^l ,\tilde{\gamma }_2^l \ne 1,}{\tilde{\gamma }_1^u \in \tilde{h}_1 ,\tilde{\gamma }_2^u \in \tilde{h}_2 ,\tilde{\gamma }_1^u \ge \tilde{\gamma }_2^u ,\tilde{\gamma }_2^u \ne 1}}\nonumber \\&\qquad \left\{ \frac{\tilde{\gamma }_1^l -\tilde{\gamma }_2^l }{1-\tilde{\gamma }_2^l }\right. \nonumber \\&\qquad \left. +\tilde{\gamma }_2^l -\frac{\tilde{\gamma }_1^l -\tilde{\gamma }_2^l }{1-\tilde{\gamma }_2^l }\tilde{\gamma }_2^l ,\frac{\tilde{\gamma }_1^u -\tilde{\gamma }_2^u }{1-\tilde{\gamma }_2^u }+\tilde{\gamma }_2^u -\frac{\tilde{\gamma }_1^u -\tilde{\gamma }_2^u }{1-\tilde{\gamma }_2^u }\tilde{\gamma }_2^u \right\} \nonumber \\&\quad =\cup _{{\tilde{\gamma }_1^l \in \tilde{h}_1 ,\tilde{\gamma }_2^l \in \tilde{h}_2 ,\tilde{\gamma }_1^l \ge \tilde{\gamma }_2^l ,\tilde{\gamma }_2^l \ne 1,}{\tilde{\gamma }_1^u \in \tilde{h}_1 ,\tilde{\gamma }_2^u \in \tilde{h}_2 ,\tilde{\gamma }_1^u \ge \tilde{\gamma }_2^u ,\tilde{\gamma }_2^u \ne 1}}\nonumber \\&\quad \quad \left\{ {\frac{\tilde{\gamma }_1^l ( {1-\tilde{\gamma }_2^l })}{1-\tilde{\gamma }_2^l },\frac{\tilde{\gamma }_1^u ( {1-\tilde{\gamma }_2^u })}{1-\tilde{\gamma }_2^u }} \right\} \nonumber \\&\quad =\cup _{\tilde{\gamma }_1^l \in \tilde{h}_1 } =\tilde{h}_1 \end{aligned}$$

(25)

$$\begin{aligned}&\left( \frac{\tilde{h}_1 }{\tilde{h}_2 }\right) \otimes \tilde{h}_2 =\tilde{h}_1 \nonumber \\&\quad =\cup _{{\tilde{\gamma }_1^l \in \tilde{h}_1 ,\tilde{\gamma }_2^l \in \tilde{h}_2 ,\tilde{\gamma }_1^l \le \tilde{\gamma }_2^l ,\tilde{\gamma }_2^l \ne 0,}{\tilde{\gamma }_1^u \in \tilde{h}_1 ,\tilde{\gamma }_2^u \in \tilde{h}_2 ,\tilde{\gamma }_1^u \le \tilde{\gamma }_2^u ,\tilde{\gamma }_2^u \ne 0}}\nonumber \\&\quad \quad \left\{ {\frac{\tilde{\gamma }_1^l }{\tilde{\gamma }_2^l },\frac{\tilde{\gamma }_1^u }{\tilde{\gamma }_2^u }} \right\} \otimes \tilde{h}_2 \nonumber \\&\quad =\cup _{{\tilde{\gamma }_1^l \in \tilde{h}_1 ,\tilde{\gamma }_2^l \in \tilde{h}_2 ,\tilde{\gamma }_1^l \le \tilde{\gamma }_2^l ,\tilde{\gamma }_2^l \ne 0,}{\tilde{\gamma }_1^u \in \tilde{h}_1 ,\tilde{\gamma }_2^u \in \tilde{h}_2 ,\tilde{\gamma }_1^u \le \tilde{\gamma }_2^u ,\tilde{\gamma }_2^u \ne 0}}\nonumber \\&\quad \quad \left\{ {\frac{\tilde{\gamma }_1^l }{\tilde{\gamma }_2^l }.\tilde{\gamma }_2^l ,\frac{\tilde{\gamma }_1^u }{\tilde{\gamma }_2^u }.\tilde{\gamma }_2^u } \right\} \nonumber \\&\quad =\cup _{{\tilde{\gamma }_1^l \in \tilde{h}_1 ,}{\tilde{\gamma }_1^u \in \tilde{h}_1 }} \left\{ {\tilde{\gamma }_1^l ,\tilde{\gamma }_1^u } \right\} =\tilde{h}_1 \end{aligned}$$

(26)

Thus, the proof of theorem 2 is complete $\square$

Definition 8

(Farhadinia 2013) Consider $\tilde{M}$ and$\tilde{N}$ as two IVHFSs on X. The component-wise ordering and the total ordering are defined as two types of ordering of IVHFSs, respectively, as follows:

$$\begin{aligned}&\tilde{M}\le \tilde{N}\quad if\quad h_{\tilde{M}}^{\sigma ( j)L} ( {x_i })\le h_{\tilde{N}}^{\sigma ( j)L} ( {x_i }),\nonumber \\&h_{\tilde{M}}^{\sigma ( j)U} ( {x_i })\le h_{\tilde{N}}^{\sigma ( j)U} ( {x_i })\nonumber \\&\quad \forall i=1,2,\ldots ,n;\quad j=1,2,\ldots ,l_{x_i }\end{aligned}$$

(27)

$$\begin{aligned}&\tilde{M}\mathop \prec \limits _- \tilde{N}\quad if\, Score( {\tilde{M}})\le Score( {\tilde{N}\,})\end{aligned}$$

(28)

$$\begin{aligned}&Score( {\tilde{M}})=\frac{1}{n}\sum \limits _{i=1}^n {\left( {\frac{1}{l_{x_i } }\sum \limits _{j=1}^{l_{x_i } } {\left[ {\frac{\,h_{\tilde{M}}^{\sigma ( j)L} ( {x_i })+h_{\tilde{M}}^{\sigma ( j)U} ( {x_i })}{2}} \right] } }\right) }\nonumber \\ \end{aligned}$$

(29)

where $h_M$ and $h_N$ are IVHFSs which represented as $h_{\tilde{M}}^{\sigma (j)} ( {x_i })=\left[ {h_{\tilde{M}}^{\sigma (j)L} ( {x_i }),h_{\tilde{M}}^{\sigma (j)U} ( {x_i })} \right]$, $h_{\tilde{N}}^{\sigma (j)} ( {x_i })=\Big [ h_{\tilde{N}}^{\sigma (j)L}( {x_i }),h_{\tilde{N}}^{\sigma (j)U} ( {x_i }) \Big ]$, respectively; also, $h_{\tilde{M}}^{\sigma (j)}$and $h_{\tilde{N}}^{\sigma (j)}$are the jth largest intervals in $h_{\tilde{M}} ( {x_i })$ and $h_{\tilde{N}} ( {x_i })$, respectively.

Assumptions The number of intervals in various IVHFEs may be different. Assume that the number of intervals in $h_{\tilde{M}} ( x)$ is denoted by $l( {h_{\tilde{M}} ( x)})$. In this respect, two assumptions are made as follows:

• (A1) In each $h_{\tilde{M}} ( x)$, all the elements have to be arranged in increasing order, and

• (A2) If $l( {h_{\tilde{M}} ( x)})\ne l( {h_{\tilde{N}} ( x)})$, then $l_x =\max \{ l( {h_{\tilde{M}} ( x)}),l( {h_{\tilde{N}} ( x)}) \}$ for some $x\in X$. Two IVHFEs such as $h_{\tilde{M}} ( x)$and $h_{\tilde{N}} ( x)$ should have the same length when compared. If $h_{\tilde{M}} ( x)$ has less elements than in$h_{\tilde{N}} ( x)$, then $h_{\tilde{M}} ( x)$ should be extended based on an optimistic approach, in which value it has to be added$( {h_{\tilde{M}} ( x)})$.

Definition 9

(Chen et al. 2013) The interval-valued hesitant fuzzy Euclidean distance measure and the interval-valued hesitant fuzzy hamming distance measure are defined, respectively, as follows:

$$\begin{aligned} d( {\tilde{h}_M ,\tilde{h}_N })= & {} \sqrt{\frac{1}{2l_{x_i } }\sum \limits _{j=1}^{l_{x_i } } {\left( {\left| {\tilde{h}_M^{\sigma (j)L} ( {x_i })-\tilde{h}_N^{\sigma (j)L} ( {x_i })} \right| ^2+\left| {\tilde{h}_M^{\sigma (j)U} ( {x_i })-\tilde{h}_N^{\sigma (j)U} ( {x_i })} \right| ^2}\right) } }\end{aligned}$$

(30)

$$\begin{aligned} d( {\tilde{h}_M ,\tilde{h}_N })= & {} \frac{1}{2l_{x_i } }\sum \limits _{j=1}^{l_{x_i } } \left( \left| {\tilde{h}_M^{\sigma (j)L} ( {x_i })-\tilde{h}_N^{\sigma (j)L} ( {x_i })} \right| +\left| {\tilde{h}_M^{\sigma (j)U} ( {x_i })-\tilde{h}_N^{\sigma (j)U} ( {x_i })} \right| \right) \end{aligned}$$

(31)

Definition 10

(Chen et al. 2013) The interval-valued hesitant fuzzy geometric (IVHFG) relation is defined below:

$$\begin{aligned}&IVHFG( {\tilde{h}_1 ,\tilde{h}_2 ,\ldots ,\tilde{h}_n })=\left( {\mathop \otimes \limits _{j=1}^n ( {\tilde{h}_j })^{\frac{1}{n}}}\right) \nonumber \\&\quad =\cup _{\tilde{\gamma }_1 \in \tilde{h}_1 ,\tilde{\gamma }_2 \in \tilde{h}_2 ,\ldots ,\tilde{\gamma }_n \in \tilde{h}_n } \left\{ {\left[ {\prod \limits _{j=1}^n {( {\tilde{\gamma }_j^L })^{\frac{1}{n}}} ,\prod \limits _{j=1}^n {( {\tilde{\gamma }_j^U })^{\frac{1}{n}}} } \right] } \right\} \nonumber \\ \end{aligned}$$

(32)

Definition 11

(Chen et al. 2013) The interval-valued fuzzy hesitant weighted geometric (IVHFWG) relation is expressed below:

$$\begin{aligned}&IVHFWG( {\tilde{h}_1 ,\tilde{h}_2 ,\ldots ,\tilde{h}_n })=\left( {\mathop \otimes \limits _{j=1}^n ( {\tilde{h}_j })^{w_j}}\right) \nonumber \\&\quad =\cup _{\tilde{\gamma }_1 \in \tilde{h}_1 ,\tilde{\gamma }_2 \in \tilde{h}_2 ,\ldots ,\tilde{\gamma }_n \in \tilde{h}_n } \left\{ {\left[ {\prod \limits _{j=1}^n {( {\tilde{\gamma }_j^L })^{w_j}} ,\prod \limits _{j=1}^n {( {\tilde{\gamma }_j^U })^{w_j}} } \right] } \right\} \nonumber \\ \end{aligned}$$

(33)

where $w=( {w_1 ,w_2 ,\ldots ,w_n })^T$ are the weight vector of $\tilde{h}_j ( {j=1,2,\ldots ,n})$ and $w_j >0,\,\sum \limits _{j=1}^n {w_j } =1$.

Definition 12

(Zhang et al. 2014) In MCGDM problems, there are two kinds of attributes such as benefit and cost types. In this respect, the cost attributes’ values are transformed to benefit attributes’ values; i.e., the interval-valued hesitant fuzzy decision matrix $( {\tilde{H}=( {\tilde{h}_{ij} })_{m\times n} })$ is normalized $( {\tilde{B}=( {\tilde{b}_{ij} })_{m\times n} })$ based on the following relations:

$$\begin{aligned} \tilde{b}_{ij}&=\left\{ {{\begin{array}{ll} {\left\{ {\left[ {\tilde{\gamma }_{ij}^l ,\tilde{\gamma }_{ij}^u } \right] } \right\} } &{}\quad {\text{ for }\,\text{ positive }\,\text{ criteria }} \\ {\left\{ {\left[ {1-\tilde{\gamma }_{ij}^u ,1-\tilde{\gamma }_{ij}^l } \right] } \right\} } &{}\quad {\text{ for }\,\text{ negative }\,\text{ criteria }} \\ \end{array} }} \right. \nonumber \\&\quad \forall i=1,2,\ldots ,m;\quad j=1,2,\ldots ,n \end{aligned}$$

(34)

3 Proposed soft computing approach based on IVHF-MCGA method

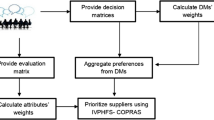
In this section, the proposed IVHF-MCGA approach is introduced, which is composed of three methods: the COPRAS method is tailored based on the IVHFSs for sorting of the candidate alternatives; the IVHF-entropy method and IVHF-CS method are developed to determine the weights of criteria and DMs, respectively. In this respect, the structure of the proposed IVHF-MCGA approach is depicted in Fig. 1.

Fig. 1

Structure of the proposed IVHF-MCGA approach

Step 1. Determine important criteria which satisfy the potential alternatives.

Step 2. Construct the interval-valued hesitant fuzzy decision matrix (IVHF-decision matrix) from a committee of DMs as follows:

$$\begin{aligned} M=\begin{array}{cc} &{} \begin{array}{lll} C_1 &{} \qquad \qquad \cdots &{} \qquad \qquad C_n \\ \end{array}\\ &{} \begin{array}{c} {A_1 } \\ \vdots \\ {A_m } \\ \end{array}\left[ \begin{array}{ccc} {\left\{ {\left[ {\mu _{11}^{L1} ,\mu _{11}^{U1} } \right] ,\left[ {\mu _{11}^{L2} ,\mu _{11}^{U2} } \right] ,\ldots ,\left[ {\mu _{11}^{Lk} ,\mu _{11}^{Uk} } \right] } \right\} } &{} \cdots &{} {\left\{ {\left[ {\mu _{1n}^{L1} ,\mu _{1n}^{U1} } \right] ,\left[ {\mu _{1n}^{L2} ,\mu _{1n}^{U2} } \right] ,\ldots ,\left[ {\mu _{1n}^{Lk} ,\mu _{1n}^{Uk} } \right] } \right\} } \\ \vdots &{} \ddots &{} \vdots \\ {\left\{ {\left[ {\mu _{m1}^{L1} ,\mu _{m1}^{U1} } \right] ,\left[ {\mu _{m1}^{L2} ,\mu _{m1}^{U2} } \right] ,\ldots ,\left[ {\mu _{m1}^{Lk} ,\mu _{m1}^{Uk} } \right] } \right\} } &{} \cdots &{} {\left\{ {\left[ {\mu _{mn}^{L1} ,\mu _{mn}^{U1} } \right] ,\left[ {\mu _{mn}^{L2} ,\mu _{mn}^{U2} } \right] ,\ldots ,\left[ {\mu _{mn}^{Lk} ,\mu _{mn}^{Uk} } \right] } \right\} } \\ \end{array}\right] _{m\times n} \\ \end{array} \end{aligned}$$

(35)

Step 3. Estimate criteria weights by the proposed IVHF-entropy method regarding DMs’ opinions.

Step 3.1. Construct the aggregated IVHF-decision matrix $( {M_\mathrm{Agg} })$ based on Definition 10 as follows:

$$\begin{aligned}&\left[ {\mu _{ij}^L ,\mu _{ij}^U } \right] =\mathrm{IVHFG}( {\tilde{h}_{p1} ,\tilde{h}_{p2} ,\ldots ,\tilde{h}_{pk} })=\left( {\mathop \otimes \limits _{k=1}^K ( {\tilde{h}_{pk} })^{\frac{1}{k}}}\right) \nonumber \\&\quad =\cup _{\tilde{\gamma }_{p1} \in \tilde{h}_{p1} ,\tilde{\gamma }_{p2} \in \tilde{h}_{p2} ,\ldots ,\tilde{\gamma }_{pk} \in \tilde{h}_{pk} } \left\{ {\left[ {\prod \limits _{k=1}^K {( {\tilde{\gamma }_{pk}^L })^{\frac{1}{k}}} ,\prod \limits _{k=1}^K {( {\tilde{\gamma }_{pk}^U })^{\frac{1}{k}}} } \right] } \right\} \nonumber \\ \end{aligned}$$

(36)

(37)

Step 3.2. Aggregate the DMs’ judgments about the relative importance of criteria $( {\tilde{h}_{wk} })$ by the following relation:

$$\begin{aligned} \upsilon _j= & {} \mathrm{IVHFG}( {\tilde{h}_{w1} ,\tilde{h}_{w2} ,\ldots ,\tilde{h}_{wk} })=\left( {\mathop \otimes \limits _{k=1}^K ( {\tilde{h}_{wk} })^{\frac{1}{k}}}\right) \nonumber \\= & {} \cup _{\tilde{\gamma }_{w1} \in \tilde{h}_{w1} ,\tilde{\gamma }_{w2} \in \tilde{h}_{w2} ,\ldots ,\tilde{\gamma }_{wk} \in \tilde{h}_{wk} }\nonumber \\&\left\{ {\left[ {\prod \limits _{k=1}^K {( {\tilde{\gamma }_{wk}^L })^{\frac{1}{k}}} ,\prod \limits _{k=1}^K {( {\tilde{\gamma }_{wk}^U })^{\frac{1}{k}}} } \right] } \right\} \end{aligned}$$

(38)

Step 3.3. Specify the $T_{ij} =\left[ {T_{ij}^l ,\text{ T }_{ij}^u } \right]$ by the following relations:

$$\begin{aligned} T_{ij}^l =\left\{ {{\begin{array}{ll} {\frac{\mu _{ij}^l }{1-\prod \limits _{i=1}^m {(1-\mu _{ij}^l )} }\,} &{}\quad {\text{ if }\,\mu _{ij}^l \le 1-\prod \limits _{i=1}^m {(1-\mu _{ij}^l )} \,\,\text{ and }\,\,1-\prod \limits _{i=1}^m {(1-\mu _{ij}^l )} \ne 0} \\ 1 &{}\quad {\text{ Otherwise }} \\ \end{array} }} \right. \end{aligned}$$

(39)

$$\begin{aligned} T_{ij}^u =\left\{ {{\begin{array}{ll} {\frac{\mu _{ij}^u }{1-\prod \limits _{i=1}^m {(1-\mu _{ij}^u )} }} &{}\quad {\text{ if }\,\mu _{ij}^u \le 1-\prod \limits _{i=1}^m {(1-\mu _{ij}^u )} \,\,\text{ and }\,\,1-\prod \limits _{i=1}^m {(1-\mu _{ij}^u )} \ne 0} \\ 1 &{}\quad {\text{ Otherwise }} \\ \end{array} }} \right. \end{aligned}$$

(40)

Step 3.4. Specify the interval-valued hesitant fuzzy degree of deviation or interval-valued hesitant fuzzy unreliability of each criterion regarding interval-valued hesitant fuzzy entropy ($E_j =[ {E_j^l ,E_j^u }])$ as follows:

$$\begin{aligned} d_j =\left[ {\left( {\prod \limits _{i=1}^m {( {1-T_{ij}^l })^{Ln( {T_{ij}^l })}} }\right) ^{-\frac{1}{Ln( m)}},\left( {\prod \limits _{i=1}^m {( {1-T_{ij}^u })^{Ln( {T_{ij}^u })}} }\right) ^{-\frac{1}{Ln( m)}}} \right] \end{aligned}$$

(41)

Step 3.5. Determine the final criteria weights $( {w_j})$ by according to DMs’ opinions.

$$\begin{aligned} w_j =\frac{\upsilon _j^l .d_j^l \left( {\sum \nolimits _{j=1}^n {\upsilon _j^u .d_j^u } }\right) +\upsilon _j^u .d_j^u \left( {\sum \nolimits _{j=1}^n {\upsilon _j^l .d_j^l } }\right) }{2\left( {\sum \nolimits _{j=1}^n {\upsilon _j^l .d_j^l } }\right) \left( {\sum \nolimits _{j=1}^n {\upsilon _j^u .d_j^u } }\right) }\quad \forall j \end{aligned}$$

(42)

Step 4. Estimate the DMs’ weights by the proposed IVHF-CS method.

Step 4.1.Establish the weighted normalized IVHF-decision matrix for each DM based on Definition 12.

$$\begin{aligned} M_k =\begin{array}{c} \begin{array}{llll} \qquad \qquad C_1 &{} \qquad \qquad C_2 &{} \qquad \cdots &{} \qquad \qquad C_n \\ \end{array}\\ \begin{array}{c} {A_1 } \\ \vdots \\ {A_m } \\ \end{array} \left( \begin{array}{cccc} \left[ {\mu _{11}^{Lk} ,\mu _{11}^{Uk} } \right] &{} \left[ {\mu _{12}^{Lk} ,\mu _{12}^{Uk} } \right] &{} \cdots &{} {\left[ {\mu _{1n}^{Lk} ,\mu _{1n}^{Uk} } \right] } \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ \left[ {\mu _{m1}^{Lk} ,\mu _{m1}^{Uk} } \right] &{} \left[ {\mu _{m2}^{Lk} ,\mu _{m2}^{Uk} } \right] &{} \cdots &{} {\left[ {\mu _{mn}^{Lk} ,\mu _{mn}^{Uk} } \right] } \\ \end{array}\right) _{m\times n} \end{array} \end{aligned}$$

(43)

Step 4.2. Estimate the interval-valued hesitant fuzzy positive ideal solution (IVHF-PIS) and interval-valued hesitant fuzzy negative ideal solution (IVHF-NIS) based on the following relations:

(44)

(45)

where the average of group decision matrix is computed as follows:

$$\begin{aligned}&\mu _{ij}^{*L} =\frac{1}{K}\sum \limits _{k=1}^K {\mu _{ij}^{Lk} }\end{aligned}$$

(46)

$$\begin{aligned}&\mu _{ij}^{*U} =\frac{1}{K}\sum \limits _{k=1}^K {\mu _{ij}^{Uk} }\end{aligned}$$

(47)

$$\begin{aligned}&\mu _{ij}^{-L} =\mathop {\min }\limits _k \left\{ {\mu _{ij}^{Lk} } \right\} \end{aligned}$$

(48)

$$\begin{aligned}&\mu _{ij}^{-U} =\mathop {\max }\limits _k \left\{ {\mu _{ij}^{Uk} } \right\} \end{aligned}$$

(49)

Step 4.3. Compute the separation measure for the matrix of each DM from the IVHF-PIS and IVHF-NIS by applying the interval-valued hesitant fuzzy Euclidean distance measure. In this regard, the distance measure is developed to the n-dimensional interval-valued hesitant fuzzy Euclidean distance measure as below:

$$\begin{aligned} \xi _k^*=\sqrt{\frac{1}{2l_{x_i } }\sum \limits _{i=1}^m {\sum \limits _{j=1}^n {\sum \limits _{\lambda =1}^{l_{x_i } } {\left( {\left| {\mu _{ij}^{Lk\sigma ( \lambda )} ( {x_i })-A_{ij}^{*L\sigma ( \lambda )} ( {x_i })} \right| ^2+\left| {\mu _{ij}^{Uk\sigma ( \lambda )} ( {x_i })-A_{ij}^{*U\sigma ( \lambda )} ( {x_i })} \right| ^2}\right) } } } } \quad \forall k \end{aligned}$$

(50)

$$\begin{aligned} \xi _k^- =\sqrt{\frac{1}{2l_{x_i } }\sum \limits _{i=1}^m {\sum \limits _{j=1}^n {\sum \limits _{\lambda =1}^{l_{x_i } } {\left( {\left| {\mu _{ij}^{Lk\sigma ( \lambda )} ( {x_i })-A_{ij}^{-L\sigma ( \lambda )} ( {x_i })} \right| ^2+\left| {\mu _{ij}^{Uk\sigma ( \lambda )} ( {x_i })-A_{ij}^{-U\sigma ( \lambda )} ( {x_i })} \right| ^2}\right) } } } } \quad \forall k \end{aligned}$$

(51)

Step 4.4. Determine the weight of each DM $( {\varpi _k })$ by considering the following relation:

$$\begin{aligned} \varpi _k =\frac{\xi _k^- }{( {\xi _k^- +\xi _k^*})\left( {\sum \nolimits _{k=1}^K {\frac{\xi _k^- }{\xi _k^- +\xi _k^*}} }\right) }\,\forall k \end{aligned}$$

(52)

Step 5. Calculate sums $p_i^k =\left[ {p_i^{lk} ,p_i^{uk} } \right]$ of positive criteria values with respect to the weighted normalized IVHF-decision matrix for each DM in Step 4.1:

$$\begin{aligned} p_i^k =\left[ {1-\prod \limits _{j=1}^r {(1-\mu _{ij}^{lk} )} ,1-\prod \limits _{j=1}^r {(1-\mu _{ij}^{uk} )} } \right] \quad \forall k,i \end{aligned}$$

(53)

where r is the number of positive criteria. It is supposed that in the IVHF-decision matrix, first columns are placed by positive criteria and negative criteria are placed after.

Step 6. Computing sums $R_i^k =[ {R_i^{lk} ,R_i^{uk} }]$ of criteria values which are negative criteria for each potential alternative with respect to weighted normalized hesitant fuzzy decision matrix for each DM in Step 4.1.

$$\begin{aligned} R_i^k =\left[ {1-\prod \limits _{j=r+1}^n {(1-\mu _{ij}^{lk} )} ,1-\prod \limits _{j=r+1}^n {(1-\mu _{ij}^{uk} )} } \right] \quad \forall k,i \end{aligned}$$

(54)

Step 7. Determine the smallest value of $R_i^k =[ {R_i^{lk} ,R_i^{uk} }]$ as follows:

$$\begin{aligned} R_{\min }^k =\left[ {\mathop {\min }\limits _i ( {R_i^{lk} }),\mathop {\min }\limits _i ( {R_i^{uk} })} \right] \quad \forall k \end{aligned}$$

(55)

Step 8. Calculate the interval-valued hesitant fuzzy relative importance of each alternative $( {Q_i^k =\left[ {Q_i^{lk} ,Q_i^{uk} } \right] })$ regarding each DM as follows:

$$\begin{aligned} Q_i^k&=\left[ P_i^{lk} +( {1-P_i^{lk} })\left( {\frac{1-\left( {\prod \nolimits _i^m {( {1-R_i^{lk} })} }\right) ^{R_{\min }^{lk} }}{1-\left( {\prod \nolimits _i^m {\left( {1-\frac{R_{\min }^{lk} }{R_i^{lk} }}\right) } }\right) ^{R_i^{lk} }}}\right) ,P_i^{uk}\right. \nonumber \\&\left. +\,( {1-P_i^{uk} })\left( {\frac{1-\left( {\prod \nolimits _i^m {( {1-R_i^{uk} })} }\right) ^{R_{\min }^{uk} }}{1-\left( {\prod \nolimits _i^m {\left( {1-\frac{R_{\min }^{uk} }{R_i^{uk} }}\right) } }\right) ^{R_i^{uk} }}}\right) \right] \forall k,i \end{aligned}$$

(56)

Step 9. Determine each $Q_i$ value by utilizing the IVHFG by considering the DMs’ weights as follows:

$$\begin{aligned} Q_i= & {} \mathrm{IVHFWG}( {Q_i^{l1} ,Q_i^{l2} ,\ldots ,Q_i^{lk} })=\left( {\mathop \otimes \limits _{k=1}^K ( {\tilde{Q}_i^k })^{\varpi _k}}\right) \nonumber \\= & {} \cup _{\tilde{Q}_1 \in \tilde{h}_{q1} ,\tilde{Q}_2 \in \tilde{h}_{q2} ,\ldots ,\tilde{Q}_k \in \tilde{h}_{qk} } \nonumber \\&\times \left\{ {\left[ {\prod \limits _{k=1}^K {( {Q_i^{lk} })^{\varpi _k^l }} ,\prod \limits _{k=1}^K {( {Q_i^{uk} })^{\varpi _k^u }} } \right] } \right\} \forall i \end{aligned}$$

(57)

Step 10. Compute the interval-valued hesitant fuzzy utility degree of each possible alternative as below:

$$\begin{aligned} N_i =\left[ {\frac{Q_i^l }{\max ( {Q_i^l })},\frac{Q_i^u }{\max ( {Q_i^u })}} \right] 100\,\% \end{aligned}$$

(58)

Step 11. Rank the alternatives by selecting the maximum value of interval-valued hesitant fuzzy utility degree by ordering relation based on Definition 8.

4 Application of the proposed IVHF-MCGA method in solving the MCGDM problems

4.1 Illustrative example 1: robot selection

The practical application from Vahdani et al. (2014) is used to show the suitability and feasibility of the proposed IVHF-MCGA method. Suppose that a manufacturing company needs a robot for implementing the material-handling assessment. In this respect, for further assessment, three robots ($R_{i}$, $i=1,2,3)$ are selected for the MCGDM problem. Also, six criteria are considered for rating the potential alternatives as follows:

• Man–machine interface ($C_{1})$;

• Programming flexibility ($C_{2})$;

• Vendor’s service contract ($C_{3})$;

• Load capacity ($C_{4})$;

• Positioning accuracy ($C_{5})$; and

• Purchase cost ($C_{6})$.

In the robot selection problem, consider four DM (${\mathrm{DM}_{k}}$, $k=1,2,3,4$) to evaluate the alternatives with respect to criteria and to choose the best robot candidate. Tables 2 and 3 provide values of hesitant linguistic variables for relative importance of criteria and ratings of the alternatives. Table 4 indicates the IVHF-decision matrix by linguistic variables, and also the relative importance of each criterion as assessed by DMs’ opinions is indicated in Table 5.

Table 2 Linguistic variables for rating the importance of criteria

Table 3 Linguistic variables for rating the potential alternatives

Table 4 Performance rating of the alternatives by linguistic variables for the first illustrative example

Table 5 Decision makers’ judgments about criteria weights for the first illustrative example

Table 6 Aggregated IVHF-decision matrix and $T_{ij}$ matrix for the first illustrative example

Table 7 Interval-valued hesitant fuzzy unreliability ($d_{j})$, aggregated DMs’ opinions ($\upsilon _j )$ and final weights of criteria ($w_{j})$ for the first illustrative example

The interval-valued hesitant fuzzy entropy method is proposed to determine the weight of each criterion. As indicated in Table 6, firstly, we establish an aggregated IVHF-decision matrix and then construct the $T_{ij}$ matrix. In this regard, the interval-valued hesitant fuzzy degree of deviation or the interval-valued hesitant fuzzy unreliability is computed and the DMs’ opinions for criteria weights are considered for decreasing the error of determining the criteria weights. Thus, the DMs’ judgments are aggregated and the final weights of each criterion are computed by Eq. (42). Regarding the mentioned results given in Table 7, the weight of each DM is also computed by the proposed IVHF-CS method as mentioned in Steps 4.1–4.4. As represented in Table 8, the separation measure is calculated using the n-dimensional interval-valued fuzzy Euclidean distance. In addition, the relative closeness and the final weight of each DM are computed.

In the following, the process of the proposed IVHF-MCGA method, the sum of positive criteria values/negative criteria values and the minimum value of negative criteria values are determined by Eqs. (53)–(55). The above-mentioned results are indicated in Tables 9 and 10. In addition, as shown in Table 11, the interval-valued hesitant fuzzy relative importance of each potential alternative and each DM ($Q_i^k )$ is computed by Eq. (56). Hence, the $Q_i^k$values are aggregated for determining the interval-valued hesitant fuzzy utility degree. Finally, the potential alternatives are ranked by selecting the maximum value of interval-valued hesitant fuzzy utility degrees. In this regard, two types of ordering as component-wise ordering and total ordering are considered to sort the interval-valued hesitant fuzzy utility degree. Thus, the proposed approach shows that the $R_{3}$ is the best alternative for the MCGDM problem. The results are compared to the Vahdani et al. (2014) method that indicates the verification and validation of the proposed IVHF-MCGA method. Results are provided in Table 12.

Table 8 Computational results for determining the DMs’ weights for the first illustrative example

Table 9 $P_{i}$ values regarding each DM for the first illustrative example

Table 10 $R_{i}$ values regarding each DM for the first illustrative example

Table 11 Final $Q_{i}$ values regarding each DM for the first illustrative example

Table 12 Final rankings based on the $Q_{i}$ values by considering two types of ordering and the comparative analysis for the first illustrative example

In addition, the aforementioned case study is solved by the decision method of Liu et al. (2014), and the same ranking results are achieved and are shown in Table 12. Therefore, the proposed IVHF-MCGA approach is investigated by comparing the ranking results with two recent fuzzy decision methods in the literature.

4.2 Illustrative example 2: industrial site selection

Another illustrative example from Wang (2014) is provided for industrial site selection problem to further investigate the proposed IVHF-MCGA approach. In this case, four DMs are employed (k=1,2,...,4) and also three candidate alternatives ($A_{1}, A_{2}, A_{3})$ are considered to select the most suitable site for building a new factory under the following six criteria:

• Climate condition ($C_{1})$;

• Regional demand ($C_{2})$;

• Expansion possibility ($C_{3})$;

• Transportation availability ($C_{4})$;

• Labor force ($C_{5})$; and

• Investment cost ($C_{6})$.

The DMs have expressed their preferences values about the candidate sites versus the selected criteria by linguistic variables and indicated in Table 13. In addition, the DMs’ judgments about the weight of each criterion are shown based on the linguistic terms in Table 14.

Table 13 Linguistic evaluations by DMs for the second illustrative example

Table 14 Decision makers’ judgments about criteria weights for the second illustrative example

Table 15 Aggregated IVHF-decision matrix and $T_{ij}$ matrix for the second illustrative example

The weight of each criterion is obtained based on the IVHF-entropy method. In this case, the aggregated IVHF-decision matrix and then the $T_{ij}$ matrix are established. Also, the IVHF-unreliability/degree of deviation is calculated and then the DMs’ opinions about the weights of criteria are aggregated. Therefore, the final weights are obtained based on the aforementioned results. The results are reported in Tables 15 and 16. In addition, the weight of each DM is obtained based on the proposed IVHF-CS method and represented in Table 17.

Table 16 Interval-valued hesitant fuzzy unreliability ($d_{j})$, aggregated DMs’ opinions ($\upsilon _j )$ and final weights of criteria ($w_{j})$ for the second illustrative example

The $P_{i}$ and $R_{i}$ values regarding preferences of DMs’ judgments are computed and indicated in Tables 18 and 19, respectively. Then, the interval-valued hesitant fuzzy relative importance of each candidate site for each DM is determined based on the sum of positive criteria values/negative criteria values. Hence, IVHF-utility degree for each candidate site is calculated based on the aggregated IVHF-relative importance of each candidate site. The mentioned results are shown in Table 20. Consequently, two types of ordering are applied to rank the candidate sites by decreasing the value of the IVHF-utility degrees. However, as represented in Table 21, the most suitable site for building a new factory is the second candidate site and the worst candidate site is $A_{3}$. Also, to validate the proposed IVHF-MCGA approach, the ranking results are compared to the method used by Wang (2014), which shows the same results.

In the previous, solving two industrial applications and comparing the ranking results with some recent decision methods from the literature are presented; then, the proposed IVHF-MCGA approach is validated for industrial selection problems. Hence, it can be concluded that the proposed IVHF-MCGA can be more accurate and reliable regarding the above analysis and indicating the review of the literature as shown in Table 1. Finally, this study has the following advantages versus recent decision methods in the literature: (1) some IVHF-operators are introduced for establishing the soft computing approach; (2) an IVHF-entropy method is proposed to determine the criteria weights; (3) a novel method based on the compromise solution is presented to specify the weight of each DM; (4) the COPRAS method is developed with IVHFSs for evaluation and selection process; and (5) the preferences of DMs’ judgments are aggregated in the last step to prevent the loss of data.

Table 17 Computational results for determining the DMs’ weights for the second illustrative example

Table 18 $P_{i}$ values regarding each DM for the second illustrative example

Table 19 $R_{i}$ values regarding each DM for the second illustrative example

Table 20 Final $Q_{i}$ values regarding each DM for the second illustrative example

Table 21 Final ranking based on the $Q_{i}$ values by considering two types of ordering and the comparative analysis for the second illustrative example

Table 22 Performance rating of the alternatives versus objective and subjective criteria

4.3 Illustrative example 3: rapid prototyping process selection

The third illustrative example about the rapid prototyping process (RPP) selection is provided by Byun and Lee (2005) and Rao (2013) as a well-known decision-making issue in the manufacturing problems to show the further applicability of the proposed IVHF-MCGA approach. In this case, six alternatives ($\mathrm{RPP}_{1}, \mathrm{RPP}_{2},\ldots ,\mathrm{RPP}_{6}$) as rapid prototyping processes (i.e., SLA3500, SLS2500, FDM8000, LOM1015, Quadra, Z402) are judged by four DMs ($k=1,2,{\ldots },4$) under six objective and subjective criteria. The following are the aforementioned criteria:

• Accuracy ($C_{1})$;

• Part cost ($C_{2})$;

• Roughness ($C_{3})$;

• Build time ($C_{4})$;

• Strength ($C_{5})$; and

• Elongation ($C_{6})$.

The performance rating of RPP candidates under the objective and subjective criteria is indicated in Table 22. In addition, the weight of each criterion based on the preferences of the DMs is presented in Table 23.

Table 23 Decision makers’ judgments about criteria weights for the third illustrative example

Table 24 Computational results of aggregated DMs’ opinions about criteria weights ($\upsilon _j )$, final weights of criteria ($w_{j})$ and DMs’ weights for the third illustrative example

Table 25 Final $Q_{i}$ values regarding each DM for the third illustrative example

In Table 24, the aggregated DMs’ opinions about the criteria weights and the final weights of criteria based on the proposed IVHF-entropy method are demonstrated. Also, the computational results of proposed IVHF-CS method are provided for determining the DMs’ weights. Finally, the interval-valued hesitant fuzzy utility degree for each candidate is calculated based on the interval-valued hesitant fuzzy relative importance. Then, the RPP alternatives are ranked by decreasing sorting. Computational results are given in Tables 25 and 26. The ranking results by comparing with Byun and Lee (2005) study indicate somewhat similar outcomes.

5 Comparative analysis

In this section, the comparative analysis is presented for the IVHF-MCGA approach and fuzzy group TOPSIS method. The reason of selecting the fuzzy group TOPSIS is that all studies, considered in illustrative examples for comparing the ranking results, are based on the concept of the TOPSIS method (i.e., closer to positive ideal solution and farther from negative ideal solution). In this case, some comparison parameters are regarded to show the profitability of the proposed approach. In fact, the comparison parameters are selected based on the Junior et al. (2014) study and the characteristics of fuzzy decision-making methods presented in Table 1. Junior et al. (2014) have compared the fuzzy AHP and fuzzy TOPSIS methods based on some appropriate comparison parameters, including adequacy to changes of alternatives and criteria, agility in decision process, time complexity, support to group decision making, number of alternatives and criteria, and modeling of uncertainty.

In this paper, some comparison parameters, including adequacy to changes of alternatives and criteria, agility in decision process, influence of DMs’ weights, and impact of first and last aggregations, that can show the efficiency and suitability of the proposed IVHF-MCGA approach are considered to compare with fuzzy group TOPSIS method in the selection problem of the rapid prototyping process. The following are the comparative analysis of comparison parameters in detail.

Table 26 Final ranking based on the $Q_{i}$ values by considering two types of ordering and the comparative analysis for the third illustrative example

5.1 Adequacy to changes of alternatives or criteria

One of interesting comparison parameters is adequacy to changes of alternatives or criteria in the decision-making process that could lead to ranking reversal in the ordering of potential alternatives or selected criteria. In this case, the adding or excluding one alternative is evaluated by both proposed IVHF-MCGA approach and fuzzy group TOPSIS method; the same ranking results are obtained. The ranking order of the alternatives in the third illustrative example by adding/excluding the candidates is achieved as $\mathrm{RPP}_6 >\mathrm{RPP}_5 >\mathrm{RPP}_1 >\mathrm{RPP}_4 >\mathrm{RPP}_2 >\mathrm{RPP}_3$. In addition, the aforementioned results are provided for adding/excluding the criteria; it means that the importance order (i.e., $C_1 >C_2 >C_5 >C_6 >C_4 >C_3 )$ has no changes.

5.2 Agility in decision process

This factor assesses the amount of required preference judgments that are assigned by the DMs or experts in both proposed IVHF-MCGA approach and fuzzy TOPSIS method under group decision procedures. Let m the number of alternatives, n the number of criteria and k the number of the DMs. As presented in Eq. (59), the fuzzy group TOPSIS method requires mnk judgments to establish the group decision matrix and also nk judgments for specifying the criteria weights.

$$\begin{aligned} \mathrm{Ag}_{n,m,k}^\mathrm{TOPSIS} =mnk+nk=nk(m+1) \end{aligned}$$

(59)

In the case of the proposed approach, the IVHF-entropy method is presented to determine the criteria weights. Although the experts’ judgments about the relative importance of each criterion can be considered in the procedure of proposed IVHF-entropy to provide an accurate solution, it is optional in the proposed decision-making process. In fact, the IVHF-entropy method can compute the weight of each criterion without the experts’ opinions about the criteria weights. Thus, this can be illustrated in Eq. (60).

$$\begin{aligned} \mathrm{Ag}_{n,m,k}^\mathrm{IVHF-MCGA} =mnk \end{aligned}$$

(60)

Therefore, as indicated in Eqs. (59) and (60), the number of judgments for the proposed IVHF-MCGA method is nk values less than the fuzzy group TOPSIS method. For example, in the third illustrative example, the fuzzy group TOPSIS has required 168 judgments while the proposed IVHF-MCGA has required 144 judgments.

5.3 Influence of decision makers’ weights

DMs’ expertise might be different in the industry based on different backgrounds; thus, considering the weight of each DM by regarding their judgments could help us to achieve a precise solution. In this respect, the effect of applying the DMs’ weights is explained based on the third illustrative example. In the application case, the weight of each DM is considered equal; then the ranking order results are:$\mathrm{RPP}_6 >\mathrm{RPP}_5 >\mathrm{RPP}_4 >\mathrm{RPP}_1 >\mathrm{RPP}_2 >\mathrm{RPP}_3$, which is slightly different from the ranking order results of fuzzy group decision method (i.e., $\mathrm{RPP}_6 >\mathrm{RPP}_4 >\mathrm{RPP}_5 >\mathrm{RPP}_1 >\mathrm{RPP}_2 >\mathrm{RPP}_3 )$. The comparative analysis based on this comparison parameter shows that the final ranking order of six candidates is affected from the DMs’ weights. It is obvious that considering the weight of each DM could lead to an accurate result of the selection problem.

5.4 Impact of first and last aggregations

In the group decision-making process, two approaches as first aggregation and last aggregation are considered to integrate the judgments of the DMs or experts: in the first aggregation approach, the preference judgments of the DMs for the rating of candidates versus selected criteria are aggregated at the first and then the desired decision-making technique is implemented. In the last aggregation approach, ratings of alternatives are provided by the DMs and considered in desired decision-making technique directly. In other words, the opinions of the DMs are aggregated in the last step of desired group decision-making technique and it is capable of preventing the loss of data. In the third illustrative example, the ranking order results based on the proposed IVHF-MCGA approach are: $\mathrm{RPP}_6 >\mathrm{RPP}_5 >\mathrm{RPP}_1 >\mathrm{RPP}_4 >\mathrm{RPP}_2 >\mathrm{RPP}_3$ and also based on the fuzzy group TOPSIS method are: $\mathrm{RPP}_6 >\mathrm{RPP}_4 >\mathrm{RPP}_5 >\mathrm{RPP}_1 >\mathrm{RPP}_2 >\mathrm{RPP}_3$. Then, this study attempts to understand the main cause in the ranking order of $\mathrm{RPP}_{1}, \mathrm{RPP}_{4},$ and $\mathrm{RPP}_{5}$. In this respect, in the first step of the proposed IVHF-MCGA, all judgments of the DMs are aggregated and the aggregated group decision-making matrix is considered for input parameters of the proposed approach. Then, it indicates that the ranking order results are: $\mathrm{RPP}_6 >\mathrm{RPP}_4 >\mathrm{RPP}_1 >\mathrm{RPP}_5 >\mathrm{RPP}_2 >\mathrm{RPP}_3$, and it can be concluded that the ranking order from the first aggregation of the proposed IVHF-MCGA is partially different from the ranking order of the fuzzy group TOPSIS.

The comparative analysis of the proposed soft computing approach and the fuzzy group TOPSIS method based on four comparison parameters indicates some interesting outcomes that show the efficiency and suitability of the proposed approach. The obtained results based on these comparison parameters are investigated for the RPP selection problem as the third illustrative example, and they might be different for other contexts in the manufacturing industry. In summary, the outcomes and findings are reported in Table 27.

Table 27 Summarized comparative analysis of the proposed soft computing approach and fuzzy group decision method

6 Conclusions and suggestions

For many manufacturing companies, the complex decision problems like the industrial selections are serious issues to increase the productivity. The multi-criteria group decision-making (MCGDM) approach could be considered in an interval-valued hesitant fuzzy (IVHF) environment to solve the industrial selection problems. This study proposed a novel group decision-making method based on the interval-valued hesitant fuzzy complex proportional assessment, called IVHF-MCGA, for the selection of the most suitable industrial candidates. The preferences of potential alternatives and the criteria weights that are judged by decision makers (DMs) are expressed by linguistic variables and then are transformed into IVHFEs. In addition, the weight of each criterion is computed by developing a new IVHF-entropy method according to the DMs’ judgments. Also, the relative importance of each DM is calculated by introducing a new IVHF-compromise solution method. Moreover, for the prevention of the data loss, the DMs’ opinions are aggregated at the end of the proposed soft computing approach along with some IVHF-operators introduced in this study. The proposed approach under uncertainty is efficient and easy to understand with the IVHF-setting. This approach improved the group decision-making process and developed the concept and theory of compromise solution and utility degree, based on interval-valued hesitant fuzzy positive and negative ideal solutions and, therefore, it could be considered as new soft computing approach for solving the evaluation and selection problems to handle uncertainty. In addition, the validity and applicability of the proposed IVHF-MCGA approach are tested based on solving three different industrial selection problems. In this respect, the obtained ranking order results are compared with some fuzzy decision methods from the literature, which are developed from the concept of TOPSIS method. Computational results show the same ranking of industrial alternatives. Also, the fuzzy group TOPSIS method has been considered to establish a comparative analysis based on four selected comparison parameters to indicate the efficiency and suitability of the proposed soft computing approach. Although the presented approach has been applied to industrial selection problems, it could be used in other fields of management and engineering for making a suitable decision, especially for manufacturing decision problems.